Towards a universal understanding of sex ratio in termites

Abstract

Termites are eusocial cockroaches whose altruist caste is constituted of males and females. While sex ratio theory predicts a balanced investment between sexes in diploid organisms, extreme deviations are observed in termites, both in altruists and alate reproductives. Here, we expand the theoretical framework for the prediction of alate population sex ratio by considering partitioned sexual and parthenogenetic reproduction, and female/male relatedness asymmetries arising from their sex-linked chromosome complexes. We consider the viewpoint of either the primary reproductives or the altruists while accounting for the effect of caste developmental systems on the sex ratio. We compile all data on alate sex ratios available to date (97 species), and found the direction of the sex ratio bias to be consistent within major taxonomic groups. We test our models, along with models of intrasexual competition, on an exploratory set of 13 species with available demographic data. Our analyses indicate that the factors explaining bias in alate sex ratio are variable and include sexual dimorphism, sex-asymmetric inbreeding, imperfect use of sexual and parthenogenetic reproduction, sex-linked genomic inheritance, intrasexual competition and caste developmental constraints. Our study provides an integrative framework for sex ratio and conflicts in termites, and closes in on a universal theory.

Introduction

Independently-founded social insect colonies develop in four stages: the colony foundation, the ergonomic stage (during which the colony grows and produces neuters), the reproductive stage, and the declining phase¹. The production of alate reproductives, the ultimate maximand of each colony, takes place during the colony’s reproductive stage. The allocation into neuters (i.e., the altruists) and dispersers (i.e., the winged reproductives, also termed alates) is a key parameter of colony fitness, as it reflects its reproductive capacity in the pool of colonies. A key parameter of sex allocation is the relative investment in male and female alates (i.e., the sex ratio). Fisher’s theory² predicts a balanced investment in diploid animals under panmixia without competition for resources between related individuals. Consequently, the numerical sex ratio of alates should deviate towards the production of the less expensive sex to reach an equal energetic investment in males and females³. The population sex ratio is considered evolutionarily stable when the fitness gain per unit of investment into each sex is equal from the viewpoint of all actors in control⁴. While sexual dimorphism between male and female alates is limited in termites, biases in alate sex ratio, sometimes extreme, have been observed^5,6,7. Inclusive fitness theory admits that various genetic and ecological factors can explain the variability in colony and population sex ratios^8,9. For each colony member, the fitness returns from the investment in alates of each sex is a function of their relatedness to males and females, as well as their respective reproductive values and success.

Conflicts may occur when sex-linked relatedness asymmetries vary between nestmates. For instance, the haplodiploid sex determination system of hymenopterans begets relatedness asymmetries, as (female) workers are three times more related to their sisters than brothers, while the queen is equally related to both her daughters and sons. Hence, in a panmictic population with sterile workers and singly-mated queens, the equilibrium alate sex ratio is 1:1 female:male for the queen and 3:1 for the workers —the ratio at which the higher relatedness of females to workers compensates for females’ lower reproductive success¹⁰. While termites are diplodiploid, with males being the heterogametic sex¹¹, translocations between sex chromosomes and autosomes can lead to a significant part of the genome being sex-linked in some species^11,12,13,14, up to ~90% (30 out of 34 chromosomes) in the Okinawan population of the drywood termite Glyptotermes nakajimai¹⁵. This peculiar genomic sex-linkage begets relatedness asymmetries between same- or opposite-sex altruists, affecting their indirect fitness, which could lead to biases in the alate sex ratio^16,17.

Another potential source of bias in the alate sex ratio is the caste differentiation system. Termites display a diversity of developmental pathways, with two main types¹⁸. Some species have a linear caste system with totipotent immatures (pseudergates or false workers) that can differentiate into soldiers, alates, and secondary reproductives (i.e., the neotenics). Other species exhibit a bifurcated caste system, in which the development of immatures irreversibly diverges early on to follow one of two developmental lines: the neuter line —with “true” workers able to moult into soldiers, or more rarely into (ergatoid) neotenics— and the nymphal line leading to the alates and (nymphoid) neotenics. While both sexes are generally distributed among castes with no apparent bias in species with false workers, sex specialisation is frequent in workers and soldiers of species with true workers, especially in the Termitidae^{18,19,20,21,22}. For example, soldiers are all male in most Nasutitermitinae and Sphaerotermitinae, while they are generally all female in Cubitermitinae, Macrotermitinae, Termitinae, and Microcerotermitinae. This strict sex specialisation in some castes may affect the alate sex ratio.

The reproductive values of male and female alates (i.e., the respective genetic contribution of males and females to future generations) vary with the breeding system. For instance, in social Hymenoptera, the reproductive value of males is higher in species with fertile workers than in species with sterile workers because the workers of the former species produce males carrying both their father’s and mother’s genes, while all males produced by the queen only carry her genes⁴. In termites, the sex-asymmetric longevity of primary reproductives and their mating with replacement reproductives (i.e., their offspring) cause asymmetries in the reproductive values of male and female alates^23,24.

The reproductive success of male and female alates depends on intrasexual competition, ultimately related to the general sex ratio at the level of the whole population. Intrasexual competition may also be influenced by adaptations to ecological factors, such as the availability of resources and the mode of individual dispersion or colony foundation. Theoretical predictions vary depending on whether individuals cooperate or compete. Under local resource enhancement (LRE), a model based on cooperation, selection should favour the overproduction of the cooperating sex, leading to either female- or male-biased alate sex ratios^25,26. This phenomenon may occur in polygynous societies initiated by related females. Local resource competition (LRC)²⁷ can happen when related colonies (or queens) compete for resources, especially in species reproducing by colony fission or budding, with daughters reproducing within their natal nest. Under LRC and queen philopatry, selection should favour a male-biased alate sex ratio to reduce competition between related females. Under local mate competition (LMC)^28,29 —a special case of LRC where male is the philopatric sex, and brothers compete for mates in a structured population— a female-biased alate sex ratio is expected as it reduces competition between related males. These three mechanisms may occur in the same population, potentially leading to split sex ratios —i.e., a bi- or multimodal distribution of colony-level sex ratios^4,30,31. For instance, as opposed to population-level predictions, colonies with low levels of resources and productivity (i.e., producing a small number of alates) are expected to mostly produce males in species under LMC and females in species under LRC, two predictions termed the “constant male” and “constant female” hypotheses³². Finally, colonies of the ant Formica exsecta with few queens (and hence low levels of LRC) display female-biased alate sex ratios, while colonies with many queens (high LRC) exhibit male-biased alate sex ratios, sometimes with male-only reproductives^30,33. In this species, queens are recruited back to their natal nest as replacement queens, leading these colonies to shift their investment towards producing more males. This situation, involving intrasexual competition between secondary reproductives, is reminiscent of neotenic queen reproduction in termites.

This manuscript bridges theoretical predictions of alate sex ratios to available empirical data across Isoptera. First, we develop further the theoretical framework to account for realistic genetic and demographic components of termites’ populations that may influence sex ratios. To do so, we expand the sex-asymmetric inbreeding sex ratio model of Kobayashi et al.²³. This model considers the viewpoint of the primary founders, assuming that biased alate sex ratios are solely explained by asymmetries in the contribution of males and females to the gene pool of the next generation —i.e., conditions that favour a greater genetic contribution of females to the next generation should increase their proportion among alates. We enhance the model by introducing (i) partitioned sexual and parthenogenetic reproduction for the production of secondary queens and female alates, and (ii) relatedness asymmetries between sexes due to genomic sex-linkage. We apply the same assumptions to derive altruist-based models while considering caste developmental constraints. These models can be used as tools to understand termite population sex ratios (Fig. 1; Supplementary Figs. 1–2). Second, we compile alate sex ratio data from 97 species to assess biases and their direction across the phylogeny and major taxonomic groupings with particular attention to factors that could explain inherent biases, such as investment-aware sex ratio measures, sexual dimorphism, productivity, and caste systems. Finally, we test our models and intrasexual competition-based models on a preliminary set of 13 species with available demographic data.

Fig. 1: Levels of sex ratio predicted by generalised models under a combination of factors.

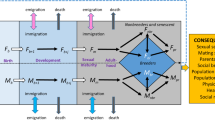
The considered factors are the sex-linked genomic fraction L (y-axis), the proportion q of parthenogenetically-produced female alates (x-axis), and the mode of production of neotenic queens (u = 0; parthenogenetically-produced, solid lines; u = 1, sexually-produced, dashed lines). We consider four populations (from left to right), composed of primaries only (p₁), primary king and neotenic queen (p₂, p₃), neotenic king and neotenic queens (p₄, p₅), and all colony types in equal proportion in the population. We present sex ratios levels for the A FG model, the B AG model, and the ASA model with either 30% (C) or 70% (D) of altruists being females. The latter two situations are respectively comparable to the observed altruists’ sex ratio in Cavitermes tuberosus¹⁰⁴ and species of Microcerotermes¹⁹. Sex ratios (s) are in the proportion of females, and s is considered biased when deviating from 0.50 (male-biased, blue; balanced, grey; female-biased, red; represented levels are: 0.10, 0.20, 0.30, 0.40, 0.45, 0.50, 0.55, 0.60, 0.70, 0.80 and 0.90). Note that L exists in the (0,1) interval to model an XY sex-determination system; and that some elevated levels of L or q required to produce a biased sex ratio are unlikely to exist in nature (see details on Supplementary Fig. 2). Termite drawings by Simon Hellemans.

Results

Patterns of alate sex ratio across termites

In total, we retrieved alate sex ratio data from 97 species (Supplementary Data 2–3). Analyses were performed on a subset of 73 species for which sufficient data were available. A likelihood ratio test on model fits indicated that productivity does not significantly affect termites’ colony sex ratios (χ² = 0.662, p = 0.42). Hartigan’s dip tests indicated significant deviations from a unimodal distribution of colony-level alate sex ratios for two species, Glyptotermes nakajimai (D = 0.149, p < 0.001) and Coptotermes lacteus (D = 0.110, p < 0.001). The bimodal distribution in G. nakajimai stems from its distinct asexual (with only females) and sexual lineages. For C. lacteus, the alate sex ratio followed a clear bimodal pattern, with neotenic-headed colonies harbouring almost only males while the sex ratios of primary-headed colonies were balanced. For these reasons, the two lineages and mating types of these species were considered separately in subsequent analyses —i.e., 73 species but 75 populations.

Across all termite species, the numerical population sex ratio of alates was balanced (mean ± SD = 0.497 ± 0.135, min-max = 0.014–1; One-sample t-test, t = −0.14, p = 0.89), as was its biomass-corrected equivalent (mean ± SD = 0.528 ± 0.136, min-max = 0.016–1; t = 1.83, p = 0.07) (Fig. 2A). Subsequent analyses were carried out on the biomass-corrected investment values (those relevant in predictive models). Investment sex ratios varied among taxonomic groups (Fig. 2A; one-way ANOVA; F_7,67 = 3.443, p = 0.003), with post-hoc tests indicating that the sex ratios of species of the clade composed of Coptotermes and Heterotermes significantly differed from the sex ratios of Termitidae (Tukey’s test; p = 0.002). Furthermore, alate population sex ratios exhibited significant phylogenetic autocorrelation (Moran’s I, I = 0.031, p = 0.024; Fig. 2B).

Fig. 2: Patterns of alate sex ratio across termites.

Sex ratios are expressed as a proportion of females, and are considered male- or female-biased for values below 0.40 or above 0.60, respectively (see methods). A Numerical population sex ratios (open circles) and their weight-corrected equivalent, either estimated from species-specific weight ratios (filled triangles) or non-specific (open triangles) (n = 73 species, 75 populations). B Maximum-likelihood phylogenetic reconstructions using full mitogenomes or single mitochondrial genes with IQ-TREE (n = 66 species, 68 populations). Asterisks indicate a significant local phylogenetic signal (at α = 0.05) using Local Moran’s I indices. Species names indicated in bold were used for model testing (Fig. 3). Error bars represent 95% confidence intervals (CI) on population sex ratios. The source data used for this figure can be found in Supplementary Data 6 (population sex ratios, CI and number of observations) and Supplementary Data 7 (the phylogenetic tree).

We first tested for deviations from a balanced sex ratio (50:50) using binomial tests and found that 32 of the 75 analysed populations (43%) were significantly female-biased, while 18 (24%) were male-biased (Supplementary Table 5). The Termitidae included 59% (19 species) of the species with a female-biased sex ratio, but only 28% (5) of male-biased species. Using more conservative thresholds (0.40–0.60), 12 out of the 75 populations (16%) displayed a female-biased sex ratio (>0.60), including eight species of Termitidae and four species belonging to other clades (Kalotermitidae: 1; Reticulitermes: 2; Rhinotermitidae: 1; binomial tests; Supplementary Table 5). Conversely, no species exhibited a male-biased population investment sex ratio (<0.40) in the Termitidae, while three species of the Coptotermes + Heterotermes clade, one species of Serritermitidae, and one species of Kalotermitidae did.

Model evaluation

Sex ratio models were tested on a subset of 13 species (14 populations) for which life history data could be retrieved (Fig. 3; Supplementary Figs. 4–5). Note that some of the parameters were approximated to the best of our knowledge. Thus, the results below should be interpreted with a grain of salt and considered semi-quantitative. Full justifications on the values of parameters, together with predicted sex ratios, are presented in Supplementary Data 5. Because these tests have reduced power owing to the low sample sizes, they should be considered preliminary.

Fig. 3: Semi-quantitative predictions of alate sex ratio.

A Founder-based generalised (FG) model predictions (filled orange circles; Eq. (2)), with primary queen (red queen symbol) and king (blue king symbol) optima based on relatedness asymmetries (Queen-RA and King-RA; Eqs. (9–10)). Predictions for Schedorhinotermes lamanianus were tested under exclusive production of neotenic queens through sexual (u = 1) or parthenogenetic (u = 0) reproduction. Predictions using the frequency of parthenogenetically-produced alates in R. speratus (q^WU = 0.345;³⁴) are reported by crosses “x”. B Altruist-based generalised (AG) model predictions (filled orange diamond), with RA-based optima from the B1-male (blue male symbol; Eq. (11)), B1-female (red female symbol; Eq. (12)). These optima are weighted in the altruist-based sex-averaged (ASA) model (Eq. (13); black pawn symbol). The fit between observed sex ratios and model predictions are presented for the C FG model; or models reflecting the resolution of interclass conflict between the founders and B1 altruists: D FGxAG and E FGxASA. Dashed lines represent an equal match between predicted and observed sex ratios, while solid lines represent regression lines. Expanded comparison of models is presented in Supplementary Fig. 5 and Supplementary Table 6. Error bars represent 95% confidence intervals (CI) on population sex ratios. The source data used for this figure can be found in Supplementary Data 5 (model parameters and predictions) and Data 6 (population sex ratios, CI and number of observations).

Overall, linear regression and phylogenetic generalised least squares tests (Supplementary Fig. 5; Supplementary Table 6) indicated that the founder- (FG) and altruists-based (AG and ASA) generalised models predicted observed population sex ratios more acurately than the LMC and LRC models; and that both the FG model (Eq. (2), with Supplementary Tables 1–2), and models averaging the FG model with the altruist-based AG (Eq. (2), with Supplementary Tables 3–4) or the sex-averaged ASA (Eq. (13), with Supplementary Tables 3–4) models were good predictors (Fig. 3C–E). The latter possibly indicates the resolution of interclass conflict between founders and altruists. However, the AG and ASA models taken alone were less accurate predictors (Fig. 3B; Supplementary Fig. 5; Supplementary Table 6). The stepwise forward model selection procedure indicated that models incorporating u, L, the altruists’ sex ratio (p_X), and the proportion of primary-headed nests (p₁) were amongst the best models (Supplementary Figs. 6–7; Supplementary Tables 7–8). Additionally, finer (species-specific) patterns could be distinguished.

Species-specific patterns

LMC and LRC models performed poorly with respect to observed sex ratios (Supplementary Figs. 4–5; Supplementary Table 6), with the notable exception of the neotenic-headed colonies of C. lacteus whose male-biased population sex ratio is compatible with the predictions of the LRC model taking inbreeding into consideration. The observed alate population sex ratio of C. formosanus also appeared consistent with LRC (see Discussion). The sex ratio of the two kalotermitid species (Neotermes connexus and Neotermes sugioi) could not be explained by any model (but see Discussion).

The FG model, identified as a good predictor in linear regression analyses (Supplementary Table 6), yielded interesting predictions on the remaining ten populations (Fig. 3A; Supplementary Fig. 5; Supplementary Data 5). Of these ten lineages, four rely on classical sexual reproduction, five exhibit AQS, and one presumably undergoes AQS. For populations using classical reproduction (Incisitermes schwarzi, the sexual lineage of G. nakajimai, the primary-headed colonies of C. lacteus, and Nasutitermes corniger), the predicted alate sex ratios did not significantly differ from the observed alate sex ratios (Fig. 3A; One-sample t-tests with FDR-corrections: p > 0.05) except for I. schwarzi (p = 0.04). For the five species known to use AQS, the predicted biases in alate sex ratios were consistent with observations (One-sample t-tests: p > 0.05), with the exception of Reticulitermes speratus and Reticulitermes lucifugus (both with p = 0.04). These differences may stem from inaccurate parameter estimations, as a more recent estimation of parthenogenetically-produced alates in R. speratus (Supplementary Data 5;³⁴) yielded an estimate fitting with empirical observation (One-sample t-test: p > 0.05). In addition, our model predicted the occurrence of AQS in Schedorhinotermes lamanianus (i.e., the production of neotenic queens through parthenogenesis, u = 0), which is in line with the known life history of this species³⁵.

Discussion

Our study compiled all available alate sex ratios of termites measured to date, encompassing data from 97 species. Our analyses indicated a slight sexual dimorphism in alates, with females on average heavier than males (Supplementary Fig. 3) —a dimorphism which tended to be weaker in non-Termitidae species⁶. We showed that significant biased investment in male and female alates occurs at the population level in some species (Fig. 2; Supplementary Table 5). Using a threshold of 2:3 females:males (0.40) and 3:2 (0.60) for male- and female-biased sex ratios³⁶, the sex ratios were more frequently biased toward female than male alates (n = 12 and 5, respectively) and no male-biased sex ratio was detected in the Termitidae (Fig. 2).

Sexual dimorphism as a cause of biased alate investment sex ratios

A substantially marked sexual dimorphism was evidenced in four species, Hodotermes mossambicus, Pseudacanthotermes militaris, and two species of Apicotermes (Supplementary Fig. 3). We could not investigate the link between the sexual dimorphism and the sex ratio in H. mossambicus as sex ratio data was not available. The alate investment sex ratios of the latter three species were female-biased at the 0.50 threshold (Supplementary Table 5), while their numerical sex ratio was balanced (Fig. 2A). Therefore, biases in alate investment sex ratio of these three species are solely due to an increased sexual dimorphism, which probably stems from their flight and pairing modalities. For instance, H. mossambicus has a desiccation-adapted physiology: alates drastically reduce their water content before the flight to compensate for their large energy reserve³⁷. This is especially so for female alates, as demonstrated by their female-to-male dry weight ratio greater than the wet weight ratio (Supplementary Fig. 3). After the flight and during colony foundation, they re-acquire water through imbibition of the ‘water-sacs’ that visibly inflate the abdomen³⁸. While the alates of most termites pair on the ground after the flight and tandem run until they settle for a site to initiate a new nest³⁹, some have unusual pairing strategies, which probably drove sexual dimorphism. In the macrotermitine Pseudacanthotermes militaris and the apicotermitine Allognathotermes hypogeus, alates leave their nests to reach the treetops where they pair and the (smaller) male grabs the (larger) female from beneath while she ensures the flight^20,40,41. The other species of Pseudacanthotermes in our dataset (P. spiniger) exhibits a milder sexual dimorphism (Supplementary Fig. 3), likely enabling their outstanding in-flight pairing strategy⁴².

Generalised models are good predictors of alate sex ratio

Models were preliminarily tested on a limited set of 13 species for which demographic data was available. It has been predicted that alate population sex ratio is female-biased in species using AQS^23,24. However, some species exhibit more variable colony life histories, potentially affecting the sex ratio in complex ways^43,44. Through fine-tuning the reproductive origin of neotenic queens (u) or female alates (q), and the sex-linked genomic fraction (L), our founder-based FG model could correctly predict smaller bias toward females for species with a combination of sexually- and parthenogenetically-produced female neotenics (e.g., Cavitermes tuberosus and Silvestritermes minutus; Fig. 3A; Supplementary Data 5). Of note, we suggest that the female-biased alate sex ratio in S. lamanianus is explained by AQS, which is in line with known features of its breeding system³⁵.

Both altruist-based models (AG and ASA) were less accurate predictors than the FG model (Fig. 3; Supplementary Fig. 5; Supplementary Table 6; Supplementary Data 5). In other words, predicting alate sex ratio based on the founding pair, which gains fitness directly, leads to more accurate estimates than doing so using the altruistic castes, which generally gain fitness indirectly. Our models provide insights into kin selection and conflicts among colony members because they differentiate between scenarios in which the queen, the king, or the altruists may enter into competition over alate sex ratio (Fig. 1; Supplementary Fig. 2).

One improvement of our generalised models (FG, AG, and ASA) is that it accounts for relatedness asymmetries between sexes arising from sex-linked inheritance (Supplementary Fig. 2A). Unfortunately, the tested species showed little variation in their sex-linked genomic fractions (Supplementary Figs. 7–8; Supplementary Data 5). Chromosome fusions during male meiosis possibly had a role early on in the evolution of termites. The sex-linked fraction of the genome ensures the maintenance of heterozygosity through males and has been hypothesised to counterbalance inbreeding in termites⁴⁵. In several species, the number of chromosomes involved in the fusions during male meiosis varies across populations^15,46. These variations offer unique targets to test the impact of sex-linked inheritance on alate sex ratio and whether it is a proximal mechanism leading to biases in termites.

Our models take into account the production of female alates by parthenogenesis, which modifies the founders’ relative contributions in the FG model (Supplementary Fig. 2B). This use of parthenogenesis increases the respective contribution of primary queens to the next generation and decreases that of primary kings. The occasional findings of fully homozygous primary queens in the mature nests of three species of Neotropical Termitinae^47,48 indicate that parthenogenetically-produced female alates significantly contribute to new colony foundation and achieve reproductive success. Updated data on such female alates in R. speratus³⁴ improved our predictions (Fig. 3A; Supplementary Data 5). These results indicate that our model efficiently incorporates complex termite colony life histories and provides evidence that sex-specific reproductive values affect the alate population sex ratios. However, the investment required for raising parthenogenetically- or sexually-produced females may not involve the same costs. In R. speratus, (i) parthenogenetic eggs are significantly larger than sexually-produced eggs, indicating that primary queens invest more resources into each parthenogenetic egg⁴⁹; and (ii) parthenogenetically-produced female alates exhibit a smaller body size than sexually-produced females³⁴.

Male bias and local resource competition

The existence of competition among neotenics is evidenced by observations of aggressive behaviour, which sometimes leads to the elimination of other neotenics^50,51. In species in which a substantial proportion of neotenic queens are produced sexually (and therefore inbreed), one advantage of producing more males (as expected under LRC) would be to limit the loss of heterozygosity in the population.

The LRC model was generally a poor predictor of alate sex ratio, except in C. lacteus (Supplementary Figs. 4–5). This species is characterised by a split sex ratio, with primary-headed colonies producing an even sex ratio and neotenic-headed colonies producing almost all-male broods (Fig. 2) —a bias originating early on in the development (probably as early as in eggs)⁵². These observations can be interpreted as signatures of LRC^4,30,33. A similar shift towards the production of male broods was reported in Coptotermes formosanus⁵³. While no data on the number of queens per colony was available for the latter, both species may have similar colony life histories, suggesting LRC. Similar male-biased alate sex ratios were identified in the related genus Heterotermes (Fig. 2). In species of Reticulitermes, a genus related to Coptotermes and Heterotermes, specific crossing among neotenic reproductives begets male-biased colony sex ratio⁵⁴. An almost all-male brood was also found in a neotenic-headed field colony of one Reticulitermes species in Japan (N. Mizumoto, pers. comm. 2023). Neoteny being frequent in the Heterotermitidae (Coptotermes + Heterotermes + Reticulitermes)⁵⁵, we postulate that competition among neotenics and split sex ratios are common in this clade.

Male-biased alate sex ratio linked to breeding systems may not be restricted to the Heterotermitidae. For instance, (i) colonies producing only male alates were reported in the nasutitermitine Nasutitermes dunensis⁵⁶; and (ii) in the termitine C. tuberosus, in which primary-headed nests produce more females than neotenic-headed nests⁴³. Additionally, (iii) the occurrence of nearly male-only reigning secondary reproductives, together with a biased alate sex ratio, is suggestive of LRC in Neotermes species^57,58,59. However, neither previous analyses⁶⁰ nor our reanalysis (Supplementary Fig. 4) provided evidence for LRC in Neotermes. Failure to properly assess LRC in N. sugioi may stem from our use of one reproductive female per nest⁶¹ (Supplementary Data 5), which may be inadequate as neotenic females may be cryptically-coloured in this species (T. Abe, pers. comm. in Myles & Chang⁵⁸). Under LRC, as little as five competing females would yield a sex ratio compatible with the observed one (~0.40).

Caste systems lead to biased alate sex ratios

Alate sex ratio may primarily depend on the primary sex ratio (see ref. ⁶²). This is especially true in species with a linear developmental pathway. However, for species with a bifurcated developmental scheme, sex specialisation may additionally impact alate sex ratio. For example, soldiers are always male in species of Trinervitermes, while workers are almost exclusively female^19,22. The systematic female-biased alate sex ratio in Trinervitermes reflects the higher production of female larvae than male larvae, as more workers are needed than soldiers during most of the year. Such female bias was conserved across species of Trinervitermes, leading to a local phylogenetic signal (Fig. 2B).

Other species exhibit a similar excess in one sex at the scale of the entire society. There is an overall excess of females in Microcerotermes, with most species having only female soldiers and female-biased worker and alate sex ratios¹⁹. Such colony-level biases imply either differential mortality between sexes (e.g., from predation due to different behaviour) or deviations from random fertilisation by X- and Y-bearing spermatozoa. Microsatellite typing and cross-breeding experiments in the species N. sugioi (with linear development) suggested that the proportion of males and females in eggs and young instars depends on the population of origin, with males being the determinant factor⁶². Furthermore, only males are able to differentiate into neotenic reproductives in Neotermes^57,58,59. Therefore, sex-specific caste potentialities have strong influences on both alate and colony-level sex ratios. Even more spectacular systems are found in a handful of species in which workers and soldiers, produced throughout the year, are of one sex only¹⁷. In our dataset, this is illustrated by both the Serritermitidae Glossotermes oculatus and the Rhinotermitidae S. lamanianus, where altruists are respectively all-male and all-female^63,64, and in which the colony-level sex ratio is biased towards the most abundant sex in the altruist castes.

Conclusions

While bearing in mind our termite sex ratio review is inherently biased with respect to the surveyed taxonomic groups (Supplementary Table 9), we unravelled that most species harbour balanced alate sex ratios when considering stringent 0.40–0.60 thresholds accounting for sampling biases^17,36. We identified the likely factors affecting sex ratio in termites to be stemming from either by-products of sexual dimorphism and sex-linked caste developmental constraints, or intrasexual competition and unequal reproductive values of male and female alates. Biases linked to competition and sex-related alate reproductive values were found in species exhibiting secondary reproduction and inbreeding, which shape many colony and population characteristics⁶⁵.

We provided an extended theoretical framework that improves our understanding of termite sex ratio in species with various breeding systems. Our framework considers the viewpoints of all actors in termite societies. We showed that conflicts between colony members over sex ratio are expected in diplo-diploid species exhibiting sex-linkage and using parthenogenesis (Supplementary Fig. 2). While worker policing has been sporadically shown in termites⁵⁰, whether conflicts between founders and altruists exist remains to be thoroughly demonstrated through controlled experiments. Accordingly, verifying the match between primary and alate sex ratios while accounting for the caste systems (linear versus bifurcated pathways) should pinpoint the actors in control.

More data on colony life histories and demography (see refs. ^66,67) are needed to deepen our understanding of both proximate and ultimate factors shaping termite sex ratio and other population features. Our tests of model theoretical predictions lack robustness due to the low number of species for which such data were available (n = 13). Indeed, knowledge on the frequency of reproductives is required to test our models but is often challenging to estimate as reproductives hide in hardwood or deep in the ground. Unfortunately, field data collection has been undervalued for decades, and researchers are not incentivised to publish these data. For instance, it took researchers over 30 years to collect accurate demographic data on N. sugioi⁶¹. We hope the framework proposed in this paper will promote collective work on data acquisition allowing more powerful tests in the future. We invite researchers to join this initiative and share their dust-taking data with the termite scientific community, through our database repository (maintained at https://github.com/sihellem/TER-SEX-DB), on which we plan to periodically update available data on termite demographics and sex ratios. Finally, we expect simulation-based approaches to eventually further improve model parameter estimations and predictions.

Methods

A comprehensive glossary of abbreviations and model factors is presented in Table 1.

Table 1 Glossary of abbreviations and model variables

Base model of sex-asymmetric inbreeding

Kobayashi et al.²³ developed a model to predict sex ratio in a population of termites. Under this model, the sex ratio is predicted from the perspective of the colony founders (the primary reproductives) throughout the colony’s lifecycle, including when replaced by neotenics upon their death. This model was initially developed in species displaying sex-asymmetric longevity and undergoing asexual queen succession (AQS)⁶⁸, in which the primary queen is replaced by multiple neotenic queens produced parthenogenetically. Upon his death, the primary king is replaced by a (sexually-produced) neotenic son. In most cases, this neotenic male results from outbreeding: he is the son of the primary king and either the primary queen or one of her parthenogenetic neotenic daughters. In such a case, the primary queen’s contribution to the progeny’s gene pool becomes three times that of the primary king. The higher the frequency of king replacement in the population, the higher the bias in reproductive value favouring female alates over male alates, which selects for a female-biased investment sex ratio in alates at the population level^23,24. In a population of colonies with n types of mating, the evolutionary stable strategy (ESS) population investment (s) in females is the class inclusive reproductive values of females (c_F), given by

$$s={c}_{F}=\mathop{\sum}\limits_{i=1}^{n}{p}_{i}{g}_{{F}_{i}}$$

(1)

where p_i and g_Fi are respectively the proportion of progeny in the ith type of mating and the genetic contribution of founders to females of that progeny (Eq. (5) in ref. ²³).

We identified three limitations to this final expression of the sex-asymmetric inbreeding model. First, it considers perfect AQS, where all neotenic queens are parthenogenetically-produced. That is, it does not consider sexually-produced neotenic queens and father-daughter inbreeding. Second, it only considers relatedness patterns at autosomal loci (b_auto), where either founder is equally related to their sons and daughters (g_Fi = b_auto). That is, it does not consider relatedness asymmetries arising from sex chromosomes. Third, it considers that progeny is only produced through conventional sexual reproduction. That is, it does not account for female alates produced parthenogenetically, carrying the undiluted primary queen’s genome.

Founder-based generalised (FG) model

Here, we develop a generalised model that addresses the three limitations of the base model by refining both the population and relatedness structures. We explicitly use reproductive values, as they reflect the expected number of gene copies transmitted to distant future generations⁶⁹, which is a useful way of considering the viewpoint of founders throughout the colony’s lifecycle, even upon their death. The ESS population sex ratio of alates in the absence of intrasexual competition, derived in terms of reproductive values of male and female alates, is obtained by

$${s}_{{FG}}={c}_{F}=\mathop{\sum}\limits_{i=1}^{n}{p}_{i}{c}_{{F}_{i}}$$

(2)

where p_i and c_Fi are the proportion of progeny and the reproductive value of females in the ith type of mating, respectively. The three modifications taken into account for estimating p_i and c_Fi are detailed below.

Refining the population structure, p _i

In this section, we specifically consider the origin of neotenic queens (Modification 1 to the base model). The replacement of reproductives in a later stage of the colony lifecycle changes the relative contributions of the original founding pair. For simplicity, we only consider the replacement of either king or queen(s) at a time and six types of mating (Supplementary Fig. 1): between (1) the original primary king and queen; (2) the primary king and sexually-produced neotenic queens; (3) the primary king and parthenogenetically-produced neotenic queens; (4) the neotenic king and sexually-produced neotenic queens; (5) the neotenic king and parthenogenetically-produced neotenic queens; and (6) the primary queen and neotenic king. The proportions p_i of progeny (with all p_i summing up to unity) are given by

$$\left\{\begin{array}{c}\begin{array}{c}{p}_{1}=\frac{{n}_{A}}{N} \hfill \\ {p}_{2}=\frac{{n}_{B}}{N}u \hfill \\ {p}_{3}=\frac{{n}_{B}}{N}u^{\prime} \end{array} \hfill \\ \begin{array}{c}{p}_{4}=\frac{{n}_{C}}{N}u \hfill \\ {p}_{5}=\frac{{n}_{C}}{N}u^{\prime} \hfill \\ {p}_{6}=\frac{{n}_{D}}{N}\hfill\end{array}\end{array}\right.$$

(3)

where u is the frequency of sexually-produced neotenic queens in the population, with u + u′ = 1; and N, n_A, n_B, n_C, and n_D are, respectively, the total number of colonies in the population, the number of colonies with both primary reproductives (i = 1), with neotenic queens and either a primary king (i = 2,3) or a neotenic king (i = 4,5), and with a primary queen and a neotenic king (i = 6). For simplicity, we assumed that u is constant across colonies with neotenic queens and that all colonies have similar productivity. Although this assumption may appear improbable given the hypothesised productivity boost in neotenic-headed colonies of AQS species^70,71, differences with primary-headed nests were not uncovered^7,43. Through this first modification, one can consider situations ranging from siblings inbreeding with all neotenics being sexually-produced (u = 1) to species under AQS with only parthenogenetically-produced neotenics (u = 0).

Refining the class reproductive values, c _Fi

We solve the class reproductive value of females in each type of mating (c_Fi) using matrix notation and the eigenvector method (as refs. ^72,73) as

$$\quad \left(\begin{array}{cc}{c}_{{F}_{i}} & {c}_{{M}_{i}}\end{array}\right)=(\begin{array}{cc}{c}_{{F}_{i}} & {c}_{{M}_{i}}\end{array})\left(\begin{array}{cc}{g}_{{PQ}\to {F}_{i}} & {g}_{{PK}\to {F}_{i}}\\ {g}_{{PQ}\to {M}_{i}} & {g}_{{PK}\to {M}_{i}}\end{array}\right)$$

(4)

where g is the genetic contribution of the primary queen (PQ) or king (PK) to female (F_i) or male (M_i) progeny, with c_Fi and c_Mi summing up to unity. In this system, c_Fi is solved as

$${c}_{{F}_{i}}= \frac{{g}_{{PQ}\to {M}_{i}}}{{g}_{{PQ}\to {M}_{i}}+\, {g}_{{PK}\to {F}_{i}}}.$$

(5)

We assume no differential survivorship between male and female alates and monogamous mating of founding pairs. Genetic contributions are derived from relatedness coefficients, and take into account sex-linked loci and the mode of reproduction.

Refining the genetic contributions, g

One may want to specifically consider the effect of sex-linkage on genetic contributions across generations (Modification 2 to the base model). Termites exhibit an XY sex-determination system (except in Stolotermes inopinus, in which males harbour an X0 sex chromosome pattern⁷⁴). This system begets sex-specific relatedness patterns, complexified by the replacement scenarios (see Supplementary Tables 1–2). In the Termitidae, the sex-linked fraction of the genome is seemingly fixed at ~10% (L = 0.10; four chromosomes involved in chromosome rings, on a total of 2n = 42), while it is highly variable in other termite families⁷⁵. Here, we use weighted average relatedness coefficients (as in Crozier & Pamilo³¹) to estimate the genetic contribution from either primary reproductive to the progeny in the ith type of mating, as

$${g}_{{case}}={{b}_{{auto}}}_{{case}}\left(1-L\right)+{{b}_{{sex}}}_{{case}}L$$

(6)

with four cases (PQ|PK→F_i|M_i); where b_auto and b_sex are, respectively, the relatedness at autosomal and sex-linked loci; and L is the sex-linked genomic fraction. Note that L is bounded to values in (0,1) to model the XY sex-determination system. One may instead want to model the X- and Y-linked fractions separately by considering them as non-recombining genetic subpopulations evolving under distinct selective pressures. By contrast, we consider here, as Roisin¹⁷, that sex-linked alleles are associated with a specific sex chromosome for several generations but can be transferred at a larger timescale. Indeed, the recombination of alleles between the X and Y chromosomes was observed^14,76. Furthermore, termites’ X and Y chromosomes appear poorly differentiated (homomorphic) on karyotypes⁷⁷, implying shuffling between autosomes and pseudoautosomes⁷⁸.

Finally, one may want to consider the occurrence of parthenogenetically-produced female alates on genetic contributions (Modification 3 to the base model). Caste and reproductive origins are not hardwired, as parthenogenetically-produced females do not always differentiate into neotenics but may also become alates. This modifies the contribution of founders to females as follows

$${g}_{{PQ|PK}\to {F}_{i}}=(1-q){g}_{{PQ|PK}\to {F}_{i,{sex}.}}+q{g}_{{PQ|PK}\to {F}_{i,{parth}.}}$$

(7)

where F_i,sex. and F_i,parth. are, respectively, sexually- and parthenogenetically-produced female progeny, g_{PQ|PK→Fi,sex.} is given by Eq. (6), and q is the proportion of female alates produced by parthenogenesis. Sex-linkage only impacts the relatedness of reproductives towards sexually-produced alates, while their relatedness towards parthenogenetically-produced females is independent of genome linkage ( g_{PQ|PK→Fi,parth.} equals b_{PQ|PK→Fi,parth.}, where b_auto equals b_sex).

Predictions of the FG model

We outline the genetic contributions of founders under simple replacement scenarios, where replacements were constrained to originate from the B1 progeny (at i = 1) (Supplementary Fig. 1; Supplementary Tables 1–2). For instance, solving c_F as in Eqs. (4–5) for a colony headed by a primary king and queen (i = 1) under near-complete sex-linkage (e.g., L = 0.99, to allow for an XY sex-determination system) and no parthenogenesis (q = 0) yields

$$\left(\begin{array}{cc}{g}_{{PQ}\to {F}_{i}} & {g}_{{PK}\to {F}_{i}}\\ {g}_{{PQ}\to {M}_{i}} & {g}_{{PK}\to {M}_{i}}\end{array}\right)= \left(\begin{array}{cc}{b}_{{sex},{PQ}\to {F}_{i,{sex}.}} & {b}_{{sex},{PK}\to {F}_{i,{sex}.}}\\ {b}_{{sex},{PQ}\to {M}_{i,{sex}.}} & {b}_{{sex},{PK}\to {M}_{i,{sex}.}}\end{array}\right)\cong \left(\begin{array}{cc}\frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2}\end{array}\right).$$

(8)

In this case, sex-linkage has no impact (L terms cancel out and the last equality is exact), Eq. (8) is solved as c_Fi = ½, and a balanced sex ratio is expected (Fig. 1A; Supplementary Fig. 2). Note that the relatedness coefficients are different than under haplodiploidy, where the lower terms b_{sex,PQ→ M} and b_{sex,PK→ M} are 1 and 0, respectively, and c_Fi is 2/3. As a second example, if only colonies headed by neotenics are considered, in a species in which 10% of the genome is sex-linked and 60% of female alates are parthenogenetically-produced (Fig. 1), c_Fi values become 0.89 under mother-son inbreeding (i = 5) and 0.49 under siblings inbreeding (i = 4). Depending on values of L and q, the FG model predicts a female-biased alate sex ratio under outbreeding and mother-son inbreeding, but a male-biased alate sex ratio under siblings or father-daughter inbreeding (Fig. 1A; Supplementary Fig. 2). An example of deriving the semi-quantitative prediction of the FG model from observed parameters is given in Supplementary Data 1. Note that our FG model is identical to the base model of Kobayashi et al.²³ when L, q, and u are nullified.

The inclusive population optimum of Eq. (2) can be compared independently to the viewpoint of each original founder (Supplementary Fig. 2) through their relatedness asymmetries towards the brood produced at each stage of the colony’s lifecycle. These estimates, based on relatedness asymmetries (RA), can be expressed as the proportion of females by:

$${s}_{{King}-{RA}}=\mathop{\sum}\limits_{i=1}^{n}{p}_{i}\frac{{g}_{{PK}\to {F}_{i}}}{{g}_{{PK}\to {F}_{i}}+{g}_{{PK}\to {M}_{i}}},$$

(9)

and

$${s}_{{Queen}-{RA}}=\mathop{\sum}\limits_{i=1}^{n}{p}_{i}\frac{{g}_{{PQ}\to {F}_{i}}}{{g}_{{PQ}\to {F}_{i}}+{g}_{{PQ}\to {M}_{i}}}.$$

(10)

Altruist-based generalised (AG) model

A model based on the viewpoint of altruists can be derived from the founder-based model. We consider the simplest case in which all broods are raised by the first brood of sterile altruists (B1) produced by the primary pair (as in Roisin¹⁷). This is a reasonable assumption, as altruists are replaced after two to three years^79,80. The AG model is obtained using the same equations as the FG model but considering the genetic contributions of female and male altruists to the alates (Supplementary Tables 3–4), instead of those from the primary queen and king.

This model is primarily affected by sex-linkage (L) and the respective indirect fitness payoff between male and female altruists: nullifying L begets identical relatedness among all nestmates. Note also that b_auto equals 0.50 in all cases, both for sexually- and parthenogenetically-produced siblings. Under mother-son inbreeding (i = 5,6), the use of parthenogenesis to produce female alates (q) does not affect relatedness patterns, so it does not affect the expected alate sex ratio either (Supplementary Fig. 2B). Depending on levels of L and q, the AG model predicts a male-biased alate sex ratio under outbreeding and mother-son inbreeding, but a female-biased alate sex ratio under father-daughter inbreeding (Fig. 1B; Supplementary Fig. 2). Note that the direction of the bias is opposite to that of the FG model, suggesting interclass conflicts.

Similarly, the AG optimum can be compared to sex-specific RA-based estimates (Supplementary Fig. 2), denoted s_X and s_Y, respectively, for female (X) and male (Y) altruists of the B1 brood:

$${s}_{Y-{RA}}=\mathop{\sum}\limits_{i=1}^{n}{p}_{i}\frac{{g}_{Y\to {F}_{i}}}{{g}_{Y\to {F}_{i}}+{g}_{Y\to {M}_{i}}},$$

(11)

and

$${s}_{X-{RA}}=\mathop{\sum}\limits_{i=1}^{n}{p}_{i}\frac{{g}_{X\to {F}_{i}}}{{g}_{X\to {F}_{i}}+{g}_{X\to {M}_{i}}}.$$

(12)

Such a comparison assumes that altruists can assess the relatedness patterns in their colony (e.g.,⁸¹). Hence, they should bias the alate sex ratio in favour of their sex to the level of their RA to female and male alates^10,17,82.

Altruist-based sex-averaged (ASA) model

The sex-specific RA-based values can also be summarised from the viewpoint of all altruists, weighted by the proportion of female (p_X) and male (p_Y) altruists across colonies:

$${s}_{{ASA}}={{p}_{X}s}_{X-{RA}}+{{p}_{Y}s}_{Y-{RA}}.$$

(13)

For simplicity, we assume that the sex ratio of altruists is constant across colonies and types of mating. Depending on the values of L and q, the ASA model predicts a male-biased alate sex ratio under father-daughter inbreeding when the altruists’ sex ratio is male-biased (Fig. 1C) and a female-biased alate sex ratio under outbreeding when the altruists’ sex ratio is female-biased (Fig. 1D).

Competition-based models

Contrarily to the approach focusing on the viewpoint and reproductive values of colony founders, one can consider the viewpoint of neotenics. In theory, intrasexual competition among neotenic reproductives (whose sex ratio can be highly biased towards one sex) may cause biased alate sex ratios. In species under AQS, nests can harbour hundreds of neotenic females reproducing with one neotenic or primary king^47,83. This female-biased sex ratio of reigning neotenics may itself suggest LMC, where one king can mate with many queens^23,84. In such a case, a female-biased sex ratio reduces competition between related males.

Here, we consider a population where the reproductive output of colonies results from neotenic-headed nests, assimilating neotenic queens to foundresses. We considered the formalisation of LMC by Hamilton²⁸, which considers a group of n unrelated foundresses, for which the ESS sex ratio expressed as a proportion of females is given by:

$${s}_{{LMC}}=1-\frac{n-1}{2n}.$$

(14)

We also considered a population of related foundresses, in which the expression becomes dependent on the consanguinity f of females⁸⁵:

$${s}_{{LMC}{{\rm{\_}}}f}=1-\frac{n-1}{2n}* \frac{1-f}{2* \left(1+3f\right)}.$$

(15)

Note that we formulated these two equations to predict the sex ratio expressed as a proportion of females (they are expressed as a proportion of males in the original works^28,85) and that the latter equation yields a constant consanguinity-dependent fraction of the former. We approximated n as the harmonic mean of queens per patch, while female consanguinity was assessed by their fixation index relative to the population, F_IT. In such LMC models, the expected sex ratio is highly female-biased when few females compete, while it equilibrates when many do (reaching panmixia conditions). Note, however, that some assumptions of these models may not apply to termite biology; and we only use these to contrast the founder- and altruist-based models.

Alternatively, the multitude of (related) neotenic queens may be in competition for resources within the nest (LRC), so that a male-biased sex ratio is expected. Note that in some species, the highly male-biased sex ratio of reigning neotenics in species of Neotermes^57,58,59 or in Coptotermes lacteus⁷ may itself be suggestive of LRC among related females. We assessed the occurrence of LRC among related queens by simply mirroring the predictions of LMC⁴. In these LRC models, the expected sex ratio is highly male-biased when few females compete, while it equilibrates when many do.

Literature survey

We carried out a comprehensive review of termite alate numerical sex ratio data published until the end of 2023, a task not undertaken since the seminal work of Jones et al.⁵. To do so, we (i) used the keywords “sex-ratio” or “sex ratio” on Google Scholar and in the bibliographic catalogue “Treatise on the Isoptera of the World”⁸⁶, and (ii) looked through the institutional collection of Isoptera offprints. This updated dataset consists of 1362 observations on 97 species (see Supplementary Data 2–3), collected from 98 references (Supplementary Note 2). We also collected data on alate sex-specific fresh or dry weights (Supplementary Data 4) from 25 references (Supplementary Note 2), retrieved using the keyword “weight”.

Demographic data for model testing was searched for the 97 species for which alate sex ratio data were available. We could retrieve data on the frequency of secondary reproductives, use of parthenogenesis for the production of neotenic queens or female alates, and sex ratio of altruists (either pseudergates or workers) for 13 species (Supplementary Data 5; Supplementary Note 2). These data were retrieved using the species name together with the keywords “parthenogenesis”, “primary”, “reproductive”, “neotenic”, “king”, “queen”, “life cycle”, or “reproductive cycle”.

Statistics and reproducibility

All analyses were performed in R v4.0.2⁸⁷, except when indicated otherwise.

Sex ratio measures

We only considered observations on species identified at the species level in the sex ratio data collected from the literature on 97 species. Colony numerical sex ratios were estimated using the number of males and females at nymphal and alate stages in species exhibiting a bifurcated developmental pathway (i.e., with “true” workers: Mastotermitidae, Hodotermitidae, Rhinotermitidae, Heterotermitidae, and Termitidae). We considered individuals at all stages in species with a linear developmental pathway (Archotermopsidae, Kalotermitidae, Serritermitidae, and Termitogetonidae) —i.e., the immatures (larvae, pseudergates, and nymphs), soldiers, alates, and neotenics. We discarded observations made on 50 or fewer individuals. We calculated the mean population numerical sex ratio and its associated 95% confidence interval (CI) for frequency-structured data using the productivity-corrected colonial sex ratios⁴.

Because of sexual dimorphism, we also converted numerical sex ratios into investment sex ratios using collected weight ratios. Females were always heavier than males: the mean wet and dry female-to-male alate weight ratios without outliers were, respectively, 1.12:1 and 1.13:1 female:male (Supplementary Fig. 3). This ratio never reached 2:1 female:male in termites (Supplementary Fig. 3; Supplementary Data 4), while it can reach ~25:1 in ants⁸⁸. We used the mean dry female-to-male alate weight ratio to convert numerical population sex ratios when species-specific data could not be obtained. Note that this approach has limitations, as female-to-male alate weight ratios were inferred from observations of alates at various stages (e.g., ready-to-fly alate, flying alate, or dealate) and dried with various drying methods (oven-dried or ethanol-dried) for dry weights. Ethanol-drying is problematic as lipids dissolve into ethanol⁸⁹, affecting investment sex-ratio estimations. This may not be a significant issue for species having males and females of similar size and weight. For example, lipid contents are similar between males and females of each caste of Reticulitermes chinensis⁹⁰. However, this might be problematic for the few species displaying a substantial sexual dimorphism, such as the macrotermitine Pseudacanthotermes militaris. We did not use a power correction to estimate investment sex ratios from dry weights, unlike in the ant literature, where a 0.7 power conversion is generally applied^88,91. An additional discussion on this conversion factor is provided in Supplementary Note 1 (with Supplementary Tables 10–11).

In this study, the sex ratio is expressed as a proportion of females (0, all-male; 1, all-female). While any statistical deviations from the neutral sex ratio (50:50) can be considered as biases under a strict definition, we also considered other thresholds accounting for variations. For instance, values of 0.375 (i.e., three females for five males, 3:5) and 0.625 (5:3) were used by Roisin¹⁷ to categorise male or female biases, respectively. Here, we considered the sex ratio to be male-biased for values below 0.40 (40:60; 2:3) and female-biased above 0.60 (60:40; 3:2) following Hu & Forschler³⁶, who statistically estimated that approaching colonial sex ratios with an error margin of ±10% was reasonable. These values were assessed to allow for detectable biases in field populations, with the rationale that smaller biases would be more difficult to ascertain given random sex ratio variations over colonies, sampling biases (e.g., developmental stage, swarm readiness), or numerical-to-investment conversion^17,36.

Patterns of alate sex ratio across termites

We assessed the patterns of sex ratios across termites using both family-level taxonomic groupings and phylogenetic tests.

(i) We used a linear mixed regression to test the (fixed) effect of productivity on colonial sex ratios with species as a random effect using the formula ‘sex ratio ~ productivity + (1 | species)’ in the ‘lmer’ function of the ‘lme4’ R package. Model fit was compared to a null model without the fixed effect using a likelihood ratio test with the ‘anova’ function of the ‘stats’ R package.

(ii) We tested for deviations from balanced population investment for each species with two-sided binomial tests using the ‘binom.test’ function of the ‘stats’ R package. P-values were corrected for multiple comparisons using the false discovery (FDR) method⁹² with the ‘p.adjust’ function.

(iii) We assessed the phylogenetic signal from population sex ratios using two methods, excluding or including phylogenetic autocorrelation. We used both categories of tests to avoid giving excessive weight to phylogenetic uncertainties. More specifically, reconstructions from nuclear genomes evidenced untractable relationships among neoisopteran families⁹³, and incongruences to topologies obtained from mitogenomes^94,95. First, we considered the families as defined in the new termite classification⁹³, with the exception of the Heterotermitidae for which we considered Reticulitermes and Coptotermes + Heterotermes separately, given their respective recent radiations following a prolonged absence of diversification^95,96. We compared the observed investment sex ratio across taxonomic groups using a one-way ANOVA after controlling for homoscedasticity with the ‘leveneTest’ function of the ‘car’ R package. The ANOVA was followed by a post-hoc multiple comparison of means with Tukey’s contrasts (function ‘mcp’), fed to the linear ‘linfct’ argument of the ‘glht’ function (‘glht(myAOV,linfct=mcp(taxonomy = “Tukey”))’; all functions from the ‘multcomp’ R package). Second, we reconstructed a maximum-likelihood (ML) phylogenetic tree using mitochondrial sequences and IQ-TREE v1.6.12^97,98. The alignment was separated into five partitions: combined rRNAs, combined tRNAs, and combined first, second, and third codon positions of protein-coding genes. We constrained the monophyly of Macrotermitinae + Sphaerotermitinae and non-Macrotermitinae non-Sphaerotermitinae Termitidae to match the topology retrieved by genome-scale reconstructions^93,99,100. The best-fit substitution models were selected for each partition using ModelFinder¹⁰¹. Local phylogenetic signals were assessed using Moran’s I and Local Moran’s I indices with the ‘phyloSignal’ and ‘lipaMoran’ functions of the R package ‘phylosignal’¹⁰², respectively. Both analyses were performed with two-sided alternatives, and p-values were obtained from 999 randomisations. The tree was also used to account for phylogenetic autocorrelation in the model evaluation procedure.

Model evaluation

For the subset of species with demographic data, we compared the observed sex ratios to theoretical predictions using four independent procedures to provide contrasted means of evaluation given the low number of observations (n = 13 species, 14 populations; Supplementary Data 5). We used both phylogeny-blind and -aware tests to account for a limited sample size and the uncertainty of phylogenetic relationships among neoisopteran families⁹³, such as the placement of Rhinotermitidae, a family represented by one species in the dataset.

Species-by-species comparisons were performed using (i) one-sample two-sided t-tests using the ‘tsum.test’ function of the ‘BSDA’ R package with the parameters ‘s.x’ set to the standard deviation of population sex ratio (from productivity-corrected 95% CI; see above), and ‘n.x’ to the number of colonies. Models predictions were then globally evaluated using (ii) Spearman’s rank correlation two-sided tests (‘cor.test’ function from ‘stats’ R package), (iii) linear regression (LM; ‘lm’ function from ‘stats’), and (iv) phylogenetic generalised least squares (PGLS). PGLS were performed with the ‘gls’ function in ‘nlme’ R package, with a phylogenetic correlation structure (‘correlation’ argument) estimating lambda using the ‘corPagel’ function (with ‘fixed = FALSE’) of the ‘ape’ R package¹⁰³. The diagonal of the variance-covariance matrix (with ‘d = diag(ape::vcv.phylo(tree))’) was set as the fixed variance weights to correct for different root to tip lengths of our non-ultrametric ML tree (argument ‘weights = nlme::varFixed(~d)’). We used Akaike’s information criterion (AIC) and Akaike weights (AICw) to determine best-fit models.

We tested the relationship between the observed sex ratios and the models’ variables using LM with stepwise forward addition of predictors as determined by a decrease in the model’s AIC. The best final model was selected based on AICw. We performed this procedure twice: once for the FG/AG models and each party’s RA optima (which all include p_i, u, L, and q as predictors), and once for the ASA model by including altruists’ sex ratio (through p_X) as an additional predictor. These tests were not performed for competition-based models owing to the lack of data (Supplementary Data 5). Models were assessed using AIC and AICw as previously described.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.