EmbSAM: cell boundary localization and Segment Anything Model for fast images of developing embryos

Abstract

Cellular shape dynamics are critical for understanding cell fate determination and organogenesis during development. However, fluorescence live-cell images of cell membranes frequently suffer from a low signal-to-noise ratio, especially during long-duration imaging with high spatiotemporal resolutions. The low ratio is caused by a tradeoff between embryo viability and phototoxicity and photobleaching of fluorescent markers, which hinders effective cell shape reconstruction, particularly in rapidly developing embryos. Here, we devise an integrative computational framework, EmbSAM, that incorporates a deep-learning-based cell boundary localization algorithm and the Segment Anything Model. EmbSAM enables accurate segmentation of three-dimensional cell membrane images for roundworm Caenorhabditis elegans embryos imaged with exceptional temporal resolution, i.e., every 10 seconds per stack. The resolved cell shapes prior to gastrulation quantitatively characterize a series of cell-division-coupled morphodynamics associated with cell position, cell division phase duration, cell division axis reorientation, cell identity, lineage, fate, among others, which can be accessed locally and online.

Introduction

Embryogenesis is the developmental process during which a single-celled fertilized egg undergoes cleavage (rapid division) along with the emergence of stereotypical spatial architectures and fate maps of numerous cells, forming a functional larva that can survive independently^1,2,3. The rapid division takes place concurrently with cell migration and cell differentiation, where cell shape changes dramatically to accommodate cell fate determination and organogenesis^4,5. Studying detailed cellular behaviors during rapid division becomes a challenging task because early embryonic mitotic phases, during which three-dimensional (3D) cell shape changes drastically, are very short. In theory, fast (high-frequency) imaging is able to reconstruct the cellular behaviors, but it can only be conducted with a relatively lower laser power to minimize accumulative photobleaching and phototoxicity. Therefore, a more sensitive cell segmentation algorithm is needed to compensate for the low signal-to-noise ratio (SNR) of the acquired images^6,7. For instance, the duration of cytokinesis, i.e., the time between the complete separation of sister cell nuclei and that of cell membranes, in early roundworm embryogenesis is roughly 2.5 min, during which the cell shape changes from spherical to dumbbell-shaped^8,9. Notably, cytokinesis often exhibits differential behaviors (e.g., differential cell division axes and durations of different phases of mitosis) along with specific cell shape dynamics depending on cell positions, cell identities, cell lineages, and cell fates. Moreover, these differential behaviors can also exist within a single cell type across successive cell cycles^{10,11,12,13,14}. The details of cytokinesis and cell shape dynamics in such a short period are commonly missed in time-lapse 3D imaging due to insufficient spatial and temporal resolutions, especially the temporal one. Moreover, many cellular properties, in particular those related to cytokinesis, also change drastically over development, such as the asymmetric partition of cell volume between sister cells and the decrease of cell sphericity within roughly 7 min at late metaphase^14,15. To enable illustration of the biological mechanisms underlying these cellular behaviors, it is essential to acquire fluorescence images of cell membranes through time-lapse 3D live-cell imaging (also called in toto imaging) at an exceptional temporal resolution, which permits reconstruction of cell shape with sufficient temporal resolution to analyze cell shape dynamics during cytokinesis. Furthermore, cell shape reconstruction is crucial for quantifying the spatiotemporal dynamics of functional molecules associated with cell membrane and cell division, such as filamentous actin (F-actin) and non-muscle myosin (NMY) that control the cell cortex stiffness and fluidity^12,16. However, because of photobleaching and phototoxicity, a tradeoff has to be applied between image quality and laser power or imaging frequency. This is especially true if both the cell identity and cell boundary need to be simultaneously resolved, with one laser channel for cell nucleus tracing and the other for cell membrane segmentation^8,17. Therefore, the development of a cell (membrane) segmentation algorithm has to take into consideration a modest quality of fluorescence image, either for the raw one or the processed one.

The transparent roundworm Caenorhabditis elegans is one of the most popular models for studying the developmental control over embryogenesis due to its precise development, including cell lineage and fate, cell migration trajectory, cell division timing and axis orientation and cell size among others (Supplementary Fig. 1)^{18,19,20,21,22,23,24}. Thus, multiple 3D cell segmentation algorithms that process time-lapse image stacks of different temporal resolutions have been devised in the past several years: spheresDT/Mpacts-PiCS at 3-min intervals²⁵, CShaper at ~1.5-min intervals⁸, and BCOMS2 at 30-s intervals¹⁵.

Apart from the customized frameworks, there are also many techniques developed for universal experimental conditions, in other words, for realizing the cell segmentation with a general computational framework, such as CellProfiler²⁶, RACE^27,, and SingleCellDetector²⁸. Recently, the Segment Anything Model (SAM) based on the Vision Transformer (ViT) architecture further revolutionized the field of computer vision, along with its truncated versions adapted to general 3D biomedical images, MedLSAM and MedSAM^{29,30,31,32,33}. The limitations of current SAM frameworks include their heavy reliance on manual input for segmentation promoters, such as seeding points or bounding boxes. Although the general SAM frameworks with these limitations may not be comparable to the customized ones when executed in the custom system (e.g., spheresDT/Mpacts-PiCS, CShaper, and BCOMS2 for the C. elegans embryo^8,15,25, they still impose a chance that the advantage of different approaches could be integrated so as to increase the overall cell segmentation performance coherently, for example, targeting the fluorescence images with a low SNR just like the ones obtained at a high temporal resolution and with a weak laser power^9,20,21.

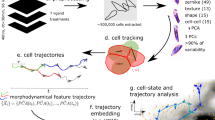
To realize cell-resolved shape reconstruction of developing embryos from fluorescence images with a low SNR, particularly those captured at high temporal resolutions on the order of 10 s or less, we devised EmbSAM, a computational framework that extends the SAM with additional cell boundary localization part containing a denoising module and a watershed module. This framework outputs 3D bounding boxes as a guide to direct the SAM to perform accurate segmentation of the cell membrane fluorescence in 2D, which can then be assembled in 3D space (Fig. 1). Evaluation using three C. elegans embryos imaged with a low SNR demonstrates that EmbSAM significantly outperforms CShaper, MedSAM, and PlantSeg, regarding 3D cell segmentation accuracy. Furthermore, EmbSAM was applied to segment six more C. elegans embryos imaged at 10-s intervals and up to the moment before gastrulation, leading to a quantitative measurement of cell shape changes for fundamental cellular behaviors (e.g., cell division and cell migration) as well as their dependence on cell positions, cell identities, cell lineages, and cell fates. The resulting data have been reformatted for both local and online analytical platforms previously made available to the public. Developmental landmarks such as post-fertilization pseudocleavage, dorsal-ventral and left-right body axes establishment, and spatial reorganization for gastrulation, are digitized and monitored over the course of time.

Fig. 1: The flowchart of EmbSAM, with time-lapse 3D fluorescence images (left) as input and lineage-resolved 3D cell shapes (bottom right) as output.

Top panel: Raw cell membrane fluorescence images were subjected to two add-on modules (denoising model highlighted with purple background and watershed module highlighted with blue background) that constitute the Cell Boundary Localization algorithm; the denoised images outputted by the denoising module are inputted into the image encoder in the SAM module³⁰, while the watershed pre-segmentation outputted by the watershed module are inputted as the prompt tokens for the mask decoder in the SAM module. The slice-by-slice segmentation results from the SAM module are subjected to 2D irregularity filter and 3D region assembling accordingly. Note that the lock icon represents frozen neural network without retraining and the unlock icon represents re-trained network with our data. Bottom panel: Raw cell nucleus fluorescence images were subjected to cell lineage tracing via StarryNite/AceTree^50,51,52, where the outputted cell position and identity label each assembled 3D cell region.

Results

Performance of EmbSAM in cell segmentation on low-SNR images

With C. elegans wild-type embryo samples “Emb1” and “Emb2” at their 4-, 6-, 7-, 8-, 12-, 14-, 15-, 24-, 26-, 28-, and ≥44-cell stages, we compared EmbSAM to CShaper^8,17 (one of the most updated algorithms customized for C. elegans embryonic images), MedSAM³³ (one of the most updated SAM algorithms generalized for biomedical images), and PlantSeg^34,35 (one of the most updated algorithms validated on both plant tissue and mouse embryonic images)(Supplemental Note 1). Considering that MedSAM was designed for segmenting 2D images and demands bounding box promoters to guide the reconstruction of 3D objects, the cell nucleus position $({x}_{{{\rm{n}}}{{\rm{uc}}}},\,{y}_{{{\rm{n}}}{{\rm{uc}}}},\,{z}_{{{\rm{n}}}{{\rm{uc}}}})$ and the conserved C. elegans embryonic cell volume (V)^8,17 documented before were utilized for constructing the required 3D bounding box promoters, a cuboid with boundaries $\left({x}_{{{\rm{n}}}{{\rm{uc}}}}\pm \root{{3}}\of{\frac{3V}{4\pi }},\,{y}_{{{\rm{n}}}{{\rm{uc}}}}\pm \root{{3}}\of{\frac{3V}{4\pi }},\,{z}_{{{\rm{n}}}{{\rm{uc}}}}\pm \root{{3}}\of{\frac{3V}{4\pi }}\right)$; therefore, the segmented 2D regions from MedSAM can be assembled into 3D regions.

In the EmbSAM segmentation, 99.73% of cells obtain fully connected 3D regions after the slice-by-slice 2D irregularity filtering. Intuitively, the EmbSAM segmentation outputs smooth and compacted cell shapes in both 2D and 3D for the whole embryo at developmental stages with a few to dozens of cells (Supplementary Fig. 2), while the segmented cell shapes from CShaper, MedSAM, and PlantSeg are coarse or uncompacted (Supplementary Fig. 3). While quantitative evaluation shows PlantSeg achieves a comparable performance to EmbSAM (reflected by Hausdorff distance) at the 12-cell stage, EmbSAM achieves both significantly larger Dice score (0.921 ± 0.061) and smaller Hausdorff distance (2.380 ± 1.530) than all CShaper, MedSAM, and PlantSeg at all developmental stages afterward^{8,17,33,34,35}, supporting its outperformance in segmentation accuracy. Compared to the coarse or uncompacted cell shapes outputted by CShaper, MedSAM, and PlantSeg, the ones by EmbSAM resemble those of the ground truth (Fig. 2A). To test if EmbSAM holds its outperformance when image is even noisier, we further added artificial Poisson noise to each voxel: for each voxel with original fluorescence brightness ${\varphi }_{\left(x,y,z\right)}$, noise was sampled from a Poisson distribution with mean and standard deviation $\sqrt{A{\varphi }_{\left(x,y\right)}}$, where the amplification coefficient $A$ took increasing values of 0.01*0 (no noise), 0.01*0.75, 0.01*0.5, 0.01*0.25, and 0.01*0.1; then all voxel brightness values were proportionally normalize to 0–255 (Supplementary Fig. 4). Across the first four noise levels, EmbSAM always achieved the largest Dice scores and smallest Hausdorff distances, while all algorithms failed at the highest noise level. This artificial noise experiment again demonstrates EmbSAM’s superior tolerance to noise and its high segmentation accuracy.

Fig. 2: The segmentation performance of EmbSAM.

A Segmentation results (exemplified by the embryo sample “Emb1”) of ground truth (1^st row), EmbSAM (2^nd row), CShaper (3^rd row), MedSAM (4^th row), and PlantSeg (5^th row) at different developmental stages. B Outperformance of EmbSAM compared to CShaper, MedSAM, and PlantSeg, revealed by Dice score (top) and Hausdorff distance (bottom). Presentation: box-and-whisker plot (colored interquartile with upper and lower quartiles as boundaries and median inside; whiskers extended to upper quartile + 1.5× interquartile range and lower quartile – 1.5× interquartile range; outliers beyond the range above). significance (one-sided Wilcoxon rank-sum test): n.s. (not significant), p > 0.10; ^*p < 0.10; ^**p < 0.05; ^***p < 0.01. Data: the embryo samples “Emb1” and “Emb2” (in toto: 4-, 6-, 7-, 8-, 12-, 14-, 15-, 24-, 26-, 28-, and ≥44-cell stage with 8, 12, 14, 16, 24, 28, 30, 48, 52, 56, and 91 data points, respectively, per embryo). C Poorer segmentation performance of EmbSAM when the denoising module and watershed module are ablated respectively, revealed by Dice score (left) and Hausdorff distance (right). The percentage of 3D cell regions with increasing or decreasing values is marked near the diagonal line. Data: the embryo samples “Emb1” and “Emb2” (in toto: 379 data points). Source data: Supplementary Data 5 for (B) and Supplementary Data 6 for (C).

Apart from algorithm benchmarking, we further validated EmbSAM’s segmentation accuracy using the manually annotated ground truth from the additional embryo sample “Emb3” first published in this work (Supplementary Fig. 5). What is more, we inspected how reproducible EmbSAM’s segmentation accuracy is by segmenting the 3D image stack slice-by-slice along all six orthogonal axes (i.e., with slicing direction along +x, –x, +y, –y, +z, and –z), which is equivalent to rotating the stack while maintaining the original slicing direction along –z. With two embryo samples, 11 developmental stages, and 379 individual cells (Fig. 2B), we consistently observed large Dice scores (0.890 ± 0.093) and small Hausdorff distances (2.856 ± 0.993) and segmented 3D cell shapes matching ground truth and indistinguishable across all six conditions, confirming EmbSAM’s reproducible segmentation accuracy regardless stack rotation or slicing direction (Supplementary Fig. 6, and Supplementary Data 1).

Further, we applied 3D shape descriptors (incl., general sphericity, Hayakawa roundness, and spreading index) to assess cell shape consistency in three contexts: (1) between EmbSAM segmentation and ground truth; (2) across individual embryos (imaged under the same experimental condition with compression) segmented by EmbSAM; (3) between uncompressed and compressed embryos (imaged under the same experimental condition respectively) segmented by EmbSAM. First, shape descriptor values from 379 individual cells in “Emb1” and “Emb2” are highly similar between EmbSAM segmentation and ground truth (Supplementary Fig. 7; $R=0.993,\,0.991,\,0.996$ accordingly, with ${R}^{2}$ from a proportional least-squares fit to test a proportional relationship), demonstrating considerable segmentation accuracy in terms of cell shape. Second, shape descriptor values in four embryo samples “Emb4” to “Emb7” (imaged under the same experimental condition with compression) are close to their averages (Supplementary Fig. 8; $R=0.851,\,0.879,\,0.753$ accordingly, with ${R}^{2}$ from a proportional least-squares fit to test a proportional relationship). This suggests both the high accuracy of measurement and a tight control of C. elegans embryogenesis variability in the scale of cell shape, similar to cell lineage and fate patterns, cell division timings and axis orientations, cell cycle lengths, cell sizes (Supplementary Fig. 8; $R=0.952$ for volume and $R=0.932$ for surface area, with ${R}^{2}$ from a proportional least-squares fit to test a proportional relationship), cell positions, and other cellular developmental properties discovered before^8,18,36,37. It should be pointed out that the variation coefficients within EmbSAM segmentation (0.072 averaged over all 379 cells and three shape descriptors) and within ground truth (0.113 averaged over all 379 cells and three shape descriptors) are both low and near to each other, supporting both the high segmentation accuracy of our algorithm and the high biological reproducibility of embryogenesis. Third, all three shape descriptor values in compressed embryo samples “Emb4” to “Emb7” exhibit a decreasing trend in comparison to those in uncompressed embryos “Emb8” to “Emb9” (Supplementary Fig. 9). This overall cell shape shift raises enduring questions about how embryogenesis maintains robustness across varying mechanical environments, such as the compressive stresses experienced in aged or nutrient-deprived adults. Beyond local compensatory cell movements³⁸, what global self-correction mechanisms are engaged to accommodate these variable cell shapes warrants further investigation, particularly using our dataset.

Substantial contribution of denoising module and watershed module

To explain why EmbSAM and MedSAM (two SAM-based algorithms sharing the same segmentation architecture but differing in their training datasets) exhibit divergent performance, we evaluated the contributions of the denoising module and watershed module. To validate these modules’ effectiveness and necessity before SAM segmentation in the EmbSAM framework, we implemented an ablation experiment for each of them: when ablating the denoising module, the inputted image moves directly to watershed module and then segmentation module; when ablating the watershed module, the cuboid with boundaries $({x}_{{{\rm{n}}}{{\rm{uc}}}}\pm \root{{3}}\of{\frac{3V}{4\pi }},\,{y}_{{{\rm{n}}}{{\rm{uc}}}}\pm \root{{3}}\of{\frac{3V}{4\pi }},\,{z}_{{{\rm{n}}}{{\rm{uc}}}}\pm \root{{3}}\of{\frac{3V}{4\pi }})$ surrounding the cell nucleus position is used as the 3D bounding box promoters (i.e., SAM prompt tokens shown in Supplementary Fig. 10) for SAM segmentation of the image outputted by the denoising module. Besides, we added these modules individually and jointly into MedSAM before its SAM segmentation. The modified MedSAM produces smooth and compacted 3D cell shapes for ≥44-cell-stage embryos, matching ground truth and appearing indistinguishable from EmbSAM (Supplementary Fig. 11). In both frameworks, omitting the denoising module led to severe cell missing, while omitting the watershed module led to unrealistic cell irregularity, underscoring their essential roles in mitigating low SNR and prompting cell boundary (generating slice-specific bounding boxes instead of MedSAM’s default rectangular 3D bounding box or 2D bounding box without automatic slice-specificity, which is yet to be refined³³ (Supplementary Fig. 12)) prior to SAM segmentation. These findings indicate that EmbSAM’s superior performance arises from its integrated denoising module and watershed module, while its segmentation module remains on par with other retrained SAM-based algorithms.

Quantitatively, the ablation experiments on EmbSAM reveal a global decline in segmentation performance following the removal of each module (Fig. 2C). While 97.76% of the 3D cell regions acquired a poorer Hausdorff distance after the denoising module removal, all of them acquired a poorer Dice score. This evidence strongly supports the pivotal role of these two modules in recognizing individual cells in noisy images and promoting the accuracy of SAM segmentation. Such severe segmentation defects in ablation experiments were mostly seen at the top and bottom of the cells (Supplementary Fig. 11), where the fluorescence signal intensity is relatively lower due to the single-layer cell membrane (compared to the double-layer ones formed by two contacting cells inside the embryo) and the loss of laser power through the z-axis (parallel to the imaging direction and perpendicular to the focal plane) in the embryo^39,40.

While the classic watershed module was also used in some other cell segmentation algorithms customized for C. elegans embryonic images^8,40,41,42, our denoising module was introduced to overcome the low SNR present in certain images. To evaluate its performance in such a goal, we compared it with two other state-of-the-art image denoisers, Noise2Void⁴³ and CARE⁴⁴ (Supplementary Note 1), using the 2D image acquired at the mid-focal plane of embryo samples “Emb1” to “Emb 3” at their ≥44-cell stage (Supplementary Fig. 13). Along the middle line $y=0$ (as a function of $x$), our denoising module reaches a brightness distribution with zero regions at cytoplasm locations and sharp peaks at membrane locations, whereas Noise2Void exhibits noticeably lower contrast. At the embryo periphery, our denoising module yields continuous, uniform membrane fluorescence; in CARE-denoised images, the membrane signal appears thin and fragmented. These results demonstrate that our denoising module offers superior performance for low-SNR C. elegans embryonic images.

Segmentation outperformance without reliance on cell nucleus information

While EmbSAM outperforms other membrane-based segmentation algorithms (i.e., CShaper, MedSAM, and PlantSeg just compared), it remains to be seen whether EmbSAM can also outperform the nucleus-assisted ones. For C. elegans embryogenesis, this is a straightforward and useful strategy to prompt the segmentation of cell membrane boundary by providing the cell nucleus position as a seed^39,40. In this context, CMap is a kind of such segmentation algorithm that very recently reconstructed a C. elegans morphological map with >95% of embryonic cells segmented at 1.5-min intervals⁴⁰. Thereof, we compare EmbSAM (only cell membrane fluorescence images) and CMap (using both cell membrane and cell nucleus fluorescence images, where the cell nucleus position is extracted and serves as a segmentation seed) as described above. Qualitatively, CMap outputs cell shapes resembling those of the ground truth, but they are coarser than both those of the ground truth and the ones by EmbSAM (Supplementary Fig. 14AB). Quantitatively, EmbSAM achieves both significantly larger Dice score and smaller Hausdorff distance than CMap at all developmental stages⁴⁰ (Supplementary Fig. 14C). These findings support EmbSAM’s outperformance in segmentation accuracy, and suggest that it more effectively discriminates cell membrane fluorescence signal from background noise, obviating the need for cell-nucleus-based seeding. By getting rid of the cell nucleus fluorescence channel, future experiments can repurpose that fluorescent label for other molecules of interest, such as the cell adhesion molecule E-cadherin (HMR-1), to quantify their dynamics in space and time with the segmented 3D cell shapes⁴⁵.

Monitoring 3D morphodynamics of cell biology event at 10-second intervals

Embryonic cell divisions proceed with drastic cell shape dynamics as fast as seconds to minutes, such as cytokinesis, which is coupled with rapid cell motion, asymmetric cell volume segregation, and fate differentiation^{10,11,13,14,21}. Since the EmbSAM framework can effectively segment the cell membrane fluorescence images with a low SNR in the embryo samples “Emb1” to “Emb3” (Fig. 2, and Supplementary Figs. 2 and 5), we further applied it to other C. elegans wild-type embryo samples, “Emb4” to “Emb9”, that were imaged at a high temporal resolution but with a weak laser intensity^9,20. Fascinatingly, the overall 3D cell shapes inside both embryos were successfully reconstructed up to the moment before gastrulation (i.e., 24-cell stage) at 10-s intervals (Supplementary Movies 1 and 2), allowing a detailed study of specific cellular behaviors and developmental landmarks with traced cell identities, lineages, and fates, as shown below^46,47,48. Based on the four embryo samples with the most imaging time points, reconstruction process from the ≤4- to ≥24-cell stages requires <11 h in total and <6 min per time point on a GPU (graphics processing unit; NVIDIA A100 40 GB PCIe), demonstrating considerable computing efficiency for broad usage (Supplementary Data 2). Note that such smooth and compact cell shapes produced by our low-SNR fast imaging cannot be reconstructed by CShaper, which was originally customized for C. elegans embryonic images^8,17 (Supplementary Figs. 3 and 15). The digital embryonic cell shape data has been reformatted for convenient access, visualization, and analysis through public platforms, including both the local software ITK-SNAP-CVE and the online website https://bcc.ee.cityu.edu.hk/cmos/embsam (user instruction in Supplementary Movies 3 and 4)⁴⁰.

Cell shape dynamics related to cell division

The cell division axis orientation and cell cycle length have been known to be regulated by various biomechanical and biochemical processes^10,13. Our segmented 3D cell shape data can illustrate the cell divisions in multiple lineages and generations at 10-s intervals, exemplified by the AB cells (the 1^st somatic founder cell derived from the 1^st cell division post fertilization) (Supplementary Fig. 16), EMS cell (the 2^nd somatic founder cell derived from the 3^rd cell division post fertilization) (Fig. 3A), MS and E cells (anterior and posterior daughter cell of EMS) (Supplementary Fig. 17), and C and P3 cells (the 3^rd somatic founder cell and remaining germline stem cell derived from the 7^th cell division post fertilization) (Supplementary Figs. 1 and 18). Each cell division is identified within a single segmented 3D cell region by a pair of mitotic sister cell nuclei (or two sets of separate reformed chromosomes after nuclear envelope breakdown) — distinct histone-labeled fluorescent domains — recognized via StarryNite/AceTree that comprises automatic tracing and manual correction^49,50,51,52. Taking the EMS cell division for a case study, the Wnt signaling from its neighbor cell, i.e., the P2 cell, controls its axis orientation and differentiation of the two daughter cells, i.e., the MS cell for mesoderm and the E cell for endoderm^53,54 (Fig. 3A, and Supplementary Movie 5). Both the separation and motion of cell nuclei and cell membrane can be vividly visualized and quantitatively characterized, at the temporal resolution three times of the previous one¹⁵ (Fig. 3A, and Supplementary Fig. 19). At the end of EMS cell division, in other words, the anaphase (starting with a symbol of cell nuclei separation and their widening gap), an increase of cell surface area is detected (Fig. 3B), in consistency with previous cell biology knowledge on cell division^55,56. The cell sphericity keeps declining as reported before¹⁵, along with the other three independent cell shape descriptors (i.e., Hayakawa roundness, spreading index, and diameter) obeying the same trend⁵⁷ (Fig. 3B). It is noteworthy that, the four embryo samples “Emb4” to “Emb7” shows lower variability in cell shape (with variation coefficient of 0.062, averaged over all five curves and all time points) is less than that of cell surface area and cell-cell contact areas (with variation coefficient of 0.342, averaged over all five curves and all time points), suggesting variability levels could substantially differ between cellular developmental properties even though they are essentially relevant (Fig. 3BC, and Supplementary Fig. 20).

Fig. 3: The segmentation results (exemplified by the embryo sample “Emb5”) of EmbSAM for the EMS cell division at 10-second intervals.

A 2D (middle plane) and 3D segmentation results viewed in the imaging direction and highlighted by the dotted cell nuclei and masked cell membranes. Shown are lateral views with the anterior of the embryo to the left. All cell identities at the first and last moments are labeled next to their cell regions. Scare bar: 10 μm. B Monotonic curves of cell surface area, general sphericity, Hayakawa roundness, spreading index, and diameter over time, shown with their data in individual embryo samples (differentially color-coded) as well as averaged over all embryo samples (black) alongside standard deviation (orange shade). C Curves of cell-cell contact area over time, shown with their data in individual embryo samples (differentially color-coded) and in average (black) with standard deviation (orange shade). For (A, B, C), the developmental time is shown, with the moment of complete cell membrane separation as time zero; For (B, C), the durations of all embryo samples are normalized to their average. Source data: Supplementary Data 7 for (B) and Supplementary Data 8 for (C).

The cell deformation with declining general sphericity, Hayakawa roundness, spreading index, and diameter during cell division is actually proceeding with the cell shape changed from spherical to dumbbell-shaped (Fig. 3A). Further exemplified by the ABpr and E cells and their neighbor cells (C and ABplp respectively), when a cell initiates its division program, it firstly turns spherical with its interface protruding toward its neighbor cell, and subsequently turns to dumbbell-shaped, squeezing its neighbor cell severely into a flat shape (Fig. 4A, B, and Supplementary Movies 6 and 7). Quantitative cell-cell contact interface curvature (defined as the reciprocal of radius of a sphere fitted to the curved contact interface) decreases continuously from positive values (indicating protrusion toward the dividing cell), through zero (indicating a flat interface), into negative values (indicating protrusion in opposite orientation to the initial one and toward the dividing cell’s neighbor)⁵⁸ (Fig. 4C, D). This implies a strong intracellular and intercellular mechanical force generated by the dividing cell. Such an intensive passive force and deformation exerted by a dividing cell on its neighbor cell appear to be a common phenomenon, further supported not only by the previously reported EMS and P2 cells (squeezed by ABa and ABp cell divisions) but also by other cells – C (squeezed by ABpr cell), ABplp (squeezed by E cell) (Fig. 4A, B), MS (squeezed by ABpl cell division), E (squeezed by ABpl cell division), among others⁵⁸ (Supplementary Figs. 21 and 22, and Supplementary Movie 8). Previous fluorescence imaging on the spatiotemporal dynamics of F-actin demonstrates its accumulation on the cell membrane near cell division and in the cytosol beyond cell division, which makes the cells get rounder and harder when it is around cell division (further validated by atomic force microscopy measurements of Young’s modulus)⁵⁹. Our data can clearly illustrate such cell-cycle-dependent cell shape dynamics at 10-s intervals, represented by the cells mentioned above when they turn spherical and dumbbell-shaped successively, squeezing their neighbor cells (relatively soft) to adapt to it (relatively hard) through severe deformation.

Fig. 4: The 3D segmentation results of EmbSAM for the drastic shape dynamics of dividing cells and newborn daughters (non-transparent), as well as their squeezed neighbors (semi-transparent) at 10-second intervals.

A E cell division that squeezes ABplp, in accordance with Supplementary Movie 6. B ABpr cell division that squeezes C, in accordance with Supplementary Movie 7. The swapped cell-cell contact interface orientation originating from the hard cell and pointing the soft cell is highlighted by the starting and ending moments of the top three rows. For (A, B), the developmental time is shown, with the moment of complete cell nuclei separation as time zero. C, D Curves of cell-cell contact interface curvature with sign changed over time, corresponding to (A, B) respectively. Data: the embryo sample “Emb5”. For (A–D), the developmental time is shown, with the moment of complete cell nuclei separation as time zero. Source data: Supplementary Data 9 for (C) and Supplementary Data 10 for (D).

Cell shape dynamics related to body axis establishment

The anaphase and telophase of cell division, defined as starting from cell nuclei separation and ending in cell membrane separation, is as fast as 2.5 min measured before^8,9. Such a short-term biological process is critical to establishing the body axes that determine the dorsal (D), ventral (V), left (L), and right (R) of an embryo (also called symmetry breaking), while the anterior-posterior (A-P) axis is determined by sperm entry and cell polarization that makes the first cell division asymmetric^60,61. While the first two cells AB and P are located in the anterior and posterior of the embryo, respectively, the second cell division taking place in AB is initiated with an axis perpendicular to the A-P axis first and then reoriented to it, making its posterior daughter ABp determining the dorsal of the embryo (Fig. 5A, and Supplementary Movie 8).

Fig. 5: The segmentation results (exemplified by the embryo sample “Emb5”) of EmbSAM for the cell division responsible for dorsal-ventral axis establishment at 10-second intervals.

A 2D (middle plane) and 3D segmentation results of the AB cell division (top, with the large skew angle of cell nuclei orientation) and P1 cell division (bottom, with the small skew angle of cell nuclei orientation), viewed in the imaging direction and highlighted by the dotted cell nuclei and masked cell membranes. Connecting lines between cell nuclei are overlaid on the time-lapse images: the dashed vector marks the initial separation orientation (serving as the baseline at the first time point), while the solid vector tracks subsequent orientation changes; the angle between these vectors in Cartesian coordinates quantifies the skew angle of cell nuclei orientation during anaphase and telophase. Shown are lateral views with the anterior of the embryo to the left. Scare bar: 10 μm. B Intuitive schematic for how the skew angle of cell nuclei orientation during anaphase and telophase is calculated – the included angle between newborn cell nuclei’s connecting lines at the first moment (marked by ${N}_{{{\rm{S}}}}$) and later moments in Cartesian coordinates. C Curves of skew angle of cell nuclei orientation of all recorded cells in the AB lineage (left) and P1 lineage (right) over time. Data: the embryo samples “Emb4” to “Emb7” (in toto: AB and P1 lineages with 60 and 27 cells respectively). For (A–C), the developmental time is shown, with the moment of complete cell membrane separation as time zero; for (C) the durations of all embryo samples are normalized to their average. D Comparison between all recorded cells in the AB lineage and P1 lineage, regarding their net skew angle of cell nuclei orientation during anaphase and telophase averaged over all embryo samples (left), and their standard deviation among all embryo samples (right). Presentation: box-and-whisker plot (colored interquartile with upper and lower quartiles as boundaries and median inside; whiskers extended to upper quartile + 1.5× interquartile range and lower quartile – 1.5× interquartile range; outliers beyond the range above). Statistical significance (one-sided t-test): n.s. (not significant), p > 0.10; ^*p < 0.10; ^**p < 0.05; ^***p < 0.01. Data: the embryo samples “Emb4” to “Emb7” (in toto: AB and P1 lineages with 60 and 27 cells respectively). E Comparison between all recorded cells in the AB lineage and P1 lineage, regarding their positional variability at the onset of anaphase and at the end of telophase. Presentation: box-and-whisker plot (colored interquartile with upper and lower quartiles as boundaries and median inside; whiskers extended to upper quartile + 1.5× interquartile range and lower quartile – 1.5× interquartile range; outliers beyond the range above). Statistical significance (one-sided t-test): n.s. (not significant), p > 0.10; ^*p < 0.10; ^**p < 0.05; ^***p < 0.01. Data: the embryo samples “Emb4” to “Emb7” (in toto: AB and P1 lineages with 10 and 6 cells respectively, per embryo). Source data: Supplementary Data 11 for (C) and Supplementary Data 12 for (D) and Supplementary Data 13 for (E).

As previous experimental observation indicated that the cell divisions in the AB lineage have a regulated reorientation during cytokinesis while the ones in the P1 lineage don’t¹¹, we measure the skew angle of cell nuclei orientation during anaphase and telophase for all cells recorded (Fig. 5B), with each time-dependent curve averaged across embryo samples “Emb4” to “Emb7”. Here, the skew angle is quantitatively defined as the included angle between two vectors in 3D space: the first connects two cell nuclei at their initial separation (serving as the baseline at the first time point), and the second connects the same cell nuclei at any subsequent time point to track orientation changes. Shown by the overall curve averaged over all cells at the temporal resolution of 10 s, the AB cells (incl., AB, ABa, ABal, ABala, ABalp, ABalpa, ABalpp, ABar, ABara, ABaraa, ABarap, ABarp, ABarpa, ABarpp, ABp, ABpl, ABpla, ABplaa, ABplap, ABplp, ABplpp, ABpr, ABpra, ABpraa, ABprap, ABprp, ABprpa, ABprpp) exhibit a stably increasing skew angle deviated from its initial direction but the P1 cells (incl., EMS, MS, MSa, E, C, Ca, Cp, D, P1, P2, P3) exhibit a stably unchanged value, faithfully supporting previous conclusion (Fig. 5C). This conclusion holds whether the durations of anaphase and telophase among embryo samples, along with the skew angle at those time points, are proportionally normalized to their length (leading to skew angle curves with an equal duration) or not (leading to skew angle curves with unequal durations) (Fig. 5C, and Supplementary Fig. 23). Although the AB cells carry substantially larger skew angle than P1 cells on average, their standard deviations among embryo samples is also larger (Fig. 5D). Alongside the more variable skew angle of AB cells, they also exhibit significantly higher positional variability (defined as root-mean-square deviation of distance vectors between a cell and all other cells, in all four embryo samples³⁷) than P1 cells, at the end of the telophase but at the onset of anaphase (Fig. 5E). This finding suggests that, beyond the previously reported cell adhesion and gap junction³⁷, regulated cell nuclei orientation skewing is another critical contributor to positional variability during embryonic development. In the future, the variability of skew angle, cell position, and other cellular developmental properties is worth joint investigation, using our data coupled with cell identities, cell lineages, and cell fates.

Following the diamond-shaped 4-cell stage with both anterior-posterior and dorsal-ventral symmetry breaking, the fourth and fifth cell divisions simultaneously taking place in ABa and ABp (anterior and posterior daughter of AB) are initiated with an axis roughly perpendicular to the plane constituted by the A-P and D-V axes; regulated by a contact-induced myosin flow demonstrated before¹⁰, the axis orientation is slightly skewed with the left daughter cells nearer to the anterior (Fig. 6A, and Supplementary Movie 9). Subsequently, the ABpl cell (left daughter of ABp) undergoes long-range migration toward the dorsal of the embryo with its migration-coupled spreading shape occurring in the middle of its lifespan^4,57 (Fig. 6B, and Supplementary Movie 10). The migration of ABpl, which has been identified with the longest distance among all cells before the 24-cell stage and has nearly the most irregular shape among all cells before the 350-cell stage^8,20, was proposed to be driven by cell adhesion regulation^9,62 and enhances the left-right symmetry breaking substantially. Interestingly, the duration of anaphase and telophase positively associates with cell volume, evidenced in both absolute coordinates (Supplementary Fig. 24A; $R=0.300$, with ${R}^{2}$ from an unconstrained least-squares fit to test a power-law relationship) and semi-log coordinates (Fig. 6C; $R=0.441$, with ${R}^{2}$ from a proportional least-squares fit to test a proportional relationship). Although previous experimental measurements and our data consistently revealed that the cell cycle length negatively associates with cell volume^21,63 (Supplementary Fig. 24B), no correlation (Supplementary Fig. 24C, $R < 0.001$, ${R}^{2}$ from an unconstrained least-squares fit) was found between the cell cycle length and duration of anaphase and telophase. This is possibily attributed to the one-order-of-magnitude difference in their timescales and distinct regulatory mechanisms without direct correlation: while cell cycle length is affected by the limited content of its regulatory molecules (e.g., nuclear pore complexes) unequally allocated during cell volume partition^13,64, the duration of anaphase and telophase is likely affected by cell-volume-dependent physical constraints — namely, the distance sister nuclei must separate and the equatorial diameter that the contractile ring must ingress through during cytoskeleton remodeling for cytokinesis^65,66.

Fig. 6: The segmentation results (exemplified by the embryo sample “Emb5”) of EmbSAM for the cell division responsible for left-right axis establishment at 10-second intervals.

A 2D (middle plane) and 3D segmentation results of the ABp cell division, viewed from the dorsal view and highlighted by the dotted cell nuclei and masked cell membranes. Shown are lateral views with the anterior of embryo to the left. Scare bar: 10 μm. The developmental time is shown, with the moment of complete cell membrane separation as time zero. B 3D segmentation results (exemplified by the embryo sample “Emb4”) of EmbSAM for the ABpl cell migration at 10-s intervals. Shown are lateral views with the anterior of the embryo to the left. ABpl is colored in red and other cells are in gray. The developmental time is shown, with the last moment before ABpl cell nuclei separation as time zero. C Positive correlation between cell volume and duration of anaphase and telophase (defined as starting from cell nuclei separation and ending in cell membrane separation as illustrated in (A). Data: the embryo samples “Emb4” to “Emb7” (in toto: 79 data points). D Significance comparison between ABpl cell and its sister and cousins (i.e., the ABal, ABar, and ABpr cells), regarding the duration of anaphase and telophase (defined as starting from cell nuclei separation and ending in cell membrane separation as illustrated in (A). Presentation: box-and-whisker plot (colored interquartile with upper and lower quartiles as boundaries and median inside; whiskers extended to upper quartile + 1.5× interquartile range and lower quartile – 1.5× interquartile range; outliers beyond the range above). Statistical significance (one-sided t-test): n.s. (not significant), p > 0.10; ^*p < 0.10; ^**p < 0.05; ^***p < 0.01. Data: the embryo samples “Emb4” to “Emb7” (in toto: 79 data points). Source data: Supplementary Data 14 for (C) and Supplementary Data 15 for (D).

The relationship between cell volume and the duration of anaphase and telophase appears in a global manner and independent of lineage: cells from both the germline lineage (i.e., P lineage) and all of its derived somatic lineages (i.e., AB, EMS, and C lineages, each with at least two cells) (Supplementary Fig. 1) intermix on both sides the fitted line, with no apparent shifts between lineages (Supplementary Fig. 24A). Notably, ABpl’s duration of anaphase and telophase is significantly shorter than those of its sister and cousins with similar size (with a relative difference of <8%), probably reflecting its unique cytoskeletal state that facilitates left-right symmetry breaking and embryo rotation^4,67 (Fig. 6D). Beyond the difference between ABpl and its sister and cousins, the cell-specific duration of anaphase and telophase is reproducible between individual embryos. Remarkably, the unidentical cells’ four duration lengths in embryo samples “Emb4” to “Emb7” (imaged under the same experimental condition with compression) fluctuate around their averages, which together considerably fit the proportional relationship (Supplementary Fig. 24D; $R=0.767$, with ${R}^{2}$ from a proportional least-squares fit to test a proportional relationship) with a small variation coefficient of $0.131\pm 0.036$. This suggests both the high accuracy of measurement and a tight control of C. elegans embryogenesis variability in the scale of cell division phase durations, similar to cell lineage and fate patterns, cell division timings and division orientations, cell cycle lengths, cell sizes (Supplementary Fig. 8; $R=0.952$, with ${R}^{2}$ from a proportional least-squares fit to test a proportional relationship), cell positions, and other cellular developmental properties discovered before^8,18,36,37.

The 10-s window in our extensive dataset provides an opportunity to analyze the spatial distribution of functional subcellular structures (i.e., contractile ring, lamellipodia, protrusion, and filopodia) over time to understand the underlying mechanism for cell division and migration, how the dividing and migrating cells interact with their neighbors, and how are multidimensional cellular properties stored in our dataset (e.g., cell division, cell migration, cell shape, cell cycle, cell identity, cell lineage, cell fate, and cell nucleus position and size (Supplementary Fig. 25)) affect each other^63,68. In the future, physical simulation of cytoskeletal dynamics is anticipated to elucidate their contributions to the cell division, migration, and deformation behaviors observed in this dataset^69,70.

Cell shape dynamics related to spatial reorganization for gastrulation

In addition to morphogenetic events driven by one or a few cell divisions, the ones proceeding over multiple rounds of cell divisions can also be characterized quantitatively at exceptional spatiotemporal resolutions. Previous experimental studies have reported that C. elegans early embryonic cells undergo spatial reorganization for gastrulation through apical-basal polarization, where all cells remain attached to the eggshell and form a cavity (blastocoel) to facilitate the upcoming cell ingression, i.e., gastrulation^46,71. In our data with a temporal resolution of 10 s, the cells keep acquiring enlarged lateral contact area and slimmer shape to get aligned on the inner surface of the eggshell regularly (Supplementary Fig. 26A). This is supplemented by a strong negative correlation observed between the relative outer surface area (contacting the eggshell) of a cell and developmental time (Supplementary Fig. 26B).

Conclusion

Quantitative and automatic reconstruction of time-lapse 3D cell shapes with fluorescently-labeled cell membranes is challenging, especially for a developing embryo, in which cells undergo rapid division and migration frequently coupled with cell fate specification and cell shape deformation. Such a challenge is even more severe when the fluorescence images exhibit a low SNR because of various experimental protocols (e.g., strains) and purposes (e.g., observing short-term or long-term biological processes) (Supplementary Fig. 27). In this paper, we successfully segmented the time-lapse 3D images with a relatively low SNR from nine C. elegans wild-type embryo samples with resolved cell identities, which had failed to be segmented by state-of-the-art algorithms. The successful segmentation is achieved by an integrative computational framework, EmbSAM, that contains a deep-learning-based denoising module and a watershed module followed by SAM, which allows accurate reconstruction of the cell shapes from multiple developing embryos (Figs. 1–3). With an exceptional temporal resolution as high as 10-s in six of the embryos, the results allow examination of the instantaneous change in cellular behaviors during rapid cell division of embryogenesis, For example, the cell shape change and nucleus movement during division and fast directional cell movement after division can be examined, together with their dependence on cell identities, cell lineages, and cell fates; upon those single-cell behaviors, whole-embryo morphogenesis including body axes establishment and spatial reorganization for gastrulation is illustrated in 3D, along with quantitative cellular properties like cell division axis reorientation and cell surface area distribution presented in the time course (Figs. 4–6). All the reconstructed time-lapse 3D cell shapes at 10-s intervals and calculated shape features (incl., cell volume, cell surface area, and cell-cell contact area) are publically available in the data format of software ITK-SNAP-CVE and website https://bcc.ee.cityu.edu.hk/cmos/embsam^40,72.

Given the high segmentation accuracy of the EmbSAM framework, it could be applied not only to the wild-type embryos but also to the perturbed ones, such as the one curated with external compression, laser ablation, and RNA interference, to uncover how a developing embryo coordinates cellular behaviors (e.g., cell division and coupled motion) to enable the faithful formation of tissues or organs^{9,11,20,38,73,74}. Preliminary test with fifteen more C. elegans wild-type and RNAi-treated embryos image reveals cell membrane segmentation is feasible with fluorescence labeling on alternative molecules, including both the homogeneously-distributed one (phosphoinositide) and the heterogeneously-distributed one (NMY-2), where the latter one (profiles biologically significant dynamics, i.e., cell cortex fluidity associated with cell division and coupled motion)^10,11,12 could replace the traditional marker for cell membrane labeling and leave more fluorescence channels for monitoring the dynamics of other molecules simultaneously (Supplementary Note 2, Supplementary Figs. 28–31, and Supplementary Data 3). Such monitoring can be customized for specific developmental stages from fertilization to late and even post embryogenesis, for the whole body or tissue/organ of interest (e.g., ACT-5 for monitoring the lumenal formation in intestinal cells) (Supplementary Fig. 32) and at flexible intervals (e.g., down to 2-s)^75,76 (Supplementary Fig. 33). Following this paradigm, more molecule dynamics in time-lapse format can be collected quantitatively by strain crossing, fluorescence imaging, and cell segmentation in a high-throughput manner. When imaging different fluorescent markers, variations in brightness or SNR will require fine-tuning of both laser power and re-trained denoising module; alternatively, for scenarios where cells lie in a 2D plane (e.g., C. elegans 1- to 4-cell stages with anterior-posterior and dorsal-ventral axes establishment), image quality could be enhanced by projecting the z-stack into a 2D image for accurate cell membrane segmentation, revealed by embryos in the preliminary test (Supplementary Note 2, Supplementary Data 4, and Supplementary Figs. 28–31).

The fluorescence images of dozens of C. elegans embryos and the reconstructed cell shapes in 2D and 3D at high temporal resolutions in this work enable systematic, detailed, and in-depth analysis of cellular behaviors, including but not limited to the ones analyzed in this paper. For example, the skew angle of cell nuclei orientation during anaphase and telophase likely reflects both the cell nucleus movement inside a cell and the whole cell body’s movement, where the orientation of a bounding box of the 3D cell body can be extracted by principal component analysis as demonstrated before⁵⁷. Classic Hertwig’s rule — namely, that how the embryonic cell division axis orientations are determined by cell nucleus movements, cell body movements, cell shapes, cell positions, cell-cell contact relationships and areas, as well as other external environments (e.g., mechanical compression) and molecular dynamics (e.g., myosin density and flow) — can be systematically investigated using our high-resolution multidimensional dataset^10,12. The identified correlations, causal relationships, and independencies among these factors are expected to facilitate the construction of new theoretical models that help predict what’s going on in reality. For instance, the cell shape change during fast cell division and cytokinesis can help understand the cell membrane mechanics, providing a reference for testing various cell membrane models established previously^9,77,78,79. Moreover, such embryo-wide cell shapes can be used to reversely infer the intracellular and intercellular mechanical properties over development, which are usually hard to measure directly^56,79,80,81. When replacing the fluorescent marker used for labeling cell membranes with those specific for other cellular or subcellular compartments (e.g., E-cadherin and F-actin), the dynamics of their related cellular behaviors, such as cell adhesion and cell stiffness, can be examined with an exceptional temporal resolution, i.e., at a 10-s or a shorter interval^82,83. All the detailed cellular or subcellular behaviors above not only help understand the biological regulation in vivo, but also facilitate the establishment of a reliable, comprehensive computational model that simulates developmental control in silico and permits virtual experiments for mechanism discovery^9,62,78,84. In the future, the EmbSAM framework could be used to analyze datasets with fluorescently-labeled cell membranes beyond the ones analyzed in this work, such as those of ascidian, fruit fly, zebrafish, and mouse, so as to broaden the cell shape data in various biological contexts^27,85,86.

In spite of the successful 3D segmentation of pre-gastrulating C. elegans embryos at 10-s intervals, performance declines at the periphery of embryos no matter they are mechanically compressed or not, leading to missing or overspreading cell regions (Supplementary Fig. 34). Estimated with representative embryo samples “Emb7” (under compression) and “Emb8” (without compression) in an 100-time-point intervals, those errors start occurring in the 500^th time points, while the save duration up to the 400^th time point ends with 22 cells for both embryos; between the 100^th and 400^th time points, the SNR of the 3D image volume (256 × 356 × 214 voxels, with a voxel resolution of 0.18 μm/pixel) was calculated to be just above 2, defining the quantitative image-quality threshold that EmbSAM can reliably deal with. The segmentation failure in embryo periphery is typical in C. elegans embryonic cell segmentation, stemming from the single fluorescent cell membrane layer at the edge, in contrast to the double layers between adjacent internal cells that boost intensity^39,40. To extend data collection into later, more challenging periods of development, one may execute a two-stage imaging protocol – proceed the single channel (nucleus fluorescence) at 1.5-min intervals (minimizing photobleaching and phototoxicity while permitting cell lineage tracing) up to the 24-cell stage, and then switch to dual channels (nucleus and membrane fluorescence) at 10-s intervals with sufficient laser power⁸⁷. On the computational front, cell segmentation algorithms could leverage spatiotemporal correlations between neighboring slices and consecutive frames (e.g., short-term consistency in cell volume and shape) to improve accuracy and robustness, instead of completely separate segmentation slide-by-slide and frame-by-frame⁸⁸.

Methods

Embryo data collection for time-lapse 3D cell segmentation

C. elegans is a well-established model animal cultured at laboratory for half a century. C. elegans is a hermaphrodite, which reproduces mostly through selfing although rare males are present and can mate with hermaphrodite⁸⁹. A total of nine C. elegans wild-type embryo samples were used for 3D image acquisition and cell segmentation in this paper, with green fluorescence labeling cell nuclei and red fluorescence labeling cell membranes ubiquitously (strains ZZY0535 and ZZY0861)^8,17,40. The images acquired according to the unified protocol⁸ were subjected to cell segmentation. These fluorescence images exhibited a significantly lower SNR (quantification detailed in Section 2.5) than those successfully segmented by CShaper before⁹⁰ (Supplementary Fig. 35), preventing them from successful 3D cell segmentation by the CShaper (one of the most updated algorithms customized for C. elegans embryonic images), MedSAM (the most updated SAM algorithm generalized for biomedical images), or PlantSeg (one of the most updated algorithms validated on both plant tissue and mouse embryonic images) algorithm^{8,17,33,34,35}. The fluorescence labeling on cell nuclei was used for cell lineage tracing (since no later than the 4-cell stage). This was conducted with StarryNite (automatic tracing) and with AceTree for visualization and manual correction^{50,51,52,91,92,93}, which produced cell identity, division timing, and position to each cell in addition to assigning cell division. A total of nine embryos were imaged in 3D at two different temporal resolutions as described below.

Three embryo samples (strain ZZY0535)^8,17 were imaged at 1.41-min intervals for 60 time points, which were imaged in 712 × 512 pixels on the xy plane with a total of 68 focal planes along the z-axis (0.09 μm/pixel for the xy plane and 0.42  μm/pixel for the z-axis, i.e., the imaging direction). Two of them were reused from our previous works^20,21; these two embryo samples (“Emb1” and “Emb2”) were used for quantitatively evaluating the cell segmentation performance. The last embryo sample (“Emb3”) was first published in this paper, for further independent cell segmentation performance evaluation.

Two embryo samples (strain ZZY0535)^8,17 were imaged at 10-s intervals. One (“Emb4”) was published in our previous work²⁰, which was imaged in 712 × 512 pixels on the xy plane with a total of 47 focal planes along the z-axis (0.09 μm/pixel for the xy plane and 0.59 μm/pixel for the z-axis, i.e., the imaging direction) for 260 time points. The other (“Emb5”) was published in our previous work⁹, which was imaged in 712 × 512 pixels on the xy plane with a total of 47 focal planes along the z-axis (0.09 μm/pixel for the xy plane and 0.59 μm/pixel for the z-axis, i.e., the imaging direction) for 300 time points. These two embryo samples exhibit cell cycle lengths strongly proportional to the ones in the embryo samples “Emb1” to “Emb3”, suggesting that the fundamental biological process was not affected by the imaging at a substantially higher temporal resolution (almost an order of magnitude) (Supplementary Fig. 27).

Another four embryo samples (strain ZZY0861)⁴⁰ were imaged at 10-s intervals for ≥650 time points, which were imaged in 712 × 512 pixels on the xy plane (0.09  μm/pixel for the xy plane). Two of them (“Emb6” and “Emb7”) were imaged with a total of 66 focal planes along the z-axis (0.46 μm/pixel for the z-axis, i.e., the imaging direction); another two of them (“Emb8” and “Emb9”) were imaged with a total of 56 focal planes along the z-axis (0.80 μm/pixel for the z-axis, i.e., the imaging direction). These four embryo samples (“Emb6” to “Emb9”) were used to reveal how the cell segmentation method will behave or fail at more challenging later stages of development.

It is worth noting that the four embryo samples “Emb4” to “Emb7” were imaged under mechanical compression according to the unified protocol⁸, whereas the two embryo samples “Emb8” and “Emb 9” were imaged without mechanical compression according to the unified protocal⁴⁰. These two groups together will facilitate direct comparison of cell segmentation performance and embryonic development modes, while the former cohort itself can facilitate assessing developmental variability from embryo to embryo^94,95.

Manual annotation for ground truth

Manual annotation of cell membranes with fluorescence images was used as ground truth, which was necessary for training and evaluating an automatic cell segmentation algorithm. In this work, multiple groups of manually annotated ground truths were used as detailed below.

For training the deep-learning-based denoising module, 16 3D volumetric images manually annotated in five C. elegans wild-type embryos (a collection of 2339 3D cell objects) were adopted from our previous work; these manually annotated ground truths (binarized images showing ideal cell regions, used as the state after denoising), together with their corresponding raw images (noisy images with blurred cell regions, used as the state before denoising) with a SNR around 5.227, roughly twice the one of EmbSAM dataset (Supplementary Fig. 35), were generated through labor-intensive efforts and serve as a standardized and reusable resource for training a deep-learning-based denoising module^8,90,96 (Supplementary Data 4). Whether the denoising module trained with high-SNR images (CShaper dataset) is sufficient for dealing with low-SNR images (EmbSAM dataset) will be evaluated in subsequent analyzes (Supplementary Fig. 35). The 3D volumetric images were subsequently sliced in the x, y, and z directions according to the corresponding recorded pixels, resulting in a total of 4096, 5696, and 2560 2D images, respectively. From these, we randomly selected 10% in each direction to construct the training dataset, which enabled comprehensive learning and adaptation, containing the imaging features on fluorescently-labeled cell shapes in different directions.

For evaluating the automatic cell segmentation performance, all the cell shapes of the embryo samples “Emb1” and “Emb2” at 4-, 6-, 7-, 8-, 12-, 14-, 15-, 24-, 26-, 28-, and ≥44-cell stages (a collection of 379 3D cell objects) were meticulously annotated with respect to all the x, y, and z directions, slice by slice and cell by cell. Besides, a total of 45 2D images (focal planes) in the embryo sample “Emb3” were manually annotated for independent performance evaluation.

Embryo data collection for alternative fluorescently-labeled molecules

For time-lapse imaging, young adult worms were dissected to free embryos. The embryos were mounted on a 3–5% (wt/vol) agarose pad with 0.5% tetramisole and sealed with Vaseline. Green fluorescent protein (GFP) and mCherry were visualized using 488 nm and 561 nm excitation lasers, respectively. Channels were imaged sequentially to eliminate bleed-through. Imaging in all channels was captured using 0.1-s exposure time and at 2- to 30-s intervals on an inverted spinning-disk confocal microscope (Olympus SpinSR10) using a Yokogawa CSU W1 scanner system, equipped with a 60×/1.4 NA objective and two Hamamatsu ORCA Flash sCMOS cameras. All movies were acquired under the control of cellSens Dimension software (Olympus), in which multi-z sections were merged into a single projected image using ImageJ⁹⁷. Images were subsequently arranged using ImageJ with small and global adjustments for contrast and brightness. Embryos with fluorescence labeling the phosphoinositide through pleckstrin homology (PH) domain (“Emb10” to “Emb15”) and non-muscle myosin II (NMY-2) (“Emb16” to “Emb24”) are involved^98,99,100.

For single-shot imaging, embryos were mounted in M9 buffer with 10 mM sodium azide (Sigma) on glass slides, and observed under the Carl Zesis LSM 980 confocal microscope equipped with a Zeiss 60×/1.40 NA oil immersion objective lens (Carl Zeiss). Lasers 488 nm were used to excite GFP. Single-plane images were taken as 6–10 sections along the z-axis at 0.2-µm intervals. Multi-z sections were acquired and merged into a single projected image using Zen software (Carl Zeiss). Images were subsequently arranged using Adobe Photoshop with small and global adjustments for contrast and brightness. Embryos with fluorescence labeling filamentous actin 5 (ACT-5) (“Emb25” to “Emb30”) are involved^75,76.

RNA interference

For standard RNA interference (RNAi), about 10 young adults were picked and cultured on RNAi plates (nematode growth media (NGM) containing 1 mM isopropylthiogalactoside (IPTG) and 100 μg/mL ampicillin) seeded with bacterial clones of target genes, and their first-generation embryos were examined after 72 h. Worms were fed with RNAi bacteria containing the L4440 empty vector plasmid as a control treatment (EV RNAi). All RNAi clones were confirmed by sequencing. For time-lapse images, the young adult worms were put in the M9 buffer and dissected by two needles to release their embryos. Embryos were then mounted on a 2% agarose pad and imaged with oil immersion objectives.

Signal-to-noise ratio evaluation for microscopy-produced cell membrane fluorescence image

For a 3D cell membrane fluorescence image ${I}_{{{\rm{r}}}{{\rm{aw}}}}\left(x,y,z\right)$ (with its brightness value $\varphi \left(x,y,z\right)$ in each voxel $\left(x,y,z\right)$ within the whole rectangular domain ${\varOmega }_{{{\rm{w}}}{{\rm{h}}}{{\rm{ole}}}}$) produced by microscopy, 3D cell regions can be segmented either manually or automatically. To delineate the cell membrane domains, we inwardly erode each 3D cell region by five voxels in all directions; voxels present in the original region but absent after erosion define the membrane domain ${\varOmega }_{{{\rm{membrane}}}}$. Next, subtracting ${\varOmega }_{{{\rm{membrane}}}}$ from ${\varOmega }_{{{\rm{w}}}{{\rm{h}}}{{\rm{ole}}}}$ defines the background (cytoplasmic and extraembryonic space) domains ${\varOmega }_{{{\rm{background}}}}$. Finally, the fluorescence within ${\varOmega }_{{{\rm{membrane}}}}$ (with voxel number ${N}_{\left(x,y,z\right)\in {\varOmega }_{{{\rm{membrane}}}}}$) derives the average membrane signal:

$${\beta }_{{{\rm{S}}}}=\frac{{\sum }_{\left(x,y,z\right)\in {\varOmega }_{{{\rm{membrane}}}}}\varphi \left(x,y,z\right)}{{N}_{\left(x,y,z\right)\in {\varOmega }_{{{\rm{membrane}}}}}}$$

(1)

while the fluorescence within ${\varOmega }_{{{\rm{background}}}}$ (with voxel number ${N}_{\left(x,y,z\right)\in {\varOmega }_{{{\rm{background}}}}}$) derives the average background noise:

$${\beta }_{{{\rm{N}}}}=\frac{\mathop{\sum }_{\left(x,y,z\right)\in {\varOmega }_{{{\rm{background}}}},\varphi \left(x,y,z\right) > 0}\varphi \left(x,y,z\right)}{{N}_{\left(x,y,z\right)\in {\varOmega }_{{{\rm{background}}}}}}$$

(2)

evaluating the SNR at the voxel resolution as ${\beta }_{{{\rm{R}}}}=\frac{{\beta }_{{{\rm{S}}}}}{{\beta }_{{{\rm{N}}}}}$.

Proposed cell segmentation framework

The proposed computational framework for cell segmentation, EmbSAM, consists of three major parts:

• 1) The cell boundary localization part for denoising fluorescence images and generating bounding boxes for each cell region. This is primarily composed of a denoising module (the deep neural network that removes small noisy components to increase the SNR of raw images) and a watershed module (the pre-segmentation for generating bounding boxes based on a watershed algorithm and obtaining approximate boundaries of the target cell to be segmented)^42,101.

• 2) The SAM part for final automatic cell segmentation²³. This accomplishes automatic cell segmentation based on a series of bounding box promoters. The SAM module maximizes the performance of the proposed framework, whose pre-trained model was trained with billions of images containing thousands of imaging conditions. It is one of the reasons that it probably can help deal with low-SNR images. For the target cells in each slice (focal plane), the bounding box produced by the cell boundary localization part was used to facilitate the SAM segmentation with 3D assembling.

• 3) The cell tracing part for assigning cell identity to the reconstructed 3D cell regions. The cell nucleus position output by StarryNite and AceTree is used to match its corresponding 3D cell region.

Image denoising using conditional normalizing flow

The image-denoising network is based on the LLFlow (Low-Light Image Enhancement with Normalizing Flow) model¹⁰¹, which utilizes a conditional normalizing flow model^102,103 informed by the Retinex theory¹⁰⁴. The workflow of step-by-step data processing and network training in this module is detailedly described in Supplementary Fig. 36 and Supplementary Note 3. Given a raw image ${I}_{{{\rm{raw}}}}$, the processing procedure includes histogram equalization, color extraction, and noise extraction followed by the RRDB (Residual-in-Residual Dense Block) module¹⁰⁵ for feature extraction, resulting in the illumination invariant color map ${G}(I_{{{\rm{raw}}}})$. The trained invertible network ${F}$ of the conditional normalizing flow can construct the transformation process of the probability distribution between the manually annotated ground truth image with low noise (${I}_{{{\rm{clean}}}}$) and its original cell membrane fluorescence image with high-noise (${I}_{{{\rm{raw}}}}$) from a latent code $J$ that aligns with the standard Gaussian distribution and ${G}(I_{{{\rm{raw}}}})$. Here, ${F}$ consists of three layers (incl., a squeeze layer and 12 flow steps), with the probability density function $P({I|}{I}_{{{\rm{ref}}}})$ in the condition (reference image) of ${I}_{{{\rm{ref}}}}$ expressed as:

$$P({I|}{I}_{{{\rm{ref}}}})=\frac{1}{2b}\exp \left(-\frac{\left|I-{I}_{{{\rm{ref}}}}\right|}{b}\right)$$

(3)

where $b$ is a positive constant related to the learning performance. Thus, the probability distribution of ${I}_{{{\rm{clean}}}}$ under the condition of ${I}_{{{\rm{raw}}}}$ can be represented as $P({I}_{{{\rm{clean}}}}|{I}_{{{\rm{raw}}}})$, and the transformation process can be represented as ${I}_{{{\rm{clean}}}}=F(J,\,{I}_{{{\rm{raw}}}})$. From the established conditions, we can derive $\int P({I}_{{{\rm{clean}}}}|{I}_{{{\rm{raw}}}})\,\partial {I}_{{{\rm{clean}}}}=\,\int P({J|}{I}_{{{\rm{raw}}}})\,\partial J$ and $J={F}^{-1}({I}_{{{\rm{clean}}}},\,{I}_{{{\rm{raw}}}})$. After applying the Jacobian correction to the probability density of $J$, we obtain:

$$P({I}_{{{\rm{clean}}}}|{I}_{{{\rm{raw}}}})={P}_{J}(J|{I}_{{{\rm{raw}}}})\left|\frac{\partial {F}^{-1}({I}_{{{\rm{clean}}}},\,{I}_{{{\rm{raw}}}})}{\partial {I}_{{{\rm{clean}}}}}\,\right|$$

(4)

To capture distributional differences between noise and cell features, a negative log-likelihood (NLL) minimization approach is utilized to maximize the probability distribution of $P({I}_{{{\rm{clean}}}}|{I}_{{{\rm{raw}}}})$ to train $F$, getting the loss function:

$${Loss}\left({I}_{{{\rm{raw}}}},\,{I}_{{{\rm{clean}}}}\right) = \, -log (P({I}_{{{\rm{clean}}}}|{I}_{{{\rm{raw}}}})) = -log {P}_{J}({J|}{I}_{{raw}})\\ -log \left|\frac{\partial {F}^{-1}({I}_{{{\rm{clean}}}},\,{I}_{{{\rm{raw}}}})}{\partial {I}_{{{\rm{clean}}}}}\,\right|$$

(5)

After training, the inference can be implemented onto all raw images beyond the manually annotated ground truths, ${\hat{I}}_{{{\rm{clean}}}}=F\left(J,\,{I}_{{{\rm{raw}}}}\right)$, deriving their low-noise outputs (Fig. 1, and Supplementary Fig. 37).

During denoising, 2D images are stacked along the z-axis to construct a 3D image resized to $(256,\,356,\,160)$ by trilinear interpolation with an even voxel resolution of $0.18\,{{\rm{\mu }}}{{\rm{m}}}/{{\rm{pixel}}}$. Then 2D slices are generated by cutting the 3D images along the x-, y-, and z-axis, followed by the denoising process in all three directions. For each pixel in space, the maximum value from its three orthogonal denoised 2D slices is adopted, so that a small-noise 3D image is recombined. This denoising step is essential for taking advantage of the complementary information in three directions regarding the 3D cell membrane fluorescence images.

Auto-seeding watershed pre-segmentation for generating bounding box promoter and locating cell boundary

The denoised volume (3D image) is fed into the watershed module for generating bounding box promoters that approach cell boundaries slice-by-slice. The workflow of step-by-step data processing in this module is detailly described in the middle row of Fig. 1. A Gaussian filter is applied for image smoothing, utilizing a Gaussian kernel size of 13 and a standard deviation of 2. The image is binarized via Otsu’s thresholding¹⁰⁶ to produce $M$, producing an intermediate 3D image, $M$, in which $C$ and $E$ represent the pixels valued 0 (cell interior and exterior) and 1 (cell boundary) respectively. Then, the watershed pre-segmentation algorithm⁴¹ from our previous work^8,42 was applied on $M$. The 3D Euclidean distance map of $M$ is obtained:

$${Ed}\left(x,y,z\right)=\mathop{\min }_{\left(x,y,z\right)\in C}\left\{{\min }_{({x}_{0},{y}_{0},{z}_{0})\in E}\left\{{\left(x-{x}_{0}\right)}^{2}+{\left(y-{y}_{0}\right)}^{2}+{\left(z-{z}_{0}\right)}^{2}\right\},10\right\}$$

(6)

Delaunay triangulation is executed on the local maximum in ${Ed}$ (potential cell centers), where the edge ${e}_{{ij}}$ between vertices $i$ and $j$ is assigned a weight by accumulating the ${Ed}$ values along ${e}_{{ij}}$:

$${W}_{{e}_{{ij}}}={\sum }_{\left(x,y,z\right)\in {e}_{{ij}}}{Ed}\left(x,y,z\right)$$

(7)

Here, vertices with an edge having a $W$ value below a threshold (numerical value: 10, with a unit of pixel in the resized 3D image, corresponding to a length of 1.8 μm in reality; empirically customized for C. elegans embryonic images by previous independent research⁴²) are clustered as the centers inside the same cell. The vertice clusters (seeding points) and the Euclidean distance map are inputted into the watershed algorithm¹⁰⁷, marking both foreground (cell interior) and background (cell exterior) regions. It is worth pointing out that the local maximum is used to find seeds rather than the traced cell nucleus position, which makes EmbSAM segmentation fully independent of the cell nucleus fluorescence and allows for future adaptation to an alternative fluorescent label (replacing the cell nucleus fluorescence channel in microscopy) on a molecule of interest (e.g., E-cadherin or HMR-1 that controls cell adhesion), enabling quantification of its spatiotemporal dynamics on top of the segmented 3D cell shapes⁴⁵. Upon completion of these steps, the binary image with only the embryo interior and exterior is converted into the one with distinct 3D cell regions (Fig. 1, Supplementary Fig. 37). For each z slice in a pre-segmented 3D cell region, the rectangle enclosing its 2D cell region (represented as $[{x}_{\min }:{x}_{\max },\,{y}_{\min }:{y}_{\max },\,{z}_{i}]$) forms a series of 2D bounding box promoters for the following SAM module.

Segment Anything Model

For each time point, both the denoised 2D images (automatically disassembled from the denoised volume along z-axis) and all the 2D bounding boxes surrounding a specific cell outputted by the watershed module were fed into the pre-trained zero-shot SAM (base vision model named vit_b)³⁰. The segmentation output of SAM is a 3D cell region comprising both background (0, cell exterior) and foreground (1, cell interior). The workflow of step-by-step data processing in this module is detailedly described in Supplementary Fig. 10.

When performing cell segmentation, the SAM module might generate multiple potential 2D regions within the same area, including noises, the target cell, or its neighboring cells. Here, we selected the largest area as the target cell region. Additionally, unreasonable irregular regions such as dispersed coralloid or starlike shapes need to be filtered, especially around the embryo’s top and bottom cell periphery where noise is higher (since the membrane lies parallel to the confocal plane and has only one single fluorescent layer) (Supplementary Fig. 38). To this end, we calculated the nondimensional irregularity of each 2D cell region, $\eta =\frac{c}{\sqrt{s}}$, where $c$ and $s$ represent its circumference and surface area respectively. For calculating a 2D cell region’s perimeter, we used the Douglas–Peucker algorithm for contour approximation, with the approximation coefficient set as 0.01¹⁰⁸. By analyzing the irregularity of 265,704 manually annotated 2D cell regions in two previous independent research^8,40,90,96, a threshold (numerical value: 9.02, with no unit) was obtained for establishing a reasonable range for 2D cell irregularity at the 99% confidence (Supplementary Fig. 39). After slice-by-slice filtering by the cell irregularity threshold, all the remaining reliable 2D regions of a target cell are assembled into 3D, reconstructing cell-identity-resolved shapes with their cell-lineage-tracing information.

Cell segmentation performance evaluation

To systematically assess the similarity between the cell segmentation results and their ground truth annotations, we adopted two widely recognized metrics for 3D object comparison^109,110:

• Dice score: The ratio of the overlapping volume to the total volume of two 3D objects.

• Hausdorff distance: The maximum distance calculated from every voxel in one 3D object to its nearest voxel in another 3D object.

In theory, a larger Dice score and a smaller Hausdorff distance indicate a higher consistency between the cell segmentation results and their ground truth annotations.

3D cell shape descriptor

The characteristics of cell shapes enclosed by their segmented cell membranes can be quantitatively described by a series of 3D shape descriptors with explicit geometric significance. Here, we adopted three 3D cell shape descriptors from our previous work as follows⁵⁷.

• Taking a perfect sphere with the same volume as the cell, “general sphericity” is defined as the ratio of its surface area to that of the cell, in other words, it describes the similarity of the cell to a perfect sphere^111,112:

  $${General\; Sphericity}=\frac{\root{{3}}\of{36\pi {V}^{2}}}{S}$$

  (8)

  where $V$ and $S$ are the volume and surface area of the cell respectively

• While “general sphericity” assesses the gross shape of a cell, “Hayakawa roundness” specifically assesses the sharpness of edges and corners, as well as the presence of the convexities and concavities on the cell surface^112,113:

  $${Hayakawa\; Roundness}=\frac{V}{S\root{{3}}\of{{abc}}}$$

  (9)

  where $a$, $b$ and $c$ are the length of the long, intermediate, and short axes of the oriented bounding box (OBB) of the cell, respectively, estimated by principal component analysis^112,114.

• Derived from a 2D definition, “spreading index” reflects the degree to which the convex hull of a cell resembles a perfect sphere, i.e., the spreading of the cell shape^115,116:

  $${Spreading\; Index}=\frac{\root{{3}}\of{36\pi {V}_{{{\rm{convex}}}}^{2}}}{{S}_{{{\rm{convex}}}}}$$

  (10)

  where ${V}_{{{\rm{convex}}}}$ and ${S}_{{{\rm{convex}}}}$ are the volume and surface area of the convex hull enclosing the cell, respectively.

• During cytokinesis, the mother cell nucleus divides into two daughter cell nuclei with locations $({x}_{{{\rm{nuc}}}1},{y}_{{{\rm{nuc}}}1},{z}_{{{\rm{nuc}}}1})$ and $({x}_{{{\rm{nuc}}}2},{y}_{{{\rm{nuc}}}2},{z}_{{{\rm{nuc}}}2})$; almost at the same time, the cell membrane elongates with the equatorial plate ingressing as a contractile ring, whose diameter keeps shrinking¹¹⁷. The equatorial plate with a contractile ring is presumed as perpendicular to the line between the two daughter cell nuclei. Hence, the plane equation is described by $({Ax}+{By}+{Cz}+D=0)$, where $\left(A,B,C\right)=({x}_{{{\rm{nuc}}}2}-{x}_{{{\rm{nuc}}}1},{y}_{{{\rm{nuc}}}2}-{y}_{{{\rm{nuc}}}1},{z}_{{{\rm{nuc}}}2}-{z}_{{{\rm{nuc}}}1})$ is its normal vector defined by the positions of the two daughter cell nuclei and ${D}$ is determined as follows. All pixels with a distance to the plane smaller than 0.5 pixels form an approximate cylinder with a height of 1 pixel, by which the diameter of the contractile ring can be derived from its surface area:

  $${Diameter}=0.18\,{{\rm{\mu }}}{{\rm{m}}}\times \left(\sqrt{1+\frac{2{S}_{{{\rm{cylinder}}}}}{\pi }}-1\right)$$

  (11)

  where ${S}_{{{\rm{cylinder}}}}$ is the surface area of the convex hull enclosing the cylinder and ${D}$ is determined by searching the smallest ${S}_{{{\rm{cylinder}}}}$.

Statistics and reproducibility

The time-lapse 3D data studied for statistics and reproducibility in this work was produced by an experimental-computational pipeline, which incorporates time-lapse 3D fluorescence imaging, cell-nucleus-based lineage tracing^50,51,52, cell-membrane-based shape reconstruction, and 2D-irregularity-based region filter for C. elegans embryos (Methods). No data were excluded in the following quantitative analyzes.

Three groups of C. elegans embryo samples with time-lapse 3D shape reconstruction were used for statistics and reproducibility study: compressed embryos imaged at 1.41-min intervals (“Emb1” and “Emb2”), compressed embryos imaged at 10-s intervals (“Emb4” to “Emb7”), uncompressed embryos imaged at 10-s intervals (“Emb8” and “Emb9”). Wherever statistics or reproducibility is studied, data from all embryos within each group were used systematically and unbiasedly.

All quantitative results are supported by significance values for statistics and at least two replicates for reproducibility, corresponding to the sample size used in previous developmental biology and spatial patterning research^118,119.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.