Hypergraph-driven spatial multimodal fusion for precise domain delineation and tumor microenvironment decoding

Abstract

Recent advancements in spatial transcriptomics have transformed tumor microenvironment research by providing insights into cellular interactions and spatial heterogeneity. A fundamental challenge is the precise delineation of spatial domains. However, existing methods remain limited in accurately identifying spatial domains, partially due to their reliance on single-view features. Moreover, these methods often struggle with many-to-many spot relationships, such as shared biological functions. To this end, we propose HAST, a hypergraph-driven spatial multimodal fusion tool for precise domain delineation and tumor microenvironment decoding. HAST integrates gene expression, spatial coordinates, and histological features to construct local hypergraphs that effectively model many-to-many spatial relationships. These local hypergraphs are dynamically aggregated into a global hypergraph, capturing higher-order interactions. To learn discriminative and biologically meaningful representations, we employ a hypergraph convolutional network, coupled with self-supervised contrastive learning, to fuse multi-view information. Extensive benchmarking across multiple datasets demonstrates that HAST outperforms state-of-the-art methods, accurately delineating spatial domains and uncovering domain-associated genes. Functional enrichment analyses further reveal biologically relevant pathways and provide novel insights into tumor microenvironment. In summary, HAST is a robust framework for decoding the spatial complexity of tumors, paving the way for precise spatial omics analyses in cancer research.

Introduction

Spatial transcriptomics (ST) has emerged as a pioneering technology that integrates gene expression with the spatial distribution of cells, offering unprecedented insights into tissue properties and pathological alterations at both the molecular and structural levels. By mapping gene expression patterns on tissue sections, ST technology provides a powerful tool for unraveling complex cellular microenvironments and tissue structures^1,2. Spatial domain identification is an essential task during the ST analysis process. It aims to delineate different functional and structural regions within a tissue based on transcriptomic data. These spatial domains usually correspond to biologically significant regions, such as tumor microenvironments or developmental regions of embryonic tissues^3,4. Therefore, accurately identifying these regions is crucial for understanding tissue-specific functions, revealing disease mechanisms, and guiding precision medicine strategies^5,6.

Traditional non-spatial clustering methods, such as Louvain⁷, and package Seurat⁸, rely solely on gene expression data to group cells into spatial domains by assessing the similarity between gene expressions. These methods demonstrate suboptimal performance, due to ignoring the spatial location information within tissues^9,10. To take account of this information, several graph-based deep learning methods are proposed, such as SpaGCN⁹, SpaceFlow¹¹, STAGATE¹², and GraphST¹⁰. These methods improve the performance of domain identification by integrating gene expression with spatial location. For instance, SpaGCN⁹ and STAGATE¹² model spatial information using a graph-based encoder, effectively capturing local spatial dependencies between spots. Moreover, SpaceFlow¹¹ employs a contrastive learning strategy that creates negative examples by randomly rearranging spatial expression graphs during training. Another method, GraphST¹⁰, combines graph convolutional networks (GCNs) with contrastive learning to derive informative and discriminative spot representations by minimizing the distance between spatially adjacent spots. Furthermore, several advanced methods have been proposed and can be applied in spatial domain identification. For example, BANKSY¹³ uses neighbor-augmented embeddings to jointly perform cell-type labeling and tissue-domain segmentation in spatial omics data. CellCharter¹⁴ integrates molecular profiles with spatial information and structural metrics to identify and compare cell niches across samples in a scalable and interpretable manner. scNiche¹⁵ is a multi-view graph-fusion autoencoder that integrates molecular and spatial information via a fusion network to derive compact single-cell niche representations. Kasumi¹⁶ leverages dual-view learning with spatial information to robustly represent tissues for improved patient stratification in spatial omics datasets.

While graph-based methods have demonstrated strong performance in well-structured tissues like the brain, they often encounter challenges in more heterogeneous contexts, such as tumor microenvironments, where spatial boundaries are ambiguous, and gene expression signals are noisy. For instance, SpaGCN⁹ acknowledges that their spatial domain detection is mainly driven by gene expression, which may lead to the discrepancy between the detected domains and the underlying tissue anatomical structure. A common limitation among these methods is their reliance on single-modality features, typically gene expression or spatial coordinates, to construct pairwise spot-to-spot graphs. Such a design makes it difficult to capture many-to-many relationships¹⁷. For example, in complex tissues, such as tumors, a spot may share key biological programs with multiple, non-adjacent neighbors, which cannot be captured by pairwise edges alone. Modeling such higher-order associations enables more accurate and biologically meaningful spatial domain delineation, especially when domain boundaries are non-contiguous or partially overlapping^18,19,20,21. Therefore, it is essential to develop models that can integrate multi-modal features and encode high-order relational structures.

Here, we propose a multi-view Hypergraph Association Spatial Transcriptomic (HAST) framework for domain identification. HAST constructs three types of modality-specific local hypergraphs separately from gene expression, spatial coordinates, and histology image features. These local hypergraphs are then adaptively aggregated into a global hypergraph to capture higher-order interactions across modalities. All hypergraphs, along with spatial gene expression patterns, are processed using hypergraph convolutional networks (HGCNs) to learn comprehensive representations. To further enhance feature discriminability, we employ self-supervised contrastive learning by corrupting vertex gene features and aligning original and corrupted representations. The final fused representations are used for spatial domain clustering. We evaluate HAST on multiple spatial transcriptomic datasets and show that it outperforms existing methods in spatial domain identification. In addition, HAST reveals fine-grained spatial and genetic information within tumor microenvironments, providing insights into complex tissue organization.

Results

Overview of HAST

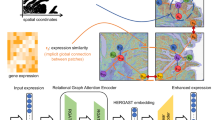
HAST is a hypergraph-based deep learning framework for spatial domain identification, as illustrated in Fig. 1. It consists of two sequential stages: (1) multi-view hypergraph construction and representation learning, and (2) representation refinement and domain identification.

Fig. 1: Schematic overview of HAST framework for spatial domain identification.

HAST consists of two stages for gene representation extraction and spatial domain identification, respectively. Stage 1 further includes two detailed steps, which are multi-view hypergraph construction and hypergraph representation learning. In stage 1, three hypergraphs ${{{{\mathcal{H}}}}}^{GC}$, ${{{{\mathcal{H}}}}}^{MS}$, and ${{{{\mathcal{H}}}}}^{SC}$ are firstly constructed from perspectives of gene correlations, morphological similarities, and spatial neighborhoods. For subsequent operation, three corrupted hypergraphs are generated by data augmentation. Then, HAST constructs a global hypergraph ${{{{\mathcal{H}}}}}_{f}$ by adaptively aggregating weighted local hypergraphs. These local and global hypergraphs, along with spatial gene expression patterns, are then processed by hypergraph convolutional networks (HGCNs) to learn comprehensive representations, obtaining the original representation Z and the corrupted representation ${Z}^{{\prime} }$. In stage 2, the self-supervised contrastive learning is applied to optimize the alignment between original and corrupted representations. Finally, the reconstructed gene expression matrix $\hat{X}$ from a multilayer perceptron (MLP) decoder is used for spatial domain clustering. Stage 3 illustrates some downstream analysis.

In Stage 1, HAST constructs three modality-specific local hypergraphs from spatial transcriptomic data using: (1) Pearson correlation to model gene expression similarity, (2) Euclidean distance of spatial coordinates to reflect physical adjacency, and (3) cosine similarity of image patch features extracted from a pre-trained Vision Transformer to represent histological morphology. Each spot is connected to its top-k similar neighbors in each modality to form a hyperedge. These three local hypergraphs are each encoded with a hypergraph convolutional network (HGCN) to generate modality-specific latent representations, detailed in “Hypergraph construction”. To integrate the three views, HAST uses an adaptive weighted hypergraph fusion module that assigns a weight to each local hypergraph based on its consistency with the fused structure. The weights are updated in a closed-form manner at each forward pass. This fused global hypergraph is further processed by an additional HGCN to model high-order, multi-view relationships, detailed in “HGCN for representation learning”.

In Stage 2, we apply self-supervised contrastive learning by corrupting the input gene matrix while maintaining the neighbor topology. The corrupted and original graphs are both passed through the encoder pipeline. Contrastive learning encourages the model to produce consistent representations for similar spots by maximizing the alignment between the original and corrupted versions of the same spot. It enhances the robustness of representations and does not enforce similarity between spatially neighboring but biologically distinct spots. Finally, a multilayer perceptron decoder reconstructs the gene expression matrix from the fused latent features. This reconstruction step retains biologically meaningful expression signals, thus providing a refined gene profile for downstream spatial domain clustering.

Performance of spatial domain identification for the DLPFC dataset

We first evaluated the spatial identification performance of HAST on the LIBD human dorsolateral prefrontal cortex (DLPFC) dataset²², which comprised spatially resolved transcriptomic profiles of 12 slices. Each slice included manually annotated white matter (WM) and four to six cortical layers. For this dataset, we compared the spatial domain identification performance of HAST with other baseline methods. As shown in Fig. 2a, HAST achieved the best overall clustering performance, measured by Adjusted Rand Index (ARI)²³, Fowlkes-Mallows Index (FMI)²⁴, and Normalized Mutual Information (NMI)²⁵. We hypothesize that the dynamic multi-view hypergraph aggregation contributes to the improved clustering performance. HAST also exhibited less variation in performance across slices than other methods, demonstrating consistent and robust clustering results with an average ARI, FMI, and NMI scores of 0.63, 0.72, and 0.70. These results represented significant performance improvements in three metrics of 15%, 9%, and 6%, respectively, compared to the second-ranked method, GraphST. Although STAGATE and GraphST showed decent clustering performance on partial slices, their overall performance was worse than HAST. Additionally, the performance of BayesSpace and SpaceFlow exhibited less variation but had much lower average scores.

Fig. 2: Performance on the DLPFC dataset.

a Boxplots of ARI scores, FMI scores, and NMI scores for eleven methods on 12 slices of the DLPFC dataset. In the boxplots, the center line represents the median, the box boundaries represent the upper and lower quartiles, the black dots denote individual slices, and the whisker lines are 1.5 × interquartile range. b H& E images, manual annotations, clustering with ARI and NMI by HAST on slice #151672 of the DLPFC dataset, and UMAP visualization. c Clustering results of baseline methods Seurat, Giotto, SpaGCN, SpaceFlow, conST, BayesSpace, STAGATE, and GraphST on slice #151672 of the DLPFC dataset using ARI and FMI. Manual annotation and clustering results for other DLPFC slices are shown in Supplementary Figs. S1--S12. Tools for visualization are from the Scanpy package. d UMAP visualization by SpaGCN, GraphST, STAGATE, and HAST on DLPFC slice #151672. e Spatial expression patterns of SVGs for domain 1 (PCP4), domain 3 (MBP), and domain 6 (HPCAL1) for slice #151673. f Heatmaps of spot similarity matrices in the latent space of HAST, HAST with only spatial location correlation HGCN encoder, HAST with only gene correlation HGCN encoder, and HAST with only morphological similarity HGCN encoder on slice #151672 of the DLPFC dataset.

Among all slices, HAST achieved the best performance on slice #151672, with the ARI of 0.70 and FMI of 0.78. Fig. 2b presents the clustering results alongside the uniform manifold approximation and projection (UMAP) visualization. Figure 2c further illustrates clustering results across baseline methods on slice #151672, revealing that Giotto performed the worst, with substantial intermixing of clusters and the ARI of only 0.11 and FMI of 0.36. Seurat exhibited a similar issue, with poorly defined cluster boundaries. BayesSpace performed slightly better but still struggled with inter-category mixing. Additionally, SpaceFlow identified distinct layers, but most of the layers do not match the annotations. SpaGCN and conST produced cluster shapes that were closer to the annotations but suffered from inconsistent category thickness. STAGATE and GraphST achieved the most annotation-aligned results among baseline methods, with ARI scores of 0.57 and 0.63, respectively. Manual annotation and clustering results for other DLPFC slices are shown in Supplementary Figs. S1–S12. Figure 2d visualized the UMAP of HAST and the three best-performing baseline methods on slice #151672. SpaGCN achieved relatively good separation between some layers, but overall exhibited less compact and clearly defined clusters. GraphST demonstrated stronger local consistency but suffered from overlap between clusters. Certain regions of STAGATE displayed mixing of different spot types. In contrast, HAST improved spatial delineation visually. While these aspects are qualitative in nature, they are aligned with the quantitative improvements observed in evaluation metrics.

To further validate the efficiency of identified spatial domains, we detected spatially variable genes (SVGs) for each domain in the case slice #151673, following the pipeline in SpaGCN. Specifically, for each target domain, we selected its top three neighboring domains using a spatial k-nearest approach. Statistical comparison was performed using a log-transformed gene expression matrix and a neighborhood-aware differential expression model that accounts for the spatial adjacency matrix. All SVG detection was performed on the original gene expression matrix rather than the reconstructed output. Among the detected SVGs, three with strong domain specificity were presented in Fig. 2e. PCP4 was identified as a key SVG in domain 1, while MBP and HPCAL1 were enriched in domains 3 and 6, respectively. These SVGs highlighted their association with spatial heterogeneity across different regions, demonstrating the ability of HAST to accurately capture spatial patterns and reveal meaningful biological insights with distinct domains^22,26. Finally, we highlighted the issue of representation collapse in the case slice #151672, which contained five spatial domains, as shown in Fig. 2f. These heatmaps illustrated the structural separability and discriminative capacity of the learned embeddings. It can be seen that embeddings learned from HAST with a specific HGCN encoder failed to produce clearly separable clusters, causing smaller-scale blocks to blend with larger or neighboring ones. In contrast, the embedding generated through HAST, which adaptively fuses multi-view hypergraphs, showed well-separated similarity blocks. It provides a representation-level explanation of why HAST captures domain boundaries more accurately.

Analysis of independent and integrated slices from the mouse brain tissue dataset

The mouse brain tissue dataset comprised two slices: anterior and posterior, with only the anterior slice manually annotated. In the anterior section (Fig. 3a), HAST accurately delineated key regions, including the olfactory bulb and dorsal pallium. Using the manual annotations from Long et al.¹⁰, HAST achieved the highest ARI and FMI scores of 0.50 and 0.52, respectively, representing a 22% improvement in ARI compared to the second-ranked GraphST. For the posterior slice (Fig. 3b), which lacked manual annotations, HAST successfully identified the cerebellar cortex (red box) and the Ammon’s horn (yellow box), aligning well with the Allen mouse brain atlas²⁷. Since manual annotations were unavailable, we evaluated clustering performance using the Silhouette Coefficient (SC)²⁸ and Davies-Bouldin index (DB)²⁹. The SC measures clustering compactness and separation, ranging from −1 to 1, with higher values indicating better clustering. The DB index assesses overall cluster quality, where lower values are preferable. HAST achieved the highest SC of 0.23 and the lowest DB of 1.36, outperforming other baseline methods.

Fig. 3: Performance on the mouse brain tissue dataset.

a H& E image of the anterior slice of mouse brain tissue dataset, manual annotation from Long et al.¹⁰ and clustering results of HAST and baseline methods on this slice measured by ARI and FMI. Colors are independently assigned for each method. b H& E image of the posterior slice of mouse brain tissue dataset, annotations from the Allen reference atlas²⁷, and clustering results of HAST and baseline methods on this slice measured by SC and DB. Colors are independently assigned for each method. c Horizontal integration of HAST, including annotations of the Allen reference atlas, results of the integration of HAST and baseline methods on anterior and posterior mouse brain tissue sections. The cerebral cortex is outlined in the red box, and the hippocampal Cornu Ammonis region is outlined in the yellow box. The remaining results of the baseline method are shown in Supplementary Fig. S13. d The UMAP visualization of HAST.

Since tissue samples can be much larger than the capture slices used in ST, horizontal integration enables the alignment of data from multiple slices. To assess the horizontal integration capability of HAST, we spliced two slices from the mouse brain tissue dataset and compared its performance against baseline methods (Fig. 3c and Supplementary Fig. S7). Following previous work, we set the number of target clusters to 26 across all methods. HAST accurately identified key brain structures, including the cerebral cortex (red box), and hippocampus (yellow box) closely matching the Allen mouse brain atlas. In contrast, other methods neglected certain structures. For example, conST failed to recognize the hippocampus. Additionally, HAST achieved the highest SC of 0.26 and the lowest DB of 1.23 among all methods, demonstrating superior clustering performance. Further analysis of the UMAP distribution (Fig. 3d) indicated that common regions in the anterior and posterior slices overlapped, whereas unique regions remained distinct. This outcome reflects the functional differences between the two slices and reveals that the integration preserves both shared and distinct tissue structures.

Specifying the tumor microenvironment in the human breast cancer dataset

In the analysis of the human breast cancer dataset, the results from HAST were closest to the manual annotation among all methods and achieved the highest ARI of 0.60 and FMI of 0.63, which was 15% higher than the second-ranked STAGATE in terms of the ARI score (Fig. 4a). It is worth noting that the clustering result proposed by HAST is more refined compared to the manual annotation. In particular, for the “Healthy_1” region, HAST divided it into Cluster 4 and Cluster 16. Analysis of differentially expressed genes (DEGs) (Fig. 4b) showed that DEGs in cluster 4 included DCN, VIM, and COL1A2, and these genes tended to play a role in cancer-associated fibroblasts (CAFs)^30,31,32. In contrast, these genes were not in DEGs of cluster 16 (Fig. 4b and Supplementary Fig. S14a). In addition, CAF marker genes (TIMP1, COL1A2, DCN) were upregulated in Cluster 4 (log2FC  > 0.5, p-value  < 0.05) (Fig. 4c), but were not up-regulated in Cluster 16 (Supplementary Fig. S14b). We also observed that GraphST also detected a cancer-related region, which is larger than Cluster 4 of HAST. While CAF marker genes are also more highly expressed in the GraphST-identified domain compared to other regions, the expression enrichment is less than that observed in HAST. Specifically, COL1A2 exhibits an expression level of 0 in Cluster 4 of GraphST, whereas it is absent in Cluster 4 of HAST. Similarly, the number of TIMP1 and DCN expressed at low levels in Cluster 4 of GraphST also exceeds that in Cluster 4 of HAST (Fig. 4c). This suggests that HAST achieved a more refined domain identification.

Fig. 4: Results on the human breast cancer dataset.

a H& E image of the human breast cancer dataset, manual annotation, and clustering results of HAST and baseline methods on this slice measured by ARI and FMI. Colors are independently assigned for each method. b Differential gene expression (DGE) analysis of Cluster 4 vs. other clusters (left) and Cluster 16 vs. other clusters (right). Each point represents a gene, with the vertical axis indicating -log10 of the p-value and the horizontal axis representing the log2FoldChange (log2FC). P-values were from the two-sided Wilcoxon rank-sum test. Significance thresholds were set at ∣log2FC∣ > 0.5 and p-value  < 0.05. c Violin plots of CAF marker genes (TIMP1, COL1A2, DCN) in Cluster 4 vs. other clusters. The vertical axis represents gene expression levels. Each violin indicates the expression distribution of a specific gene, and the width indicates the frequency. The central white line represents the median, the thick black bar within each violin is the interquartile spacing, and the whisker line extends from the 25th and 75th percentiles to 1.5 × interquartile range. d GO analysis of Cluster 4 vs. other clusters. The vertical axis represents GO terms, while the horizontal axis represents -log10 of the p-value. GO enrichment analysis was conducted using a one-sided hypergeometric test, with p-values adjusted for multiple comparisons using the Benjamini-Hochberg method.

To further confirm that Cluster 4 corresponded to the cancerous region, we conducted gene ontology (GO) enrichment analysis (Fig. 4d). Compared to other clusters, DEGs in Cluster 4 were significantly enriched in molecular functions such as transforming growth factor beta (TGF-β) binding, cellular components such as collagen-containing extracellular matrix, and biological processes such as extracellular matrix organization (adjusted p-value  < 0.05). These GO terms suggest that Cluster 4 exhibits key cancer-related biological features^33,34,35, including extracellular matrix remodeling, active cancer signaling pathways, platelet involvement in tumor progression, and enhanced protein synthesis, further supporting its strong association with the characteristics of breast cancer tissue. In conclusion, by multimodal integration of HAST, we identified that Cluster 4 corresponds to a tumor microenvironment densely populated by CAFs, revealing the molecular characteristics of CAF-enriched regions.

Performance on the HER2+ dataset, the zebrafish melanoma dataset, and the Visium HD dataset

The HER2+ dataset also consists of breast cancer tissue slices, albeit much smaller in size. We evaluated the clustering performance of HAST, SpaGCN, SpaceFlow, conST, and GraphST on eight slices with manual annotations (Fig. 5a and Supplementary Figs. S15 and S16). HAST outperformed other baseline methods across all slices. Specifically, for the two slices in Fig. 5a, HAST achieved ARI scores of 0.25 and 0.18, significantly surpassing GraphST, which recorded scores of 0.1 and 0.05, respectively. Notably, the number of clusters in the second slice was smaller for both HAST and GraphST than for manual annotations. This discrepancy is attributed to both methods performing refinement steps, as detailed in “Representation refinement” which merge smaller clusters with others. Biologically, the merged clusters did not exhibit strong separation in gene expression or morphology, suggesting the merging is reasonable. Users can also disable this step if they prefer to retain all small clusters for downstream analysis.

Fig. 5: Performance on the HER2+ dataset and analysis of the zebrafish melanoma dataset.

a Two groups of H& E images in the HER2+ dataset, manual annotation, and clustering results of HAST and GraphST measured by ARI and FMI. The remaining results of other baseline methods and slices are shown in Supplementary Figs. S15 and S16. b H& E image, annotation of zebrafish melanoma on slices A and B from Hunter et al.², clustering results of HAST on slices A and B with SC and DB, and corresponding UMAP visualizations. Baseline methods results are shown in Supplementary Fig. S17. c DGE analysis of the interface domain versus other domains on slice A (up) and B (down). Each point represents a gene, with the vertical axis denoting the -log10 of the p-value and the horizontal axis denoting the log2FC. P-values were from the two-sided Wilcoxon rank-sum test. Significance thresholds were set at ∣log2FC∣ > 0.25 and p-value  < 0.05. d GO analysis for the identified interface domain versus other domains on slices A (left) and B (right). The vertical axis represents GO terms, while the horizontal axis represents -log10 of the p-value. GO enrichment analysis was conducted using a one-sided hypergeometric test, with p-values adjusted for multiple comparisons using the Benjamini-Hochberg method. e Clustering results of HAST and GraphST measured by ARI and FMI on one patch of a Visium HD data. The remaining results of other baseline methods and slices are shown in Supplementary Fig. S18.

In the zebrafish melanoma dataset, we analyzed tissue slices A and B. Hunter et al.² used scRNA-seq data to classify interface clusters into muscle-like and tumor-like subclusters. However, independent analysis of ST data proved insufficient to accurately identify clusters, especially in smaller regions where scRNA data were not integrated. In slices A and B, the domain identification results from HAST closely matched the annotations provided by Hunter et al. (Fig. 5b). In the UMAP visualization, Cluster 7 in slice A and Cluster 14 in slice B serve as interfaces, connecting the two primary regions of muscle and cancer. In contrast, other baseline methods, although capable of recognizing the cancer-muscle interface, exhibited reduced accuracy (Supplementary Fig. S17). For instance, in Slice A, STAGATE identified larger interface regions, while SpaceFlow mistakenly included normal muscle tissue within the interface cluster boundaries. In slice B, GraphST barely recognized the interface region correctly. Additionally, DEGs identified by HAST included genes such as zgc:158463, si:dkey-153m14.1, RPL41, and hspb9 (Fig. 5c). These DEGs reflect the reciprocal regulation between muscle tissue and cancer cells. GO enrichment analysis of the interface between slices A and B revealed enrichment in pathways related to translation, cytoplasmic translation, and ribosome assembly (Fig. 5d). These results underscore the active transcription and translation processes occurring at the interface, further supporting previous findings.

To assess the scalability and effectiveness of HAST under high spatial resolution, we further evaluated it on the Visium HD dataset. Due to the ultra-high resolution of this dataset, we divided the tissue into multiple patches and selected representative ones (20,000 cells per patch) for benchmarking to ensure GPU memory feasibility across baseline methods. Among these, the performance of HAST and GraphST on two representative patches is shown in Fig. 5e, where HAST demonstrates finer spatial boundary delineation and more coherent domain structures. Quantitatively, HAST outperforms GraphST and other baselines in both ARI and FMI. Additional comparison results involving SpaGCN, STAGATE, SpaceFlow, conST, KASUMI, and cellcharter, as well as evaluations on other Visium HD patches, are provided in Supplementary Fig. S18. These findings suggest that HAST remains robust and effective under high-resolution settings, highlighting its potential for fine-grained spatial analysis across different spatial transcriptomics technologies.

The ablation studies of HAST

To verify the contribution of the different parts of the HAST, we conducted ablation experiments on the loss function and network architecture separately. Supplementary Fig. S19a and S20a present the clustering results on the four datasets when varying the loss function, with w/o indicating the exclusion of the specific loss function. The removal of both contrastive losses resulted in an average ARI score reduction of 20.3% across four datasets. When the individual losses, ${{{{\mathcal{L}}}}}_{{{{\rm{SCL}}}}}$ and ${{{{\mathcal{L}}}}}_{{\mbox{C}}{\mbox{\_}}{\mbox{SCL}}}$, were added, the average ARI scores improved by 3.8% and 6.9%, respectively. The best performance was achieved when both contrastive losses were incorporated. This indicated that contrastive losses improved the quality of representations by pulling similar vertices closer together and pushing dissimilar vertices further apart.

Supplementary Fig. S19b and S20b evaluated the role of various modules within the network structure. Firstly, we only used a spatial correlation GCN ${{{{\mathcal{G}}}}}^{SC}$ as the encoder. When replacing it with the spatial correlation HGCN ${{{{\mathcal{H}}}}}^{SC}$, the average ARI score improved by 4.3%. Besides, as different HGCN modules were progressively incorporated, the average ARI scores improved by 2.5%, 5.7%, and 4.4%. This improvement could be attributed to the local-global hypergraph encoder, which defined higher-order relationships across multiple views, enabling richer feature interactions. By extending spot relationships from simple first-order adjacencies to more complex contextual dependencies, the model effectively captured a broader spectrum of topological relationships. Supplementary Fig. S19c and S20c further illustrated the performance of using a single modality to construct a graph or hypergraph. It can be seen that HGCN consistently outperforms GCN. In addition, among the three modalities, graph or hypergraph construction using histological features and gene correlation is superior to that using spatial locations.

We then tested HAST with varying numbers of HVGs on the DLPFC dataset and observed that the performance remains stable, with changes in ARI and NMI within  ± 5%, as shown in Supplementary Fig. S21. This suggests that HAST is robust to moderate variations in HVG selection. We finally selected 3000 HVGs as a default based on empirical evaluation across datasets, balancing expression diversity and computational efficiency.

In HAST, we applied ViT-B/32, pre-trained on ImageNet-1K, as the default morphological encoder. No fine-tuning was performed. To evaluate robustness, we further tested Prov-GigaPath³⁶, a large foundation model pre-trained on whole-slide histopathology images, and ResNet-50³⁷, a classical CNN-based encoder loaded with ImageNet-pretrained weights. Performance across these encoders on the DLPFC dataset is provided in Supplementary Fig. S23. The results demonstrate that HAST performs best when using ViT-B/32 as the image encoder, validating it as an effective and efficient morphological feature extractor.

Finally, we conducted ablation experiments on the choice of hyperparameters in HAST. These include radius r in the post-clustering spatial smoothing, neighbor k in hypergraph construction, and the parameters λ₁ and λ₂ for balancing reconstruction loss and contrastive loss. Related experimental results are shown in the Supplementary Fig. 23. For radius r, HAST achieves optimal performance with r = 40 for DLPFC, mouse brain tissue, human breast cancer, and r = 20 for HER2+, balancing noise smoothing and functional boundary preservation. For the number of neighbors, k = 3 yields the best trade-off between accuracy and stability across datasets. λ₁ and λ₂ are set to 10 and 1 to avoid contrastive loss dominating the training process.

Discussion

Spatial transcriptomic domain identification plays a pivotal role in deciphering tissue architecture and cellular interactions. While existing graph-based methods have advanced the integration of gene expression and spatial coordinates, their reliance on single-view pairwise graphs limits their ability to capture the intricate many-to-many relationships inherent in complex tissues, such as tumor microenvironments, where distinct spatial domains may share similar gene expression profiles but differ in histological structure or spatial organization. In this study, we proposed HAST, a multi-view hypergraph framework that integrates gene expression, spatial location, and histology images to model higher-order interactions and refine representations through self-supervised contrastive learning. Comprehensive experiments demonstrate that HAST outperforms state-of-the-art methods across diverse datasets and provides biologically interpretable insights into spatial domains.

Unlike conventional graph-based models that rely on predefined pairwise relationships, HAST dynamically aggregates three complementary hypergraphs-gene correlation, morphological similarity, and spatial neighborhoods-to capture both local and global structural dependencies. The adaptive weighting mechanism helps mitigate the impact of low-quality or noisy modalities by dynamically adjusting the contribution of each feature view, improving robustness in cases where specific modalities may provide less informative signals. The integration of self-supervised contrastive learning further enhances discriminative power. By perturbing gene expression features while preserving hypergraph topology, HAST learns invariant representations that align neighboring spots and separate dissimilar regions^38,39. This strategy mitigates overfitting and improves generalization. For instance, in the DLPFC dataset, HAST achieved sharp domain boundaries that closely matched manual annotations, while methods like SpaGCN and GraphST exhibited spatial dispersion or oversmoothing. In conclusion, the performance advantage of HAST over prior methods can be attributed to two key innovations. First, the hypergraph fusion framework enables richer relational modeling by capturing higher-order and cross-view associations, rather than relying solely on pairwise spot relationships. Second, the inclusion of the morphological view brings in spatial tissue structure information derived from H&E images, which complements the gene and spatial views with histological features. Our ablation studies confirm that both components are essential, and their integration leads to significant performance improvements.

In practical scenarios involving multiple slices from the same tissue type, HAST can be flexibly applied either slice-by-slice or in an integrated fashion. For instance, in the mouse brain dataset, HAST is trained across concatenated slices, allowing it to uncover shared and distinct spatial structures. This joint modeling benefits from the shared biological context while preserving unique slice-level heterogeneity.

HAST’s ability to resolve fine-grained spatial domains has significant implications for understanding tissue heterogeneity. In the human breast cancer dataset, HAST identified a CAF-enriched subcluster within the “Healthy_1” region, validated by upregulated markers (DCN, COL1A2) and GO terms related to extracellular matrix remodeling^30,32. Such precision is critical for delineating tumor-stroma interfaces and identifying therapeutic targets³⁵. Similarly, in zebrafish melanoma, HAST uncovered interface regions with active transcriptional activity, marked by ribosome-related genes (RPL41, hspb9), suggesting a transitional zone between tumor and muscle tissues^2,32. These findings underscore the capacity of HAST to reveal spatially resolved molecular mechanisms that are often obscured in conventional analyses.

HAST could be further improved in the following aspects: First, the computational complexity of HAST increases with hypergraph size, posing challenges for large-scale datasets. Future work could explore mini-batch training or graph sparsification to enhance scalability. Second, the current implementation relies on predefined hyperparameters, which may require optimization for tissues with varying spatial resolutions. Automating hyperparameter selection via meta-learning or Bayesian optimization could improve adaptability. Third, HAST can be extended to integrate multi-omics data (e.g., proteomics, epigenetics) or single-cell RNA-seq references, enabling joint analysis of cellular states and spatial contexts. Furthermore, our current framework operates on 2D slices independently, extending HAST to analyze aligned serial tissue sections for 3D spatial domain identification represents a compelling future direction. This will require datasets with accurate inter-slice registration or inherently 3D transcriptomic measurements, which are emerging with platforms such as Stereo-seq and 3D Slide-seq.

Methods

Data description

Five publicly available ST datasets and histological images obtained from different platforms are employed (Supplementary Table S1). The first is the DLPFC Dataset, which comprises twelve slices from three individuals, acquired using the 10 × Visium platform²². Each individual contributes four slices, sampled at 10 μm and 300 μm intervals, with section sizes ranging from 3460 to 4789 spots, capturing 33,538 genes. Each section is manually annotated, containing five to seven distinct regions. The second dataset is the mouse brain tissue from the 10 × Genomics Data Repository. This dataset consists of two sections with 2695 and 3355 spots. Fifty-two manually labeled regions from the Allen brain atlas²⁷ are used as references. The third is the human breast cancer sample sourced from the 10 × Genomics Data Repository, which contains 3798 spots and 36,601 genes, with 20 manually annotated regions. The fourth dataset of the HER2+⁴⁰ breast tumor includes 36 tissue sections from eight patients. Eight annotated sections manually labeled by pathologists are used in this study. The last is the zebrafish melanoma dataset² retrieved from the NCBI GEO database. Two tissue sections with 2179 and 2677 spots are selected and analyzed.

Data preprocessing

For spatial clustering, HAST incorporates gene expression counts, spatial location data, and histological images. The top 3000 highly variable genes (HVGs) are first selected. Gene expression counts are subsequently normalized by library size and log-transformed using the SCANPY package⁴¹. The normalized gene expression counts are finally standardized to zero mean and unit variance as input for the HAST model. For image data, HAST extracts coordinate-centered sub-images of size 224 × 224 based on spatial location coordinates. The spatial resolution of the original H&E images is determined by the imaging platform of each dataset. For datasets based on the 10x Visium platform, the resolution is approximately 0.253 μm per pixel. Each extracted sub-image thus corresponds to an area of approximately 57 μm  × 57 μm.”, which is basically comparable to the size of a spot. These sub-images are normalized and finally encoded into feature vectors.

For datasets involving multiple tissue slices, HAST supports both slice-wise processing and cross-slice integration. When spatial alignment is feasible, we merge the spot-level data across slices and apply joint training and clustering, as demonstrated in the mouse brain dataset. Otherwise, HAST is applied to each slice independently.

Hypergraph construction

HAST first constructs hypergraphs to learn latent representations from three perspectives: gene correlations, morphological similarities, and spatial neighborhoods.

Gene correlation matrix. Gene expression correlation of cells helps improve clustering accuracy by revealing biological similarities and potential functional links between cells. In addition, it helps reduce noise interference and supports further analysis of cellular functions. For the gene expression correlation weight GC_ij, we calculate it through the gene expression vectors g_i and g_j from spots s_i and s_j by

$$GC\left({s}_{i},{s}_{j}\right)=G{C}_{ij}=\frac{\left({g}_{i}-\overline{{g}_{i}}\right)\cdot \left({g}_{j}-\overline{{g}_{j}}\right)}{{\big\Vert {g}_{i}-\overline{{g}_{i}}\big\Vert }_{2}{\big\Vert {g}_{j}-\overline{{g}_{j}}\big\Vert }_{2}},$$

(1)

where $\overline{{g}_{i}}$ and $\overline{{g}_{j}}$ are the mean value of g_i and g_j, which come from the gene expression matrix X.

Morphological similarity matrix. Morphological information reveals spatial relationships between cells and microenvironmental features by providing insights into the morphological structure of cells. Combining morphological information can better distinguish cells with similar functions but different spatial locations, and assist in identifying tissue structures and cellular states. To utilize this information, we extract a 224 × 224 pixel image patch centered at each spot’s spatial coordinate from the histology image. These sub-images are then fed into a pre-trained Vision Transformer⁴², which serves as the image encoder to generate spot-wise morphological feature vectors. The morphological similarity weight MS_ij between s_i and s_j is calculated by cosine similarity and defined as

$$MS\left({s}_{i},{s}_{j}\right)=M{S}_{ij}=\frac{{m}_{i}\cdot {m}_{j}}{{\big\Vert {m}_{i}\big\Vert }_{2}{\big\Vert {m}_{j}\big\Vert}_{2}},$$

(2)

where m_i and m_j represent the morphological features for spots s_i and s_j.

Spatial correlation matrix. For spatial location information, we calculate the Euclidean distance between spots to quantify the effect of spatial information on determining similar cell states. The spatial correlation weight SC_ij is represented as

$$SC\left({s}_{i},{s}_{j}\right)=S{C}_{ij}=\sqrt{{\left({x}_{i}-{x}_{j}\right)}^{2}+{\left({y}_{i}-{y}_{j}\right)}^{2}},$$

(3)

where (x_i, y_i) and (x_j, y_j) are coordinates of spots s_i and s_j.

After completing the matrix computations, we construct three hypergraphs based on the gene correlation matrix GC, morphological similarity matrix MS, and spatial correlation matrix SC. For each spot, we define a neighbor set within each matrix and select the k most similar neighbors. Specifically, for GC and MS, we choose the k neighbors with the highest correlation. For SC, k neighbors with the smallest spatial distance are selected.

With the neighbor set ${{{{\mathcal{N}}}}}^{GC}$, ${{{{\mathcal{N}}}}}^{MS}$, and ${{{{\mathcal{N}}}}}^{SC}$, we define each vertex i and its set of neighbors as a hyperedge e_i. The hypergraphs ${{{{\mathcal{H}}}}}^{GC}$, ${{{{\mathcal{H}}}}}^{MS}$, and ${{{{\mathcal{H}}}}}^{SC}$ are then constructed for the three matrices, respectively. Each hypergraph ${{{\mathcal{H}}}}$ can be represented as a set ${{{\mathcal{V}}}}$ of vertices and a set ${{{\mathcal{E}}}}$ of hyperedges: ${{{\mathcal{H}}}}=\{{{{\mathcal{V}}}},{{{\mathcal{E}}}}\}$, ${{{\mathcal{E}}}}=\{{e}_{i}| {e}_{i}=\{i,{{{{\mathcal{N}}}}}_{i}\}\}$.

HGCN for representation learning

In this step, the top 3000 highly variable genes are selected. Then, we log-transform the original gene expression matrix and normalize it⁴¹. For subsequent contrastive learning, we generate corrupted hypergraphs by data augmentation. Specifically, given a hypergraph ${{{\mathcal{H}}}}$ and a normalized gene expression matrix X, the corrupted hypergraph is created by randomly shuffling the gene expression vectors between vertices while maintaining the topology of the original hypergraph. The corrupted hypergraph and shuffled gene expression matrix are denoted as ${{{{\mathcal{H}}}}}^{{\prime} }$ and ${X}^{{\prime} }$.

HGCN-based encoder. To extract the spot latent representation from the gene expression matrix, we design an HGCN-based encoder. The HGCN can effectively capture the higher-order correlations between vertices in the hypergraph ${{{\mathcal{H}}}}$, making it well-suited for handling complex neighboring structures. Specifically, the encoder takes the hypergraph ${{{\mathcal{H}}}}$ and the expression matrix X as input and utilizes the HGCN to learn the latent representation z_i of spot i. In HGCN, the structure of the hypergraph is represented by the adjacency matrix H ∈ R^N×M, where N denotes the number of spots, and M represents the number of hyperedges. Vertex features are aggregated and propagated through hyperedges. Formally, for the layer l, the vertex representation is updated as

$${X}^{(l+1)}=\sigma \left({D}_{v}^{-1/2}HW{D}_{e}^{-1}{H}^{\top }{D}_{v}^{-1/2}{X}^{(l)}{\Theta }^{(l)}\right),$$

(4)

where X^(l+1) is the output of the l-th layer and σ is the ReLU function for nonlinear activation. D_v ∈ R^N×N is the vertex degree matrix, D_e ∈ R^M×M is the hyperedge degree matrix. W ∈ R^M×M is the weight matrix of the hyperedge, and Θ is the learnable parameter matrix that maps the input features to the latent representation space.

Adaptive weighted hypergraph fusion. Different views provide complementary information, making the fusion of the three hypergraphs into a more informative and robust global hypergraph beneficial for the clustering task. However, due to the noise and the incompleteness of the original features, some views may not correctly reflect the actual topology between vertices. Therefore, we adaptively assign weights to each hypergraph during hypergraph fusion, ensuring a more reliable structure representation. Specifically, we minimize the sum of the squared differences of the weighted Frobenius paradigms between H_f and all H^v by adjusting H_f:

$${H}_{f}={\min }_{{H}_{f}}{\sum }_{v}^{V}{w}_{v}\parallel {H}_{f}-{H}^{v}{\parallel }_{F}^{2},$$

(5)

where V = [GC, MS, SC], and w_v is the weight or each view. According to⁴³, we compute the w_v using the inverse distance of fusion adjacency matrix H_f and each latent adjacency matrix H^v, which is expressed as

$${w}_{v}=\frac{1}{\parallel {H}_{f}-{H}^{v}{\parallel }_{F}}.$$

(6)

Based on the obtained weights, the fusion adjacency matrix H_f is updated in each forward pass by

$${H}_{f}=\frac{{\sum }_{v}{w}_{v}{H}^{v}}{{\sum }_{v}{w}_{v}}.$$

(7)

At the start of training, latent hypergraphs from different views are assigned equal weights. As training progresses, these weights are adaptively updated based on the differences between the matrices, ensuring that high-quality local hypergraphs, those closely aligned with the fusion hypergraph, receive higher weights. Simultaneously, less reliable hypergraphs are assigned smaller weights, effectively mitigating the negative impact of noise.

With the fusion adjacency matrix H_f, we sum the outputs of the three HGCNs to obtain the global features. An additional HGCN is then applied as the final layer of the encoder to derive the original representation Z. Similarly, for the corrupted gene expression matrix ${X}^{{\prime} }$, the same process is used to obtain the corrupted original representation ${Z}^{{\prime} }$. The representation Z is then fed into a decoder composed of two linear layers to reconstruct it into the original gene expression space. Specifically, the decoding process is defined as

$$\hat{X}=(ReLU(Z{W}_{1}+{b}_{1})){W}_{2}+{b}_{2},$$

(8)

where $\hat{X}$ is the reconstructed gene expression matrix. W_1,2 and b_1,2 are the weights and biases for linear transformations. To fully leverage the gene expression matrix, we train the model by minimizing the self-reconstruction loss ${{{{\mathcal{L}}}}}_{{{{\rm{rec}}}}}$ of the gene expression data, which is defined as

$${{{{\mathcal{L}}}}}_{{{{\rm{rec}}}}}={\left\Vert X-\hat{X}\right\Vert }_{F}^{2}.$$

(9)

Representation refinement

To further enhance the robustness and discriminative ability of the feature representation, we employ a self-supervised contrastive learning strategy for the latent space representation after encoding. Specifically, for a vertex in the hypergraph, the representation vectors of its neighbors constitute the local context of the vertex. The representation vector of the vertex itself, along with its local context, forms a positive pair, while its representation vector and the local context from the corrupted hypergraph form a negative pair. Through self-supervised contrastive learning, we maximize the mutual information of positive pairs while minimizing the mutual information of negative pairs. This approach ensures that neighboring vertices in the hypergraph topology are encouraged to have similar representations, whereas disjoint or unrelated vertices are assigned dissimilar representations. The contrastive loss ${{{{\mathcal{L}}}}}_{{{{\rm{SCL}}}}}$ can be defined as

$${{{{\mathcal{L}}}}}_{{{{\rm{SCL}}}}} = - \frac{1}{2N}\left( {\sum }_{i=1}^{N} {{\mathbb{E}}}_{(X,H)}\left[\log \Phi \left({z}_{i},{g}_{i}\right)\right] \\ +{{\mathbb{E}}}_{({X}^{{\prime} },{H}^{{\prime} })}\left[\log \left(1-\Phi \left({z}_{i}^{{\prime} },{g}_{i}\right)\right)\right]\right),$$

(10)

where z_i is the representation of vertex i, and g_i denotes its local context vector. ${z}_{i}^{{\prime} }$ is the corresponding representation from the corrupted hypergraph. The discriminator Φ is a learnable neural network, which is defined as Φ(h, c) = c^⊤Wh + b, where c is the embedding of the context (e.g., original spot), h is the embedding of either a positive or negative sample, and W is a learnable weight. The output logits are used to classify positive and negative pairs in the contrastive loss. To ensure stability and balance in the model, we introduce a symmetric contrastive loss ${{{{\mathcal{L}}}}}_{{\mbox{C}}{\mbox{\_}}{\mbox{SCL}}}$ for the corrupted hypergraph, leveraging the fact that its topology remains identical to the original hypergraph. This loss function is designed to maintain consistency and enhance the model’s robustness, which is formalized as

$$\begin{array}{l}{{{{\mathcal{L}}}}}_{{\mbox{C}}{\mbox{\_}}{\mbox{SCL}}}=-\,\dfrac{1}{2N}\left({\sum }_{i=1}^{N}{{\mathbb{E}}}_{({X}^{{\prime} },{H}^{{\prime} })}\left[\log \Phi \left({z}_{i}^{{\prime} },{g}_{i}^{{\prime} }\right)\right]\right.\\ \qquad\qquad\, \left.+{{\mathbb{E}}}_{(X,H)}\left[\log \left(1-\Phi \left({z}_{i},{g}_{i}^{{\prime} }\right)\right)\right]\right),\end{array}$$

(11)

where ${g}_{i}^{{\prime} }$ is the local context vector of vertex i from the corrupted hypergraph. In summary, the representation learning of HAST is optimized by minimizing both the reconstruction loss and the contrastive loss, with the overall training loss defined as

$${{{\mathcal{L}}}}={\lambda }_{1}{{{{\mathcal{L}}}}}_{{{{\rm{rec}}}}}+{\lambda }_{2}\left({{{{\mathcal{L}}}}}_{{{{\rm{SCL}}}}}+{{{{\mathcal{L}}}}}_{{\mbox{C}}{\mbox{\_}}{\mbox{SCL}}}\right),$$

(12)

where λ₁ and λ₂ are weighting coefficients used to balance the effects of the reconstruction loss and the contrastive loss. The reconstruction loss preserves fine-grained gene expression patterns, while the contrastive loss improves cluster separability. Together, they enable the model to learn embeddings that are both biologically consistent and structurally discriminative.

After completing the training, we cluster the spots into different spatial domains using the reconstructed spatial gene expression matrix $\hat{X}$ generated by the decoder, combined with the non-spatial clustering algorithm mclust⁴⁴. For datasets with ground-truth annotations (e.g., DLPFC), we directly set the number of clusters to match the number of manually annotated domains. For datasets without annotations (e.g., mouse brain posterior, zebrafish melanoma), we adopt the same number of clusters as used in related works^2,10 to ensure a fair comparison.

To mitigate noise in the clustering results that could impact downstream biological analyses, we perform an additional optimization step. Specifically, for each spot, the spots located within a predefined radius r are considered its neighbors. HAST then reassigns the spot to the domain that corresponds to the most common label among its neighboring spots. This optional post-processing step is intended to smooth noisy assignments and improve spatial coherence, especially for isolated or borderline spots. While it helps reduce spurious small clusters, users should be aware that it may also merge small but potentially meaningful clusters. This step can be disabled if fine-grained cluster preservation is desired.

Implementation details

For all datasets utilized in the experiments, we employ ViT-B/32, pre-trained on ImageNet-1K, to extract morphological features, with the size of sub-images set to 224 × 224. In HAST, the number of nearest neighbors k for hypergraph construction is set to 3. The hyperparameters of the loss function, λ₁ and λ₂, are assigned values of 10 and 1. The Adam optimizer is used for optimization, with a learning rate of 0.001 and 600 training epochs. For the compared methods, we use the source code and the suggested parameter settings provided by the authors. All training is conducted on a single NVIDIA 4090 GPU.

Baseline methods

To demonstrate the effectiveness of HAST for spatial clustering, we compare HAST with ten state-of-the-art methods: Seurat⁸, Giotto⁴⁵, Kasumi¹⁶, cellcharter¹⁴, SpaGCN⁹, SpaceFlow¹¹, BayesSpace⁴⁶, conST⁴⁷, STAGATE¹², and GraphST¹⁰. Three metrics, the Adjusted Rand Index (ARI), Fowlkes-Mallows Index (FMI), and Normalized Mutual Information (NMI), are used for evaluating the difference between the clustering results and the manual annotations. Two metrics, the Silhouette Coefficient (SC) and Davies-Bouldin index (DB), are used for evaluating the clustering results without manual annotations.

Statistics and reproducibility

This study utilized publicly available datasets. Sample sizes were not predetermined using statistical methods; instead, we adopted the sample sizes reported in previous studies. Following a comprehensive quality assessment, all data were included in the analysis. It should be noted that the experiments were not randomized.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.