Introduction

Locality is a fundamental concept in modern physics, implying that the Hamiltonian consists of a sum of terms with local interactions1,2,3,4. However, describing many-body systems in terms of local interactions is often an approximation and not always a reliable one5. Long-range (LR) power-law interactions (1/rα) are typical non-local interactions that are both of fundamental and practical importance, appearing ubiquitously in nature and in numerous experimental systems of current interest, such as trapped-ion6,7, nitrogen-vacancy centers8,9, and programmable Rydberg atom arrays10,11. On the theoretical side, LR interactions are widespread and lead to qualitatively different physics, including modifications to the Mermin-Wagner12,13 and Lieb-Schultz-Mattis theorems14,15, the breakdown of the entanglement area law for gapped phases or the conformal symmetry at criticality16,17,18,19, modifications to the Lieb-Robinson bounds20,21, as well as modifying the critical behavior at phase transitions22,23,24,25,26,27,28,29.

On a different front, symmetry-protected topological (SPT) phases, as a typical class of quantum matter beyond the Landau-Ginzburg paradigm, have attracted much attention in the past few decades30,31,32,33,34. Although the bulk energy gap plays a crucial role in defining SPT phases, recent progress35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64 has revealed that many key features of topological properties persist even with non-trivial couplings between the boundary and the gapless bulk. This extension is termed gapless topological phases41,44,46,48, which exhibit non-trivial gapless topological behaviors, including algebraically localized edge modes48, non-trivial conformal boundary conditions52,53, and universal bulk-boundary correspondence in the entanglement spectrum54.

From an experimental point of view, it is inevitable to consider the influence of LR interactions when implementing non-trivial topological phases in state-of-the-art quantum simulators. To date, various studies65,66,67,68,69 have demonstrated qualitative changes of physical properties under LR interactions in gapped non-interacting topological phases, including the emergence of massive edge modes16,17,70 and bulk-boundary correspondence71,72. However, it is not immediately clear whether LR interactions can have a significant impact on gapless topological phases. This is because the gapless bulk is usually sensitive to LR interactions, while topological properties often remain robust against them. Therefore, it is valuable to address the following intriguing questions: how does the gapless topological phase respond to LR interactions, and do LR interactions induce quantum phases with non-trivial gapless topological behaviors unreported before?

To conclusively address the aforementioned issues, in this work, we focus on investigating the simplest type of gapless topological phase—the symmetry-enriched Ising quantum critical point (QCP). We concentrate on a one-dimensional (1D) cluster Ising model featuring LR antiferromagnetic (AFM) interactions, which is amenable to powerful density matrix renormalization group (DMRG) simulations73,74,75,76,77. We conduct comprehensive simulations to investigate the ground-state phase diagram as a function of the cluster interaction strength λ and the LR power exponent α. For large values of α, the ground state manifests as an AFM (cluster SPT) phase for λ below (above) a critical value λc, separating a symmetry-enriched Ising QCP48. Conversely, for small α < αc ~ 1.0, the cluster SPT phase gradually crossovers to a different SPT phase characterized by algebraic correlations and edge modes, unique to the LR interacting system. Meanwhile, the symmetry-enriched Ising QCP is extended into a critical line with non-trivial topology for α < αc.

Results and discussion

The model

We consider the following LR interacting Hamiltonian for spins on a lattice of length L (see Fig. 1a)

$${H}_{{{{\rm{LRCI}}}}}={\sum}_{i < j}\frac{(1-\lambda )}{{d}_{ij}^{\alpha }}{\sigma }_{i}^{z}{\sigma }_{j}^{z}+\lambda {\sum}_{j}{\sigma }_{j-1}^{z}{\sigma }_{j}^{x}{\sigma }_{j+1}^{z}\,,$$
(1)

where \({{{{\boldsymbol{\sigma }}}}}_{i}^{x,y,z}\) represents the Pauli matrix on site i. The parameter α is the power exponent of the LR interaction, and dij is the distance between sites i and j, which is ∣i − j∣ and \(\min (| i-j| ,L-| i-j| )\) for open (OBC) and periodic (PBC) boundary conditions, respectively. Here, OBC refers a “natural” open boundary which excludes the interaction terms crossing over the bond (L, 1). This model respects a global \({{\mathbb{Z}}}_{2}\times {{\mathbb{Z}}}_{2}^{T}\) symmetry generated by \(P=\mathop{\prod }_{i = 1}^{L}{\sigma }_{i}^{x}\) and \(T={{{\mathcal{K}}}}\) (the complex conjugate). It is noted that the LR AFM interaction terms compete with each other and the ground-state energy is still an extensive quantity linear with L, therefore, the implementation of a Kac rescaling is not necessary and the system is thermodynamically stable in our case (see Supplementary Note 1). Notably, for α → ∞, Eq. (1) reduces to the nearest neighbor short-range (SR) cluster Ising model (black square in Fig. 1b), which can be exactly solved via the Jordan-Wigner transformation78,79,80,81,82, and can be realized in triangular optical lattices in ultracold atom systems83,84. The parameter λ governs the competition between the Ising and cluster interactions, driving the system toward different phases, including AFM and cluster SPT phases78. The phase transition between them belongs to the symmetry-enriched Ising universality class, featuring unconventional algebraically localized edge modes with two-fold degeneracy44,48,54,55,63, which are absent in gapped topological phases with only SR interactions.

Fig. 1: Model and phase diagram.
figure 1

a A schematic plot of the long-range (LR) cluster Ising spin chain, where the blue dashed line (green-filled ellipsoid) represents the LR antiferromagnetic (AFM) interaction (cluster interaction). Here, λ is the strength of the cluster term, α is the LR exponent, and dij is the distance between two sites. b The global ground-state phase diagram of the Hamiltonian (1) exhibits AFM (the blue region), symmetry-protected topological (SPT) (the yellow region), and algebraic SPT (the pink region) phases, along with the symmetry-enriched Ising universality (c = 1/2, black line) and a topological non-trivial critical line (ceff > 1/2, red line). The blue markers are determined by the peak position of the effective central charge ceff along fixed 1/α lines (here, ceff is the fitted coefficient of the logarithmic entanglement entropy). The black square indicates the exact critical point λ = 0.5 in the short-range limit 1/α → 0. The black dashed line represents a rough crossover boundary between the SPT and algebraic SPT phases. The gray diamonds are determined by the position where ceff is decreased below 0.01 along fixed α lines for α < 1.0. Simulations are performed with the system size L = 96 under periodic boundary conditions (PBC).

Full size image

For general α, Eq. (1) is no longer exactly solvable, and we can only resort to numerical simulations. It is noted that the model is also related to the LR transverse field Ising model through the SPT entangler79. Consequently, the LR cluster Ising model shares the same bulk universality class as the LR transverse field Ising model and, therefore, exhibits the same critical exponents and effective central charge ceff. Specifically, along the critical lines, the critical exponents and ceff change monotonically with varying α for α < αc, while for α > αc, they remain unchanged and consistent with the SR Ising universality class. However, in this work, we employ large-scale DMRG simulations to focus on the boundary topological physics of the LR model, which is entirely different from the LR transverse field Ising model under OBC (see Supplementary Note 1). The details regarding the simulation are introduced in the Methods. We focus on the model for both sufficiently strong and weak LR interactions, exploring the phases and phase transitions arising from the interplay between topology and LR interactions.

Algebraic topological phases

To investigate the effect of LR interactions on quantum phases, we compute the connected spin-spin correlation function and the non-local SPT string correlation function, as defined in Supplementary Note 5. It is important to note that LR interactions do not significantly affect the AFM long-range order for λ < λc, as demonstrated in Supplementary Note 5 and previous works17. Therefore, in this work, we primarily focus on the influence of the LR interaction on the gapped SPT phase and the symmetry-enriched Ising QCP.

In the SR limit 1/α → 0, our numerical results show AFM and cluster SPT phases for λ < 0.5 and λ > 0.5, respectively, in agreement with previous studies55,78,79 (see Supplementary Note 3). In the presence of LR interactions, the simulation also verifies the stability of the gapped SPT phase. Figure 2a, b depict a double logarithmic plot of the connected spin-spin correlation \(\left\vert {C}_{{{{\rm{c}}}}}^{zz}(r)\right\vert\) and string correlation CSPT(r) versus lattice distance r for various α within the gapped SPT region (e.g., λ = 0.55), revealing anomalous behaviors of the correlation functions. Specifically, \(| {C}_{{{{\rm{c}}}}}^{zz}(r)|\) displays a hybrid behavior that is exponential decay at short distances and algebraic decay at long distances and changes to purely algebraic decay at all distances around αc ~ 1.0. Concurrently, as α increases, the power exponent γs of the long-distance decay for \(| {C}_{{{{\rm{c}}}}}^{zz}(r)|\) changes from a constant to a value that depends linearly on α, as shown in Fig. 3a. Additionally, the long-distance behavior of CSPT(r) changes from “long-range order” to purely algebraic decay also around αc ~ 1.0 (see Supplementary Note 5 for more results). These properties are similar to critical states in SR interacting systems. However, as demonstrated in Supplementary Note 4, a finite bulk energy gap Δb within the SPT region persists even for sufficiently small α ≲ αc.

Fig. 2: Evidence for the algebraic topological phase.
figure 2

The double logarithmic plot of a the connected spin-spin correlation \(| {C}_{{{{\rm{c}}}}}^{zz}(r)|\) and b the SPT string correlation CSPT(r) versus the lattice distance r for LR exponents α = 0.3(red cross), 1.8 (orange triangle), 3.0 (blue square) along the fixed cluster strength λ = 0.55 line with system size L = 200 under open boundary condition (OBC). c The entanglement spectrum {ξk} (L = 96 under PBC) and d the magnetization profile \(\left\vert \left\langle {\sigma }_{i}^{z}\right\rangle \right\vert\) (L = 200 under OBC) within the typical algebraic SPT region for α = 0.3 and λ = 0.55. The inset in (d) shows the algebraic decay of the magnetization near the boundary as the bulk is approached; the dashed line is the least-squares fitting according to \(\left\vert \left\langle {\sigma }_{i}^{z}\right\rangle \right\vert \sim 1/{i}^{{\gamma }_{{{{\rm{m}}}}}}\). The index k counts the spectrum from the lowest-lying levels, and i labels the site position. The markers are data from numerical calculations.

Full size image
Fig. 3: Behaviors of correlation exponents and effective central charge.
figure 3

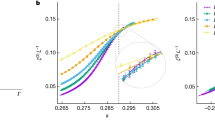
a The algebraic decaying exponent (marked by triangles) of the connected spin-spin correlation, γs, as a function of the LR power α along fixed cluster strength λ = 0.55 and 0.65 lines. b The power-law exponent of the magnetization near the boundary, γm, as a function of α along λ = 0.55 and λ = 0.65 lines (see the inset in Fig. 2d, for example). c The entanglement entropy S(l) as a function of the cord length \(\ln (L/\pi \sin [\pi l/L])\) at the estimated critical points for α = 3.0 (green square) and 0.6 (blue circle), respectively. The dashed lines are least-squares fittings according to Eq. (2); the slope of the fitted line κ is used to define the effective central charge ceff ≡ 3κ. d The effective central charge as a function of the cluster strength λ along fixed α = 3.0 (green square) and 0.6 (blue circle) lines. The critical points are estimated by the peak positions of the effective central charge marked by the vertical dashed lines. The inset investigates the finite-size effect (system sizes L = 64 (gray diamond), 80 (red cross), and 96 (blue circle)) of the effective central charge for α = 0.6, indicating that the algebraic SPT phase is stable in the thermodynamical limit. Simulated system size is L = 96 under PBC for (c), (d). The error bar in (a, b) is the standard deviation in the least-squares fittings.

Full size image

To explicitly demonstrate the robustness of topological features for λ > λc in the presence of LR interactions, we present the bulk entanglement spectrum (as defined in Supplementary Note 3) and the magnetization profile \(\left\langle {\sigma }_{i}^{z}\right\rangle\) for particular values of α. For α → ∞, the ground state corresponds to the gapped SPT phase, as evidenced by the four-fold degeneracy in the bulk entanglement spectrum and the obvious magnetization near the boundaries compared with the system bulk34,41,52,53,54. For finite α, the four-fold degeneracy in the lowest-lying level of the entanglement spectrum and the edge magnetization remains robust against the LR interactions, as depicted in Fig. 2c, d for α = 0.30 and λ = 0.55 as an example. More importantly, the localization form of the edge magnetization (or, in other words, how fast it decays when approaching the bulk) changes from a hybrid behavior to a purely algebraic decay as α decreases below αc ~ 1.0, as shown in the inset of Fig. 2d. It is also noted that the power exponent γm of the long-distance decay for \(\left\vert \left\langle {\sigma }_{i}^{z}\right\rangle \right\vert\) exhibits similar behavior to γs, as seen in Fig. 3b and Supplementary Note 5 and Supplementary Note 6. These numerical observations strongly suggest that, despite having a finite bulk gap, these topological phases exhibit non-trivial gapless topological behaviors akin to symmetry-enriched Ising QCP48,57. Hence we term these phases as algebraic topological phases (the light red region above the black dashed line in Fig. 1b). It is worth emphasizing that the change from the SPT phase to the algebraic SPT phase is not a phase transition but a crossover since the bulk remains gapped throughout. However, within the algebraic SPT region, both the correlation function and topological edge modes display algebraic decay, and more importantly, the entanglement entropy shows logarithmic growth behavior (see Supplementary Note 2 for details). These properties endow the algebraic SPT phase with a critical-like character fundamentally distinct from the conventional SPT phase. In this sense, we identify a different topological phase that arises solely from the LR interaction without any SR counterpart. Furthermore, as seen in the inset of Fig. 3d, the effective central charge remains finite as the system size increases within the algebraic SPT phase, indicating that the critical nature of this phase is stable in the infrared limit, rather than being merely an intermediate energy-scale physics.

Topological non-trivial critical line

Having explored the ground-state phase diagram, we now investigate the quantum phase transition between AFM and SPT phases for typical values of α. To obtain the transition point, we have performed extensive DMRG simulations, which cost millions of computational CPU time, to examine the finite-size scaling of the entanglement entropy. It is well accepted that entanglement entropy can provide a convenient way to extract universal properties of quantum criticality.

In particular, for 1D critical systems described by conformal field theories, the central charge c of the underlying theory can be extracted from the logarithmic scaling of the entanglement entropy via the Calabrese-Cardy formula85,86,87,

$$S(l)=\frac{c}{3}\ln \left[\frac{L}{\pi }\sin \left(\frac{\pi l}{L}\right)\right]+{S}_{0}\,,$$
(2)

where l the interval length, L the total system size, and S0 a non-universal constant. In Fig. 3c, the entanglement entropy is displayed as a function of the cord length \(\ln (L/\pi \sin [\pi l/L])\), respectively, at two critical points, and an explicit logarithmic scaling can be observed there. It is noted that we find the conformal symmetry of the critical point becomes broken around αc ~ 1.0 as α decreases (see Supplementary Note 7 for details). Nevertheless, we can still define an effective central charge by using Eq. (2) for the non-conformal region to characterize the universality class of the LR model88 (see Supplementary Note 2 for details).

To estimate the QCP, we calculate the effective central charge ceff as a function of the cluster strength λ along fixed α lines as exhibited in Fig. 3d. For α = 0.6 < αc, we note that ceff remains finite above λc but decreases to zero as λ increases further, indicating an intermediate region associated with the algebraic SPT phase, which violates the entanglement area law16. Conversely, ceff nearly vanishes below the λc (due to finite-size effects), as the AFM-ordered phase obeys the entanglement area law, even in the presence of strong LR interactions17. It is shown that ceff exhibits a sharp peak as the ground state is driven from the AFM phase into the SPT phase, and the peak position is a faithful estimation of the critical point. We see that the critical point λc of the transition decreases upon decreasing LR power exponent α. Intuitively, as the LR interaction decays more slowly (smaller α), the Ising part of the Hamiltonian becomes more frustrated, and the cluster part will be more favored. In the following, the topological features of the critical line will be studied at the critical points determined from ceff.

As pointed out by Verresen et al.48, the critical point of the SR cluster Ising model exhibits non-trivial topological properties such as algebraically localized edge modes caused by the non-trivial charge of the symmetry-flux operator under the time-reversal symmetry. Therefore, it is natural to examine whether these properties are robust against the LR AFM interaction. Specifically, we confirm the two-fold topological degeneracy in the edge modes by computing the bulk entanglement spectrum at the critical points for α = 3.0 and 0.5, respectively, as shown in Fig. 4a, b. Similarly, Fig. 4c shows that the boundary magnetization at the critical point remains finite, directly proving the existence of critical edge modes even for sufficiently strong LR interactions (e.g., α = 0.5 here). The additional numerical results for other α along the critical line, as shown in Supplementary Note 3, indicate that the entire critical line exhibits topologically protected edge modes. Moreover, we present the results of the critical edge mode splitting versus system size L for typical values along the critical line in Fig. 4d and Supplementary Note 7. The results unambiguously show that these edge modes are stable and consistently maintain algebraic decay behaviors for any finite α, as the finite-size splitting of the edge modes Δe ~ 1/Lb with b > 1 decays parametrically faster than the finite-size bulk gap Δb ~ 1/Lz where z ≤ 1 (see Supplementary Note 7 for details). Consequently, we find that the LR interaction expands the symmetry-enriched Ising QCP into a critical line with non-trivial topology. It is also worth noting that the effective central charge ceff as a function of the LR power exponent α along the critical line, as shown in Supplementary Note 2, starts to increase around αc ~ 1.0, indicating a crossover into a different topological universality class. This is also consistent with the crossover boundary between the SPT and algebraic SPT phases, as depicted in Fig. 1b. Hence, combined with the characteristics of the algebraic SPT phase mentioned above, we find that for both the gapped SPT phase and symmetry-enriched Ising QCP, LR interactions do not close or open the bulk energy gap, but unambiguously exhibit non-trivial gapless topological behaviors, as revealed by algebraically localized topologically protected edge modes and power-law decay correlation functions.

Fig. 4: Evidence for the topological non-trivial critical line.
figure 4

The entanglement spectrum {ξk} (purple circles) at the critical points for LR exponents a α = 3.0 (λc ≈ 0.457) and b α =  0.5 (λc ≈ 0.253). The index k counts the spectrum from the lowest-lying levels; the simulated system size is L = 96 under PBC. c The magnetization profile (green circle) at the critical point for a sufficiently small α = 0.5 with L = 120. d The size scaling of the edge mode splitting Δe ≡ E1 − E0 by including a small boundary perturbation \(0.1({\sigma }_{1}^{x}{\sigma }_{2}^{z}{\sigma }_{3}^{z}+{\sigma }_{L-2}^{z}{\sigma }_{L-1}^{z}{\sigma }_{L}^{x})\) at the critical point for α = 0.5. The blue crosses are obtained from exact diagonalization calculations, and the green circles are numerical data. The red dashed line is the least-squares fitting according to Δe = a/Lb. c, d are simulated under OBC.

Full size image

Discussion

To gain a physical understanding of the numerical results, we first focus on the low-energy theory of the LR model from the perspective of the renormalization group (RG). Under the RG flow, the LR interaction will flow to operators in the infrared continuum field theory and correspond to both a local part SL and a non-local part SH. Depending on α, the non-local part can be irrelevant for large α or relevant for small α5,28 at the criticality. When the non-local part flows to strong coupling, the conformal symmetry will not emerge in the infrared. Away from the criticality, the competition between the local and non-local parts contributes to the hybrid behavior in the correlation function for any finite α, as argued in refs. 69,89. Since the effective central charge is defined via the entanglement entropy, the non-local interaction will create more entanglement between the disjoint regions, leading to an increase in ceff as α decreases89,90.

To understand the stability of the critical edge modes against LR interactions, we consider the open chain with a finite-size L. The local operators \({\sigma }_{1}^{z},{\sigma }_{L}^{z}\) commute with the Hamiltonian, and the four-fold degenerate ground states are given by,

$$\left\vert {\uparrow }_{{{{\rm{L}}}}}{\downarrow }_{{{{\rm{R}}}}}\right\rangle \pm \left\vert {\downarrow }_{{{{\rm{L}}}}}{\uparrow }_{{{{\rm{R}}}}}\right\rangle \,,\quad \left\vert {\uparrow }_{{{{\rm{L}}}}}{\uparrow }_{{{{\rm{R}}}}}\right\rangle \pm \left\vert {\downarrow }_{{{{\rm{L}}}}}{\downarrow }_{{{{\rm{R}}}}}\right\rangle \,,$$
(3)

where L(R) denotes the leftmost (rightmost) site. These four edge modes are robust in the SPT phase with LR interactions for general α. When driving the system to the critical line, regardless of the strength of the LR interaction, the boundary spins generate an effective \({\sigma }_{1}^{z}{\sigma }_{L}^{z}\) coupling due to the existence of bulk critical fluctuations. This coupling changes the edge mode degeneracy from four to two, i.e., \(\left\vert {\uparrow }_{{{{\rm{L}}}}}{\downarrow }_{{{{\rm{R}}}}}\right\rangle \pm \left\vert {\downarrow }_{{{{\rm{L}}}}}{\uparrow }_{{{{\rm{R}}}}}\right\rangle\). In short, the critical line exhibits robust two-fold degenerate edge modes for any finite α.

To understand the non-trivial topology in the algebraic SPT phase, we note that the crossover values for correlation functions and edge magnetization are both around αc ~ 1.0. This implies that when α < αc, the ground state resembles critical states, and the string operator with the slowest algebraic decay can be regarded as a symmetry-flux operator and is charged under the anti-unitary time-reversal symmetry, which enforces the topological-protected edge modes similar to the case of the symmetry-enriched Ising QCP48. Hence, this qualitatively explains the crossover from the gapped SPT to the algebraic SPT phase near αc ~ 1.0.

Conclusions

In summary, we have conducted large-scale numerical simulations to demonstrate the ground-state properties of a spin-1/2 chain with LR interactions, unveiling various exotic phases and phase transitions as a function of the cluster interaction strength λ and the LR power exponent α. For large α > αc ~ 1.0, the phase diagram exhibits the AFM long-range order, the gapped SPT phase, and a symmetry-enriched Ising criticality between them. Conversely, the results for sufficiently small but finite values of α < αc are particularly intriguing. The connected correlation function and topological edge modes gradually change to purely algebraic decay within the gapped SPT region λ > λc, implying the onset of algebraic topological phases featuring non-trivial gapless topological behaviors without any SR counterpart. Moreover, the non-trivial topological properties at the Ising QCP persist for finite α and extend into a different topological universality class with ceff > 1/2 when α < αc. Generalizing these findings to more exotic topological phases, such as topological order and intrinsically gapless SPT phases, is a fascinating and challenging direction for future study. From the perspective of experimental realizations, LR interacting spin chains hold the potential for implementation in state-of-the-art quantum circuit platforms91,92. It has been proposed that highly entangled quantum matter and unconventional phase transitions can be observed in quantum circuits93,94,95,96,97,98,99,100,101,102,103, which may be useful to demonstrate our findings experimentally (briefly discussed in Supplementary Note 8). Hence, our findings open an avenue toward exploring and understanding gapless topological phases of matter.

Methods

Density matrix renormalization group (DMRG)

To solve the ground state of the LR interacting cluster Ising model, we conducted extensive DMRG simulations73,74,75,76 using the matrix product state (MPS)77. Over the past few decades, DMRG has emerged as a powerful tool for studying 1D quantum many-body systems with local interactions. However, when dealing with 1D quantum systems featuring LR interactions, the ground state no longer necessarily adheres to the so-called entanglement area law104, which can hinder an efficient MPS representation. In our specific scenario, the ground-state phase diagram (see Fig. 1b) exhibits area law or logarithmic entangled phases (as well as critical points). Despite the complexity induced by LR interactions, a faithful MPS representation remains feasible by employing a sufficiently large MPS bond dimension for finite-size systems.

In practice, we simulated finite systems of an even total length, i.e., \(L\in 2{{\mathbb{Z}}}^{+}\), under OBC or PBC with a maximum MPS bond dimension set to 512. Once the MPS energy has converged up to the order 10−8, the DMRG sweeping route would be stopped; the resulting MPS can be treated as a faithful representation of the true ground state. It is noted that the initial MPS is chosen as one of the Néel states for two reasons: (i) for OBC, there is no spin-flip operator σx in the Hamiltonian acting on the leftmost (L) or rightmost (R) boundary site, it is thus necessary to set the two boundary spins to anti-parallel directions, namely, \(\left\vert {\uparrow }_{{{{\rm{L}}}}}{\downarrow }_{{{{\rm{R}}}}}\right\rangle\) or \(\left\vert {\downarrow }_{{{{\rm{L}}}}}{\uparrow }_{{{{\rm{R}}}}}\right\rangle\), so that the calculation is converged to the correct ground-state manifold. We have verified that the doubly degenerate ground states indeed have two anti-parallel directed boundary spins via exact diagonalization calculations (see Supplementary Note 1 for the numerical evidence). Of course, one can also choose the product state \(\mathop{\prod }_{i = 1}^{L}{\left\vert +\right\rangle }_{i}\), where \({\sigma }_{i}^{x}{\left\vert +\right\rangle }_{i}={\left\vert +\right\rangle }_{i}\), as the starting point. The product state respects the global symmetry \(P=\mathop{\prod }_{i = 1}^{L}{\sigma }_{i}^{x}\) and finally converges to a superposition \(\left\vert {\uparrow }_{{{{\rm{L}}}}}{\downarrow }_{{{{\rm{R}}}}}\right\rangle +\left\vert {\downarrow }_{{{{\rm{L}}}}}{\uparrow }_{{{{\rm{R}}}}}\right\rangle\). Compared to the former choice, the latter one usually requires a larger MPS bond dimension to achieve the same accuracy level. (ii) for PBC, the main quantity under investigation is the entanglement entropy and its spectrum. More specifically, the non-trivial topological property of the critical point is partly identified by the double degeneracy of the lowest-lying level of the entanglement spectrum. If the MPS is initialized to be the product state \(\mathop{\prod }_{i = 1}^{L}{\left\vert +\right\rangle }_{i}\), a doubly degenerate entanglement spectrum would be obtained within the AFM phase (spontaneously symmetry breaking happens only in the thermodynamic limit). To have a clear distinction between the AFM phase, cluster SPT phase, and the non-trivial critical point, it is useful to artificially break the P symmetry at the beginning. By initializing the MPS as one of the Néel states, the resulting degeneracy of the lowest-lying level of the entanglement spectrum would be 1, 2, and 4 for the AFM phase, topological critical point, and cluster SPT phase, respectively.

Additionally, we would like to note that it is common to include a Kac factor as a coefficient of the LR ferromagnetic interaction to preserve the Hamiltonian extensively in the community. In the present scenario, however, the LR interaction is antiferromagnetic (or frustrated). It means it is impossible to simultaneously minimize all LR terms \({\sigma }_{i}^{z}{\sigma }_{j}^{z}/{d}_{ij}\), therefore, the ground-state energy of the LR cluster Ising Hamiltonian can still be an extensive quantity, which is linear with the size L. We have numerically verified a clear linear dependence of the ground-state energy Eg with respect to the system size L for sufficiently small α ≲ 1.0, therefore, the Kac factor is not necessary in our case (see Supplementary Note 1 for the numerical evidence).