Introduction

Due to the penetrating, non-ionizing and cost-effective properties, microwave (MW) imaging has shown significant potential in a wide range of applications, including indoor mapping, non-destructive testing, through-wall imaging, quality evaluation and security scanning1,2,3. MW imaging is particularly beneficial as it allows for non-destructive examination of the internal structure or composition of critical components in industries4. Moreover, MW can be used to penetrate certain materials and create images of objects that are hidden behind barriers. This offers MW imaging a non-invasive and non-cooperative screening capability in security applications, as well as accurate quantitative estimation of the electromagnetic properties of tissues in healthcare5. Conventionally, MW imaging is performed using linear and/or single polarized transmitter and receiver antennas to capture the intensity of MW fields6. Given that electromagnetic waves are vectorial in nature, this intensity-only imaging flattens multiple degrees of freedom of MW, leading to the loss of high-dimensional information. In recent years, polarization imaging has been of great importance in science and technology due to its potential to reveal rich information of the vectorial nature of electromagnetic fields7,8,9,10. Because polarization information is well maintained in harsh environments and sensitive to the change on surfaces or interfaces, polarization imaging is widely used in target sensing as well as life sciences and provides a variety of information about object’s surface structure and anisotropy that are ignored by ordinary intensity detection11,12.

Although great progress has been made for MW polarization imaging6,13, there is still extensive room for further research in this field. On one hand, since different targets have unique polarization characteristics, polarization filtering is highly desired for selective imaging of specific polarized MW field when superimposed MW fields with distinct polarization states coexist14. However, simultaneous polarization filtering and imaging of MW remains difficult and commonly requires a complex combination of bulky devices in imaging systems. On the other hand, polarization imaging with subwavelength spatial resolution is challenging at MW frequencies15. Subwavelength imaging techniques typically rely on scanning antennas in MW fields. Initial developments have shown that it is possible to have an image resolution of one-tenth of the wavelength but the resolution obtained by using conventional scattering measurements is not sufficiently good16.

Holography is a technique to manipulate the wavefront of electromagnetic fields and provides an efficient way for imaging17,18,19. Unlike normal photographs, holographic images contain both amplitude and phase information of the optical field from an object, which is realized through a two-stage process20. The first stage consists of the interference of a signal wave with a reference wave and the holographic storage of interference patterns with spatial variation in light intensity. The second stage relies on scalar field diffraction where a probe light beam illuminates the recorded hologram and the signal wavefront is reconstructed in the diffracted field. In the last few years, polarization holography has become a prominent research area due to its unique capability to extract polarization information of light waves21,22,23,24. Polarization holography is generally realized through forming an optical polarization-modulated pattern7 and further generating a polarization hologram in photo-anisotropic media25,26. So far, research on polarization holographic imaging has been focused on optical bands. Extending the applicability of polarization holography to MW regime would address the aforementioned limitations and reveal diverse intriguing applications.

In this work, atom-based polarization holography (APH) is proposed for all-optical polarization-filtered imaging of MW with subwavelength spatial resolution. A kind of atomic polarization holograms is recorded based on periodic photoinduced atomic anisotropy and its MW-dependent diffraction property is characterized in terms of Jones theory combined with the optical Bloch equation. It is experimentally demonstrated that MW with specific polarization state can be filtered from multiple polarized MW fields through holographic diffraction of APH and selective polarization imaging of the filtered MW field can be realized with a spatial resolution of 500 μm at the frequency of 14.997 GHz, validating the subwavelength imaging capability. Our work extends the capabilities of polarization holography from the optical band to MW band and could enrich the fields of holography and MW imaging.

Results

Atom-based polarization holography

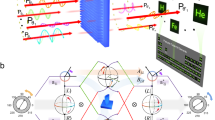
Schematic diagram of APH is depicted in Fig. 1a. Two 509-nm coherent laser beams, marked as R1 and R2, are employed as recording light. The polarization states of R1 and R2 are controlled separately with quarter-wave and half-wave plates. A polarization holographic light field (PHLF) is formed via the interference between asymmetrically polarized recording beams at a small angle of θ in a cubic vapor cell encapsulating cesium atoms. On the other hand, an 852-nm laser is employed as probe light that is regulated to linearly polarized along the y-axis with a polarizer. After passing through PHLF along the z-axis, the probe light is diffracted and the holographic diffracted field is measured with a photodetector. MW with a frequency of 14.997 GHz is generated using a signal generator (Rohde & Schwarz, SMA100B) and a horn antenna. A metal plate is placed 6 cm away from the antenna to form standing waves. While the horn antenna and metal plate remain stationary, the remaining setup components are mounted on a removable platform for MW standing wave imaging. Within PHLF, probe light couples the ground state |1〉 (6S1/2 (F = 4)) and intermediate state |2〉 (6P3/2 (F = 5)) of atoms. The recording field couples state |2〉 and a Rydberg state |3〉 (65S1/2)27. Transitions between state |3〉 and another Rydberg state |4〉 (64P3/2) can be driven with MW fields. The constructed four-level atomic system is shown in Fig. 1b.

Fig. 1: Atom-based polarization holography.
figure 1

a Experimental setup of APH. A tunable PHLF is generated in a vapor cell through holographic interference of two asymmetrically polarized recording beams. A probe light passes through the vapor cell along the z-axis and is diffracted by the holographically induced atomic structure. The diffracted probe field is detected with a photodetector for all-optical polarization imaging of MW fields. P polarizer, H half-wave plate, Q quarter-wave plate, PS polarization splitter, M mirror, VC vapor cell, DM dichroic mirror, PD photodetector. b Constructed four-level atomic system within PHLF. c Principle of photoinduced atomic anisotropy. Linearly polarized probe light can be decomposed into two circularly polarized components with equal intensity and opposite handedness. When the recording light field is elliptically polarized, absorption of RCP and LCP components of probe light becomes different for the two-photon pumped atomic medium, resulting in photoinduced atomic anisotropy.

Full size image

Photoinduced atomic anisotropy

When the recording light field is elliptically polarized, the atomic medium becomes anisotropic based on two-photon transition, as verified in Fig. 1c. The linearly polarized probe light can be decomposed into right-handed and left-handed circularly polarized (RCP and LCP) components with the same light intensity. For the transitions of 6S1/2 (F = 4) → 6P3/2 (F = 5) → 65S1/2 (F = 4), the RCP component of probe light drives transitions between Zeeman sublevels |mF1 = m〉 and |mF2 = m + 1〉, whereas the LCP component mediates transitions |mF1 = m〉 to |mF2 = m − 1〉28,29,30. As the recording field is LCP (see left side of Fig. 1b), the population of Zeeman sublevel |mF2 = −3〉 of 6P3/2 state can be optically pumped towards |mF3 = −4〉 of 65S1/2 state. However, |mF2 = −5〉 is not coupled to 65S1/2 manifold according to the selection rule for electric dipole transition. In this case, the LCP component of probe light is absorbed through the excitation process, while the RCP component can pass through the atomic medium with low loss due to the electromagnetically induced transparency effect31,32 that refers to quantum interference of double optical transitions to make the absorption of the weak probe field vanish (Supplementary Note 1). Conversely, as the recording field is RCP (see right side of Fig. 1b), the atomic medium is made transparent for LCP component of probe light based on transitions |mF1 = 4〉 → |mF2 = 3〉 → |mF3 = 4〉. The RCP component of probe light is absorbed during the excitation process of |mF1 = 4〉 → |mF2 = 5〉. Consequently, there is a difference in absorption of RCP and LCP probe components for two-photon pumped atomic medium, leading to photoinduced anisotropy that depends on the polarization state of the recording light field.

Principle of all-optical MW imaging through APH

APH is on the basis of photoinduced atomic anisotropy with periodic modulation. We start from the Jones theory in terms of PHLF33. The generalized Jones vectors of R1 and R2 are expressed as

$${{{{\bf{E}}}}}_{{{{\bf{1}}}}}=\left(\begin{array}{c}{J}_{1 {{{\rm{\mu }}}}}{{{{\rm{e}}}}}^{{{{\rm{i}}}}{\upphi }_{1{{{\rm{\mu }}}}}(x)}\\ {J}_{1 {{{\rm{\nu}}}} }{{{{\rm{e}}}}}^{{{{\rm{i}}}}{\upphi }_{1{{{\rm{\nu }}}}}(x)}\end{array}\right)={A}_{1}\left(\begin{array}{c}\cos {\chi }_{1}\,\cos {\gamma }_{1}-{{{\rm{i}}}}\,\sin {\chi }_{1}\,\sin {\gamma }_{1}\\ \sin {\chi }_{1}\,\cos {\gamma }_{1}+{{{\rm{i}}}}\,\cos {\chi }_{1}\,\sin {\gamma }_{1}\end{array}\right){{{\rm{{e}}}}}^{{{{\rm{i}}}}2\pi x/\Lambda (\theta )}$$
(1)
$${{{{\bf{E}}}}}_{{{{\bf{2}}}}}=\left(\begin{array}{c}{J}_{2{{{\rm{\mu }}}}}{{{{\rm{e}}}}}^{{{{\rm{i}}}}{\upphi }_{2{{{\rm{\mu }}}}}(x)}\\ {J}_{2{{{\rm{\nu }}}}}{{{\rm{{e}}}}}^{{{{\rm{i}}}}{\upphi }_{2{{{\rm{\nu }}}}}(x)}\end{array}\right)={A}_{2}\left(\begin{array}{c}\cos {\chi }_{2}\,\cos {\gamma }_{2}-{{{\rm{i}}}}\,\sin {\chi }_{2}\,\sin {\gamma }_{2}\\ \sin {\chi }_{2}\,\cos {\gamma }_{2}+{{{\rm{i}}}}\,\cos {\chi }_{2}\,\sin {\gamma }_{2}\end{array}\right){{{\rm{{e}}}}}^{-{{{\rm{i}}}}2\pi x/\Lambda (\theta )}$$
(2)

where φ, χ, γ, and A represent the phase, polarization azimuth, polarization ellipticity and amplitude of R1 and R2, respectively. Λ(θ) in the phase term is a tunable parameter related to θ. PHLF is described with \({{{{\bf{E}}}}}_{{{{\bf{PH}}}}}{=}{{{{\bf{E}}}}}_{{{{\bf{1}}}}}{+}{{{{\bf{E}}}}}_{{{{\bf{2}}}}}\) which is only determined by the physical properties of recording light and not affected by MW. E2 can be decomposed into two sub-vectors that are orthogonal and parallel to E1, respectively. On one hand, as R1 interferes with the orthogonal polarization component of R2 (R2o), a polarization holographic field is formed. The light intensity of the holographic field keeps constant, while the polarization state is modulated periodically in space. On the other hand, as R1 interferes with the parallel polarization component of R2 (R2p), an amplitude holographic field is formed simultaneously with a characteristic pattern of bright and dark fringes. Therefore, the optical pattern of PHLF can be regarded as the superposition of polarization and amplitude holographic fields.

Figure 2a–d shows the simulated polarization and amplitude patterns of PHLF. We introduce the Poincaré sphere with Stokes parameters (S1, S2, S3) as Cartesian coordinates to provide a visual method for representing polarization states34. Each state of polarization is represented by a unique point on the sphere with longitude 2χ and latitude 2γ. In terms of holographic interference of R1 and R2o, the generated polarization holographic pattern traces a closed trajectory on the Poincaré sphere, constrained to the red circular path in Fig. 2a–d. When R1 and R2o are linearly polarized along x- and y-axes, respectively, with the same light intensity, the polarization pattern in Fig. 2(a) exhibits linear → RCP → linear → LCP → linear polarization modulation. When R1 and R2o are orthogonally elliptically polarized, the plane of red circle is rotated along the S2-axis of the Poincaré sphere (see Fig. 2(b)). As R1 and R2o become right- and left-handed circularly polarized, respectively, with an intensity ratio of 2:1, the plane of red circle moves towards point R1 due to intensity dominance. As presented in Fig. 2c, the handedness and ellipticity of polarization holographic field remains constant, while polarization azimuth is spatially modulated. As R1 and R2o are ±45° linearly polarized with the intensity ratio of 2:1, periodic modulation of polarization azimuth, handedness and ellipticity is achieved (see Fig. 2d).

Fig. 2: Polarization patterns of the polarization holographic light field that results from the interference of R1 and R2o and is independent on microwaves.
figure 2

a R1 and R2o are orthogonally linearly polarized along x- and y-axes, respectively, with the same intensity. Points A–D are on the red circle whose plane is perpendicular to the line joining R1 and R2o. Points A and C are on the S2-axis. Points B and D are on the S3-axis. b R1 and R2o are elliptically polarized with the same intensity. Points B and D are on the S2-axis. Points A and C are in the middle of B and D. c R1 is RCP and R2o is LCP with an intensity ratio of 2:1. Points A and C are on the longitude passing through the S1-axis of the Poincaré sphere. Points B and D are in the middle of A and C. d R1 and R2o are ±45° linearly polarized, respectively, with an intensity ratio of 2:1. Points A and C are on the equator of the Poincaré sphere. Points B and D are in the middle of A and C. e Experimental validation of the simulated polarization pattern of c using a linear polarizer. Due to spatial polarization modulation within PHLF, the light intensity distribution captured by a CMOS camera varies with the rotation of the polarizer’s optical axis that is marked with a purple arrow.

Full size image

The polarization pattern of PHLF is validated experimentally using a linear polarizer, as presented in Fig. 2e. R1 and R2 are controlled to RCP and LCP, respectively, with an intensity ratio of 2:1. In this case, the polarization pattern is the same as Fig. 2c and no interference fringes exist because the polarization state of R2 is orthogonal to that of R1. A CMOS camera is applied to capture the light intensity distribution of PHLF, as shown in the first row of Fig. 2e. A linear polarizer is placed in front of the CMOS camera and the direction of the polarizer’s optical axis is marked with a purple arrow in Fig. 2e. As we rotate the polarizer’s optical axis, the light intensity distribution of the transmitted light field changes. The maximum and minimum light intensities correspond to the regions where the polarization azimuth of PHLF is parallel and orthogonal to the polarizer’s optical axis, respectively. We find good agreement between the experimental data and simulation, confirming the validity of PHLF.

Periodic distribution of atomic anisotropy can be induced by the polarization pattern of PHLF, forming a kind of atomic polarization holograms. Referring to the theory of Rydberg atom-based subwavelength imaging35,36, when MW interacts with atomic polarization holograms, the Hamiltonian matrix of APH system under rotating-wave approximation is

$${{{\bf{H}}}}=\frac{\hslash }{2}\left(\begin{array}{cccc}0 & {\Omega }_{{{{\rm{p}}}}}^{\ast } & 0 & 0\\ {\Omega }_{{{\rm{{p}}}}} & -2{\Delta }_{{{{\rm{p}}}}} & {\Omega }_{{{\rm{{PH}}}}}^{\ast }(x) & 0\\ 0 & {\Omega }_{{{\rm{{PH}}}}}(x) & -2({\Delta }_{{{\rm{p}}}}+{\Delta }_{{{{\rm{PH}}}}}) & {\Omega }_{{{\rm{{M}}}}}(x,y)\\ 0 & 0 & {\Omega }_{{{\rm{{M}}}}}^{\ast }(x,y) & -2\left({\Delta }_{{{\rm{{p}}}}}+{\Delta }_{{{\rm{{PH}}}}}-{\Delta }_{{{\rm{{M}}}}}\right)\end{array}\right)$$
(3)

where Δ is frequency detuning and \(\Omega ={{\wp }}\cdot {{{\bf{E}}}}/\hslash\) is Rabi frequency with \({{\wp }}\) being the transition dipole moment that is sensitive to the polarization of electromagnetic fields (Supplementary Note 2). Subscripts p, PH and M represent probe light, PHLF and MW, respectively. ΔPH is controlled by the frequency detuning of recording light. In this work, Ωp is constant and ΩM(x, y) of polarized MW fields varies in x–y plane. Different from the Rydberg atom-based quantum sensing configuration and electromagnetically induced gratings, ΩPH(x) is described as a space-dependent combination of RCP and LCP polarization components according to Jones theory, which is expressed as

$${\Omega }_{{{\rm{{PH}}}}}(x)= \frac{1}{2}[({J}_{1{{{\rm{\mu }}}}}-{{{\rm{i}}}}{J}_{1{{{\rm{\nu}}}} }){{{\rm{{e}}}}}^{{{{\rm{i}}}}2\pi x/\Lambda (\theta )}+({J}_{2{{{\rm{\mu}}}}}-{{{\rm{i}}}}{J}_{2{{{\rm{\nu }}}}}){{{\rm{{e}}}}}^{-{{{\rm{i}}}}2\pi x/\Lambda (\theta )}]{\Omega }_{{{\rm{{R}}}}}\\ +\frac{1}{2}[({J}_{1{{{\rm{\mu }}}}}+{{{\rm{i}}}}{{{{\rm{J}}}}}_{1{{{\rm{\nu }}}}}){{{{\rm{e}}}}}^{{{{\rm{i}}}}2\pi x/\Lambda (\theta )}+({J}_{2{{{\rm{\mu }}}}}+{{{\rm{i}}}}{{{{\rm{J}}}}}_{2{{{\rm{\nu }}}}}){{{\rm{{e}}}}}^{-{{{\rm{i}}}}2\pi x/\Lambda (\theta )}]{\Omega }_{{{\rm{{L}}}}}$$
(4)

where ΩR and ΩL are Rabi frequencies of the normalized RCP and LCP components of PHLF, respectively. Λ(θ) is essentially the period of the atomic polarization hologram. APH system considering the presence of decoherence is described by optical Bloch equation \(\partial {{{\boldsymbol{\rho }}}}/\partial t=-i[{{{\bf{H}}}},{{{\boldsymbol{\rho }}}}]/\hslash +\varGamma ({{{\boldsymbol{\rho }}}})\) where ρ is the density matrix and Γ is contributed from the spontaneous emission and decoherence37. With the solution of ρ21 under the steady-state condition (\(\partial {{{\boldsymbol{\rho }}}}/\partial t=0\)), we obtain the optical susceptibility of probe light, given by \({\chi }_{{{{\rm{p}}}}}={N}_{0}{|{{{{\boldsymbol{\wp }}}}}_{{{{\bf{21}}}}}|}^{2}{\rho }_{21}/({\varepsilon }_{0}\hslash {\Omega }_{{{{\rm{p}}}}})\) in which N0 is atomic density (Supplementary Note 3). Consequently, the transmission function of the atomic polarization hologram is38

$$T(x)=\exp [i\phi (x)\xi ]\cdot \exp [-\alpha (x)\xi ]$$
(5)

where \(\phi (x)={k}_{p}{{\mathrm{Re}}}({\chi }_{p})\) and \(\alpha (x)={k}_{p}{\mbox{Im}}({\chi }_{p})\) correspond to phase and absorption modulations, respectively. ξ is the interaction length of light fields and kp is the wave vector of probe light. The far-field diffraction property of the atomic polarization hologram is calculated through Fourier transformation of Eq. (5).

Figure 3 shows simulated phase and absorption modulations of the atomic polarization hologram along the x-axis. From left to right, ΩM equals 5σ, 15σ, 30σ, and 40σ, respectively, where σ denotes the decoherence rate. The frequency detuning of recording light ΔPH is fixed at 10σ. Λ(θ) defines the distance for one complete modulation cycle of ϕ(x) and α(x). In terms of spatial phase modulation in Fig. 3a, the pattern of ϕ(x) is manipulated by ΩM, with ϕ(x) < 0 for ΩM < 2ΔPH and ϕ(x) > 0 for ΩM > 2ΔPH. For spatial absorption modulation in Fig. 3(b), α(x) remains positive for any ΩM, while its pattern is also governed by ΩM. Under constant MW field strength, ΩM scales with the transition dipole moment which depends on the polarization of MW. Though MW fields do not affect the optical pattern of PHLF, the diffraction properties, described by T(x), of the atomic polarization hologram induced by PHLF incorporate the action of MW, resulting in a MW-polarization-dependent holographic diffracted field. This MW-to-optical conversion enables polarization filtering and imaging in MW regime via APH.

Fig. 3: Normalized phase and absorption modulations of the atomic polarization hologram versus x.
figure 3

a Phase patterns of atomic polarization holograms when ΩM equals 5σ, 15σ, 30σ and 40σ, respectively, from left to right. Spatial distribution of ϕ(x) is manipulated by ΩM that depends on the polarization of MW. b Absorption patterns of atomic polarization holograms with the same ΩM as (a). Spatial distribution of α(x) can also be modulated by the polarization of MW. Other specific parameters are Ωp = 0.5σ, ΩR1 = ΩR2 = 10σ, Δp = ΔM = 0 and ΔPH = 10σ with σ being the decoherence rate.

Full size image

Subwavelength imaging and polarization filtering in MW regime

In the experiment, we begin with polarization imaging of a single MW standing wave. MW generated by the signal source is set to a fixed power of −45 dBm. MW is initially controlled to linearly polarized along the y-axis and amplitude-modulated (AM) at 57 kHz with modulation frequency synchronized to the detection system. The CMOS camera is employed to detect the light intensity distribution of diffracted probe light. The experimental result is shown in the inset of Fig. 4a. Then, we apply the photodetector to measure the diffracted light field around 57 kHz and optical AM signals are obtained, called holographic AM signals. The experimentally detected holographic AM signal is presented in Fig. 4a. The peak of holographic AM signals appears at 57 kHz. For other frequencies, the noise strength is much weaker than the peak.

Fig. 4: Polarization imaging of microwave standing waves with subwavelength spatial resolution.
figure 4

a Holographic AM signals are obtained by detecting the diffracted probe field at the frequency of 57 kHz using the photodetector. Inset: light intensity distribution of the diffracted field of APH is measured with the CMOS camera. b All-optical APH imaging of MW standing wave characterized by nodes and antinodes with spatial resolution of 500 μm. The Poincaré sphere on the right indicates the polarization state of MW (χ = 90°). c Polarization imaging for 45° linearly polarized MW (χ = 45°). As the polarization state of MW varies, the diffraction of APH is regulated, leading to the modulation of imaging. d When MW is controlled to horizontally polarized (χ = 0°), the holographic AM signal at each pixel point reaches the minimum value compared with (b) and (c). e Detected standing wave formed by right-handed circularly polarized MW. Error bars in b–e denote the standard error obtained from 10 measurements.

Full size image

Subwavelength polarization imaging of MW fields is achieved experimentally by spatially mapping MW distributions along the x-axis with a step size of 500 μm, matching the diameter of the probe light spot. When MW is vertically polarized (χ = 90°), the detected image of MW standing wave is demonstrated in Fig. 4b with the Poincaré sphere indicating the polarization state of MW. At the antinode of MW standing wave, the peak value of AM signal is −74.58 dBm. At the node, the peak of AM signal decreases to the minimum value of −92.07 dBm. The distance between the measured antinodes is 1 cm which is half the wavelength of MW. Then, MW is controlled to diagonally polarized (χ = 45°) in Fig. 4c by rotating the horn antenna. The standing-wave image varies with MW polarization. At the same location in Fig. 4b, c, the signal strength of the former is greater than that of the latter. When MW is horizontally polarized (χ = 0°) in Fig. 4d, AM signal at each pixel point is further weakened. In Fig. 4b–d, the proportion of signal strength decrease at the antinode is not strictly the same as that at the node of MW standing waves. The discrepancy arises from standing-wave effects induced by MW reflections at the metal plate, combined with stray reflections from other components in the experimental setup. These unintended reflections introduce noise and weaken the proportionality. For right-handed circularly polarized MW in Fig. 4e, the holographic AM signal strength also shows a periodic distribution during field mapping. The unusual phenomenon is that the amplitude of signal strength variation in Fig. 4e is smaller than that in Fig. 4b–d. Based on the theoretical analysis of electromagnetic wave superposition (Supplementary Note 4), we find that the polarization components along y- and z-axes of MW can form standing waves individually. For circularly polarized MW, the phase difference between the two polarization components is π/2. This results in the spatial overlap between the node of x-polarized standing wave and the antinode of the y-polarized standing wave, creating a configuration where the nodal regions of the total standing wave formed by circularly polarized MW exhibit non-vanishing field intensity. Experimental detection (dots with error bars) of MW fields are consistent with theoretical results (curve) in Fig. 4b–e. Consequently, APH imaging is sensitive to the polarization of MW and the associated subwavelength spatial resolution is 500 μm (λMW/40) for 14.997 GHz MW with the wavelength of 2.00 cm.

When superimposed MW fields with distinct polarization states coexist, polarization filtering for selective MW imaging is achievable through holographic diffraction. Dependence of α(x) and ϕ(x) on ΔPH are verified theoretically in Fig. 5 under the conditions of ΩM = 20σ, 40σ and 60σ. In Fig. 5a–c, as ΔPH is manipulated from −40σ to 0, the value of normalized α(x) first decreases then increases. With ΔPH increasing to 40σ, α(x) is sharply attenuated to 0 and then enhanced gradually. Changing behaviors of α(x) versus ΔPH at the location of x = 3Λ (red boxes in Fig. 5a–c) are presented in Fig. 5d–f. There are two special points in each figure, marked as A and B with subscripts for different ΩM, where α(x) equals 0. When ΩM = 20σ, 40σ and 60σ, ΔPH at A1–A3 are −10σ, −20σ and −30σ, respectively, and 10σ, 20σ and 30σ for B1–B3. Therefore, there are two specific ΔPH, marked as ΔPH(0), at which no absorption modulation exists for the atomic polarization hologram along the x-axis.

Fig. 5: Polarization filtering for selective microwave imaging based on holographic diffraction of atom-based polarization holography.
figure 5

a–c Absorption modulation patterns of the atomic polarization hologram versus ΔPH under the conditions of ΩM = 20σ, 40σ and 60σ, respectively. d–f Changing behaviors of α(x) in the red boxes of (a–c). For ΔPH at points Ai and Bi (i = 1, 2, 3), α(x) equals 0 and no absorption modulation exists along the x-axis. g–i Dependence of phase modulation of the atomic polarization hologram on ΔPH for the same ΩM as (a1–a3). j–l Changing behaviors of ϕ(x) in the red boxes of (g–i). ϕ(x) = 0 along the x-axis when ΔPH are at the points Ci and Di (i = 1, 2, 3). The values of ΔPH at A1–A3 (B1–B3) are one-to-one corresponding to those at C1–C3 (D1–D3). Through controlling the frequency detuning of PHLF, MW with specific polarization state can be imaged selectively from superimposed fields of multiple polarized microwaves through APH diffraction.

Full size image

In addition, the pattern of ϕ(x) is also determined by ΔPH (see Fig. 5g–i). As ΔPH is manipulated from −40σ to 40σ, the normalized ϕ(x) first decreases then increases and again decreases. Variation of ϕ(x) at x = 3Λ in red boxes in Fig. 5g–i are demonstrated in Fig. 5j–l. Similarly, there are also two ΔPH(0), marked as C and D with subscripts, where ϕ(x) = 0 along the x-axis. The values of ΔPH at A1–A3 (B1–B3) are one-to-one corresponding to those at C1–C3 (D1–D3). Moreover, ΔPH(0) changes with ΩM and thus is sensitive to the polarization of MW. Consequently, there is no holographic diffraction at ΔPH(0) because neither absorption nor phase periodic modulation exists. By controlling ΔPH, imaging the MW field with specific polarization state can be achieved through holographic diffraction.

To experimentally demonstrate the polarization filtering characteristic of APH, two horn antennas are employed to generate two MW standing waves with different polarization states. The two antennas at a distance of 0.5 cm are oriented approximately along the x-direction with a small angle. The polarization states of two MWs are marked with P1 and P2. The two antennas generate MW standing waves simultaneously and holographic imaging of the superimposed field at ΔPH = 12.8 MHz is shown in Fig. 6(a). Within the area of 0 cm ≤ x ≤ 1.2 cm and 0 cm ≤ y ≤ 0.2 cm, the superimposed MW standing waves are indistinguishable. Polarization directions of P1 and P2 are marked with arrows. Firstly, we control ΔPH to 20.7 MHz to selectively image the P1-polarized MW. Figure 6b verifies that a sinusoidal strength distribution is filtered from the superimposed MW fields through holographic diffraction. The strength variation period of the filtered standing wave is half of the MW wavelength. Then, ΔPH is regulated to 32.4 MHz for selective imaging of P2-polarized MW field. Similarly, a standing wave in Fig. 6c is filtered from Fig. 6a. Figure 6c demonstrates that the signal strengths of the filtered MW standing wave are notably lower than those observed in Fig. 6b. This experimental result is consistent with the spatial strength distribution pattern quantified in Fig. 4, primarily attributed to the polarization-sensitive property of APH.

Fig. 6: Experimental demonstration of the polarization filtering characteristic of atom-based polarization holography.
figure 6

(a) Two- and one-dimensional imaging of two superimposed MW standing waves at ΔPH = 12.8 MHz. The two MW-generating horn antennas are oriented approximately along the x-direction with a small angle and separated by a distance of 0.5 cm. The polarization directions of the two MWs are χ = 15° and 75°, marked with P1 and P2 arrows. (b) Selective imaging of P1-polarized MW by manipulating ΔPH to 20.7 MHz. The detected signal strength varies in a sinusoidal distribution with a period of 1 cm, revealing that the P1-polarized MW standing wave is filtered from the superimposed fields. (c) Selective imaging of P2-polarized MW by controlling ΔPH = 32.4 MHz. (d) Two- and one-dimensional images detected by APH at ΔPH = 12.8 MHz for the superimposed standing waves of a vertically linearly polarized MW and a RCP MW. The polarization states of two MWs are marked as P3 and P4. (e) Selective imaging of the standing wave formed by RCP MW at ΔPH = 35.3 MHz. (f) Polarization filtering for all-optical detection of linearly polarized MW standing wave at ΔPH = 19.2 MHz. Error bars in (a-f) denote the standard error obtained from 10 measurements.

Full size image

Deviation between experimental data and theoretical prediction is observed in Fig. 6b, c, which exceeds the discrepancy noted in Fig. 4b–d. This enhanced mismatch arises from the experimental challenge of precisely controlling ΔPH to achieve ΔPH(0), which introduces unintended modulation of T(x) by the filtered MW. Our experimental results also reveal that the detected signal strength in Fig. 6a is greater than the sum of measured signal strength in Fig. 6b, c at identical spatial positions. This discrepancy arises from two reasons. On one hand, manipulation of ΔPH reduces the diffraction efficiency of the recorded atomic polarization hologram, leading to diminished signal strength. On the other hand, though the two MWs are incoherent, their spatial superposition introduces residual coherent interactions.

In addition, experimental results for polarization filtering of superimposed standing waves formed by a vertically linearly polarized MW and a RCP MW are presented in Fig. 6d–f. When ΔPH is modulated to 35.3 MHz, the standing wave formed by RCP MW can be selectively detected. As ΔPH is controlled to 19.2 MHz, the vertically linearly polarized standing wave is filtered by APH. At the antinodes of two filtered standing waves, the detected signal strengths are both higher than the simulation results. The reason is that MW is vertically linearly polarized at the antinode of the standing wave formed by RCP MW. As a result, near the antinode, the polarization filtering effect becomes insignificant.

Discussion

In summary, we have proposed APH based on photoinduced atomic anisotropy for simultaneous polarization filtering and subwavelength imaging in MW regime via an all-optical configuration. Controllable PHLF is generated through holographic interference of two coherent light beams with asymmetric polarization states, leading to the formation of a kind of atomic polarization holograms. The diffraction property of the atomic polarization hologram depends on the polarization of MW fields, which is theoretically analyzed in terms of Jones theory and the optical Bloch equation. For MW with different polarization states, the transmission function of the atomic polarization hologram is regulated by the Rabi frequencies of polarized MW, resulting in the variation of light intensity of holographic diffracted field. This MW-to-optical conversion extends polarization holography from optical-band to MW-band applications. Moreover, APH is demonstrated experimentally by imaging the standing-wave fields of polarized MW with the frequency of 14.997 GHz. The detected images are sensitive to MW polarization and the subwavelength spatial resolution of APH imaging is 500 μm that is one-fortieth the wavelength of MW (λMW/40). APH also allows for polarization filtering of superimposed MW fields. Selective imaging of the MW field with specific polarization state can be achieved through holographic diffraction by controlling the frequency detuning of PHLF.

According to Eqs. (3)–(5), APH imaging exhibits broadband applicability across millimeter- and centimeter-wave bands. Resonant enhancement occurs when MW frequencies match Rydberg-Rydberg transition frequencies, enabling all-optical polarization imaging in MW regime is able to be realized, thereby revealing the broadband property of APH. Moreover, the spatial resolution of APH imaging is mainly determined by the spot size of probe light. In order to achieve higher resolution, lenses with higher numerical aperture can be used. It has also been proven that vortex light carrying orbital angular momentum can be focused to the order of a hundred nanometers. This provides a method for higher-resolution imaging, which is one of our next research directions.

Compared with conventional MW imaging techniques using antenna arrays and metasurfaces, our proposed APH enables polarization-filtered subwavelength imaging in MW regime and shows the potential in harnessing vectorial information in an ultra-wideband frequency range. For antenna arrays, subwavelength polarization imaging remains challenging and electric field distortion could be induced via the coupling between the measured electric field and the detecting antenna39. For metasurfaces, their optical properties are largely set in the fabrication process and cannot be tuned40. In contrary, APH enables polarization imaging with subwavelength resolution and has less scattering and distortion for MW detection. APH is also actively tunable by controlling the frequency detuning and wavelength of recording light to realize selective and broadband polarization imaging. Though MW imaging based on Rydberg atoms has been previously reported41, we further realize selective imaging of MW with a specific polarization state from superimposed MW fields through holographic diffraction based on the filtering characteristic of polarization holography. We anticipate broader applications of APH in vast fields, including high-contrast medical imaging, interference-resistant target detection and non-destructive material inspection.

Methods

Specific experimental parameters

Diameters of the two recording beams are both 0.8 mm. Powers of R1 and R2 are initially set as 40 mW and modulated separately with attenuators. The diameter of the probe light is controlled to 500 μm with a lens system. The power of the probe light is 15 μW. The side length of the cubic vapor cell is 30 mm. The 852-nm probe beam is generated with an extended-cavity diode laser and split using a polarization beam splitter. One light beam is applied for laser frequency stabilization and the other is employed for APH imaging. Frequency stabilization is realized through saturation absorption spectroscopy corresponding to the transition of 6S1/2 (F = 4) → 6P3/2 (F = 5) of Cs atoms. On the other hand, we use the electromagnetically induced transparency effect of atomic absorption spectra to stabilize the frequency of recording beams. To suppress additional standing waves due to MW reflections in other directions, the surface of the metal plate is polished to minimize MW scattering and MW-absorbing materials are applied at the plate edges.

Decoherence matrix calculation

Decoherence matrix \(\varGamma [{{{\boldsymbol{\rho }}}}]\) is obtained when Γ acts on the density matrix. The expression of the decoherence matrix is \(\varGamma ({{{\boldsymbol{\rho }}}})={\sum}_{{m}}({\varGamma }_{{m}}{{{\boldsymbol{\rho }}}}{\varGamma }_{{m}}^{{{\dagger}} }-\{{\varGamma }_{{m}}^{{{\dagger}} }{\varGamma }_{{m}},{{{\boldsymbol{\rho }}}}\}/2)\) where { } represents the anticommutator and \({\varGamma }_{{m}}\) is the jump operator. Considering spontaneous emission, possible transition processes are |2〉 → |1〉, |3〉 → |2〉, |3〉  → |4〉 and |4〉 → |1〉. Transition |3〉 → |4〉 can be neglected because its spontaneous emission rate is much smaller than those of other processes. The decoherence rates of |2〉 → |1〉, |3〉 → |2〉 and |4〉 →  |1〉 are σ2, σ3 and σ4, respectively, corresponding to m = 2, 3, 4 for \(\varGamma [{{{\boldsymbol{\rho }}}}]\). Using \({\varGamma }_{m}=\sqrt{{\sigma }_{m}}|j\rangle \langle k|\), the decoherence matrix can be calculated.