Acoustic blackbody through instability-induced softening

Abstract

Perfect wave absorption across all wavelengths is forbidden by the causality principle. Here we demonstrate an approach that circumvents this fundamental limitation in acoustics by coupling unstable components to achieve zero static modulus. Both heuristic model simulations based on different mechanisms (electromagnetic and mechanical) demonstrate the same ultra-broadband absorption exceeding 95% at all wavelengths greater than 114 times the absorber thickness, with simultaneous efficient reciprocal radiation capabilities. Theoretical analyses reveal that, counter-intuitively, this strategy approaches ideal blackbody behavior as thickness approaches zero. These findings indicate that fundamental physical constraints no longer prevent blackbody realization, leaving only material limitations as the remaining challenge.

Introduction

The blackbody, an ideal absorber capturing 100% of incident wave energy across all wavelengths, has been fundamental in physics since Kirchhoff’s proposal¹. Kirchhoff and Planck’s work on blackbody radiation underpins modern thermodynamics and quantum mechanics, with the blackbody remaining both a theoretical ideal and the ultimate goal in absorption research. This pursuit has driven diverse material developments in optics and acoustics. Examples include carbon nanotubes^2,3, coherent perfect absorbers^4,5,6,7, and composite metamaterials^8,9,10 for electromagnetic waves, as well as porous materials¹¹ and resonator-based metamaterials^12,13,14,15 for sound. The absorption-radiation reciprocity further implies that advances in absorption often yield equally efficient radiation mechanisms^3,16, underscoring the dual nature of blackbody research.

Despite these advancements, scientists have long recognized the practical impossibility of realizing an ideal blackbody. As Planck noted¹⁷ that “all approximately black surfaces which may be realized in practice show appreciable reflection for rays of sufficiently long wave lengths.” This limitation stems from a universal constraint imposed by the causality principle^13,18,19,20, applicable across all wave types and materials. Recent efforts to overcome these constraints have explored active control schemes^21,22, time-variance^{23,24,25,26,27,28,29,30,31,32}, and relaxed boundary conditions^33,34,35. However, true blackbody absorption has remained elusive. To understand this fundamental limitation and provide potential solutions, we must first examine the causality constraint on absorption in detail.

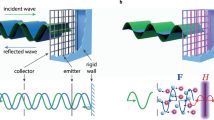
To do so, consider a classic acoustic micro-perforated plate (MPP) absorber: a rigid plate with micron-sized holes backed by a closed cavity (Fig. 1)^13,36,37. When subjected to an external sound pressure p with wavelength λ, the air in the cavity (blue cylinder) expands and compresses, driving air molecules through the micropores in a piston-like motion and dissipating sound energy via reciprocating friction. We characterize this system using two parameters: the MPP’s acoustic impedance ${Z}_{{{{\rm{mpp}}}}}=(p-{p}^{{\prime} })/\bar{v}$, where ${p}^{{\prime} }$ is the sound pressure behind the MPP and $\bar{v}$ is the surface-averaged air velocity through the holes; and the cavity’s effective bulk modulus ${B}_{{{{\rm{eff}}}}}=-{p}^{{\prime} }V/\delta V$, with δV being the change of the cavity’s volume V. These parameters determine the system’s absorption ratio (detailed in the “Absorption and Radiation” subsection in the Methods):

$$\alpha (\lambda )=1-{\left|\frac{{B}_{{{{\rm{eff}}}}}(\lambda )\lambda +i2\pi dc[\rho c-{Z}_{{{{\rm{mpp}}}}}(\lambda )]}{{B}_{{{{\rm{eff}}}}}(\lambda )\lambda -i2\pi dc[\rho c+{Z}_{{{{\rm{mpp}}}}}(\lambda )]}\right| }^{2},$$

(1)

where ρ and c are air density and sound speed, and d is the cavity thickness.

Fig. 1: Instability raises absorption limit.

Cavity air behind MPP (black) acts as a spring (stiffness k = SB_∞/d, where B_∞ = γp_atm is air’s static modulus, S is area, and d is depth). An unstable component (negative spring ${k}^{{\prime} }$) reduces effective B_∞, thereby increasing absorption’s causal limit, 4π²dρc²/B_∞, in Eq. (3). The critical condition occurs when unstable energy (${E}^{{\prime} }$ in red) cancels the original elasticity (E in blue), reaching a new neutral condition with B_∞ = 0.

To quantify overall absorption, we introduce $\Sigma \equiv -\int_{0}^{\infty }\ln [1-\alpha (\lambda )]d\lambda$, representing the total energy loss across the spectrum. For thin cavities and negligible plate thickness, approximating Z_mpp(λ) and B_eff(λ) by their long-wave (static) limit values Z_∞ and B_∞ yields:

$$\Sigma =\frac{2{\pi }^{2}dc}{{B}_{\infty }}\left({Z}_{\infty }+\rho c-\left\vert {Z}_{\infty }-\rho c\right\vert \right).$$

(2)

A limitation then emerges: as Σ increases with Z_∞, a saturated value 4π²dρc²/B_∞ exists when Z_∞ ≥ ρc. Even though Eq. (2) is derived from a specific example, its limit is general. Due to the causal nature of materials, we have previously demonstrated a fundamental inequality applicable to all passive absorbers^13,18:

$$\Sigma \le \frac{4{\pi }^{2}d\rho {c}^{2}}{{B}_{\infty }}.$$

(3)

This inequality reveals a profound implication: an ideal acoustic blackbody cannot exist at a finite thickness because its perfect absorption (α = 1) for all wavelengths yields an infinite Σ, which violates the causality constraint.

Another key insight from Eq. (3) is that lowering B_∞ increases the absorption limit. However, reducing the elastic modulus presents significant challenges. For gas in a cavity, B_∞ depends on the thermodynamic process. In typical near-adiabatic conditions, B_∞ = γp_atm, where γ > 1 is the gas’ adiabatic index and p_atm is atmospheric pressure. Effective heat exchange can decrease B_∞ to p_atm under isothermal conditions, but this is the lower limit for gas-filled cavities. Adding solid phases inevitably increases the modulus. While opening the back cavity could theoretically achieve zero B_∞, it requires an impractically large space³³. Recent studies on negative and zero stiffness in metastructures^{38,39,40,41,42} offer a promising approach to reduce B_∞, potentially leading to higher absorption^43,44.

In this work, we present a theoretical framework that circumvents the causality constraint in acoustics by achieving zero static modulus (B_∞ = 0). Our approach leverages instability mechanisms to neutralize the system’s elasticity (illustrated in Fig. 1), thereby removing the fundamental physical barrier to blackbody realization. We demonstrate this principle through two distinct passive implementations—one electromagnetic and one mechanical—both exhibiting ultra-broadband absorption exceeding 95% at wavelengths greater than 114 times the absorber thickness, along with reciprocal ultra-broadband radiation efficiency approaching unity across the same frequency ranges. Theoretical analyses reveal that this strategy approaches ideal blackbody behavior as thickness approaches zero, indicating that fundamental physical constraints no longer prevent blackbody realization.

Results and discussion

Instability-induced softening

To realize a cavity with zero static modulus, we introduce instability mechanisms that neutralize the system’s inherent elasticity. The following theoretical framework will characterize how unstable elements interact with conventional elastic components to achieve this condition. We now start from deriving the mathematical foundation for this approach.

Consider sealing a cavity by an elastic plate with potential energy E = ∫λ_iklm∂_ku_i∂_mu_ldV, where λ_iklm is the elastic modulus tensor, ∂_k = ∂/∂x_k, and u_l represents the local displacement. When coupled with an unstable system, the plate experiences an additional potential term that can be generally expressed as:

$${E}^{{\prime} }=\int\left(-{\lambda }_{iklm}^{{\prime} }{\partial }_{k}{u}_{i}{\partial }_{m}{u}_{l}-{\kappa }_{il}{u}_{i}{u}_{l}\right)dV,$$

(4)

resulting in a new potential energy:

$$E=\int\left[\left({\lambda }_{iklm}-{\lambda }_{iklm}^{{\prime} }\right){\partial }_{k}{u}_{i}{\partial }_{m}{u}_{l}-{\kappa }_{il}{u}_{i}{u}_{l}\right]dV.$$

(5)

This formulation reveals two fundamental mechanisms for introducing instability: (i) a negative elastic contribution ($-{\lambda }_{iklm}^{{\prime} }$) that counteracts the system’s intrinsic stiffness, and (ii) a position-dependent force term ( − κ_il) that generates destabilizing forces. As we will demonstrate in subsequent sections, these two mechanisms can be physically realized through mechanical and electromagnetic implementations, respectively.

For harmonic oscillations with frequency ω = 2πc/λ, the equation of motion becomes:

$${\omega }^{2}{\rho }_{{{{\rm{pl}}}}}{\delta }_{il}{u}_{l}+{\partial }_{k}\left[\left({\lambda }_{iklm}-{\lambda }_{iklm}^{{\prime} }\right){\partial }_{m}\right]{u}_{l}+{\kappa }_{il}{u}_{l}=0,$$

(6)

where ρ_pl denotes the plate’s density distribution. The corresponding Green’s function ${g}_{lq}(x,{x}^{{\prime} })$ can be expressed using eigenmodes ${\phi }_{l}^{(n)}(x)$ under Neumann boundary condition on the upper and lower surfaces^45,46:

$${g}_{lq}(x,{x}^{{\prime} })={\sum}_{n}\frac{{\phi }_{l}^{(n)}(x){\phi }_{q}^{(n)}({x}^{{\prime} })}{{\rho }_{n}({\omega }_{n}^{2}-{\tilde{\omega }}_{n}^{2}-{\omega }^{2})},$$

(7)

where the summation spans all eigenmodes, with: ${\rho }_{n}=\int{\phi }_{i}^{(n)}{\rho }_{{{{\rm{pl}}}}}{\delta }_{il}{\phi }_{l}^{(n)}dV$, ${\omega }_{n}^{2}=-\int{\phi }_{i}^{(n)}{\partial }_{k}({\lambda }_{iklm}{\partial }_{m}){\phi }_{l}^{(n)}dV/{\rho }_{n}$, and ${\tilde{\omega }}_{n}^{2}=\int{\phi }_{i}^{(n)}[-{\partial }_{k}({\lambda }_{iklm}^{{\prime} }{\partial }_{m})+{\kappa }_{il}]{\phi }_{l}^{(n)}dV/{\rho }_{n}$.

With applied pressure ${p}^{{\prime} }$ on the upper surface, the plate’s displacement is ${u}_{l}(x)=\oint {g}_{lq}(x,{x}^{{\prime} })[{p}^{{\prime} }-{p}_{{{{\rm{cavity}}}}}({x}^{{\prime} })]d{S}_{q}^{{\prime} }$. Given the cavity’s reaction pressure p_cavity = − ρc²δV/V for long waves under adiabatic condition, solving for δV = − ∮u_ldS_l and substituting into B_eff’s definition yields

(8)

For frequencies near $\sqrt{{\omega }_{0}^{2}-{\tilde{\omega }}_{0}^{2}}$, when the response is dominated by one eigenmode, ${\phi }_{l}^{(0)}$, this simplifies to:

$${B}_{{{{\rm{eff}}}}}\simeq \rho {c}^{2}+V{\rho }_{0}\frac{{\omega }_{0}^{2}-{\tilde{\omega }}_{0}^{2}-{\omega }^{2}}{{\left(\oint {\phi }_{l}^{(0)}d{S}_{l}\right)}^{2}}.$$

(9)

The critical insight emerges from Eq. (9): B_eff can be reduced to zero at zero-frequency (B_∞ = 0) when:

$${\rho }_{0}{\tilde{\omega }}_{0}^{2}={\rho }_{0}{\omega }_{0}^{2}+\frac{\rho {c}^{2}}{V}{\left(\oint {\phi }_{l}^{(0)}d{S}_{l}\right)}^{2},$$

(10)

resulting in:

$${B}_{{{{\rm{eff}}}}}=-{\omega }^{2}V\frac{\int{({\phi }_{l}^{(0)})}^{2}\rho_{{\rm{pl}}} dV}{{\left(\oint {\phi }_{l}^{(0)}d{S}_{l}\right)}^{2}}.$$

(11)

Equation (10) represents the theoretical foundation of our approach: the unstable potential’s 0th eigencomponent precisely cancels the system’s elasticity at zero frequency. As illustrated in Fig. 1, the energy increase in the elastic system during deformation (blue curve) is compensated by the unstable component (red curve), resulting in no apparent energy changes externally (black line). This zero-modulus state (B_∞ = 0) enables full absorption at zero frequency when an MPP with Z_mpp = ρc is placed in front of the plate, as shown in Eq. (1).

To approach an ideal acoustic blackbody, we must minimize the frequency-dependent term in Eq. (11). This requires a normalized eigenmode ${\phi }_{l}^{(0)}=1/\sqrt{S\sigma }{z}_{l}$ representing a piston-like motion for the plate, where S and σ are the plate’s surface area and thickness, and z_l is the unit normal direction. An ideal implementation would allow the plate to move freely in the cavity while maintaining sufficient rigidity.

For such piston-like motion, ω₀ ≃ 0, ρ₀ ≃ m/(Sσ) with m = ∫ρ_pldV being the plate’s mass, and

$${B}_{{{{\rm{eff}}}}}\simeq (1-\eta )\rho {c}^{2}-{\omega }^{2}md/S,$$

(12)

where $\eta =m{\tilde{\omega }}_{0}^{2}/(\rho {c}^{2}S/d)$ characterizing the energy ratio between the unstable potential and the inherent elasticity. The criterion in Eq. (10) simplifies to η = 1, which we can interpret physically as a force balance:

$${F}_{i}^{{\prime} }=\partial {E}^{{\prime} }/\partial {u}_{i}=-{u}_{i}\rho {c}^{2}S/d=-{p}_{{{{\rm{cavity}}}}}S=-{F}_{{{{\rm{cavity}}}}},$$

(13)

showing that the unstable force precisely offsets the force from the rear cavity.

It is worth noting that our theoretical framework deliberately simplifies the system by neglecting dissipation in the elastic body, as these effects are typically small compared to the dominant instability mechanism. However, this simplification does not diminish the validity of our approach. In the “Micro-Perforated Plate (MPP) and System Dissipation” subsection in the Methods, we will show that this elastic dissipation can be equivalently treated as an additional correction to the dissipation of an MPP placed in front of the plate.

Two implementations

To validate our theoretical framework, we present two distinct implementations that achieve zero static modulus through different instability mechanisms. Despite their contrasting physical principles, both designs produce remarkably similar acoustic behavior, confirming the generality of our approach.

Our implementations share a common structural foundation: a cylindrical cavity (radius a = 25 mm, depth d = 65 mm) with a rigid inner surface sealed by a specially designed composite plate (Fig. 2). This plate comprises a PMMA [Poly(methyl methacrylate)] thin sheet reinforced by ribs and connected to a wrinkled soft PDMS (Polydimethylsiloxane) ring (insets of Figs. 3a, 4a and detailed in the “Numerical Models” subsection in the “Methods”). The wrinkled ring minimizes added elasticity while the reinforcing ribs ensure piston-like motion—critical for approximating the ideal eigenmode in Eq. (12). This composite plate effectively couples with incident sound waves while providing a stable platform for introducing controlled instability.

Fig. 2: Two implementations of instability-induced softening.

a Electromagnetic implementation: Halbach array of magnets with systematically oriented magnetization directions (green arrows) creates a quadrupole field interacting with a current-carrying coil (red). b Normalized unstable energy (η) versus current (I). c Mechanical implementation: six spoke-shaped beams with T-shaped cross-sections provide negative stiffness under compression. d Normalized unstable energy versus beam end displacement (δL). In both implementations, scenario 1 shows the absorption process with MPP while scenario 2 depicts the sound emission process. Symbols in (b, c) represent numerical simulations with curves as guides to the eye. Both systems achieve equivalent acoustic performance despite their different physical mechanisms.

Fig. 3: Electromagnetic implementation performance.

As current approaches the critical value (η = 1), both absorption and radiation approach unity over an increasingly broad bandwidth. a B_eff/(ρc²): normalized effective bulk modulus; b α: absorption coefficient spectra; c ε: radiation efficiency spectra; circles: simulation results; curves: theoretical predictions.

Fig. 4: Mechanical implementation performance.

Despite the different physical mechanism, the results mirror those of the electromagnetic implementation at equivalent η values (controlled by compression levels) in Fig. 3. a B_eff/(ρc²): normalized effective bulk modulus; b α: absorption coefficient spectra; c ε: radiation efficiency spectra; circles: simulation results; curves: theoretical predictions.

The electromagnetic implementation exploits position-dependent forces (the κ_il term in our framework) through magnetic-current interactions. As shown in Fig. 2a, a copper wire coil (0.55 mm thick, single turn, 26.5 mm radius) is bonded to the plate surface. Surrounding this coil, a Halbach cylinder formed by 16 ring magnets with systematically oriented magnetization (green arrows) generates a quadrupole magnetic field characterized by B_r = 2Kz and B_z = − 2K(r − r₀), where (r₀, 0) denotes the ring’s center (inset of Fig. 2a) and K is a constant proportional to the magnetization⁴⁷. When current flows through the coil with density J, any vertical displacement u_z induces a Lorentz force F_z = 2KJu_z∫dV that amplifies the displacement. This creates an unstable potential:

$${E}^{{\prime} }=-KJ{u}_{z}^{2}\int\,dV,$$

(14)

which corresponds to $\kappa_{il}=KJ\delta_{i3}\delta_{l3}$ in our theoretical framework, with all ${\lambda }_{iklm}^{{\prime} }=0$.

The mechanical implementation, by contrast, leverages negative stiffness (the ${\lambda }_{iklm}^{{\prime} }$ term) through controlled buckling. As illustrated in Fig. 2c, six spoke-shaped PMMA beams (2 mm wide) with T-shaped cross-sections connect to the plate’s center via a hollow column. Under compression with stress σ_ik, these beams generate an unstable potential⁴⁸:

$${E}^{{\prime} }=-\frac{1}{2}\int{\sigma }_{ik}{\partial }_{i}{u}_{l}{\partial }_{k}{u}_{l}dV,$$

(15)

corresponding to ${\lambda }_{iklm}^{{\prime} }=(1/2){\sigma }_{lm}{\delta }_{ik}{\delta }_{lm}$ in our framework, with all κ_il = 0.

Despite these fundamental differences, both systems can be precisely tuned to achieve the critical zero-modulus condition. In the electromagnetic case, we adjust the current I (Fig. 2b), while in the mechanical case, we control the preset displacement δL at beam ends (Fig. 2d). We designed both systems to have identical mass (m = 1 g), ensuring they would exhibit the same frequency-dependent behavior according to Eq. (12).

Figures 3a, 4a confirm this prediction, showing nearly identical effective moduli for both implementations at equivalent normalized unstable energy (η). As η approaches 1, both systems achieve near-zero effective modulus over a wide frequency range, with excellent agreement between simulation results and theoretical predictions. Minor deviations at shorter wavelengths stem from high-order cavity modes not captured in our simplified model.

The similarity between these physically distinct implementations validates our unified theoretical framework, confirming that instability-induced softening can effectively neutralize a system’s elasticity regardless of the specific mechanism employed.

Reciprocal absorption and radiation

Our theoretical framework predicts not only enhanced absorption but also improved radiation efficiency—a manifestation of the fundamental absorption-radiation reciprocity principle. Here we demonstrate both capabilities with quantitative measurements.

For sound absorption, we couple our softened cavity with an MPP that provides the necessary dissipation with minimal frequency dispersion (scenario 1 in Fig. 2a and c). The MPP’s acoustic impedance is characterized by (the “Micro-Perforated Plate (MPP) and System Dissipation” subsection in the Methods):

$${Z}_{{{{\rm{mpp}}}}}\simeq \frac{32\nu \rho \tau }{{\ell }^{2}\varphi }-i\frac{\rho (51\ell +80\tau )}{60\varphi }\omega ,$$

(16)

where τ is thickness, ℓ is pore diameter, φ is porosity, and ν is air’s kinematic viscosity. We optimize these parameters (τ = 0.5 mm, ℓ = 0.3 mm, φ = 0.78%) to make the real part equal to ρc, satisfying the impedance-matching condition for maximum absorption.

As shown in Figs. 3b, 4b, both implementations exhibit virtually identical absorption spectra at equivalent η values, with excellent agreement between simulations and theoretical predictions from Eq. (1). As η approaches 1, the absorption bandwidth dramatically expands, reaching α = 1 at infinite wavelengths. The absorption increases with wavelength—contrary to conventional materials—exceeding 95% when λ > 114d and 99% when λ > 261d.

For radiation, we remove the MPP and apply a driving pressure p_drive directly to the plate (scenario 2 in Fig. 2a, c). The radiation efficiency, defined as the ratio of radiated to driving pressure, follows:

$$\varepsilon (\lambda )={\left| \frac{{p}_{{{{\rm{radiation}}}}}}{{p}_{{{{\rm{drive}}}}}}\right| }^{2}={\left| \frac{i2\pi \rho {c}^{2}d}{{B}_{{{{\rm{eff}}}}}(\lambda )\lambda -i2\pi \rho {c}^{2}d}\right| }^{2}.$$

(17)

As illustrated in Figs. 3c, 4c, both implementations achieve near-perfect radiation efficiency when η = 1, with ε approaching unity over an increasingly broad bandwidth as B_eff approaches zero. Conventional systems, by contrast, exhibit poor radiation efficiency at long wavelengths due to nonzero effective modulus.

The symmetry between the absorption and radiation spectra for both implementations provides compelling evidence of the absorption-radiation reciprocity principle. This symmetry confirms that our approach not only creates an effective absorber but simultaneously an effective radiator—a dual nature of blackbody.

Overcoming causality constraint: blackbody

We now examine the causality constraint on absorption. As shown in Fig. 5a, Σ increases without bound as current approaches I_cr where η = 1, ultimately diverging due to vanishing B_∞. This behavior contrasts sharply with traditional cavity-backed MPP absorption, where improvement through reduced perforation size is bounded by the maximum value predicted in Eq. (3). For pore sizes below a critical value ℓ₀, Σ saturates at this limit (Fig. 5b), a phenomenon first reported in ref. ¹³. While theoretical curves derived from Eq. (1) show excellent agreement with simulation data (circles) at lower currents in Fig. 5a, the discrepancy at high currents arises from the finite frequency band of numerical simulations, which cannot fully capture the extremely broadband absorption behavior.

Fig. 5: Overcoming causality constraint.

a Normalized absorption integral Σ/ (4π²d) vs. current I. I_cr: critical current. b Σ/(4π²d) vs. MPP pore size ℓ for the same cavity and MPP. ℓ₀ = 0.3 mm: critical pore size. Circles: simulation results; curves: theoretical predictions.

Despite these improvements, absorption at the critical condition η = 1 deteriorates rapidly for short waves, prompting two fundamental questions: Can we approach true blackbody absorption, and are there other limiting principles? To address these questions, we rewrite Eq. (12) to include cavity high-order modes:

$${B}_{{{{\rm{eff}}}}}=\left[\frac{\omega d}{c}\cot \left(\frac{\omega d}{c}\right)-\eta \right]\rho {c}^{2}-{\omega }^{2}\frac{md}{S}.$$

(18)

Setting m = 0, η = 1, and Z_mpp = ρc for simplicity, Eq. (1) yields:

$$\alpha ={\left[1+{\left(\frac{\lambda }{4\pi d}\right)}^{2}+\frac{{\cot }^{2}(2\pi d/\lambda )}{4}-\frac{\lambda \cot (2\pi d/\lambda )}{4\pi d}\right]}^{-1}.$$

To quantify the deviation from ideal blackbody behavior, we define a measure Δ (shaded areas in Fig. 6a):

$$\Delta =\int_{0}^{\infty }[1-\alpha (\lambda )]d\lambda =1.64d.$$

(19)

This relationship, validated by numerical simulations (Fig. 6b), reveals that perfect blackbody absorption is achievable as d approaches zero, with the only practical limitation being the required critical unstable potential that diverges as it  ~ 1/d. In practice, it requires either a divergent current in the electromagnetic implementation or divergent compressing stress in the mechanical implementation. The radiation behavior follows a similar trend toward blackbody characteristics, characterized by

$$\int_{0}^{\infty }[1-\varepsilon (\lambda )]d\lambda =3.29d,$$

(20)

further confirming the system’s dual absorption-radiation nature.

Fig. 6: Towards an acoustic blackbody.

a Absorption spectra for various sample thicknesses d; shaded area Δ: deviation from ideal blackbody. b Simulated (stars) and theoretical (line) Δ vs. d. Δ approaches zero as d decreases.

Conclusion

We have demonstrated that instability-induced softening can effectively reduce the static bulk modulus of acoustic systems to zero, circumventing the fundamental causality constraints on wave absorption. Our implementations using two fundamentally different physical mechanisms—electromagnetic forces and mechanical buckling—not only validate the achievement of ultra-broadband absorption and radiation efficiency but also confirm the generality of our theoretical framework.

Most significantly, our analysis reveals that achieving ideal acoustic blackbody behavior faces no fundamental physical barriers. The remaining challenges are purely practical, relating to material limitations rather than physical principles. The electromagnetic implementation requires managing substantial current without excessive heating, while the mechanical implementation must sustain enormous compressive stress without structural failure.

Experimental realization faces several technical challenges. Ultra-low frequency measurements would require techniques beyond conventional impedance tubes, while operating at the critical zero-stiffness point introduces extreme sensitivity to environmental fluctuations and nonlinear behaviors. Controlling these unstable systems would necessitate sophisticated feedback mechanisms—precise current regulation for the electromagnetic implementation and adaptive compression control for the mechanical system. Nevertheless, the theoretical benefits demonstrated by both implementations suggest these practical challenges are worthwhile targets for future experimental work. These advancements could benefit noise control in urban environments and transportation, ultra-sensitive acoustic sensors for medical and industrial diagnostics, and next-generation loudspeakers that can operate across wider frequency ranges.

The generality of the causality constraint⁴⁹ suggests potential applications of our approach beyond acoustics. By using controlled instability to manipulate material properties, similar principles could extend to other wave phenomena, such as electromagnetic absorption/emission through artificially engineered material parameters. This opens new perspectives in material science and device design across different physical domains, potentially enabling previously unattainable performance in areas ranging from vibration isolation to energy harvesting and stealth technologies.

Methods

Absorption and radiation

Consider a compact planar array of identical cylindrical cavities, each with depth d and cross-sectional area S. Following Hooke’s law, a uniform external pressure ${p}^{{\prime} }$ applied to the cavities’ openings produces an average surface displacement $\bar{u}$:

$$\bar{u}=\delta V/S={p}^{{\prime} }d/{B}_{{{{\rm{eff}}}}},$$

(21)

where B_eff is the effective bulk modulus. The corresponding specific acoustic impedance is:

$$Z=\frac{{p}^{{\prime} }}{-i\omega \bar{u}}=\frac{-1}{i\omega }\frac{{B}_{{{{\rm{eff}}}}}}{d}=\frac{-\lambda {B}_{{{{\rm{eff}}}}}}{i2\pi dc}.$$

(22)

For cavities with MPP fronting, the normal reflection coefficient becomes:

$$r=\frac{Z+{Z}_{{{{\rm{mpp}}}}}-\rho c}{Z+{Z}_{{{{\rm{mpp}}}}}+\rho c}=\frac{{B}_{{{{\rm{eff}}}}}\lambda +i2\pi dc(\rho c-{Z}_{{{{\rm{mpp}}}}})}{{B}_{{{{\rm{eff}}}}}\lambda -i2\pi dc(\rho c+{Z}_{{{{\rm{mpp}}}}})},$$

(23)

yielding the absorption coefficient α = 1 − ∣r∣² as expressed in Eq. (1).

For radiation analysis without MPP, we apply a uniform driving pressure p_drive to the cavities’ openings. The resulting piston-like motions generate a plane wave with amplitude ${p}_{{{{\rm{radiation}}}}}=i\omega \rho c\bar{u}$. At the openings, the total pressure satisfies ${p}^{{\prime} }={p}_{{{{\rm{drive}}}}}+{p}_{{{{\rm{radiation}}}}}$. Combining with Eq. (22), we obtain the drive-to-radiation conversion efficiency:

$$\varepsilon ={\left| \frac{{p}_{{{{\rm{radiation}}}}}}{{p}_{{{{\rm{drive}}}}}}\right| }^{2}={\left| \frac{-\rho c}{Z+\rho c}\right| }^{2}={\left| \frac{i2\pi \rho {c}^{2}d}{{B}_{{{{\rm{eff}}}}}\lambda -i2\pi \rho {c}^{2}d}\right| }^{2},$$

(24)

as shown in Eq. (17).

Numerical models

Electromagnetic implementation

Our numerical models for the electromagnetic implementation integrate the unstable Lorentz force from a quadrupole magnetic field with a cavity sealed by a composite plate designed for piston-like motion. We employ finite element method (FEM) via COMSOL Multiphysics to solve the relevant differential equations, encompassing both electromagnetic and acoustic components.

The electromagnetic simulation solves static Maxwell equations for permanent magnets. We calculate the Lorentz force as F = L∮ J × BdS, where L is coil length, J is current density, and B is the magnetic field vector, integrated over the coils’ cross section. As shown in Fig. 7, for coils in the quadrupole field’s symmetry plane, F is vertical. The key parameter $\int \kappa_{33}dV=-F_z/(2u_z)$ is determined by calculating F_z for a small vertical displacement u_z. This parameter serves as the crucial link between the electromagnetic and acoustic simulations.

Fig. 7: Magnetic field distribution of the Halbach array.

Black arrows: local magnetic field directions with lengths proportional to field intensity; white arrows: magnetization orientations of individual magnets; central circle: current carrying coil.

To minimize the required current through maximizing magnetic field strength, we employ a ring-shaped Halbach cylinder comprising 16 Neodymium magnets (Fig. 7). The magnetization directions (white arrows) of adjacent magnets differ by π/8, generating a nearly perfect quadrupole field in the ring-shaped central region. The cylinder, with outer and inner radii of 1.5 mm and 0.325 mm, respectively, maintains a 50 μm clearance from the coil (central circle)—sufficient for displacements corresponding to 96 dB airborne sounds above 10 Hz. A 100 μm vertical gap in the magnet cylinder prevents plate-magnet collision during vibration while maintaining the integrity of the internal magnetic field.

In the acoustic model, we directly utilize the $-2\int\kappa_{33}dV$ value obtained from the electromagnetic simulation as the stiffness coefficient of a virtual spring attached on the coil. This approach allows us to incorporate the electromagnetic instability into the acoustic simulation without directly coupling the full electromagnetic equations.

Mechanical implementation

To harness the buckling effect in the plate-cavity structure, we designed a spoke structure composed of six PMMA beams arranged in a 60-degree equiangular distribution. This spoke structure is positioned parallel to the composite plate and connected to its center via a thin hollow rod along the axial direction. Uniform compression of the six beams from their ends introduces unstable potential energy to the plate, enhancing its sensitivity and creating the desired softening effect.

We employ FEM via COMSOL Multiphysics in a two-step simulation approach. First, static structural mechanics simulates the deformation of the solid system when a given displacement occurs at the end of the beams. Based on these results, sound in the air is then introduced as a perturbation, and the response and acoustic behavior of the entire system are simulated through coupled pressure acoustics and structural mechanics. In our numerical model, the buckling beams have a thickness of 0.35 mm and width of 2 mm. Their T-shaped cross-section is specifically designed to suppress unwanted lateral modes, ensuring the primary buckling occurs in the desired direction.

Composite plate and eigenmodes

To achieve uniform piston-like motion despite the localized forces from the unstable components, we designed a composite plate structure (Figs. 8a, 9a). A PMMA plate is reinforced with a hexagonal lattice frame to enhance rigidity. Additionally, a soft PDMS wrinkled ring on the plate’s edge allows free movement along the cavity without significant restoring forces from the fixed edges.

Fig. 8: Eigenmodes of the electromagnetic implementation.

a Schematics of the composite plate and coil. b–g First 6 eigenmodes and eigenfrequencies of the system, comprising the composite plate, back cavity, and unstable magnetic force (modeled as a spring foundation with negative spring constant).

Fig. 9: Eigenmodes of the mechanical implementation.

a Schematics of the composite plate and buckling beams. b–g First 6 eigenmodes and eigenfrequencies of the system, comprising the composite plate, back cavity, and buckling beams.

To validate this design, we analyzed the eigenmodes of the complete system (composite plate, back cavity, and virtual spring/buckling beams) with free boundary conditions on the plate’s outer surface, as shown in Fig. 8 for the electromagnetic implementation and Fig. 9 for the mechanical implementation.

The results reveal a first eigenmode with a near-zero frequency for both implementations (0.257 Hz for the electromagnetic system and 0.181 Hz for the buckling system). These extremely low frequencies approximate the theoretically expected zero-frequency mode, which arises from the neutral equilibrium state illustrated in Fig. 1. These near-zero modes confirm that our system closely achieves the desired cancellation of elasticity by instability.

In these first modes, the composite plate’s motions closely approximate piston-like behavior. Higher eigenmodes (>780 Hz) couple weakly with external plane waves, further supporting our design’s effectiveness. This piston-like approximation over a wide frequency band underpins the accuracy of our theoretical predictions.

Micro-perforated plate (MPP) and system dissipation

The proposed broadband absorption relies on the low dispersion impedance of MPP. An MPP can be modeled as a lattice of short, narrow tubes distributed on a sound-opaque matrix. For a tube with length much shorter than the wavelength, the equation of aerial motion is^50,51:

$$-i\omega \rho v(r)-\frac{\rho \nu }{r}\frac{\partial }{\partial r}\left[r\frac{\partial v(r)}{\partial r}\right]=\frac{\Delta p}{\tau },$$

(25)

where Δp is the sound pressure difference across the tube and r is the radial coordinate. The solution for particle velocity v(r), considering viscosity effects at the tube surface (v = 0 at r = ℓ/2), is:

$$v(r)=\frac{i\Delta p}{\tau \rho \omega }\left[1-\frac{{J}_{0}(\sqrt{i\omega /\nu }r)}{{J}_{0}(\sqrt{i\omega /\nu }\ell /2)}\right].$$

(26)

For pore diameters and inter-pore distances small compared to the wavelength, the MPP’s acoustic properties are described by impedance Z_mpp:

$${Z}_{{{{\rm{mpp}}}}} \equiv \frac{\Delta p}{\bar{v}}=\frac{\Delta p\oint dA}{\varphi \oint vdA}\\ =-i\omega \frac{\rho \tau }{\varphi }\frac{{J}_{0}\left[\sqrt{i\omega /(4\nu )}\ell \right]}{{J}_{2}\left[\sqrt{i\omega /(4\nu )}\ell \right]}-i0.85\omega \frac{\rho \ell }{\varphi }\\ \simeq 32\frac{\nu \rho \tau }{{\ell }^{2}\varphi }-i\frac{51\ell +80\tau }{60\varphi }\rho \omega +\frac{{\ell }^{2}\tau }{576\nu \varphi }\rho {\omega }^{2}\cdots .$$

(27)

Here, the term  − i0.85ωρℓ/φ is Ingard’s correction for air motion near tube ends⁵². The real 0th-order term indicates constant dissipation over all frequencies. Low dispersion is achieved with small ℓ, maximizing the contrast between the 0th- and higher-order terms. The consistency between the numerical simulation results based on thermoviscous acoustics shown in Fig. 5b and the predictions derived from Eq. (27) validates the accuracy of our impedance expression. Figure 10 shows the simulated absorption spectra used in Fig. 5b.

Fig. 10: Absorption coefficient of an MPP with varying pore size ℓ, backed by a 65 mm air chamber.

The red curve indicates the critical pore size that achieves total absorption at resonance.

While our previous analysis idealized solid systems as non-dissipative, real systems inevitably contain some dissipation. To evaluate this impact, we introduce the viscosity tensor μ_iklm⁴⁸, which adds a new term  − iω∂_k(μ_iklm∂_m)u_l to Eq. (6). This modification leads to a revised Green’s function⁴⁶:

$${g}_{lq}(x,{x}^{{\prime} })={\sum}_{n}\frac{{\phi }_{l}^{(n)}(x){\phi }_{q}^{(n)}({x}^{{\prime} })}{{\rho }_{n}({\omega }_{n}^{2}-{\tilde{\omega }}_{n}^{2}-{\omega }^{2}-2i\omega {\beta }_{n})},$$

(28)

where ${\beta }_{n}=-\int{\phi }_{i}^{(n)}{\partial }_{k}({\mu }_{iklm}{\partial }_{m}){\phi }_{l}^{(n)}dV/(2{\rho }_{n})$. For frequencies near $\sqrt{{\omega }_{0}^{2}-{\tilde{\omega }}_{0}^{2}}$, the effective bulk modulus becomes:

$${B}_{{{{\rm{eff}}}}}\simeq \rho {c}^{2}+V{\rho }_{0}\frac{{\omega }_{0}^{2}-{\tilde{\omega }}_{0}^{2}-{\omega }^{2}}{{(\oint {\phi }_{l}^{(0)}d{S}_{l})}^{2}}-2i\frac{V{\rho }_{0}{\beta }_{0}\omega }{{(\oint {\phi }_{l}^{(0)}d{S}_{l})}^{2}}.$$

(29)

According to Eq. (1), the additional term compared with Eq. (9) is equivalent to adding a constant real impedance valued as $2S{\rho }_{0}{\beta }_{0}/{(\oint {\phi }_{l}^{(0)}d{S}_{l})}^{2}$ to Z_mpp. Therefore, if necessary, the system’s viscosity can be treated as a correction to the MPP’s impedance, allowing for precise modeling of real-world implementations of both the electromagnetic and mechanical systems.