Introduction

During the last two decades, cryogenic microwave experimentation for GHz frequencies has evolved tremendously. The development of the required microwave components is mainly motivated by their strong potential in a variety of quantum applications, including on-chip ferromagnetic resonance (FMR), electron spin resonance (ESR), and nuclear magnetic resonance, as well as research and applications in spin-based and superconducting qubits1,2,3,4. Superconducting materials play an essential role in these experiments, providing the ability to route the microwave signals with limited losses and low noise. For example, they can be used to fabricate resonators with large quality factors employed in so-called circuit quantum electrodynamics (QED)5. Currently, most of the measurement schemes rely on an interface between these low-temperature superconducting circuits and external commercially available RF components, such as arbitrary waveform generators, mixers, oscillators, digitizers, cryogenic amplifiers, circulators, and directional couplers.

The need for this equipment and the coupling between such a specialized RF circuitry anchored at room temperature to cryostats’ cold stages decreases the available space inside the cryostats while hampering both cooling power and system scalability. As such, it is an important task to look for alternative solutions that bring most of these RF components as close as possible to the device under test, preferably, to the chip itself. Significant advancements have been made in the development of cryo-CMOS technology. A key challenge in cryo-CMOS design is the power consumption of the devices, which could exceed the available cooling power of a dilution refrigerator operating at 20 mK6,7,8,9,10. Superconducting technology presents a compelling alternative to overcome the problem of heat dissipation altogether due to its inherently dissipationless nature. The core of many cryogenic electronic components is composed of two weakly coupled superconducting banks, constituting what is known as a Josephson junction (JJ). Its quantum mechanical nature results in a set of unique electronic functionalities not found in conventional electronics. A JJ can act as an AC current—DC voltage transducer and can be used as a voltage-controlled oscillator11. When biased with a fixed DC voltage VDC, a resulting AC current with frequency νj = VDC/Φ0 is generated, with 1/Φ0 = 2e/h = 483.6 MHz μV−1 where Φ0 is the magnetic flux quantum, e the elementary charge, and h Planck’s constant. Inversely, JJs can respond in a resonant, or phase-locked, manner to the frequency νac of the radiation field they are subjected to12,13. This resonant response manifests itself as constant-voltage plateaus, so-called Shapiro steps at integer steps n, in the voltage–current (VI) characteristics of the junction at voltage values, Vn = nΦ0νac. The position of the voltage plateaus Vn depends only on the flux quantum and the driving frequency νac.

Due to these characteristics, JJs have been extensively studied for the generation and detection of RF signals11,12,14,15,16,17,18,19,20,21. Recently, these elements have garnered renewed interest as low-power-dissipating on-chip sources. A common strategy in these devices is to couple the JJ to a resonator, enabling coherent radiation with a narrow linewidth due to excitation of resonant modes22,23,24,25,26,27,28,29,30. However, this approach sacrifices the tunability of the emission frequency by locking it to the resonance, while simultaneously increasing the device footprint. In addition, conventional JJs typically employ an insulating barrier as a weak link, necessitating reliable, but complex fabrication processes. This insulating barrier, which is typically an oxide layer, is a source of two-level-system losses31,32,33. An alternative approach that can potentially solve these problems involves the use of non-conventional planar junctions with a normal-metal weak link (see Fig. 1b). This design only requires that superconducting islands are deposited onto a metallic transport bridge, hence substantially simplifying the fabrication process. The utility of superconductor-normal-superconductor (SNS) junctions has been demonstrated by Peugeot et al., who successfully implemented on-chip spectroscopy using a single JJ coupled to an ancillary cavity34. The potential of a single JJ for emission and detection applications is limited mainly due to its low response (or radiation power) and small impedance35,36. The linewidth of an unshunted single junction emission is also limited by low-frequency fluctuations on the DC bias, being directly proportional to the junction resistance37,38. Several of the aforementioned challenges can potentially be overcome by using JJ arrays (JJAs) containing many junctions. Arrays of JJs have been implemented in different configurations in the past22,23,35,36,37,38,39,40,41,42,43,44,45,46,47,48. They provide design flexibility as the number of junctions permits optimizing the array impedance, which allows for better integration24,36,37,39, while offering robustness against non-uniformities in the JJA43,49. When using JJAs instead of a single JJ, applying a low magnetic field allows for a large in-situ tuning of the junctions' critical current50,51,52 and, consequently, its radiation power and linewidth – see Supplementary Note 1. Another unique property of JJAs is their ability to reach superradiant emission if several junctions are coherently coupled, or phase-locked, allowing the linewidth Δν to be reduced below the single junction limit, as Δν ~ 1/[(Nx − 1)(Ny − 1)], where Nx and Ny are the numbers of superconducting islands in the array in the x and y directions, respectively23,24,37,39. Furthermore, the output power P is also enhanced significantly, scaling with the number of junctions as P ~ (Nx − 1)(Ny − 1)24,35,37,42,53.

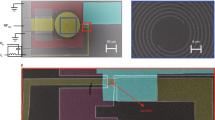
Fig. 1: Josephson junction array device with magnetic field-tunable voltage-current (VI) curves.
figure 1

a Schematic of the devices, consisting of two metallic transport bridges each containing a superconducting Josephson junction array (JJA), labeled top and bottom. The arrays can be individually biased with a DC current, I, and share a radio frequency (RF) pickup contact. Separate contacts are present to measure the voltage, V, over the junctions. b Schematic overview of the used stack. The superconductor (SC) is indicated in blue and the gold weak links in golden. c False-colored Scanning electron microscope (SEM) image of a representative array (MoGe-top). The design parameters Sx, Sy, dx, dy and the resulting unit cell area A are indicated in the figure. d Average junction dynamical resistance, Rj as a function of applied DC current, I, and frustration, \(\tilde{f}\), for the top (MoGe-top) and bottom (MoGe-bot) array at 300 mK. The weak link critical current, \({I}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}(\tilde{f})\) is shown as black dots. Gray dashed vertical lines sequentially indicate \(\tilde{f}\) = 1/4, 1/3, 1/2, 1, and 2. e Average junction voltage, Vj, as a function of applied DC current, I, for the top (red dashed) and bottom (blue) arrays, at frustrations \(\tilde{f}\) = 0, 1, and 2, obtained at 300 mK. Horizontal black dashed lines indicate junction voltages according to the relation V = Φ0νac with νac = 4 and 8 GHz (the C-band). The inset shows the VI curve for \(\tilde{f}=0\) up to 6.5 mA.

Full size image

In order to accomplish these promising perspectives, the design and properties of JJAs need to be carefully considered. For instance, it is important to tailor the junctions’ critical current and resistance, such that an applied current across the junction induces a voltage lying in the interval associated with emission in the desired frequency band. In this work, we explore the unique properties of 2D planar JJ arrays for on-chip generation and detection of microwave signals for quantum information processing. We have developed a robust design for JJAs that allows a DC voltage over the junctions to generate signals in a wide frequency range. These junctions can be manufactured by depositing superconducting islands on top of a normal metal, facilitating the fabrication process and ensuring a small device footprint. The results are reproduced for several JJAs, utilizing different materials and fabrication methods. We discuss the impact of different fabrication choices on the superconducting properties of the arrays and reveal the crucial role the device geometry and the impedance of the environment play in the detection of Josephson radiation. Although coherent emission remains evasive, we identify important factors related to the improvement of these devices for use as radiation sources. Finally, we demonstrate that the same SNS arrays can be used as detectors for radiation in the GHz range. This allows us to propose the design of a GHz spectroscopy device fully operated by DC sources, striving to harness the potential of SNS junction arrays to eliminate the need for RF circuitry altogether.

Results

The C-band of microwave frequencies, spanning from 4 to 8 GHz, is a sweet spot for circuit QED and quantum computing applications. From a practical perspective, RF electronics is commonly optimized to work in this frequency range. From a fundamental viewpoint, the C-band lies well below the superconducting gap frequency, avoiding quasiparticle poisoning, and is sufficiently high in frequency to ensure that effects of thermal energy on the resonator state remain negligible at millikelvin temperatures. As proof of principle, the 4–8 GHz range will be the targeted frequency window for this study. As the emission frequency is linked to the voltage over the junction via the Josephson relations, the envisioned JJA design should have the required fabrication flexibility to tailor the weak link critical currents (\({I}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\)), associated with the onset of the dissipative regime in the array, and the dissipative state average single junction resistance (Rj)35,54. This enables controlled access to the voltage state in the range Vj = VDC/(Nx − 1) ≈ 8.27–16.54 μV corresponding to the Josephson radiation frequency \({\nu }_{{{{\rm{j}}}}}=\frac{{V}_{{{{\rm{j}}}}}}{{\Phi }_{0}}\) within 4–8 GHz, where Vj stands for the average voltage across an individual JJ along the bias direction x. Moreover, the fabrication process should be highly reproducible, enabling the fabrication of arrays of nearly identical junctions37,54.

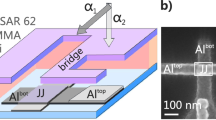
To achieve the above requirements, we fabricate devices as schematically presented in Fig. 1a – for details on the fabrication steps, see the Methods section. SEM images of this device can be found in the Supplementary Fig. 4 and Supplementary Note 5. They consist of two normal metal Ti/Au transport bridges, each decorated with an array of regularly spaced square superconducting islands, either of Au-capped Mo78Ge22 or of NbTiN, thus defining planar SNS junctions in the long diffusive regime as shown in Fig. 1b, c13,54. The islands have nominal sizes Sx = Sy = 500 ± 25 nm and are separated by dx = 100, 200, 300, or 400 nm and dy = 200 nm, as depicted in the SEM image in Fig. 1c. During the experiment, the voltage is measured over 38 junctions parallel to the current direction, and 13 perpendicular to the current direction. Including two bridges in each device allows us to test the reproducibility of our fabrication process, as well as the uniformity of the superconducting behavior, by separately biasing each array. In total, we have investigated ten JJAs and, in the remaining of this work, we will report on selected representative devices, as listed in Methods section. A high degree of reproducibility was achieved for all studied samples.

Using SNS junctions instead of tunnel junctions brings some important advantages to the design. First, SNS junctions demonstrated a broad dissipative state far below the critical temperature Tc, defined at the onset of the transition to the non-dissipative state as the sample is cooled down13,55. Secondly, \({I}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\) in SNS junctions depends decisively on the ratio between the interisland spacing and the normal metal coherence length (ξN)54. As the latter length scale (ξN(Tc) ≈ 70 nm) is within the range of state-of-the art fabrication processes, it provides a design knob to tune the device response. Thus, designing devices with such JJAs allows tuning of the emitted power depending on the application, by simply adjusting the total amount of junctions and their arrangement (Nx, Ny, dx and dy)36,38.

To test reproducibility and sample uniformity, we probe the magnetic field (B) dependence of the VI characteristics of separate arrays within a single device. Two mechanisms contribute to the Rj(I, B) response, shown in Fig. 1d. First, the critical current of individual junctions exhibits a Fraunhofer-like pattern as a function of B, with periodicity related to the junction’s area56. Second, there is an interplay between the superconducting vortices and the two-dimensional array. When the vortex lattice is commensurate with the array, vortices are distributed forming a periodic stable configuration, resulting in an increased \({I}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\)51,52,57. The magnetic fields at which this happens are called matching fields, defined as \({B}_{k}=k\frac{{\Phi }_{0}}{A}\), with Φ0 the magnetic flux quantum, A the unit cell area of the JJA (see Fig. 1c), and k a rational number. The value of k represents the average number of flux quanta contained per unit cell. It is convenient to express the magnetic field acting on the array in reduced units, known as frustration, \(\tilde{f}=\frac{BA}{{\Phi }_{0}}=\frac{B}{{B}_{1}}\).

Figure 1d simultaneously presents the average single junction resistance Rj = dVj/dI of two identically designed MoGe arrays on the same device (MoGe-top and MoGe-bot) at 300 mK. The behavior is investigated as a function of bias current in magnetic fields between  −9 and 9 mT. The results are obtained by measuring VI curves at different fields with 30 μT steps. For negative \(\tilde{f}\) values, we present results for the top array, while those for the bottom array are shown for positive \(\tilde{f}\) (see Fig. 1a for reference). If the arrays have equivalent properties, the matching peaks should be mirrored around \(\tilde{f}=0\), as evidenced in the figure. The black dots mark \({I}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\), determined as the current value at which Vj = 1 μV. Two features are immediately recognized. First, results from both arrays are nearly indistinguishable, with \({I}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}(0)\) equal to 495 and 493 μA for the top and bottom bridge, respectively. Second, clear matching features are observed at both integer and fractional (i.e., 1/2, 1/3, ...) frustrations. The presence of pronounced matching peaks in the \({I}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}(\tilde{f})\) curves in Fig. 1d that are symmetrical with respect to \(\tilde{f}=0\) is thus an indication of uniformity in fabrication and superconducting properties across the array.

For \(I > {I}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\), the arrays enter the dissipative state and the operational emission conditions35,38. In Fig. 1e, we investigate individual VI curves at different matching fields for the top (dashed red lines) and bottom bridges (solid blue lines). For \(\tilde{f}\) = 0, 1, and 2, the observed Vj falls into the voltage range associated with Josephson radiation in the C-band, represented by the two horizontal dashed lines (with Rj = 0.33 Ω in the linear section). It is important to stress that this convenient voltage range coinciding with the C-band frequency range is the result of careful fabrication and design choices, tuning \({I}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\) and Rj for a given temperature. Nevertheless, at \(\tilde{f}=0\), the VI characteristic is slightly non-linear close to the values corresponding to emission at 4 GHz. It is known that non-linearity in the VI behavior will lead to undesired higher harmonics in the radiated frequency spectrum38. Another problem we identify (see Supplementary Note 1) is that the radiation is highly sensitive to voltage differences between different junctions in the non-linear part of the VI curve. Therefore, the radiation produced in this regime has a larger linewidth and decreased intensity at the desired frequency. To mitigate this problem, one can benefit from the inherent magnetic field commensurability effects at \(\tilde{f}=1\) and 2 to access a more linear section of the VI curve within the C-band, while maintaining vortex stability and avoiding detrimental effects of flux flow. Alternatively, the VI characteristics could be further tuned by optimizing the array geometry, to ensure a linear regime for all desired frequencies. The inset of Fig. 1e shows VI curves for the top and bottom arrays spanning the full voltage state. The dissipative state sets in around 0.5 mA, when the junction’s critical current is exceeded. A second transition just above 5 mA, i.e., much higher than the required current to operate the device in the desired frequency range, indicates the transition of the superconducting islands to the normal state caused by local heating at large currents, which is found to be almost identical for the MoGe islands in the top and bottom JJAs [5.15 mA (top) and 5.13 mA (bottom)]. This current and voltage range also sets the upper frequency limit for the emission of these particular MoGe devices around 55 GHz (Vj = 114 μV), indicating that it is possible to use JJAs as high-frequency radiation sources for different applications.

After characterizing the arrays’ response to a DC current bias, we tested their ability to generate Josephson radiation in the 4–8 GHz range using a signal analyzer, as described in the Methods section. The power spectral density S(ν) is measured as a function of Vj/Φ0, where ν is the probed frequency. Figure 2a shows results for MoGe-bot operated at 300 mK and \(\tilde{f}=1\). The regions of higher S (shown in darker brown) follow the expected Josephson frequency’s first harmonic, highlighted by the black dashed line labeled νj. The displayed line has been shifted by 40 MHz to compensate for a difference between the measured voltage and the actual junction voltage due to the placement of the voltage contacts. A less intense second harmonic signal can also be observed at 2νj. This analysis demonstrates that simply by varying the DC voltage across the array, we are able to produce a measurable and tunable radiation in the GHz range transmitted through the normal metal transport bridge.

Fig. 2: DC voltage-tunable Josephson emission.
figure 2

a Power spectral density S as a function of frequency ν and junction voltage Vj, with Vj converted to units of Hz using the Josephson equation. Data is for MoGe-bot at 300 mK and frustration \(\tilde{f}=1\). The maximum value of the colorbar is set to 0.5 ⋅ 10−8 fW Hz−1 to increase the visibility of the graph. The dashed lines respresent the expected Josephson frequency νj and its harmonic 2νj. b Selected spectra of the radiation map in panel a (solid symbols) and fits (solid lines). Vertical dashed lines indicate the expected Josephson frequency. c Integrated power Pν over bias voltage for MoGe-bot (d top) as a function of frequency ν at frustrations of 0 (red) and 1 (blue). e The power integrated over voltage (red) and the measured white noise power spectral density (cyan) at frustration \(\tilde{f}=0\), both normalized to their maximum value for MoGe-bot (f top). The white noise is an average of 25 measurements with a biasing current of 6.0–6.5 mA at a frustration of \(\tilde{f}=0\).

Full size image

Figure 2a also shows that the emitted radiation power is frequency dependent, as highlighted by the apparent gap in the signal around 7 GHz. Note that the maximum value of the colorbar is set to 0.5 ⋅ 10−8 fW Hz−1 to increase the visibility of the graph. The Supplementary Movie 1 contains a video depicting all measured S(ν) spectra that compose Fig. 2a. The non-uniform emission profile can also be seen in Fig. 2b, which shows six individual S(ν) spectra, where the height of each peak varies. From these individual spectra, we extract the radiation power and linewidth. These spectra are chosen at equally spaced voltage intervals indicated in panel a by vertical lines and named V1 until V6. In panel b, solid lines are Voigt fits of each observed radiation peak, while vertical dashed lines represent the expected Josephson frequency for each spectrum. The spectrum at V1 is chosen to represent the value at which the measured radiation power is maximum, \(P={P}_{\max }\). P is obtained by numerically integrating S(ν) over the full frequency range. In this case, the power is 11.9 fW and the full width at half maximum is 106.5 ± 0.1 MHz. This leads to a maximal power efficiency, defined as the ratio between the output and input powers, of about 10−7, which is consistent with the efficiency observed for tunable radiation originating from vortex movement in superconducting superlattices58. Importantly, the observed radiation from the source is not coherent, as suggested by the fact that the linewidth of the detected signal is much larger than the theoretical lower bound for an unshunted single junction. The latter is limited by Johnson noise and directly proportional to the junction’s resistance, leading to an estimate of 4 MHz for the studied devices18,35,38. The observed broad linewidth is likely caused by a distribution in the junction properties, due to non-uniformities in fabrication52.

Figure 2c investigates the obtained power spectral density for the array MoGe-bot at \(\tilde{f}\) = 0 and 1 by integrating S(ν) over all voltages at each frequency. We label this quantity as Pν. The results show a decrease in the magnitude of Pν as \(\tilde{f}\) is increased – similar to the behavior of \({I}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\) shown in Fig. 1e and in accordance with results obtained from the current driven resistively shunted junction (RSJ) model for a single junction13,59 (see Supplementary Note 2). In addition to this, the RSJ model predicts (i) that the radiated power increases smoothly and monotonically as the voltage across a JJ increases; and (ii) that the power of the second harmonic radiation is proportional to the first harmonic component. In contrast to these predictions, Fig. 2c shows a highly non-monotonic behavior for Pν(ν), which directly reflects the trends observed in S(ν) in panel b. There is an enhancement of the signal at specific frequencies (e.g., 3.7 and 5.2 GHz) and a suppression at others (e.g., 7 GHz). This spurious behavior is likely caused by the uncontrolled impedance of the environment, where the shape of the transport bridge or the bonding wires might cause parasitic resonant modes to couple to the signal. Similar behaviors were reported in previous on-chip sources34,45.

This is further supported by comparing the results from Fig. 2c with those from Fig. 2d, which are obtained for MoGe-top. As shown in Fig. 1d, the two arrays have analogous superconducting responses, suggesting that the different Pν(ν) curves observed are not related to the profile of the Josephson radiation emitted by the arrays, but result from a frequency-dependent transfer function related to the transport bridge, wirebonds, and the sample holder that connect the emitter (JJA) and the receiver (output line). This hypothesis is reinforced by the results in Fig. 2e, f. The red curves represent the same data as in panels c and d at \(\tilde{f}=0\), but here they are plotted normalized to \({P}_{\nu ,\max }\). In cyan, we present the normalized power spectral density, \(S/{S}_{\max }\), observed when the Josephson radiation is replaced by a white noise radiation source (see Methods). As \(S/{S}_{\max }\) presents features closely related to \({P}_{\nu }/{P}_{\nu ,\max }\) for both arrays, the modulation in the detected power are independent of the source and thus not related to the emission of the JJAs. The differences in the radiation profile depending on the position of the array in the device (top or bottom in Fig. 1a) were consistently observed for all measured samples.

The previous results establish that MoGe/Au SNS JJAs can be operated as DC voltage-tunable GHz radiation sources. As shown in Fig. 3a and in the inset, the amorphous MoGe JJAs have a Tc = 6.5 K, defined at the onset of the transition to the dissipative state as the sample is cooled down. Nevertheless, MoGe has a few important drawbacks as a material in nanodevice applications and superconducting circuitry. Particularly, the superconducting properties (e.g., critical temperature) are strongly dependent on the exact stoichiometry of the MoGe compound. To control the stoichiometry, a pulsed laser deposition is needed during fabrication, which limits the uniformity of the thin films and compromises the use of lithographic steps. To tackle these issues, boost the critical temperature of the chosen superconductor, and test the robustness of the radiation mechanism, we fabricated new devices in NbTiN60,61,62,63,64,65. This material has a bulk Tc of 17.3 K66 and around 14 K for films with thickness of 20–40 nm67. The NbTiN islands are embedded on similar Au transport bridges as the MoGe devices using a top-down approach as described in the Methods section. While all devices have the same number of junctions, the horizontal interisland spacing dx is varied from 100 to 400 nm. Figure 3a shows the Rj(T) characteristics of these samples, where the bias current is far below the critical current. The curves present two transition temperatures, as expected for normal metallic films decorated with coupled superconducting islands55,68. At Tc = 12 K, for all devices, a normal state-superconducting transition indicates that the NbTiN islands retain superconductivity despite the presence of the underlying Au layers. At lower temperatures, labeled as \({T}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\), the devices enter a non-dissipative state as the superconducting islands are effectively coupled by the underlying Au bridge, such that \({T}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\) sets the upper limit at which the devices can emit Josephson radiation. We observe that \({T}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\) decreases from 6.4 to 1.8 K as dx increases from 100 to 400 nm, highlighting the effect of the interisland spacing on the coupling between the islands. Fig. 3b further demonstrates this effect, as the \({I}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\) at 0.3 K decreases with increasing dx. Another important ingredient influencing the coupling is the normal metal coherence length (ξN)68. As ξN is directly related to the electronic mean free path via \({\xi }_{{{{\rm{N}}}}}\approx 0.58\sqrt{\frac{\hslash {v}_{{{{\rm{f}}}}}}{2\pi {k}_{{{{\rm{B}}}}}T}l}\)54, the resistivity of the Au bridge affects the interisland coupling and \({T}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\). The data in Fig. 3a corroborate that trend as we observe a large difference between Tc and \({T}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\) for the NbTiN samples, for which the Au bridge has a resistivity around 53 Ωnm. For comparison, the Au bridge in the MoGe samples has a resistivity of 16 Ωnm, 3.3 times lower than what we obtained for the NbTiN samples. Thus, we identify the quality of the metallic transport bridge as a crucial ingredient affecting device performance. Figure 3c presents a set of VI curves for the devices NbTiN100 and NbTiN200. The colored solid lines are results obtained at 300 mK, while the gray horizontal lines highlight the boundaries of the C-band. We can observe that, although NbTiN100 has a higher \({T}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\), one has to carefully consider the operation conditions of the source, as the linear part of the resistive state of the VI lies outside of the C-band at low temperatures. The same is true for NbTiN200, however, as we demonstrate by the dashed line of matching color, it is not only possible to tune the VI characteristics by magnetic fields, but also by temperature, gaining access to a more linear emission regime at 2 K for this device. Finally, Fig. 3d confirms voltage-tunable radiation emission for NbTiN200 at 2 K, while we again observe a modulation of the measured power resulting from the transfer function of the normal transport bridge as discussed above. The differences in superconducting materials and fabrication processes confirm the robustness of the proposed approach of using JJAs as GHz radiation sources and allow us to envisage a better integration with future devices. Another important consideration is that at increasing temperatures, Johnson noise becomes more prominent while, at the same time, the power of the radiation decreases with decreasing \({I}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\) (see Supplementary Note 3 and 4). Consequently, it remains important to boost the power efficiency of the source and search for approaches that allow for coherent emission from the array.

Fig. 3: Effect of interjunction spacing, dx, and temperature, T, on DC voltage-tunable Josephson emission in NbTiN Josephson junction arrays (JJAs).
figure 3

a Junction resistance Rj as function of temperature for NbTiN100–400 and MoGe-bot. The vertical gray dashed lines indicate the weak link critical temperature \({T}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\) for the NbTiN array with dx = 400 nm, the superconducting critical temperature, Tc, of MoGe at 6.5 K and of NbTiN at 12 K. The inset shows a zoom near the transition of MoGe at Tc = 6.5 K. b The dependency of the weak link critical current, \({I}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\), on dx for NbTiN100–400 at 0.3 K. c VI curves for NbTiN100 (blue) and NbTiN200 at 0.3 K (red line) and 2 K (red dashed line). d Power spectral density S as a function of frequency, ν, and junction voltage Vj, converted to units of Hz using the Josephson equation. Data is for NbTiN200 at 2 K.

Full size image

Discussion

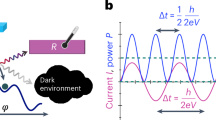
In the previous section, we fabricated JJAs that operate as on-chip DC-voltage tunable GHz range radiation sources, using different fabrication techniques. These devices are capable of working at different temperatures and applied fields. Poor coupling between the emitted signal and the output line compromises the ability to deliver the signal to different points of a hypothetical circuit as would be necessary, for instance, to excite or read out a qubit. Therefore, it is required to optimize the design of the transport bridge to allow for better coupling with the radiation. A critical step toward this goal is to embed the arrays into an impedance-matched coplanar waveguide, allowing a well-controlled environment impedance while also reducing the length of wirebonds, avoiding losses to the environment and guaranteeing that the transmitted power is not modulated in frequency. This can be achieved with a similar material arrangement as the one presented here, with a normal metal transport bridge decorated with superconducting islands, as Au waveguides can transmit the signal with low losses69. An even better transmission could be achieved employing superconducting waveguides. In such a case, the junctions need to be defined by etching the weak links in the superconducting film. In any case, numerical results based on finite element analysis can help to understand the ideal JJA-waveguide configuration maximizing the transmission and power efficiency of the devices. Furthermore, a substantial margin of performance improvement could be obtained by achieving coherent radiation emission, for which the observed linewidth should decrease below that of a single junction. A common strategy to improve the power efficiency of high frequency generators is to couple the emitting source to a cavity22,23,24,25,26,27,28,29,30. However, the price to pay in this alternative design is the lack of frequency tunability offered by the JJAs, as only resonant modes will be transmitted. A more appealing mechanism to achieve coherent radiation is intrinsic coupling via the quasiparticle mechanism37, which does not rely on an external resonance or RF drive. To achieve coherent emission through this mechanism and reduce the signal linewidth, it is crucial to consider the normal metal coherence length, a length scale describing the coherent transport of Cooper pairs through the junction. As Jain et al. propose, this can be achieved by fabricating junctions with sizes in the order of the normal metal coherence length37. The possible response of an improved source that takes these issues into consideration is schematically represented in Fig. 4a, highlighting the uniform and sharp radiation emitted when the source is biased at different voltages, Vsrc, akin to Fig. 2b.

Fig. 4: Proposed on-chip microwave measurement platform using Josephson junction arrays (JJA) as radio frequency (RF) emitter and detector.
figure 4

The top panels show a the ideal power spectral density, S, as a function of frequency, ν, of the JJA source at different voltages Vsrc; b the transmission S21 as a function of frequency for a λ/2 co-planar waveguide (CPW) resonator, with νr the resonance frequency; and c the experimentally obtained detector voltage \({V}_{\det }\) as function of the detector bias current \({I}_{\det }\) of the MoGe-det sample with (red) and without RF irradiation of a signal with amplitude ∣Vrf∣ together with the possible JJA detector response in the proposed platform. d A schematic representation of the DC-operated microwave co-planar waveguide platform consisting of a JJA source, a λ/2 resonator, and a JJA detector, where I represents the bias current and V represents the voltage over the arrays.

Full size image

Yet, there is another enticing potential use of JJAs in the context of cryogenic high-frequency experiments. The emergence of giant Shapiro steps when the arrays are excited by an alternating signal allows these devices to be also used as a GHz range detector22,70,71. Figure 4c demonstrates such features, as measured in the VI of MoGe-det at 450 mK and \(\tilde{f}=0\) when it is irradiated by a 2 GHz signal with amplitude ∣Vrf∣ = 1410 mV. Meanwhile, at zero power, no Shapiro steps are visible if a DC current is driven through the array. When MoGe-det is irradiated by the RF signal, \({I}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\) is reduced from 210 μA to zero and giant Shapiro steps with a height of 4.14 μV reveal that all the columns with junctions in the array are contributing to the Shapiro response upon an external excitation. Therefore, by applying a bias measuring current Idet below \({I}_{{{{\rm{c}}}}}^{{{{\rm{wl}}}}}\) and continuously probing the DC voltage Vdet, it is possible to know if the detector array is being irradiated by an alternating signal or not17,72. More details on the characterization of MoGe-det can be found in the Supplementary Note 6.

The possibility of an optimized JJA source and a well-characterized JJA detector allows us to propose a GHz-range measurement platform, that could be easily integrated with other on-chip electronics due to the flexible fabrication technique and small footprint. In such a device, two JJAs are embedded in a single transmission line: one acting as an ideal microwave source and the other as a microwave power detector. This is represented schematically in Fig. 4d. As discussed throughout this text, both source and detector can be operated solely by DC circuitry. The waveguide transmits the signal from the ideal source to the detector while allowing for the coupling of different physical systems to the radiation. An illustrative example of a system that can be tested is a λ/2 coplanar waveguide resonator that is capacitively coupled to the central waveguide, as shown in Fig. 4. Such a component attenuates the transmitted radiation, except at a characteristic resonance frequency, νr73. Figure 4b shows the typical S21 transmission coefficient measurement of a λ/2 resonator, revealing a sharp increase in transmittance at νr. The presence of the resonator then drastically modifies the signal arriving at the detector, suppressing the power if ν ≠ νr, such that Vdet(Vsrc) tends to zero at all frequencies different from νr, as represented in Fig. 4c. In this example, the detector is biased slightly below the critical current, where the sensitivity to changes in the VI curve is larger. That way, the proposed device is able to probe the resonance frequency without requiring an external GHz source, a spectrum analyzer, a vector network analyzer, or any specialized radio frequency wiring or circuitry, drastically simplifying the requirements for spectroscopic measurements. In essence, the proposed measurement platform can be operated using only DC components and will allow GHz transmission measurements at cryogenic temperatures, replacing commonly employed RF components. Moreover, the frequency range is not limited to the C-band, but can be further extended up to the superconducting gap frequency, such that the device can be used, for instance, as an FMR or an ESR probe1,2. Our results indicate that this proposal could serve as a viable solution for an RF platform compatible with existing technologies. While the technology is not yet fully mature, we have identified key challenges that must be addressed for its broader application.

In summary, we have fabricated low-temperature GHz radiation sources that are operated solely by standard DC components. The sources are comprised of an SNS JJ array, which is coupled to a normal metal transmission bridge. We demonstrate that the emitted frequency is effectively tuned by the junction voltage according to the Josephson equations. In addition, we have determined important design parameters to optimize the VI characteristics that allow the JJA to emit in the 4–8 GHz regime. The design is robust and can be used with different fabrication techniques. The choice to employ JJAs in the device design allows us to further tune the source behavior by changing temperature, applied magnetic fields, and material choice. We investigate the effect of all these parameters on the radiation while revealing that the coupling of the signal with the underlying transport bridge plays a determinant role in how the signal travels to different parts of the circuit. Moreover, we also demonstrate that the same arrays can be used to detect high-frequency radiation. Lastly, we propose a GHz-range spectroscopy device fully operated by DC components, that could be easily integrated with other on-chip circuits, without drastically increasing device footprint. Such a device can substitute currently employed bulky and expensive RF circuitry by bringing source and detector together on the same chip, empowering future improvements in high-frequency characterization and quantum technology.

Methods

Sample fabrication

The studied MoGe devices consist of Mo78Ge22/Au JJAs fabricated on top of Ti/Au transport bridges grown on natively oxidized silicon (300 nm silica) substrates. The substrates are first spin-coated with a co-PMMA/PMMA positive resist double layer. The transport bridge patterns are transferred to the resist by electron beam lithography (EBL) and later developed for 35 s in a 1:1 MIBK:IPA solution. The reaction is stopped by introducing the sample in IPA for 30 s. Then, a 5 nm Ti sticking layer and a 30 nm Au layer are grown over the pattern by molecular beam epitaxy, both with a growth rate of 0.18 Ås−1. The transport bridge is revealed after lift-off in acetone. A second spin-coating and EBL procedure is conducted to define the array patterns. Following development, a 25 nm layer of Mo78Ge22 and a 5 nm Au layer are deposited by pulsed laser deposition with pulse width 5–8 ns at a repetition rate of 80 Hz. The final device is ready after a second lift-off procedure in acetone. The results presented in this paper are obtained from devices fabricated on three separate Si/SiO2 substrates. Overall, we have verified radiation in the 4–8 GHz range arising from seven devices fabricated in five separate substrates, confirming the reproducibility of the effect. The NbTiN samples are fabricated on a 100-Si/SiO2 wafer with a 400 nm oxide layer grown via a wet oxidation process. First, a 5 nm Ti adhesion layer is evaporated using electron beam evaporation in a physical vapor deposition system (Lesker PVD 225) followed by an in-situ deposition of a 25 nm Au layer. Subsequently, a 25 nm NbTiN layer is sputtered on the gold surface using a near-ultra high vacuum magnetron sputtering system (DCA Metal Sputter System). The NbTiN pattern is defined using EBL in a Raith e-beam system with a negative-tone e-beam resist (ma-N 2403) which is developed in MF-319 developer. The NbTiN is then etched using reactive ion etching in an Oxford Plasmalab 100 system with a CF4/O2 plasma mixture (90 sccm CF4, 22.5 SCCM O2) to achieve the desired pattern. Afterward, the resulting structure is cleaned in MREM 400. The Au transport bridges are patterned using a subsequent round of EBL employing the same type of resist and developer as before. This pattern is etched in an Oxford Ionfab 300 system via secondary ion mass spectrometry, with a slight overetch to ensure complete removal of Au. Stable Si atom counts confirm this etching process. The resist is removed with MREM 400 and the final structures are verified with SEM imaging.

Low-temperature transport and RF measurements

Low-temperature (0.3–4.2 K) measurements were carried out in a Janis He3-SSV-2 cryostat customized for measurements in the 4–8 GHz range, depicted in Fig. 5. Perpendicular magnetic fields are applied in the sample space using a superconducting coil that allows fields up to 7 T, the required current is supplied using a Keithley 2400 source. The input RF line is attenuated by 60 dB. The output line has a non-reciprocal double-stage isolator (LNF-CICIC4_8A 4–8 GHz Cryogenic Dual Junction Circulator) at the 0.3 K temperature stage, blocking external radiation. A high electron mobility transistor (LNF-LNC4_8C) amplifies the signal with 42 dB at the 4 K stage. Both RF lines have a 50 Ω impedance. Additionally, eight DC lines allow to operate the devices and measure their VI characteristics. For the emission experiments, a room-temperature π-filter with a cutoff frequency of 1 MHz and a low-temperature LC copper powder filter are used to strongly attenuate unwanted signals through the DC lines in the 10 kHz–10 GHz range. These filter stages are not present for the detection measurements. Bias currents are applied using a Keithley 2400 sourcemeter, while the sample voltage is monitored by a Keithley 2182A nanovoltmeter. The RF signal generated by the sample is amplified by 30 dB at room temperature and detected with a frequency sweep using a FSIQ26 signal analyzer from Rhode & Schwarz. For the detection experiments, the RF excitation is provided by a signal generator SMY02 by Rhode & Schwarz, with a maximum frequency of 2 GHz. The RF voltage source acts as an RF current source because its impedance is large compared to the sample impedance.

Fig. 5: Schematic representation of the cryostat used in the radio frequency (RF) experiments.
figure 5

The DC lines in cyan are filtered at room temperature using π-filters and at the 300 mK stage using a home-made copper powder filter. The resulting RF output signal passes the circulator at 300 mK, gets amplified by a high-electron-mobility-transistor amplifier (HEMT) at 4 K and again at room temperature, and then passes through a DC blocker to the spectrum analyzer (SA). The input RF line (in red) for the Shapiro measurements is attenuated by a total of 60 dB.

Full size image

List of devices

An overview of the samples with their relevant design parameters is shown in Table 1. The list contains the device number, the superconducting material, the position on the device (top or bottom) and geometrical parameters dx, dy, Sx, Sy (see Fig. 1) and Nx, while Ny = 14. With the exception of Device 2, all devices have two JJA, one at the top and another at the bottom bridge, as represented schematically in Fig. 1a. The devices on which we report are those having the same number of islands on the top and bottom bridge, allowing for a direct comparison between their behavior. Similar and consistent high-frequency emission was nevertheless detected for all other devices, irrespective of the number of junctions.

Table 1 List of design parameters for all the reported samples, the number of islands perpendicular the current direction Ny = 14 is fixed for all devices
Full size table

Data analysis

Following the measurement of each emission spectrum, a background signal was recorded with a signal analyzer when no bias was applied, which was subtracted from the data. The resulting spectrum was then compensated to account for 72 dB of amplification in the output line. The emission spectra were analyzed using Voigt function fits. While a single junction is expected to exhibit a Lorentzian lineshape, small Gaussian deviations in properties across the JJA can result in a broadening of the lineshape. Consequently, the Voigt function, which represents a convolution of a Lorentzian and a Gaussian, provided a more accurate representation of the observed lineshape.

White noise generation

If the JJAs are biased by DC currents above Ic of the MoGe islands, in the range of 6–6.5 mA and at 300 mK, no Josephson radiation is expected as all components of the device are in the normal state. Therefore, the dissipating currents running through the device will cause Joule heating in the metallic transport bridge, inducing Johnson noise, with a power spectral density S = 4kBTR, independent of ν74. Through this process, the transport bridge acts as a source of white noise radiation, equally emitting at all frequencies.