Incorporating external fields in analog Ising machines

Abstract

Ising machines are specialized devices designed to efficiently solve combinatorial optimization problems. They consist of artificial spins that evolve towards a low-energy configuration representing a problem’s solution. Most realistic problems require both spin-spin couplings and external fields. In Ising machines with analog spins, these interactions scale differently with the continuous spin amplitudes, leading to imbalances that affect performance. Various techniques have been proposed to mitigate this issue, but their performance has not been benchmarked. We address this gap through a numerical analysis. We evaluate the time-to-solution of these methods across three distinct problem classes with up to 2400 spins. Our results show that the most effective way to incorporate external fields is through an approach where the spin interactions are proportional to the spin signs, rather than their continuous amplitudes.

Introduction

Combinatorial optimization problems (COPs) lie at the heart of numerous computational challenges in disciplines that range from industry to fundamental science. Some examples are problems in logistics¹, finance², biology^3,4, job scheduling⁵, and traffic flow regulation⁶. Many of these problems are nondeterministic polynomial-time (NP) complete, making it exceptionally challenging to develop efficient algorithms to solve them. Today, such problems are demanding vast amounts of energy, with high-performance computing centers persistently dedicating substantial resources to them⁷.

One promising solution is the use of specialized hardware rather than general-purpose digital computers. More specifically, there has been a surge of interest in Ising machines (IMs): hardware implementations designed to find low-energy states of the Ising model, defined by the following Hamiltonian:

$${{\mathcal{H}}}\left(\{{\sigma }_{i}\}\right)=-\frac{1}{2}{\sum }_{i,j}^{N}{J}_{ij}{\sigma }_{i}{\sigma }_{j}-{\sum }_{i}^{N}{h}_{i}{\sigma }_{i}.$$

(1)

Here, σ_i ∈ { − 1, 1} are Ising spins, and N is the total number of spins. J_ij and h_i denote the real-valued strengths of the spin couplings and external fields, respectively.

It has been shown that it is possible to formulate any problem within the NP complexity class as an Ising model with only polynomial overhead^8,9. The ground state, i.e., the configuration of binary spins with the lowest energy according to Eq. (1), then corresponds to the optimal solution of the optimization problem.

Many IM implementations have been proposed so far¹⁰. Some implementations are constructed using spins that are intrinsically binary, such as implementations based on quantum annealing¹¹, probabilistic p-bits^12,13, spatial light modulators¹⁴, and memristor Hopfield neural networks¹⁵. Others utilize analog spins, which take continuous values while satisfying constraints that enforce both the COP structure and spin bistability. Examples are Ising machines based on degenerate optical parametric oscillators^16,17, opto-electric oscillators¹⁸, electrical resonators¹⁹, memristor crossbar arrays²⁰, and polariton condensates^21,22. In this paper, we focus on Ising machines with analog spins.

In general, analog IMs are modeled by a set of differential equations. The time evolution of the amplitude of spin i, denoted ${s}_{i}\in {\mathbb{R}}$, is described as:

$$\frac{d{s}_{i}}{dt}={{{\mathcal{F}}}}_{i}\left({s}_{i},\alpha ,\beta {I}_{i}\right),$$

(2)

where ${{\mathcal{F}}}$ is a nonlinear function, α is the linear gain, β is the interaction strength. I_i is the local field of spin i, which can be modeled as follows:

$${I}_{i}={\sum}_{j}{J}_{ij}{s}_{j}+{h}_{i}.$$

(3)

The IM’s energy, as given by Eq. (1), can be evaluated with spin amplitudes mapped to binary spins via ${\sigma }_{i}={{\rm{sgn}}}({s}_{i})$, where ${{\rm{sgn}}}(\cdot )$ denotes the sign function.

While some studies have considered tasks that require external fields^{23,24,25,26,27,28}, the emphasis in benchmarking IMs (both with binary and analog spins) remains largely on problems that do not require such fields, such as the Max-Cut problem²⁹. This focus contrasts with the requirements of most industrially relevant COPs, which necessitate external fields for their encoding into an IM³⁰.

For IMs with analog spins, implementing external fields can be challenging. This is clear from Eq. (3), where as the spin amplitudes decrease, the spin coupling terms (∝ J_ijs_j) are weakened relative to the external fields (∝ h_i), potentially causing the latter to dominate. Conversely, when spin amplitudes exceed one, the couplings may dominate instead. Since embedding a COP into an IM requires careful tuning of the values of J_ij and h_i, such imbalances may undermine the IM’s performance.

In the past, various techniques have been proposed to mitigate this issue^26,27, but their impact on the IM’s performance has not yet been benchmarked. In this work, we address this gap by conducting a numerical study. Moreover, we include an alternative method that substitutes J_ijs_j for ${J}_{ij}\,{{\rm{sgn}}}({s}_{j})$ in Eq. (3). This method was originally proposed for ballistic simulated bifurcation^31,32, a specific type of analog IM where ${{\mathcal{F}}}$ in Eq. (2) is a linear function (whereas a nonlinear function is used in this work) and spins evolve with momentum rather than following a gradient method. While this binarization method is uncommon in other analog IMs¹⁰ and has not been included in earlier studies of imbalances between spin couplings and external fields³³, we will show that it is particularly effective for incorporating external fields and outperforms the previously proposed techniques.

We apply all methods to three different problem classes, each requiring a distinct mapping to embed problems into an Ising machine: (a) Sherrington–Kirkpatrick (SK) Hamiltonians with random external fields, which we generated ourselves, (b) quadratic unconstrained binary optimization (QUBO) problems from BiqMac’s Beasley benchmark set³⁴, and (c) Max-3-Cut problems, where graphs are generated using the Rudy generator³⁵. While SK problems serve as a general benchmark—sampling J_ij and h_i from Gaussian distributions rather than relying on a structured mapping—the other two classes represent typical ways external fields emerge in problem embeddings (see “Results” for details).

In addition to the techniques discussed above, we also explore a simple recalibration of the external fields by rescaling them with a constant factor, i.e., replacing h_i by ζh_i in Eqs. (1) and (3) where $\zeta \in {\mathbb{R}}$. This adjustment essentially modifies the embedding process of COPs and can be easily combined with any of the prior methods. This constant rescaling has been proposed in previous works^27,33, where it was suggested to enhance the performance of IMs. In this work, we show that such a constant rescaling can indeed be necessary when encoding COPs with soft constraints, such as for Max-3-Cut problems. However, for COPs without such constraints, such as in the SK and Beasley problems, this rescaling removes the guarantee that the ground-state spin configuration solves the COP, resulting in an incorrect COP embedding.

Methods

Transfer function

Ising machines with analog spins rely on nonlinear dynamics to establish bistable spin amplitudes. This bistability is typically realized through a pitchfork bifurcation, which can be achieved via different nonlinear functions ${{\mathcal{F}}}$ in Eq. (2). A prior study compared many nonlinear functions³⁶, and showed that the following nonlinearity achieves the best performance:

$$\frac{d{s}_{i}}{dt}=-{s}_{i}+\tanh \left(\alpha {s}_{i}+\beta {I}_{i}\right).$$

(4)

This nonlinearity is commonly employed to incorporate the saturation of the spin amplitudes, often observed in experimental setups^18,37. Its good performance can be attributed to its inherent suppression of amplitude inhomogeneity, a common source of error when mapping COPs to IMs with analog spins³⁶. Moreover, this nonlinearity is particularly well-suited when external fields are present. Indeed, as described in the introduction, external fields (∝ h_is_i) dominate over the spin couplings (∝ J_ijs_is_j) when spin amplitudes are small (|s_i|≪ 1). Conversely, spin couplings dominate when the spin amplitudes exceed one. Eq. (4) now constrains the spin amplitudes to the range [− 1, 1], thereby excluding the latter scenario. For these reasons, the remainder of this work exclusively considers the hyperbolic tangent nonlinearity.

Annealing scheme

At the start of a simulation of the IM, the spin amplitudes are initialized near zero, and their evolution is tracked over time by numerically integrating Eq. (4). Specific details are provided in Supplementary Note 1. The interaction strength β is increased at each timestep, following a commonly used linear annealing scheme^38,39:

$$\beta (t)={\beta }_{0}+{v}_{\beta }t.$$

(5)

Here, β₀ is the initial β-value and v_β is the annealing speed. As also detailed in Supplementary Note 1, we choose a relatively low and constant noise strength while integrating Eq. (4).

Methods to incorporate external fields

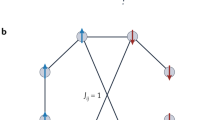
In this manuscript, we will compare the performance of four methods for incorporating external fields, which we outline below. For each of these methods, we will illustrate the spin dynamics using a 3-spin COP, which is visualized in Fig. 1a, and for which the ground state configuration is (–1,1,–1).

Fig. 1: Four methods of incorporating external fields applied to an exemplary COP.

a Example of a 3-spin COP with ground state configuration (–1,1,–1). The spins are indicated as σ₀, σ₁, and σ₂. Spin-spin couplings J_ij are shown as wavy lines, and external fields h_i as red arrows. The ground state is indicated with blue arrows. (b)-(e) Spin evolution under the methods described in Eqs. (3) and (6) to (8), respectively. In b, the initial direction of the spins (dotted lines) is given by h_i/(1 − α), independently of the spin-spin couplings J_ij. Methods in c–e are designed to prevent the external fields from dominating the spin-spin couplings. The inset in e shows a zoom-in near β = 0.

The original external fields

All considered methods essentially modify the local field of spin i, as originally defined by Eq. (3). Hence, we will further refer to Eq. (3) as the “original external fields”. For the 3-spin COP of Fig. 1a, the evolution of the spin amplitudes under Eqs. (3) to (5) is visualized in Fig. 1b where β₀ = 0. As we start to increase β, the spins initially follow the dotted lines. As shown in Supplementary Note 2, these dotted lines correspond to $\frac{d{s}_{i}}{d\beta }=\frac{{h}_{i}}{1-\alpha }$, such that the spin dynamics at low β are determined by the external fields h_i, independent of the spin couplings J_ij. As the amplitudes grow, the spin couplings strengthen (the first term in Eq. (3) grows), causing spin 2 to flip and leading to the ground state configuration (-1,1,-1).

Thus, for this simple COP, the IM successfully overcomes the initial field-driven behavior. However, for more complex problems, this may not always be the case. As discussed in the introduction section, an imbalance between the spin couplings and the external fields can undermine the validity of the COP embedding. This occurs because the information encoded in the couplings J_ij is effectively ignored when |s_i| is small (cf. Eq. (3)), even though it is essential for solving the COP. In such cases, the Ising spins are drawn toward the sign(h) configuration, which acts as a distractor in the spin dynamics.

The mean absolute spin method

One way to address the imbalance between spin couplings and the external fields is to rescale the external fields with the mean of the absolute values of the spin amplitudes²⁷, leading to the following local field:

$${I}_{i}={\sum }_{j=1}^{N}{J}_{ij}{s}_{j}+{h}_{i}\frac{1}{N}{\sum}_{k}\left\vert {s}_{k}\right\vert .$$

(6)

This approach ensures that the external field terms scale linearly with the spin amplitudes, consistent with the scaling of the spin couplings.

Figure 1c shows the evolution of the spins following this approach. We observe that the spin amplitudes remain zero until they bifurcate into the ground-state solution. Hence, this method prevents the external fields from dominating over the spin couplings.

We observe that the origin (s_i = 0, ∀ i) is a stable fixed point up to a certain β value, at which the spins bifurcate. Ideally, β₀ would be set equal to this critical value. However, as explained in Supplementary Note 3, determining this exact value is challenging, and we further choose to set β₀ = 0 when using the mean absolute spin method. Although a heuristic could, in principle, estimate β₀ more accurately and potentially improve performance, we do not explore that direction here. As shown in Supplementary Note 3, the choice of β₀ has only a moderate effect and does not influence our conclusions in the remainder of this work.

The auxiliary spin method

An alternative method to rescale the external fields is provided by the “auxiliary spin method”²⁶. It introduces an auxiliary spin amplitude s_N+1, and replaces each external field h_i by a coupling between spin i and the auxiliary spin. The local field of spin i is modified as follows:

$${I}_{i} = \left\{\begin{array}{ll}{\sum }_{j=1}^{N}{J}_{ij}{s}_{j}+{h}_{i}{s}_{N+1},\quad &{{\rm{if}}}\,i < N+1,\\ {\sum }_{j=1}^{N}{h}_{j}{s}_{j},\hfill &{{\rm{if}}}\,i=N+1,\end{array}\right.\\ = {\sum }_{j=1}^{N+1}{J}_{ij}^{{\prime} }{s}_{j},\quad {{\rm{where}}}\,{{{\bf{J}}}}^{{\prime} }=\left[\begin{array}{cc}{{\bf{J}}}&{{\bf{h}}}\\ {{{\bf{h}}}}^{T}&0\end{array}\right].$$

(7)

Hence, applying this technique only requires the implementation of spin couplings.

It can be shown that if s_opt is the optimal solution to the original Ising problem of Eq. (1), then (s_opt, 1) and ( − s_opt, − 1) are degenerate solutions of the system with the auxiliary spin²⁶. Hence, if the auxiliary spin amplitude takes a negative value, all spins are flipped before evaluating the IM’s energy via Eq. (1).

Figure 1d illustrates the evolution of the spins using this method. Similar to the mean absolute spin approach, the spin amplitudes remain zero until they bifurcate into the ground-state solution. However, for the auxiliary spin method, we show in Supplementary Note 4 that the β-value at this bifurcation can be easily calculated, allowing us to set β₀ to this value.

The spin sign method

The spin sign method^31,32 defines the local field of spin i as follows:

$${I}_{i}={\sum}_{j}{J}_{ij}\,{{\rm{sgn}}}({s}_{j})+{h}_{i}.$$

(8)

Figure 1e shows the evolution of the spins following this approach where we set β₀ = 0. The inset provides a more detailed view near β₀. For this simple COP, we observe that the spin sign method first explores the surroundings of the origin. Once the signs of the spins correspond to the COP’s solution, the local fields remain at constant values such that the spin amplitudes continue to grow linearly until they saturate.

To the best of our knowledge, the spin sign method has not previously been studied in detail for COPs with external fields. We hypothesize that it is particularly well-suited for this more realistic setting, as it inherently preserves the relative magnitudes of the spin couplings with respect to the external fields, i.e., as defined in the binary Hamiltonian of Eq. (1). That is, these magnitudes are directly determined by the values of J_ij and h_i and are independent of the continuous spin amplitudes s_i. Whereas both the mean absolute spin method and the auxiliary spin method approximately achieve this balance by multiplying the external fields with a continuously-valued time-varying correction factor, the spin sign method achieves this in a more direct and accurate way (also see Supplementary Note 12).

Scaling external fields by a constant

Previous works have proposed to rescale the external fields by a constant $\zeta \in {\mathbb{R}}$^27,33, thereby substituting h_i for ζh_i in Eqs. (3) and (6) to (8). However, these works did not provide any insights into why this rescaling technique should be adopted and for which COPs it is effective.

Embedding a COP into an IM determines the values of J_ij and h_i. For many COPs, such as SK problems and Beasley problems, this embedding guarantees that the ground state of Eq. (1) corresponds to a solution of the COP. Hence, it is counterintuitive to set ζ ≠ 1, since this modifies the energy landscape of Eq. (1), thereby eliminating this guarantee. For example, if we substitute h_i with ζh_i in Eq. (1) and set ζ ≫ 1, the external fields dominate the system, resulting in a ground-state configuration ${{\rm{sgn}}}({h}_{i})$. In this scenario, the spin couplings—which encode information that is essential to solving the COP—are effectively disregarded.

For some problems, such as Max-3-cut, so-called soft constraints are used to embed a COP. These constraints are implemented by adding terms to the energy function of Eq. (1), such that violating these constraints incurs an energy penalty. These terms come with a prefactor that indicates the importance of the corresponding constraint. However, when using soft constraints, the ground-state configuration will only solve the COP if the prefactors of all constraints are set to appropriate values. Specifically, for Max-3-Cut problems, we will demonstrate that determining the correct prefactor is challenging for realistically-sized COPs, but surprisingly, this issue can be resolved by applying a factor ζ ≈ 0.6.

Results

In this section, we discuss the performance of the rescaling techniques introduced in the previous section. We do this using three different problem classes, which are introduced in the following subsections.

The IM’s performance is evaluated using the time-to-solution (TTS) metric, which represents the total time needed to reach the target state with 99% probability. It is defined as:

$${{\rm{TTS}}}=\left\{\begin{array}{ll}T,\hfill &{{\rm{if}}}\,P > 0.99,\hfill \\ T\frac{\log (0.01)}{\log (1-P)},\quad &{{\rm{if}}}\,0 < P\le 0.99,\\ \infty ,\hfill &{{\rm{if}}}\,P=0,\hfill \end{array}\right.$$

(9)

where P is the probability of reaching the target state, and T is the (dimensionless) time window over which Eq. (4) is integrated. Whenever possible, the ground state is chosen as the target. When the ground state is unknown, a target energy is chosen corresponding to the best-known solution, as detailed in later sections.

Whereas T is typically treated as a hyperparameter⁴⁰, which leads to the performance measure ${\min }_{T}{{\rm{TTS}}}\left(T,P(T)\right)$, here we choose to set T as the average simulation time required to reach the target state across successful runs. This choice provides a practical approximation of the TTS, as it demands fewer computational resources for evaluation, compared to treating T as a hyperparameter. We estimate the values of P and T over 100 runs.

The performance of the IM depends on the choice of the linear gain α and the annealing speed v_β (cf. Eqs. (4) and (5)). Given a COP and a method to incorporate external fields (cf. “Methods”), these hyperparameters are optimized, and the corresponding value of ${\min }_{\alpha ,{v}_{\beta }}{{\rm{TTS}}}$ is reported. For the Max-3-Cut problems, an additional hyperparameter specific to the Ising formulation is optimized (see later). Unless stated otherwise, the constant rescaling factor ζ, introduced in the previous section, is set to 1. Where relevant, it is treated as an additional hyperparameter. Further details about the hyperparameter optimization procedure are provided in the Supplementary Note 1.

Sherrington–Kirkpatrick Hamiltonians with random external fields

The first type of problem we consider is a Sherrington–Kirkpatrick (SK) spin glass. The goal of this task is to find the configuration of binary spins σ_i ∈ { − 1, 1} that minimizes the Hamiltonian in Eq. (1), where the elements of the coupling matrix are drawn from a Gaussian distribution⁴¹ (with zero mean and standard deviation 1). We extend the SK spin glass model with external fields that are drawn from the same Gaussian distribution.

We considered problems with 50, 100, 150, and 200 spins, generating 10 instances for each size. For problems with 50 spins, the ground state was obtained via an exact solver⁴². The larger problems could not be solved using this exact solver with our computational resources. Therefore, we used the state-of-the-art approximate solver PySA, which is based on simulated annealing with parallel tempering⁴³. The parameters used can be found in Supplementary Note 5. The energies obtained by this solver are equal to the lowest energies found by the Ising machine for problems with 100 and 150 spins. However, for the problems with 200 spins, the Ising machine sometimes finds lower energies than PySA. Therefore, we define the lowest energy found by the Ising machine (across all methods to incorporate external fields) as the target energy. Since our primary focus is on the relative comparison of different methods for implementing external fields, this choice has no impact on the validity of our conclusions.

Figure 2 compares the various methods to incorporate external fields (cf. “Methods”) in terms of TTS when solving SK problems. Each subfigure compares two methods. Each dot on the plot represents a problem. The x (y)-coordinate of a dot is the TTS when the problem is solved using the method on the horizontal (vertical) axis. Hence, the diagonal line represents the situation where both methods have the same TTS. A dot in the upper left (lower right) of figure denotes a problem that is solved faster by the method on the horizontal (vertical) axis.

Fig. 2: Performance comparison between different methods to incorporate external fields for SK Hamiltonians with random external fields.

Comparison of the time-to-solution (TTS) for SK Hamiltonians solved using the spin sign method (Eq. (8)) compared to the three alternative approaches: a the original external fields (Eq. (3)), b the auxiliary spin method (Eq. (7)) and c the mean absolute spin method (Eq. (6)). Dots in the grey area on the right denote combinatorial optimization problems (COPs) that could be solved by the spin sign method within the allocated compute time of ${t}_{\max }=1{0}^{4}$, but not by the method on the x-axis (TTS = ∞, SR = 0). The spin sign method can solve more problems within the allocated time than the other methods, and it generally requires less time to do so.

Figure 2a compares the original external field method of Eq. (3) with the spin sign method of Eq. (7). 22 of the 40 COPs are positioned in the grey region on the right, indicating TTS = ∞ when using the original external fields. This means that for each of these 22 problems and across all tested hyperparameter values, the original external fields failed to reach the target energy in all 100 runs within the maximum time of ${t}_{\max }=1{0}^{4}$ (cf. Eq. (9)). In contrast, the spin sign method successfully solved these instances, yielding a finite TTS. The remaining 18 COPs could be solved by either of the two methods. 14 of them were solved faster by the original external fields, while 4 were solved faster using the spin sign method.

In both Fig. 2b and c, one of the 40 problems appears in the grey region on the right. Although not visible in the plots, this data point corresponds to the same COP, which could only be solved by the spin sign method, while the other three methods failed.

Figure 2b and c appear similar, but Fig. (c) has more dots below the diagonal, indicating that the auxiliary spin method is generally faster than the mean absolute spin method.

In Supplementary Note 10, we provide the values of the success rate and the average runtime T of successful runs corresponding to the TTS values of Fig. 2.

Overall, the spin sign method performs best for the SK problems. While it solves all considered COPs, the original external fields fail on more than half. Both the auxiliary spin method and the mean absolute spin method solve all but one COP; however, the latter is generally slower, while the former is only slightly slower than the spin sign method on average, making it the second-best-performing for these problems.

As discussed in “Methods”, previous works proposed to scale external fields by a constant factor $\zeta \in {\mathbb{R}}$. Ref. ³³ indicates that the IM’s performance, averaged over SK problems with at most 16 spins, is highly sensitive to the choice of ζ. However, in the Supplementary Note 6, we show that this sensitivity is due to the small problem size. Our results indicate that applying a scaling factor different from 1 is generally not beneficial here, reinforcing that ζ = 1 is the best choice for solving SK problems. This is explained by the fact that setting ζ ≠ 1 removes the guarantee that the ground state spin corresponds to the problem’s optimal solution.

Quadratic unconstrained binary optimization problems

The problems analyzed in this section are the Beasley instances from the BiqMac library³⁴. These are examples of QUBO problems, meaning that they are defined using binary variables x_i ∈ {0, 1}. Given a symmetric matrix Q, the goal is to find the configuration x that minimizes the objective function x^TQx.

These problems can be mapped to the Ising model using the following transformation:

$${x}_{i}=\frac{{\sigma }_{i}+1}{2}.$$

(10)

While the original QUBO formulations of these problems include only quadratic terms (∝ x_ix_j), Supplementary Note 7 shows that applying Eq. (10) results in both spin couplings (∝ σ_iσ_j) and external fields (∝ σ_i). Many COPs of interest are naturally defined as QUBO problems, making the transformation of Eq. (10) a common mechanism that gives rise to external fields in IMs.

The ground state energies for Beasley problems with up to 250 spins are provided in the BiqMac library³⁴. For problems with 500 spins, the exact ground state is not known. For these problems, we use the upper bounds provided in the BiqMac library³⁴ as target values.

Figure 3 compares the various methods to incorporate external fields, as defined in “Methods”, in terms of TTS, when applied to the Beasley problems. Figure 3a compares the original external fields of Eq. (3) to the spin sign method of Eq. (8). 17 of the 40 COPs appear at the rightmost edge of the plot, indicating that they could not be solved using the original external fields, while they could be solved using the spin sign method.

Fig. 3: Performance comparison between different methods to incorporate external fields for Beasley problems.

Comparison of the time-to-solution (TTS) for Beasley problems solved using the spin sign method (Eq. (8)) compared to the three alternative approaches: a the original external fields (Eq. (3)), b the auxiliary spin method (Eq. (7)) and c the mean absolute spin method (Eq. (6)). Dots in the grey area on the right denote combinatorial optimization problems (COPs) that could be solved by the spin sign method within the allocated compute time of ${t}_{\max }=1{0}^{4}$, but not by the method on the x-axis (TTS = ∞, SR = 0).

Figure 3b compares the auxiliary spin method of Eq. (7) with the spin sign method of Eq. (8). The plot looks similar to Fig. 3a, and our results indicate that the same 17 COPs at the right edge of Fig. 3a could also not be solved using the auxiliary spin method.

Figure 3c compares the mean absolute spin method of Eq. (6) with the spin sign method of Eq. (8). This time, only 5 COPs of the 40 could be solved exclusively by the spin sign method. Looking at the COPs that could be solved using either of the two methods, which are displayed in the white region of the plot, we see that the spin sign method generally reaches a solution faster.

Overall, we conclude from Fig. 3 that the spin sign method performs best as it can solve more Beasley problems than the other methods. The mean absolute spin method is the second-best-performing method as it solves more COPs than the original external fields and the auxiliary spin method. The latter two methods yield comparable performance.

As explained in “Methods”, it has been proposed in the past to multiply the external fields by a constant factor, but this removes the guarantee that the ground state spin configuration solves these problems. In Supplementary Note 6, we demonstrate that applying a factor different from 1 is generally not beneficial for Beasley problems, consistent with our findings for SK problems.

Max-3-Cut problems

The goal of the Max-3-Cut problem is to partition the vertices of an undirected graph into three sets, maximizing the number of edges that connect different sets, i.e., maximizing the so-called cut-value. In other words, we seek the best possible vertex coloring using 3 colors. In this section, we consider graphs generated using the rudy generator^34,35,44,45. To benchmark the IM’s performance, the problems are solved to optimality using the publicly available max_k_cut package⁴².

Max-3-Cut serves as a fundamental example of a COP requiring multivariate integer variables. Such problems are native to the Potts model, an extension of the Ising model, and are typically embedded in an Ising machine using one-hot encoding. This encoding introduces external fields, as will be explained in the next section.

Ising formulation

We utilize the Max-3-Cut Ising formulation as described in Ref. ³⁰. We denote the sets of vertices and edges in the graph as V and E, respectively. For every vertex v ∈ V, a triplet of binary variables is introduced: x_v,i where i ∈ {1, 2, 3}. x_v,i equals 1 if vertex v has color i, and 0 otherwise. The energy is defined as follows:

$${{\mathcal{H}}}=A{\sum}_{v\in V}{\left(1-{\sum }_{i = 1}^{3}{x}_{v,i}\right)}^{2}+B{\sum}_{(uv)\in E}{\sum }_{i=1}^{3}{x}_{u,i}{x}_{v,i},$$

(11)

where A and B are positive scalars. The first term enforces that all variable triplets {x_v,1, x_v,2, x_v,3} are one-hot encoded since this positive term only vanishes if every triplet contains a single 1 and two 0’s, ensuring the vertex colors are well-defined. The second term enforces the maximization of the cut value since an energy penalty is added for every edge that connects vertices with the same color. The ratio B/A denotes the relative importance of the two constraints.

The binary variables in Eq. (11) can be transformed to Ising spins using Eq. (10). As detailed in Supplementary Note 7, this allows us to rewrite the energy as follows:

$${{\mathcal{H}}}= \, \frac{A}{4}{\sum }_{v}{\sum }_{i\ne j}{\sigma }_{v,i}{\sigma }_{v,j}+\frac{B}{4}{\sum }_{(uv)\in E}{\sum }_{i=1}^{3}{\sigma }_{u,i}{\sigma }_{v,i}\\ +\zeta {\sum }_{v}{\sum }_{i=1}^{3}\left(\frac{A}{2}+\frac{B}{4}{{\rm{deg }}}(v)\right){\sigma }_{v,i},$$

(12)

where deg(v) denotes the degree of vertex v. Note that we multiplied the external fields (∝ σ_v,i) by $\zeta \in {\mathbb{R}}$. Whereas Eqs. (11) and (12) are only strictly equivalent when ζ = 1, we will show in the next section that setting ζ ≠ 1 is a necessary modification for the IM to achieve good performance.

Scaling external fields by a constant counters mapping errors

As explained in “Methods”, it is generally not expected that rescaling the external fields with ζ ≠ 1 will improve the performance of an IM. Such a rescaling can eliminate the guarantee that the ground-state configuration solves the COP in question. In the previous sections, we confirmed that ζ is generally best put to 1 when solving an SK problem or Beasley problem.

However, we will show now that this is not the case for the Max-3-Cut mapping of Eq. (12). The inspiration for this approach comes from Ref. ²⁷, which found that setting ζ ≈ 0.6 is optimal for a structure-based drug design problem of which the mapping also contains one-hot encoding constraints and edge constraints, similar to Eq. (12), along with additional external fields. While the usefulness of this rescaling was observed, its underlying reasons were not explained. In this section, we will clarify why this rescaling works for Max-3-Cut.

First, we show that all implementation methods for external fields fail when ζ = 1, but not when ζ ≈ 0.6. For each of these methods, Fig. 4 compares the case where ζ is fixed at 1 to the case where ζ is optimized within [0, 1.2]. In other words, the x-axis represents ${\min }_{\alpha ,{v}_{\beta },\frac{B}{A}}{{\rm{TTS}}}$ for ζ = 1, while the y-axis represents ${\min }_{\alpha ,{v}_{\beta },\frac{B}{A},\zeta }{{\rm{TTS}}}$. As expected, all points lie on or below the diagonal, since tuning ζ can only maintain or improve performance relative to fixing ζ = 1. Across all four methods, several problems fall into the gray region on the right side of the figure. These instances cannot be solved with ζ = 1 but become solvable when ζ is optimized within [0, 1.2]. Many of the remaining points show that optimizing ζ can yield improvements in TTS by several orders of magnitude.

Fig. 4: Performance comparison between using ζ = 1 and the optimal ζ for Max-3-Cut problems.

Comparison of the time-to-solution (TTS) for Max-3-Cut problems between using ζ = 1 and using the optimal ζ that minimizes the TTS. Results are shown for a the original external fields (Eq. (3)), b the auxiliary spin method (Eq. (7)), c the mean absolute spin method (Eq. (6)) and d the spin sign method (Eq. (8)). Data points in the grey area on the right denote combinatorial optimization problems (COPs) that could not be solved using ζ = 1 (TTS = ∞, SR = 0), given the allocated compute time of ${t}_{\max }=1{0}^{4}$.

Figure 5 shows the optimal value of ζ as a function of the graph size. Each data point denotes the average optimal value across 10 problems of the same size. The standard deviation is represented by a shaded area. For all four rescaling methods, the optimal value of ζ converges to ~0.6. Although the optimal ζ may deviate from 0.6 in some cases, fixing ζ = 0.6 generally yields comparable performance to using the instance-specific optimal value, as shown in Supplementary Note 8. This is not the case for other fixed values such as ζ = 0.4 or ζ = 0.8, which tend to result in worse performance.

Fig. 5: Optimal ζ values (which minimize TTS) as a function of the number of spins.

Each dot represents the mean optimal value across 10 Max-3-Cut problems. Shaded areas represent the standard deviation.

This result is consistent with a prior study that identified ζ = 0.6 as the optimal value for a similar problem that also uses one-hot encoding, but with k > 3²⁷ (recall that k = 3 here). This suggests that the value ζ = 0.6 holds for a broader class of problems using one-hot encoding.

We now show that the reason why this rescaling is necessary stems from the structure of Eq. (12). As explained in “Methods”, the ground state configuration of a mapping that contains soft constraints will only solve the COP under consideration when the prefactors of those constraints are set to adequate values. It is often guaranteed that good values for these prefactors exist, but they are not necessarily a priori known³⁰. Consequently, given a value of B/A, we can determine the error of the mapping in Eq. (12) as follows. On the one hand, we obtain the highest achievable cut-value (the number of edges connecting different sets in the partition) via an exact Max-k-Cut solver⁴². On the other hand, we determine the cut-value of the ground state of Eq. (12) via an exhaustive search over the spin configurations. The difference between these respective cut values is defined as the error.

Figure 6 shows the error of Eq. (12) as a function of B/A and ζ for an arbitrary Max-3-Cut problem of 30 spins. In the white region, outlined by a green dashed line, the ground-state configuration of Eq. (12) correctly solves the COP. For the blue cells, we verified numerically that the one-hot encoding constraints (the terms of Eq. (12) with prefactor A) are violated, leading to ill-defined vertex colors. Consequently, the ground-state configuration is not a valid solution in these cells, such that the error is nonzero.

Fig. 6: Error of the Max-3-Cut mapping (Eq. (12)) as a function of $\frac{B}{A}$ and ζ for the g05_10.0 graph.

For every set of values $(\frac{B}{A},\zeta )$, the ground state configuration of Eq. (12) is determined via exhaustive search. The error is defined as the difference between the cut value of this configuration and the optimal cut value (obtained via an exact solver⁴²). The region where the ground-state configuration solves the Max-3-Cut problem is surrounded by a green dashed line. Grey cells indicate that the ground state is degenerate, including at least one configuration that does not solve the Max-3-Cut problem.

It is important to note that in Fig. 6, the range of valid B/A values is broader for ζ = 0.6 compared to ζ = 1. In general, as the graph size increases for ζ = 1, it turns out that the mapping remains correct only for progressively smaller values of B/A, as larger values violate the one-hot encoding constraints. Interestingly, this issue does not arise for ζ = 0.6. As detailed in Supplementary Note 9, we confirmed these findings for small graphs by evaluating the error of Eq. (12) (requiring an exhaustive search as also used in Fig. 6) and extended them to larger graphs based on the strong correlation between the correctness of the mapping and the success rate.

Although decreasing B/A could theoretically eliminate mapping errors at ζ = 1, this would require an unrealistic resolution of the interaction parameters, making the approach impractical. In contrast, choosing ζ = 0.6 yields good performance across a much broader range of B/A values, significantly reducing sensitivity to parameter choices. Moreover, as shown in Supplementary Note 8, using ζ = 0.6 generally results in similar TTS as the optimal ζ ∈ [0, 1.2]. Hence, we conclude that setting ζ = 0.6 effectively mitigates mapping errors caused by violations of the one-hot encoding constraint, without requiring impractically small values of B/A.

Comparison of external field implementations

Figure 7 compares the TTS of the methods to incorporate external fields (cf. “Methods”) for Max-3-Cut problems with ζ = 0.6. In addition to the graphs studied earlier in this section, we now include the first five graphs from the Gset benchmark set⁴⁵. They each consist of 800 graph nodes, corresponding to 2400 Ising spins. Their target energies for the TTS measure are given by the best known solutions from Ref. ⁴⁶. Most data points lie below the diagonal or in the grey area on the right, indicating that the spin sign method generally outperforms the alternative methods. Its dominance is particularly clear for the larger Gset instances: the spin sign method successfully solves all five, whereas the other methods generally fail. Only one instance, G4, is also solvable using the auxiliary spin method, and in this case, it achieves a solution roughly three times faster. However, the auxiliary spin method fails to solve the remaining four problems, highlighting the superior reliability, performance, and scalability of the spin sign method. The maximally achieved cut-values for each of the methods are provided in Supplementary Note 11. Overall, as with the SK and Beasley problems, we find that it again performs best for the Max-3-Cut problems, but that a key prerequisite for good performance is setting ζ ≈ 0.6.

Fig. 7: Performance comparison between different methods to incorporate external fields for Max-3-Cut problems.

Comparison of the time-to-solution (TTS) for Max-3-Cut problems, using ζ = 0.6, solved using the spin sign method (Eq. (8)) compared to the three alternative approaches: a the original external fields (Eq. (3)), b the auxiliary spin method (Eq. (7)) and c the mean absolute spin method (Eq. (6)). Dots in the grey area on the right denote combinatorial optimization problems (COPs) that could be solved by the spin sign method within the allocated compute time of ${t}_{\max }=1{0}^{4}$, but not by the method on the x-axis (TTS = ∞, SR = 0). The spin sign method generally solves the COPs faster than the other methods. We include 5 large-scale graphs (⋆) from the Gset benchmark set⁴⁵ to provide additional support for the scalability of the approach.

Hardware considerations

In the previous section, we have shown that the spin sign method is the most effective approach to incorporate external fields in analog IMs. Additionally, it can easily be implemented in hardware using, for example, a comparator in electronic systems. Moreover, analog spin amplitudes are often measured before computing the local fields I_i^{16,17,18,19,20,21,22}. In such setups, a one-bit resolution measurement device can enforce the spin sign method, provided this only affects the local field computation and preserves the analog nature of the spins.

Whereas the spin sign method offers the best performance and can be implemented in hardware relatively easily, the mean absolute spin method performs worse and further complicates the calculation of I_i. Indeed, in addition to the standard matrix-vector multiplication, it requires computing the mean absolute spin value. This is a global operation: at each iteration, the amplitudes of all spins must be collected, their absolute values summed, and the result divided by N. Unlike local operations, which are typically easier to implement in hardware, this global aggregation demands extending an existing platform with additional electrical circuitry or optical components to perform the required computation.

The auxiliary spin method, though less effective than the spin sign method, may still be useful when directly implementing external fields in hardware is challenging. Indeed, some analog hardware implementations of Ising machines that perform matrix-vector multiplications without relying on digital components like field-programmable gate arrays are specifically optimized for pairwise spin interactions^14,47. Adding single-spin terms to incorporate external fields may require additional optical components or electrical circuitry, which could reduce scalability or stability. However, since the auxiliary spin must connect to all spins affected by an external field, it can pose difficulties in hardware that does not allow for all-to-all coupling^11,14,48. Moreover, while this method is often cited as a justification for excluding external fields from hardware implementations^26,31,48,49, we emphasize that this approach is not ideal, as it leads to suboptimal performance.

Hence, the spin sign method not only provides the best performance but is also relatively easy to implement compared to the auxiliary spin and mean absolute spin methods.

Conclusion

The initial implementation of external fields in IMs with analog spins, Eq. (3), is prone to imbalances in magnitude between the external fields and the spin couplings. To address this, the mean absolute spin method of Eq. (6) and the auxiliary spin method of Eq. (7) were proposed in the past.

In this work, we demonstrate that the spin sign method of Eq. (8) consistently outperforms the earlier approaches across three distinct problem classes. For SK, Beasley, and Max-3-Cut problems, it enables solving more COPs within the allotted time, and generally achieves faster solutions than any of the other methods.

Although the spin sign method was previously shown to be effective for ballistic simulated bifurcation^31,32, its use has remained largely confined to that setting, where ${{\mathcal{F}}}$ in Eq. (2) is linear and spin dynamics involve momentum. It has not been widely adopted in other analog IMs¹⁰ nor included in prior studies on balancing spin couplings and external fields³³. Moreover, to the best of our knowledge, it has not yet been studied in detail for problems with external fields. In this work, we show that the problems with external fields, which better represent real-world COPs, are exactly the scenarios where this method flourishes.

The reason for this is its inherent ability to preserve the relative magnitudes between spin couplings and external fields, such that they accurately describe the magnitudes of all terms in the binary Hamiltonian of Eq. (1). In contrast, the mean absolute spin method and auxiliary spin method essentially rely on heuristic time-varying rescalings of the external fields that only approximate this balance.

Such approximations can distort the energy landscape imposed on the IM, deviating from the intended Hamiltonian of Eq. (1). This is closely related to the problem of spin inhomogeneity, where frustration causes unequal spin amplitudes that attenuate the effective spin couplings and ultimately degrade performance^36,50. The spin sign method naturally alleviates such issues by preserving the correct relative magnitudes of external fields and spin couplings.

It is important to highlight that the auxiliary spin method falls short in performance, despite being widely used in practice. This approach is commonly adopted to avoid the direct implementation of external fields, meaning that only quadratic interactions need to be implemented^26,48,49. Our results show that this approach is not the most effective in practice. In contrast, adopting the spin-sign method can significantly improve IM performance.

Beyond refining IM dynamics, we shed light on the embedding process of certain COPs. Contrary to some prior works, we showed that the external fields should not be rescaled with a constant ζ ≠ 1 for problems without soft constraints, such as SK and Beasley problems. However, we confirmed that such a rescaling can be necessary when soft constraints are used, as in Max-3-Cut. While this necessity had been observed before, we identified the underlying reason: with ζ = 1, one-hot encoding constraints are often violated due to the finite resolution of interaction parameters. Choosing ζ ≈ 0.6 restores the embedding’s correctness for the problems considered here. Notably, prior work also found this value to be optimal for one-hot encoding with more than three states²⁷, suggesting its robustness. Since many COPs represent multivariate variables using one-hot encoding, this insight is valuable for the Ising machine community. Moreover, since real-world COPs often involve numerous soft constraints—particularly when using IMs—it may be worthwhile to explore whether similar rescalings could benefit other types of soft constraints.