Introduction

Temporal networks serve as fundamental models for describing associations and interactions in dynamic complex systems1,2,3,4,5,6, with applications across biology7, society8, and engineering9. In a typical temporal network, nodes represent elements, and links represent pairwise associations or interactions. Unlike static networks, links in temporal networks are intermittently active and display rich temporal features10,11,12,13,14. Topological structure15,16,17,18 and temporal properties19,20,21,22,23 jointly shape the dynamic characteristics on temporal networks. Empirical studies confirm that interactions frequently involve groups rather than only pairs24,25,26,27. Such higher-order interactions are not reducible to a linear superposition of pairwise links. Instead, they are more faithfully represented by simplicial complexes or hypergraphs28,29,30,31,32,33. Moreover, the presence of higher-order interactions often gives rise to nonlinear phenomena. Examples include discontinuous transitions, multistability, and intermittency, which exhibit significant difference from those on pairwise networks34,35,36,37. Consequently, complex systems with temporal higher-order interactions are likely to exhibit richer dynamical behaviors. Although still underexplored, some early studies have shown that temporal features in higher-order interaction networks can significantly affect dynamical behavior, including altering convergence speed and the steady states38,39.

Based on empirical data, studies of temporal higher-order interaction have revealed numerous nontrivial phenomena. Interactions of different orders exhibit heterogeneous activity levels and durations40,41. All orders display temporal burstiness40, and both intra- and cross-order interactions show complex correlations42. In various contexts, higher-order interactions follow distinct growth and decay dynamics40,41 and exhibit pronounced temporal-topological correlations43. In order to capture these features, several generative frameworks based on temporal simplicial complexes and hypergraphs have been proposed to capture these features41,42,44,45,46,47. Inspired by activity-driven models48, simplicial activity-driven model44 extends links to simplices, providing an analytically tractable model of temporal higher-order networks driven by node activity. Higher-order activity-driven model45 generalizes this framework to temporal hypergraphs. Emerging activity temporal hypergraph model47 further incorporates short- and long-term memory to reproduce realistic topological and temporal features. Another perspective focuses on individual behavior. Iacopini et al.41 reproduce empirical growth and decay dynamics by allowing individuals to switch between groups. Group attractiveness model46 embeds individuals in Euclidean space and uses spatial proximity to generate higher-order interactions. Discrete auto regressive hypergraph model42 directly formulates evolution among different orders of interactions and introduces memory effects to capture cross-order evolutions.

Most existing models treat higher-order interactions as fundamental modeling components. They specify either the probability distribution of higher-order interactions evolving or the transitions of each individual among different interactions. With the assumption that higher-order interactions already exist, most approaches focus on fitting real-world data, while few investigate the microscopic mechanisms underlying their emergence. In contexts such as face-to-face contact, high-resolution temporal data usually record only pairwise interactions49,50,51. Higher-order interactions are then inferred by identifying cliques of links that are activated within the same short time window41,42,44,45,46,47. However, empirical studies show that pairwise links usually exhibit low activity, which makes it unlikely for the independent co-occurrence of multiple links52. Recent work also indicates that link activations often depend on the states of other links23,53, and this dependency has been leveraged to predict the dynamics of temporal pairwise54 and higher-order55 networks. Therefore, it is crucial to reveal the emergence and evolution of higher-order interactions from microscopic pairwise link activity.

In this paper, we introduce a Pairwise-Induced Temporal Higher-Order Network model (PITHON) based on a simple collaborative mechanism among links. In PITHON, higher-order interactions are modeled as simplices, where an active k-simplex represents a temporal interaction among k + 1 individuals. Collaboration between pairwise interactions can lead to the spontaneous emergence of higher-order interactions, offering a potential explanation for the formation of temporal higher-order interactions observed in certain real systems. PITHON captures key empirical patterns including overall activity levels, interaction durations, cross-order dynamics, and temporal-topological correlations. PITHON offers flexible tuning capabilities to generate temporal higher-order networks, including underlying topology, activity rates, and evolutionary timescales. By mitigating the scarcity of high-quality temporal higher-order network data, PITHON helps researchers to derive the influence of temporal higher-order features on dynamical processes. It also provides a data foundation for deep learning approaches in the field of complex systems.

Results

From pairwise event stream to temporal simplicial complexes

Real-world interactions are complex, but the recorded datasets are simple. In many empirical studies of the population \({{\mathcal{V}}}=\{{v}_{1},{v}_{2},\ldots ,{v}_{n}\}\), only pairwise interactions are recorded: if two individuals vi and vj interact at least once during the interval [t, t + Δt), the event (vi, vj, t, t + Δt) is logged. In this way, the sequence of interactions is abstracted as an event stream \(I=\{(l,t,t+\Delta t)| l=\{{v}_{1},{v}_{2}\},{v}_{1},{v}_{2}\in {{\mathcal{V}}}\}\)49,50,51. At each time t, we define the active link set \({{{\mathcal{L}}}}_{t}=\{\,l| (l,t,t+\Delta t)\in I\}\), and thus obtain the instantaneous graph \({{{\mathcal{G}}}}_{t}=({{\mathcal{V}}},{{{\mathcal{L}}}}_{t})\). Any clique of size greater than two in \({{{\mathcal{G}}}}_{t}\) indicates a simultaneous group interaction at time t. We therefore regard each such clique as a higher-order interaction. This construction yields a simplicial complex because every face of a clique is again a clique. Formally, we define the simplicial complex \({{{\mathcal{H}}}}_{t}\) so that its 0-simplices are the nodes in \({{\mathcal{V}}}\), its 1-simplices are the links in \({{{\mathcal{G}}}}_{t}\), and its higher-order simplices correspond to all cliques in \({{{\mathcal{G}}}}_{t}\). The graph \({{{\mathcal{G}}}}_{t}\) thus corresponds exactly to the 1-skeleton of \({{{\mathcal{H}}}}_{t}\). Since every clique is filled (e.g., the presence of links {v1, v2}, {v1, v3}, and {v2, v3} necessarily implies the simplex {v1, v2, v3}), there is a one-to-one correspondence between \({{{\mathcal{G}}}}_{t}\) and \({{{\mathcal{H}}}}_{t}\). As time progresses, the sequence \({\{{{{\mathcal{H}}}}_{t}\}}_{t = 1}^{T}\) forms a temporal simplicial complex that captures the dynamics of higher-order interactions.

Pairwise-induced temporal higher-order network

Most existing temporal higher-order network models directly prescribe rules for forming and dissolving higher-order interactions. We aim to develop a generative model that regulates only the evolution of pairwise interactions. In this model, higher-order interactions emerge spontaneously, which matches the dynamics and correlations seen in empirical data. Motivated by this goal, we propose the PITHON model. The behavior of PITHON suggests that higher-order structures in real-world systems may emerge spontaneously from the coordinated evolution of pairwise interactions.

In PITHON, each individual corresponds to a node in an underlying network \({{\mathcal{G}}}=({{\mathcal{V}}},{{\mathcal{L}}})\). Its simplicial complex is denoted by \({{\mathcal{H}}}\). \({{{\mathcal{H}}}}^{(k)}=\{\,h\in {{\mathcal{H}}}| | h| =k+1\}\) represents the set of all k-simplices. Each link \(l\in {{{\mathcal{H}}}}^{(1)}={{\mathcal{L}}}\) has a binary state process Xl(t) ∈ {0, 1} for \(t\in {{\mathbb{R}}}^{+}\). State 1 indicates that the two individuals of l interact at time t. We posit that higher-order interactions emerge from the simultaneous activation of adjacent links. Specifically, each link’s state is determined by its intrinsic activation mechanism, as well as the states of its neighboring links. The likelihood of forming a higher-order interaction increases as more neighboring links become active simultaneously. Thus, the instantaneous transition rate for link l switching from state s to 1−s at time t is

$${q}_{s}^{l}(t)=(1-\sigma )\,{\tau }_{s}^{-1}+\sigma \left({\tau }_{0}^{-1}+{\tau }_{1}^{-1}\right)\ \frac{{\sum }_{m\in {\partial }_{l}}\delta \left({X}_{m}(t),1-s\right)}{| {\partial }_{l}| }.$$
(1)

Here ∂l is the set of links adjacent to l, and \(\delta \left({X}_{m}(t),1-s\right)\) is a Kronecker delta function, equal to 1 iff Xm(t) = 1−s, and 0 otherwise. The first term \((1-\sigma )\,{\tau }_{s}^{-1}\) represents the intrinsic transition mechanism of link l, where τs is the mean sojourn time in state s. The second term captures the collaborative effect: as more neighbors occupy the target state 1 − s, the transition rate increases. The parameter σ ∈ [0, 1) balances intrinsic dynamics and neighbor collaboration (σ = 0 yields independent links). The specific derivation process can be found in the “Methods” section. For a fixed topology \({{\mathcal{G}}}\), PITHON is fully specified by three parameters (τ0, τ1, σ). To clarify interpretation, we set α = τ1/(τ0 + τ1) and τ = τ1. The tunable parameters (α, τ, σ) then control: (i) α ∈ (0, 1), the expected link activity rate; (ii) \(\tau \in {{\mathbb{R}}}^{+}\), the global time scale; and (iii) σ ∈ [0, 1), the collaborative strength.

The transition rates govern the activation of links \(l\in {{{\mathcal{H}}}}^{(1)}\). For any higher-order simplex \(h\in {{{\mathcal{H}}}}^{(k)}\) with k > 1, let \({{{\mathcal{H}}}}_{h}^{(1)}=\left\{\,l\in {{{\mathcal{H}}}}^{(1)}| l\subseteq h\,\right\}\) denote the set of its 1-dimensional faces. We define the state of h by

$${X}_{h}(t)\ =\ {\prod}_{l\in {{{\mathcal{H}}}}_{h}^{(1)}}{X}_{l}(t),$$
(2)

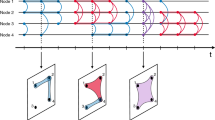
i.e., h is active iff all its constitutive links are active. As shown in Fig. 1, the 2-simplex is active whenever all its constituent links are in state 1. Otherwise, if any link flips to state 0, the 2-simplex becomes inactive. Based on the above stochastic process, we can efficiently generate temporal simplicial complex using the Gillespie algorithm56,57 (see “Methods” for the specific algorithm).

Fig. 1: Evolution of simplex states over time.
figure 1

a A local region of the underlying simplicial complex \({{\mathcal{H}}}\), consisting of three nodes u, v, and w along with their three links, which together form a single 2-simplex. b The time evolution of each simplex’s state: coloured intervals denote active state 1, while white intervals represent inactive state 0 (blue intervals indicate link activity, orange intervals denote 2-simplex activity). The snapshots above illustrate the active simplicial complex at several time points. c How the time-dependent transition rates \({q}_{0}^{\{u,v\}}\) and \({q}_{1}^{\{u,v\}}\) for link {u, v} vary over time.

Full size image

The state of a higher-order simplex is a nonlinear function of multiple link states. Analyzing the emergence of higher-order interactions requires the joint distribution of all link states. Since adjacent links interact, their states within a connected component are dependent, forcing us to consider the full joint state space. In this representation, the explicit time dependence of individual transition rates disappears, and the system becomes a time-homogeneous Markov process. We can then assemble the corresponding microstate transition-rate matrix Q. In this case, the system’s long-term behavior can be characterized by the stationary distribution π of its microstates (see “Methods” for the detailed description). For each simplex h, define the active-state set \({S}_{h}=\{{{\bf{X}}}| {X}_{l}=1\ \forall \,l\in {{{\mathcal{H}}}}_{h}^{(1)}\}\). Its expected activity rate is

$$\langle {a}_{h}\rangle \ =\ {\sum}_{{{\bf{X}}}\in {S}_{h}}{\pi }_{{{\bf{X}}}}.$$
(3)

When σ = 0, the activity rate of any k-simplex is \({\alpha }^{(k+1)k/2}\), which is equal to the probability that all \((k+1)k/2\) links activate simultaneously under independent link dynamics. As σ increases, the marginal link activity rate remains α, but higher-order simplices become more active. In the limit σ → 1, the activity rate of any k-simplex converges to α, corresponding to fully synchronized link activity. A simplex cannot be more active than its constituent links. Analytic results and simulations in Fig. 2 both show that, as σ increases from 0 toward 1, the activity rate of k-simplices rises monotonically from \({\alpha }^{(k+1)k/2}\) to α. This range demonstrates the flexibility of PITHON in generating any desired level of higher-order activity.

Fig. 2: Collaborative promotes the emergence of higher-order interactions.
figure 2

This figure shows how the expected activity rate 〈ak〉 and expected duration 〈tk〉 vary with the collaborative strength σ. Both analytical predictions and Monte Carlo simulation results are displayed for comparison, based on a fully connected underlying network of 5 nodes. a The curves computed from Eq. (3) and the scatter points from simulation for the mean activity rate of each order. b The curves computed from Eq. (4) and the scatter points from simulation for the mean durations. Model parameters are α = 0.3, τ = 60, and the maximum simulation time is 108.

Full size image

We also consider the expected duration of higher-order interactions. Let the set Ih denote all intervals [t+, t−) during which simplex h is active. The expected duration of h is then defined as \(\left\langle {t}_{h}\right\rangle ={\mathbb{E}}\{{t}^{-}-{t}^{+}| [{t}^{+},{t}^{-})\in {I}_{h}\}\). This quantity can also be analytically computed using the transition-rate matrix Q, i.e.,

$$\left\langle {t}_{h}\right\rangle ={\phi }_{h}^{-1}.$$
(4)

Where ϕh denotes the average deactivation rate of h (see “Methods” for the detailed description). In addition to τ directly influencing interaction duration, Fig. 2 also demonstrates that the parameter σ affects interaction duration as a byproduct of facilitating collaboration. When σ = 0, links deactivate independently. In this case, the expected duration satisfies \(\left\langle {t}_{h}\right\rangle =\tau [(k+1)k/2]^{-1}\), which corresponds to the average overlap of \((k+1)k/2\) independent intervals of mean length τ. Increasing σ enhances collaboration among adjacent links, which suppresses state flips and thus prolongs \(\left\langle {t}_{h}\right\rangle\). As σ → 1, the system becomes trapped in fully active or inactive configurations, and \(\left\langle {t}_{h}\right\rangle \to \infty\). Therefore, collaboration not only boosts higher-order activity but also extends its persistence. This demonstrates that rich, long-lived higher-order interactions can emerge solely from pairwise collaboration.

In addition to model parameters, we investigate the influence of underlying topology on higher-order interactions. To ensure a sufficient number of triadic closures and to control network density, we generate underlying networks using the Watts–Strogatz model at varying mean degrees. We then measure the activity rate of simplices of different orders. As shown in Fig. 3, pairwise activity remains constant across mean degree, whereas higher-order activity rate decreases in denser networks when all parameters are fixed. Equivalently, achieving a given level of higher-order activity in a denser network requires a higher collaborative strength. This behavior arises because each link aggregates the states of all neighbors equally. As the number of neighbors increases, the influence of any single neighbor diminishes, hindering spontaneous higher-order interaction formation.

Fig. 3: The effect of underlying network structure on simplex activity.
figure 3

The figure shows the average activity rate of simplices of different orders, as obtained from Monte Carlo simulations, for underlying networks with varying average degree. The dashed lines represent the mean activity rate of each simplex order, and the error bars indicate one standard deviation. The simulated underlying network is a Watts–Strogatz network with 100 nodes and a rewiring probability of 0.2, with α = 0.1. The maximum simulation time is 104, and the simulation was repeated 104 times.

Full size image

Empirical studies reveal a correlation between temporal and topological proximity: interactions that are close in time tend to involve nodes that are close in the underlying network43. Such correlations may arise from time-dependent activity patterns tied to network structure or from external factors influencing both topology and timing. For example, in face-to-face networks, physical proximity implies that geographically nearby individuals are network-close and their interactions are close in time. In online or collaborative networks, members with similar interests form links and often interact within the same time window. Although PITHON relies solely on local collaboration, where each link updates based on its own state and the states of its neighbors, it indirectly reproduces the long-range correlation. For k-order interactions, we quantify this correlation by defining the normalized expected topological distance under a temporal threshold Δt, denoted μ(k)(Δt) (see “Methods” for the detailed description). Figure 4 shows μ(k)(Δt) as a function of Δt for various simplex orders and collaborative strengths σ. Whenever σ > 0, the mean topological distance grows with temporal threshold. This behavior indicates a significant positive correlation between time and topology, consistent with empirical data. Additionally, this correlation becomes stronger as σ increases and is more pronounced for higher-order interactions than for pairwise interactions. It should be noted that temporal-topological correlations may not be solely related to collaboration. Other factors such as the network topology and activity rate may also exert complex influences. In this work, we focus only on the qualitative impact of collaboration on these correlations.

Fig. 4: Temporal-topological correlation of interactions.
figure 4

The figure shows the variation of the average relative topological distance μ(k) for k-order interactions as a function of the temporal threshold Δt, for different collaborative strengths σ. a The temporal-topological correlation for 1-order interactions. b The temporal-topological correlation for 2-order interactions. The simulated underlying network is a Watts–Strogatz network with 50 nodes, an average degree of 4, and a rewiring probability of 0.2. The parameters used are α = 0.2, τ = 60, and the maximum simulation time is 104, repeated 103 times.

Full size image

Reproducing the characters of empirical data

To validate PITHON in reproducing real-world interaction patterns, we analyze three face-to-face contact event streams collected via wearable Radio Frequency IDentification (RFID) devices:

  • Workplace49: contacts among employees in an office building in France.

  • Malawi50: contacts among residents of a rural village in Malawi.

  • Baboons51: contacts among Guinea baboons within an enclosure at a primate research center in France.

These datasets span a wide variety of settings, from workplace to daily life, and from human societies to animal groups. They reveal diverse and rich patterns of collective contact. Each participant wore an RFID tag that exchanged packets with any other tag within 1–1.5  m, at least once per second. If two tags exchanged packets during a 20 s window, a single pairwise contact event is recorded for that interval50. These spatial and temporal scales capture dynamics relevant to information diffusion and pathogen transmission.

We infer the optimal parameters (α*, τ*, σ*) by matching the model’s higher-order dynamics to those observed empirically in the temporal simplicial complex. PITHON operates in continuous time, whereas the datasets have a minimum resolution of Δt = 20 s. Therefore, simulated contacts are discretized for comparison. If a simulated link is active at least once within a time window, it is considered continuously active throughout that window. If it remains active for n consecutive windows, a single contact of duration Δtn is recorded. This discretization necessarily overestimates both activity rates and durations. As Table 1 shows, empirical link activity rates are uniformly low. In the limit α → 0, the discretized mean link activity rate admits the approximation \(\hat{a}\simeq (1+\Delta t/\tau )\,\alpha\), which yields the estimator \({\alpha }^{* }(\tau )=\hat{a}/(1+\Delta t/\tau )\) (see “Methods” for the detailed description). Since no closed-form solution exists for σ and τ, σ* and τ* are determined via grid search. With α* fixed to match the empirical mean 1-simplex activity rate, we choose σ* to match the empirical mean 2-simplex activity rate

$${\bar{a}}^{(2)}=\frac{1}{| {{{\mathcal{H}}}}^{(2)}| }{\sum}_{h\in {{{\mathcal{H}}}}^{(2)}}{a}_{h},$$
(5)

and choose τ* to match the empirical mean 1-order interactions duration

$${\bar{t}}^{(1)}=\frac{{\sum}_{h\in {{{\mathcal{H}}}}^{(1)}}{\sum}_{[{t}^{+},{t}^{-})\in {I}_{h}}({t}^{-}-{t}^{+})}{{\sum}_{h\in {{{\mathcal{H}}}}^{(1)}}| {I}_{h}| }.$$
(6)

Because σ also influences durations and τ affects α* via discretization, σ and τ are optimized jointly. For each candidate τ, σ*(τ) is found by setting the 2-simplex activity rate error to zero. For each candidate σ, τ*(σ) is found by setting the 1-order interactions duration error to zero. The intersection of these two curves yields the optimal pair (σ*, τ*). This procedure is illustrated in Fig. 5, and the optimal parameters are listed in Table 1.

Table 1 Overview of each dataset and the model’s optimal fitting parameters
Full size table
Fig. 5: Optimal parameters search for model fitting to empirical data.
figure 5

The figure illustrates how the model parameters σ and τ are tuned to match the empirical mean 2-simplex activity rate \({\bar{a}}^{(2)}\) and the mean 1-order interactions duration \({\bar{t}}^{(1)}\). Columns from left to right correspond to the Workplace (a, d), Malawi (b, e), and Baboons (c, f) datasets. The first row (a–c) shows heatmaps of the mean 2-simplex activity rate relative error for different (σ, τ), with the dashed curve indicating, for each τ, the collaborative strength σ*(τ) that minimizes the absolute value of error. The second row (d–f) shows heatmaps of the mean 1-order interactions duration relative error for different (σ, τ), with the dashed curve indicating, for each σ, the time scale τ*(σ) that minimizes the absolute value of error. The intersection point of σ*(τ) and τ*(σ), marked by a dot in each panel, denotes the optimal parameter pair (σ*, τ*). Each (σ, τ) combination was simulated 100-times and averaged.

Full size image

As shown in Fig. 6, simulations with the fitted parameters reproduce the observed 1-simplex and 2-simplex mean activity rates and 1-order interactions mean durations. They also reproduce the decay of activity rate and duration across higher orders. Empirically, both metrics are observed to decay approximately exponentially with simplex order, which reflects the increasing difficulty of coordinating larger groups. This agreement supports that PITHON can capture the intrinsic mechanisms underlying hierarchical interaction patterns.

Fig. 6: Empirical interaction dynamics and model fit.
figure 6

Columns from left to right correspond to the Workplace (a, d), Malawi (b, e), and Baboons (c, f) datasets. The first row (a–c) shows the mean activity rate \(\bar{a}\) of simplices of each order in the real data and in the model simulations. The second row (d–f) shows the mean duration \(\bar{t}\) of interactions of each order for both empirical and simulated data. Error bars denote one standard deviation, and each model estimate is averaged over 103 Monte Carlo runs.

Full size image

Beyond aggregate activity levels and durations, the fine-grained evolution of each higher-order interaction is examined40,41,42. Specifically, we test how a higher-order interaction forms. It may arise from scratch, where isolated nodes directly coalesce. Alternatively, it may form progressively through the accumulation of lower-order interactions. We also examine how such interactions dissolve. They may break down directly into isolated nodes or gradually through the successive loss of lower-order links. For each k-order interaction, the highest order \(k^{\prime} \in \{0,1,\ldots ,k-1\}\) of the interactions among its k + 1 individuals is identified in the interval before activation, and similarly after deactivation. If states were independent across time, this distribution over \(k^{\prime}\) would match the normalized simplex activity levels (as shown in Fig. 6). But empirical and simulated results in Fig. 7 exhibit a bias: activations and deactivations often occur via \(k^{\prime}\)-faces close to k, and the pre- and post-distributions are nearly symmetric. In particular, for 3-order interactions, it is almost impossible for them to appear or disappear directly from isolated individuals. These observations reveal strong cross-order correlations in higher-order interactions. Accurate reproduction of this pattern by PITHON indicates that pairwise collaboration is a plausible microscopic mechanism underlying cross-order dynamics. In some metrics (e.g., panels g and h), the data generated by PITHON show notable differences from the real data. This discrepancy may be due to the sparsity of higher-order interactions in the empirical dataset, where the distribution derived from a limited number of samples is likely to deviate from the true distribution.

Fig. 7: Empirical cross-order evolution of interactions and model fit.
figure 7

The figure shows, from top to bottom, the Workplace (a–d), Malawi (e–h), and Baboons (i–l) datasets, comparing empirical data and model simulations. For each k-order interaction, we examine the distribution of the highest-order interaction \(k^{\prime} \in \{0,1,\ldots ,k-1\}\) among its k + 1 nodes in the time window immediately before activation (after deactivation). The first column (a, e, i) and second column (b, f, j) correspond to pre-distributions and post-distributions for 2-order interactions respectively. The third column (c, g, k) and fourth column (d, h, l) correspond to pre-distributions and post-distributions for 3-order interactions respectively. To mitigate the sparsity of the data, we set the total simulation time to 103 times the total duration of the empirical data.

Full size image

Lastly, the temporal-topological correlations in the empirical datasets are validated. Figure 8 shows significant positive correlations between temporal and topological distances for interactions of all orders. These correlations are reproduced by PITHON. In large datasets, the computation of all same-order interaction pairs is computationally intensive. Each dataset is partitioned into 5 equal time segments. Within each segment, μ(k)(Δt) is computed and then averaged across segments. To eliminate biases from nested overlaps among higher-order interactions, pairs of interactions sharing any common link are excluded from the correlation analysis. Although PITHON’s collaborative mechanism is confined to local neighborhoods and produces Markovian dynamics, it nevertheless captures the global temporal-topological correlations observed in empirical networks, thereby validating its effectiveness.

Fig. 8: Empirical temporal-topological correlations of higher-order interactions and model fit.
figure 8

The figure plots, for each k-order interaction, the mean relative topological distance μ(k) as a function of the temporal distance threshold Δt. Columns from left to right correspond to the Workplace (a, d), Malawi (b, e), and Baboons (c, f) datasets, comparing empirical measurements and model simulations. The first row (a–c) shows the temporal-topological correlation for pairwise interactions, while the second row (d–f) shows the correlation for 2-order interactions. Error bars denote one standard deviation, and each model curve is averaged over 100 Monte Carlo runs.

Full size image

Discussion

The emergence and evolution of higher-order interactions is one of the central questions in temporal higher-order network research. In this work, we propose a minimal model, PITHON, which regulates only the collaborative mechanism among adjacent links. The evolution of higher-order interactions then follows solely from these link dynamics. Analytical results show that the collaborative strength σ controls the activity of higher-order interactions across their theoretical range. We also find that collaboration not only affects higher-order activity levels but also prolongs interaction durations. This effect promotes the emergence of more persistent interactions. PITHON’s local collaboration mechanism among neighboring links generates pronounced global temporal-topological correlations at every simplex order, and these correlations become stronger as σ increases. To test PITHON’s empirical fit, we take advantage of several face-to-face contact datasets spanning humans and animals, live and workplace environments. We fit the model’s parameters (α*, τ*, σ*) by matching three metrics: mean 1-simplex activity rate, mean 2-simplex activity rate, and mean 1-order interaction duration. Without further tuning, PITHON reproduces higher-order activity rates and durations, as well as temporal-topological correlations and cross-order evolution patterns. As a simple yet powerful framework, PITHON captures multiple features of real temporal higher-order systems, suggesting that pairwise collaboration is a plausible mechanism underlying higher-order emergence. Moreover, given the scarcity of high-quality temporal higher-order data, PITHON provides an efficient and flexible method to generate realistic synthetic datasets, which supports deeper studies of dynamical processes on temporal higher-order networks and enables data-driven advances in generative artificial intelligence for complex systems58,59.

As an early attempt to generate temporal higher-order networks from pairwise dynamics, PITHON still needs further improvements. First, it assumes homogeneous dynamics for simplicity, while real systems exhibit rich heterogeneity in activity levels, timescales, and attention to different neighbors. Extending the framework to heterogeneous parameters and fitting real systems within an expanding parameter space remains a problem. Deep learning techniques may offer a potential solution to this problem60,61,62. Second, PITHON’s evolution is Markovian and cannot capture temporal burstiness and rhythmic behavior over long time scales arising from memory effects or external drivers. However, balancing the intrinsic burstiness of link dynamics and the correlations among links may present fundamental challenges46. Some recent studies have introduced time-dependent parameters to reproduce temporal heterogeneity in link dynamics through external modulation47,52. How such heterogeneous temporal patterns across different timescales can be regulated and reproduced through a unified mechanism remains an open question. Finally, PITHON demonstrates that simple pairwise collaboration suffices to reproduce empirical higher-order dynamics in face-to-face interaction scenarios. We also expect it to be applicable in other systems, including but not limited to the brain and ecosystems. Nevertheless, different real-world systems may rely on diverse microscopic mechanisms, and the intrinsic mechanisms of non-clique higher-order interactions cannot be simply attributed to collaborative effects. In summary, we hope this work inspires further investigation into microscopic mechanisms of temporal higher-order interaction formation and stimulates the development of more realistic generative models for temporal higher-order networks.

Methods

The generative model and its properties

In PITHON, each individual corresponds to a node in an underlying network \({{\mathcal{G}}}=({{\mathcal{V}}},{{\mathcal{L}}})\). Its simplicial complex is denoted by \({{\mathcal{H}}}\). Each link \(l\in {{{\mathcal{H}}}}^{(1)}\) has a binary state process Xl(t) ∈ {0, 1} for \(t\in {{\mathbb{R}}}^{+}\). The instantaneous transition rate for link l switching from state s to 1 − s at time t is

$${\frac{\partial }{\partial \epsilon }\Pr \left({X}_{l}(t+\epsilon ) = 1-s\bigg| {X}_{l}(t) = s\right)\bigg| }_{\epsilon \to {0}^{+}}={q}_{s}^{l}(t),$$
(7)

where

$${q}_{s}^{l}(t)=(1-\sigma )\,{\tau }_{s}^{-1}+\sigma \,{\lambda }_{s}\ \frac{{\sum }_{m\in {\partial }_{l}}\delta \left({X}_{m}(t),(1-s)\right)}{| {\partial }_{l}| }.$$
(8)

Here, ∂l is the set of links adjacent to l, \(\delta \left({X}_{m}(t),1-s\right)\) is a Kronecker delta function, equal to 1 iff Xm(t) = 1 − s, and 0 otherwise. τs is the mean sojourn time in state s, σ ∈ [0, 1) balances intrinsic dynamics and neighbor collaboration, and λs scales the collaborative strength.

Although states 0 and 1 are symmetric, attention is typically given to the activity rate of links. Intrinsic dynamics produce an activity rate τ1/(τ0 + τ1). To prevent collaboration from changing this baseline, we assume that when neighbors occupy state 1 − s with probability τ1−s/(τ0 + τ1), the transition rate is independent of σ. Setting

$$\frac{\partial }{\partial \sigma }\left[(1-\sigma ){\tau }_{s}^{-1}+\sigma \,{\lambda }_{s}\frac{{\tau }_{1-s}}{{\tau }_{0}+{\tau }_{1}}\right]=0$$
(9)

yields \({\lambda }_{s}={\tau }_{0}^{-1}+{\tau }_{1}^{-1}\). Substituting it into the rate in Eq. (8) gives

$${q}_{s}^{l}(t)=(1-\sigma )\,{\tau }_{s}^{-1}+\sigma \left({\tau }_{0}^{-1}+{\tau }_{1}^{-1}\right)\ \frac{{\sum }_{m\in {\partial }_{l}}\delta \left({X}_{m}(t),1-s\right)}{| {\partial }_{l}| }.$$
(10)

This choice makes the average transition rates identical to the non-collaborative case when neighbors occupy the opposite state with their stationary probabilities.

For any higher-order simplex \(h\in {{{\mathcal{H}}}}^{(k)}\) with k > 1, the state of h is fully determined by the states of its 1-dimensional faces, then \({X}_{h}(t)\ =\ {\prod }_{l\in {{{\mathcal{H}}}}_{h}^{(1)}}{X}_{l}(t)\). We denote the joint state vector by \({{\bf{X}}}={\left[{X}_{l}\right]}_{l\in {{{\mathcal{H}}}}^{(1)}}\), so that the state space has size \({2}^{| {{{\mathcal{H}}}}^{(1)}| }\). The continuous-time transition-rate matrix \({{\bf{Q}}}=[\,{q}_{{{\bf{X}}},{{\bf{X}}}^{\prime} }]\) of size \({2}^{| {{{\mathcal{H}}}}^{(1)}| }\times {2}^{| {{{\mathcal{H}}}}^{(1)}| }\) is specified by

$${q}_{{{\bf{X}}},{{\bf{X}}}^{\prime} }=\left\{\begin{array}{ll}{q}_{s}^{l}(t) \quad \hfill &\,{{\mbox{if}}}\,{{\bf{X}}}^{\prime} \,{{\mbox{differs\; from}}}\,{{\bf{X}}}\,{{\mbox{only\; at}}}\,{X}_{l}=s,\ X^{\prime} =1-s,\\ -{\sum }_{{{\bf{X}}}^{\prime\prime} \ne {{\bf{X}}}}{q}_{{{\bf{X}}},{{\bf{X}}}^{\prime\prime} }\quad &\,{\mbox{if}}\,{{\bf{X}}}^{\prime} ={{\bf{X}}},\hfill\\ 0\quad \hfill &\,{{\mbox{otherwise}}.}\hfill\,\end{array}\right.$$
(11)

The transition rates of joint states are time-homogeneous and define a finite-dimensional Markov process. Under irreducibility and aperiodicity, a unique stationary distribution π exists which satisfies

$${{\boldsymbol{\pi }}}\,{{\bf{Q}}}={{\bf{0}}},\quad {{\boldsymbol{\pi }}}\,{{\bf{1}}}=1.$$
(12)

For each simplex h, define the active-state set \({S}_{h}=\{{{\bf{X}}}| {X}_{l}=1\ \forall \,l\in {{{\mathcal{H}}}}_{h}^{(1)}\}\). Its expected activity rate is

$$\langle {a}_{h}\rangle \ =\ {\sum}_{{{\bf{X}}}\in {S}_{h}}{\pi }_{{{\bf{X}}}}.$$
(13)

Consider the expected duration of higher-order interactions. In PITHON, a higher-order simplex h’s interaction deactivates iff one of its constituent links flips from 1 to 0. For each X ∈ Sh, let \({{{\bf{X}}}}_{l}^{-}\) denote the state obtained by setting the state of link l ⊆ h to 0. Then the average deactivation rate of h is

$${\phi }_{h}=\frac{{\sum}_{{{\bf{X}}}\in {S}_{h}}{\pi }_{{{\bf{X}}}}{\sum}_{l\in {{{\mathcal{H}}}}_{h}^{(1)}}{q}_{{{\bf{X}}},{{{\bf{X}}}}_{l}^{-}}}{{\sum}_{{{\bf{X}}}\in {S}_{h}}{\pi }_{{{\bf{X}}}}}.$$
(14)

Hence,

$$\left\langle {t}_{h}\right\rangle ={\phi }_{h}^{-1}.$$
(15)

For example, consider a triangular underlying network with three nodes and three links. The joint state of its three links can be encoded as {000, 001, 010, 011, 100, 101, 110, 111}, where each position denotes the state of one link. Substituting this encoding into Eq. (11) yields the transition-rate matrix Q. By solving Eq. (12) for the stationary distribution, we obtain the steady-state vector π, where

$$\left\{\begin{array}{rcl}{\pi }_{000}&=&\frac{{(1-\alpha )}^{3}(1-\alpha \sigma )(2-\sigma -\alpha \sigma )}{\left(1-2\alpha \sigma +{\alpha }^{2}\sigma \right)\left(2-\sigma -2\alpha \sigma +{\alpha }^{2}\sigma \right)},\\ {\pi }_{001}={\pi }_{010}={\pi }_{100}&=&\frac{{(1-\alpha )}^{2}\alpha (1-\sigma )(2-\sigma -\alpha \sigma )}{\left(1-2\alpha \sigma +{\alpha }^{2}\sigma \right)\left(2-\sigma -2\alpha \sigma +{\alpha }^{2}\sigma \right)},\\ {\pi }_{011}={\pi }_{101}={\pi }_{110}&=&\frac{(1-\alpha )\alpha (1-\sigma )\left(2\alpha +\sigma -4\alpha \sigma +{\alpha }^{2}\sigma \right)}{\left(1-2\alpha \sigma +{\alpha }^{2}\sigma \right)\left(2-\sigma -2\alpha \sigma +{\alpha }^{2}\sigma \right)},\\ {\pi }_{111}&=&\frac{\alpha \left(2\alpha +\sigma -4\alpha \sigma +{\alpha }^{2}\sigma \right)\left(\alpha +\sigma -3\alpha \sigma +{\alpha }^{2}\sigma \right)}{\left(1-2\alpha \sigma +{\alpha }^{2}\sigma \right)\left(2-\sigma -2\alpha \sigma +{\alpha }^{2}\sigma \right)}.\end{array}\right.$$
(16)

Here, πΔ = π111 is the expected activity rate of the 2-simplex in this network. ϕΔ = ∣q111,111∣ denotes the deactivation rate of the 2-order interaction, and its reciprocal-τ/[3(1 − σ)]-is the expected active duration.

PITHON-based algorithm for generating temporal simplicial complex

Based on PITHON, we can use the Gillespie algorithm56,57 to generate temporal simplicial complex. The inputs are the underlying network \({{\mathcal{G}}}\), the model parameters (α, τ, σ), and the maximum simulation time \({T}_{\max }\). The basic procedure is outlined in the pseudocode Algorithm 1.

Algorithm 1

Pairwise-induced temporal higher-order network

Require: Underlying network \({{\mathcal{G}}}\), model parameters (α, τ, σ), and final time \({T}_{\max }\)

Ensure: Time series of simplex states \({\{{X}_{h}(t)\}}_{h\in {{\mathcal{H}}}}\)

1: build simplicial complex \({{\mathcal{H}}}\) from \({{\mathcal{G}}}\)

2: t ⇐ 0

3: for link \(l\in {{{\mathcal{H}}}}^{(1)}\) do

4:  Xl(t) ⇐ 1 with probability α, and 0 with probability 1 − α

5:  \({q}^{l}\Leftarrow (1-\sigma )\,{\tau }_{{X}_{l}(t)}^{-1}+\sigma \left({\tau }_{0}^{-1}+{\tau }_{1}^{-1}\right)\ {\sum }_{m\in {\partial }_{l}}\delta \left({X}_{m}(t),1-{X}_{l}(t)\right)/| {\partial }_{l}|\).

6: end for

7: for simplex \(h\in {{{\mathcal{H}}}}^{(k)},k > 1\) do

8:  \({X}_{h}(t)\Leftarrow {\prod }_{l\in {{{\mathcal{H}}}}_{h}^{(1)}}{X}_{l}(t)\)

9: end for

10: \({Q}_{{{\rm{total}}}}\Leftarrow {\sum }_{l\in {{{\mathcal{H}}}}^{(1)}}{q}^{l}\)

11: while \(t < {T}_{\max }\) and Qtotal > 0 do

12: draw \(\Delta t \sim {{\rm{Exp}}}({Q}_{{{\rm{total}}}})\)

13: t ⇐ t + Δt

14: choose link l* with probability \({q}^{{l}^{* }}/{Q}_{{{\rm{total}}}}\)

15: \({X}_{{l}^{* }}(t)\Leftarrow 1-{X}_{{l}^{* }}(t)\)

16: for simplex h with \({l}^{* }\subseteq {{{\mathcal{H}}}}_{h}^{(1)}\) do

17:  \({X}_{h}(t)\Leftarrow {\prod }_{l\subseteq {{{\mathcal{H}}}}_{h}^{(1)}}{X}_{l}(t)\)

18: end for

19: for link l ∈ {l*} ∪ ∂l* do

20:  update\(\,\,{q}^{l}\Leftarrow (1-\sigma )\,{\tau }_{{X}_{l}(t)}^{-1}+\sigma \left({\tau }_{0}^{-1}+{\tau }_{1}^{-1}\right)\ {\sum }_{m\in {\partial }_{l}}\delta \left({X}_{m}(t),1-{X}_{l}(t)\right)/| {\partial }_{l}|\).

21: end for

22: update \({Q}_{{{\rm{total}}}}\Leftarrow {\sum }_{l\in {{{\mathcal{H}}}}^{(1)}}{q}^{l}\)

23: end while

Temporal-topological correlations

In empirical datasets, interactions that occur close in time tend to involve nodes that are close in the underlying network43. To quantify this temporal-topology correlation, for two interaction events \({i}_{1}=({h}_{1},{t}_{1}^{+},{t}_{1}^{-})\) and \({i}_{2}=({h}_{2},{t}_{2}^{+},{t}_{2}^{-})\), we define the temporal distance

$${d}_{{{\rm{temp}}}}({i}_{1},{i}_{2})=\left| \frac{{t}_{1}^{+}+{t}_{1}^{-}}{2}-\frac{{t}_{2}^{+}+{t}_{2}^{-}}{2}\right|$$
(17)

and the topological distance

$${d}_{{{\rm{topo}}}}({i}_{1},{i}_{2})=\frac{1}{| {h}_{1}| \ \,| {h}_{2}| }{\sum}_{{v}_{1}\in {h}_{1}}{\sum}_{{v}_{2}\in {h}_{2}}d({v}_{1},{v}_{2}),$$
(18)

where d(v1, v2) is the shortest-path distance in the underlying network. Here, we adapt a definition that differs from the traditional one43 in order to distinguish the distances between higher-order interactions with varying degrees of overlap. For k-simplices, the normalized mean topological distance with temporal threshold Δt is defined as

$${\mu }^{(k)}(\Delta t)=\frac{{\mathbb{E}}\{{d}_{{{\rm{topo}}}}({i}_{1},{i}_{2})| {h}_{1},{h}_{2}\in {{{\mathcal{H}}}}^{(k)}\wedge {d}_{{{\rm{temp}}}}({i}_{1},{i}_{2}) < \Delta t\}}{{\mathbb{E}}\{{d}_{{{\rm{topo}}}}({i}_{1},{i}_{2})| {h}_{1},{h}_{2}\in {{{\mathcal{H}}}}^{(k)}\}}.$$
(19)

It is straightforward to see that \({\lim }_{\Delta t\to +\infty }{\mu }^{(k)}(\Delta t)=1\).

Fitting the optimal α in empirical data

In a simplified setting, the relationship between continuous-time activity rate and observed discretized activity rate is approximated. Consider a two-state continuous-time Markov process, where the system transitions from state 0 to 1 at rate \({\tau }_{0}^{-1}\) and from state 1 to 0 at rate \({\tau }_{1}^{-1}\). The probability \(\hat{a}\) that the process is in state 1 at least once during an interval of length Δt (and hence the discretized activity rate) is

$$\hat{a}=1-\frac{{\tau }_{0}}{{\tau }_{0}+{\tau }_{1}}{e}^{-\Delta t/{\tau }_{0}}=1-(1-\alpha ){e}^{-\Delta t\alpha /[\tau (1-\alpha )]}.$$
(20)

In the limit α → 0, the approximation \(\hat{a}\simeq (1+\Delta t/\tau )\,\alpha\) is obtained. Thus, the optimal parameter is approximated by \({\alpha }^{* }(\tau )=\hat{a}/(1+\Delta t/\tau )\).