Abstract
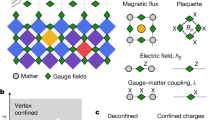
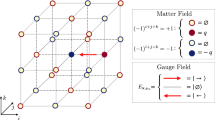
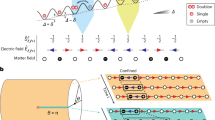
Understanding strongly interacting quantum field theories is a central challenge in theoretical physics, with direct relevance to nuclear, high-energy and condensed matter systems. Here we present a quantum algorithm for compact lattice Quantum Electrodynamics in 2+1 dimensions with dynamical fermionic matter. Using a variational quantum approach, we extract the static potential between charges across Coulomb, confinement, and string-breaking regimes. Our method employs a symmetry-preserving, resource-efficient circuit to prepare ground states, enabling accurate calculations on the Quantinuum H1-1 trapped-ion device and emulator, in agreement with noiseless simulations. Moreover, we visualize the electric field flux configurations that mainly contribute to the wave function of the quantum ground state, giving insights into the mechanisms of confinement and string-breaking. These results are a promising step forward in the grand challenge of solving higher dimensional lattice gauge theory problems with quantum computing algorithms.
Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Code availability
A python code implementation for the truncation scheme as well as quantum circuit construction is available at ref. 53.
References
Wilson, K. G. Confinement of Quarks. Phys. Rev. D. 10, 2445–2459 (1974).
Rothe, H. J. Lattice Gauge Theories: An Introduction (World Scientific Publishing Company, 2012).
Gattringer, C. & Lang, C. Quantum Chromodynamics on the Lattice: An Introductory Presentation, vol. 788 (Springer Science & Business Media, 2009).
Gross, F. et al. 50 years of quantum chromodynamics. Eur. Phys. J. C. 83, 1125 (2023).
Polyakov, A. M. Quark confinement and topology of gauge groups. Nucl. Phys. B 120, 429–458 (1977).
Wen, X.-G. Quantum Field Theory of Many-body Systems. (Oxford University Press, New York, NY, 2004).
Knechtli, F. & Sommer, R. String breaking as a mixing phenomenon in the SU(2) Higgs model. Nucl. Phys. B 590, 309–328 (2000).
Philipsen, O. & Wittig, H. String breaking in nonAbelian gauge theories with fundamental matter fields. Phys. Rev. Lett. 81, 4056–4059 (1998).
Bali, G. S. QCD forces and heavy quark bound states. Phys. Rept. 343, 1–136 (2001).
Loan, M., Brunner, M., Sloggett, C. & Hamer, C. Path integral Monte Carlo approach to the U (1) lattice gauge theory in 2+ 1 dimensions. Phys. Rev. D. 68, 034504 (2003).
Bender, J., Emonts, P., Zohar, E. & Cirac, J. I. Real-time dynamics in 2 + 1d compact QED using complex periodic gaussian states. Phys. Rev. Res. 2, 043145 (2020).
Banuls, M. C. et al. Simulating lattice gauge theories within quantum technologies. Eur. Phys. J. D. 74, 1–42 (2020).
Bauer, C. W. et al. Quantum simulation for high-energy physics. PRX Quantum 4, 027001 (2023).
Di Meglio, A. et al. Quantum computing for high-energy physics: state of the art and challenges. PRX Quantum 5, 037001 (2024).
Funcke, L., Hartung, T., Jansen, K. & Kühn, S. Review on quantum computing for lattice field theory. PoS LATTICE2022, 228 (2023).
Banerjee, D. et al. Atomic quantum simulation of dynamical gauge fields coupled to fermionic matter: from string breaking to evolution after a quench. Phys. Rev. Lett. 109, 175302 (2012).
Wiese, U.-J. Ultracold quantum gases and lattice systems: quantum simulation of lattice gauge theories. Ann. der Phys. 525, 777–796 (2013).
Zohar, E., Cirac, J. I. & Reznik, B. Quantum simulations of lattice gauge theories using ultracold atoms in optical lattices. Rep. Prog. Phys. 79, 014401 (2015).
Magnifico, G., Felser, T., Silvi, P. & Montangero, S. Lattice quantum electrodynamics in (3+ 1)-dimensions at finite density with tensor networks. Nat. Commun. 12, 3600 (2021).
Zohar, E. & Reznik, B. Confinement and lattice quantum-electrodynamic electric flux tubes simulated with ultracold atoms. Phys. Rev. Lett. 107, 275301 (2011).
Cochran, T. A. et al. Visualizing dynamics of charges and strings in (2 + 1)D lattice gauge theories. Nature 642, 1–6 (2025).
De, A. et al. Observation of string-breaking dynamics in a quantum simulator. Preprint at https://arxiv.org/abs/2410.13815 (2024).
González-Cuadra, D. et al. Observation of string breaking on a (2+ 1) D Rydberg quantum simulator. Nature 642, 1–6 (2025).
Quantinuum H1-1. https://www.quantinuum.com/products-solutions/system-model-h1-series (2024).
Kogut, J. & Susskind, L. Hamiltonian formulation of wilson’s lattice gauge theories. Phys. Rev. D. 11, 395–408 (1975).
Robson, D. & Webber, D. Gauge theories on a small lattice. Z. Phys. C. Part. Fields 7, 53–60 (1980).
Ligterink, N., Walet, N. & Bishop, R. A many-body treatment of hamiltonian lattice gauge theory. Nucl. Phys. A Nucl. Hadronic Phys. 663, 983c–986c (2000).
Nielsen, H. B. & Ninomiya, M. No go theorem for regularizing chiral fermions. Phys. Lett. B 105, 219–223 (1981).
Susskind, L. Lattice fermions. Phys. Rev. D. 16, 3031–3039 (1977).
Haase, J. F. et al. A resource efficient approach for quantum and classical simulations of gauge theories in particle physics. Quantum 5, 393 (2021).
Mathis, S. V., Mazzola, G. & Tavernelli, I. Toward scalable simulations of lattice gauge theories on quantum computers. Phys. Rev. D. 102, 094501 (2020).
Chandrasekharan, S. & Wiese, U.-J. Quantum link models: a discrete approach to gauge theories. Nucl. Phys. B 492, 455–471 (1997).
Hashizume, T., Halimeh, J., Hauke, P. & Banerjee, D. Ground-state phase diagram of quantum link electrodynamics in (2 + 1)-d. SciPost Phys. 13, https://doi.org/10.21468/SciPostPhys.13.2.017 (2022).
Notarnicola, S. et al. Discrete abelian gauge theories for quantum simulations of qed. J. Phys. A Math. Theor. 48, 30FT01 (2015).
Meth, M. et al. Simulating 2d lattice gauge theories on a qudit quantum computer. Preprint at https://arxiv.org/abs/2310.12110 (2023).
Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014).
Nakanishi, K. M., Fujii, K. & Todo, S. Sequential minimal optimization for quantum-classical hybrid algorithms. Phys. Rev. Res. 2, 043158 (2020).
Ostaszewski, M., Grant, E. & Benedetti, M. Structure optimization for parameterized quantum circuits. Quantum 5, 391 (2021).
Kohda, M. et al. Quantum expectation-value estimation by computational basis sampling. Phys. Rev. Res. 4, 033173 (2022).
Tranter, A. et al. InQuanto: quantum computational chemistry. https://www.quantinuum.com/products-solutions/inquanto (2022).
DeCross, M., Chertkov, E., Kohagen, M. & Foss-Feig, M. Qubit-reuse compilation with mid-circuit measurement and reset. Phys. Rev. X 13, 041057 (2023).
Sivarajah, S. et al. t\(\left\vert {{{\rm{ket}}}}\right\rangle\): a retargetable compiler for NISQ devices. Quantum Sci. Technol. 6, 014003 (2020).
Quantinuum H2-1. https://www.quantinuum.com/products-solutions/system-model-h2-series (2024).
Crippa, A. et al. Towards determining the (2+1)-dimensional Quantum Electrodynamics running coupling with Monte Carlo and quantum computing methods. Commun. Phys. 8, 367 (2025).
Farrell, R. C., Illa, M., Ciavarella, A. N. & Savage, M. J. Scalable Circuits for Preparing Ground States on Digital Quantum Computers: The Schwinger Model Vacuum on 100 Qubits. PRX Quantum 5, 020315 (2024).
Granet, E., Ghanem, K. & Dreyer, H. Practicality of a quantum adiabatic algorithm for chemistry applications. Phys. Rev. A. 111, 022428 (2025).
Luescher, M. Symmetry-breaking aspects of the roughening transition in gauge theories. Nucl. Phys. B 180, 317–329 (1981).
Lüscher, M. & Weisz, P. Quark confinement and the bosonic string. J. High. Energy Phys. 2002, 049 (2002).
Nogueira, F. S. & Kleinert, H. Quantum electrodynamics in 2+ 1 dimensions, confinement, and the stability of u (1) spin liquids. Phys. Rev. Lett. 95, 176406 (2005).
Chagdaa, S., Galsandorj, E., Laermann, E. & Purev, B. Width and string tension of the flux tube in su (2) lattice gauge theory at high temperature. J. Phys. G: Nucl. Part. Phys. 45, 025002 (2017).
Caselle, M., Cellini, E. & Nada, A. Numerical determination of the width and shape of the effective string using stochastic normalizing flows. J. High Energ. Phys. 2025, 1–30 (2025).
Peng, C. et al. Hamiltonian lattice formulation of compact Maxwell-Chern-Simons theory. Preprint at https://arxiv.org/abs/2407.20225 (2024).
Crippa, A. QED_Hamiltonian/v0.0.2, https://github.com/ariannacrippa/QC_lattice_H (2024).
Paulson, D. et al. Simulating 2d effects in lattice gauge theories on a quantum computer. PRX Quantum 2, 030334 (2021).
Di Matteo, O. et al. Improving hamiltonian encodings with the gray code. Phys. Rev. A 103, 042405 (2021).
Jordan, P. & Wigner, E. P.Über das paulische äquivalenzverbot (Springer, 1993).
Quantinuum nexus, https://nexus.quantinuum.com/ (2024).
Pino, J. M. et al. Demonstration of the trapped-ion quantum CCD computer architecture. Nature 592, 209 (2021).
Ryan-Anderson, C. Pecos: performance estimator of codes on surfaces. https://github.com/PECOS-packages/PECOS (2018).
Ryan-Anderson, C. et al. Realization of real-time fault-tolerant quantum error correction. Phys. Rev. X 11, 041058 (2021).
Yamamoto, K., Manrique, D. Z., Khan, I. T., Sawada, H. & Ramo, D. M. Quantum hardware calculations of periodic systems with partition-measurement symmetry verification: Simplified models of hydrogen chain and iron crystals. Phys. Rev. Res. 4, https://doi.org/10.1103/PhysRevResearch.4.033110 (2022).
Jackson, C. & van Enk, S. J. Detecting correlated errors in state-preparation-and-measurement tomography. Phys. Rev. A 92, 042312 (2015).
Acknowledgements
We acknowledge Henrik Dreyer and David Zsolt Manrique for a careful review of the manuscript, and Irfan Khan for discussions on the qubit reuse automatic compilation. We thank the entire Quantinuum NEXUS team. We thank Davide Materia for sharing his work on the employment of the mutual information in quantum chemistry. We are grateful to Enrique Rico Ortega, Francesco Di Marcantonio and Maria Cristina Diamantini for fruitful discussions on the topic. This work is supported with funds from the Ministry of Science, Research and Culture of the State of Brandenburg within the Centre for Quantum Technologies and Applications (CQTA). A.C. is supported in part by the Helmholtz Association Innopool Project Variational Quantum Computer Simulations (VQCS). This work is funded by the European Union’s Horizon Europe Frame-work Programme (HORIZON) under the ERA Chair scheme with grant agreement no. 101087126.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
A. Crippa is the corresponding author of this manuscript. A. Crippa developed the quantum circuits and carried out the calculations in the Hamiltonian formalism with exact diagonalization, variational quantum computing approach and on quantum hardware. K. Jansen supervised the project and contributed to discussions of the results. E. Rinaldi applied the necessary transpilation and error mitigation techniques to run on the ion trap device and supervised the quantum hardware runs. All authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Or Katz and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Crippa, A., Jansen, K. & Rinaldi, E. Analysis of the confinement string in (2+1)-dimensional Quantum Electrodynamics with a trapped-ion quantum computer. Commun Phys (2026). https://doi.org/10.1038/s42005-025-02465-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-025-02465-8