Main

Advances in fields such as robot hardware development1,2, motion and interaction control3, interaction policy design4, vision, motion and task planning, learning5 and human–robot interaction6, have led to systematic approaches for implementing skilful and versatile physical robotic manipulation capabilities called ‘manipulation skills’. Considering that many workplaces may be automated in the near future and that important steps have been made to increase robotic manipulation performance7,8, manipulation skills have gained increasing interest from various application domains9,10,11,12 involving manual work. Human workers can rely on systematic curricula that have been specifically developed for their profession. For example, in Germany, there are various well-established standard works on professional industrial training13, such as those described in refs. 14,15,16. However, no such curriculum exists for robots when learning manipulation skills.

If robots are to work in such applications, they require sophisticated tactile capabilities to ensure their safe, reliable and efficient integration into human-centred processes. Such capabilities, which we refer to as robot skills, have been the subject of extensive research efforts, such as object–action complexes17,18, combinations of hierarchical task structures with low-level motion and interaction controllers19,20,21, a cognitive architecture that recognizes and imitates actions22, or goal-directed action sequences that consist of motor primitives23. Other approaches are based on Riemannian manifolds24 or geometric fabrics25 or are learned end-to-end, such as refs. 26,27. Recently, vision–language–action models have gained increasing popularity as more relevant robot data have become available4,28. In this work, we focus on three important issues: the missing scalability of the solution skills, the integration of learning and task constraints such as safety and robustness, and the need for a clear mapping from process specification to skill implementation.

To address these problems, we propose a new taxonomy-based approach for manipulation skills that integrates control and learning on a basic level. Several taxonomies have been proposed for anthropomorphic robotic hands where different grasps are classified into a hierarchical structure29,30. However, taxonomies that classify robot skills remain rare. Ref. 31 introduced an assembly taxonomy that decomposes complex assembly tasks into simple skills that can be reused to reduce the programming time and overhead, whereas ref. 32 combined planning methods and compliant manipulation schemes to classify typical household tasks.

We consider our taxonomy as a first step towards developing a systematic curriculum for robotic manipulation, which would allow us to constructively scale to arbitrary skills with unmatched versatility. Additionally, we introduce a formalism for tactile skills that could seamlessly integrate well-understood manipulation processes and their constraints and connect to learning capabilities.

The proposed integration of process specifications, a taxonomy and a tactile skill framework can also be viewed as an end-to-end approach informed by requirements. In robotics, end-to-end frameworks typically map available sensory inputs to motor torque outputs using, for example, large neural networks to represent the policy33,34. Instead, we seek a mapping from a process description of physical manipulation to a parametric representation of a tactile skill. Both are constructed with a compatible formalism and, thus, can be framed as a joint learning problem. Compared to common sensor-to-torque approaches, the solution space is much smaller, such that it can be more efficiently sampled and learned. Although the approach introduced in this manuscript is not limited to a particular subset of robotic manipulation skills, we focus on well-established manufacturing processes as a highly relevant application domain with notable spillover potential. Also note that we performed our studies with a widely used state-of-the-art manipulator with seven degrees of freedom (DoF) and equipped with a standard rigid end effector. While highly specialized machines are more suited to individual skills and can execute them with higher performance than this manipulator, but our results should be compared with other general-purpose manipulators. Furthermore, all objects are grasped with form closure.

Results

Tactile skill

We first introduce the concept of a tactile skill as a computational policy–controller–learner complex that, together with a tactile platform, constitutes the system class of tactile robots. Figure 1 depicts the overall architecture of a tactile skill, which is composed of three fundamental components as described in its definition. A nomenclature explaining all symbols used in the following is presented in appendix 1 in the Supplementary Information.

Fig. 1: Tactile skill architecture.
figure 1

\({\dot{{\bf{x}}}}_\mathrm{d}\) is the desired twist, fd the desired wrench, τd the desired joint torque, \(\dot{{\bf{x}}}\) is the actual twist of the robot, fext the external wrench, Ω the percept vector, \({\mathcal{Q}}\) the performance of the skill, θπ the policy parameters and θc the controller parameters.

Full size image

Definition 1

(Tactile skill) A tactile skill integrates (1) a tactile policy, which encodes coordinated desired wrench and twist commands, and drives (2) a tactile controller that simultaneously regulates and tracks compliance and contact force by generating inputs to (3) a tactile platform that represents the low-level joint dynamics integrating the actual physical system and delivering the percept vector Ω to measure the performance \({\mathcal{Q}}\) that is used to (4) learn the policy and control parameters θπ and θc, respectively.

Definition 2

(Tactile policy) A tactile policy πd encodes and generates coordinated twist and wrench commands \({{\bf{\pi }}}_\mathrm{d}={[{\dot{\bf{x}}}_\mathrm{d}^\mathrm{T},{{\bf{f}}}_\mathrm{d}^\mathrm{T}]}^\mathrm{T}\) to drive the tactile controller based on the percept vector Ω and policy parameters θπ.

A particularly useful instance of a tactile policy πd can be constructed using dynamic movement primitives35. Any suitable dynamical system with appropriate geometric properties is a potential candidate. A possible combined system with dynamic movement primitives for both motion and wrench is defined by

$$\begin{aligned}{\ddot{{\mathbf{p}}}}_\mathrm{d}&={{\varTheta}}_{\uppi,\mathrm{p}_{1}}\left[{{\varTheta}}_{\uppi,\mathrm{p}_{2}}({{\mathbf{p}}}_\mathrm{g}-{{\mathbf{p}}}_\mathrm{d})-{\dot{{\mathbf{p}}}}_\mathrm{d}\right]+{({\bf{\upgamma}}^\mathrm{T}(\alpha (t)){{I}}_{N\times 1})}^{-1}{{\varTheta}}_{\uppi,\mathrm{p}_{3}}\bf{\upgamma}(\alpha (t))\alpha (t),\\ {\dot{\bf{\upeta}}}_\mathrm{d}&={{\varTheta}}_{\uppi,\mathrm{r}_{1}}\left[\,{{\varTheta}}_{\uppi,\mathrm{r}_{2}}\,2\,\log^{r}({{\mathbf{r}}}_\mathrm{g}\otimes {\bar{{\mathbf{r}}}}_\mathrm{d})-{\bf{\upeta}}_\mathrm{d}\,\right]\\&+{({\bf{\upgamma}}^\mathrm{T}(\alpha (t)){{I}}_{N\times 1})}^{-1}{{\varTheta}}_{\uppi,\mathrm{r}_{3}}\bf{\upgamma}(\alpha (t))\alpha (t),\\ {\dot{{\mathbf{r}}}}_\mathrm{d}&=\frac{1}{2}{\bf{\upeta}}_\mathrm{d}\otimes {{\mathbf{r}}}_\mathrm{d},\\ {\ddot{{\mathbf{f}}}}_\mathrm{d}&={{\varTheta}}_{\uppi,\mathrm{f}_{1}}\left[{{\varTheta}}_{\uppi,\mathrm{f}_{2}}({{\mathbf{f}}}_\mathrm{g}-{{\mathbf{f}}}_\mathrm{d})-{\dot{{\mathbf{f}}}}_\mathrm{d}\right]+{({\bf{\upgamma}}^\mathrm{T}(\alpha (t)){{I}}_{N\times 1})}^{-1}{{\varTheta}}_{\uppi,\mathrm{f}_{3}}\bf{\upgamma}(\alpha (t))\alpha (t),\\ \dot{\alpha}&=-\bf{\uptheta}_{\uppi,\alpha}\alpha,\end{aligned}$$
(1)

where ⊗ denotes the quaternion product, pg and pd the goal and desired positions, rg and rd the goal and desired orientations in quaternion representation, ηd the desired angular velocity and \(\bar{{\bf{r}}}\) the conjugated orientation quaternion. γ(α(t)) is the Gaussian basis function vector with N elements driven by the synchronizing joint phase variable α. The matrices Θ[] = diag{θ[]} parameterize the dynamical system and the Gaussians. See appendix 2 in the Supplementary Information for more details.

Several more example policies are presented in appendix 7 in the Supplementary Information. These are described in the time domain for clarity, although in the actual system they would be encoded into a form like equation (1). Note that in our implementation the measured external wrench fext is used at the policy level to inform the policy-switching conditions.

Definition 3

(Tactile controller) A tactile controller is driven by the tactile policy πd (the desired twist and wrench). It is parameterized by θc and informed by the percept vector Ω. It generates effort-level commands to the physical system (the tactile platform) through a generalized interaction control framework that simultaneously regulates or tracks motion and force.

For simplicity, we use an impedance control architecture36 combined with force application and regulation using tactile measurements Ωt ∈ Ω. Overall, the closed-loop system can be written as

$${{\mathbf{f}}}_{{\rm{ext}}}={M}_{x}({\mathbf{q}})\ddot{{\mathbf{x}}}+{D}_\mathrm{d}({M}_{x}({\mathbf{q}}),{{\boldsymbol{\theta}}}_{\rm{c,k}},{{\boldsymbol{\theta}}}_{\rm{c,d}})\dot{\tilde{{\mathbf{x}}}}+{K}_\mathrm{d}({{\boldsymbol{\theta}}}_{\rm{c,k}})\tilde{{\mathbf{x}}}+{{\mathbf{u}}}_\mathrm{f}({{\boldsymbol{\Omega}}}_\mathrm{t}),$$
(2)

where fext is the external wrench. \(\tilde{{\bf{x}}}={\bf{x}}-{{\mathfrak{f}}}_\mathrm{q2a}({{\bf{x}}}_\mathrm{d})\) denotes the motion error where \({{\mathfrak{f}}}_\mathrm{q2a}\) is a transformation from quaternion to axis-angle representation. Mx(q) denotes the Cartesian mass matrix37, where q are the joint angles. Kd is the desired positive definite and diagonal stiffness matrix, which is parameterized by θc,k, where k indicates the parameters for the stiffness matrix. Dd is the desired positive definite damping matrix based on an appropriate damping design38, where θc,d are the damping factors. uf(Ωt) is a feedback term that yields an output based on a measured tactile quantity Ωt. The specific richness of the tactile information Ωt depends on the specificity of the tactile platform. In the simplest case, uf is a time-dependent feedforward wrench trajectory. A more complex option is a force controller39, where Ωt = fext. With further advances in force and tactile sensing, future tactile platforms will leverage the measurement of pressure and shear stress distribution Ωt = iνj. For details, refer to sections ‘Contact event chain’ and ‘Tactile-feedback level’ in appendix 3 in the Supplementary Information, which describe the propagation of contacts into the internal robot structure and how the richness of Ωt determines the tactile feedback level of the given tactile platform.

Tactile platform

A tactile platform is a real-world physical realization that is close to the ideal robot dynamics and model. It incorporates the structure of tactile perception of external contacts through the contact event chain. It connects the tactile skill framework with the environment. A formal definition and technical specification details are provided in appendix 3 in the Supplementary Information.

Learning

Learning is an integral part of a tactile skill. Each parameter can evolve during learning. Specifically, the set of all parameters \({{\bf{\uptheta }}}_{i}={[{{\bf{\uptheta }}}_{\text{c},i}^\mathrm{T},{{\bf{\uptheta }}}_{\uppi ,i}^\mathrm{T}]}^\mathrm{T}\) at episode i is evaluated using a performance evaluator. The computed quality metric \({\mathcal{Q}}\) guides the selection of parameters for the next episode θi+1, that is, \({{\bf{\uptheta }}}_{i+1}={\mathcal{L}}({{\mathcal{Q}}}_{i},{{\bf{\uptheta }}}_{i})\), where \({\mathcal{L}}\) represents the learning method at hand and the performance evaluator measures the quality metric \({\mathcal{Q}}\) based on the convex combination:

$${\mathcal{Q}}(\boldsymbol{\Omega})=\sum_{l=1}^{n}\,{{\mathcal{Q}}}_{l}(\boldsymbol{\Omega})\,{\omega}_{l},\quad {\omega}_{l}\le 0,\quad\sum_{l=1}^{n}{\omega}_{l}=1,$$
(3)

of performance measures \(\{{{\mathcal{Q}}}_{l}({\boldsymbol{\Omega }})\}\). The choice of weights ωi is part of the cost function design and depends on the desired overall performance objectives. Details of the learning method used are provided in Methods.

Tactile skill representation in the state space

All the above elements of a tactile skill can be integrated into its unified state-space representation:

$$\begin{aligned}{\mathbf{y}}(t)&:= {\left[{{\mathbf{x}}}_\mathrm{d}{(t)}^\mathrm{T},{\dot{{\mathbf{x}}}}_\mathrm{d}{(t)}^\mathrm{T},{{\mathbf{f}}}_\mathrm{d}{(t)}^\mathrm{T},{\dot{{\mathbf{f}}}}_\mathrm{d}{(t)}^\mathrm{T},{\mathbf{x}}{(t)}^\mathrm{T},\dot{{\mathbf{x}}}{(t)}^\mathrm{T}\right]}^\mathrm{T},\\ \dot{{\mathbf{y}}}(t)&={\mathcal{A}}(t,{\mathbf{y}}(t),{\bf{\uptheta}}_{\uppi},{\bf{\uptheta}}_\mathrm{c})+{\mathcal{B}}(t,{\bf{\uptheta}}_\mathrm{c}){\mathbf{u}}(t),\\ {\mathbf{z}}(t)&={\mathcal{C}}(t,{\bf{\uptheta}}_\mathrm{c}){\mathbf{y}}(t)+{\mathcal{D}}(t,{\bf{\uptheta}}_\mathrm{c}){\mathbf{u}}(t),\end{aligned}$$
(4)

where y(t) is the state vector, \({\mathcal{A}}\) the system matrix, \({\mathcal{B}}\) the input matrix, \({\mathcal{C}}\) the output matrix, \({\mathcal{D}}\) the feedthrough matrix, u(t) the control vector and z(t) the output vector. θπ and θc are the parameter vectors of the tactile policy and the tactile controller, respectively, and u(t) is the total control vector:

$${\mathbf{u}}(t)=\left[\begin{array}{c}{({\bf{\upgamma}}^\mathrm{T}(\alpha (t)){{{I}}}_{N\times 1})}^{-1}{{{\varTheta}}}_{\uppi,\mathrm{p}_{3}}\bf{\upgamma}(\alpha (t))\alpha (t)\\ {({\bf{\upgamma}}^\mathrm{T}(\alpha (t)){{{I}}}_{N\times 1})}^{-1}{{{\varTheta}}}_{\uppi,\mathrm{r}_{3}}\bf{\upgamma}(\alpha (t))\alpha (t)\\ {({\bf{\upgamma}}^\mathrm{T}(\alpha (t)){{{I}}}_{N\times 1})}^{-1}{{{\varTheta}}}_{\uppi,\mathrm{f}_{3}}\bf{\upgamma}(\alpha (t))\alpha (t)\\ {{\mathfrak{f}}}_{\rm{q2a}}({{\mathbf{x}}}_\mathrm{d}(t))\\ {{\mathfrak{f}}}_{\rm{q2a}}({\dot{{\mathbf{x}}}}_\mathrm{d}(t))\\ {{\mathbf{u}}}_\mathrm{f}({\boldsymbol{\Omega}}_\mathrm{t}(t))\\ {{\mathbf{f}}}_{{\rm{ext}}}(t)\end{array}\right].$$
(5)

Details of the system components are presented in appendix 2 in the Supplementary Information.

For clarity, we treat estimated and measured sensory quantities alike. We assumed the bandwidth to be consistently high enough and relevant errors to be comparably negligible, meaning that they are handled by lower-level loops so that the policy generator does not need to treat them explicitly. To our knowledge, current off-the-shelf technology complies with these assumptions. The stability and performance of the specific measurement and controller set-up depend on various factors, which go beyond the scope of this work.

Taxonomy

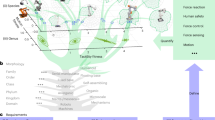
A tactile skill is the output of the taxonomy of manipulation skills (TMS), which encodes the skill selection process. The input to the taxonomy is the process specification. It is the interface used by process experts, such as technicians, robot operators and shop-floor workers, to frame their process knowledge. The developed TMS connects the two domains of process-centric and robot-centric representations. Specifically, it allows a user to map a given process specification to a unique tactile skill using its underlying classification scheme. Figure 2 visually explains this mapping process. Each rank answers a specific question, as stated in the bottom left. This is done for the example of Ethernet plug insertion. The details are given below.

Fig. 2: Taxonomy of manipulation skills.
figure 2

This visualization shows the ranks of the taxonomy and how a given process specification may propagate through it to output a tactile skill.

Full size image

Process specification

A process p is specified by the process operations that are needed to achieve the process objective and the process requirements. There are four process states: initial state s0, error state se, final state s1 and policy state sπ. The policy state sπ contains a number of process operations. The process requirements are formalized by the transitions δ ∈ Δ that connect the process operations and three boundary conditions (\({{\mathcal{C}}}_{{\rm{pre}}}\), \({{\mathcal{C}}}_{{\rm{err}}}\) and \({{\mathcal{C}}}_{{\rm{suc}}}\)) that determine the switching between the top-level states:

  • The precondition \({{\mathcal{C}}}_{{\rm{pre}}}({\mathcal{O}})={c}_{1,{\rm{pre}}}({\mathcal{O}})\wedge\cdots\wedge{c}_{n,{\rm{pre}}}({\mathcal{O}})\) checks whether the process is ready to start and switches from s0 to sπ.

  • The error condition \({{\mathcal{C}}}_{{\rm{err}}}({\mathcal{O}})={c}_{1,{\rm{err}}}({\mathcal{O}})\vee\cdots\vee{c}_{n,{\rm{err}}}({\mathcal{O}})\) is triggered by an irreversible failure. It immediately terminates the process and enters the error state se from s0 or sπ.

  • The success condition \({{\mathcal{C}}}_{{\rm{suc}}}({\mathcal{O}})={c}_{1,{\rm{suc}}}({\mathcal{O}})\wedge\cdots\wedge{c}_{n,{\rm{suc}}}({\mathcal{O}})\) indicates the successful execution of the process. Its activation triggers a switch from s0 or sπ to s1.

The boundary conditions depend on a set of objects \({\mathcal{O}}\) that constitute the process environment. An object \(o\in\mathcal{O}\) is characterized by its Cartesian pose To and possibly also physical properties such as mass, centre of mass or inertia. All objects have a unique identifier (object) and a handle (o1).

The TMS input process specifications are supplied by process experts using established standards like the German curricula for trainees in metalworking40, electronics16 and mechatronics15. These standards and associated norms form the backbone of various industrial processes by delineating boundary conditions, procedural steps, requisites and goals. Process experts leverage these resources to configure automation tasks and streamline their optimization.

By removing the need for explicit robotics expertise, our framework reduces the reliance on integrators, thereby minimizing planning complexities and financial burdens. As a first step, the TMS encompasses processes such as machine-tending (operating levers and pressing buttons), assembly (insertion) and material-processing (bending and cutting).

Skill synthesis

We devised a synthesis procedure to formally close the gap between process specification and skill implementation. The selection of a robot manipulation policy πd(Ω, θπ) from a desired manipulation process p is expressed by

$${\mathcal{T}}={{\mathcal{T}}}_{1}\circ {{\mathcal{T}}}_{2}\circ {{\mathcal{T}}}_{3}\circ {{\mathcal{T}}}_{4}:{p}\to {{\bf{\uppi }}}_\mathrm{d},$$
(6)

where \({\mathcal{T}}\) is the taxonomic algorithm that maps p to a unique πd. Then πd is jointly learned with the controller using a suitable algorithm (the policy and controller parameters θπ and θc are learned) such that \({{\bf{\uppi }}}_\mathrm{d}^{* }={{\bf{\uppi}}}_\mathrm{d}({\boldsymbol{\Omega }},{{\bf{\uptheta }}}_{\uppi }^{* })\) and \({{\bf{\uptau }}}_\mathrm{d}^{* }={{\bf{\uptau }}}_\mathrm{d}({{\bf{\uptheta }}}_\mathrm{c}^{* })\) are the optimal policy and controller solving p. The algorithm steps \({{\mathcal{T}}}_{1}\) to \({{\mathcal{T}}}_{4}\) correspond to the ranks in the taxonomy. Π0 is the initial set of all available policies. \({\mathcal{T}}\) iteratively narrows Π0 down to a single πd by executing the following steps, which are currently still done manually but can be automated:

  1. (1)

    The domain rank \({{\mathcal{T}}}_{1}\) selects policies based on their desired wrench fd: Π1 = {πd ∣ fd(t) = 0 ⊕ fd(t) = const. ⊕ fd(t) ∈ {fd,1, …, fd,n} ⊕ fd = g(t)}, where g(t) is an arbitrary function that drives the evolution of the wrench and ⊕ is an exclusive or.

  2. (2)

    The class rank \({{\mathcal{T}}}_{2}\) selects policies that reach s1, that is the ones that can, in principle, adhere to the boundary conditions of p: Π2 = {πd ∣ s(t) = s1 for t → ∞}.

  3. (3)

    The subclass rank \({{\mathcal{T}}}_{3}\) selects policies that follow the process operations defined by Δ: Π3 = {πd∣δ → true ∀ δ ∈ Δ}.

  4. (4)

    The instance rank \({{\mathcal{T}}}_{4}\) selects the policy with the fewest parameters: \({\varPi}_{4}={{{\uppi}}}_{\mathrm{d}}={c}(\{{\mathbf{\uppi}}_{\mathrm{d}}{\mid}{\rm{min}}_{\vert{{\mathbf{\uptheta}}}_{\uppi}\vert}{{{\uppi}}}_{\mathrm{d}}{\in}{\Pi}_{\mathrm{o,p}}\})\). c represents a choice if more than one policy is left. Furthermore, the parameter domain \({\mathbb{D}}={f}_{{\mathbb{D}}}({{\bf{\uptheta }}}_{\uppi },{{\bf{\uptheta }}}_\mathrm{c},{\mathbb{C}})\) is determined by system and process constraints \({\mathbb{C}}\). This (so far manual) step is represented by \({f}_{{\mathbb{D}}}\).

The rationale behind \({{\mathcal{T}}}_{4}\) selecting the policy with the fewest parameters is to facilitate the subsequent learning problem. Furthermore, we empirically found in refs. 41,42 that process-driven and tailored policies generally outperform more complex and initially unspecific ones (for example, modern vision–language–action models), if a strict specification is provided, that is a narrow problem is to be solved in principle.

The synthesis procedure for our two examples, Ethernet plug insertion and cutting cloth, is described below. More details are provided in appendix 6 in the Supplementary Information. In these examples, we use fg and fg,d to denote the 1-DoF grasp force measured by the gripper and the desired grasp force.

Synthesis 1

Inserting an Ethernet plug

Process specification:

$$\begin{array}{l}{\mathcal{O}}=\{{{o}}_{1},{{o}}_{2},{{o}}_{3}\},\,{{\mathcal{C}}}_{{\rm{pre}}}=\{\;{f}_{{\rm{g}}}\ge {f}_{{\rm{g,d}}}\},\,{{\mathcal{C}}}_{{\rm{err}}}=\{\;{f}_{{\rm{g}}} < {f}_{{\rm{g,d}}}\},\\\,{{\mathcal{C}}}_{{\rm{suc}}}=\{{{{T}}}_{{{o}}_{1}}\in {\mathcal{U}}({{o}}_{3})\},\\\varDelta=\{{\delta }_{1,2}:= {{T}}_{{o}_{1}}\in\mathcal{U}({{o}}_{2}),{\delta }_{2,3}:= {f}_{{\rm{ext}},z} > {f}_{{\rm{contact}}}\}\end{array}$$

fcontact is a contact threshold and fext,z is the z-axis component of the external wrench.

  1. (1)

    The process involves a search behaviour with complex interaction forces. \({{\mathcal{T}}}_{1}\) yields

    $$\varPi_{1}=\{{\bf{\uppi}}_{\mathrm{d},13},{\bf{\uppi}}_{\mathrm{d},14},{\bf{\uppi}}_{\mathrm{d},15},{\bf{\uppi}}_{\mathrm{d},16},{\bf{\uppi}}_{\mathrm{d},17},{\bf{\uppi}}_{\mathrm{d},18},{\bf{\uppi}}_{\mathrm{d},19},{\bf{\uppi}}_{\mathrm{d},20},{\bf{\uppi}}_{\mathrm{d},27},{\bf{\uppi}}_{\mathrm{d},28},{\bf{\uppi}}_{\mathrm{d},32}\}.$$
  2. (2)

    Policies that can reach the final state s1 are selected by \({{\mathcal{T}}}_{2}\) to be

    $${\varPi}_{2}=\{{\bf{\uppi}}_{\mathrm{d},17},{\bf{\uppi}}_{\mathrm{d},20},{\bf{\uppi}}_{\mathrm{d},27},{\bf{\uppi}}_{\mathrm{d},28},{\bf{\uppi}}_{\mathrm{d},32}\}.$$
  3. (3)

    Policies not guaranteed to reach the process substates are removed, so that \({{\mathcal{T}}}_{3}\) yields

    $${\varPi}_{3}=\{{\bf{\uppi}}_{\mathrm{d},27},{\bf{\uppi}}_{\mathrm{d},28},{\bf{\uppi}}_{\mathrm{d},32}\}.$$
  4. (4)

    From Π3, the least complex policy is selected by \({{\mathcal{T}}}_{4}\) to be πd,27.

Synthesis 2

Cutting cloth

Process specification:

$$\begin{array}{l}{\mathcal{O}}=\{{{o}}_{1},{{o}}_{2},{{o}}_{3},{{o}}_{4},{{o}}_{5}\},\,{{\mathcal{C}}}_{{\rm{pre}}}=\{\mathrm{f}_{{\rm{g}}}\ge \mathrm{f}_{{\rm{g,d}}}\},\,{{\mathcal{C}}}_{{\rm{err}}}=\{\mathrm{f}_{{\rm{g}}} < \mathrm{f}_{{\rm{g,d}}},{{\mathbf{f}}}_{{\rm{ext}}} < {{\mathbf{f}}}_{{\rm{cut}}}\},\\{{\mathcal{C}}}_{{\rm{suc}}}=\{{{{T}}}_{{{o}}_{1}}\in {\mathcal{U}}({{o}}_{5})\},\\{{\varDelta}}=\{{\updelta}_{1,2}:= {{{T}}}_{{{o}}_{1}}\in {\mathcal{U}}({{o}}_{2}),{\updelta}_{2,3}:= {{\mathbf{f}}}_{{\rm{ext}}} > {{\mathbf{f}}}_{{\rm{cut}}},{\updelta}_{3,4}:= {{{T}}}_{{{o}}_{1}}\in {\mathcal{U}}({{o}}_{4})\}\end{array}$$

fcut is the desired cutting force.

  1. (1)

    The process requires a constant cutting force, but it also has phases without any contact. Thus, \({{\mathcal{T}}}_{1}\) yields

    $${\varPi}_{1}=\{{\bf{\uppi}}_{\mathrm{d},22},{\bf{\uppi}}_{\mathrm{d},24},{\bf{\uppi}}_{\mathrm{d},26},{\bf{\uppi}}_{\mathrm{d},30},{\bf{\uppi}}_{\mathrm{d},31}\}.$$
  2. (2)

    Policies that can reach the final state s1 are selected by \({{\mathcal{T}}}_{2}\) to be

    $$\varPi_{2}=\{{{\bf{\uppi }}}_{\mathrm{d},26},{{\bf{\uppi }}}_{\mathrm{d},31}\}.$$
  3. (3)

    Policies not guaranteed to reach the process substates are removed, so that \({{\mathcal{T}}}_{3}\) yields

    $$\varPi_{3}=\{{{\bf{\uppi }}}_{\mathrm{d},26}\}.$$
  4. (4)

    From Π3, the least complex policy is selected by \({{\mathcal{T}}}_{4}\) to be πd,26.

Experimental study

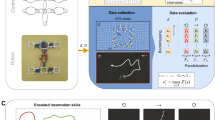
We implemented solution skills based on our Graph-Guided Twist-Wrench Policy (GGTWreP) framework41 (Fig. 4; see Methods for details). The framework encodes expert knowledge about robotics through process-tailored policies with low-level control parameter spaces. It is connected to the process specification through the TMS. This approach allows for sample-efficient learning and tuning by seamlessly combining knowledge from various domains and state-of-the-art machine learning. To illustrate the power of this approach, we implemented 28 real-world manipulation skills using the GGTWreP framework (Fig. 5 and Supplementary Table 1). Overall, high performance levels could be achieved with minimum execution time and contact moments. We injected artificial errors e at the kinesthetically taught poses of the skills to test their robustness to disturbances from exteroception (which is explained in more detail in Methods). The injected errors \({\bf{e}} \sim {{\mathcal{U}}}_{[{{\bf{e}}}_\mathrm{l},{{\bf{e}}}_\mathrm{u}]}\) follow a uniform distribution with lower bound el and upper bound eu.

Table 1 summarizes the achieved performance, the robustness against goal pose randomization, and the average and standard deviation of these metrics. The skills were either autonomously learned or tuned by a domain expert using the simple procedure detailed in Methods. Surprisingly, the seeming disadvantage of having to design a large number of different skills is mitigated because the vast majority of policies can be transferred without modification within the same skill class. Thus, we used one policy for each skill class and needed only to adapt (or relearn) the parameters \({\bf{\uptheta }}={\left[{{\bf{\uptheta }}}_{\uppi }^\mathrm{T},{{\bf{\uptheta }}}_\mathrm{c}^\mathrm{T}\right]}^\mathrm{T}\) to find the new optimum. Some policies are even directly transferable between different classes. When looking at the building blocks of our policies, we may say that many manipulation processes can be solved by using a small toolset of building blocks, which confirms that the proposed approach is versatile enough to be relevant for realistic scenarios.

Table 1 Experimental results
Full size table

As a final verification case, we solved the assembly of an industrial bottle-gripping mechanism, which is widely used in large numbers in bottle-filling plants. The mechanism is a part of a rapidly rotating filling machine, and it grabs and holds bottles during the filling process. This assembly involves eight successive steps using various skills, including insertion, screwing, placing and grasping, and it features a range of physical properties for different materials (aluminium or plastic) and high-precision tolerances <0.1 mm. More details, such as formal skill descriptions and the step-by-step assembly process, can be found in appendix 9 in the Supplementary Information. We verified the approach by running the application n = 50 times. The final execution time required for the assembly was 100 s, and the success rate was 100 %. Note that we cannot disclose any information about our collaboration partner using this device due to confidentiality reasons and that this work has neither been financed nor influenced by this collaboration.

Discussion

The TMS introduced in this paper allows us to encode robot controls and policies by connecting formal process definitions with compatible models of tactile skills. By leveraging established process definitions and the experimentally validated GGTWreP framework, the TMS provides a systematic approach for developing a comprehensive manipulation curriculum for robots.

A key question in effectively using the TMS is how to identify proven solutions for industrial manufacturing processes directly from the taxonomy, which would enable robots to use them as foundational process data for their manipulation capabilities. Human vocational training curricula seem well suited for this purpose. In Germany, these curricula cover over 130 state-certified technical apprenticeships (out of over 320 in total), such as industrial mechanic, mechatronics technician, electronics technician and tool mechanic, and roughly 34,000 DIN norms. They contain definitions for standard processes that are taught to 0.5 million technical apprentices each year based on specialized standard literature15,40. In Germany, Switzerland and Austria, these curricula are standardized at the national level. This standardization has evolved over a century, beginning with the establishment of the Chamber of Commerce and Industry in 1842, followed by the founding of Deutsches Institut für Normung (DIN) in 1917, Schweizerische Normen-Vereinigung in 1919 and Österreichisches Normungsinstitut in 1920.

If robots are to automate today’s industry and become useful assembly assistants, following such established industrial curricula may provide a foundation of prior knowledge for formalizing and then learning and extending these skills. Although these curricula are intended for human use, such as in vocational schools or as an everyday reference for professionals, considering recent advances in large language models (LLMs), it seems reasonable to (at least partially) automate the transformation of these curricula into formal tactile robot skills. This could lead to the creation of a taxonomy of skills and would essentially form a solid starting point for a robot curriculum.

The clear descriptions with transferable parameters and the built-in learning capabilities of the GGTWreP framework yield a high degree of versatility. These features may enable process experts without specific robotics knowledge to deploy robots in the field with little configuration time. As a first use case, we implemented 28 tactile skills from manufacturing industry. The implementation exhibited robust behaviour and high performance in various automation tasks that have been subjected to significant process disturbances. Importantly, the simple transfer of policies and the efficient learning through the parameter vector θ demonstrate the versatility enabled by the taxonomy.

Energy consumption

As this approach enables the learning of a wide range of skills in realistic settings, the issue of energy consumption in real-world 24/7 skill acquisition settings is important. Therefore, we compare the computational energy required for our approach with that of an exemplary state-of-the-art deep learning system, as illustrated in Fig. 3 (details can be found in appendix 4 in the Supplementary Information). The GGTWreP model41 (see Fig. 4) used in this work is compared with the deep deterministic policy gradient method (DDPG)43. The results indicate that using current state-of-the-art data-based methods to learn many skills may have substantial resource demands, as was anticipated, for example, in ref. 44. However, using the GGTWreP framework requires an order of magnitude less energy than DDPG. We compare these approaches to highlight potential limitations and expenses of data-driven methods in contrast to structured methodologies. We anticipate that these insights will hold substantial significance for forthcoming industrial applications, particularly those intended for extensive scaling. Additionally, on the right of Fig. 3 we show bar plots that compare the achieved success rate and performance of the two methods on the cylinder insertion problem from the taxonomy (see Fig. 5).

Fig. 3: Energy demand comparison.
figure 3

a, Comparison of the energy required to learn a great number of skills. We compare the DDPG algorithm with the GGTWreP framework. b, Comparison of the final performance of successful episodes for both approaches averaged over several experiments.

Full size image
Fig. 4: An architectural overview of the GGTWreP framework.
figure 4

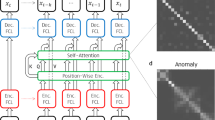
The learning layer generates parameters for downstream layers. The skill state layer selects the appropriate policy state, which is executed by the policy layer. Generated commands are sent to the control layer, and the system layer then forwards torque commands to the robot hardware while receiving the latest robot state. This state is processed by the state and model estimator to produce an updated world state, which is made available to all layers.

Full size image
Fig. 5: Experimental set-ups.
figure 5

Experimentally validated skills are shown with the set-up used in the context of the taxonomy. For clarity, we indicate the taxonomy ranks as domain (D), class (C) and subclass (S). Instances are omitted because they are represented by the pictures.

Full size image

Limitations and outlook

Limitations of the current implementation of GGTWreP include that manual design is required to reuse its process-tailored models for different classes. However, recent works, such as ref. 45, indicate that LLMs could create such policies in a scalable way. Furthermore, the current scope of our taxonomy was limited to a moderate set of manipulation skills and serial manipulators with linear two-fingered grippers; we did not consider interactions with soft materials, which could be addressed by integrating suitable controllers. As we do not make assumptions about the robot controller, it would be possible to extend the presented approach to processes that involve deformable objects46.

A related aspect is the flexibility required of the grasping device. Current industrial processes are typically rigid. They disregard unexpected variations and treat deviations as faults rather than opportunities for adaptation. Future robots must overcome these limitations if they are to be applied in domains requiring complex processes like textile manufacturing. Although our approach does not yet handle gripper slippage or object shifts during interactions, promising directions for future developments include: (1) automated additive manufacturing of task-specific optimized gripper fingers47 and (2) compliant or force-controlled grippers equipped with tactile sensors to enhance robustness and to adapt nominal tactile policies to varying conditions48.

We plan to extend the experimental work to even more manipulation processes and skills, which would also require us to extend the taxonomy to other domains and robot systems. Specific examples are bimanual tasks in the household service domain, including skills such as handing items to humans or supporting them physically. In fact, further efforts conceptually building upon the framework described in this manuscript have already been carried out49. Furthermore, the integration of the GGTWreP framework with state-of-the-art deep learning techniques may open up possibilities to make the skill models more generic.

Finally, the formal architecture of the TMS, with its well-defined semantics, could provide an automated library for high-level robot programming languages that have become widespread in recent years (see, for example, ref. 2). In this context, we plan to use LLMs and vision–language models to generate formal process definitions from natural language input. By using its synthesis procedure to generate new skills on the fly from user input and its ability to learn them, it could become a programming tool for non-experts. However, a caveat of this approach is that the amount of data required to build proper, specialized LLMs or vision–language models is typically very large and implies extensive community effort. Our initial thoughts on this topic are provided in appendix 10 in the Supplementary Information.

Methods

GGTWreP framework

To implement process-compatible tactile skills, we rooted our efforts in the GGTWreP framework41, which has several hierarchical layers, with each layer modelling a different aspect of tactile manipulation. This multilayered structure descends from a learning layer down to the hardware system layer that is directly connected to the physical robot platform, which is coupled to the real world (Fig. 4). \({\bf{w}}\in {\mathcal{W}}\) denotes an element of the world state space \({\mathcal{W}}\), containing, for example, the robot poses, external forces or object positions. Ω denotes the percept vector, which contains information received by internal or external sensors. Appendix 1 in the Supplementary Information provides a nomenclature for all symbols used in the following.

Layers

The framework layers are described in detail in the sections below. Each layer receives inputs and extra parameters from the layer above and provides outputs to the layer below. The layers also provide constraints \({\mathbb{C}}\) in the context of the task and the limits of the system. These constraints model the limits of a valid input to the respective layer (for example, the maximum admissible velocity). The state and model estimator updates and provides the world state w with the other components based on the percept vector Ω and internal models. Figure 4 provides an overview of the GGTWreP framework with its different layers.

  • The learning layer proposes parameters for the next episode in a learning process based on the parameters and quality metric of the previous episode.

  • The skill state layer controls a state machine that governs the discrete behaviour of the system.

  • The policy layer holds a set of (in general) ordinary differential equations embedded into a graph structure, which produce coordinated twist and wrench commands.

  • The control layer implements a unified force and impedance controller that is fed by the policy layer commands and provides desired motor commands for the system layer. This layer also contains safety mechanisms to meet the system and process constraints. It also contains safety mechanisms that ensure that the system and process constraints are fulfilled.

  • The system layer is the lowest layer. It sends motor commands from the control layer to the robot hardware. It provides the current robot state to the other layers.

Objects

A skill is instantiated through objects \({\mathcal{O}}\) that define the environment relevant to the skill, which is like the definition of manipulation processes introduced above. Note that all skills also contain an end effector as a default object. It has the handle EE.

Learning layer

The learning layer executes a learning algorithm that proposes a parameter candidate \({{\bf{\uptheta }}}_{i+1}\in {\mathbb{D}}\) for episode i + 1 based on the parameters θi and quality metric \({{\mathcal{Q}}}_{i}\) of the previous episode i and passes the candidate to the skill state layer. \({\mathbb{D}}\) is the parameter domain and is informed by the constraints \({\mathbb{C}}\). The learning layer is represented by the functional mapping:

$${f}_\mathrm{l}:{\mathbb{D}},{{\bf{\uptheta }}}_{i},{{\mathcal{Q}}}_{i}\to {{\bf{\uptheta }}}_{i+1}.$$
(7)

Skill state layer

The skill state layer contains a discrete two-layered state machine that consists of four skill states: initial state s0, policy state sπ, error state se and final state s1. s0 denotes the beginning, s1 is active at the end, se represents the end state if an error occurs, and sπ activates the policy layer. Three transitions govern the switching behaviour at the top level of the state machine. They directly implement the boundary conditions from the process specification introduced above. Additionally, some of the default conditions come from the physical realities of the robot system:

  • The default precondition \({{\mathcal{C}}}_{\text{pre},0}=\{{{{T}}}_{{\rm{EE}}}\in \text{ROI}\}\) states that the robot has to be within a suitable region of interest (ROI) depending on the task at hand.

  • The three default error conditions \({{\mathcal{C}}}_{\text{err},0}=\{| {{\bf{f}}}_{{\rm{ext}}}| > {{\bf{f}}}_{{\rm{ext,max}}},{{{T}}}_{{\rm{EE}}}\notin \text{ROI},t > {t}_{{\rm{max}}}\}\) state that the robot may not leave the ROI, exceed the maximum external forces or exhaust the maximum time for skill execution. fext,max is a positive vector.

The policy state sπ contains a state machine layer known as the manipulation graph. It implements the policy state from the process specification. In this graph G(Πg, Δ), Πg denotes the set of policies (nodes) and Δ the set of transitions (edges). The transitions are conditions that, if true, switch the current policy according to the graph structure. The skill state layer is represented by the functional mapping:

$${f}_{s}:{\mathcal{O}},{{\bf{\uptheta }}}_{\pi },{\bf{w}}\to s,{s}_{\uppi ,k},$$
(8)

where s is the current skill state and sπ,k the kth substate in the policy state.

Policy layer

The policy layer contains a set of ordinary differential equations Πg. Each system represents one policy πd and implements one process state while maintaining the stated conditions. The currently active πd is determined by the skill state layer. The policy layer functional mapping is expressed as:

$${f}_{{\uppi}}:s,{s}_{{\uppi} ,k},{{\mathbf{\uptheta}}}_{\uppi},{\mathbf{w}}\to {{\mathbf{\uppi}}}_{\mathrm{d}}.$$
(9)

For s ≠ sπ, a default policy

$${\mathbf{\uppi}}_{\mathrm{d}}=\left[\begin{array}{c}{\dot{{\mathbf{x}}}}_{\mathrm{d}}\\ {{\mathbf{f}}}_{\mathrm{d}}\end{array}\right]=\left[\begin{array}{c}{\mathbf{0}}\\ {\mathbf{0}}\end{array}\right],\quad{f}_{{\rm{g,d}}}={f}_{{\rm{g}}},$$

is activated, where fg denotes the current grasp force. Note that fg,d is the desired grasp force for the end effector of the robot and is passed directly to the robot. For clarity, it was omitted from Fig. 4.

Control layer

The control layer receives commands πd from the policy layer and calculates the desired motor commands τd. We chose a basic form of unified force and impedance control:

$${\bf{\uptau}}_\mathrm{d}={{{J}}}_{x}{({\mathbf{q}})}^\mathrm{T}\left[{{\mathbf{f}}}_\mathrm{d}-{K}_\mathrm{d}({\bf{\uptheta}}_{\rm{c,k}})\tilde{{\mathbf{x}}}-{D}_\mathrm{d}({M}_{x}({\mathbf{q}}),{\bf{\uptheta}}_{\rm{c,k}},{\bf{\uptheta}}_{\rm{c,d}})\dot{\tilde{{\mathbf{x}}}}\right].$$
(10)

\(\tilde{{\bf{x}}}={\bf{x}}-{{\mathfrak{f}}}_\mathrm{q2a}({{\bf{x}}}_\mathrm{d})\) denotes the motion error and \({{\mathfrak{f}}}_\mathrm{q2a}\) is a transformation from quaternion to axis-angle representation. Kd is the desired positive definite stiffness matrix, Dd is the desired positive definite damping, and θc,d and θc,k are the damping factors and stiffness gains. Mx(q) denotes the Cartesian mass matrix37.

Architecturally, the control layer is encoded by the functional mapping

$${f}_{\mathrm{c}}:{{\mathbf{\uppi}}}_{\mathrm{d}},{{\mathbf{\uptheta}}}_{\mathrm{c}},{w}\to {{\mathbf{\uptau}}}_{\mathrm{d}}.$$
(11)

Furthermore, the control layer hosts safety mechanisms such as value and rate limitations, collision detection, reflexes and virtual walls.

System layer

The system layer is expressed by the functional mapping

$${f}_\mathrm{h}:{{\bf{\uptau }}}_\mathrm{d}\to {\boldsymbol{\Omega }}.$$
(12)

It defines the control/sensing interface for the hardware system and other devices in the robot and encapsulates any subsequent hardware-specific control loops.

State and model estimator

The state and model estimator holds all the models for internal and external processes. Examples of internal models are the estimated mass matrix \(\hat{{{M}}}({\bf{q}})\), Coriolis forces \(\hat{{\bf{C}}}({\bf{q}},\dot{{\bf{q}}})\) and gravity vector \(\hat{{\bf{g}}}({\bf{q}})\). External models describe the state of environmental elements, such as the physical objects handled by the robot. For example, if the robot were to place an object at a new location, a model of the object would be updated with the new pose. The estimator continuously updates the models using Ω. Its functional mapping is

$${f}_\mathrm{i}:{\boldsymbol{\Omega }}\to {w}.$$
(13)

Task frame

The task frame T defines a coordinate frame OTT relative to the origin frame of the robot O. πd is then calculated in the task frame and transformed through OTT into the frame of the origin.

Implementation example

In this section, the steps from a process to a skill implementation is outlined for the two process examples inserting an Ethernet plug and cutting a piece of cloth. The details of the policy selection through \({\mathcal{T}}\) can be found in appendix 6 in the Supplementary Information together with a visualization in Supplementary Fig. 1.

Inserting an Ethernet plug

In general, an insertion process involves fitting one object into another by aligning their geometries to achieve a form fit. In an industrial context, this process is essential for tasks such as part-mating. Process experts may use specialized literature, such as ref. 50 and norms51, which is a source of process constraints and requirements, such as maximum forces, velocities and so on. In the GGTWreP framework, these constraints can be directly represented as \({{\mathbb{C}}}_\mathrm{s}\), \({{\mathbb{C}}}_{\uppi }\), \({{\mathbb{C}}}_\mathrm{c}\) and \({{\mathbb{C}}}_\mathrm{h}\). These constraints set the limits of the parameter domain for the skills \({\mathbb{D}}\). To underline the performance of our approach (also for learning) and the difficulty of the addressed insertion problems, we compare related work in appendix 8 in the Supplementary Information. In the following, we outline details of the skill implementation based on the GGTWreP framework.

Process specification

The process specification states that the insertable o1 has to be moved towards an approach pose o3. From there, contact is established in the direction of the container o2. Finally, the insertable has to be inserted into the container:

$$\begin{array}{l}{\mathcal{O}}=\{{{o}}_{1},{{o}}_{2},{{o}}_{3}\},\,{{\mathcal{C}}}_{{\rm{pre}}}=\{\;{f}_{{\rm{g}}}\ge {f}_{{\rm{g,d}}}\},\,{{\mathcal{C}}}_{{\rm{err}}}=\{\;{f}_{{\rm{g}}} < {f}_{{\rm{g,d}}}\},\,{{\mathcal{C}}}_{{\rm{suc}}}=\{{{{T}}}_{{{o}}_{1}}\in {\mathcal{U}}({{o}}_{3})\},\\\varDelta=\{{\delta }_{1,2}:= {{{T}}}_{{{o}}_{1}}\in {\mathcal{U}}({{o}}_{2}),{\delta }_{2,3}:= {f}_{{\mathrm{ext},z}} > {f}_{{\rm{contact}}}\}.\end{array}$$

Conditions

There is a default precondition that the robot has to be within the user-defined ROI and an implementation-specific precondition that the robot must have grasped the insertable o1. The default error conditions are that the external forces and torques must not exceed a predefined threshold, the ROI must not be left and the maximum execution time must not be exceeded. Additionally, the robot must not lose the insertable o1 at any time. Note that, for clarity, we do not explicitly show the default conditions in Supplementary Fig. 1. The process specification states that, to be successful, o1 has to be matched with o2. In the implementation, this is expressed by a predefined maximum distance \({\mathcal{U}}({{o}}_{2})\).

Policies

The insertion skill model consists of three distinct phases: (1) approach, (2) contact and (3) insert. The approach phase uses a simple point-to-point motion generator to drive the robot through free space to o3. The contact phase drives the robot into the direction of o2 until contact has been established, that is, when external forces that exceed a defined contact threshold fcontact have been perceived. The insertion phase attempts to move o1 to o2 by pushing downwards with a constant wrench, while employing a Lissajous figure to overcome friction and material dynamics. Additionally, a simple motion generator controls the orientation of the end effector and its lateral motion towards the goal pose. A grasp force fg,d is applied simultaneously to all three phases to hold o1 in the gripper.

Cutting a piece of cloth

A cutting process is characterized by dividing an object into two parts using a cutting tool such as a knife. Again, process experts may use specialized literature such as ref. 52 to define a process specification and set up its optimization. In the following section, we outline the details of the skill implementation using the GGTWreP framework.

Process specification

The process specification states that the knife o1 has to be moved towards an approach pose o3. From there, contact is established in the direction of the surface o2. Then, o1 is moved towards a goal pose o4 while maintaining contact with the surface. Finally, o1 is moved to a final retract pose o5. fcut is the desired cutting force:

$$\begin{aligned}{\mathcal{O}}&=\{{{o}}_{1},{{o}}_{2},{{o}}_{3},{{o}}_{4},{{o}}_{5}\},\,{{\mathcal{C}}}_{{\rm{pre}}}=\{\;{f}_{{\rm{g}}}\ge {f}_{{\rm{g,d}}}\},\,{{\mathcal{C}}}_{{\rm{err}}}=\{\;{f}_{{\rm{g}}} < {f}_{{\rm{g,d}}},{{\mathbf{f}}}_{{\rm{ext}}} < {{\mathbf{f}}}_{{\rm{cut}}}\},\,\\ {{\mathcal{C}}}_{{\rm{suc}}}&=\{{{{T}}}_{{{o}}_{1}}\in {\mathcal{U}}({{o}}_{5})\},\\ {{\varDelta}}&=\{{\updelta}_{1,2}:= {{{T}}}_{{{o}}_{1}}\in {\mathcal{U}}({{o}}_{2}),{\updelta}_{2,3}:= {f}_{{\mathrm{ext},z}} > {f}_{{\rm{cut}}},{\updelta}_{3,4}:= {{{T}}}_{{{o}}_{1}}\in {\mathcal{U}}({{o}}_{4})\}\end{aligned}$$

Conditions

There is a default precondition that the robot has to be within the user-defined ROI and an implementation-specific precondition that the robot must have grasped the knife o1. The default error conditions are that the external forces and torques must not exceed a predefined threshold, the ROI must not be left and the maximum execution time must not be exceeded. Additionally, the robot must not lose the knife o1 at any time, and fext,z < fcontact must be maintained when moving from o3 to o4 in π3. The process specification states that, to be successful, o1 has to be moved towards o5.

Policies

The cutting skill model consists of four distinct phases: (1) approach, (2) contact, (3) cut and (4) retract. The approach phase uses a simple point-to-point motion generator to drive the robot through free space towards o3. The contact phase drives the robot into the direction of o2 until contact has been established, that is, when external forces that exceed a defined contact threshold fcontact have been perceived. The cut phase moves o1 to o4 using a point-to-point motion generator combined with a constant downward-pushing wrench. The retract phase moves o1 to o5 using a point-to-point motion generator. A grasp force fg,d is simultaneously applied to all four phases to hold o1 in the gripper.

Experimental set-up

All experiments use the following off-the-shelf hardware:

  • A Franka Emika robot arm2,53: A 7-DoF manipulator with link-side joint torque sensors and a 1-kHz torque-level real-time interface, which allowed us to directly connect the GGTWreP framework to the system hardware.

  • A Franka Emika robot hand: A standard two-fingered gripper that was sufficient for the processes considered.

  • Intel NUC: A small PC with an Intel i7 CPU, 16 GB RAM and a solid-state drive. Note that our learning approaches do not require GPU acceleration or distributed computing clusters.

Software: The GGTWreP framework was implemented using a software stack developed at the Munich Institute of Robotics and Machine Intelligence. The code can be downloaded from ref. 54.

For the validation experiment, we executed each skill model 50 times on the same set-up. A single trial involved executing a particular skill model until it terminated. When appropriate, we used artificial errors e to offset the manually taught goal poses of the skill in the validation experiment to simulate a more realistic process environment with major disturbances. For example, in typical industrial environments, the moving parts of heavy machines cause process disturbances that impact the precision of the robot. The process-specific experiment set-ups are depicted in Fig. 5. Supplementary Table 1 provides a short description of the skills and lists the selected policy and the injected pose error when the latter is available. For the validation experiment and the optimization experiments (both autonomous learning and manual tuning), roughly 6,000 episodes were run in total. Taking into account the optimization times and set-up times (physically adjusting the environment around the robot for the next experiment), the experimental work took about one net month to complete.

Learning and tuning skills

The parameters for tactile skills \({\bf{\uptheta }}={\left[{{\bf{\uptheta }}}_\mathrm{c}^\mathrm{T},{{\bf{\uptheta }}}_{\uppi }^\mathrm{T}\right]}^\mathrm{T}\) were partially learned and partially manually tuned. The parameter learning procedure is based on our previous work, such as refs. 41,42,55. We used the physical experimental set-ups and goal poses described in ʽResultsʼ.

Algorithm for partitioning the parameter space

We used the parameter space partition algorithm that was introduced in ref. 42. The algorithm runs for k generations with ne episodes per generation. For each episode i, parameters θi were sampled ~ q(a) in a hypercube sample space with q(a) as the sampling policy. These were translated into a solution space and applied to the optimization problem. The resulting reward ri was stored together with the parameters θi. When an episode was unsuccessful, the reward ri was set to a negative value, ri = −1. This was done to ensure that there was a negative classification in the update step. At the end of each generation, the sampling policy q(a) was updated. The sampling policy q(a) consists of two elements: a proposal policy p(a) and a filtering policy f(p(a)). p(a) generated parameter candidates until one was accepted by the filtering policy f(p(a)). Specifically, p(a) proposed parameters θi, which were then evaluated by the filtering policy f(θi). The filtering policy was implemented as a nonlinear support vector machine.

Proposal policy

At the beginning, the proposal policy was a Latin hypercube sampler56, as there was then not enough data to generate meaningful parameter proposals. Instead, the available solution space was evenly sampled. After the first generation, a uniform random sampler was used. In later generations, assuming sufficient data were available, a Gaussian mixture model was used as the policy.

Filtering policy

The filtering policy is a nonlinear support vector machine with radial-basis-function kernels. It was used only if enough successful (in the sense of a successful skill execution) samples were available to ensure a robust estimation.

Optimization procedure

Each optimization procedure was run for ne = 200 episodes. Optimization minimized the execution time and contact moments in two separate experiments. Each episode had the following steps:

  • The learning algorithm proposed policy and controller parameters \({{\bf{\uptheta }}}_{i}={\left[{{\bf{\uptheta }}}_{\uppi ,i}^\mathrm{T},{{\bf{\uptheta }}}_{\mathrm{c},i}^\mathrm{T}\right]}^\mathrm{T}\).

  • A skill was executed with θi, and the measured quality metric \({{\mathcal{Q}}}_{i}\) was fed back to the algorithm.

  • A predefined reset procedure moved the robot on a path back to its initial state.

Thereafter, all the skills converged to an optimal parameter set θ⋆, which was used in the experiments presented. Detailed examples for this skill-learning approach can be found in refs. 41,42. The procedure for manual parameter tuning is like autonomous learning, except that the role of the learning algorithm is taken by an expert programmer.