Introduction

The research of nanometric topological spin textures, such as magnetic skyrmions, contributes significantly to the fundamental understanding of emerging magnetism1,2,3,4. These spin arrangements exhibit unique and non-trivial topological properties, providing insights into the behavior of quantum materials and the interplay between topology and magnetism5. Understanding and manipulating nanometric spin textures have promising implications for future spintronic technologies4,6. Nanometric skyrmion, one prototypical two-dimensional (2D) topological spin texture, is characterized as a topological object defined by topological charge or skyrmion number1,

$$Q=\int \frac{{d}^{2}r}{4\pi }{{{{{{\boldsymbol{n}}}}}}}_{r}\cdot \left(\frac{\partial {{{{{{\boldsymbol{n}}}}}}}_{r}}{\partial x}\times \frac{\partial {{{{{{\boldsymbol{n}}}}}}}_{r}}{\partial y}\right)$$
(1)

Here \({{{{{{\boldsymbol{n}}}}}}}_{r}\) is a unit vector of magnetic moments. It promises potentially faster, energy-efficient, and compact electronic components and may serve as building blocks for information processing6,7, contributing to the realization of more robust and scalable computers. While the impact of nanometric topological spin textures is promising, there are challenges to overcome, such as precise control and manipulation of these structures, addressing issues related to stability and scalability, and resolving three-dimensional (3D) magnetic states in topological magnets.

The topological nature of skyrmion-related spin textures, which includes spin (anti) hedgehogs, plays a crucial role in determining their stability8,9,10. Skyrmion refers to the traditional 2D topological spin textures that have been confirmed through various advanced imaging techniques, such as Lorentz transmission electron microscopy (Lorentz TEM)11, scanning tunneling microscopy (STM)12,13, and magnetic force microscopy (MFM)10, in bulky magnets with a broken inversion symmetry in their crystal structure and heterostructured films with spin-orbital interaction (Dzyaloshinskii–Moria interaction (DMI))14. On the other hand, spin (anti) hedgehog refers to the 3D spin textures predicted theoretically in the context of broken skyrmion strings9,10. To gain insights into the dynamic behavior of spin hedgehogs and their interactions with other magnetic structures like skyrmion strings, and hence to understand the topological stability of these spin textures, the advanced 3D magnetic imaging technique is desirable, which enables the visualization of spin (anti) hedgehogs and their dynamics, offering the means to comprehend the influence of external factors such as temperature on the stability and dynamics of skyrmion structures.

While various imaging techniques exist, such as electron tomography15,16 and X-ray nanotomography17,18, achieving high-resolution, non-invasive, and quantitative 3D imaging of magnetic structures remains a significant challenge. Quantitatively measuring these topological objects in three dimensions is less explored, and current methods may not provide a complete and accurate representation of the intricate topology of the magnetic states. While high-resolution magnetic imaging techniques provide detailed insights into the spin states in magnets, there are still limitations. For instance, the non-destructive imaging technique—Lorentz TEM—allows the exploration of dynamic changes in the magnetic phase over time without altering the sample19 and its applications are particularly valuable in materials science, physics, and spintronics, where understanding the magnetic structures is essential. However, Lorentz TEM only offers qualitative information about the magnetic field distribution within materials. This limitation prompts the need for complementary techniques, such as the transport-of-intensity technique, to derive quasi-quantitative information about magnetization textures20,21. In addition, to achieve 3D magnetic imaging through tomographic Lorentz TEM, the tilt-angle range is constrained to ±50°, causing a missing-wedge problem that can potentially compromise either the spatial resolution or accuracy of the 3D field distribution in materials22.

While atomic-resolution 3D electron tomography is well-established in characterizing the 3D crystal structure of materials23, quantitative evaluation of complex spin textures through 3D magnetic imaging, particularly 3D magnetic phase imaging, remains less explored. Challenges arise from intricate hardware, reconstruction processes, and lower time resolution (typically requiring several hours or days) associated with electron holography15,16. These factors hinder topologically-resolved mapping of 3D spin textures and the dynamics of emergent spin (anti)hedgehogs in magnets. The latter requires high spatial resolution as well as a time-resolved 3D tomographic technique. Therefore, improving time and spatial resolutions in 3D magnetic phase imaging would enhance its effectiveness. However, the magnetic field generated by magnetic lenses in the electron microscope, which is used to align the electron beam and magnify the spatial resolution for imaging, may alter the fine spin textures and modify the overall magnetic states within materials. Overcoming this bottleneck is vital for the progress of 3D magnetic imaging microscopy.

This study presents integrated differential-phase contrast (iDPC) imaging24, which is based on the DPC microscopy (DPCM)25,26,27,28 (see the “Methods” section), to observe magnetic vortices and metastable skyrmion strings within the magnets of (Fe0.63Ni0.3Pd0.07)3P29 and FeGe30 with non-centrosymmetric crystal structures in three dimensions. The experimental setup efficiently suppresses the external magnetic field applied to the sample to below 0.2 mT. The scalar field corresponds to the phase information of spin textures within magnets. In Lorentz TEM or DPCM with a Lorentz mode, the in-plane magnetic components (equivalent to magnetic field B) are perpendicular to the electron beam, causing deflection of the electrons due to their Lorentz force interaction with the B-field. Consequently, the phase shift arising from the electron deflation allows for the imaging of the scalar field of spin textures present within the TEM samples using Lorentz TEM or DPCM (see details in the “Methods” section). In comparison with Lorentz TEM, this phase imaging, conducted in an in-focus scanning transmission electron microscopy (STEM) mode25,26, quantitatively provides the spatial distribution of magnetic fields in magnet with a high spatial resolution approaching atomic scale31. The enhanced spatial resolution enables the visualization of spin (anti) hedgehogs involved in magnetic vortices closed to sample surfaces. Notably, the time resolution achieved is ~10 min in capturing datasets for 3D scalar field reconstructions. This capability facilitates the investigation of the melting dynamics of metastable skyrmion strings, accompanied by the generation of spin (anti) hedgehogs.

Results and discussion

Development of iDPC tomography to visualize vortices in skyrmion strings

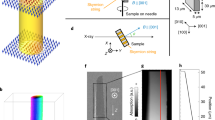
To develop 3D magnetic imaging of spin textures through advanced transmission electron microscopy, we first target the zero-field skyrmion strings at room temperature (RT) in a thin (Fe0.63Ni0.3Pd0.07)3P (FNPP) magnet with a broken-inversion-symmetry crystal structure, as shown schematically in Fig. 1a, to avoid the external field impacting spin textures during sequential tilting of the thin sample. The sample geometry is illustrated in Fig 1b: the plate plane is perpendicular to the c-axis; the longer side and the shorter one measure 4 and 2 μm, respectively. Its thickness ranges from 240 to 280 nm along the y-axis and from 240 to 300 nm along the x-axis (Fig. 1c). In FNPP, the anisotropic DMI vectors result in a orthogonal stripe domain structure29,32,33,34. Upon the out-of-plane magnetic fields, the 2D antiskyrmion29 (Fig. 1d) and skyrmion29 (Fig. 1e) textures show up at relatively low field (~250 mT) and high field (~ 400 mT) in the thin plates, respectively. Meanwhile, such 2D spin textures extend in the thickness direction to form 3D spin textures in the relatively thicker samples under specific conditions33. The zero-field elliptical skyrmions consisting of the inner vortex marked by a yellow arrow (Fig. 1f) can be created through the FC process32. Note here that this vortex-like texture should be topologically distinguished from the vortex core in trivial bubble domains observed in the uniaxial ferromagnets with centrosymmetric crystal structures35,36,37, wherein the DMI is absent.

Fig. 1: The scalar field maps of spin textures observed by tomographic differential-phase-contrast microscopy (DPCM) at a field-free scanning transmission electron microscopy (STEM) mode in a magnet (Fe0.63Ni0.3Pd0.07)3P (FNPP).
figure 1

a The schematics of the non-centrosymmetric crystal structure of M3P (M: Fe, Pd, Ni) with the space group of I\(\bar{4}\) (S4 symmetry). b Schematic of the thin plate showing its dimensions. c Profiles of the thickness versus sample position along the x- (left panel) and y- (right panel) axes, respectively. d and e Simulated spin textures for antiskyrmion (d) and elliptical skyrmion (e) based on material parameters of the FNPP at room temperature (RT). f Integrated DPC (iDPC, phase) image observed in the FNPP plate showing mixtures of stripes and elliptical skyrmions (ellipses). g and h Scalar-field maps of elliptical skyrmions in the XY-planes g at the center (z = 130 nm) and h on the bottom surface (z = 0). The small white arrows denote vortex-like textures appearing on the surface of the elliptical skyrmion (h) while absent at the center of the skyrmion (g). i A three-dimensional (3D) configuration of an elliptical skyrmion, as indicated by a dashed-line yellow arrow in f, showing two separated vortices emerging near the top and bottom surfaces of the elliptically cylindrical skyrmion. j Top-view of the elliptical skyrmion string.

Full size image

To visualize such elliptical skyrmions and clarify the vortex textures, we develop a 3D phase imaging technique at RT. We tilt the sample from ⎯55° to +55° in 2° intervals to capture tilt series of 2D phase images, which are used for the reconstructions of 3D phase maps of elliptical skyrmion strings (see details in the “Methods” section). Figure 1g, h present the XY-plane scalar field maps of the strings at the center of the sample (Fig. 1g) and on the bottom surface (Fig. 1h), respectively, revealing that the vortex is discerned on the surface while absent around the center, as denoted by white arrows. The inner structure of the two separated vortices near two surfaces, as well as the outer circular Bloch domain wall (cylinder) of the skyrmion string, is well grasped from the 3D scalar field distribution of skyrmion string (Fig. 1i). Note that these two vortices can only be distinguished in 3D field maps, whereas they appear as a single vortex from the top view (shown in Fig. 1j). Importantly, at the two ends of vortices, possible singularities, such as spin hedgehog and anti-hedgehog emerge, similarly to the hedgehog–antihedgehog pair predicted theoretically at the ends of the broken skyrmion string8,9,18,22. According to our recent micromagnetic simulations and vector field tomography observations33, these surface vortices may arise from the demagnetization effect in this anisotropic DMI magnet with uniaxial magnetic anisotropy29,33. Further theoretical studies, together with the reconstructed vector field information, may rule out the topological nature of such surface vortices involved in the elliptical skyrmion strings.

Skyrmion strings and their melting dynamics

Next, we approach 3D phase imaging of topological spin textures by varying temperatures to visualize the dynamics of spin (anti) hedgehog directly and gain insight into the stability of metastable skyrmion strings. We examine the magnetic phase diagram in a thin helimagnet FeGe, whose crystal structure is shown in Fig. 2a, with sample dimensions of 4 μm × 2 μm × 0.26 μm, as shown in Fig. 2b, by systematically observing 2D real-space magnetic configurations. After cooling the plate by applying the normal field from a temperature above TC, the zero-field metastable skyrmions (Fig. 2c, d) appear in a wide temperature T range below 240 K (Supplementary Fig. 1), while they are converted to the helical state above 240 K below the TC close to 280 K. Such zero-field metastable skyrmion strings are promising candidates for future spintronic elements due to their intriguing topological properties. Therefore, understanding the stability of such 3D metastable topological objects is desirable, but it remains elusive owing to the limited exploration of the spin texture’s dynamics in three dimensions.

Fig. 2: 3D scalar field maps of metastable skyrmion strings in a helimagnet FeGe visualized by iDPC tomography at zero field.
figure 2

a The schematic of the crystal structure of FeGe with the space group of P213. b The phase diagram observed in a FeGe thin plate with an approximate thickness of 260 nm. The labels H, C, SkX, FC and FM represent the helical structure, conical structure with a wavevector q perpendicular to the plate plane, hexagonal skyrmion lattice, field cooling, and field-polarized ferromagnetic state, respectively. Dashed green (labeled “A”) and blue (labeled “B”) lines represent the field cooling (FC) procedures from 300 K (above the helical ordering temperature TC) to the target temperatures of 180 K (green) and 95 K (blue), respectively. Open circles indicate data points used for capturing iDPC images. c and d 2D vector field maps of metastable SkX observed at zero field. In c, the image was captured at 180 K following a 160-mT FC procedure, while in d, it was observed at 95 K after a 130-mT FC procedure. e and f The corresponding 3D scalar field maps of one unit cell of the metastable SkX at 180 K (e) and 95 K (f). In e, the hexagonal lattice is composed of cylinder-shaped skyrmion strings (entirely uniform scalar fields along the z-direction) obtained in the “A” area. In f, the lattice is triangular and composed of deformed skyrmion strings observed in the “B” area. g and h The cylinder-shaped skyrmions (g) and heavily deformed skyrmion strings (h) were calculated in the thin FeGe with negligible magnetic anisotropy (g) and with in-plane surface anisotropy (h), respectively. Equi-spin surfaces with mz = 0 are shown. Insets show 2D vector field maps of skyrmion strings.

Full size image

The 2D vector field maps presented in Fig. 2c, d illustrate the configurations of two zero-field hexagonal skyrmion lattices (SkXs) at different temperatures: a relatively higher temperature of 180 K in Fig. 2c and a lower temperature of 95 K in Fig. 2d. Despite an in-plane rotation of almost 30° in SkX orientation, possibly influenced by varying the magnitude of cooling fields (160 mT for SkX formation in Fig. 2c and 130 mT for SkX generation in Fig. 2d), no significant difference is observed in these 2D vector field maps. However, the 3D scalar field maps of these metastable skyrmion strings reveal notable distortions at the relatively lower temperature of 95 K (Fig. 2f), particularly for the strings approaching the sample surface. The deformation of skyrmion strings plays a crucial role in their breakage or fusion within the bulk, ultimately leading to the formation of spin hedgehogs and anti-hedgehogs. This process could potentially collapse skyrmion strings and impact their stability. In contrast, cylinder-shaped strings without distortion are evident at the relatively higher temperature of 180 K (Fig. 2e), aligning with the temperature range exhibiting a thermodynamically stable SkX phase, as indicated by the red-colored region in Fig. 2b.

The 3D scalar field maps of metastable skyrmion strings obtained by electron tomography provide a clear depiction of the topological features of metastable states in three dimensions. This confirmation aligns with theoretical predictions regarding the uniformity of magnetic skyrmions normal to the spin-rotating plane within the robust SkX phase stabilized by thermal fluctuations9,10. However, these metastable skyrmion strings exhibit deformation when the temperature is much lower than the transition temperature (T ≪ TC).

The micromagnetic simulations with and without the surface anisotropy in FeGe, as shown in Fig. 2g and h, respectively, have reproduced the aforementioned metastable skyrmion strings observed at 180 K (Fig. 2e) and 95 K (Fig. 2f). The presence of surface anisotropy could be a possible origin of the deformation of metastable skyrmion strings. Although the surface anisotropy is small compared with other magnetic energy terms, it can still have a significant effect on the spin textures38. As a magnetic interaction, the surface anisotropy is expected to be a function of temperature. We tried different values of the surface anisotropy to mimic the temperature trend and observed that the skyrmion string begins to deform (Fig. 2h) and reproduce the experimental result, as shown in Fig. 2f, only when the surface anisotropy is above a certain threshold (~150 μJ m⎯2). Accordingly, the surface anisotropy, in combination with the different temperature and magnetic field parameters used for the field cooling process, may give rise to deformed skyrmion strings. Note here that although the experimental observation can be explained by adding the surface anisotropy in the system, other possible origins, such as the pinning by the impurities, cannot be completely ruled out. The pinning is more effective at lower temperatures, while it is smeared out at higher temperatures.

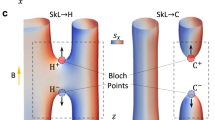
To explore the spin (anti) hedgehog’s dynamics involved in SkX and, hence, to find its stability or collapse mechanism in the heating process, the sequential temperature profiles of their 3D scalar field maps have been observed. Before comprehending the 3D field distributions in skyrmion strings, 2D phase images (Fig. 3a–c) and a series of Lorentz TEM images (Supplementary Fig. 1) at several temperature points in a heating run depict the collapse of SkX with an increase in the sample temperature: below 200 K, the hexagonal metastable SkX, with a fixed crystal orientation, remains robust (Fig. 3a, b); between 200 and 220 K, some skyrmion arrays begin to deform and extend somewhat along a SkX orientation (Fig. 3c); between 220 and 240 K, the SkX mostly transforms into helical domains (periodic bright and dark stripes in Supplementary Fig. 1e) accompanied by skyrmion clusters; above 240 K, the helical domains completely replace the skyrmions (Supplementary Figs. 1, 2).

Fig. 3: The melting dynamics of metastable 3D skyrmion strings observed using iDPC tomography with the increase of temperature.
figure 3

a–c 2D phase images of a zero-field metastable SkX after 130 mT-FC at several temperatures in a heating run: a 95 K, b 200 K, c 220 K. d–i 3D scalar field maps of the surrounding area by smaller red rectangles in a–c demonstrating the melting dynamics of the skyrmion strings with increasing temperature: d, g independent strings at the lowest temperature, 95 K; e, h “H”-shape skyrmion strings connected to each other around the center at 200 K; f, i the curved stripe domains with surface modulations accompanying skyrmion strings at 220 K. j–l Relaxations of metastable skyrmion strings at zero fields evaluated with micromagnetic simulations: j cylinder-shape SkX; k “H”-shape skyrmion strings; l stripe domains with surface modulations. Insets in k and l show schematics of spin hedgehog and anti-hedgehog textures.

Full size image

The mechanism for the collapse of the SkX with an increase in temperature is elucidated through 3D magnetic imaging. At lower temperatures, such as 95 K, isolated skyrmion strings crystallize into a hexagonal SkX, although some strings deform (Fig. 3d and g). As the temperature increases up to 200 K, each skyrmion string connects to one another along one axis of SkX while maintaining a robust lattice form (Fig. 3e). Intriguingly, these connections occur around the string’s center but vanish as they approach the two (top and bottom) surfaces (Fig. 3h), resulting in “H”-shaped skyrmion strings. Magnetic simulations reproduce these “H”-shaped strings composed of pairs of spin hedgehogs and antihedgehogs9,10,22, as shown in Fig. 3k, contrasting with the cylindrical skyrmion strings (Fig. 3j). With a further increase in temperature to 220 K, the connections extend to the sample surfaces, and helical domains with surface modulations become evident, as discerned in Fig. 3f and i. These observations are supported by micromagnetic simulations (Fig. 3l). The sequential temperature-dependent 3D magnetic imaging of the metastable SkX clarifies the melting mechanisms of skyrmion strings: the emergence of spin (anti)hedgehogs around the string center and their dynamics with increasing temperature results in fusion of skyrmion strings, and hence melting or unwinding such metastable spin textures. The transition path from metastable skyrmion strings to helical structure depends on the external magnetic field, as predicted by previous theoretical study9. At low (high) magnetic fields, the (anti)hedgehogs tend to be nucleated in the bulk (at the surface). This difference may be due to the stability of chiral bobbers carrying (anti)hedgehogs at their ends. At a low magnetic field, the chiral bobber is more stable in the bulk, while at a high field, it is more stable close to the surface. Since the present experiments were performed at zero-magnetic fields, it is reasonable that the transformation begins from the bulk. In other words, the present experimental observations confirm the previous theoretical predictions.

The revelations from the 3D scalar field maps, as depicted in Fig. 4, provide a deeper understanding of the dynamical and topological behavior of metastable skyrmions under thermal fluctuation. The scalar field distributions of metastable skyrmion strings in the XY-plane are highlighted at the top (Fig. 4a, d, and g), center (Fig. 4b, e, and h), and bottom (Fig. 4c, f, and i) surfaces at temperatures of (Fig. 4a–c) 95 K, (Fig. 4d–f) 200 K, and (Fig. 4g–i) 220 K, respectively. The data indicate that topological aspects are preserved, and the topological charge remains a constant integer of 1 along the strings at lower temperatures, such as 95 K. However, at a relatively higher temperature of 200 K, the topological charge, as well as the shape of the skyrmions, undergoes modification in the bulk (Fig. 4e), although it is preserved close to the sample surfaces (Fig. 4d and f). This suggests a heat-induced evolution of topological spin textures, leading to the fusion of skyrmion strings and consequently to the emergence of spin (anti)hedgehogs. Upon further temperature increase to 220 K, the fusion of skyrmion strings extends to the sample surface (Fig. 4g), triggering the transformation of skyrmions into helical domains via heavily distorted states of the strings (Fig. 4g–i). In addition to exploring the metastability of skyrmion strings, 3D magnetic imaging highlights the intricate interplay among temperature, topological charge, and the topological aspects of spin textures, providing valuable insights into the thermal dynamics of metastable topological spin textures.

Fig. 4: Scalar-field maps of metastable skyrmion strings in the XY-planes with varying the z-value and temperature.
figure 4

a, d, g Images at the top surface. b, e, h Images at the center. c, f, i Images at the bottom surface. a–c 95 K. d–f 200 K. g–i 220 K.

Full size image

Conclusions

The use of cryogenic 3D magnetic imaging, complemented by its temperature profiles, presents a groundbreaking achievement as it directly confirms theoretical predictions. This innovative approach not only provides empirical evidence but also opens up a new avenue for exploring the intricacies of 3D spin textures. The insights gained from this study have the potential to significantly advance our understanding of complex magnetic phenomena and pave the way for further discoveries in the realm of spintronics and related fields.

Methods

Bulk sample preparation

Single crystals of (Fe0.63Ni0.3Pd0.07)3P and FeGe were grown by a self-flux method29 and chemical vapor transport2, respectively. Powder X-ray diffraction and selected-area electron diffraction confirmed their crystal structures with the \(I\bar{4}\) space group for (Fe0.63Ni0.3Pd0.07)3P and P213 symmetry for FeGe, respectively.

Preparation of thin plane sample

Thin plates of (Fe0.63Ni0.3Pd0.07)3P and FeGe with around 260-nm thicknesses were prepared by thinning bulky samples using a dual-beam system (Helios 5UX, Thermo Fisher Scientific). The thin-sample extraction process was conducted at 30 kV using a Ga-ion beam. The thin plates were then gently polished using a Ga-ion beam at 2 kV to remove the damaged surface layer.

Cryogenic (S)TEM tomography

A liquid-nitrogen-cooling holder with high tilt angles (maximum tilt angles: ±70°), specifically the Gatan Elsa model, is utilized alongside a commercial transmission electron microscope ((S)TEM; Talos F200X, Thermo Fisher Scientific). This setup enables cryogenic (S)TEM imaging. Atomic-scale cryogenic (S)TEM tomography is employed for observing structures in the standard (S)TEM mode under a high magnetic field of ~2 T. In comparison, nanoscale (S)TEM tomography is utilized to obtain magnetic induction maps at the low-magnification (S)TEM mode, varying the normal magnetic field from 0 to ±1.5 T.

Integrated differential-phase-contrast (iDPC) microscopy

Differential phase contrast (DPC) is a method that exploits the phase shift of the electron wave as it passes through a specimen25,26. DPC microscopy (DPCM) uses a convergent electron beam (Supplementary Fig. 3a) to scan across a sample (Supplementary Fig. 3b and c) and a segmented detector (Supplementary Fig. 3d) to collect signals from the transmitted electrons, allowing the extraction of phase (φout (x, y) in (Supplementary Fig. 3a) information, providing magnetic information in materials, according to the equation25

$${{\varphi }}_{{{{{\rm{out}}}}}}(x,y)={{{{{{\rm{C}}}}}}}_{{{{{{\rm{E}}}}}}}\int V\left(x,y,z\right){{\rm {d}}z}-\frac{{{{{{\rm{e}}}}}}}{{{\hslash }}}\int A\left(x,y,z\right){{\rm {d}}z},$$
(2)

where \({C}_{{\rm {E}}},\)V, e, ћ, and A are a constant, the electrostatic potential, electron charge, Plank constant, and the vector potential related to magnetic induction (field). The DPC collects the phase shift related to the shift of the center of mass (CoM) of the electron and detects the intensity I of electron wave24 as

$${I}_{x}={I}_{{{{{\rm{1}}}}}}-{I}_{{{{{\rm{3}}}}}}={{{{{{\rm{|}}}}}}\Delta {{{{{\varphi }}}}}_{x}{{{{{\rm{|}}}}}}}^{2}$$
(3)
$${I}_{y}={I}_{2}-{I}_{4}={{|}\Delta {{\varphi }}_{{y}}}{|}^{2}$$
(4)

Here, \(\Delta {\varphi }_{x}\) and \(\Delta {\varphi }_{y}\) are Fourier transforms of φout (x, y), and I1–I4 are the intensities detected by each detector (Supplementary Fig. 3d), respectively. It indicates that the DPC can directly measure the phase shift (Supplementary Fig. 3e).

When the electron beam with a wavelength λ passes through a magnetic material with infinite thickness t (Supplementary Fig. 3b), the beam should be deflected, resulting in the beam shift (the down panel in Supplementary Fig. 3b) by a Lorentz force arising from the in-plane magnetic components in the magnets. The deflected angle θ is proportional to the in-plane magnetic components (equivalent to magnetic field B), as shown in the following equation25:

$$\theta =\frac{e\lambda }{{{\hslash }}\upsilon }{\bf {B}}t$$
(5)

Therefore, the scalar field, corresponding to the phase information of spin textures within the magnet, can be visualized through DPCM with a Lorentz mode.

Traditional phase contrast methods in (S)TEM involve adding a phase plate to the microscope, but integrated DPC (iDPC) is a technique used to enhance the contrast in imaging samples based on their phase information and helps to enhance the signal-noise ratio (Supplementary Fig. 3g) in comparison with that obtained by DPC (Supplementary Fig. 3f), and hence the visibility of weakly scattering features in materials. The iDPC is linearly proportional to the phase shift24,31,39, which corresponds to the B-field, as shown in e in the relevant magnetic materials, described as

$${{I}}^{{{{{{{\rm{iDPC}}}}}}}}\propto \frac{e}{{{\hslash }}}\left(\int {-B}_{y}\left(x,y,z\right){{{{{{\rm{d}}}}}}x}+\int {B}_{x}\left(x,y,z\right){{{{{{\rm{d}}}}}}y}\right).$$
(6)

While iDPC can provide valuable information about the nanoscale structure and composition of materials, it is sensitive to variations in sample thickness, and careful considerations need to be taken to account for these effects during image interpretation. To obtain a high-quality tilt series of 2D iDPC images, it is crucial to select a sample area with a relatively uniform thickness. Achieving optimal performance in iDPC requires stable instrument conditions to accurately capture phase information.

Tomographic iDPC

The tomographic iDPC is a valuable technique that enhances phase contrast and spatial resolution, leading to high-resolution 3D magnetic imaging to map tiny spin textures in magnets. In analogy to other electron tomographic techniques, first, the stage shifts in the tilt series projection images are corrected manually using the “Align Image by line ROI” plugin within the open-source image analysis software40 by selecting a line across two easily identifiable landmarks in each image in the tilt series. Next, Inspect3D (Thermo Fisher Scientific) is used to correct the tilt series misalignments through an iterative cross-correlation technique. Band-pass filters and Hanning window are employed in this process to enhance the features in the tilt series in order to get a better cross-correlation data output. This alignment process is set to iterate 5 times with a tilt axis update at every run, ensuring progressively refined alignment. The aligned tilt series is then subsequently reconstructed using the sequential iterative reconstruction technique (SIRT) with 10 iterations. SIRT is chosen for its balance between computational efficiency and reconstruction quality. This iterative nature ensures convergence towards optimal 3D representation. The reconstructed data are then visualized using Avizo software (Thermo Fisher Scientific). Segmentations are performed to extract key features in the 3D models of the magnetic features and a smoothening filter is applied for better visual output.

Micromagnetic simulations in three dimensions

The micromagnetic simulations were performed using Mumax341. To simulate the spin textures in a chiral magnet FeGe, material parameters employed in the simulations are: exchange interaction A = 4.75 pJ m⎯1, Dzyaloshinskii–Moriya interaction D = 0.853 mJ m⎯2, and the saturation magnetization Ms = 384 kA m⎯1 42. The magnetic dipole–dipole interaction was also included in the simulations. The cell size is 3 nm × 3 nm × 3 nm. The periodic boundary condition was employed within the skyrmion plane, while the open boundary condition was employed perpendicular to the skyrmion plane. For the simulations with surface anisotropy (Fig. 2h), an easy-plane type magnetic anisotropy Ks = 200 μJ m⎯2 was employed. The stable spin textures were obtained through energy minimization using the conjugate gradient method. For Fig. 3j–l, the process of a skyrmion lattice transformed into a helix state was simulated with the relaxation process initiated by flipping spins between skyrmions.