Introduction

Dislocations are linear defects in the crystal structure that cause misalignments in the regular three-dimensional lattice pattern. They govern several critical aspects of plastic deformation, including yield strength, work hardening, ductility, creep resistance, and fatigue resistance1. Under extreme high-rate loading events, dislocation motion transitions from thermally activated glide to ballistic transport2. This transition leads to interactions between rapidly moving dislocations and phonons within the lattice. The resulting significant drag effect can excessively embrittle metallic materials leading to catastrophic failures at high strain rates3,4,5.

The altered bonding states within the core regions of dislocations alter the phonon density of states (DOS) by introducing localized vibrational modes6, contributing additional peaks in the phonon spectrum distinct from those in a perfect lattice, and causing variations in bond strength that shift phonon frequencies7. Dislocations also distort the surrounding lattice, modify the vibrational properties of nearby atoms, and exhibit significant anharmonicity, broadening phonon modes and increasing scattering rate8. Similar to the quantization of lattice vibrations, i.e., phonons, a quantized version of a crystal dislocation, i.e., dislons, has been defined for a more precise understanding of the dislocation-phonon interaction9,10,11. From this perspective, confinement and quantization are closely related because confinement in a physical system often leads to the quantization of certain properties9,12. Just as the quantum treatment of dislocation-electron interactions introduced new strategies for optimizing the electrical and thermal properties of materials9,13, quantum confinement of dislocations could also result in unique mechanical behaviors.

In stabilized nano-crystalline and nanostructured metals and alloys, where three-dimensional grain boundary network and/or precipitate spacing is often in the nanometer range, such dislocation confinement may indeed be feasible14. If proven, the confinement effect could be particularly significant in the dynamic deformation of metals, where interactions between dislocations and phonons are the predominant mechanisms. Here we present conclusive proof that phonon drag in metals has been completely damped out, even at strain rates as high as 109 s−1. Such phenomena only manifest if the dislocations are constrained to glide within extremely short distances, on the scale of nanometers. This restriction lowers their terminal velocity well below the shear-wave speed which would typically be observed in bulk materials (i.e., not being constrained). Consequently, their interaction with phonons diminishes, leading to a suppressed phonon drag effect.

This is a noteworthy observation, especially given that the dislocation-phonon drag regime at ultra-high strain rates remains largely unexplored. This gap exists primarily due to the lack of systematic methods to characterize this regime beyond the capabilities of conventional high-rate experiments, such as the Kolsky bar and Taylor impact tests (104−105 s−1)4,15. The recent advancement of laser-induced microprojectile impact testing (LIPIT) enabled studies of deformation behavior at ultra-high strain rates (beyond 106 s−1)16,17,18,19,20. The findings presented here were made possible by developing an impression-based approach that integrates LIPIT with spherical nanoindentation. The key in our approach is to produce spherical impressions with similar geometries and volumes yet employ mechanistically distinct deformation regimes in microprojectile impact and spherical nanoindentation. The mechanistic difference enables us, by developing a theoretical framework, to isolate and characterize the dislocation-phonon drag regime up to 109 s−1. In this study, we apply our approach to Cu-3Ta, a model thermo-mechanically stable nanocrystalline (NC) alloy.

Results

In-situ microprojectile impact

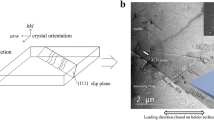
As illustrated schematically in Fig. 1a, individual silica microprojectiles were accelerated by the laser-induced ablation of a sacrificial film and then impacted an NC Cu-3Ta target. Figure 1b is an exemplar in-situ snapshot showing a silica microprojectile impacting onto and rebounding from the target. Figure 1c shows the coefficient of restitution (CoR), i.e., the ratio of rebound and impact velocities, as a function of the impact velocity for both NC Cu-3Ta and pure Cu21. The CoR monotonically decreases as the impact velocity increases for both Cu and NC Cu-3Ta since more energy is dissipated as plastic works at higher impact velocities. However, we note a significantly higher CoR for NC Cu-3Ta compared to pure Cu. In fact, the CoR for NC Cu-3Ta is larger than typical values reported for pure metals21,22,23,24 and coarse-grained alloys25 at a comparable range of impact velocities by several factors. We attribute this unusually high CoR to the much higher strength of NC Cu-3Ta owing to significant grain boundary strengthening and dispersion strengthening from Ta nanoclusters.

Fig. 1: In-situ measurements of microprojectile impact data of NC Cu-3Ta.
figure 1

a Schematic representation of the LIPIT setup. b A multi-exposure snapshot showing a 21-µm-diameter rigid microprojectile impacting onto and rebounding off an NC Cu-3Ta target. c Comparison of coefficient of restitution as a function of impact velocity for pure Cu and NC Cu-3Ta. The data for pure Cu was reproduced from our previous work21. The error bars were determined based on the resolution of the LIPIT snapshots.

Full size image

Plastic work and strain rate sensitivity

Figure 2a–d shows four representative impressions on NC Cu-3Ta resulting from spherical nanoindentation at increasing strain rates of 1, 10, and 100 s−1, and from microprojectile impact at 593 m/s (characteristic strain rate of 6 × 108 s−1). The laser confocal microscopy reconstructions show that these impressions have comparable deformation volumes. We measured the plastic work during both nanoindentation and microprojectile impact (SI Eq. S1 and S2). From 1 s−1 to 100 s−1, our measurements show only a marginal increase in plastic work per unit deformation volume from 4.02 to 4.09 and 4.14 nJ/µm3, respectively. This is in line with the relatively low strain rate sensitivities of the FCC metals in the thermal activation regime3. However, what is surprising is the relatively subtle increase in plastic work per unit impression volume, reaching only 4.76 nJ/µm3, for the impact impression in Fig. 2d despite a significant increase in strain rate by ~8 orders of magnitude to 6 × 108 s−1. To provide context, we compare the measured 1.18 times increase in plastic work per unit deformation volume from nanoindentation to microprojectile impact in NC Cu-3Ta with the fourfold increase reported for pure Cu at comparable deformation volumes and rates in our previous work5.

Fig. 2: Geometrical reconstruction of impressions and comparison of plastic work per unit impression volume across different strain rates, from nanoindentation to microprojectile impact.
figure 2

Laser confocal microscopy reconstructions of four impressions produced by spherical nanoindentation at strain rates of a 1 s−1, b 10 s−1, c 100 s−1, and d LIPIT at strain rate of 6 × 108 s−1 (impact velocity of 593 m/s). e Plastic work normalized by impression volume as a function of effective strain rate (\(\dot{\varepsilon }={v}_{{{\rm{i}}}}/h,\) with \({v}_{{{\rm{i}}}}\) being the impact velocity and \(h\) being the indentation depth). The indentation and impact data were compared only at comparable impression strain levels (\(\varepsilon =h/2.4a=\)0.21 ± 0.02, with \(a\) being the half-width of the impression59) to exclude possible strain hardening effects from the data. The error bars for the nanoindentation data points represent the standard deviation from multiple repeated measurements. For the LIPIT data points, the error bars were calculated based on the resolution of the LIPIT snapshots and laser confocal microscopy.

Full size image

The above analysis suggests minimal embrittlement at ultra-high strain rate in NC Cu-3Ta. To further confirm this observation, we plot the plastic work normalized by impression volume as a function of the effective strain rate for NC Cu-3Ta and Cu in Fig. 2e. The data for Cu clearly shows two different mechanistic regimes. The indentation data which we can fit with a power law with m = 0.015 as the exponent represents the thermal activation regime. The measured strain rate sensitivity in the thermal activation regime is comparable to the reported data4,21. The same power law form cannot fit the microprojectile impact data for Cu. We observe a transition to a linear relationship between the normalized plastic work and the strain rate. The exponent of unity is indeed expected when dislocations enter the ballistic transport regime, and the dislocation-phonon drag is the dominant deformation mechanism4,5. Turning to the indentation and impact data for NC Cu-3Ta we observe no apparent mechanistic regime change. The power law relationship fitting the indentation data (thermal activation regime) can also fit the microprojectile impact data. Our result clearly suggests that the increase in plastic work from indentation to impact in NC Cu-3Ta can be primarily attributed to thermal activation. It is interesting to note the significant role of dislocation-phonon drag in Cu (and the lack thereof in NC Cu-3Ta), making pure Cu as hard as an NC alloy with nanoclusters at ultra-high strain rates.

Thermal activation vs. dislocation-phonon drag; mechanistic contributions

The analysis presented above, while clearly suggestive of a suppressed dislocation-phonon regime in Cu-3Ta, remains empirical. In what follows, we present a mechanistic theoretical framework (see Supplementary Information Section 2 for the theoretical development) to isolate and quantify the dislocation-phonon drag contribution. First, we reformulate the classic equation for the thermal activation stress (Supplementary Information Equation S3–S5) incorporating the plastic work term that we directly measure experimentally:

$${({W}_{{{\rm{p}}}})}^{p}={({W}_{{{\rm{p}}}0})}^{p}-\frac{{({W}_{{{\rm{p}}}0})}^{p}}{{{g}_{0}}^{\frac{1}{q}}}{\left[\frac{kT}{\mu {b}^{3}}{{\mathrm{ln}}}(\frac{{\dot{\varepsilon }}_{0}}{\dot{\varepsilon }})\right]}^{\frac{1}{q}}$$
(1)

Equation 1 reveals a linear relationship between \({({W}_{{{\rm{p}}}})}^{p}\) and \({\left[\frac{kT}{\mu {b}^{3}}{{\mathrm{ln}}}(\frac{{\dot{\varepsilon }}_{0}}{\dot{\varepsilon }})\right]}^{\frac{1}{q}}\). We extrapolated this linear relationship with the experimentally measured plastic work at strain rates of 1, 10, and 100 s−1 to the rates comparable to those induced by microprojectile impact (107–109 s−1) for predicting the plastic work associated with thermal activation at ultra-high rates (see Supplementary Information Fig. 1). The difference in plastic work between the extrapolated nanoindentation data and the measured microprojectile impact data is then the true contribution from the dislocation-phonon drag at ultra-high rates.

Figure 3a, b shows the plastic work as a function of deformation volume for pure Cu and NC Cu-3Ta under nanoindentation and microprojectile impact. For pure Cu, there is a large difference in plastic work between the microprojectile impact (solid red line) and the extrapolated nanoindentation (dashed blue line) indicating a significant contribution from dislocation-phonon drag. For NC Cu-3Ta, on the other hand, the microprojectile impact plastic work, and the extrapolated indentation plastic work collapse into one curve (Fig. 3b), indicating suppressed ballistic transport of dislocations and consequently only minimal dislocation-phonon drag effect. While the plastic work induced by dislocation-phonon drag is in the range of 148–644 nJ for the studied impact velocity range in pure Cu, it is reduced by orders of magnitude to 0.7–70 nJ in NC Cu-3Ta. These results clearly show the ability of NC Cu-3Ta to suppress ballistic dislocation transport at ultra-high strain rates, up to 109 s−1.

Fig. 3: Theoretical analysis separates the phonon drag contribution from thermal activation.
figure 3

Plastic work as a function of impression volume for microprojectile impact, nanoindentation, and extrapolations to the impact strain rate regimes (107–109 s−1) distinguishing the thermal activation and dislocation drag plastic work contributions for a Cu and b Cu-3Ta.

Full size image

Discussion

Our results presented above provide compelling evidence for the suppressed ballistic transport of dislocations in the NC Cu-3Ta alloy at ultra-high strain rates. That is, the thermal fluctuations with which dislocation overcomes the barriers at low strain rates (indentation) remain the dominant deformation mechanism at ultra-high strain rates (microprojectile impact). The lack of the dislocation drag regime in NC Cu-3Ta is physically plausible only if the dislocation-phonon interactions are suppressed, which is surprising given the ultra-high strain rates induced during microprojectile impact5. The three-dimensional network of NC grain boundaries and Ta nanoclusters confine dislocations in nanometer scales. In such a confined environment, the dislocation-phonon interaction can be viewed from a quantized dislocation perspective. According to the dislon theory, the nature of dislocation-phonon interactions is influenced by the phonon frequency in conditions13. Atomistic simulations indicate that in NC Cu-3Ta, Ta nanoclusters disrupt the Cu lattice and shift the acoustic phonon DOS to lower frequencies7. This shift in phonon modes toward lower frequencies, which also occurs with increasing temperature, is a hallmark of thermal expansion and anharmonicity. Consequently, NC Cu-3Ta is expected to exhibit a more pronounced phonon drag on dislocations compared to pure Cu. In the following, we demonstrate that confining dislocations at the nanometer scale suppresses dislocation-phonon interaction, resulting in the minimal dislocation drag regime observed experimentally.

To analyze dislocation behavior further, we consider the treatment proposed by Gillis and Kratochvil1,26 for the acceleration of a single dislocation under a given applied shear stress and with the presence of a drag force that resists its motion. The acceleration of the dislocations can be expressed as a function of dislocation velocity:

$$a(v)=\frac{{\tau }_{{{\rm{AP}}}}{\beta }^{3}}{\rho b}-\frac{\bar{B}v\beta }{\rho {b}^{2}}$$
(2)

Where \({\tau }_{{{\rm{AP}}}}\) is the applied shear stress (see Supplementary Information Section 3, Equation S7–S9), \(\beta =\sqrt{1-{v}^{2}/{v}_{{{\rm{s}}}}^{2}}\) in which v and vs are the dislocation velocity and shear wave velocity, respectively, and ρ is the mass density of Cu. We used Eq. 2 to estimate the normalized dislocation velocity (v/vs) as a function of the distance traveled within a Cu matrix (Supplementary Information Equation S10 and S11). Figure 4 shows that dislocations initially accelerate to high velocities albeit at a decreasing rate due to the drag force. In this case dislocation asymptotically reaches a steady-state velocity of ~0.6 vs after traveling ~85 nm in the Cu matrix. The estimation aligns with prior studies that the steady-state velocity is typically well below the shear wave speed27,28,29,30,31, and specifically ranges from 0.5 to 0.7 vs for dislocations gliding in copper single crystals under similar levels of applied stress32,33.

Fig. 4: Dislocation travel distance as a function of dislocation velocity normalized by the shear wave velocity for NC Cu-3Ta.
figure 4

The dashed purple line indicates the Ta nanocluster spacing (6.4 nm). The gradient background indicates that as the dislocation accelerates from an interrupted glide (v = 0) to a velocity approaching the shear wave velocity, the dominant deformation mechanism transitions from thermal activation to dislocation-phonon drag.

Full size image

The length scale for dislocations to reach steady state velocity is available in pure Cu with grain sizes in the micrometer regime, and a steady state velocity of ~0.6 vs is indeed high enough to trigger significant dislocation-phonon interactions8,34,35,36. As a dislocation accelerates under high applied stress, its continuous gliding generates a strain field around the dislocation37. Consequently, anharmonicities in the dislocation strain field38 contribute to the overall strength of the dislocation-phonon interactions. That is, as the dislocation strain field expands, more phonons are scattered by the dislocation, resulting in stronger dislocation-phonon interactions. For a dislocation within a single crystal Cu, the expansion of the dislocation strain field is negligible for dislocation velocities up to ~0.5 vs (refs. 1,39). This results in a low drag force in the so-called phonon viscosity regime40 where a linear relationship between the drag force and the dislocation velocity is expected. However, as the dislocation velocity exceeds ~0.5 vs, the dislocation strain field expands significantly, resulting in the breakdown of the phonon viscosity regime and a sudden orders of magnitude increase in the energy consumed by dislocation-phonon interactions41. At a steady state velocity of ~0.6 vs, significant dislocation-phonon interactions will dominate the plastic deformation of the Cu matrix.

The NC grains and the Ta nanoclusters, on the other hand, significantly limit the available mean free path in NC Cu-3Ta. To confirm this, we performed scanning transmission electron microscopy (STEM) with both bright field (BF) and high angle annular dark field (HAADF) characterizations on both as-processed and deformed NC Cu-3Ta samples. Our TEM observations of the microstructures in the as-processed state show that the average spacing of the Ta nanoclusters is 6.4 ± 1.6 nm (see Fig. 5b), and the average spacing between the Ta clusters and NC grain boundaries is 6.7 ± 2.4 nm (see Fig. 5c). The nanometer-scale cluster-cluster and cluster-grain boundary spacings are closely linked to the NC grain sizes in the NC Cu-3Ta alloy. Increasing the grain sizes requires the coarsening of nanoclusters, which reduces their number density and consequently increases the cluster spacings via Ostwald ripening42,43,44. This can result in a significantly larger dislocation acceleration distance, enhancing dislocation drag. A high volume of grain boundaries can also act as dislocation sinks45,46,47,48,49, reabsorbing dislocations nucleated during high strain rate impacts and thereby suppressing dislocation-phonon drag. In such conditions, the mean free path available for dislocations to travel in the NC Cu-3Ta is one order of magnitude smaller than the minimum mean free path necessary for the dislocations to reach the steady state velocity. Even without considering the decelerating effect of the Ta nanoclusters due to their strain field interactions with dislocations, we expect a terminal velocity of ~0.38 vs (see the dashed line in Fig. 4) before dislocations are stopped by the nanoclusters. The extremely small mean free path available in the NC Cu-3Ta limits the dislocation velocities in a regime where no significant strain field expansion and interactions with phonons are attainable. This aligns with our experimental measurements, which show an insignificant drag regime, as depicted in Fig. 3b.

Fig. 5: As-processed and post-deformed microstructures beneath the surface of a representative nanoindentation impression and a microprojectile impact impression in NC Cu 3-Ta alloys.
figure 5

a, d, g represent the low magnification STEM BF images of the nanocrystalline grains for as-processed, nanoindentation, and impact samples, respectively; b, e, h represent the higher magnification STEM HAADF images of the high density of Ta-based clusters residing in the lattice as well as along the grain boundaries of the Cu-based matrix for as-processed, nanoindentation and impact sample, respectively; c, f and i show the magnified STEM BF images of a limited number of dislocations surrounding the Ta nanoclusters for as-processed, and been pinned by Ta nanoclusters for nanoindentation and impact samples, respectively. The red arrows in c, f and i highlight some exemplar dislocations.

Full size image

The short mean free path is a necessary condition for suppressing the dislocation drag regime but not sufficient. The short mean free path should be maintained during the deformation. That is, the microstructure should be thermo-mechanically stable under the extreme conditions of stress, strain, and adiabatic temperature rise induced by impact. Traditional NC metals and alloys have been reported to lose their microstructure stability when subjected to low strain rate plastic deformation50. For example, rapid and extensive grain growth was reported for NC Cu under room temperature nanoindentation51. Similar grain coarsening was observed in both NC Ni-Fe and NC Co-P alloys after tensile tests50 and in NC Ni under compression52. This microstructural instability was reported to be even more pronounced in NC Ta subjected to higher rate shock compression53. Our TEM results, on the other hand, demonstrate that the microstructure of NC Cu-3Ta remains stable over a wide range of strain rates spanning from 1 to 109 s−1. Specifically, the grain sizes (~100 nm, Fig. 5a), and the diameter (~4 nm, Fig. 5b) and spacing (~6 nm, Fig. 5c) of Ta nanoclusters in as-processed NC Cu-3Ta, remain nearly constant in both nanoindentation (Fig. 5d–f) and microprojectile impact impression (Fig. 5g–i). This aligns with previous works about the high stability of coherent Ta nanoclusters in NC Cu-3Ta which can prevent grain boundaries from migrating due to a large Zener pinning force54,55,56.

The stable NC structures and Ta nanoclusters in NC Cu-3Ta should result in consistently short mean free paths for dislocations over a wide range of strain rates. The stability in the mean free path, observed in both nanoindentation and impact impression should similarly retard the dislocation motions in both cases. Consequently, the formation of similar residual dislocation structures and activities in both impressions is expected. Indeed, the number of residual dislocations is limited in both cases, with mobile dislocations (Fig. 5c) interacting and becoming pinned by Ta nanoclusters and NC grain boundaries (Fig. 5f, i). Atomistic simulations7,55,57 also predicted this pinning behavior, finding that the NC grain boundaries and closely spaced Ta nanoclusters can prevent dislocations from attaining steady-state velocities at which phonon-dislocation interactions become dominant. Therefore, we confirm that dislocation-phonon drag is significantly suppressed in thermo-mechanically stable NC Cu-3Ta over a wide range of strain rates spanning from 1 to 109 s−1.

Conclusions

The study provides valuable insights into the mechanical behavior of NC Cu-3Ta alloy under ultra-high strain rates, achieved via LIPIT. With the careful design of spherical microprojectile impact and nanoindentation we achieved geometrically similar deformation but at different mechanistic regimes. We developed a theoretical framework to decouple the contribution of dislocation-phonon drag from thermally activated dislocation glide. Our findings revealed a significant suppression of dislocation-phonon drag, a phenomenon that typically dominates plastic deformation in pure copper at high rates. This suppression is attributed to the extremely short mean free paths available for dislocations within the NC matrix, constrained by the presence of Ta nanoclusters. These clusters, spaced ~6.4 nm apart, prevent dislocations from accelerating to velocities sufficient to induce significant phonon scattering, thereby altering the material’s deformation mechanism even under extreme conditions. These results provide conclusive evidence that phonon drags in metals can be entirely damped out at ultra-high strain rates, particularly when dislocations are confined to glide within several-nanometer range distances.

In the context of Cu-3Ta, the dislocations are effectively confined within nanometer-scale regions, akin to electrons in a quantum well. This confinement alters their dynamic properties, preventing them from reaching the ballistic transport regime typically associated with high strain rates. Our findings suggest that this unique behavior is not only due to the physical confinement of dislocations but also to the stability of the NC structure, which maintains its integrity across a broad range of strain rates. We hope that the reported unique behavior in metals, along with the associated mechanistic insights, will inspire further research to substantiate and expand upon these initial findings. This study shall open exciting opportunities for designing materials with tailored mechanical properties by exploiting the interplay between dislocation dynamics and nanostructure confinement. Future research could incorporate experimental characterizations and molecular dynamics simulations to enhance our understanding of dislons and quantum mechanical effects in metals. Specifically, can controlling dislocation velocity under constrained and overdriven conditions lead to phenomena such as phonon engineering? This would complement possible manipulations of the type, location, density, and movement of dislocations which we leave as a direction for future studies.

Methods

Materials and specimen preparation

A batch of monodisperse non-porous silica microspheres with diameter of 20 ± 2 µm and a density of 2.0 g/cm3 was purchased from Sigma-Aldrich (Missouri, USA). The pure Cu plates were purchased from Alfa Aesar (Ward Hill, USA) and have a recrystallized average grain size of 6 ± 2 μm5. The NC Cu-3Ta powders were manufactured through high-energy mechanical alloying at cryogenic temperatures. The NC Cu-3Ta powders were subsequently consolidated into bulk samples via equal channel angular extrusion7,44,55,58. The NC Cu-3Ta target substrates were polished to a nominally 0.05 µm mirror finish prior to nanoindentation and microprojectile impact experiments.

Nanoindentation tests

Nanoindentation tests were conducted on the NC Cu-3Ta alloys using a micromechanical testing stage (Alemnis AG, Switzerland) with a spherical diamond tip (d = 10 μm). We performed microprojectile impact experiments first and characterized the resulting impressions using laser-confocal microscopy to measure their depths and volumes. Based on these measurements, we then aimed for specific nanoindentation depths in the nanoindentation experiments to ensure that both methods covered the same range of deformation volumes and depths. We performed nanoindentation tests under constant strain rates of 1 s−1, 10 s−1, and 100 s−1 and with a range of indentation depths from 1 to 5 μm.

Microprojectile impact tests

Microprojectile impact tests were performed using an in-house built all-optical ballistic setup. A 9 ns duration pulse laser (Quantel Q-smart 850) was used as the excitation laser entailing a repetition rate of 10 Hz and a maximum energy per pulse of 460 mJ at a wavelength of 532 nm. The excitation laser is focused using a focusing lens (LA1131-YAG, f = 50 mm) on a launch pad assembly including a 210 µm thick glass substrate, a 100 nm thick chromium (Cr) film, and a 60 µm thick polyurethane (PU) film. A small amount of silica particles was applied to the PU film of the launch pad using a spatula, followed by a few drops of ethanol. The particles were evenly distributed with a provided tissue, and the ethanol was allowed to evaporate completely. A single microprojectile can be launched by focusing an excitation laser onto the chromium film in which the focused area is ablated to generate a high-pressure plasma and cause rapid expansion of the PU film. The microprojectile speed can be changed by adjusting the laser energy from 1 to 20 mJ. A SuperK FIANIUM FIR-20 picosecond white laser purchased from NKT Photonics (Birkerød, Denmark) was used to illuminate the microprojectiles. The illumination laser pulse entails a repetition rate spanning from 150 kHz to 78 MHz (corresponding to a pulse interval spanning from 6.67 µs to 12.8 ns). With a predefined pulse interval for the illumination laser pulses, we can capture the microprojectile traces using an ORCA-Fusion CMOS camera (C14440-20UP) with a frame rate of 23.2 fps. We scale our original images, which are 2304×2304 pixels, to real-world dimensions of 1028 µm by 1028 µm through calibration with a R1L1S5P stage micrometer. By measuring the distance between two consecutive or multiple microprojectiles and dividing by the time intervals, we can measure both the impact and rebound velocities of the microprojectiles with an uncertainty of ±2%. We can also measure the diameter of the microprojectiles for each LIPIT shot.

Post-mortem characterization

We use a Keyence VK-X260 Laser-Scanning Profilometer to measure the volume and profiles of the nanoindentation and microprojectile impressions. All post-mortem secondary electron and ion contrast images were taken using a ThermoFisher Scientific Helios G4 UX dual-beam focused ion beam/scanning electron microscope (SEM). The secondary electron images were taken with the SEM column operated at 20 keV, while the ion contrast images were taken with the ion column operated at 30 keV using a beam current of 26 pA and 3 µs. The TEM samples for the as-received, nanoindenter, and LIPIT conditions were prepared using the conventional lift-out technique using the same dual-beam microscope. The initial trenching and thinning of the liftout was performed at 30 keV, while the final thinning was started at 5 keV and finished at 2 keV to minimize Ga damage. The TEM lamella of as-processed NC Cu 3-Ta alloy was extracted from a location that is far from any nanoindentation or microprojectile impact impressions to exclude the effects of deformation on the microstructure. The TEM lamellas of nanoindentation impression and microprojectile impact impression were extracted from the center of the impressions. The STEM was performed using a JEOL 2100 F TEM operated at 200 kV. In order to fully characterize the microstructures and the damage imparted from the various testing conditions, both bright-field and HAADF images were acquired.