Introduction

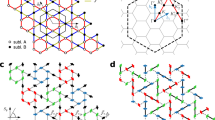
The kagome lattice antiferromagnet is the embodiment of high geometric frustration in two dimensions1. However, a number of other lattices based on triangular motifs come close if we consider suppression of ordered moment2,3. Examples of other highly frustrated Archimedean lattices are the star, bounce, trellis and maple-leaf lattices. A common feature of these lattices is that material realizations are extremely rare4; metal-organic approximate versions exist for the star5 and trellis lattice6. Concerning the maple-leaf lattice (MLL) (see Fig. 1a)7, the situation is slightly more promising8,9 as a number of minerals with quantum spins like bluebellite Cu6IO3(OH)10Cl10, mojaveite Cu6TeO4(OH)Cl10, fuettererite Pb3Cu6TeO6(OH)7Cl511, sabelliite (Cu,Zn)2Zn[(As,Sb)O4](OH)312 and spangolite Cu6Al(SO4)(OH)12Cl ⋅ 3H2O13,14,15,16 have been found; besides, some semi-classical maple-leaf lattice antiferromagnets like MgMn3O7 ⋅ 3H2O17 and Na2Mn3O718,19 are known. Here, we focus on spangolite, which has been characterised magnetically20 with evidence of a non-magnetic ground state. However, the nature of the singlet ground state remains a riddle with various speculative scenarios of either isolated or interacting dimers and trimers having been discussed in ref. 2, but none found to be in complete agreement with observed magnetic features. In this manuscript, we address this long-standing issue by first employing ab-initio density functional theory (DFT) calculations to reliably ascertain the magnetic interactions, which are shown in Fig. 1a, and found to be antiferromagnetic on the dimer (J1) and triangular (J4 and J5) bonds, and ferromagnetic on the hexagons (J2 and J3). The resulting magnetic Hamiltonian is analysed employing state-of-the-art tensor network (TN) simulations based on infinite projected entangled simplex states (iPESS)21 and infinite projected entangled simplex operators (iPESO)22 ansätze, to assess both its ground state as well as finite magnetic field and finite-temperature behaviour.

Fig. 1: Structure and Heisenberg Hamiltonian parameters of spangolite.
figure 1

a Distorted maple-leaf lattice realized in spangolite. The bonds represent the exchange interactions Ji, with thickness scaled in proportion to their values. J1 to J5 are named with ascending Cu-Cu distance, while Jt1, Jt2 (triangles), Jd (dimer) and Jh1, Jh2 (hexagon) are used in the literature. b Crystal structure of spangolite Cu6Al(SO4)(OH)12Cl ⋅ 3H2O20 with DFT relaxed hydrogen positions. c Five exchange interactions constituting the maple-leaf lattice, determined by DFT energy mapping, as function of on-site interaction strength U. The vertical line indicates the U value for which the couplings match the experimental Curie-Weiss temperature, and for this U we have antiferromagnetic J1 = 95.0(2) K, J4 = 28.2(1) K and J5 = 41.6(2) K and ferromagnetic J2 = −23.9(1) K and J3 = −24.2(1) K.

Full size image

Our results lend support to a picture of a dimerized ground state characterised by strong singlet formation on the dimer bonds (J1 in Fig. 1a), which can be ascribed to the presence of a large antiferromagnetic coupling on these bonds. Since these singlets are coupled via appreciable ferromagnetic correlations on the hexagons, they cannot be viewed as being isolated. The ground state is thus composed of correlated dimers and can be viewed as a dressed version of the exact dimer product state23. The behaviour of the magnetic susceptibility with temperature is found to be in qualitative agreement with experiment. For a quantitative match of the calculated susceptibility, a smaller spin gap would be required which would consequently lead to a higher maximum; it is plausible that once an experimental low temperature crystal structure becomes available, redetermination of the Hamiltonian could yield a slightly smaller J1 and larger frustration, yielding a smaller spin gap. The finding of a substantially reduced effective magnetic moment at high temperatures (in agreement with experiment) compared to that expected of six S = 1/2 spins lends support to a ground state composed of non-trivially correlated dimers. This is indeed confirmed by the obtained ground state spin correlation profile, which features significant spin-spin correlations on the triangular and hexagonal bonds. We do not see any evidence of the formation of strongly bound clusters or trimers, which would require invoking additional orbital moments as speculated in ref. 20. Under the application of a magnetic field, the resulting magnetisation curve displays plateaus at 1/3 and 2/3 of the saturation magnetisation characterised by a translationally invariant pattern of spin-spin correlations. The temperature evolution of the magnetisation curve shows a relatively faster melting of the 1/3 compared to the 2/3 plateau.

Results

Heisenberg Hamiltonian

We begin our study of spangolite by determining the parameters of the Heisenberg Hamiltonian

$$H={\sum}_{i < j}{J}_{ij}{{{\bf{S}}}}_{i}\cdot {{{\bf{S}}}}_{j}$$
(1)

using the density functional theory based energy mapping technique. This approach has proven instrumental for the understanding of various Cu2+ based minerals like centennialite24, henmilite25, birchite26, kapellasite27 as well as PbCuTe2O6 (idealized coloalite28)29. The first step is to establish the best possible crystal structure, including all hydrogen positions. For this purpose, we use the structure determined by Fennell et al.20, adding to it the missing H3 position from Hawthorne et al.16. We then carefully relax all six hydrogen positions using the full potential local orbital (FPLO) code30 and the generalized gradient approximation (GGA)31 exchange correlation functional. The resulting crystal structure is shown in Fig. 1b. The structure is characterised by Cu2+ maple-leaf layers where Al3+ ions fill the centers of the hexagons. The metal hydroxide layers are well separated by sulfate groups and water molecules, indicating a high level of two-dimensionality of the material.

We now proceed to extract the Heisenberg Hamiltonian parameters of Eq. (1) by DFT energy mapping (see Method section for details). We can resolve the five nearest-neighbour exchange interactions which make up the distorted maple-leaf lattice of spangolite. We also determine seven longer range couplings which turn out to be less than one percent of the largest coupling and which we ignore in our subsequent analysis. The values of the first five exchange interactions are plotted in Fig. 1c as function of the on-site interaction strength U. The relevant value of U, determined by demanding that the mean-field estimate of the Curie-Weiss temperature matches the experimental value of θCW = −29.4 K20 is marked by a vertical line (note that we redetermined θCW from the experimental data as explained in the Method section). The resulting Hamiltonian parameters, which are the basis for our further investigation are given in Table 1. Spangolite is found to be characterised by a unique network of three antiferromagnetic and two ferromagnetic couplings shown in Fig. 1a. The largest coupling, antiferromagnetic J1, defines dimers. The two weaker antiferromagnetic couplings J4 = 0.297J1 and J5 = 0.437J1 define triangles, and the two ferromagnetic couplings J2 = − 0.252J1 and J3 = − 0.254J1 form the hexagons of the maple-leaf lattice.

Table 1 Exchange interactions of spangolite obtained by DFT energy mapping and compared to bluebellite
Full size table

In order to understand the unique features of spangolite, it is instructive to compare it to bluebellite which has been investigated in refs. 32,33,34 (see Table 1). The dimer coupling J1 ≡ Jd which is strong for both spangolite and bluebellite is nearly equal in magnitude but opposite in sign, antiferromagnetic and ferromagnetic, respectively. This implies that a dimer singlet picture is the natural starting point to understanding the physics of spangolite as all other couplings are clearly subdominant. In contrast, in bluebellite, strong ferromagnetic Jd bonds compete with even stronger antiferromagnetic triangles, which leads to a very different starting point based on antiferromagnetically frustrated triangles.

The two sets of hexagon bonds J2, J3 (Jh1, Jh2) are both ferromagnetic and of nearly equal magnitude in spangolite, while in bluebellite they are nearly equal in magnitude but of opposite signs. This leads to inherently strongly frustrated hexagons in bluebellite but unfrustrated hexagonal units in spangolite. Hence, this points to completely different frustration mechanisms at play in the two materials. Furthermore, the hexagonal couplings in bluebellite are  ~60% of the strongest coupling and cannot simply be treated as a perturbation of a parent order determined by Jt1 and Jd couplings. On the other hand, for spangolite, the hexagonal couplings are only  ~20% of the dimer coupling and do not alter the picture of weakly correlated dimers. In the following, we will analyse the properties of the spangolite Hamiltonian using state-of-the-art tensor network techniques.

Tensor network ansatz

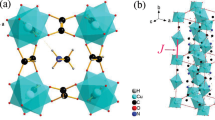
The study of the spangolite Hamiltonian is based on numerical tensor network simulations in the thermodynamic limit. TNs are efficient representations of quantum many-body systems, that encode the probability amplitudes of a (thermal) quantum state as a contraction of a network of local tensors. The tensors are interconnected by auxiliary, virtual indices as shown in Fig. 2a, whose maximal dimension is called the bond dimension χB of the TN (bulk bond dimension). It is a control parameter that can be systematically increased to improve the accuracy of the ansatz. Tuning the bond dimension changes the number of variational parameters in the TN and thereby the amount of quantum entanglement that can be captured. Tensor networks offer efficient numerical simulations with only a polynomial scaling in the number of particles, thus overcoming the exponential barrier by targeting the low-entanglement sector of the full Hilbert space35,36. In our study, we employ infinite projected entangled simplex states (iPESS)21 and infinite projected entangled simplex operators (iPESO)22 for the simulation of ground states and thermal states, respectively. In this context, the TN is used as an ansatz for the full many-body system, consisting of a unit cell of different tensors that generates a translationally invariant quantum state. The simple update steps for the iPESS and iPESO networks visualized in Fig. 2b, c are described Supplementary Notes 2 and 3, together with the coarse-graining scheme shown in Fig. 2d, and other details of the TN implementation.

Fig. 2: Tensor network setup for the simulations of spangolite.
figure 2

a Infinite projected entangled simplex state and operator ansatz for the simulations of spangolite. A coarse-graining of the two spins on J1 bonds results in a regular kagome lattice, on which the tensor network is defined. Here, green tensors reside on the coarse-grained sites, encompassing the physical degrees of freedom, while gray tensors mediate quantum correlations through purely virtual bonds, linking the former. While quantum states \(\left\vert \psi \right\rangle\) have one physical index (represented by the black vertical lines), thermal states ρ(β) need two physical indices (both black and gray vertical lines). b, c Simple update step for the iPESS ground state (T = 0 K) and iPESO thermal state (T > 0 K). The imaginary time evolution gate is first absorbed into a triangle configuration to evolve the states. Applying a higher-order singular value decomposition (SVD) with truncation (tSVD) to the bulk bond dimension χB recovers the individual tensors. d Coarse-graining the six spins in the elementary unit cell results in a square lattice TN, whose contraction is approximated by fixed-point environment tensors shown in gray, using a corner transfer matrix renormalization group procedure. The unavoidable approximations are controlled by an environment bond dimension χE.

Full size image

Ground state without magnetic field

The ground state for the spangolite Hamiltonian can be represented with a single geometrical unit cell of six spins. Due to the strong antiferromagnetic interaction on J1 bonds, it is dominated by a dimerization of the connected spins. The remaining antiferromagnetic interaction terms contribute only weakly to the structure, however, there exist nonnegligible ferromagnetic correlations on the hexagonal bonds. Due to the chosen coarse-graining, the two spins on J1 bonds are treated exactly as a single tensor site, and entanglement with neighbouring sites is only weak. The chosen TN ansatz is therefore ideal and the simple update algorithm leads to accurate results. More sophisticated procedures, such as variational optimisation37 are limited to smaller bond dimensions and not superior here. The ground state energy vs. the inverse iPESS bond dimension is shown in Fig. 3a. Quantum correlations are already seen to be well captured with an ansatz of χB = 8, and a larger bond dimension does not substantially decrease the energy further. A fit of the six largest data points reveals a good estimate for the infinite bond dimension limit (χB → ∞), for which we extrapolate to an energy of

$${E}_{0}/{J}_{1}=-0.4066(4).$$
(2)

The energy is found to be lower compared to that of an exact dimer product state (on J1 bonds), which has an energy per site of E/J1 = − 0.375. The spatial pattern of nearest-neighbour spin-spin correlations 〈Si ⋅ Sj〉 reveals the expected strong dimerization of the ground state on J1 bonds. It is shown as the inset of Fig. 3a. The spins on the hexagons show weak ferromagnetic alignment, while the spins on triangle configurations are nearly uncorrelated. Thus, the ground state cannot be characterised by isolated singlet formations on the dimer bonds alone, but instead these dimers are correlated (due to ferromagnetically correlated hexagonal bonds) forming a correlated dimer liquid with a lower energy.

Fig. 3: Ground state of spangolite.
figure 3

a Ground state energy vs. inverse bond dimension χB for the ground state of the spangolite Hamiltonian without magnetic field. The inset shows the spatial pattern of nearest-neighbour spin-spin correlations, revealing the strong dimerization. b The equal-time spin structure factor S(q) for an exact dimer state on J1 bonds34,47 and (c) for the ground state of the spangolite Hamiltonian at bond dimension χB = 8. The extended Brillouin zone is marked by a white hexagon.

Full size image

In order to further characterize the ground state, we compute the equal-time spin structure factor

$$S({{\bf{q}}}) = \sum\limits_{i,j}\sum\limits_{m,n}{e}^{\dot{\iota }{{\bf{q}}}\cdot ({{{\bf{R}}}}_{i}-{{{\bf{R}}}}_{j})}{e}^{\dot{\iota }{{\bf{q}}}\cdot ({{{\bf{b}}}}_{m}-{{{\bf{b}}}}_{n})}\\ \times \left\langle {{\bf{S}}}({{{\bf{R}}}}_{i}+{{{\bf{b}}}}_{m})\cdot {{\bf{S}}}({{{\bf{R}}}}_{j}+{{{\bf{b}}}}_{n})\right\rangle.$$
(3)

Here, (i, j) denotes the summation over unit cells and (m, n) the additional summation over the six-site basis of the maple-leaf lattice. By exploiting translational invariance, one sum over unit cells can be removed, and the structure factor can be computed by a CTMRG resummation scheme38,39,40, accounting for the appropriate phase factors and spin operators while absorbing tensors into the environment tensors. This scheme typically needs large environment bond dimensions χE to reach convergence. However, due to the large gap in our system (cf. the width of the zero-magnetisation plateau below), the calculations of the structure factor can be converged with moderate χE. In order to have a defined reference, we show the structure factor for the spangolite ground state in comparison to an exact dimer state on J1 bonds in Fig. 3b, c. While the exact dimer state is representable with an iPESS at bond dimension χB = 1, i.e., a product state of coarse-grained dimers, the structure factor for spangolite is computed at χB = 8 to balance accuracy and the computational cost of the CTMRG routine. The similarity in the structure factor for the spangolite ground state with the exact dimer one confirms the strong dimerization, however, it is slightly smeared compared to the exact dimer state.

Thermal state and heat capacity

Before investigating magnetic properties of the spangolite Hamiltonian, we compute thermal state properties without a magnetic field using iPESO simulations at a large bulk bond dimension χB = 24 with mean-field environments22. Thermal states are obtained by successively cooling an infinite-temperature state with infinitesimal steps δβ = 10−4 down to low temperatures. From the thermal state energy we can compute the heat capacity C = ∂U/∂T. Results are shown in Fig. 4a. The heat capacity C/T features a pronounced peak at T ~20 K.

Fig. 4: Thermodynamic properties of spangolite.
figure 4

a Specific heat divided by temperature showing a pronounced peak at T ~ 20 K. The inset shows the thermal state energy, that converges to the ground state energy for low temperatures, alongside the accumulated truncation error of the simple update cooling procedure, that stays below ε ~ 10−2 throughout the full range of temperatures. b Magnetic susceptibility over temperature. The high-temperature regime (T > 1000 K for the simulation, T > 250 K for the experiment) is fitted with a Curie-Weiss law to extract the CW temperature in Table 2. The inset shows the effective magnetic moment. The theoretical susceptibility data have been scaled by a factor of  ~0.68 to match the high-temperature tail as explained in the text.

Full size image

In the inset we show the thermal state energy alongside the truncation error in the simple update cooling procedure. The thermal state energy converges to the ground state energy of Fig. 3a for low temperatures, indicating that the procedure does not get stuck in local minima during the cooling. The truncation error can be used to probe the accuracy of the simulations. It stays below ε ~ 10−2 down to T = 1 K, which is a good indication that the chosen bond dimension for the thermal state simulations is sufficiently high.

Magnetic susceptibility

To further characterize the spangolite Hamiltonian, we computed the variation of the magnetic susceptibility with temperature using the iPESO thermal state algorithm. To this end, we choose again a bulk bond dimension of χB = 24 and an accurate infinitesimal temperature step of δβ = 10−4, leading to a maximally accessible temperature of 1/δβ = 104 K. Expectation values are computed using the mean-field environment, which is reasonable due to the high bond dimension and temperature, and low entanglement in the system. Fortunately, we can directly compare our theoretical simulations of the model Hamiltonian to experimental measurements on spangolite. The magnetic susceptibility is computed from the magnetisation along the direction of the field according to

$${\chi }_{{{\rm{M}}}}(T)={\frac{\partial {m}_{z}(T)}{\partial {h}_{z}}{\bigg| }}_{{h}_{z}\to 0}.$$
(4)

Our results, alongside the data extracted from ref. 20 are shown in Fig. 4b. The main feature of a sharp peak and the high-temperature tail are correctly recovered by our tensor network simulations. A numerical fit of the high-temperature regime (T > 1000 K for the simulation, T > 250 K for the experiment) with a Curie-Weiss law

$${\chi }_{{{\rm{M}}}}(T)=\frac{C}{T-{\theta }_{{{\rm{CW}}}}}$$
(5)

is used to extract the Curie-Weiss temperature θCW. The fit results in parameters given in Table 2. The simulations show a peak at a slightly higher temperature (T = 59 K) compared to experiment (T = 44 K) and a quicker decline of the magnetic susceptibility, indicating a non-magnetic ground state already at higher temperatures. From the Curie-Weiss constant C we can compute the effective magnetic moment

$${\mu }_{{{\rm{eff}}}}=\sqrt{\frac{3{k}_{B}C}{{N}_{A}{\mu }_{\rm B}^{2}}}.$$
(6)

The extracted value from the TN simulations is slightly larger compared to the experimentally estimated one, see Table 2. However, our calculations capture the substantial reduction in μeff compared to the expected value for the spangolite formula unit, which has μeff = 10.39 μB/f.u. for the six spin-1/2s20. This reflects the fact that the ground state cannot be viewed as either being composed of isolated dimers or explained by a model of dimers interacting with a mean-field41,42,43 and confirms the description of the ground state obtained from TN simulations. In order to match the high-temperature tail of the susceptibility to the experimental data, we need to scale the Weiss constant C by a factor of  ~0.68. The experimental finding is that the expected effective moment of μeff = 10.39 μB for a unit cell of six Cu S = 1/2 is reduced to μeff = 4.75 μB which is only 46% of the expected value and corresponds to a reduced spin value of S = 0.14. Theoretically, we find a reduction of the effective moment to μeff = 5.82 μB which is 56% of the expected value and corresponds to a reduced spin value of S = 0.20. Thus, our simulations capture the major part of the moment reduction but fall a bit short. The missing reduction in the magnetic moment could be related to enhanced frustration upon introduction of inter-layer couplings which are inevitably present in the real material. The fact that our calculated susceptibility vanishes at a somewhat higher temperature than in experiment indicates an overestimation of the formation of dimers, which could result from a slightly too high value for J1 in the model Hamiltonian. The iPESO ansatz itself is biased towards the formation of dimers on J1 bonds as well, however, the large bulk bond dimension χB = 24 should allow sufficient correlations to neighbouring sites to counteract this bias. Using C = χMT in Eq. (6), we can plot the effective magnetic moment as function of temperature as shown in the inset of Fig. 4b. While neither experiment nor simulation data for the effective moment completely saturate at room temperature, our result approaches a slightly lower value compared to the experiment, in agreement with the preceding discussion.

Table 2 Parameters of the numerical fit of the Curie-Weiss law of the magnetic susceptibility
Full size table

Magnetisation plateaus

Finally, we study the spangolite Hamiltonian in an external magnetic field. Due to the strong antiferromagnetic interaction on J1 bonds, the system retains a non-magnetic ground state up until hz ~ 56 T. In the T = 0 K simulations we have used unit cells of six, twelve and eighteen spins in order to capture more complicated ground state structures. Upon tuning the magnetic field, we find the emergence of magnetisation plateaus at values of mz/mS = 1/3 and 2/3 of the saturation value mS = 1/2. The full magnetisation curve is shown in Fig. 5a. It is interesting to note that we do not find the 1/6, 2/9 and 2/7 plateaus observed in the magnetisation curve of the exact dimer product ground state44. This provides further evidence that the ground state of the spangolite Hamiltonian is not formed by isolated singlets but more appropriately viewed as a correlated dimer state due to the presence of ferromagnetic correlations on the hexagonal bonds connecting the dimers.

Fig. 5: Magnetisation curves of spangolite.
figure 5

a Zero temperature magnetisation of the spangolite Hamiltonian over the magnetic field hz at χB = 8, using CTMRG environments with χE = 64. Below hz ~ 56 T the strong antiferromagnetic J1 interaction leads to a vanishing magnetisation. Two plateaus at 1/3 and 2/3 of the saturation mS = 1/2 are found. b Magnetisation curve of spangolite at finite temperatures. The insets show the melting of the mz/mS = 1/3 and 2/3 magnetisation plateaus as an effect of increasing temperature. c, d Nearest-neighbour spin-spin correlations and local Sz expectation values for the 1/3 and 2/3 magnetisation plateaus, corresponding to values of c hz = 70 T and d hz = 90 T, respectively.

Full size image

The spin-spin correlations in both the 1/3 and 2/3 plateaus are translationally invariant and thus representable within a six site unit cell. Those plateaus satisfy the conventional condition for a magnetisation plateau to emerge, namely, \({N}_{{{\rm{u}}}}S(1-{m}_{z}/{m}_{{{\rm{s}}}})\in {\mathbb{Z}}\)45,46, where Nu is the number of sites in the unit cell for the ground state and S is the spin quantum number which, in the present case, is S = 1/2. For the aforementioned quantities, we obtain values of 2 and 1 for the 1/3 and 2/3 plateaus, respectively. The spatial pattern of spin-spin correlations and z-component of the magnetisation is shown in Fig. 5c, d.

Finally, we analyse the stability of the observed plateaus with respect to temperature. To this end, we simulate the spangolite Hamiltonian in a field over a temperature range T  ∈  [0.1 K, 1000 K] at a fixed bond dimension of χB = 24 using mean-field environments to compute expectation values. Here we use a slightly larger temperature step δβ = 10−3 to achieve more efficient cooling. The unit cell is set to six spins. While the infinite-temperature states are fully disordered without any magnetisation, the simple update cooling procedure recovers the two plateaus at low temperatures. A set of fixed temperature slices is shown in Fig. 5b. In the inset we show the melting of both plateaus. Noticeably, they melt rather symmetrically from the low and high field limits, respectively. Due to the smaller width, the 1/3 magnetisation plateau is more susceptible to thermal effects and starts melting sooner than the 2/3 plateau.

Discussion

Employing a combination of density functional theory based energy mapping and tensor network simulations, we investigated the ground and thermal state properties in the presence of a magnetic field of a distorted maple-leaf lattice as realized in spangolite (Cu6Al(SO4)(OH)12Cl ⋅ 3H2O). The DFT Hamiltonian features the largest coupling, antiferromagnetic J1 on the dimer bonds, while the subleading antiferromagnetic couplings, J4 = 0.297J1 and J5 = 0.437J1 define the triangles. A noteworthy aspect of the Hamiltonian is the presence of substantial ferromagnetic interactions, J2 = − 0.252J1 and J3 = − 0.254J1 on the hexagons. The pattern of spin-spin correlations in the ground state consequently features strong singlet formation on the dimer bonds, and sizeable ferromagnetic correlations on the hexagonal bonds which connect the dimers. Interestingly, the spins on the triangles are nearly uncorrelated. Thus, our picture of a non-trivially correlated dimer ground state accounts for the appreciable reduction in magnetic moment at high temperatures observed in experiment, thereby resolving a long-standing puzzle. It also effectively rules out a scenario of a ground state composed of either isolated dimers or dimers interacting with a mean-field, and dispenses with the need of invoking more complicated mechanisms which have been speculated about earlier. We find a good agreement with the experimentally observed behaviour of the magnetic susceptibility. The magnetisation curve of spangolite does not show the presence of 1/6, 2/9, and 2/7 plateaus which are expected for an exact dimer product configuration. This lends further evidence of a correlated dimer ground state. We find that the 1/3 and 2/3 plateau states are fully translation invariant. With increasing temperature, the 2/3 plateau appears more robust compared to the 1/3 plateau.

Much of the recent theoretical efforts in search of exotic non-magnetic states on the maple-leaf lattice have focused on the purely antiferromagnetic model47,48,49. However, lately the explorations of models with mixed ferro-antiferro couplings (with antiferromagnetically coupled hexagons and ferromagnetic coupling on triangles and dimer bonds) have unveiled a variety of dimer orders encompassing an island of putative quantum spin liquid behaviour50. In a similar vein, there could be a putative quantum spin liquid lurking around the corner proximate to the observed correlated dimer ground state. To this end, it would be worthwhile to perform a thorough investigation of the mixed ferro-antiferro parameter space of the spangolite Hamiltonian, which features ferromagnetically coupled hexagons and antiferromagnetic coupling on triangles and dimer bonds. This might also enable us to ascertain whether the observed dimerized phase could potentially be viewed as an instability of proximate quantum spin liquids, which have lately been classified in ref. 51.

Our study of spangolite is the second detailed elucidation of the Hamiltonian of a maple-leaf material, the first being the recent investigation of bluebellite34. Both minerals share the distortion pattern of the ideal maple-leaf lattice with five inequivalent nearest-neighbour bonds and the fact that the Hamiltonian is dominantly antiferromagnetic, but modified by two ferromagnetic exchange interactions. As the resultant physics, spin singlet formation versus valence bond solid ground state for spangolite and bluebellite, respectively, vary considerably, it is a worthwhile endeavor to understand the other known copper minerals with maple-leaf lattice, mojaveite, fuetterite and sabelliite, as well. Their maple-leaf lattices are also distorted, promising new patterns of antiferromagnetic and ferromagnetic bonds. The example of bluebellite17 suggests that synthesis of the minerals is possible and can lead to a reduction of the lattice distortions. A next step could be efforts to synthesize material variations, for example by replacing chlorine by bromine and thus to further extend the richness of quantum spin systems with maple-leaf structure.

Methods

Density functional theory based energy mapping

We use all electron density functional theory calculations with a full potential local orbital (FPLO) basis set30. For the prediction of the hydrogen atom positions, we use a generalized gradient approximation (GGA) exchange correlation functional31. We determine the Heisenberg Hamiltonian parameters from total energies where we correct for the strong electronic correlations on the Cu2+ 3d orbitals by a DFT+U functional52. For the energy mapping approach, we classify all 4096 possible spin configurations for the twelve Cu2+ ions in the unit cell after removing the symmetry. We find that the 364 distinct classical energies allow us to resolve twelve Heisenberg Hamiltonian parameters. We fix the Hund’s rule coupling for Cu 3d as JH = 1 eV, in agreement with many previous studies24,29. We then perform the energy mapping approach for six values of the onsite interaction value U (see Fig. 1c). We choose the appropriate value for spangolite by demanding that the Curie-Weiss temperature calculated as

$${\theta }_{{{\rm{CW}}}} = \frac{1}{3}S(S+1)\left({J}_{1}+{J}_{2}+{J}_{3}+{J}_{4}+{J}_{5}+{J}_{15}+{J}_{16}\right.\\ +\left.{J}_{17}+{J}_{18}+{J}_{19}+{J}_{21}+{J}_{23}\right)$$
(7)

agree with the experimental value of θCW. For this purpose, we reconsider the Curie-Weiss fit performed in ref. 20. We use a fitting ansatz developed recently by Pohle and Jaubert53 for spin liquids:

$${\left.\chi T\right\vert }^{{{\rm{fit}}}}= \frac{1+{b}_{1}\exp [{c}_{1}/T]}{a+{b}_{2}\exp [{c}_{2}/T]}\\ C= \frac{1+{b}_{1}}{a+{b}_{2}},\quad {\theta }_{{{\rm{CW}}}}=\frac{{b}_{1}{c}_{1}}{1+{b}_{1}}-\frac{{b}_{2}{c}_{2}}{a+{b}_{2}}$$
(8)

Note that this ansatz has recently allowed us to assign a Curie-Weiss temperature to nabokoite54. The fit is excellent throughout the temperature range (see Supplementary Fig. 1) and allows us to revise the Curie-Weiss temperature of spangolite to θCW = − 29.4 K, which is somewhat smaller than the result of the traditional χ−1 fit of θCW = − 38 K.

As a consistency check, we have evaluated the theoretical magnetic susceptibility that we obtained with the DFT Hamiltonian given in Table 1 in the same way as the experimental susceptibility (see Supplementary Fig. 2). The fit with the ansatz of Eq. (8) yields Weiss constant C and Curie-Weiss temperature θCW that are in good agreement with experiment.

Tensor network ansatz

The construction of the tensor network state proceeds by coarse-graining the two spins on the dominant antiferromagnetic J1 bonds in the maple-leaf lattice, which then maps it to a regular kagome lattice. Due to its corner-sharing triangles, a TN setup on the dual honeycomb lattice in the form of iPESS and iPESO is very well suited to capture the multipartite quantum correlations therein. The general TN setup is shown in Fig. 2a, where the stretched hexagons denote coarse-grained lattice sites, each represented by a single green tensor in b and c. In the chosen TN ansatz, those tensors reside on the links of the honeycomb lattice, so that additional three-index simplex tensors have to be introduced to connect them (gray tensors). Quantum states, represented by an iPESS, have only a single physical index per lattice site tensor, while thermal density matrices, represented by an iPESO, have two. This is shown in the figure as black, and both black and gray indices, respectively. A single unit cell consists of three lattice tensors (capturing six spins), together with two simplex tensors. Importantly, tensor networks in the thermodynamic limit offer the possibility of choosing arbitrary unit cells, that are repeated periodically to generate the 2D lattice. This gives us the possibility to determine the actual structure of the targeted states based on energy comparisons of different configurations55. Each elementary unit cell of the honeycomb TN can be further coarse-grained into an effective tensor on a regular square lattice, as described in Supplementary Fig. 4. It allows to combine six spins on the original maple-leaf lattice into a single tensor. This is important to compute accurate expectation values, for which we use a corner transfer matrix renormalization group (CTMRG)56,57,58 procedure, as shown in Fig. 2d. The contraction of the infinite square lattice introduces an additional control parameter, the environment bond dimension χE. In our simulations we use system sizes of six, twelve and eighteen spins. Both ground and thermal state simulations are based on the very efficient simple update procedure21,22,59,60. It is an approximate, yet reliable algorithm frequently used in TN simulations. The main refinement parameters, i.e., the bond dimensions and the infinitesimal cooling step in the finite-temperature simulations, are carefully chosen to achieve sufficient accuracy and accessible temperature ranges while balancing the numerical effort. Details about the simple update for iPESS and iPESO, as well as the calculation of expectation values are presented in the Supplementary Note 3.