Introduction

In the midst of a drought, resource managers, media, and the public often want to know when the drought will end1,2,3,4. Long-duration droughts take a toll on ecosystems (e.g. refs. 5,6) and reduce flows in watersheds (e.g. refs. 4,7) and municipal water supplies (e.g. ref. 8). Thus, water resource managers seek information on how long a drought will likely last—or the probability of drought recovery by a certain date—in order to make better management decisions, including when to tighten and relax water restrictions.

This question emerged for California in 2022 as the state faced its third consecutive hot and dry year, placing ~90% of the state in extreme to exceptional drought that September, according to the US Drought Monitor (USDM)9. Due to the compounded water deficits from multiple drought years, municipal and state agencies prepared to issue large water allocation cuts to agriculture if conditions did not improve10, while Coalinga, California received a $1.2 million award from the state for an emergency water transfer as the city approached day zero water11. However, the 2023 water year brought record breaking precipitation which led to drought recovery: by summer 2023, the state was drought-free, according to the UDSM, and water use restrictions were lifted.

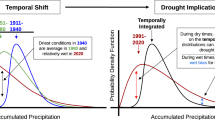
As there are many types of drought (e.g. hydrologic, ecological, etc.)12, there are also a range of definitions of drought recovery1,2,13. Broadly, however, drought recovery reflects an abatement of moisture deficits, and thus requires receiving adequate moisture to satisfy current water demand plus a surplus of moisture to recover from the previous deficit1,2,14. It is therefore dependent on drought severity and on subsequent meteorological conditions (e.g. precipitation and atmospheric evaporative demand). The more severe the initial drought, the more surplus moisture is needed to recover2. Elevated temperatures in months following the initial drought can increase atmospheric evaporative demand, leading to even further water deficits1,3. Conversely, surplus moisture, often a product of above average precipitation, can lead to drought recovery1,15.

Efforts to assess the anticipated longevity of drought, and measures to cope with drought impacts, aim to determine the probability of drought recovery (PDR) by a certain time. These efforts consider how drought indicators (e.g., streamflow, soil moisture, drought indices) may evolve in subsequent months. Seasonal drought and hydrologic forecasts that incorporate initial conditions and climate forecasts have skill at up to 12-month lead-times in the western US, which can inform PDR2,12,16,17. Likewise, forecast skill has been demonstrated for efforts that leverage historic analogs such as ensemble streamflow prediction16,17,18 or analogs based on historical soil moisture19. However, reliance on historical analogs assumes hydrometeorological stationarity—which may be increasingly unreliable due to anthropogenic climate change (hereafter referred to as ‘climate change’)18,20,21.

Much of the southwestern US has experienced exceptional and persistent drought for the past two decades, due to a combination of natural variability and climate change. The western US is broadly characterized by cool, wet winters with significant interannual variability in precipitation and hot, dry summers with high atmospheric evaporative demand (Supplementary Fig. 1). Though much of the recent observed reduction in precipitation is likely due to natural variability22, climate change has increased atmospheric evaporative demand in the hot, dry seasons across the western US3,6,23,24, and has thus increased the frequency with which hot conditions co-occur with dry conditions25,26. Studies have attributed the observed rapid intensification of drought onset (‘flash droughts’) and increased overall severity of droughts in this region to climate change23,24,27. Other studies have employed models which suggest both projected increases in frequency and duration of droughts due to climate change, which is in part dependent on the initial severity of drought28,29. Yet, to the best of our knowledge, no study has yet examined whether and how climate change has affected observed PDR once in drought.

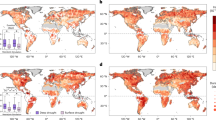
Here, we quantify how observed PDR has changed across the western US and attribute how much of that change is due to climate change. To do so, we calculate PDR using the self-calibrating Palmer Drought Severity Index (scPDSI)30,31, a widely-used drought indicator whose calculation is based on reference evapotranspiration (ETo) and precipitation. We calculate PDR for five macroscale basins (HUC2 watersheds) across the western US: the Upper and Lower Colorado Basins (UCB, LCB), the Great Basin (GB), the Pacific Northwest (PNW), and California (CA) (Fig. 1). We use a multiple-lines-of-evidence approach, leveraging observational scPDSI data (1901–2023; Fig. 1), an experimental approach that initializes each month with severe drought conditions and applies observational data to examine potential drought recovery, and scPDSI calculated from 23 models participating in the Coupled Model Intercomparison Project Phase 6 (CMIP6)32. The observational and experimental data also include counterfactual scPDSI estimates which omit anthropogenic trends in background mean climate (as defined by the CMIP6 multi-model mean during 1901–2023), which allow us to isolate how climate change has contributed to observed changes. Recovery was defined as non-drought conditions (scPDSI ≥30th percentile) occurring in each of the 24 months immediately following severe drought (scPDSI ≤10th percentile) (USDM; Fig. 1), and PDR for each month calculated as the percentage of recoveries across the time period of interest19. We calculated PDR for each dataset for different time periods, climate scenarios, and seasons. A detailed description of the approaches can be found in Materials and Methods.

Fig. 1: Map of the study region, encompassing five watersheds defined using 2-digit Hydrologic Unit Codes (HUC2), and distribution of observational scPDSI values for each watershed.
figure 1

The five watersheds are the Upper Colorado Basin (UCB, HUC2 14), the Lower Colorado Basin (LCB, HUC2 15), the Great Basin (GB, HUC2 16), the Pacific Northwest (PNW, HUC2 17), and the California Basin (CA, HUC2 18). Bias-corrected distribution of observational scPDSI values are shown for the historical (gray, 1901–1980) and recent (red, 2000–2023) time periods, as well as the counterfactual for the recent time period, with the first order trends attributable to climate change removed (blue). Drought and drought recovery definitions are shown for each region in the boxplots as horizontal brown and blue lines, respectively.

Full size image

Results

Drought recovery is less likely in part due to climate change

We find that drought recovery was slower over the past two decades than in previous decades across much of the western US (Fig. 2). Historically (1901–1980), PDR 18 months after severe drought was 44–65% across the five regions in the observational data (top row), with the highest PDR in UCB and LCB and the lowest PDR in PNW (Fig. 2). Note, the low historical PDR in PNW reflects the exceptional and persistent drought experienced by the region in the 1920s–1930s (Fig. 3). Hence, there is little detectable change in PNW in the recent time period (2000–2021) as a product of internal variability. However, PDR was significantly lower in month 18 across the other regions during 2000–2021 (PDR = 30–47%) compared to 1901–1980 (PDR = 56–65%) using the observational data. Indeed, in both the observational and experimental data, PDR is ~25–50% lower in the recent period in California and the three southwestern basins (LCB, UCB, and GB). Notably, as the experimental traces are initialized to the same drought magnitude, these results suggest the observed decreases in PDR are not related to the initial severity of drought.

Fig. 2: Probability of drought recovery (PDR) using observational data (top), experimental data (middle), and model-based data (bottom).
figure 2

Drought recovery defined as scPDSI >30th percentile for 1901–1980; horizontal gray line indicates unconditional probability based drought recovery definition. Probabilities refer to drought recovery in months following drought. For the observational and model-based data, recovery is calculated for all dates in which the region was in drought (scPDSI <10th). For the observational and experimental panels, stars indicate statistically significant differences (p < 0.05) between the observed and counterfactual traces (red, McNemar’s test) and the historical (1901–1980) and recent (2000–2021) traces (black, t-test). The bottom panels depict the multi-model mean PDR estimate. Statistically significant differences between the historical and recent traces are indicated by the presence of black stars, and are defined as the multi-model-mean recent trace falling outside of the 95% CI of the means for the historical trace. Note, all regions in model-based panels show significant reductions when defining 2000–2040 as the contemporary period (Supplementary Fig. 4).

Full size image
Fig. 3: Time series of PDR 18 months after severe drought conditions are met.
figure 3

Probabilities are shown using a sliding 21-year window updated every 5 years centered on the date of interest (e.g. 1950 uses 1940–1960). Drought and recovery are defined as scPDSI <10th percentile and >30th percentile, respectively, based on 1900–1980. Horizontal gray line shows the multi-model-mean PDR for 1900–1980. For the observational data (brown), only windows with sufficient number of drought instances (n ≥ 15) are included. PDR from experiments using observational data are shown in green, while PDR from CMIP6 models are shown in black. The black line and gray ribbon show the multi-model mean and 95% CI of the multi-model mean, respectively. The red line and ribbon indicate the median time of emergence (ToE) based on climate model output.

Full size image

Counterfactual simulations that exclude the first-order influence of climate change suggest the reduced PDR is partially due to climate change (Fig. 2, top and middle row). In southwestern basins, one-third to all of the observed decreases in PDR in month 18 are explained by anthropogenic climate trends. Indeed, the largest water deficit anomalies (ETo minus precipitation) in the counterfactual are found for the southwestern regions, and are largely due to heightened ETo from climate change (Supplementary Fig. 2). For PNW and CA, while the climate change contribution is statistically significant for portions of the experimental traces, the contribution is lower.

Drought recovery calculated directly from climate model simulations shows qualitatively similar results as observations: models simulate that PDR is statistically significantly reduced in recent decades relative to much of the 20th century for some regions (Fig. 2, bottom row). When accounting for uncertainty across the 23 models, we find statistically significant reductions in PDR for LCB, PNW, and CA. However, unlike the attributable differences in observational and experimental data, the largest modeled reductions in PDR were in PNW and CA. In month 18, models suggest PDR is 17% (±6%) lower in PNW and 13% (±5%) lower in CA, yet ~0–10% lower for Southwest regions. As with the experimental traces (Fig. 2, middle row), supplementary analysis indicates that the recent reductions in PDR in the model-based data are independent from initial depth of drought and largely insensitive to the specific PDSI thresholds used (Supplementary Fig. 3).

Over the past century, PDR 18 months following severe drought shows evidence of both significant multidecadal variability in observations as well as a more recent trend toward reduced drought recovery, with all regions having low PDR post-2000 (Fig. 3). Observational and experimental data capture this variability, with low PDR during historical protracted droughts (e.g. PNW in ~1930) as well as high PDR during historical wet periods (e.g. LCB ~ 1980). However, this high multidecadal variability in PDR from observations limits our ability to detect trends.

Instead, the climate model-based mean PDR estimates depict a decline in PDR for all regions in recent decades. For each model, we estimate a Time of Emergence (ToE) of when the signal of climate change emerges from internal variability. The median, model-based ToE is earliest for CA, PNW, and LCB, ranging from 1980 to 1995, before the recent time period (2000–2021) in Fig. 2 (ToE range of estimates across models in Supplementary Fig. 5). Note that while PNW experiences a median ToE in 1980 using model-based data, it does not have observational emergence. Conversely, the median ToE estimate for UCB is 2010. Therefore, in recreating Fig. 2 using a window centered on 2020 (2000–2040), which reflects contemporary conditions, a statistically significant climate signal emerges for this region (Supplementary Fig. 4).

Decreased PDR is driven by increasing ETo in non-winter months

In each region, modeled PDR has slowed in non-winter months with climate change, largely due to increases in ETo (Fig. 4, experimental results in Supplementary Table 2). For all regions except GB, at least three-quarters of models suggest slowing recovery in spring (AMJ) and/or summer (JAS) months. For example, for CA, the median change in model-based PDR during summer in the contemporary period (2000–2040) was ~1.5 percentage points slower per month compared to the historical period (or ~4.5 percentage points slower across the season, Fig. 4). The models depict strong, statistically significant increases in ETo in the non-winter months for all regions (Supplementary Fig. 6), which is the main contributor to the decrease in the simple water balance (P-ETo) shown in Fig. 4. As PDSI is a water balance model that accounts for both precipitation and ETo, our results thus suggest that the slowing PDR in non-winter months is largely forced by anthropogenic increases in ETo.

Fig. 4: Boxplots depict the monthly change in PDR anomaly between the historical (1900–1980) and contemporary (2000–2040) traces (Δ(PDR anomaly) / Δ(month)).
figure 4

Monthly values are binned by season (JFM, AMJ, JAS, OND). The upper and lower bounds of the box depict the interquartile range from the 23 CMIP6 models. Negative values mean that historical drought recovery probabilities increased faster month-to-month than they do in the contemporary period. The p-value refers to statistical significance in the difference between winter and summer. The brown boxplots depict the P-ETo climatological anomaly across models for the contemporary time period.

Full size image

Modeled changes in drought recovery vary between winter and summer months for PNW and CA, with statistically significant differences between warm and cool season values (Fig. 4). For these regions, over half of the models suggest that climate change corresponds to faster recovery in winter months, with median PDR increases of 0.1-1.4 percentage points per month compared to the historical time period, due to increased precipitation (Supplementary Fig. 6).

It now takes longer to recover from drought

Finally, we demonstrate that it now takes on average ~1–4 months longer to recover in UCB, LCB, PNW, and CA, using model-based data (Fig. 5). The models suggest that under historical climate (1901–1980), it took around one year following severe drought to recover, whereas under contemporary climate (2000–2040) it takes on average 13–16 months (Fig. 5). The lengthened recovery time is significant for all regions (t-test p-value < 0.05) except GB, with 15–21 of 23 models showing longer times to recovery. Note, the model-based estimates show no significant change for GB due to modeled winter gains largely offsetting modeled non-winter losses. However, the experimental results (Supplementary Fig. 7) suggest lengthened recovery time for GB due to climate change.

Fig. 5: Number of months to reach drought recovery for the historical (1901–1980) and contemporary (2000–2040) time periods, using model-based data.
figure 5

For each simulation, the median number of months to recovery for each drought was taken from which multi-model medians were derived. If recovery did not occur within a 24-month period, the value was assigned as 25. Boxplots depict interquartile range across the 23 CMIP6 models.

Full size image

Discussion

Together, the observational, experimental, and model-based data indicate that drought recovery across the western US is less likely today compared to the historical time period, and further suggest that climate change accounts for some of that change (Figs. 2 and 3). The remaining change is likely due to internal variability22,23 or potential biases in CMIP6 modeling related to land-surface feedbacks in arid location and seasons33. Notably, this result is relatively insensitive to our choice of threshold used for drought and drought recovery definitions as well as the severity of initial drought conditions (Fig. 2, Supplementary Fig. 3). This decrease in recovery probability translates to slower recovery, and thus longer drought duration, with the model-based data suggesting it now takes an additional ~1–4 months due to climate change to recover (Fig. 5).

Our results indicate that human-caused climate change has slowed drought recovery during non-winter months, via increasing ETo (Fig. 4). These findings are consistent with studies that have found that in the western US, the largest increases in ETo have occurred during the warm season, which exacerbates drought24,34,35. Notably, while these increases in ETo have reduced PDR, over the southwestern basins, they have occurred against a backdrop of anomalously low precipitation over the past two decades, largely due to natural variability, which likely accounts for the remaining observed reduction in PDR22. However, for coastal basins, climate model output suggests that slight increases in winter precipitation (Supplementary Fig. 6) lead to improved probability of recovery in winter (Fig. 4); similarly, for winter, the experimental data show smaller reductions in compared to other seasons, and in some cases modest gains (Supplementary Table 2). While there is substantial uncertainty in how climate change has affected precipitation in the western US36, models suggest future intensification of winter precipitation over much of the western US, and this increased interannual variability in precipitation may somewhat favor drought recovery in winter (e.g. refs. 37,38,39). Yet, our model-based PDR results suggest that such winter gains currently fail—and will continue to fail—to offset the ETo-driven non-winter losses (Fig. 3). These seasonal patterns are important from a management perspective12,39,40. In the case of a winter drought, recovery can be expected to be harder over the following dry season than it used to be, thereby lengthening time to recovery through the dry season.

Our multiple-lines-of-evidence approach allowed for addressing several challenges presented by using observational data alone (e.g. refs. 41,42). First, in using both observational and model-based data, we accounted for uncertainty stemming from the limitations presented by each type of data. Furthermore, the experimental data and the model-based data addressed the challenge of small sample sizes presented by the observational data, and allowed for assessing the effect of severity of drought on PDR (Supplementary Fig. 3). While the experimental data shifts the magnitude of drought recovery probabilities up, the rate of month-to-month change in recovery probabilities is unaffected2. Moreover, the model-based data allowed both for examining inter-model uncertainty via calculating PDR for each model, and for identifying the climate change signal in PDR when taking the multi-model mean (e.g., Figs. 2–4).

This approach thus allowed for differentiating unique patterns in changing recovery probabilities between the southwestern and coastal regions. The climate signal is present in the observational and experimental data for the southwestern regions, but the signal is weaker for coastal regions (Fig. 2). Indeed, as found by other studies7,21,23,24, these results suggest that the mean shifts in temperature and ETo are having the strongest persistent impacts over the Colorado Basins. Conversely, for the Great Basin, the lack of a signal in the model-based data is consistent with studies that have found a later ToE for in soil moisture as a drought indicator for the Great Basin21, particularly when simulating directly from GCMs24. However, the presence of a strong signal for coastal areas in model-based data may reflect a combination of high internal variability present for the coastal regions and anthropogenically forced changes in variability43. Coastal regions may be more affected by this due to the higher observed interannual precipitation variability. For California, much of the winter precipitation comes in the form of atmospheric rivers with high interannual variability that have been associated with ending drought events15. Additionally, a strong tendency has been demonstrated for high-frequency interannual variability in winter precipitation in the Sierra Nevada and much of California44, which would facilitate drought recovery in certain years.

While our results find that climate change has affected drought recovery when defined using scPDSI, there are numerous drought indicators that have different climate sensitivities and memories, suggesting that our results may differ for other metrics. For instance, scPDSI accounts for changes in precipitation and ETo, yet does not capture changes in hydroclimatic variables such as snowpack, which is an important part of the western US’s hydrology3. Studies have demonstrated that increased temperatures from climate change have reduced springtime snowpack, due to a shift in rain versus snow and due to early melt45, which leads to lower soil moisture in the warm summer months. Thus, it is likely that this analysis offers conservative estimates of reductions in drought recovery probability due to climate change. Yet, we still find a substantial slowing of recovery, leading to longer-lasting droughts with slower recovery times.

This slowing recovery has tangible negative impacts: on reduced water flows across the western US, including stressing the already over-allocated Colorado Basin3,7,40, and leading to deficits in ecosystems, such as poor forage on rangelands6,46 and forest mortality47. Moreover, slowing drought recovery means that the risk of day zero water will increase absent changes in water management, making the experience of Coalinga, CA a more common occurrence. This highlights the need for increased water resiliency, involving placing less demand on water during drought, such as through water conservation and adaptive agricultural systems48, and broader scale water adaptations, such as managed aquifer recharge to smooth effects across wet and dry times39. The models suggest that as warming continues from climate change, drought recovery probabilities will decline further over the coming decades (Supplementary Fig. 4), increasing the need for drought planning efforts to factor in longer duration droughts and adaptation approaches to reduce detrimental drought impacts on society and the environment.

Materials & methods

Data

Monthly gridded (0.25° resolution) observational precipitation (pr), minimum and maximum temperature (Tmin, Tmax), wind speed, actual vapor pressure, and downward shortwave radiation for 1901–2023 were retrieved23, with forcing datasets updated through 2023. Specific humidity (SH) was then derived from these data. Additionally, general circulation model (GCM) data were retrieved in order to increase the sample size and account for the effect of climate change on changing variability. Monthly pr, Tmin, Tmax, wind speed, SH, and downward shortwave radiation were retrieved from 23 different climate models participating in CMIP6 across a total of 130 ensemble members for historical (1850–2014) and future (SSP2-45) forcing experiments (hereafter referred to as ‘model-based’ data) (Supplementary Table 1)32. These data were used to calculate monthly observational and model-based ETo following the ASCE Penman-Monteith approach49, and subsequently observational and model-based scPDSI (using 1950–2016 as the reference period).

The counterfactual observational data were then created by subtracting the GCM-based multi-model mean trends in pr, average temperature (tas), windspeed, SH, and shortwave radiation from the observational fields, thereby capturing average conditions in a world without anthropogenic climate change. We use multi-model means for the purpose of developing counterfactuals, as such models largely mute internal variability as simulated by models but leave behind an estimate of trends due to anthropogenic forcing. Notably, the counterfactual only removes first-order changes in monthly averages from each climate variable and does not account for anthropogenic influences on higher-frequency climate variability. As such, the counterfactual preserves the variability of the observational record. The counterfactual scPDSI data were calibrated using the observational data (rather than counterfactual data).

Processing data

Spatially-averaged monthly time series of scPDSI, tas, pr, and ETo were calculated for each of the five 2-digit hydrologic unit code (HUC2) regions: the Upper Colorado Basin (HUC 14), the Lower Colorado Basin (HUC 15), the Great Basin (HUC 16), the Pacific Northwest Basin (HUC 17), and the California Basin (HUC 18) (Fig. 1). For the model-based data, data were first resampled to 0.1 degree using bilinear interpolation before taking spatial means.

Models were then examined to determine if any model culling was needed. This involved examining climatological biases in tas, pr, and ETo relative to observational data (Supplementary Fig. 1) as well as trends in these variables during 1901–2022 (Supplementary Fig. 8). Based on these examinations, no models were removed.

Creating the experimental data

The experimental dataset was created by initializing each month with scPDSI = −4 and running independent scPDSI calculations for the subsequent 24 months using the spatial mean of the observed and counterfactual ETo and precipitation data for each basin. This additionally required initializing soil moisture to the 2nd percentile of each monthly data given the theoretical construct of scPDSI where the 2nd percentile of data yields a value of −4. This approach not only increased the sample size of drought observations to provide a more statistically robust sample but also controls for drought magnitude.

Calculating drought recovery

Drought and drought recovery were defined as falling below the 10th percentile and arriving above the 30th percentile, respectively, for each month based on the 1901–1980 baseline data. These definitions follow the US Drought Monitor (USDM) percentile breaks: under the 10th percentile corresponds to severe (D2) to exceptional (D4) drought, while over the 30th percentile corresponds to no drought. Therefore, historical analogs were defined as historical droughts (scPDSI <10th percentile). For the observational and experimental data, the scPDSI value corresponding to drought was selected based on the observational data, and the same dates corresponding to drought were selected for the counterfactual experiment. Furthermore, for the experimental data, the definitions were used from the observational data. Finally, to assess uncertainty associated with choice of thresholds, PDR for model-based data was additionally calculated for two alternate thresholds for drought and recovery definitions (Supplementary Fig. 3).

Drought recovery may be defined in a number of ways. For example, it may be defined as reaching non-drought conditions in any previous month, regardless of whether subsequent months are drought-free. However, in the case of a limited sample size, this approach risks a single month of recovery dominating the probability curve, whereby all subsequent months are redefined as ‘recovered’. Therefore, for this study, drought recovery was defined as arriving in non-drought conditions in the month of interest (e.g. for PDR in month 18, recovery in, not by, month 18). To calculate the probability of drought recovery (PDR) in a specific month (mt), the data were subset to all dates in drought (m0), and for the subsequent 24 months (mt), we tabulated whether conditions were still in drought (scPDSI <drought recovery definition) or out of drought (scPDSI >= drought recovery definition). Raw probabilities were then calculated by summing the binaries and then dividing that sum by the total number of drought instances. Therefore, PDR was calculated for the full period of record minus the final 24 months.

PDR was calculated separately for observational data, counterfactual data, and each GCM ensemble member. For GCMs containing more than one ensemble member, we calculate PDR as the mean drought recovery from individual ensembles. Finally, we calculate a multi-model mean PDR as an evenly weighted average of probabilities across the 23 models.

PDR was estimated for different time periods: historical (1901–1980), recent (2000–2021) (two years before the end of the historical data to calculate m1…m18), and, for the model-based data, contemporary (2000–2040). The contemporary time period is centered on 2020, and provides modeled anthropogenic forcing that more closely resembles current conditions.

Several tests were used to determine statistical significance. To test for significant differences between the observed and counterfactual traces from the observational data, McNemar’s test was run. McNemar’s test is used for paired categorical data. As the observed and counterfactual traces are, by design, paired, this test identifies significant differences between the binaries of recovered and not recovered. To compare the historical and recent traces for the observational and experimental data, a t-test was run on the distribution of scPDSI values for each month following drought. For both tests, a p-value threshold of <0.05 was used to indicate statistical significance. Finally, to test for significance between the historical and recent traces using the model-based data, the 95% confidence interval (CI) was calculated by bootstrapping the PDR values across the 23 models, and significance was defined as when the mean PDR in the recent trace falls outside of the CI of the historical traces for each model. Uncertainty related to the percent change in PDR is calculated as the percent change in multi-model-mean recent trace from the lower and upper bounds of the CI of the historical trace.

To calculate how PDR has changed over time, PDR was calculated for moving 21-year windows every 5 years (Fig. 3). For the model-based data, PDR for month 18 was first calculated for each simulation. Then for each model, the mean was taken across the corresponding simulation-specific PDR estimates. Using these model-mean PDR estimates, the time of emergence (ToE) was calculated for each model as when PDR first falls below, and then consistently (through 2050) remains below, the average PDR from 1900 (1880–1920) to 1980 (1960–2000). The multi-model ToE was then calculated as the median across the 23 ToE estimates.

To calculate the seasonal divergences, for each model, PDR was calculated for each season (JFM, AMJ, JAS, OND) for the historical (1901–1980) and contemporary (2000–2040) time periods. The historical PDR was then subtracted from the contemporary PDR, yielding the monthly attributable difference in PDR. Next, the attributable difference in each month was subtracted from the subsequent month, yielding an estimate of rate of change in attributable differences. These rate of change estimates were then subset into seasons, and the mean value for each season for each model depicted in the boxplots. To determine statistical significance in seasonal differences, a Welch one-way ANOVA test was run comparing cool season (Oct-Mar) and warm season (Apr-Sep) values. Finally, the precipitation and ETo anomalies were derived by subtracting climatological values for the contemporary from the historical time periods.

To determine the number of months for recovery, scPDSI values were tabulated for the 24 months after initial drought conditions were met. If the recovery did not occur in the 24-month period, the value was assigned as 25. For the experimental data, the median number of months to recovery for each time period (historical and contemporary) was taken. For the model-based data, the median number of months to recovery was taken for each simulation, and then the median for each model taken.