Introduction

In the face of accelerating sea-level rise and intensifying extreme weather, floods have become the most frequent and destructive natural hazard worldwide1,2,3. Anthropogenic climate change, coupled with widespread land-use modifications, has amplified both the magnitude and recurrence of extreme flood events, resulting in escalating losses of lives and assets4—particularly across Southeast Asia5, where the greatest exposure is observed6,7,8,9. This vulnerability is further exacerbated by rapid urban expansion and unsustainable groundwater extraction in low-lying coastal zones, which accelerate land subsidence and compound the impacts of sea-level rise and storm surges5,10,11. Simultaneously, the degradation of coastal wetlands, a critical buffer against storm impacts, has diminished the natural capacity to trap sediments and dissipate wave energy12,13,14. Together, these intertwined processes have substantially eroded flood resilience worldwide and underscore the critical need for high-resolution risk assessments at a global scale.

Global evidence indicates a high likelihood of concurrent riverine and oceanic flooding in coastal regions, arising from anomalous river discharge and elevated sea levels15,16,17. Such interdependent flood mechanisms give rise to compound flood events that can substantially intensify overall impacts by deepening inundation, prolonging flood duration, and widening the spatial extent of floods18,19,20,21,22. Joint-probability-based approaches have been widely used to quantify the dependence between riverine and oceanic floods globally15,17,18. However, these methods require event selection based on specific flood sources (e.g., storm surges or river overflows), whereas extreme water levels can result from events that are not extreme themselves23,24, which may introduce bias in compound flood estimates. Recent studies have incorporated conditional simulation frameworks into compound flood modeling25,26, without requiring strict event pre-classification. This methodological shift has facilitated the global-delta-scale assessments of compound flood risk27, offering insights into the spatial patterns of compound floods. However, these approaches may underestimate hazard levels in future-oriented decision-making, as emerging extremes are unlikely to be captured by past statistics. From a mechanistic perspective28,29,30, the riverine and oceanic floods under multiple probabilities can plausibly co-occur. This highlights the need for a combined metric that captures the potential volume of compound flooding that coastal communities would need to manage.

In economic terms, flood risk is often expressed as expected annual damage, defined as the integration of socio-economic losses over the full spectrum of flood return periods31,32. As urbanization increasingly expands into flood-prone regions5,33,34, population exposure rises, flood risk assessments that focus solely on economic losses tend to bias estimates toward high-income regions33. In contrast, low-income countries are disproportionately exposed to floods and face greater vulnerability35,36. Accordingly, the hazard-exposure-vulnerability (HEV) framework is commonly employed to assess flood risk37,38,39,40. However, existing global flood risk assessments based on the HEV framework that incorporate population exposure often rely on a single return period, typically the 1-in-100-year event, and a narrow set of indicators (e.g., flood depth or inundation extent)33,41. These approaches can introduce systematic biases in risk estimation: focusing on a single return period neglects both low-frequency and high-frequency catastrophic floods42, while considering inundation extent or depth in isolation may misrepresent the flood volume relevant for flood management43. These limitations underscore the need for a more integrated metric that systematically characterizes the full spectrum of flood hazards.

Exposure and vulnerability are equally critical components of flood risk, given the inherently impact-driven nature of risk assessments. Prior studies have frequently used population as a proxy for flood exposure5,33,40, and in the absence of high-resolution geospatial vulnerability data, Gross Domestic Product (GDP) is often adopted as a surrogate for economic vulnerability41,44. This assumption rests on the premise that flood-related economic losses scale with the level of economic development. However, this simplification tends to skew flood risk concentration toward economically developed regions, potentially obscuring vulnerabilities in lower-income areas. Empirical evidence suggests that areas with higher GDP are more likely to invest in flood protection, resulting in more advanced flood defense systems and consequently lower flood-related mortality and economic losses45,46,47. To account for the mitigating effects of economic development on flood risk, some studies have used inverted GDP as a vulnerability indicator41,45. Moreover, recent research also emphasizes that income inequality within high-GDP areas can erode the benefits of economic development, leading to disproportionately high flood impacts even in wealthy nations48,49. These findings highlight the complex and multidimensional nature of vulnerability and underscore the need for data-driven approaches that account for hazard-society interactions to improve the robustness of vulnerability.

Here, we introduce a probability-adjusted compound flood volume (Vpc) metric to represent potential coastal compound flood hazard, which integrates riverine and oceanic flood volumes across multiple return periods under a physically plausible co-occurrence assumption. Secondly, we propose a data-driven vulnerability metric derived from the Vpc-GDP relationship, expressed as the ratio between observed and maximum potential hazard for a given GDP level. Finally, we integrate compound flood hazard, population exposure, and empirical vulnerability to derive the global Potential Coastal Compound Flood Risk (PCCFR) at a 0.1 degree resolution (~10 km at the equator) and then aggregated the results to the subnational scale. To examine how different vulnerability assumptions influence risk estimates, and to validate the performance of our empirical approach, we compare three scenarios: (i) raw GDP (risk-taking), (ii) inverted GDP (risk-averse), and (iii) empirical vulnerability (data-driven risk-neutral). The global mapping of PCCFR serves as an initial screening tool to identify potential compound flood risk hotspots, helping to prioritize regions where more detailed local assessments and adaptive restoration efforts are most urgently required.

Results and discussion

Global mapping of potential coastal compound flood hazard

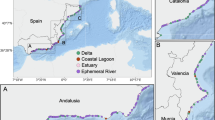
Coastal regions are increasingly susceptible to the simultaneous occurrence of river overflows and storm surges15. Figure 1A–E illustrates the spatial distribution of compound flood hazards across high-risk river deltas, including the Ganges, Pearl, Niger, Mississippi, and Rhine. Figure 1b reveals pronounced spatial heterogeneity in Vpc within deltas. To further disentangle the sources of Vpc, we analyze the probability-adjusted riverine (Vpr) and oceanic (Vpo) flood volumes, alongside their relative contributions (Vpo / Vpr) across these deltas (Fig. 1c–e). As shown in Fig. 1b–d, compound flood exhibits spatial patterns that diverge from those associated with riverine-only or oceanic-only flood events in deltaic hotspots. These spatial discrepancies highlight a key limitation of assessing riverine and oceanic hazards separately, which misrepresents the true extent and dynamics of coastal flood hazards. Neglecting these interactions can substantially underestimate compound flood hazard, especially in low-lying coastal systems. A robust characterization of potential compound flooding for future-oriented decision-making requires an integrated framework that explicitly accounts for the co-occurrence of riverine and oceanic floods.

Fig. 1: Spatial pattern of flood hazard in deltaic hotspots.
figure 1

a The global locations of major deltaic hotspots. A–E Close-up views of five key deltas: the Ganges River Delta, Pearl River Delta, Niger River Delta, Mississippi River Delta, and Rhine River Delta. b–e The deltaic hotspots of probability-adjusted compound flood volume Vpc, probability-adjusted oceanic flood volume (Vpo), probability-adjusted riverine flood volume (Vpr), and their ratio (Vpo/Vpr).

Full size image

As illustrated in Fig. 1c, d, oceanic floods attenuate gradually inland due to progressive energy dissipation mechanisms compounded by increasing topographic resistance with distance from the shoreline50. Conversely, riverine flood intensity tends to diminish downstream toward the coast, driven by a combination of reduced channel slope and expanding channel width, which collectively lower peak flood magnitudes51. Figure 1e illustrates a spatial gradient in Vpo / Vpr, with an increasing trend from inland to coast. This gradient underscores a fundamental transition in the prevailing flood hazard regime: riverine-driven flooding dominates inland regions, while oceanic influences become increasingly significant closer to the coast. The spatial gradient in flood dominance provides essential guidance for designing targeted and adaptive compound flood management strategies, enabling more effective risk mitigation in vulnerable coastal systems.

Socio-economic exposure to potential coastal compound flood hazard

Globally, around 117.19 million people and USD 1.63 trillion in assets are exposed to potential coastal compound flood hazards. To further compare socio-economic exposure to compound and single-source floods, we analyze the conditional distribution of population and assets exposure given five quantiles of riverine (Vpr), oceanic (Vpo), and compound floods (Vpc) (Fig. 2a, b). The results reveal that considering exposure based solely on oceanic floods distorts spatial patterns, overestimating exposure in low-hazard areas (the first quintile, Q1) and underestimating it in high-hazard zones (the fifth quintile, Q5) relative to compound flood scenarios. Similarly, focusing only on riverine floods substantially underestimates socio-economic exposure. These findings underscore the need to integrate multiple flood sources for more accurate, risk-informed decision-making.

Fig. 2: Population and assets exposed to flood hazards.
figure 2

a Conditional distribution of population exposure given different quintiles of compound (Vpc), riverine (Vpr), and oceanic (Vpo) flood. b Conditional distribution of economic exposure given different quintiles of compound (Vpc), riverine (Vpr), and oceanic (Vpo) floods. c Country rankings based on the share of high (Vpc) grids. d Country rankings based on the share of population exposed to high (Vpc). e Country rankings based on the share of assets exposed to high (Vpc).

Full size image

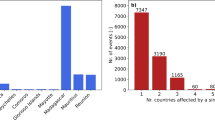
Analysis of the continental distribution of grid cells within Q5-Vpc and their socio-economic exposure reveals that Asia carries the heaviest burden, comprising 54.83% of grid cells within Q5-Vpc and accounting for the largest shares of population (87.29%) and GDP-based asset exposure (49.85%) (Supplementary Fig. 1). At the national level, Fig. 2c–e illustrate that Bangladesh accounts for the largest share of grid cells within Q5-Vpc (14.85%) and the highest population exposure to Q5-Vpc (25.71%), while the Netherlands exhibits the highest share of asset exposure to Q5-Vpc (37.40%). Importantly, several countries exhibit disproportionate exposure relative to their share of grid cells within Q5-Vpc. For example, while the Netherlands holds only 7.31% of grid cells within Q5-Vpc, it accounts for 37.40% of asset exposure. Similarly, Bangladesh hosts 14.85% of grid cells within Q5-Vpc, but contributes 3.92% of asset exposure. These imbalances highlight a key limitation of flood risk assessments based solely on the spatial extent of hazard, which may obscure the underlying socio-economic asymmetries in exposure. We further evaluate the distribution of Q5-hazard grids and associated exposure derived from single-source floods (either riverine or oceanic) at both continental and national levels, as shown in Supplementary Figs. 1 and 2.

Linking V pc and GDP: a data-driven vulnerability function

Understanding the relationship between Vpc and GDP is essential for accurately quantifying the influence of economic development on hazard, as well as assessing the potential return of flood management. Figure 3 illustrates a scale-dependent relationship between Vpc and GDP: at the subnational level, a power-law trend emerges, with exponents generally decreasing for high- to lower-income regions. In contrast, the relationship exhibits an inverted-U pattern at the grid scale. This divergence likely stems from intra-regional income inequality, previously shown to amplify disaster impacts48,49, which tends to be obscured in aggregated subnational analyses. These differences in the Vpc-GDP relationship across spatial scales underscore the importance of deriving vulnerability functions at the appropriate resolution for engineering design and policy evaluation, ensuring that investment returns are assessed with greater precision and contextual relevance.

Fig. 3: The relationship between compound flood hazard and economic level.
figure 3

a The global subcountry-level relationship. b–e The subcountry-level relationship stratified by income groups: high income (b), upper middle income (c), lower middle income (d), and low income countries (e). f The global 0.1 degree grid-level relationship. g–j The grid-level relationship stratified by income groups: high income (g), upper middle income (h), lower middle income (i), and low income countries (j). Colors of the points represent elevation; the red lines in penal (a–e) is the powerlaw fitting lines; the red line in panel (f) is upper envelope curve represented by 99.9% quantile regression.

Full size image

The relationship between Vpc and GDP at the grid scale echoes the Environmental Kuznets Curve (EKC), which posits a similar inverted-U shaped relationship between economic growth and environmental degradation52,53. While previous studies often attribute flood hazard initially increases with GDP as exposure intensifies, then declines as flood defenses and planning catch up with development46, it should be noted that the hazard maps used here do not account for existing protection infrastructure. Therefore, other factors, such as land-use patterns and socio-economic distribution, may also contribute to the observed trend3. For example, in practice, urban planning often prioritizes locating high-income production and densely populated communities in relatively low-flood-risk zones. Supplementary Fig. 3 illustrates that both the turning points and peak Vpc values of the inverted-U pattern differ across countries, with low-income regions tending toward lower peaks. These results potentially reflect differences in climate, topography, economic capacity, and infrastructure investment across countries53,54,55.

While GDP and its inverse are commonly employed as proxies for economic or social vulnerability5,33,41,45, such approaches typically assume a uniform relationship between wealth and flood resilience, potentially masking spatial heterogeneity of vulnerability. Here, we introduce a data-driven vulnerability grounded in the empirical Vpc-GDP dynamics at the grid level. Specifically, we fit an upper-envelope function to capture the maximum observed hazard at each GDP level worldwide (Fig. 3f). This upper envelope serves as a benchmark for potential hazard, against which actual hazard can be compared. We define the systemic vulnerability as the ratio between observed Vpc and its fitted upper bound, capturing how close a region comes to its maximum expected hazard given its economic conditions. This metric reflects how economic development modulates potential flood hazard and provides a scalable, data-driven measure of flood vulnerability.

Global mapping of potential coastal compound flood risk

To evaluate how different vulnerability functions influence PCCFR estimates, we compare three scenarios: (i) raw GDP (risk-taking), (ii) inverted GDP (risk-averse), and (iii) empirical vulnerability (data-driven risk-neutral). The GDP-based vulnerability function reflects a risk-taking scenario, assuming that rapid economic growth proceeds with negative flood defenses investment. In contrast, the inverted GDP formulation embodies a risk-averse perspective, assuming that economic development aligns with positive flood defenses investment. Our empirical approach grounds vulnerability in the observed relationship between Vpc and GDP, capturing actual trade-offs between economic development and flood defense investment.

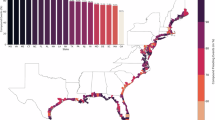
Under the empirical vulnerability scenario, Asia exhibites the highest 35.22% internal high-risk grid cells (the fifth quintile, Q5), followed by Africa (20.21%), Europe (17.02%), South America (9.89%), and North America (2.31%) (Table 1, Fig. 4a). Subnational analyses reveal that Vietnam contributes six of the top fifteen highest-risk administrative units—namely Nam Dinh, Thai Binh, Hai Phong, Hung Yen, Binh Dinh, and Quang Nam—while Bangladesh contributes four: Barisal, Chittagong, Sylhet, and Dhaka. Other high-risk units include Rayong (Thailand), Macao (China), West Bengal (India), Gifu (Japan), and Pyongyang (North Korea) (Fig. 5a). These areas are typically characterized by low-lying coastal geography, high population density, and relatively limited flood resilience, as indicated by the proximity of observed flood hazards to their maximum potential intensity. Such conditions render these regions acutely vulnerable to coastal compound flood.

Fig. 4: Global distribution of Potential Coastal Compound Flood Risk (PCCFR) at 0.1 degree grid-scale.
figure 4

a Risk-neutral empirical vulnerability. b Risk-taking scenario. c Risk-averse scenario.

Full size image
Fig. 5: Global distribution of subnational Potential Coastal Compound Flood Risk (PCCFR) under different scenarios.
figure 5

a Risk-neutral empirical vulnerability. b Risk-taking scenario. c Risk-averse scenario. Grid-scale PCCFR values were categorized into five quintiles (Q1–Q5) to indicate relative risk, with Q5 representing the highest risk. Pie charts show the proportion of grid cells in each risk quintile within each continent.

Full size image
Table 1 Percentages of compound flood risk quintiles across continents under three vulnerability functions
Full size table

Under the risk-taking scenario, the internal proportion of high-risk grid cells is 36.96% in Asia, 28.76% in Europe, 7.55% in Africa, 5.26% in South America, and 2.78% in North America (Table 1, Fig. 4b). At the subnational level, high-income coastal regions dominate the top ranks in flood risk, driven by their low-lying topograph and high asset exposure (Fig. 5b). This scenario offers insights into flood risk under growth-oriented pathways with minimal adaptation. Under the risk-averse scenario, the internal proportion of high-risk grid cells is 35.22% in Asia, 20.21% in Africa, 17.02% in Europe, 9.89% in South America, and 2.31% in North America (Table 1, Fig. 4a). Subnationally, high-risk units are concentrated in low-income, high-hazard regions, particularly across South and Southeast Asia (Fig. 5c). These areas combine high hazard exposure with limited economic capacity, underscoring the urgent need to prioritize flood mitigation in lower-income regions.

Comparative results show that using GDP as a proxy for economic vulnerability tends to concentrate high PCCFR estimates in high-income regions. Conversely, using the inverse of GDP shifts perceived risk toward low-income regions by presuming that poverty uniformly increases social vulnerability. These two vulnerability functions rely on a priori assumptions and fail to capture the non-linear, context-specific dynamics that shape flood impacts. The contrasting results from different vulnerability functions show that assumptions about vulnerability can strongly alter where flood risk is perceived to be highest, with implications for transnational, national, and regional policy decisions. By comparison, the empirical vulnerability metric provides a data-driven, risk-neutral assessment that accounts for integrating the ratio between observed and potential hazard, providing a more balanced basis for identifying priority areas in coastal flood risk management.

Conclusion

Our scenario-based PCCFR model combines compound flood hazard, population exposure, and empirical vulnerability. Global maps show that high-risk areas are largely concentrated in major low-lying, densely populated river deltas, including the Ganges, Pearl, Niger, Mississippi, and Rhine. Asia accounts for the largest internal share of high-risk grid cells (35.22%), followed by Africa (20.21%), Europe (17.02%), South America (9.89%), and North America (2.31%) under the empirical vulnerability scenario. At the subnational level, high-risk administrative units are clustered in Southeast Asia, including Bangladesh, Vietnam, Thailand, China, India, Japan, and North Korea. This global PCCFR mapping provides a screening tool for identifying hotspots and prioritizing regions for detailed assessment and targeted adaptation.

The potential coastal compound flood hazard metric, Vpc, linearly sums riverine and oceanic flood volumes under a physically plausible co-occurrence scenario rather than explicitly calculating joint probability. Given that flood protection infrastructure is typically designed under conservative assumptions56,57, this approach provides an estimate of the conservative potential compound flood volume at each grid cell, supporting design-oriented risk assessment under deep uncertainty in hazard co-occurrence. Moreover, Vpc is derived from multiple return periods based on long-term flood simulations, providing a robust representation of flood variability and large-scale hazard patterns beyond individual short-term events. Therefore, incorporating this metric into planning efforts allows decision-makers to enhance resilience. Although compound flooding may amplify inundation depth and spatial extent beyond a simple linear sum of riverine and oceanic floods21,22, such interactions are expected to have a limited effect on total flood volume due to the conservation of flood volume43,58,59. Nonetheless, we acknowledge that compound floods can intensify impacts beyond the sum of their individual sources, and future work should evaluate these nonlinear compounding mechanisms to improve the precision of compound flood hazard estimates.

While GDP-based approaches have been widely used as simplified proxies for vulnerability41,44,45, they often obscure the complex relationship between economic development and adaptive capacity. Our approach derives vulnerability from the empirically observed relationship between Vpc and GDP, thereby reflecting real-world adaptive responses and offering a more robust basis for prioritizing flood resilience investments. This data-driven framework is both flexible and context-sensitive, allowing for its application across diverse socio-economic and geographic settings.

In all, the developed PCCFR model is flexible and context-sensitive, enabling its application across diverse socio-economic settings. However, the current results do not explicitly account for detailed local-scale analyses that account for site-specific hydrology, ecology, and socio-economic conditions; the PCCFR model should be regarded as a strategic tool for value-based prioritization rather than precise prescriptions for adaptive restoration. Building on our earlier work that established the ecohydrological fitness of Blue Carbon Ecotones (BCEs) worldwide60, the present study further focuses on site-specific flood risk due to future compounding events. Although methodologically independent, their integration bridges ecosystem health with disaster risk information, enabling a cross-scale framework that supports a value-based prioritization of adaptation actions. Future development of flood risk assessments should incorporate additional eco-environmental drivers (e.g., hydrological, ecological, and socio-economic information) together with high-resolution representations of gray infrastructure, to better capture the localized dynamics and to inform adaptation planning.

Methods

Global flood hazard dataset

Flood inundation data at 30 arc-seconds (~1 km at the equator) were obtained from the World Resources Institute’s Aqueduct Floods Hazard Dataset (2020 version). The dataset provides riverine and oceanic flood inundation (depth and extent) for multiple return periods (5, 10, 25, 50, 100, 250, 500, and 1000 years), separately. In this dataset, riverine and oceanic flooding are treated independently, and interactions between the two flood types are not accounted for. To illustrate the data structure used in this study, Supplementary Figs. 4, 5 present a regional example of flood inundation depths across multiple return periods for each source. These return periods represent the average interarrival time of flood events of varying magnitudes. A higher return period corresponds to a flood event of greater magnitude. Specifically, Aqueduct Floods generated present-day (2010) flood datasets for multiple return periods through the following steps61:

  • Riverine flooding refers to inundation caused by river overflow, driven by accumulated rainfall and surface runoff. The dataset covers river basins with an upstream area greater than 10,000 km2. The present-day riverine flood hazard for multiple return periods was derived by fitting extreme value distributions to inundation outputs simulated by the PCR-GLOBWB hydrological model for the period 1960–199955.

  • The oceanic flood represents flooding from storm surges and occurs along coastlines around the world. The present-day oceanic flood inundation for multiple return periods was derived by fitting Gumbel distributions to annual maximum sea levels extracted from the Global Tide and Surge Reanalysis (GTSR) dataset for the period 1979–201462.

To evaluate the potential misalignment between riverine and oceanic flood datasets, we conducted a sensitivity analysis using time series daily precipitation data, as consistent flood time series are not available and precipitation is the primary driver of flood simulation models61. Moreover, precipitation also captures the decadal variability of large-scale climate modes (e.g., North Atlantic Oscillation (NAO), El Niño-Southern Oscillation (ENSO))63,64, thereby serving as a suitable proxy for evaluating temporal sensitivity between the two hazard sources. Specifically, we compared extreme daily precipitation (95th and 99th percentiles, P95/P99) across three time windows: 1960-1999 (riverine flood period), 1979–1999 (the overlapping period), and 1979–2014 (oceanic flood period) for five representative river deltas considering their flooding criticality (the Ganges, Pearl, Niger, Mississippi, and Rhine river deltas). The results show that, although different time windows are subject to decadal climate variability (e.g., NAO and ENSO), the long-term (~40-year) datasets capture relatively stable regional precipitation characteristics (Supplementary Table 2), indicating that different time windows of riverine and oceanic floods have a limited effect on our conclusions.

Potential coastal compound flood hazard

We calculate the Probability-adjusted Compound Flood Volume (Vpc) at 30 arc-seconds to represent potential coastal compound flood hazard. Vpc integrates riverine and oceanic flood volumes across multiple return periods under a physically plausible co-occurrence assumption (assuming a co-occurrence probability of 1), without relying on explicit joint-probability calculations (Eq. (4.1)). Specifically, Vpc comprises two components: Probability-adjusted Oceanic (Vpo) and Riverine (Vpr) flood volumes, which were calculated as in Eqs. (4.3) and (4.4), respectively. Moreover, the hazard layers used in this study do not account for existing flood protection measures (such as ecohydrological factors and anthropogenic infrastructures), and thus, Vpc represents potential flood hazards under unmitigated conditions.

$${V}_{pc}={V}_{po}+{V}_{pr}$$
(4.1)

where, Vpc: Probability-adjusted Compounding Flood Volume. Vpo: Probability-adjusted Oceanic Flood Volume; Vpr: Probability-adjusted Riverine Flood Volume.

To compare our approach with the joint-probability based compound flood, we computed the joint exceedance probability of riverine and coastal floods (Pjoint) using the Gumbel Copula in a pixel-by-pixel manner. Due to the lack of continuous historical observations of flood volume, synthetic time series for both riverine and coastal flood volumes were generated from their cumulative distribution functions (CDFs) to capture their statistical dependence. In calculating Pjoint, flood occurrence for both sources was defined using the moderate-event threshold corresponding to a 5-year return period. We then derived a joint-probability-weighted compound flood volume (Vpc_joint) as Eq. (4.2). Supplementary Fig. 6 compares the spatial patterns of Vpc and Vpc_joint in the Ganges River Delta, a well-recognized hotspot of compound flooding. While both metrics exhibit broadly similar spatial distributions, Vpc_joint is consistently lower than Vpc, reflecting the adjustment for the likelihood of simultaneous riverine and coastal flooding. This result indicates that our Vpc provides a more conservative representation of grid-scale compound flood hazard.

$${V}_{pc\_joint}=({V}_{pr}+{V}_{po})\times {P}_{joint}$$
(4.2)

Given the distinct spatial patterns of oceanic and riverine floods, we introduce the Vpo/Vpr to distinguish their dominant contributions. A ratio greater than 1 suggests that oceanic flooding dominates, whereas a ratio less than 1 indicates that riverine flooding is the primary flood hazard.

$${V}_{po}={\sum }_{j=5}^{1000}({A}_{oj}\times {D}_{oj}\times {P}_{j})$$
(4.3)

where, j: return period of 5, 10, 25, 50, 100, 250, 500, 1000 years; Vpo: Probability-adjusted Oceanic Flood Volume; Aoj: Oceanic Flood Area for the j-th return period; Doj: Oceanic Flood Depth for the j-th return period; and Pj: annual exceedance probability for j-th return period.

$${V}_{pr}={\sum }_{j=5}^{1000}({A}_{rj}\times {D}_{rj}\times {P}_{j})$$
(4.4)

where, Vpr: Probability-adjusted Riverine Flood Volume; Arj: Riverine Flood Area for the j-th return period; Drj: Riverine Flood Depth for the j-th return period.

Socio-economic exposure

We considered population and assets as indicators of socio-economic exposure. Gridded population data at 30 arc-seconds were obtained from WorldPop65, while GDP data at 1 km resolution were derived from calibrated nighttime light observations66. Both datasets, for the year 2010, were resampled to the resolution of the compound flood hazard maps (30 arc-seconds) for analysis.

To compare population and asset exposure to coastal compound floods versus single-source floods, we divided affected areas into five quintiles (Q1–Q5, from lowest to highest) based on the Vpc values of each grid cell. Using these thresholds, we then quantified the exposure of population and assets considering only oceanic flooding or only riverine flooding. To further investigate the spatial patterns of socio-economic exposure in high-hazard zones, we focused on high-Vpc grids (Q5) and calculated their distribution at both continental and national scales.

Empirical vulnerability

We introduce a data-driven vulnerability (Ne) grounded in the empirical Vpc-GDP dynamics at the grid level. Specifically, we fit an upper-envelope function to capture the maximum observed hazard at each GDP level worldwide (Fig. 3f). This upper envelope serves as a benchmark for potential hazard, against which actual hazard can be compared. We define the systemic vulnerability as the ratio between observed Vpc and its fitted upper bound, capturing how close a region comes to its maximum expected hazard given its economic conditions. For each grid i, Ne is calculated as Eq. (4.5). Ne closer to 1 indicates regions approaching their maximum potential hazard. When computing vulnerability at the 30 arc-seconds resolution, we found that GDP exhibits limited spatial heterogeneity, resulting in histograms with GDP values concentrated within a narrow range (Supplementary Fig. 7b, d). This lack of variability makes it difficult to robustly capture the empirical relationship between GDP and Vpc. To address this issue, we compute vulnerability on a coarser 0.1 degree grid, which more effectively captures the spatial variability of both GDP and flood hazard (Supplementary Fig. 8b, d). All subsequent risk calculations involving vulnerability are therefore conducted on the 0.1 degree resolution.

$${N}_{e}=\frac{{V}_{pc}}{{f}_{envelope}(GDP)}$$
(4.5)

where, fenvolope(GDP) represents the quadratic quantile regression at the 99.9th percentile between Vpc and GDP.

Potential coastal compound flood risk for different risk-perception’s vulnerability

We calculate global coastal compound flood risk based on the HEV framework (Eq. (4.6)). The GDP-based vulnerability (Nt) reflects a risk-taking scenario, assuming that rapid economic growth proceeds with negative flood defenses investment. As evidence shows that regions with higher GDP are more likely to invest in flood protection45, and thus possess more advanced flood defenses46, resulting in fewer flood-related fatalities and economic losses47, In contrast, the inverted GDP formulation (Na) embodies a risk-averse perspective, assuming that economic development aligns with positive flood defenses investment. Our empirical approach grounds vulnerability (Ne) in the observed relationship between flood hazard and GDP, capturing actual trade-offs between economic development and flood defense investment.

$$PCCFR=\root{{3}}\of{{V}_{pc}\times {E}_{p}\times \Bigg\{\begin{array}{ll}{N}_{e}, & risk\,-\,neutral\,empirical{V}_{pc}-GDP\,vulnerability\\ {N}_{a}=1/GDP, & risk\,-\,averse\,vulnerability\hfill \\ {N}_{t}=GDP, & risk\,-\,taking\,vulnerability\hfill \end{array}}$$
(4.6)

Where, Vpc: Potential coastal compound flood hazard; Ep: population exposure. Each components used in the PCCFR calculation were divided into 10 quantiles, with each assigned values from 0.1 to 1.0. This quantile-based normalization allows for consistent comparison across variables with different units and magnitudes, reduces the influence of outliers, and enables integration into a unified systemic risk, where higher values correspond to higher risk. Then we apply the cubic root because, given normalized inputs, the product of the HEV components always lies between 0 and 1. Their raw product can become disproportionately small. The cubic root restores scale through the geometric mean, yielding a more balanced integration of the three factors, consistent with the approach of Fox et al.41.