Introduction

Over the past decade, many studies have developed regression-based and machine learning models for predicting the risk of complex genetic disorders1. Despite progress, their performance still falls short of the estimated limits based on heritability2. Meanwhile, efforts to identify functional genome components and environmental factors influencing heritable disorders have advanced. In polygenic disorders, where heritability is spread across many genes, leveraging current genomic knowledge could improve risk estimation. One study showed that using trait-specific functional priors increased polygenic prediction accuracy by 5%3. However, machine learning models have yet to fully utilize genomic knowledge, requiring new methods to handle the changes in data dimensionality and characteristics.

As an example, we focused on type-2 diabetes mellitus (T2D), which afflicts 6.3% of the world’s population4,5. Genome-wide association studies (GWASs) of T2D have been successful in identifying hundreds of genetic variants6,7. Studies using machine learning models to classify people with and without T2D have been less successful; model performances are lower than expected relative to the heritability of T2D and the classification performance of diseases with similar heritability8,9,10. This poor performance may stem from several factors. One possibility is that the genetic risk for T2D is more complex, involving numerous small-effect loci across the genome, unlike type-1 diabetes, where risk is concentrated in a single region11. If so, more sophisticated models may be needed to capture this complexity.

The complexity of machine learning models has its drawbacks12. A complex model can capture patterns specific to the training data. If these patterns are more effective at classification than the real effects, the model may prioritize them, leading to “overfitting.” This means the model performs well on training data but struggles with unseen data that lack the same patterns. One example of a model learning patterns specific to training data and failing to generalize is when it is trained with population stratification13. In population stratification, cases and controls in the training data have systematic ancestry differences. A model may use these variant frequencies between ancestry groups to classify cases and controls, but it ends up classifying ancestry rather than disease. When tested on data without the same ancestry imbalance, the model’s disease classification performance will drop.

Although ancestry can confound analyses, modeling ancestry alongside genotype data can improve prediction14,15 due to differing sampled case/control ratios within different ancestries or the interaction between genetic risk and a factor in which ancestry acts as a proxy. While these factors are undoubtedly important for clinical implementations of genetic risk models, the goal of many studies, including ours, is to better understand the genetic basis of the disorder, which motivates efforts to minimize the confounding effects of ancestry on genetic risk modeling.

In GWAS and polygenic risk score models, population stratification is typically controlled by including principal components (PCs) as covariates to assess associations and derive risk scores16. Most ancestry information is thought to be captured in the top PCs, so removing their effects allows the model to detect true disease risk. However, linear adjustments may not fully address ancestry-specific differences in allele frequencies. Since many machine learning models can learn non-linear relationships, it’s crucial to account for potential non-linear ancestry effects. In this work, we tackle this by using a within-model adjustment that reverses the gradient during gradient descent17. This “adversarial task” helps the model unlearn ancestry, reducing its reliance on ancestry confounds.

One cause of overfitting complex models is the high number of parameters in a model18. Many machine learning models can achieve near-perfect accuracy on randomly labeled data if the number of parameters far exceeds the number of samples19. This is particularly relevant in GWAS studies, where genetic variants can number in the millions, while the number of study participants is far fewer. A common way to reduce overfitting is to limit the number of variants used18, but this may hinder model performance if true risk variants are excluded.

In this study, we develop a classification model using convolutional neural networks (CNNs) to limit the number of model parameters without removing genetic variants. CNNs are widely used in image recognition due to their ability to learn local patterns and efficiently reduce high-dimensional features. Several studies have shown the effectiveness of CNNs on genetic data, focusing on disease classification or annotation prediction based on genotype values20,21. Here, we create a CNN guided by genetic annotations, aiming to produce a low-dimensional representation of disease-relevant genetic variants. We hypothesize that training a CNN informed by genomic context will improve classification performance relative to current approaches. We also test whether using gradient reversal layers to create adversarial multi-task networks could control for ancestry confounding while preserving disorder classification accuracy. We find that CNN models using genomic context and neural network models constrained to context-enriched genetic variants significantly outperform polygenic risk score methods in classifying T2D. We show that adversarial ancestry adjustment effectively removes ancestry information from these models without reducing classification performance. Finally, we find that context-informed models capture unique and generalizable risk patterns, indicating that combining genomic context with within-model ancestry adjustment is a promising direction for advancing genetic risk prediction.

Methods

Data acquisition and preprocessing

We applied for and obtained genotype and phenotype data from the UK Biobank22, a prospective cohort study of over 500,000 individuals in the United Kingdom under application number 60050. Access to UK Biobank data is available to bona fide researchers through application to the UK Biobank (www.ukbiobank.ac.uk/register-apply). All UK Biobank participants provided informed consent at recruitment and can withdraw consent at any time. The UK Biobank received ethical approval from the Northwest Multi-Center Research Ethics Committee (reference no. 16/NW/0274). We applied for and accessed genotype and phenotype data from the Wellcome Trust Case-Control Consortium (WTCCC) under the application titled “Using Genomic Context Informed Genotype Data and Within-model Ancestry Adjustment to Classify Complex Genetic Diseases”. Access to WTCCC data is available to bona fide researchers through application to the Sanger Data Access Committee (https://edam.sanger.ac.uk). The WTCCC project received ethical approval from the South East Multicentre Research Ethics Committee (ref no. 05/Q0106/74). All WTCCC participants provided written informed consent. The UK Biobank genotype data were generated by a combination of the UK Biobank Axiom array and UK BiLEVE Axiom array. 1037 sample outliers, multi-allelic single nucleotide polymorphisms (SNPs), and SNPs with a minor allele frequency (MAF) < 1% were removed, resulting in 641,018 SNPs23. These were used to impute ungenotyped SNPs, leading to a dataset of 73,355,667 variants. For our analyses, based on our training subset, we removed all SNPs with MAF < 1%, all SNPs with > 5% missingness, all individuals with > 5% missingness, and one member of any estimated kinship equal to or closer than second-degree relatives using Plink. We randomly split the data into training (70%), validation (15%), and testing subsets (15%). In each subset, we performed 1:1 case-control matched pairing based on age and sex using MatchIt24,25. The training, validation and test subsets had 55,168, 11,712, and 11,648 records, respectively. The SUNY Upstate IRB determined that this project did not meet the definition of human subject research (Project ID: 2241318-1).

Context informed data matrix (CID)

Model overview and input

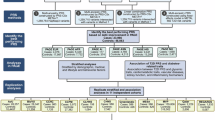
Simplified diagrams of model architectures, inputs, and outputs are shown in Fig. 1. An overview of the models used in our analysis is shown in Table 1. The genotype input used in our NN models is the number of minor alleles at each SNP for each person, ranging from 0, when neither chromosome contained the alternate allele, to 2, when both chromosomes contained the alternate allele. The additional input used in our CNN models is a CID, which contains each SNP along with information about that SNP. The CID’s columns represent each SNP; rows contain the genomic annotations and disorder risk values for each SNP. Figure 2 shows a simplified CID.

Fig. 1: Simplified model architecture diagrams.
figure 1

The Black arrows represent the layers that connect each input to each output. The green arrows represent the positive feedback from backpropagation that aims to minimize error. The unfilled/white arrows represent stop gradient layers, which prevent the task from changing the weights in all layers upstream from the stop gradient layer. Red arrows represent gradient reversal layers of adversarial tasks, which reverse the direction of the weight changes and maximize loss for the task in any layer upstream from the gradient reversal layer. a represents the PC NN model, b represents the Geno-PC model, c represents the Geno-PC-T2D model, d represents the Geno-T2D Track-PC model, e represents the Geno-T2D Adv-PC model, f represents the CID-T2D Track-PC model, g represents the CID-T2D Track-PC/Geno model, h represents the CID Specific model, and i represents the Geno Specific model. An overview of these models can be found in Table 1. Note that some models, like (f) vs (g) and (h) vs (i), differ only in the way gradients flow during backpropagation, illustrated by the color of the arrows. The blue rectangles represent the input data, and the blue circles represent the transformed input that has been reduced to fewer dimensions. Task specific output layers are present for each task in each model. Principal component (PC), Type 2 Diabetes (T2D), Context Informed Data matrix (CID), Genotype (Geno), Adversarial (Adv), Convolutional (Conv).

Full size image
Fig. 2: An illustrative example of a portion of a context-informed data matrix (CID).
figure 2

A CID is constructed for each person within the study. For each person, the annotation values are multiplied by the allele count at each SNP and the resulting individualized annotation matrix is used as input into machine learning models. Type 2 Diabetes (T2D), Single Nucleotide Polymorphism (SNP), micro Ribonucleic Acid (miRNA), Transcription Factor Binding Site (TFBS).

Full size image
Table 1 Overview of Machine Learning Models
Full size table

For each individual, the CID, which largely contains information about each SNP that does not change between individuals, is multiplied by the genotype values of the individual prior to model training. For all models, we used a binary variable representing the presence of the International Statistics Classification of Disease 10th revision (ICD-10) code for T2D, E11, for each individual as the label to be predicted. Our models output values from 0 to 1 with the goal of minimizing the error in predicting the label for each individual.

Genomic annotations

The genomic annotations provided information on whether the SNP occurs at a location known to be a miRNA binding site, DNase hypersensitivity site, CPG island, gene, intron, 5’ untranslated region (UTR), 3’ UTR, splice site, promoter, or transcription factor binding site using the AnnotationHub26 and VariantAnnotation27 packages in R. We did this by loading the SNP locations and annotation ranges and then finding the overlaps between the two. Any SNP that had an overlapping location with an annotation was coded as a 1 for that annotation or was otherwise coded as a zero. We included whether the SNP was a coding variant using the same overlap method.

We also added annotations indicating whether the SNP was within the range of each of the 20 gene sets most associated with T2D among gene sets in the lowest 10% standard error in MAGMA gene set analysis28. We used the lowest 10% standard error threshold to ensure that the resulting gene set annotations were dense due to using larger gene sets and gene set association was consistent in the training subset as determined by MAGMA gene set analysis. The results of MAGMA gene set analysis on the training subset can be found in Supplementary Data.

Risk values

To give the model information about documented disease risk associations, we added the log odds ratios for each SNP from an external GWAS on T2D6 to the CID. Only SNPs present in both the UK Biobank data and the external GWAS were included in the model. To reduce the computational cost of this analysis, we further reduced the number of SNPs for ML models by only including SNPs that were associated with T2D in the external GWAS at p ≤ 0.01. This reduction left us with 11,730 SNPs for machine learning models. We also included odds ratios from correlated disorders based on genetic correlations calculated by GWAS Atlas29. From the list of the 100 most correlated traits with T2D, we selected traits that had ICD-10 codes available in the UK Biobank data. The included traits were overweight and obesity, disorders of lipoprotein metabolism and other lipidemias, essential hypertension, chronic ischemic heart disease, cholelithiasis, angina pectoris, other disorders of the urinary system, and pain in the throat and chest. We performed GWASs on these traits using genotyped UK Biobank individuals that were not included in our machine learning models. The top ten PCs were used as covariates in the model to adjust for population stratification. We included the log odds ratios calculated from these GWASs in the CID.

Correlation to Annotation

It is likely that, for most SNPs, the risk associated with the SNP is due to another genetic change that is associated with the SNP through linkage disequilibrium30. To account for this, we added an annotation for each previously described binary annotation that indicates the maximum squared correlation each SNP has to a SNP with the binary annotation. Correlations were calculated using Plink31. In cases where the SNP has the annotation, the correlation is 1, and the resulting annotation value is identical to the original annotation value.

Model hyperparameter optimization

Within TensorFlow32, we used the KerasTuner33 framework to optimize the hyperparameters of our models. Using the Hyperband search algorithm, we searched for the optimal number of genomic convolutional blocks, number of filters within each block, filter and pool width within each block, number of dense layers, number of nodes and dropout rate within each layer, gradient reversal weights, L2 regularization presence and factor, number of epochs, and learning rates. The objective of the search algorithm was to maximize the area under the receiver operating characteristic curve (AUC) in the validation subset for classification tasks and maximize the validation subset R2 for regression tasks.

Detecting and adjusting ancestry confounding with PCs and adversarial learning

ML models use all information available to them to produce the best performance possible. This can result in models that perform well mainly due to a confounding variable. To address confounding by ancestry, we ran a PCs analysis using the SNPs that were not included in our ML models nor correlated with the SNPs (r2 < 0.2) that were used in the ML models. We extracted the top ten PCs, as is frequently used for ancestry inference16 and used them as labels in several models.

To establish whether population stratification was an issue, we built the “PC NN” model (Fig. 1a) using the ancestral PCs to predict T2D status. To determine if the subset of SNPs used as predictors in our model could recreate the PCs within the model, we used the genotype data as input in a neural network model that predicted the PCs (“Geno-PC” model, Fig. 1b). We determined the effectiveness of all model architectures in estimating the PCs with mean squared error (MSE) and R2. In models that had a positive R2 value, we also tracked T2D classification AUC from the PC estimates.

To test if a neural network could classify T2D and estimate PCs using the same layers, we designed a multi-task model with both tasks sharing all layers except output layers (“Geno-PC T2D” model, Fig. 1c). An additional task classifying T2D from the PC estimates was used to compare classification performance between the PC estimates and the true PCs.

To test whether, in classifying T2D from genotype data, our model inadvertently uses PC-like ancestral information, we built a multi-task model where one task classified T2D from the genotype input and another task estimated PCs (“Geno-T2D Track-PC” model, Fig. 1d) from the output of the dense layers. In this model, we used a stop gradient layer between the PC estimation task and the dense layers, which stops backpropagation. By using this layer, we stopped training such that the task estimating PCs did not influence the dense layers upstream from the layer unique to their tasks. This strategy allows us to track the performance of a task, in this case, PC estimation, without interfering with shared layer training. If the PC estimation task was predictive, this would suggest the model classifying T2D from genotype data used ancestral information that could be directly transformed into PC estimations.

To test whether we could teach the network not to use ancestry information when predicting T2D, we built a multi-task model (“Geno-T2D Adv-PC” model, Fig. 1e) with the same two tasks as the previous model but replaced the stop gradient layer with a gradient reversal layer, a technique initially developed in the domain adaptation field of machine learning17. This layer reverses the direction of gradients in gradient descent, thereby directing the weights in the layers upstream of the gradient reversal layer to adjust in a way that maximizes the error in the task, instead of the typical minimization. Unlike the fast gradient sign method, which creates “adversarial examples” by using gradients to create a new example that maximizes loss, the gradient reversal layer creates a continuous “adversarial task” by reversing the gradient from back propagation from the task-specific layers of the selected task throughout model training. The “adversarial task” directs the model to find ancestry-invariant patterns by penalizing classification strategies that lead towards more accurate estimation of ancestral PCs. Layers that are downstream of the gradient reversal layer still adjust weights in a way that minimizes error in the task. This means the adversarial task still attempts to minimize error and accurately estimate PCs in the layers that are unique to the task, thereby leaving adjustment of shared layers as the only option in maximizing error. We used this architecture to remove any PC-like ancestry information from the shared layers. If the model is unable to estimate PCs, it suggests the ancestry information present within the PCs is not being used in the shared layers.

CNN model architecture for genomic data

In all our CNN models, we used the matrices as input into genomic convolutional blocks, which are repeating units within the model that contain a combination of 1D convolutional layers with ReLU activation functions, pooling layers, and batch normalization layers. Within convolutional layers, the convolutional filters require spatial invariance, meaning that a signal at one part of the two-dimensional data structure has the same meaning as the same signal anywhere else in the data structure. This is true for images, for which convolutional layers were originally developed. In contrast, the height dimension of the context-informed data matrix used as input in our model, which represents the annotation information at each SNP location, lacks spatial meaning. Consequently, filters at different heights could convey vastly different meanings, thereby violating spatial invariance. To address this issue, we set the height of each convolutional filter equal to the total number of rows present in the matrix to assure that output signals from one part of the matrix were equivalent to those from another part. Given that spatial invariance was violated along the genome, with the columns representing SNPs in the CID, we set the hyperparameter selection range of convolutional width to 1–20. This range was used to allow the model to set the convolutional width to 1 if having convolutional filters containing more than a single SNP was disruptive to model performance due to the violation of spatial invariance, while also allowing for wider convolutional filters if that was beneficial to model performance. After each 1D convolutional layer, the output was fed into a batch normalization layer. After the genomic convolutional blocks, the output was used as input into one or more dense layers with ReLU activation functions, depending on hyperparameter optimization. Finally, we used a dense layer with a sigmoid activation function to produce an output prediction of the T2D status for each person. We used the Adam optimizer and binary cross-entropy loss function to train our models.

To test whether genotype-only models and context-informed genotype models can share the same features, we trained a CNN model that had two input sources that shared intermediate layers but have separate input-specific T2D classification tasks (“CID-T2D Track-PC” model, Fig. 1f). This means that the two input sources undergo the same transformations in the shared layers, but the output of those transformations is different because the input sources are different. The inputs into this model differ in that the CID input contains annotation information for each SNP, whereas the genotype input has copies of the genotype data, such that it is the same shape as the CID input to allow layer sharing. The input specific output layers then optimize T2D classification based on the result of the transformations in each input source. One input was the CID as previously described. The second input was the genotype data portion of the CID replicated such that it had the same dimensions as the CID. Both inputs shared all layers except the output layer specific to each input/task. If both tasks can classify T2D, it would suggest that there are similarities in the patterns used in the two input types. A PC estimation task with a stop gradient layer was used to track whether ancestry information was used within the model.

To test whether overlaps in the patterns found and used in both tasks are present when only training the CNN with CID input, we trained another CNN model (“CID-T2D Track-PC/Geno” model, Fig. 1g). In this model, we used the same base structure as the “CID-T2D Track-PC” model but used a stop gradient layer prior to the output layer of the genotype-only model, thereby preventing the task from training layers besides the output layer unique to the task. If the task is still able to classify T2D diagnosis with these constraints, it suggests that at least some of the similarities in the patterns used for both tasks are used even when not directed to find shared patterns.

To test whether the CNN with CID input can find patterns that the genotype-only model cannot use to classify T2D, we built a third CNN model (“CID Specific” model, Fig. 1h). In this model, the stop gradient layers in the “CID-T2D Track-PC/Geno” model were replaced with gradient reversal layers. This effectively forces the shared layers away from any patterns that could be used by the genotype-only input to classify T2D. Likewise, the shared layers are forced away from using ancestry information that could be used to estimate PCs. If the CID input can classify T2D using the same layers as the genotype-only input, it would suggest that the CID input can model patterns that the genotype-only input is not able to model. To test whether the CNN with genotype input can find patterns the model with CID input cannot, we built a similar model (“Geno Specific” model, Fig. 1i) that switched the main and adversarial tasks of the “CID Specific” model.

To test whether the “Specific” models contained non-overlapping T2D risk information, we built a model that used a combination of the risk features generated by the “Specific” models to predict T2D. To do this, we concatenated the output from the final intermediate layer in both models. This combined output was used as input into a neural network model (“Combined Specific” model) with the task of classifying T2D diagnosis. We compared the performance of this combined model to the performance of the “Specific” models individually.

Logistic regression models and model comparison

We fit logistic regressions using multiple PRS methods on all available SNPs comparisons. For standard PRS, we used Plink to prune correlated SNPs and calculate polygenic risk scores (PRSs)31. We also calculated PRS scores using LDpred234 and PRS-CS35. We adjusted all PRSs for ancestry by regressing the PCs on the PRSs and keeping the residual. We used this residual in the generalized linear model (glm) function within the base stats package in R to fit a logistic regression using only the training subset. We predicted the test subset T2D status and the performance within the test subset to compare with other models. We used AUC to measure performance in the test subset. AUC confidence intervals were computed with 2000 stratified bootstrap replicates using the pROC R package36. We also used the pROC package to compare the performance between models with DeLong’s test for two correlated ROC curves.

Feature importance and generalization analyses

We used integrated gradients37 on our trained NN and CNN models to identify the features that were most influential in separating cases and controls. The output from Integrated Gradients is a value for each input feature for each person representing how much that feature contributed to the prediction of that person’s T2D status. To estimate overall feature importance, we compared the mean attributions in cases and controls for each feature using t-tests. We adjusted for multiple comparisons in our feature importance analyses using Bonferroni correction. There is significant and reasonable concern that the features used in ML algorithms are somewhat specific to the data used to train the model18. To test generalization, we used data from the WTCCC, which included 2922 T2D cases and 2922 controls after applying the same QC steps we used for the UK Biobank data38. Genotypes for these data were imputed using the 1000 Genomes Project Phase 3 reference panel. Since the SNPs used in the original model were not all present in the WTCCC data, we re-ran the analysis for the best-performing models using only SNPs present in both WTCCC and UK Biobank data. We performed all other steps as described in previous sections, with the WTCCC data as an additional withheld subset. We assessed generalization by comparing AUC across models and data sets. We also looked for overlap in significant feature importance results across data sets.

Statistics and reproducibility

Statistical analyses were conducted in R (version 4.3.1). Machine learning models were implemented in Python (version 3.8.5) using TensorFlow (version 2.9.1) and associated libraries. Model performance was evaluated using area under the ROC curve (AUC) with 95% confidence intervals estimated from 2000 stratified bootstrap replicates. Differences between models were tested with DeLong’s test for two correlated ROC curves. Feature importance values were estimated using Integrated Gradients and compared between cases and controls using two-sample t-tests with Bonferroni correction for multiple comparisons. All statistical tests were two-sided. Principal component estimation accuracy was evaluated using MSE and R². Models were trained using a training subset (n = 55,168), hyperparameters were optimized using a validation subset (n = 11,712), and performance was tested using a test subset (n = 11,648), all from the UK Biobank dataset. We tested model generalizability using external WTCCC data (n = 5844).

Results

In the following, “genotype data” refers to the set of genotypes used as input to the models, “GWAS PCs” refers to ancestrally informative PCs estimated from the full set of GWAS SNPs and “ML PC estimates” refers to PCs estimated in machine learning models using genotype data as input. Table 2 shows the performance of all models on the test subset. Descriptions of each model’s results can be found in the supplementary results. The hyperparameter optimization ranges and values are in Table 3.

Table 2 Machine Learning Model Results
Full size table
Table 3 Hyperparameter Optimization Ranges
Full size table

Adversarial ancestry adjustment

Two of our models (shown in Fig. 1a, b) showed that both GWAS PCs and ML PC estimates were significantly predictive of T2D. The prediction of T2D using GWAS PCs and the prediction of T2D using ML PCs estimates were not significantly different (p = 0.65, Delong’s test for two correlated ROC curves). This illustrates the issue that within model correction may be necessary to avoid using potentially confounding ancestry information in classification modeling. Models that used adversarial tasks for ancestry (shown in Fig. 1e, h, i) all increased the ML PC estimates MSE as intended, ensuring that the model could not accurately recreate GWAS PCs and therefore could not use the ancestry information within those PCs to improve the classification of T2D. All models with an adversarial ancestry task had an R2 < 0 for the PC estimation task, indicating that the model’s predictions are worse predictions than using the mean.

Classification model performance and comparison

The best performing NN model was the “Geno-T2D Adv-PC” model (Fig. 1e), with an AUC of 0.66 (95% CI: 0.65–0.67). The best performing CNN model was the “CID-T2D Track-PC/Geno” model (Fig. 1g) with an AUC of 0.65 (95% CI: 0.64–0.66). In comparison, the best performing PRS method used LDpred2 to predict T2D with an AUC of 0.63 (95% CI: 0.62–0.64). The best performing CNN and NN models were both significantly more predictive than the best PRS method (p = 0.009 and p = 0.001, Delong’s test for two correlated ROC curves) despite using only 11,730 SNPs compared to 979,891 SNPs used in the PRS methods.

Feature importance and generalization analyses

SNPs with significantly different mean attributions between cases and controls in the test subset for the “Geno-T2D Adv-PC”, “CID-T2D Track-PC/Geno”, and “CID Specific” models can be found in Supplementary Data. In all three models, the significant SNPs based on feature importance did not have significantly different GWAS association p-values compared to the SNPs that were not significant based on feature importance. In a generalization analysis, which was restricted to overlapping SNPs in the WTCCC and UK Biobank data sets, model performance decreased but all models were still significantly predictive of T2D. In the LDPred2 PRS model, which used 1,088,838 SNPs, the AUC was 0.56 (95% CI: 0.55–0.58) in the test subset and 0.54 (95% CI: 0.53–0.56) in the WTCCC data. In the “Geno T2D Adv PC” model, which used 9626 SNPs, the AUC was 0.62 (95% CI: 0.61–0.64) in the test subset and 0.62 (95% CI: 0.60–0.64) in the WTCCC data. In the “CID-T2D Track-PC/Geno” model, which used the same 9626 SNPs, the AUC was 0.58 (95% CI: 0.56–0.60) in the test subset and 0.60 (95% CI: 0.58–0.62) in the WTCCC data. In feature importance analysis, comparing the results in the test subset and WTCCC data, there was one overlapping significant SNP in the “Geno T2D Adv PC” model, rs12244851, and two overlapping significant SNPs in the “CID-T2D Track-PC/Geno” model, rs11996576 and rs3818717.

Discussion

Our findings show that incorporating genetic annotations for common variations provides additional insights relative to polygenic risk score approaches. To our knowledge, we are the first to use convolutional layers with genomic context, and our results suggest these methods can find unique, generalizable risk patterns. As far as we are aware, this study is also the first to apply gradient reversal layers in genomic machine learning, proving useful for adjusting ancestry and testing hypotheses. We found that relying solely on the top ten PCs is insufficient for removing ancestry-related confounding. Therefore, within-model control methods are essential to prevent ancestry confounding in predictive models.

In a large dataset of over 70,000 subjects, the “PC NN” model (Fig. 1a) significantly predicted T2D using the top 10 PCs from a PCA based on SNPs not included or in linkage disequilibrium with SNPs used to estimate our models. The “Geno-PC” model (Fig. 1b) showed that the genotype information we use as predictors can accurately estimate PCs. Taken together, these two models show that machine learning models can recreate ancestry information and use that information to classify T2D diagnosis and, likely, other disorders. The “Geno-PC-T2D” model (Fig. 1c) tested this ancestry inference to disorder diagnosis pathway directly and resulted in T2D classification performance not significantly different from classifying directly from GWAS PCs. The “Geno-T2D Adv-PC” (Fig. 1e) did not perform any worse than the “Geno-PC-T2D” model (Fig. 1c), despite eliminating the latter model’s ability to estimate PCs. Since the layers within the Geno-T2D Adv-PC model were forced away from using ancestry information, it is likely that nodes of the model that had been occupied with ancestry inference were used to represent additional real risk features of T2D.

In traditional machine learning approaches, it’s difficult to know if ancestry influences a model. Our solution uses a subtask that estimates ancestry-adjusted PCs from the output of layers used in the main classification task. This subtask cannot affect the shared layers’ weights due to a stop gradient layer. Without it, backpropagation would alter the main classification layers to improve PC estimation, encouraging the use of ancestry information. Instead, the stop gradient layer monitors whether ancestry data is used without altering the main network. If significant PC estimation occurs with the stop gradient, it indicates ancestry information is present in the shared layers. In this case, the stop gradient can be replaced by a gradient reversal layer, which flips the direction of weight changes from gradient descent in the upstream layers. This causes the model to maximize errors in PC estimation, avoiding ancestry use. This effect is shown by comparing the MSE in Fig. 1d, e, where replacing the stop gradient with a gradient reversal layer increases the PC estimation MSE from 1.70 to 2.32. The strength of this adversarial task can be adjusted to eliminate ancestry information. If more detailed ancestry data is available, it can also be used similarly. Studies have shown that genetic risk models, primarily developed on people of European ancestry, do not generalize well to other ancestral groups39,40. Adversarial ancestry tasks would reduce this discrepancy by finding ancestry-invariant patterns.

In the “CID-T2D Track-PC” model (Fig. 1f), we trained a model to predict T2D with two types of inputs. The inputs were a “CID Input” that uses genomic context information and a “genotype input” that did not use genomic context information. The input types trained and used the same shared layers, apart from output layers that were not shared. The classification performance resulting from the two input types were similar. This suggests that the input types can find and use the same patterns within the data to classify T2D. This result was expected since the two input types share the same genotype information.

However, the CID-T2D Track-PC/Geno model (Fig. 1g), which only allowed the CID input to train the shared layers, found that the CID input was significantly better at classifying T2D compared to genotype input that did not train the shared layers (p = 2e-16, Delong’s test for two correlated ROC curves). This shows that while the two input types share similarities in their ability to represent the risk of T2D, CID input can create unique risk representations that improve prediction beyond what can be represented by genotype data alone.

Our use of gradient reversal layers to create adversarial tasks in the “CID Specific” model and “Geno Specific” model further separated out input-dependent features. While both models’ performance declined relative to other CNN models, the inputs for the non-adversarial tasks still had AUCs that were statistically significant. In comparison, the adversarial task input (genotype input for the “CID Specific” model and CID input for the “Geno Specific” model) was unable to significantly classify T2D using the same shared layers used by the main input. This suggests that the risk representations within the models leading to T2D classification were specific to the non-adversarial input. Our feature importance analysis also suggests that the CNN models are finding different risk patterns compared to our NN models. There was only a 2% overlap in significantly predictive SNPs between the “Geno-T2D Adv-PC” and the “CID Specific” models.

One explanation of the unique risk representations is that they represent the same underlying risk features but are constructed in a way that can only be used with one input type. To test this theory, we trained the “Combined Specific” model, which combines the features of the final intermediate layers of the “CID Specific” and “Geno Specific” models. If the features from the “Specific” models were overlapping, one would expect the model using the features from both models to have the same classification performance. We found that the “Combined Specific” model was significantly better at classifying T2D compared to both individual models. This suggests that the risk representations found in the “Specific” models are at least in part specific to those input types. This suggests that some of the genetic risk for T2D can be transformed into higher-order risk features using genomic context (features from the “CID Specific” model) while other risk cannot be transformed with the set of genomic context information used in our analyses. Further investigation of the genetic variants and higher-order risk features used and developed in these models could reveal insights for future genetic risk modeling efforts.

The performances of our NN and CNN models improves on prior results. One study reported an AUC of 0.60 (95% CI: 0.59–0.61) when using a gradient boosted and LD-adjusted heuristic polygenic score and an AUC of 0.61 when using LDpred polygenic scoring41,42. The same study reported an AUC of 0.58 in an LD-unadjusted polygenic risk score and an AUC of 0.58 when using traditional pruning and thresholding polygenic scoring methods, which is like our polygenic risk score methods and results. Another study that investigated many different models and feature encodings reported a maximum AUC in T2D across all models/encodings of 0.5943. We used the LDpred234 polygenic scoring method and saw an improvement compared to these prior results, with an AUC of 0.63 (95% CI: 0.62–0.64). Our best genotype (“Geno-T2D Adv-PC” model, AUC: 0.66, 95% CI: 0.65–0.67) and CID (“CID-T2D Track-PC/Geno” model, AUC: 0.65, 95% CI: 0.64–0.66) models are both improvements over these prior studies and our own polygenic scoring results. While these are significant improvements, they are small; further advances will be necessary to reach the goal of clinical utility.

Classification models may be useful for identifying genetic variants that predict T2D. Our feature importance analyses of the “Geno-T2D Adv-PC”, “CID-T2D Track-PC/Geno”, and “CID Specific” models had 352, 57, and 62 SNPs with statistically significant differences in mean attributions between cases and controls in the test subset (see Supplementary Data). These SNPs did not have significant differences in association with T2D compared to the other SNPs used in the models. This suggests that information beyond the differing allele rates between cases and controls are driving the importance of the significant SNPs, which may be worthy of further investigation. They may also be specific to the models and data used in our study due to overfitting. We addressed generalizability of our models’ prediction in this study by presenting classification model performance only in a withheld testing subset of data that were not used to train or optimize the model and by testing performance in an external WTCCC dataset.

Several limitations may have reduced our models’ ability to classify T2D. Due to computational issues, we only used a small subset of the genetic variants. Using more variants might increase the CNNs’ ability to detect local patterns since the genetic variants would be spaced closer together and the distance between variants would be more uniform. Insufficient optimization of hyperparameters may have also limited the performance of our models. In more complex models, the hyperparameter space becomes too large to efficiently explore all possible solutions. Therefore, it is likely that our model architectures are not the optimal solution. Further exploration of the hyperparameter space could improve results. The annotations used to create the CID may not be the best combination of information. Adjustments to the genomic context information might improve our results. There has been some evidence that population structure may not be fully captured by just the top PCs, so residual ancestry information could still influence the model44. Our model’s ability to account for ancestry depends on the PCs used in the adversarial task. It is possible that other ancestry data are still included in the model and used in classification. Including more PCs as labels in adversarial tasks may further reduce the models’ reliance on ancestry information, minimizing the potential confounding effect of population stratification. On the other hand, our focus on minimizing ancestry information in the models may come at the cost of some predictive power. It is possible that some of the genetic risk features learned by the models in our study may be strengthened or weakened by the presence of gene-gene or gene-environment interactions present specifically in certain ancestry groups. Further study of ancestry-variant genetic risk will further our understanding and modeling of disorders like T2D. In addition, while the comparable classification performance between withheld UK Biobank and WTCCC data sets suggests model generalizability, the limited overlap between significant feature importance results suggest that different features led to the similar performance and since most of the individuals in these data sets are of European ancestry, generalization to other ancestries is unknown. The most generalizable modeling strategy would likely be to train a single model using multiple data sets. This could lead to more generalizable classification models and feature importance results.

In summary, we have described CNN/NN architectures that combine genomic context-informed genotype data, and within model ancestry detection/adjustment. Our results indicate that this may be a useful direction for improving our ability to classify complex genetic disorders and detect SNPs that are significantly predictive of disease. While classification performance remains too low for clinical utility and earlier detection of T2D risk, incremental improvements such as those reported here may get to the point of clinical utility in the future.