Introduction

Rapid and accurate autofocusing is an important issue in imaging technologies1,2. There has been increasing research on passive autofocusing techniques (i.e., techniques that do not require any distance measurement by laser range-finders or similar sensors) in recent years. These techniques can be classified into the following categories: traditional methods using image information for autofocusing, such as contrast-based autofocusing and phase autofocusing3,4,5,6 or evaluating advanced local differential focus measures7 and the use of artificial intelligence approaches, such as the deep learning autofocusing techniques8,9,10. However, the AI-based methods require a large number of image sequences, being computationally intensive, and being applicable only to specific scenes11,12. Conventional imaging techniques rely on surface array detectors; however, surface array detectors are expensive and sometimes unresponsive in special wavelength bands such as infrared and terahertz.

Single-pixel imaging (SPI) is a novel imaging technique13, which was invented in connection with compressed sensing. In SPI, optical information is modulated by a spatial-optical modulator and projected onto a single-point photosensitive detector. SPI originally appeared in connection with compressive sensing, where a complete image of the target is constructed using an algorithm by varying the modulation patterns of the spatial-optical modulator and obtaining measurements. Here we employ SPI in an original way for a real-time evaluation of a focusing criterion.

The typical advantages of SPI over conventional imaging techniques14 are as follows. First, SPI has high sensitivity. Conventional imaging techniques typically use an array of pixels to capture an image, in which each pixel is responsible for recording the intensity of light at a specific location. However, SPI takes a different approach and captures image information by measuring the total light intensity in the entire scene. This global measurement approach makes SPI highly sensitive and capable of capturing extremely faint light signals15. Second, SPI responds over a wide spectral range. Different wavelengths of light have different properties and information; therefore, the ability to acquire images over a wide spectral range is critical for many applications. SPI uses a single-point detector with a much wider response spectrum, making it valuable for important applications in bands such as infrared and terahertz16. Since SPI actually performs a spatial integration of the incoming light, it is very robust to noise.

The use of non-imaging methods to achieve fast focusing is of great value for many systems, such as conventional surface arrays and new SPI. Recently, Shaoting Qi et al. studied dual-modulation image-free active self-focusing and its application to Fourier SPI17. However, this technique requires the addition of auxiliary grating devices, which increases the complexity of the imaging systems. Zilin Deng et al. proposed an autofocus technique that employs Fourier coefficients as a criterion18. Ten Fourier coefficients are acquired at each position and combined as a criterion for autofocus; the number of detections required at each position is 30 when using a three-step phase-shift method. However, universal rules for selecting quantitative spectral values for a large number of rich images are lacking.

In this paper, we aim at a development of a novel autofocusing technique that should work in real time, should be robust to noise in image data, should be implemented directly in the camera hardware and should not require any additional range measurement. To meet all these requirements, we propose to use focusing criterion which is based on image moments. To achieve the desired speed, we propose a real-time technique for moment calculation by means of SPI.

We provide a detailed theoretical analysis of the universal autofocusing judgment rules. The moment values of the target image at different positions of the imaging lens are obtained by direct detection, and the central moments are used as a criterion to search for the position of the imaging lens with the smallest central moment to achieve autofocusing. In comparison with traditional image processing autofocusing methods, our method is a non-imaging autofocusing method with extremely fast data acquisition, transmission, and processing. It manifests higher autofocusing speed with only three detection intensity values at different positions18 and does not require additional devices, such as gratings17. Moreover, our method can be applied to diverse real-world images.

Methods

If the image is not perfectly focused, it appears blurred, which means its high frequencies are suppressed. If the scene is flat, the blurred image \(g(x,y)\) can be modeled as a convolution of a focused image f(x,y) and a point spread function h(x,y)19; the convolution symbol is denoted by *, where (x,y) are the coordinates of the two-dimensional (2D) image

$$g(x,y)=(f\ast h)(x,y).$$
(1)

In case of images of 3D scenes, the convolution model holds only locally and/or approximately.

Common assumptions are the positivity of the image

$${\int }_{\!\!\!\!\!-\infty }^{\infty }{\int }_{\!\!\!\!\!-\infty }^{\infty }f(x,y)dxdy \, > \, 0$$
(2)

and overall conservation of energy in the imaging system

$${\int }_{\!\!\!\!\!-\infty }^{\infty }{\int }_{\!\!\!\!\!-\infty }^{\infty }h(x,y)dxdy=1.$$
(3)

In case of out-of-focus blur, h(x,y) is a constant function inside a polygon which has the same shape as the aperture of the camera. If the aperture is fully open, h(x,y) is a circle (see Fig. 1). For a detailed explanation of out-of-focus blur see20, Chapter 6.

Fig. 1: Examples of real point spread functions (PSF’s) that cause out-of-focus image blur.
figure 1

Circular PSF of a fully open aperture (left) and polygonal PSF’s of partially open aperture. The shape is given by diaphragm blades. The images of the PSF’s were obtained as photos of a single bright point far from the focus distance.

Full size image

Now we explain how image moments are changed under wrong focus. Geometric moment of order (p + q) of image f is defined as

$${m}_{pq}^{(f)}={\int }_{\!\!\!\!\!-\infty }^{\infty }{\int }_{\!\!\!\!\!-\infty }^{\infty }{x}^{p}{y}^{q}f(x,y)dxdy.$$
(4)

Since geometric moments are not shift-invariant, we work with central moments upq(f) that are independent on the position of the object in the field of view of the camera

$${u}_{pq}^{(f)}={\int }_{\!\!\!\!\!-\infty }^{\infty }{\int }_{\!\!\!\!\!-\infty }^{\infty }{(x-{x}_{c})}^{p}{(y-{y}_{c})}^{q} \, f(x,y)dxdy,$$
(5)

where (xc, yc) are the coordinates of the centroid of f(x,y)

$${{x}}_{{c}}{=}\frac{{{m}}_{{10}}}{{{m}}_{{00}}}{,} \, {{y}}_{{c}}{=}\frac{{{m}}_{{01}}}{{{m}}_{{00}}}.$$
(6)

The moments of the blurred image g(x,y) can be expressed in terms of moments of the original image f(x,y) and the point spread function h(x,y) as follows21:

$${m}_{pq}^{(g)}={\sum}_{i=0}^{p}{\sum}_{j=0}^{q}\left(\begin{array}{c}p\\ i\end{array}\right)\left(\begin{array}{c}q\\ j\end{array}\right){m}_{ij}^{(h)}{m}_{p-i,q-j}^{(f)}$$
(7)
$${u}_{pq}^{(g)}={\sum}_{i=0}^{p}{\sum}_{j=0}^{q}\left(\begin{array}{c}p\\ i\end{array}\right)\left(\begin{array}{c}q\\ j\end{array}\right){u}_{ij}^{(h)}{u}_{p-i,q-j}^{(f)}.$$
(8)

To derive a moment-based focus measure, we employ the second-order moments. First-order moments do not carry enough information about the focus and higher-order moments do not bring any advantage over the second order. So, from (8) we obtain

$${M}_{1}={u}_{20}^{(g)}={u}_{00}^{(h)}{u}_{20}^{(f)}+2{u}_{10}^{(h)}{u}_{10}^{(f)}+{u}_{20}^{(h)}{u}_{00}^{(f)}$$
(9)
$${M}_{2}={u}_{02}^{(g)}={u}_{00}^{(h)}{u}_{02}^{(f)}+2{u}_{01}^{(h)}{u}_{01}^{(f)}+{u}_{02}^{(h)}{u}_{00}^{(f)}.$$
(10)

Since the imaging system is assumed to be energy-preserving, we have u(h)00 = 1. Because u10 = u01 = 0 for arbitrary function, Eqs. (9) and (10) obtain the form

$${M}_{1}={u}_{20}^{(g)}={u}_{20}^{(f)}+{u}_{20}^{(h)}{u}_{00}^{(f)},$$
(11)
$${M}_{2}={u}_{02}^{(g)}={u}_{02}^{(f)}+{u}_{02}^{(h)}{u}_{00}^{(f)}.$$
(12)

The moments u20(h) and u02(h) are in fact variances of the PSF in x and y direction, respectively. The variance σ of the PSF indicates the degree of spatial dispersion of light energy; a smaller variance implies a more concentrated distribution of the PSF, leading to sharper images, whereas a larger variance corresponds to a more dispersed PSF distribution and thus, blurrier images22. The larger blur, the higher these moments. In the optimal focus position we have u20(h) = u02(h) = 0 and both M1 and M2 reach their minimum (note that the other moments in Eqs. (11) and (12) are always positive and independent on the focus setting).

Therefore, M1 and M2 can be used to measure the degree of image blurring whatever the particular PSF is. Taking M1 + M2 as the criterion is even more convenient choice—this quantity measures the blur in both directions and is invariant to image rotation. To calculate the central moments, we use the relationship between the center of mass and the geometric moments. The central moments of the blurred image g(x,y) can be expressed as

$${M}_{1}={u}_{20}^{(g)}={m}_{20}^{(g)}{-}_{{m}_{00}^{(g)}}^{{m}_{10}^{{(g)}^{2}}},$$
(13)
$${M}_{2}={{u}}_{02}^{(g)}={m}_{02}^{(g)}-\frac{{m}_{01}^{{g}^{2}}}{{m}_{00}^{(g)}}.$$
(14)

Hence, only an algorithm for calculating geometric moments is sufficient to evaluate our focus measure.

Traditional moment calculation from the definition replaces the integral in Eq. (4) by a sum over all image pixels. This is expensive as it requires O(N2) operations for an N × N image. To reduce this complexity to O(1), we take the advantage of SPI and optical modulation unit called digital micromirror device (DMD). We spatially modulate the image by a polynomial, which is equivalent to multiplication. Then the entire modulated image is captured by a single-pixel detector, which is equivalent to integration of the modulated light over the field of view. The obtained scalar value is the image moment, which corresponds to the polynomial used for modulation. By changing the pattern on DMD, we can calculate any set of moments in real time.

To describe this process formally, we multiply the scene information using a series of modulation patterns Bn(x, y), and use a single-pixel detector to record the total amount of light In reflected or transmitted from the scene, where n denotes the index of the modulation pattern

$${I}_{n}={\int }_{\!\!\!\!\!-\infty }^{\infty }{\int }_{\!\!\!\!\!-\infty }^{\infty }f(x,y){B}_{n}(x,y)dxdy.$$
(15)

If

$${B}_{n}(x,y)={x}^{p}{y}^{q}$$
(16)

Then obviously In = mpq.

Using the detected value as the geometric moments, fast acquisition and calculation of the central moments can be achieved. Being a non-imaging method, the proposed method does not require image acquisition of the target and requires only a small amount of computation and data, which enables fast and accurate autofocusing. Compared to existing methods17,18, this method does not require additional hardware devices, and the modulation sampling intensity values are lower with higher efficiency. At the same time, the integration of the light into a single value ensures the robustness to noise. The generated modulation patterns are shown in Fig. 2. When the scene information is modulated using B1, B2, B3, B4, and B5, the detected intensity values correspond to geometric moments m00, m10, m20, m01, and m02 of the scene, respectively. Notice, to enhance the clarity of the modulation pattern boundaries in the plotting, a black border has been added at each boundary of the modulation modes for better visibility.

Fig. 2: The modulation patterns for geometric moment calculation.
figure 2

B1, B2, B3, B4, and B5 are used to obtain m00, m10, m20, m01, and m02 values. (Note that the image coordinates use a Cartesian coordinate system with the origin at the lower left corner.)

Full size image

Results

Simulations results

In the first series of experiments, we used computer simulations only. No actual DMD and SPI were used. The aim of these experiments is to demonstrate that M1, M2, and M1 + M2 can actually measure the level of blur in images and to identify slight differences between them. We performed this study using 256 × 256 pixel binary and grayscale images, as shown in Fig. 3. The images were convolved with different types of point spread functions to simulate various out-of-focus blur types. The absolute difference in distance between the imaging lens at different positions and the reference focused position corresponds to the degree of blurring. Thus, we can simulate the entire image focusing process, from defocus to focus and back to defocus, by changing the position of the imaging lens.

Fig. 3: Images for simulating experiments.
figure 3

Binary images img1 and img2 and gray-level images img3 and img4 used for the simulation experiments.

Full size image

Through theoretical analysis, it is observed that M1 represents the image variance in the horizontal direction, M2 represents the variance in the vertical direction, and M1 + M2 includes variances in both horizontal and vertical directions. Using Eqs. (13) and (14), we obtained the central moments M1 and M2 of the simulated images with different defocus levels. To normalize them, both image central moments M1 and M2 were divided by the central moments of the original focused image.

Gaussian point spread function

For the first set of simulation experiments, the commonly used isotropic 2D truncated Gaussian function was chosen as the point spread function23

$${h}({x}{,}{y})=\frac{1}{2\pi {\sigma }^{2}}exp -\frac{1}{2}\left(\frac{{x}^{2}}{{\sigma }^{2}}+\frac{{y}^{2}}{{\sigma }^{2}}\right)$$
(17)

The sequence of blurred images with different blur size σ (σ = 0.5–5, intervals of 0.5) is shown in Fig. 4.

Fig. 4: Defocused images of objects with different levels of blurring.
figure 4

a–d A sequence of blurred images of img1, img2, img3, and img4, respectively. As σ increases, the images become more blurred.

Full size image

The central moments M1 and M2 of the images in Fig. 3 were calculated using Eqs. (13) and (14), respectively. The parameter σ in Fig. 5 corresponds to the position z of the imaging lens set. For the focused image, the imaging lens position is z = 0. Ten different values of σ were considered. When z > 0, σ = z/2, simulating back defocus; when z < 0, σ = −z/2, simulating front defocus. The value of σ represents the degree of blurring in the defocused image. The larger the σ value, the greater the blurring, while the smaller the σ value, the lesser the blurring. The vertical coordinates in Fig. 5 show the normalized central moments M1 and M2 of the simulated images at different degrees of defocus divided by the central moments of the focused images. Thus, when the imaging lens is in the focus position, the central moments M1 and M2 of the focused image are equal to 1.

Fig. 5: The variation of central moments during the process of isotropic blurring of the images.
figure 5

Relationship between central moments (M1, M2, and M1 + M2) and variance (σ) of the 2D Gaussian point spread function for img1 (a), img2 (b), img3 (c), and img4 (d).

Full size image

The central moments M1 and M2 vary with variance σ, and the results are shown in Fig. 5. The magnitudes of the central moments of the image progressively decrease as the images approach proper focus (z = 0). For isotropic images, like img1, when the PSF has equal variance σ in both the x and y directions, the resulting blurred image’s M1 and M2 moments are identical. For anisotropic images, such as img2, img3, and img4, despite having a PSF with equal variance σ in x and y directions, the M1 and M2 moments of their blurred versions are distinct. However, both approach their minima at the focal point (z = 0). In this case, any of the three moments (M1, M2 or (M1 + M2)/2) can be used as a focus criterion.

For the next set of simulation experiments, considering the possibility of different variations in the point spread function along the x and y axes, we employ an elliptic 2D Gaussian function

$${h}({x}{,}{y}){=}\frac{{1}}{{2}{\pi }{{\sigma }}_{{x}}{{\sigma }}_{{y}}}exp {-}\frac{{1}}{{2}}\left(\frac{{{x}}^{{2}}}{{{\sigma }}_{{x}}^{{2}}}{+}\frac{{{Y}}^{{2}}}{{{\sigma }}_{{y}}^{{2}}}\right)$$
(18)

was chosen as the point spread function to simulate anisotropic optical systems. The sequence of blurred images with different variances σx and σy (σx = 0.5–5, intervals of 0.5; σy = 1–10, intervals of 1) is shown in Fig. 6.

Fig. 6: Defocused images of objects with different levels of blurring.
figure 6

a–d A sequence of blurred images of img1, img2, img3, and img4, respectively. σx and σy are the variance of the 2D Gaussian point spread function in the horizontal and vertical directions, respectively. As σx and σy increases, the images become more blurred.

Full size image

Table 1 provides a detailed description of the relationship between the position z of the imaging lens system and the variance of the Gaussian function. The first row of Table 1 shows the position z of the imaging lens system, while the second row displays the variations in the isotropic Gaussian function variance σ. The third and fourth rows show the variations of the variances σx and σy, respectively.

Table 1 Relationship between focus position x and Gaussian function variance
Full size table

We calculated the moments M1 and M2 of the image using Eqs. (13) and (14), respectively. The parameter σ in Fig. 7 corresponds to the position z of the imaging lens. When z > 0, we set σx = z/2, σy = z, simulating back defocus; when z < 0, σ = −z/2, σy = −z, that simulates front defocus. The vertical coordinates in Fig. 7 are the central moments of the blurred images and are normalized by dividing by the central moment of the original focused image. Due to the variance of the elliptical 2D Gaussian function differs in the x and y directions (that is, σx ≠ σy), for isotropic images such as img1, the central moments M1 and M2 of the image will also be different.

Fig. 7: The variation of central moments during the process of anisotropic blurring of the images.
figure 7

Relationship between central moments (M1, M2 and M1 + M2) and variance (σx and σy) of the elliptic 2D Gaussian point spread function for img1 (a), img2 (b), img3 (c), and img4 (d).

Full size image

According to the results in Figs. 5 and 7, it can be observed that regardless of whether the point spread function is an isotropic Gaussian function or an anisotropic Gaussian function, the central moments of the image effectively reflect the degree of image blurring. The central moment values serve as a reliable criterion for determining focus in both of these cases.

Performance analysis

In this section, we delve into the impact of noise on the accuracy of autofocusing and meticulously evaluate the robustness and reliability of the proposed autofocusing criterion when confronted with typical noise disturbances. To comprehensively understand the potential implications of noise on the focus determination mechanism, we simulate the introduction of prevalent noise types found in imaging systems onto test images: Gaussian noise. This analytical step aims to reveal the performance of the method under complex real-world conditions, ensuring that the proposed approach is not only effective under ideal circumstances but also remains sturdy when faced with practical challenges.

Let g(x,y) represent the noise-free blurry image, and n(x,y) denote the additive noise. The resulting noisy blurry image, g’(x,y), is then given by

$$g{'}(x,y)=g(x,y)+n(x,y)$$
(19)

The moments M’ of the noisy image can be expressed as

$${M}^{\prime }={{u}}_{pq}^{(g^{\prime})}={{{u}}}_{{pq}}^{(g)}+{{{u}}}_{pq}^{(n)}={M}+{{M}}_{n}$$
(20)

Where M is the moment of the image, and Mn is the moment of the noise.

Suppose the additive noise follows a Gaussian distribution with mean 0 and variance Var(N), For zero-mean noise, assuming the noise function is n(x,y), then E[n(x,y)] = 0, and thus we have:

$$E[{M}_{n}]={\int }_{\!\!\!\!\!-\infty }^{\infty }{\int }_{\!\!\!\!\!-\infty }^{\infty }E[{x}^{p}{y}^{q}n(x,y)] \, dxdy=0$$
(21)

This means that the contribution of the noise to the expected value of image moments is zero, E[M’] = E[M]. Zero-mean noise, due to its property of having a zero expectation value, is averaged out during the calculation of image moments, making its effect on them mild, thus preserving the stability of image moments. For specific instances of noise appearance, the expected value of the moments may be non-zero but still very low. This is because particular forms of noise might introduce some offset, causing the expected value of the moments to deviate slightly from zero. Nevertheless, such deviations are usually very small and can be negligible for most practical applications. The central moment values of a noisy image primarily depend on the central moment values of the original image. Therefore, during the blurring process, changes in the central moments are still predominantly influenced by the point spread function.

Next, we analyze the characteristics of central moment variations in blurred images under noisy conditions using the four images depicted in Fig. 3. To simulate blur, we convolve the images with isotropic two-dimensional Gaussian point spread functions of varying variances(σ = 0.5–5, intervals of 0.5), followed by the addition of Gaussian noise with a mean of 0 and a variance of 0.01, as illustrated in Fig. 8. After noise addition, the signal-to-noise ratios (SNRs) for Images 1 through 4 are measured to be 20.02 dB, 10.73 dB, 15.07 dB, 14.01 dB, respectively.

Fig. 8: Noisy defocused images of objects with different levels of blurring.
figure 8

a–d A sequence of Gaussian noise blurred images of img1, img2, img3, and img4, respectively. As σ increases, the images become more blurred.

Full size image

Similarly, we used Eqs. (13) and (14) to calculate the central moments M1 and M2 for images with varying degrees of blur, including the presence of noise, as depicted in Fig. 9. It is evident that all three focus measures perfectly pinpoint the focus, demonstrating the robustness of the method despite the introduced noise.

Fig. 9: The variation of central moments during the isotropic blurring process of the noisy images.
figure 9

Relationship between central moments (M1, M2, and M1 + M2) and variance (σ) of the 2D Gaussian point spread function for img1 (a), img2 (b), img3 (c), and img4 (d), under Gaussian noise conditions.

Full size image

Taking the analysis a step further, we added Gaussian noise at varying variance to the images and computed the changes in the central moments of the images with added noise. Specifically, for img1, we applied Gaussian noise with variance of 0.01, 0.02, 0.05, and 0.1. The outcomes of this process are illustrated in Fig. 10 below. Images subjected to these noise variance exhibited respective signal-to-noise ratios (SNRs) of 20.02 dB, 17.01 dB, 13.18 dB, and 10.23 dB. Likewise, the effects of different noise variance on the central moments of blurred images are showcased in Fig. 11. From these results, it becomes evident that even at an SNR as low as 10 dB, using central moments as a metric for determining focus remains robust and effective.

Fig. 10: Noise images for simulating experiments.
figure 10

Img1 with Gaussian noise of different variance, where the noise variance for a, b, c, and d are 0.01, 0.02, 0.05, and 0.1, respectively.

Full size image
Fig. 11: The variation of central moments during the isotropic blurring process of noisy image1.
figure 11

The relationship between the central moments of img1 with Gaussian noise of different variance and the variance (σ) of a 2D Gaussian point spread function, where the noise variance for a, b, c, and d are 0.01, 0.02, 0.05, and 0.1, respectively.

Full size image

Our simulation conclusions reveal that under conditions of varying noise variance, a proportional relationship exists between the degree of image blur and its central moments. Therefore, it is possible to perform autofocus by searching for the minimum value of one of the three examined focus measures, thereby affirming the feasibility and robustness of utilizing central moments as a metric for assessing and optimizing image focus in a wide range of scenarios and challenges.

Generally, it is recommended to use preferably M1 + M2, because this criterion is rotation invariant and isotropic. For our constructed optical verification system, the point spread function is symmetric along the horizontal and vertical directions on the optical axis. Therefore, the central moment M1 can be taken as the standard parameter for obtaining the position of the focal point. In this case, three modulation modes (B1, B2, and B3) are used to obtain the values of geometric moments (m00, m10, and m20), and then the central moment M1 is calculated. Leaving out M2 speeds-up the process without sacrificing the accuracy of the focus point detection.

Real experiments results

Experimental hardware design

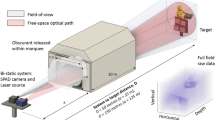
To verify the proposed autofocusing technique in practice, we designed an experimental hardware system (see Fig. 12). A light source is used to illuminate the object. The light passes through the lens and reaches a digital micromirror device (DMD).

Fig. 12: The experimental hardware for testing the proposed autofocus technique.
figure 12

The light illuminates the object, passes through the lens, is modulated on the Digital Micromirror Device (DMD) and continues to the single-pixel detector. The experiment is monitored by a mobile phone.

Full size image

DMD displays a 2D modulation pattern generated by a computer. In our case, low-order polynomials are used to modulate the image (see Fig. 1). The patterns are loaded onto the DMD using the spatial dithering method24. The modulated optical signal is captured by a single-pixel detector. The SPI value, which is in fact an optically calculated image geometric moment, is passed to a computer to calculate central moments and to evaluate the focus measure. This process is iterated over a certain range of the lens positions and the position providing the optimal focus is determined as the minimum of the criterion function.

A light-emitting diode (LED) (M530L4-C1, Thorlabs) with a maximum power of 200 mW, wavelength of 530 nm, and bandwidth of 35 nm was used as the light source. A combined lens set was used as the imaging lens set and was placed on a motorized displacement stage (Zolix TSA100-B) with a total travel distance of 100 mm. For the same traveling distance, four experiments with different focusing speed were conducted to verify the effectiveness of the method proposed in this paper by controlling the moving speed of the motorized displacement stage. The moving speed was 10, 15, 20, and 30 mm s−1, respectively. The total distance traveled by the imaging lens was 60 mm. Focusing was performed by gradually moving closer to and then further away from the focal point. The light modulator (DMD) was a Texas Instruments Discovery V7000 with 1024 × 768 micromirrors (the effective usage area of DMD is the middle 768 × 768 micromirrors).The modulated light from the DMD was reflected using a silver-plated mirror, the reflected light was collected using a convex lens with a focal length of 31.5 mm, and the modulated light signal was captured by a single-pixel detector (PDA100A2 Thorlabs). The detector output signals were sampled and acquired using a high-speed digitizer (ADLINK PCI-9816H).

Experimental results

Autofocusing experiments were conducted using the system described above. Two objects were manufactured of a metal plate with hollow patterns, as shown in Fig. 13. During the experiment, the imaging lens moved horizontally at a constant speed to change the image of the object on the DMD. The modulation time of the three patterns modulated by the DMD was set to 1000 µs, and the sampling rate of the acquisition card was 100 kHz. Equation (13) was used to calculate the central moment of the object at different imaging lens positions.

Fig. 13: Objects used for the experiments.
figure 13

a The letters “USTC” and b part of the USAF1951 resolution plate.

Full size image

When the imaging lens moves to different positions within the range, the change of the central moment of the object “USTC” is shown in Fig. 14. Figure 14a–d shows the results for focusing speeds of 10, 15, 20, and 30 mm s−1, respectively. The central moment was calculated using the detections under pattern modulation of modes B1, B2, and B3 at different focusing positions (the patterns were pre-computed and stored off-line). The blue curves are the calculated data for the central moment. The horizontal axis represents distance in millimeters, and the central moment is plotted along the vertical axis. To eliminate the impact of noise, fluctuations in the detector signals, and other factors, the calculated central moment data curves were fitted using the curve fitting method. This process ensured a smooth data curve, shown in orange. As shown in Fig. 14, the four experiments initially approached the focal point and then moved away. As the lens moved, the imaging pattern transitioned from blurry to clear and back to blurry. The orange smooth-fitting curves in Fig. 14a–d show that the central moment of the objects in all four experiments reached its minimum at the focal point (z = 30 mm). Because of the time interval between the signal acquisition by the acquisition card and the start of lens movement, the central moment curve initially exhibits a period of flatness. From Fig. 14a–d, it can be observed that the central moment is minimum at the same position (z ≈ 29.4 mm) for each of the four focusing speeds, indicating that the corresponding optical system has the same focal point.

Fig. 14: Experimental results for the USTC object.
figure 14

a–d The results under moving speeds of 10, 15, 20, and 30 mm s−1, respectively. i–vii are the photographed images using a Xiaomi 13 mobile phone when the imaging lens moved at the positions of 0, 10, 20, 30, 40, 50, 60 mm, respectively. e–g The Hadamard single-pixel reconstructions of the object 10 mm left of the focal point, at the focal point of the central moment minimum, and 10 mm to the right of the focal point, respectively (see Supplementary Movie 1 for more details).

Full size image

The image of the object on the DMD during the 10 mm s−1 speed experiment was for illustration captured using a Xiaomi 13 mobile phone, and the results are shown in the images indicated by the black dashed arrows in Fig. 14a. The seven images in Fig. 14(i–vii) are images of the objects captured when the imaging lens moved approximately to positions 0, 10, 20, 30, 40, 50, and 60 mm, respectively. In the supplement (see “Supplementary Movie 1”), some distortion can be observed in the images due to the shooting angle of the mobile phone. The angle between the mobile phone lens and the DMD target surface is ~45°.

In addition to video, taking by the mobile phone, we performed another test that enables visual assessment. In addition to polynomial modulation, which was used for moment calculation, we applied modulation by Hadamard basis functions.

Then the SPI values can be used for image reconstruction. This process is known as the Hadamard single-pixel imaging and was originally employed in compressed sensing. We employed the differential Hadamard single-pixel imaging technique and utilized 32,768 Hadamard patterns to reconstruct the image on a 128 × 128 pixel grid (note that for a complete reconstruction, this technique requires two times more SPI values than the number of reconstructed pixels)25,26,27,28,29.

The reconstructions are shown in Fig. 14e–g. Figure 14f shows the image at the focused position, whereas Fig. 14e, g show the imaging results at 10 mm to the left of the approximate focus position (green dots on the curves in Fig. 14b–d) and 10 mm to the right (yellow dots on the curves in Fig. 14b–d), respectively. The object image appears the sharpest at the calculated focal point, which supports the results measured by the mobile and illustrates the effectiveness of the proposed method.

Figure 15 shows the results of an identical experiment conducted on the resolution plate shown in Fig. 13b. The blue curves in Fig. 15a–d represent the original central moment data of the object obtained by the imaging lens at various positions using the detections under pattern modulation of modes B1, B2, and B3 at different focusing positions. The orange curves show the results of fitting the original blue data curves to achieve a smoothed representation. The black dashed arrows pointing to i–vii in Fig. 15a are the images of the object captured with a Xiaomi 13 mobile phone when the imaging lens moved about 0, 10, 20, 30, 40, 50, and 60 mm, respectively. In the supplemental document (see “Supplementary Movie 2”), some distortion can be observed in the images due to the shooting angle of the mobile phone.

Fig. 15: Experimental results for the USAF1951 resolution plate.
figure 15

a–d The results under moving speeds of 10, 15, 20, and 30 mm s−1, respectively. i–vii are the photographed images using a Xiaomi 13 mobile phone when the imaging lens moved at the positions of 0, 10, 20, 30, 40, 50, 60 mm, respectively. e–g The Hadamard single-pixel reconstructions of the object 10 mm left of the focal point, at the focal point of the central moment minimum, and 10 mm to the right of the focal point, respectively(see Supplementary Movie 2 for more details).

Full size image

The central moment values of the object in all four experiments shown in Fig. 15a–d varied from large to small and then to large, and the image reached the focal point when the central moment value was the smallest. Regardless of the focusing speed, the minimum value of the central moment was reached at the same position (z ≈ 29.35 mm).

The Hadamard single-pixel reconstruction was used again to visualize the results (see Fig. 15e–g).

It is worth noting that the proposed technique actually works in real time. The modulation frequency of the DMD was up to 22.2 kHz, and each calculation required three modulation modes. Therefore, the achievable frequency for obtaining the focus parameters is 7.4 kHz. In other words, calculation of focus parameters, including signal modulation and single-pixel detection, requires negligible time comparing to the time of traveling of the lens from one distance to another.

Conclusion

In this study, a moment-detection fast autofocusing technique was proposed, and the effectiveness of the method was verified through theoretical and experimental analysis. The main advantages of the proposed technique are as follows: First, it assesses image sharpness and focus quality in real time using a non-imaging hardware-implemented method and achieves accurate focusing results. Unlike local differential focus criteria, the moment-based measure is integral and hence robust to noise. Even in the presence of noise and with a low signal-to-noise ratio, the method still performs well. On the other hand, there exist a limitation of our method which is implied by the global nature of the moments. To be precise, our focus measure requires objects on a black background along the image borders. If this is not the case, we face so-called boundary effect, which means that the moment values of the blurred image are influenced by the objects laying outside the visual field. Fortunately, if the blur is small comparing to the image size, the boundary effect does not violate the performance of the method significantly. The single-pixel moment-detection fast autofocusing technology reduces the cost and complexity. Comparing to active techniques, our method does not require any distance measurement using a rangefinder or a similar device and our method does not need any timing circuits. In comparison with traditional image processing-based autofocusing techniques, where the entire image is captured in each focus position and the focus measure is calculated numerically, our technology uses one light detection unit to measure the light intensity. Both approaches of course require scanning along the optical axis, so they need to move the lens. This simplified structure renders the technology more practically and conveniently for various applications. Furthermore, our technique utilizes a single-pixel detector, which performs well even under low-light conditions. It has advantages in acquiring optical signals within specific wavelength bands, such as the infrared and terahertz ranges. Moreover, this single-pixel moment detection fast autofocusing method requires only three single-pixel detection values at each focus position, which results in less computational data and faster focusing. In summary, the proposed single-pixel moment-detection fast autofocusing technique provides an innovative solution for achieving fast and accurate autofocusing. This technique has significant advantages in the field of autofocusing, including high speed, accurate focusing, low cost, and low complexity, making it ideal for application in various imaging and projection fields.