Introduction

Lithium-ion battery packs (LIBPs) play a crucial role in electrified transportation systems. The cost of LIBPs has a substantial impact on the manufacturing expenses of electric vehicles (EVs), typically representing 25% of the total EV production cost1, and 75% of the powertrain cost2. LIBPs can experience a range of faults and failures over time, and many of these issues are challenging to detect directly through sensor measurements. Failure to detect and identify these faults can lead to accelerated battery degradation and, in the worst case, trigger a battery fire or explosion3, ultimately leading to increased replacement or warranty costs4. One of the main functions of a battery management system (BMS) should be capable of is detecting and identifying these faults early enough to avoid severe consequences and potential thermal runaway5.

Various fault types can occur in LIBPs, potentially leading to severe consequences including thermal runaway. Common faults include internal and external short circuits, contactor failures, blown fuses, cooling system malfunctions, and sensor reading errors, etc. Internal short circuits are a primary cause of thermal runaway6, often triggered by mechanical abuse, dendritic growth, or internal flaws that lead to direct contact between the positive and negative electrodes within the battery7. External short circuit refers to the direct connection between the positive and negative terminals outside the battery. It can arise from multiple causes, such as deformation or crushing of the battery case, seal failures that permit dust or moisture infiltration, shorted sampling harnesses, or degraded high-voltage insulation8. Several studies have addressed internal9,10,11 and external12,13 short circuit fault detection by analyzing anomalies in the BMS measurements of current and voltage signals. LIBPs typically incorporate hundreds of sensors to ensure safe and efficient operation, including voltage, current, temperature, position and gas sensors14. However, the likelihood of faults occurring in any sensor increases with the number of sensors. As the BMS essential functions rely on the accuracy of the collected measurements from the sensors, neglecting any of the sensor reading faults could lead to incorrectly reporting data to the driver and several safety hazards. Advanced anomaly detection BMS algorithms15,16 are essential to enable a reduction in sensor count, ultimately lowering sensor replacement costs and BMS system failure.

Battery fault detection methods can be generally grouped into threshold-based method and model-based method14,17. Threshold-based methods detect faults mostly by measured cell or pack voltage anomalies18,19,20,21. The measured cell and pack voltages demonstrate a correlation with several electrical faults14; however, voltage is less sensitive to the temperature of the cell and may not be sufficient to detect thermal faults where the temperature change is quite minor. There are various thermal faults that can occur in the LIBPs without causing immediate temperature rise or voltage variation, including cooling pump failure, partial or complete coolant flow blockage in a pack or module, loss of coolant pump control (resulting in too little or not enough coolant flow), and temperature sensor measurement error. Detecting these thermal faults from voltage anomalies is challenging, yet they can lead to battery cells operating in unusual conditions, potentially accelerating battery degradation and posing safety hazards. Model-based method detects faults by monitoring the error between sensor measurement and model estimation. A few studies have developed LIBP thermal fault detection systems based on measured temperature signals, which detects higher than normal heat generation by the battery22 and detects the possibility of thermal runaway occurring23. However, such thermal faults are relatively easy to detect, as they result in a significant temperature rise. Consequently, these methods may be insufficient for distinguishing more nuanced faults, such as partially blocked coolant channels, which are investigated in this paper.

Typically, an accurate thermal model serves as the key to a thermal fault detection algorithm’s success in reliably identifying thermal anomalies. Battery temperature estimation models can be mainly catheterized into four types24, namely electrochemical impedance based25, full-order thermal model26, reduced-order lumped parameter model27, and data-driven model28. Electrochemical impedance-based method generally relies on the temperature dependency of battery impedance obtained from electrochemical impedance spectroscopy (EIS) tests25,29. Therefore, it needs a specially designed excitation generator for onboard impedance measurement, which would inevitably increase the hardware cost and complexity. The full-order thermal model utilizes partial differential equations (PDEs) to represent the thermal behavior of battery cells30. While it offers high-fidelity insights into the internal thermal distribution of the battery, solving these PDEs in real-time is impractical due to the limited computational power available in onboard BMS systems. To address the computational challenges of full-order models, reduced-order lumped parameter (LP) models31,32,33,34 have been developed by incorporating reasonable assumptions and applying model order reduction techniques. In LP models, simple circuit components such as the current source, capacitors, and resistors are used to mimic heat generation, heat accumulation, and heat transfer. However, it is challenging for LP models to effectively monitor thermal states of a battery pack due to limited temperature sensors in a battery system. Also, LP models often require specialized tests conducted in a laboratory environment. Consequently, the performance of physical models for real-life operation, especially when considering battery degradation, can be sub-optimal.

Data-driven thermal models, particularly neural networks (NNs), have been utilized in several studies to estimate battery core and surface temperature28,35,36,37,38. NNs can be trained from both laboratory test data and real-life operation data. The laboratory data helps establish a foundational understanding, while the real-life data ensures that the NN can adapt to the dynamics and sometimes unpredictable conditions it may face in deployment. Nevertheless, data-driven models lack physical meaning, making their performance sensitive to data faults and outliers. This feature poses challenges to the robustness of data-driven thermal models. Additionally, machine learning models are prone to overfitting to specific training datasets, which can result in poor generalization and suboptimal performance under new or varying operating conditions. To overcome these limitations, combining data-driven algorithms with existing thermal models offers a promising approach39, enhancing robustness and reliability compared to purely data-driven methods. Machine learning models offer adaptability to new and dynamic conditions but lack interpretability and generalizability. Conversely, physics-based models ensure robustness, explainability, and applicability across different chemistries and sizes. By integrating the two, the proposed model achieves adaptability while maintaining reliability and accuracy, making it suitable for diverse applications and fault detection in battery systems. However, integrating physics-based and data-driven models for temperature estimation remains in its early stages24, particularly for the more complex pack-level applications.

This work proposes a model-based method for detecting and identifying thermal faults in a battery pack before any protection limits are reached. The key contributions are as follows: 1) Temperature Estimation Model. A highly accurate temperature estimation model, which integrates a physics-based thermal model and a feedforward neural network (FNN) is built. This model achieves a root mean square error of 0.39 °C and a maximum error of 1 °C for US06 discharge and 6C charge profiles at 15 °C. 2) Thermal Fault Detection and Identification Method. A battery thermal fault detection and identification method is proposed. This method compares measured temperatures with estimated temperatures to identify and classify fault types accordingly. To experimentally validate the concept, the algorithm is applied to a 72-cell air-cooled battery pack with one temperature sensor per cell. It only requires measurements from eight of the 72 temperature sensors for effective fault detection. Faults were applied to the pack during electric vehicle drive cycles, and the algorithm was able to detect and identify each fault type within about 45 min, well before any temperature limits were reached.

As the EV space expands, with a clear trajectory towards software centered vehicles, our proposed method strives to offer early fault insights to drivers, fleet managers, and original equipment manufacturers before faults escalate to severe levels. These insights are crucial for all stakeholders to implement corrective measures promptly and avert catastrophic battery failures. The primary goal of our approach is not only to mitigate safety concerns associated with driving electric vehicles but also to curtail the operational costs of running these vehicles, thereby reducing the overall cost of ownership. Notably, our method stands out as it doesn’t necessitate the installation of additional components, sensors, or parts. The fault detection method was rigorously tested and validated under real-life drive cycles, high C-rate charging conditions, and diverse fault scenarios using an actual battery pack. The pack validation featured a temperature sensor ratio of one per nine series-connected cells, reflecting typical production designs, thereby demonstrating the method’s practical reliability and robustness.

Results and Discussion

Validation of integrated physics and deep neural network based temperature estimation model

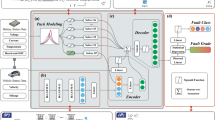
A highly accurate battery pack temperature estimation model composed of a physical-based thermal model integrated with a machine learning-based model, as illustrated in Fig. 1, is the first main contribution of this work. The model receives inputs including the state of charge (SOC) of each individual cell, the battery pack current, and the temperature at the air inlet. It then processes these measurements to output an estimated temperature for each cell.

Fig. 1: Overview of the proposed LP + FNN integrated battery pack thermal model.
figure 1

a Integrated LP + FNN thermal model. b Lumped parameter pack thermal model. It estimates the temperature of individual cells by accounting for thermal conduction through bus bars and convective heat transfer from airflow between cells. c Lumped parameter cell thermal model. It is used in b to simulate each individual cell’s thermal behavior within a pack LP thermal model. d Correlation coefficients between measured cell temperature rise and other measured or estimated values. Parameters with high correlation scores are selected as inputs to the FNN model.

Full size image

In this work, the fan speed was fixed, ensuring that inlet wind speed and pressure remained approximately constant throughout the experiments. As a result, the inlet air temperature is the only variable that mainly impacted the thermal behavior of the system. Additionally, parameters such as wind speed and pressure are typically not measured in air-cooled battery packs and therefore would not be available as inputs for a thermal model designed for practical implementation in a BMS. This consideration ensures the model remains both accurate and practical for real-world applications.

The estimated temperature assumes proper operation of the pack (i.e., no faults), and the difference between measured and estimated temperature is therefore used in the fault detection process. The physical-based model consists of a LP thermal model, shown in Fig. 1b, which is developed using the thermal parameters of each component in the pack, including cells, tabs, and airflow. This model is coupled with an electrical equivalent circuit model (ECM) to calculate the cell loss and to estimate the temperature of each battery cell. The machine learning model employs a FNN to create an improved estimate of cell temperatures. To determine the inputs for the FNN, a Spearman’s rank correlation analysis is performed on a range of measurement and estimation values which could be used as inputs, and the results are illustrated in Fig. 1d. The analysis results show a strong correlation between the measured cell temperature rise and the temperature rise estimated by the LP thermal model, \(\Delta {\hat{T}}_{LP}\). Furthermore, low-pass filters are applied to the current and voltage measurements since they can effectively add memory information by taking the average of measurements over the last many time steps40. According to the correlation analysis, pack voltage and its filtered values have no correlation with measured temperature rise as expected, since battery loss is not a function of voltage on its own. In contrast, pack current measurements, especially filtered current with 1 mHz frequency low-pass Butterworth filter, have a strong correlation with measured temperature rise due to cell loss being current dependent. The values which are most highly correlated with temperature were selected as FNN inputs, including cell temperature rise estimated with the LP thermal model (\(\Delta {\hat{T}}_{LP}\)), current with a 1 mHz (If) corner frequency filter, air inlet temperature (Ta), and the cell SOC.

To prove the benefits of the proposed integrated thermal model, three LIBP temperature estimation models were compared, including a physics-based LP model on its own, a FNN model on its own, and a model which integrates the LP and FNN (LP+FNN) models together. The models were tested using standard vehicle drive cycles and different C-rate charges, which were not included in the model characterization or training data sets. The test data include the UDDS, LA92, HWFET, and US06 drive cycles and charge profiles ranging from 4 C to 10 C rates at ambient temperatures of 15 °C and 25 °C. These drive cycles range from city and less aggressive to urban and aggressive driving conditions.

Figure 2b presents the estimated versus measured temperature for cell#1 for a US06 discharge and 6 C-rate charge profile applied at 15 °C (test profile illustrated in Fig. 2(a)), which is one of the highest temperature rise cases. Measured temperature steps in increments of 1 °C, which is the resolution of the pack temperature sensing unit. The FNN model by itself struggled to estimate the cell temperature, and has a high root mean square error (RMSE) and maximum error of of 2.6 °C and around 5 °C respectively. The LP model has better accuracy than the FNN model, with an RMSE of 1.4 °C and a maximum error of around 2 °C. In contrast, the LP+FNN model achieved a significantly improved accuracy compared to both LP and FNN models on their own, with just 0.39 °C RMSE and 1 °C maximum error at 15 °C for US06 discharge and 6C charge profiles.

Fig. 2: Temperature estimation accuracy comparison between LP, FNN, and LP+FNN models.
figure 2

a, b Performance comparison for the test profile with US06 discharge and 6C charge profiles at 15 °C on cell#1. a, The US06 discharge and 6C charge profile. b Temperature estimation accuracy comparison on cell#1. c Temperature estimation RMS errors for all testing profiles on 8 cells. The average RMSE for LP, FNN, and LP+FNN models are 1.30 °C, 1.84 °C, and 0.45 °C, respectively.

Full size image

In Fig. 2c, the error of each temperature estimation model is presented for eight different testing profiles. The plot shows the average error between the model and measurements for each of the 72 temperature sensors installed in the 72-cell battery pack. The average RMSE ranges from 0.8 to 1.7 °C, 0.9 to 3.4 °C and 0.3 to 0.6 °C for the LP, FNN and LP+FNN models, respectively. The LP+FNN model is shown to accurately estimate the surface temperature of the cells over a range of thermal conditions with an RMS error about 1/3 to 1/4 of the LP and FNN models. This shows that either model on it own is not sufficient to provide the highly accurate estimate of temperature which is necessary for the temperature anomaly driven model proposed in this paper. These results underscore the efficacy of FNN+LP models in modeling cell thermal behavior by integrating information from both physical thermal parameters and machine learning training derived from experimental data. This highly accurate temperature estimation model forms the basis of the fault detection algorithm proposed in the subsequent section.

Fault detection algorithm validation

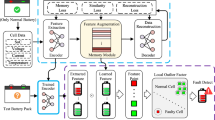
Figure 3 illustrates the function of the proposed fault detection and identification method. It works by comparing the measured and the modeled battery pack temperatures and then identifying faults according to temperature residual error calculation and evaluation. To emulate real-world scenarios where there are relatively few temperature measurements across the pack, only eight temperature sensors were utilized in the fault detection algorithm. The algorithm first calculates the residual error between the measured and LP+FNN modeled temperature for each of the eight measurement points. The residual probability value gi is then calculated based on a mathematical formulation of the residual error. If gi exceeds any of the threshold boundaries, a fault is detected and the fault is identified based on the eight error flag values. For example, if all error flags are high, this indicates a failure of the coolant pump, while if just two adjacent flags are high it indicates the cooling manifold of individual battery module is blocked. This robust fault detection approach is the second main contribution of the paper, and is described in detail in the Methods section and Supplementary Fig. 1. As summarized in Table 1, the fault detection algorithm is capable of identify several different cases - e.g., no/Low flow, high flow, module blockage, and sensor failure - all of which are validated by introducing the specific fault to the physical battery pack.

Fig. 3
figure 3

Overview of the proposed fault detection and identification method.

Full size image
Table 1 Summary of fault-free and faulty tests performed on air-cooled pack
Full size table

In Fig. 4a, the fault detection algorithm was validated on a prolonged driving scenario, composed of a US06 drive cycle discharge, 6 C-rate charge, UDDS discharge, 4 C-rate charge, LA92 discharge, and 8 C-rate charge, all at 15 °C. The charge and discharge rates were very high because the pack tested has a high power capability, making it suitable for a plug-in hybrid with a very short all electric range for example. At the beginning of the profile, during the US06 cycle, the system was fault-free. Then, after eight minutes, the fan was switched off for 36 minutes throughout two fast charges and an additional drive cycle discharge. Then, the fan was switched on again for an hour and 17 minutes during the UDDS discharge and 4C charge, which is sufficient time for the cells to return to their non-fault status. The fan speed was then increased to 200% of its nominal value at the beginning of the LA92 profile, which lasts for 45 minutes, and was finally returned to its nominal speed.

Fig. 4: Validation of the fault detection method under specific conditions. The cases considered involve Fan Off and Fan Speed 200% faults at a temperature of 15 °C.
figure 4

a Cells' measurements and fan status. The test cycles include US06 discharge and 6C charge, UDDS discharge and 4C charge, LA92 discharge and 8C charge. b temperature residuals and fault flags status. 16 minutes After fan turns off, 8 high fault flags appear. 9 minutes after fan speeds up from 100% to 200%, 8 low fault flags appear.

Full size image

Figure 4b shows measured and estimated battery pack temperatures, and the corresponding residuals (e) and the accumulated log of the commutative probability of the residual (g) values. Furthermore, fault flags and identified fault types are recorded according to the analysis of residuals. At the beginning, the system shows no fault flags. Then after 20 minutes, 12 minutes after the fan was turned off, the first two high flags were recorded from cell#24 and cell#60, indicating the temperatures of these cells were higher than expected. A waiting window of 10 min after the first fault flag occurs was used, and all eight sensors showed high flags after this waiting period. According to the logic flowchart illustrated in Supplementary Fig. 1, the fault was then identified as no/low flow by the algorithm, since this fault case is defined as occurring when there are five or more high flags. The proposed algorithm was therefore demonstrated to detect the fan failure fault 22 minutes (10-minute wait window) after fan is turned off and 9 minutes before the battery pack temperature reaches its highest temperature of 45 °C. This feature ensures the user or the battery management system has enough time to react to the fault, preventing the battery pack from being damaged or the vehicle from halting operation unexpectedly. The fault is then cleared sixteen minutes after the fan was turned back on when the residuals all went back within the μ ± 3σ error threshold, as discussed in the Methods section. This shows that it is necessary to record faults in the memory in the BMS so that there is a record of intermittent faults. The fan speed was then increased to 200% and it took nine minutes for the system to record the first low flag from cell#13, indicating that pack temperature was lower than expected. After the ten minute waiting time window, eight low flags were recorded, which was identified based on the flag conditions as pack airflow higher than the setpoint. The residual threshold μ ± 3σ for low flag is tuned to be −2.36 °C which is lower than 2.62 °C of the high flag (absolute value comparison), to reflect the truth that temperature rising is more common and severe than decreasing in our experimental cases and real-life applications.

The algorithm was experimentally validated for a wide array of cases, including air/liquid flow blockage and temperature sensor fault, as is shown in Table 1. In Supplementary Fig. 3, fan speed was halved at the beginning of the UDDS cycle to simulate another more challenging No/Low fault case. After 45 minutes, five high flags were recorded, indicating temperature of these cells is higher than expected and low flow fault was effectively detected and identified. In the case shown in Supplementary Fig. 4, we blocked airflow between cell #24 and cell #36 to simulate module blockage fault. Two high flags were recorded during the 10-minute waiting window on cell #24 and # 36, declaring airflow blockage fault was identified by our model. Additionally, we designed four experimental cases to simulate faults related to failed temperature sensors in Supplementary Fig. 5. These include applying offsets of +1/+2 °C on sensor #49 and scaling adjustments of  −0.05%/ −0.1% on sensor #60. The proposed fault detection algorithm was tuned to successfully detect faults when a +2 °C offset was applied to sensor #49 or a  −0.1% scaling adjustment was applied to sensor #60, while it bypassed cases with a +1 °C offset or  −0.05% scaling adjustment which are within sensor precision tolerance.

Throughout these test cases, which cover 6.5 h of operation and 11 charge discharge cycles, there was not a single false fault flag and the faults were identified in a relatively short time, between 13 and 45 minutes, demonstrating the overall robustness of the approach. The proposed thermal fault detection method accounts for current operational conditions but recognizes the potential impact of battery aging on model accuracy. To address this, incorporating automated ECM parameter updates is suggested as a direction for future work to enhance long-term adaptability and minimize aging-related errors.

Conclusion

Integrating a physical thermal model and a deep neural network-based thermal model is a promising route for creating highly accurate thermal models which are necessary for the proposed lithium-ion battery thermal fault detection algorithm. The developed battery pack thermal model, by combining a LP thermal model with FNN model achieves a very low 0.5 °C RMS error across a range of challenging conditions, compared to 1.3 °C RMSE for an LP model on its own and 1.8 °C RMSE for an FNN model on its own. This high-accuracy thermal model is employed as the cornerstone of the proposed battery pack thermal fault detection algorithm, which applies a unique residual based fault detection approach. The algorithm is experimentally validated using a 72-cell air-cooled battery pack. It requires measurements from only eight of the 72 temperature sensors installed in the pack and successfully detects multiple faults, including sensor faults, cooling fan failure, airflow blockage, and airflow exceeding the setpoint. Each fault type is detected and identified within about 45 min, well before the battery reaches excessive temperatures for the faulty cooling system cases. This quick detection time ensures that the user or battery management system has enough time to react to and repair battery pack faults, thus prolonging battery lifetime and preventing damaged and unexpected loss of operation of the vehicle. While the thermal modeling methodology and algorithm was demonstrated for an air cooled pack, the approach is generalized and could be applied to a pack cooled in any ways (e.g. liquid, refrigerant, heat pipe, etc). The proposed algorithm is key to the creation of future smart battery packs, which would have a wide range of different types of fault detection and identification algorithms, ensuring safe and reliable operation, and predictable repair, throughout the life of the pack.

While the current model demonstrates robust accuracy in controlled laboratory environments, opportunities remain to expand its robustness to field variability and long-term applicability. Future work will focus on integrating real-time aging updates to enhance predictive accuracy over cell aging process. Additionally, the model will be adapted to field conditions with uncontrollable ambient temperatures, ensuring its effectiveness across diverse applications. These advancements aim to improve the model’s adaptability, enabling broader real-world implementation.

Methods

Data generation

Supplementary Fig. 6a shows the air-cooled LIBP utilized in this study, which is a prototype high power pack, suitable for hybrid or plug in hybrid vehicle applications, with a total energy of 1.3 KWh and 266 V nominal operating voltage. This battery pack consists of 72 series-connected SB Limotive cells, as shown in Supplementary Fig. 6b, each with 5.2 Ah nominal capacity and 3.7 V nominal voltage. The detailed specifications of the pack and cell can be found in Table S1. Several characterization and drive cycle tests are conducted on an individual cell and the pack to develop cell and pack thermal model, as illustrated in Tables S2 and S3.

Integrated LP+FNN battery thermal model

In this study, the concept of integrating a physical model and a machine learning model, shown in Fig. 1, is proposed to develop an accurate thermal model of a multi-cell LIBP. A detailed illustration of how the thermal parameters are determined can be found in Supplementary Note 1.

The LP cell model shown in Fig. 1c is adopted to model the thermal behavior of one cell, where the thermal mass and the generated heat are assumed to be concentrated in the center of the cell. The heat is generated at the core and then transferred from the core to the surface of the battery by thermal conduction. The heat generation, absorption and transfer can be described by the heat balance equations described follows:

$${P}_{{{{\rm{loss}}}} = }{P}_{{{{{\rm{loss}}}}}_{{{{\rm{irr}}}}}}+{P}_{{{{{\rm{loss}}}}}_{rev}}$$
(1)
$${P}_{{{{{\rm{loss}}}}}_{{{{\rm{irr}}}}}}={I}^{2}{R}_{{{{\rm{Ch}}}},{{{\rm{Dch}}}}}$$
(2)
$${P}_{{{{{\rm{loss}}}}}_{rev}}=-I{T}_{c}\frac{dOCV}{dt}$$
(3)
$${m}_{b}{C}_{b}\frac{d{T}_{c}}{dt}={P}_{{{{\rm{loss}}}}}+\frac{({T}_{c}-{T}_{s1})}{(2{R}_{c,eq})}+\frac{({T}_{c}-{T}_{s2})}{(2{R}_{c,eq})}$$
(4)

Where RCh,Dch is the electrical equivalent charge or discharge resistance, OCV is the cell open circuit voltage, mb is the weight of the battery, Cb is the specific heat capacity of the cell, Tc is the core temperature and Ts1,Ts2 are the surface temperature of the two largest area sides of the battery cell. Ploss is the total power loss and Rc,eq is the thermal lumped core thermal resistance of the battery.

The core thermal resistance is divided equally between the cell surface into two halves to mimic the left and right sides of a prismatic cell. In lithium-ion batteries, the heat is generated from two sources, including irreversible and reversible heat losses41. The irreversible heat losses represent the ohmic losses of the internal cell components, including electrodes, tabs, and chemical reactions. They can be represented by an equivalent electrical resistance that consumes power in the form of heat as in (2). The reversible power losses represent the change in the entropy of the chemical reactions. The reversible heat losses can be calculated by multiplying the rate of the change of the battery open circuit voltage (OCV), battery current (I) and core temperature (Tc) as in (3). Reversible loss is neglected in the analysis since it usually contributes only a small amount to heat generation and the entropic heating coefficient is difficult to measure without specialized equipment. Finally, the summation of these heat components is assumed to be transferred by conduction to the surface of the cell.

A thermal LP model for an air-cooled multi-cell pack is developed using the thermal parameter of each component in the pack, including cells, tabs, and airflow, as shown in Fig. 1b. The heat is generated at the core of each cell and transferred from the core of the cell to the surface by conduction has thermal properties represented by thermal resistance. Then the heat is assumed to transfer from the two largest area surfaces (Ax) to the air by convection. The other cells’ surfaces (Ay and Az) are isolated with plastic casing and printed circuit boards (PCBs), and the heat transfer through these surfaces is neglected. The heat transfer is initiated by each cell and transferred to the adjacent cell by conduction and to the airflow by convection means which are presented by lumped contact (Rcc) and channels (Rh) thermal resistances. The core and contact thermal lumped resistance is considered fixed for all cells assuming identical cells properties and connections, while the channels thermal resistances vary due to the variation of the airflow between cells. In addition, the heat capacity of the pack components other than the cells is lumped and is represented by two shunt thermal masses (mcCc) added to each cell side. The governing thermal equations describing the heat generation and transfer between every two adjacent cells can be written as follows:

$$\begin{array}{c}{m}_{b}{C}_{b}\frac{d{T}_{c,i}}{dt}={P}_{{{{{\rm{loss}}}}}_{i}}+\frac{{T}_{c,i}-{T}_{s1,i}}{2{R}_{c,eq}}+\frac{{T}_{c,i}-{T}_{s2,i}}{2{R}_{c,eq}}\quad i\in N\\ \,{{{\rm{Side1:}}}}\,\,{m}_{c}{C}_{c}\frac{d{T}_{s1,i}}{dt}+\frac{{T}_{s1,i}-{T}_{c,i}}{2{R}_{c,eq}}+\frac{{T}_{s1,i}-{T}_{a}}{{R}_{h,i}}+\frac{{T}_{s1,i}-{T}_{s2,i-1}}{{R}_{cc}}=0\\ \,{{{\rm{Side2:}}}}\,\,{m}_{c}{C}_{c}\frac{d{T}_{s2,i}}{dt}+\frac{{T}_{s2,i}-{T}_{c,i}}{2{R}_{c,eq}}+\frac{{T}_{s2,i}-{T}_{a}}{{R}_{h,i+1}}+\frac{{T}_{s2,i}-{T}_{s1,i+1}}{{R}_{cc}}=0\end{array}$$
(5)

Where mcCc is pack distributed lumped heat capacity of the pack components other than cells in J/K. Rh,i is the lumped channel resistance of the cell#i. Rcc is the equivalent lumped thermal resistance of the tap connecting two adjacent cells and N is the total number of cells in one module, Ta is the inlet air temperature which is always equal to the chamber ambient temperature.

To build a machine learning model that could mimic the thermal behavior of the battery pack, a FNN machine learning structure is selected as shown in Supplementary Fig. 7. Previous work28 demonstrated that FNN, combined with external filters, achieved lower error and better modeling accuracy than long short-term memory network (LSTM) for temperature estimation tasks. Furthermore, the proposed model is designed to operate on a BMS, where computational efficiency is crucial. Compared to LSTM and other temporal machine learning methods such as gated recurrent units (GRU), FNN offers a lighter and more computationally efficient solution, making it ideal for integration into resource-constrained BMS environments. This balance of accuracy and efficiency makes FNN a suitable choice for the proposed model. Details of FNN development can be found in Supplementary Note 2. Different measured parameters are collected from the pack during operation, including cell voltages, pack voltage, pack current, cell SOC, cell temperature rise, and inlet air temperature. Using all measurements will impact the complexity of the training process, and in some cases, it leads to over-fitting42. Hence, Spearman’s rank correlation is performed between the different inputs and the output, measured temperature rise for one cell43, to obtain the best features to input to the FNN model. The correlation coefficients for each measurement with the cell surface temperature rise are listed in Fig. 1d. Based on the correlation study, the filtered current with 1 mHz (If) corner frequency, the cell SOC, air inlet temperature (Ta), and estimated LP model cells’ temperature rise (\(\Delta {\hat{T}}_{LP}\)) are selected as optimal FNN model inputs. Supplementary Fig. 8 shows the structure of the investigated FNN temperature estimation models for one cell, including inputs, layers, activation functions, and output.

Multi-fault detection and identification method

The proposed method for fault detection relies on assessing the residuals derived from the variance between measured and modeled temperatures. Initially, these residuals are generated and subjected to evaluation, leading to the subsequent determination of fault presence and type. The calculation of the residual (ej) involves the disparity between the sensor readings and model temperatures, as indicated in Equation (6). Notably, a cumulative probability model, as described in refs. 44,45, is employed for fault assessment. Residual data from fault-free test cases are fitted to a normal probability density function, yielding the mean value (μ) and the variance (σ) of the residuals. For the error values which exceed μ ± 3σ, and are therefore well outside the normal distribution of the data, the log of the probability distribution function (PDF) of the error data is summed using equations (7) to (8) to calculate the g function. Employing the logarithm of the probability density function offers the advantage of assigning greater weight to residuals with lower probabilities, i.e., those with large error values lying far beyond the μ ± 3σ residual thresholds. This characteristic, illustrated in Supplementary Fig. 9, facilitates expedited fault detection. Fault determination is accomplished by analyzing the g values in instances where measured temperatures exceed modeled temperatures and vice versa. The g function accumulates each time a residual surpasses three standard deviations threshold (μ ± 3σ), resetting to zero when the residual reverts within these thresholds. A fault flag is then employed when the g value exceeds pre-established limits (J), as defined in Equation (9). This methodology achieves robust and fast detection of faults by only accumulating residual error values which are well outside the distribution of error experienced in a fault free battery pack, and by weighting larger errors more heavily.

The fault identification methodology accumulates the residual and assesses a fault flag value (F) for each sensor, based on the g function. Subsequently, each fault type is determined based on the number and characteristics of the fault flags. A fault is declared when one or more flags are present for a period exceeding ten minutes. The specific fault type is then determined based on the nature and quantity of the accumulated flags.

For instance, if a flag F is logged for a solitary sensor, a sensor failure fault is declared, indicating there is no issue with the cooling system and that a single sensor is reading inaccurately. If two to four consecutive sensors exhibit a high flag F, a module blockage fault is declared in the corresponding sub-module(s), indicating that those specific modules are not being cooled sufficiently. No/low flow fault is declared when more than four high F flags are tallied within the window time, indicating the majority of the battery pack is exhibiting temperatures higher than expected. Discrimination between fan/pump failure and low air/coolant flow faults can be achieved by adjusting a specific threshold level of the g value for each fault. Lastly, if more than one low F flag is recorded, a high flow fault is declared, indicating that the fan/pump is not operating as expected. In this study, only a single fault occurring at once is considered when identifying a fault.

The equations used to determine fault flag status are as follows:

$${e}_{i}(k)={T}_{m,i}(k)-{\hat{T}}_{LP+FNN,i}(k)\quad i\in \{\,{\mbox{cell}}\,\#1,13,24,36,37,49,60,72\}$$
(6)
$${g}_{i}(k)=\left\{\begin{array}{ll}{g}_{i}(k-1)-\log \left(PDF\left({e}_{i}(k)\right)\right)\quad &\,{{{\rm{if}}}}\,\,{e}_{i}(k) \, > \, \mu +3\sigma \\ {g}_{i}(k-1)+\log \left(PDF\left({e}_{i}(k)\right)\right)\quad &\,{{{\rm{if}}}}\,\,{e}_{i}(k) \, < \, \mu -3\sigma \\ 0\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad &\,{{{\rm{if}}}}\,\,\mu -3\sigma \le {e}_{i}(k)\le \mu +3\sigma \end{array}\right.$$
(7)
$$PDF(x)=\frac{1}{\sigma \times \sqrt{2\pi }}{{{{\rm{e}}}}}^{-0.5{(\frac{x-\mu }{\sigma })}^{2}}$$
(8)
$${F}_{i}(k)=\left\{\begin{array}{lcr}\,{{{\rm{High}}}}\,&&\,{{{\rm{if}}}}\,\,{g}_{i}(k) \, > \, {J}_{1}\\ \,{{{\rm{Low}}}}\,&&\,{{{\rm{if}}}}\,\,{g}_{i}(k) \, < \, {J}_{2}\\ \,{{{\rm{Null}}}}\,&&\,{{{\rm{if}}}}\,\,{J}_{1} \, > \, {g}_{i}(k) \, > \, {J}_{2}\end{array}\right.$$
(9)

where F is the fault flag and reads high for cases where measured temperature exceeds modeled temperature and vice versa J1 and J2 are fault thresholds that are tuned using fault free test cases on battery pack such that faults are not declared under normal operating conditions. Details about residual and fault thresholds determination can be found in Supplementary Note 3.

The proposed algorithm is designed to be chemistry- and size-agnostic, ensuring applicability across a variety of battery configurations. Although it was validated using a pack suitable for a plug-in hybrid electric vehicle (PHEV) with a short all-electric range, the method’s reliance on cumulative temperature estimation errors ensures adaptability to larger battery systems. For batteries with slower temperature rise behaviors, such as those in long-range EVs, the fault detection decision time may be slower. However, this can be adjusted by fine-tuning the fault detection thresholds (J1 and J2) using fault-free operational data, enabling faster or slower fault detection based on application requirements. Furthermore, to extend the algorithm’s applicability, we included tests at high C-rates, replicating real-world EV charging conditions. These additional validations confirm the robustness of the algorithm in diverse scenarios, making it suitable for both PHEVs and EVs.