Cascaded guidance, state estimation, and control for depth tracking of underactuated autonomous underwater vehicles

Abstract

Cascaded guidance, state estimation, and control systems have been successfully implemented in autonomous underwater vehicles. However, disordered convergence sequences among subsystems fundamentally induce system oscillations and instabilities. Here, we introduce a temporal-sequencing-convergent cascaded guidance, state estimation, and control system for depth-tracking of underactuated autonomous underwater vehicles. It establishes an ordered convergence architecture: state estimation converges first with a planning window t_d, followed by control execution with a planning time window t_c, and guidance finally converges with a planning time window t_f, adhering to a temporal-sequencing-convergent criterion t_d < t_c < t_f. This architecture, validated through experiments, ensures stable and efficient depth-tracking performance owing to well-ordered convergence of subsystems. Conversely, experiments violating the temporal-sequencing-convergent criterion exhibited prominent oscillatory depth-tracking responses. Our method outperformed selected approaches, achieving a lower average depth-tracking error of 1.32 cm under sudden external disturbances. Notably, even with prominent pitch-tracking errors using a PD controller, our proposed guidance design also showcased remarkable attack-angle compensation capability, thereby maintaining precise depth-tracking performance.

Introduction

Over the past few decades, unmanned marine vehicles have witnessed tremendous development. In particular, autonomous underwater vehicles (AUVs) have emerged as pivotal platforms for diverse marine applications, including scientific investigations, resource exploration, seabed mapping, underwater salvage, emergency rescue, etc¹. Unlike remotely operated vehicles, AUVs do not need to establish a connection to a mother ship via cables, allowing for higher autonomy and a wider range of marine operations. Recent research has increasingly focused on underactuated AUV systems, which feature control inputs insufficient for direct six-degree-of-freedom motion control. For the rudder-propeller-driven underactuated AUVs, a critical challenge lies in the depth-tracking control task, which has become an essential capability for these vehicles.

Generally, the depth-tracking control task for underactuated AUVs can be transformed into a pitch-tracking control problem through kinematic modelling. Specifically, it is essential to establish a constraint that links the depth-tracking error to the desired pitch angle, thereby reducing the AUV’s degrees of freedom. This is also referred to as the guidance law design. It should be noted that the depth-tracking kinematic model involves an attack angle for AUVs, associated with the vehicle’s surge and heave linear velocities, both of which are highly sensitive to the nonlinear dynamics and unknown external disturbances². Therefore, a compensation angle should be introduced in guidance law design to mitigate the attack angle. At the vehicle dynamic layer, the control system’s primary objective is to achieve accurate tracking of the desired pitch angle, as its control performance inevitably affects the depth-tracking accuracy. To ensure the precise execution of the guidance and control systems, state estimation should achieve fast convergence to provide accurate estimated states for these two systems. As illustrated in Fig. 1, state estimation should converge first to offer the depth-tracking guidance and the pitch-tracking control with precise feedback states. The pitch-tracking control system then converges to ensure accurate execution of the desired pitch angle provided by the guidance. Finally, the guidance converges, achieving depth-tracking convergence at the kinematic level via the controlled pitch angle.

Fig. 1: The proposed temporal-sequencing-convergent (TSC) cascaded guidance, state estimation, and control (GSC) system for depth tracking of underactuated autonomous underwater vehicles.

It thereby enables a decoupling control strategy characterized by a temporal convergence sequence: state estimation converges first, pitch-tracking control follows, and depth-tracking guidance finally converges.

As mentioned above, the compensation of attack angle remains a pivotal challenge in guidance law design for underactuated AUVs. In recent decades, line-of-sight (LOS) guidance laws have been widely used in underwater vehicles^3,4,5,6,7,8. Conventional LOS guidance neglects the influence of attack angle, resulting in inadequate path-following performance⁹. To address this issue, numerous improved LOS-based guidance laws have been proposed to compensate for the attack angle. Particularly, these enhancements can be mainly divided into integral LOS (ILOS) and adaptive LOS (ALOS)¹⁰. These LOS-based methods shared a similar structure, expressed as θ_G = ϕ + θ₁ ± tan⁻¹(kz_e + θ₂), where θ_G denotes the desired guided angle, ϕ represents the path rotational angle, k is a predefined gain, z_e is defined as the tracking error, θ₁ is the compensation angle in ALOS methods, and θ₂ is employed for ILOS methods. The proportional LOS guidance law was proved to be uniformly semiglobally exponentially stable when applied to the autopilot control of marine vehicles¹¹. Subsequent studies^{12,13,14,15,16} proposed similar ILOS guidance laws that formulated the compensation angle θ₂ as an integral action of the tracking error z_e. Additionally, Liu^17,18 and Du¹⁹ developed their LOS guidance law designs that incorporated an estimation of the attack angle via nonlinear observers. In the research work of Fossen¹⁰ and Duan²⁰, ALOS guidance laws were similarly structured as an adaptive angle θ₁ formulated as an integral action of the tracking error z_e to compensate for the attack angle. However, these studies exhibit noticeable limitations, including the assumptions of a small or constant attack angle, the time-lag effects induced by the integral action, the complex integral structure with various gains, and the inadequate tracking performance under time-varying external disturbances. These factors collectively exhibit challenges to achieving finite-time tracking convergence via the guidance system.

In addition, the pitch-tracking control performance directly dominates the tracking accuracy of the aforementioned guided pitch angle and has a significant impact on the underactuated AUV’s depth-tracking accuracy. Classical PID controller have been widely used in AUVs due to its simple structure and minimal parameter requirements. However, challenging issues are to resist the unknown external disturbances and the nonlinear hydrodynamics, coupled with multi-degree-of-freedom motions, which lead to inadequate pitch-tracking performance of PID controller. At present, numerous advanced control algorithms have been developed, including sliding mode control (SMC), model predictive control (MPC), fuzzy logic control, and intelligent learning control, which aim to effectively handle the aforementioned challenging control issue. In the research work of Tanakitkorn²¹, Shet²², Qiao²³, and Patre²⁴, various advanced SMC-based control frameworks were developed, including super twisting SMC, adaptive non-singular integral terminal SMC, fast fuzzy terminal SMC, to reduce chattering in control inputs and handle unknown vehicle dynamics and external disturbances. In the research work of Yang⁵, Wei²⁵, Shen²⁶, Rout⁷, and Heshmati²⁷, several MPC-based control system designs were developed, including the distributed Lyapunov-based MPC, nonlinear MPC, and explicit MPC, to take into account practical constraints, computational burden, unknown vehicle dynamics as well as external disturbances. In the research work of Xiang²⁸ and Yu²⁹, robust fuzzy adaptive control systems were proposed to compensate for unknown vehicle dynamics and manage control truncations between unsaturated and saturated inputs. Moreover, intelligent control frameworks, including reinforcement learning and neural networks, were proposed by Guo³⁰, Song³¹, Jiang³², Hadi³³, and Wang⁶ to analyse large datasets for autonomous decision making and enhance control robustness in complex working conditions. However, these control methods often require a large amount of computational resources, training time periods, and data samples, which inevitably limit their learning effectiveness. Although advanced control methods achieve superior performance, greater complexity exists in control structures with increasing control gains. Similarly, these factors present challenges to guarantee control convergence within the prescribed timeframe.

State estimation can be broadly classified into model-based and model-free approaches. Model-based observer design employs detailed disturbance modelling to construct estimation mechanisms that enable comprehensive compensation for multi-source disturbances, including environmental disturbances, model nonlinearities, and system uncertainties^34,35. However, the accuracy of disturbance modelling and the optimization of gain parameters critically affect estimation performance. In contrast, differentiator-based approaches, which are independent of system dynamics and unaffected by environmental disturbances or modelling uncertainties, have found widespread applications in unmanned systems³⁶. However, these methods exhibit prominent chattering in highest-order state estimation, necessitating gain optimization to stabilize them. Furthermore, governing their finite-time convergence properties is still a challenging issue.

In summary, guidance, state estimation, and control subsystems operate at distinct hierarchical layers. When a lower-layer subsystem exhibits a slower convergence rate than an upper-layer subsystem, unstable states of the lower-layer subsystem propagate upward through the upper-layer subsystem. This induces internal oscillations in cascaded systems, which degrade cascaded system stability and amplify nonlinear coupling effects among them. To address these challenging issues, we propose a temporal-sequencing-convergent (TSC) cascaded guidance, state estimation, and control (GSC) system for depth-tracking of underactuated AUVs. It consists of three TSC steps: (1) State estimation achieves prioritized convergence to provide accurate feedback states; (2) Pitch-tracking controller subsequently converges to precisely track the desired pitch angle; and (3) Guidance system ultimately converges to achieve oscillation-suppressing depth-tracking control under stabilized pitch-tracking feedback. Inspired by Newton’s second law, a mechanical system’s acceleration determines the variations of its position and velocity over time, which can be adopted to adjust the system’s convergence rate. This paper aims at constructing three planning-time-based accelerations for the depth-tracking guidance with a planning time window t_f, the differentiation-based state estimation with a planning time window t_d, and pitch-tracking control with a planning time window t_c, based on state constraints among their tracking errors and velocities. Under settings of t_d <t_c <t_f, the TSC depth-tracking control task can be archived when these planning-time-based accelerations are sufficiently executed. Notably, to the best of our knowledge, this control concept of realizing desired acceleration subject to constraints of position and velocity has not been reported in the field of underwater vehicle control. Focusing on the underactuated AUV’s depth-tracking control problem, this paper has the following contributions.

• (1) A TSC cascaded GSC system design has been developed for the underactuated AUV depth-tracking control task, such that: 1) State estimation achieves prioritized convergence to provide accurate state feedback; 2) Pitch-tracking control subsequently converges to precisely track the desired pitch angle; 3) Guidance finally ensures the depth-tracking convergence via the desired pitch-tracking regulation. In this context, the problem of intensified coupling effects and oscillatory responses caused by an unreasonable convergence sequence across the cascaded systems can be fundamentally resolved, thereby enhancing the GSC system stability.

• (2) By setting planning time windows t_d <t_c <t_f for the cascaded state estimation, control, and guidance, respectively, their planning-time-based desired accelerations have been executed, thereby enabling the regulation of their convergence time accordingly. Therefore, the temporal-sequencing convergence of the cascaded GSC system can be achieved.

• (3) The proposed TSC cascaded GSC system design has been validated through experiments and comparative studies with selected approaches, demonstrating its effectiveness and superiority. Notably, even with prominent pitch-tracking errors using a PD controller, the proposed guidance law can rapidly and accurately compensate for the attack angle with precise depth-tracking performance.

• (4) The proposed TSC cascaded GSC architecture exhibits strong generalizability, as it imposes minimal dependency on the precise dynamic model of marine vehicles and can be directly extended to other control tasks (e.g., yaw heading control). This hierarchical convergence strategy with planning time windows t_d <t_c <t_f is not only effective for AUV depth tracking but also adaptable to other autonomous marine vehicles (e.g., unmanned surface vessels or underwater robots), demonstrating broad engineering applicability.

Results

Robotic system overview

The underactuated AUV prototype features a streamlined single-turn torpedo-shaped layout. The main features of this prototype are listed in Table 1. As shown in Fig. 2a, b this streamlined shape is obtained from the Myring linear equation, which describes a minimal hydrodynamic resistance for a specific aspect ratio. The AUV is powered by a classical stern rudder system combined with a main propeller. The tail has four identical rectangular rudders that are symmetrically aligned at 90° to each other and defined by the NACA 0021 profile. The propeller is directly driven by a brushless DC motor that operates at 12 V and has a maximum power output of 180 W. It has a maximum rotational speed of 3800 rpm, a maximum thrust of 70 N, and can operate at a pressure depth of 300 m. The AUV’s main configuration is divided into three compartments: bow section, amidships section, and stern section. The main propeller and rudders are installed in the stern section. The amidships section houses waterproof electronics and sensors, with propulsion in the stern. The bow section is made to cover required payloads. With a total length of 1.03 m and a diameter of 0.14 m, the AUV’s bow, midships, and stern sections have lengths of 0.11 m, 0.74 m, and 0.18 m, respectively.

Fig. 2: The underactuated autonomous underwater vehicle prototype.

a Depth-tracking control experiment in the towing tank. b The components and structure of the prototype. c Hardware architecture and internal device connection diagram.

Table 1 Main Features of AUV Prototype

The design of the AUV’s hardware system is depicted in Fig. 2c. The system integrates onboard modules with a ground station providing remote operation support. The primary components of the ground control station are a communication module and a monitoring computer. The AUV and monitoring computer can communicate by radio, WiFi, or optical cable. The AUV’s onboard control system employs a lumped control approach, wherein all components are connected to a single onboard computer. Due to limitations in peripheral interface resources, various devices, such as the inertial measurement unit, depth gauge, and power meter, are connected via the IIC bus, facilitating a one-master and multiple-slave communication configuration. The angle measurement accuracy of the inertial measurement unit is less than 0.5 degrees, while the measurement accuracy of the depth gauge is less than 2 mm.

Proposed guidance based on a second-order depth-tracking kinematic system

Initially, a second-order depth-tracking kinematic model was developed. The model reveals the first-order derivative of attack angle directly governs its depth-tracking acceleration, thereby serving as the model’s control input. Consequently, the depth-tracking error and its associated velocity were employed as the state constraints to formulate the desired depth-tracking acceleration. The first-order derivative of the estimated attack angle was then formally developed using this desired depth-tracking acceleration. It is worth noting that the desired pitch angle specified by the guidance law was assigned as the control reference to be attained by the control system. As a result, the pitch-tracking control needs to converge before the depth-tracking guidance. Therefore, the convergence time of the guidance system should be longer than that of the control system, specifically t_c <t_f.

To validate the finite-time convergence property of the proposed guidance method, the planning time duration t_c for the pitch-tracking control system was set to 9 s, while the planning time duration t_f for the depth-tracking guidance system was set to 6 s, 10 s, and 13 s for comparison purposes. The experimental depth-tracking guidance results are illustrated in the left subplots of Fig. 3, while the pitch-tracking control results are shown in the right subplots of Fig. 3. A depth reference of 2 meters was employed as a step signal. The depth-tracking guidance results in the first subplot verified that the longer the planning time duration t_f was set, the slower the depth-tracking guided convergence rate became. In the right-hand subplots of Fig. 3, we set a uniform planning time duration t_c = 9 s to ensure synchronous convergence of the desired pitch angle through the pitch-tracking controller. As evidenced by the second subplot, the pitch-tracking errors converged simultaneously at approximately 20 s. This observation not only validates the accuracy of uncertainty estimation shown in the fourth subplot but also demonstrates the effectiveness of finite-time control law presented in the fifth subplot. Thus, it is recommended to set t_c <t_f for smooth depth-tracking performance. Upon reaching the desired depth, the AUV exhibited minimal depth-tracking overshoot, owing to the overshoot-free polynomial planning trajectory design.

Fig. 3: Experimental depth-tracking guidance results and pitch-tracking control results.

The left subplots provide experimental depth-tracking guidance results using our proposed attack-angle update rate. The right subplots present pitch-tracking performance achieved by our control method.

The guidance system’s planning time durations with t_f = 10 s and t_f = 13 s were specifically configured to exceed the controller’s t_c = 9 s, ensuring the depth-tracking guidance converges after the pitch-tracking controller. This design stems from the fact that the depth-tracking guidance convergence depends on precise control performance of the desired pitch-tracking angle. The depth-tracking results in the left subplots of Fig. 3 demonstrate stable convergence after 20 s (first subplot), enabled by accurate attack angle estimation (fourth subplot), thereby validating the effectiveness of the proposed TSC cascaded system design. Under reversed sequencing (t_f = 6 s <t_c = 9 s), the guidance system was forced to converge prior to pitch-tracking stabilization. This disordered convergence introduced dynamic coupling from the pitch-tracking control into the depth-tracking guidance, generating oscillations in depth tracking results. These oscillations were indeed observed in both the depth-tracking response and attack angle estimation under t_f = 6 s <t_c = 9 s.

Proposed controller based on a second-order pitch-tracking dynamic system

A second-order pitch-tracking dynamic model was similarly derived, utilizing the vehicle’s elevator angle as its control input. The pitch-tracking error and its velocity were then employed as state constraints to formulate the desired pitch-tracking acceleration. The control law for the elevator angle was designed to realize this desired pitch-tracking acceleration. As previously mentioned, the control system was expected to realize the desired pitch angle provided by the guidance system. The precision of pitch tracking is of paramount importance, as it directly affects the depth-tracking convergence rate of the guidance system. Therefore, it is recommended that the convergence of the pitch-tracking control task should be faster than that of the depth-tracking guided task of the guidance system.

The pitch-tracking results presented in the right subplots of Fig. 3 were obtained with a fixed planning time duration t_c = 9 s using the pitch-tracking controller. Analysis of the second subplot indicates that the pitch-tracking errors consistently achieved synchronous convergence at approximately 20 s, even when the depth-tracking guidance system employed different planning time durations. The experimental results confirmed the effectiveness of the uncertainty estimation method shown in the fourth subplot and demonstrated the robustness of the finite-time control law presented in the fifth subplot. With the assistance of the proposed pitch-tracking controller, when the pitch-tracking angle converged to the desired pitch angle, the guidance system design acquired accurate pitch angles for depth tracking regulation.

Noise-filtering differentiator based on a second-order integration

At the beginning of each sampling period, a second-order time-based polynomial was fitted to most recent measurement data using the least-squares. The first-order and second-order derivatives of this polynomial served as the nominal states, subject to measurement noises. Similarly, the estimated position error and its velocity constraints were applied to formulate the estimated acceleration with planning time window t_d = 2 s. Note that the measurement noises associated with the nominal states were lumped together into the estimated acceleration. Subsequently, a linear regression filter was implemented to suppress measurement noise from the estimated acceleration. This denoised acceleration was then integrated to update the estimation of position and velocity. It is noteworthy that the differentiator was responsible for providing feedback states to both the guidance system and control system. Therefore, the differentiator’s convergence should be faster than that of the control and guidance systems, ensuring that t_d <t_c <t_f.

In guidance system design, the depth-tracking error and its filtered velocity were provided by a differentiator. In control system design, the pitch-tracking error and its filtered velocity were provided by another differentiator. The experimental results shown in the right subplots of Fig. 4 indicate that the filtered results of both the depth-tracking error and the pitch-tracking error converged to the measured values within a short time duration, thereby verifying its finite-time convergence property.

Fig. 4: State-filtering results from differentiators and experimental comparisons of selected methods.

The left subplots show the state-filtering results of our proposed differentiator. The right subplots display comparative results of selected guidance and control methods. The other three comparative methods consist of proportional-derivative (PD) control with the proposed guidance under external disturbances, terminal sliding mode control (TSMC) with adaptive line-of-sight (ALOS) guidance in the absence of external disturbances, and active disturbance rejection control (ADRC) with ALOS guidance under external disturbances.

Performance comparison of selected methods

Given that the pitch-tracking control accuracy directly affects the depth-tracking guidance performance, comparative experiments were conducted to evaluate different control and guidance methods. These experiments primarily included the proposed GSC cascaded design with external disturbances, PD control with proposed guidance and external disturbances, terminal sliding mode control (TSMC) with ALOS guidance and without external disturbances, and active disturbance rejection control (ADRC) with ALOS guidance and external disturbances. The comparative experimental results are illustrated in the right subplots of Fig. 4. Due to the elevator’s saturation, the proposed control method achieved pitch-tracking convergence within 2 degrees after 16 s. In comparison to the PD, TSMC, and ADRC methods, the proposed control method exhibited a faster convergence rate, higher tracking accuracy, and reduced overshoot. A comprehensive analysis of the experimental data within the final 60 s is presented in Table 2, which includes the following indices: average absolute error (AAE), standard deviation of tracking error (SDE), maximum absolute error (MAE), integral of absolute control input (IACI), and standard deviation of control input (SDCI). Compared to the ALOS guidance, the data listed in Table 2 demonstrate that the proposed guidance system with PD controller and proposed controller exhibited superior performance in the depth-tracking task. It should be noted that although the PD control had an average absolute pitch-tracking error of about 11.42 degrees, the average absolute depth-tracking error was about 2.8 cm. Because the tracking error of pitch angle induced by PD control was promptly estimated and compensated in attack-angle estimation, as shown in the left-second subplot of Fig. 4. Compared to ALOS guidance with TSMC and ADRC control methods, the proposed method outperformed them in the depth-tracking control task with the AAE of 1.3 cm, the SDE of 1.6 cm, and the MAE of 6.1 cm. The reason is that the depth-tracking velocity employed by the proposed guidance enabled more rapid adjustment of attack-angle compensation than that achieved by other methods. Consequently, the comparative experimental results validated the effectiveness of the proposed guidance method.

Table 2 Experimental comparisons of depth-tracking performance among selected methods

Ballast water was selected as an external disturbance during a specified period of the experiment. When the AUV encountered an external disturbance arising from ballast water, its depth-tracking behavior was adversely impacted, resulting in sudden deviations from the depth reference of 2 meters, as shown by the results of ADRC method in the left-first subplot of Fig. 4. Given that variations in depth-tracking error and its velocity were directly affected by prompt execution of the desired acceleration, experimental results of proposed method verified that the execution of desired acceleration facilitated an immediate adjustment of attack angle, thereby enabling the AUV to rapidly counteract the external disturbance on its depth-tracking motion.

Discussion

In this study, we investigated a TSC control framework to design cascaded GSC systems for depth-tracking control of underactuated AUVs. Although previous studies have addressed the feasibility of similar cascaded system designs, the impact of successive convergence properties among the cascaded systems on closed-loop stability has not been thoroughly examined. Drawing inspiration from Newton’s second law, the changes in position and velocity of a system are uniquely determined by its acceleration. Consequently, we found that the prompt control execution to achieve the desired acceleration, constrained by position and velocity, was an effective way to realize temporal-sequencing convergence of the system. This principle underpinned our proposed TSC cascaded GSC system design.

In previous studies, adaptive guidance laws based on the integral action of tracking error have been widely developed. However, achieving finite-time convergence within a specified time duration remains challenging, and issues such as integral time delay and overshoot phenomena persist. To address these issues, we derived a second-order depth-tracking kinematic model that utilized the first-order derivative of attack angle as the model’s control input. Using our proposed finite-time control theory, the update law of estimated attack angle was formulated as a combined expression of both the depth-tracking error and its velocity. Notably, the proposed estimation of the attack angle was an integral action of both the depth-tracking error and its velocity. Compared to the ALOS guidance method, our innovative guidance design accounted for the influence of tracking-error velocity, thereby overcoming oscillatory tracking responses induced by only considering the integration of depth-tracking error in earlier studies. Furthermore, the proposed depth-tracking guidance not only achieved finite-time convergence but also mitigated depth-tracking overshoot. Remarkably, even with prominent pitch-tracking errors from control system, such as the average absolute pitch-tracking error of approximately 11 degrees observed in PD control experiments, our proposed guidance could still promptly and accurately compensate for this pitch-tracking error in the attack-angle estimation. Consequently, a high-precision depth-tracking guided task was accomplished, with an average absolute error of 2.8 cm in the presence of external disturbances.

For state estimation and control systems, early studies have investigated cascaded system designs for various observers and controllers. Considering that guidance, state estimation, and control are cascaded systems, these studies could not well eliminate the coupling effects among them. This challenge not only requires extensive parameter tuning work but also limits the potential implementation in complex working conditions. Based on our proposed finite-time control theory, a differentiator was developed that serves as state estimation, using the tracking error and its velocity constraints to derive the estimated acceleration. The integral action of the estimated acceleration was then utilized to update the estimation of position and velocity, thereby achieving finite-time convergence of the differentiator. In the control system design, the desired pitch-tracking acceleration was derived based on the constraints of pitch-tracking error and its velocity. The estimation of the unknown uncertainty term was updated through the integral action of desired acceleration, facilitating the finite-time convergence of control system. By setting appropriate planning time windows for guidance, state estimation, and control, i.e., t_d <t_c <t_f, we can achieve their successive convergence in time domain while effectively mitigating the cascade coupling effects among them.

The fine-tuning control parameters have been a challenging issue, which often involve numerous control parameters without any physical meanings. This requires repeated adjustments for time-varying operating conditions, thereby limiting practical implementations. In contrast, the proposed finite-time control method categorized control parameters into three types: a mass-like or moment-like gain, a polynomial planning time window, and a dimensionless integral gain of uncertainty term, as shown in elevator’s control law in Eq. (12). These parameters had clear physical meanings, making them easier to be adjusted and more conducive to practical implementation.

Overall, this paper investigated a TSC cascaded GSC system design for underactuated AUVs. The proposed control strategy focused on realization of the desired acceleration provided by a planning polynomial, utilizing error constraints of position and velocity. When reasonable polynomial planning time windows were predefined, i.e., t_d <t_c <t_f, the proposed temporal-sequencing convergence of state estimation, control, and guidance was achieved. Compared to the ALOS guidance, our proposed guidance approach could be used in a cascade system with other control methods, such as PD control, and also had good depth-tracking control performance. This improvement was primarily attributed to an accurate attack-angle compensation for the depth-tracking error in the proposed guidance law design.

The proposed TSC cascaded GSC architecture provides several research topics for future investigation. Firstly, its minimal reliance on precise dynamic models facilitates convenient extension to other types of underactuated marine robotic systems, and even to non-marine dynamic-constrained systems such as unmanned aerial and ground vehicles. Secondly, by implementing the TSC strategy with planning time windows t_d <t_c <t_f, this TSC cascaded GSC methodology can be effectively extended to multi-task control scenarios including the horizontal or three-dimensional tracking control. Furthermore, future research could explore the integration of the TSC cascaded GSC architecture with intelligent control frameworks such as reinforcement learning or neural networks, which would maintain system robustness while further reducing the need for empirical parameter tuning. These research directions would bridge the gap between theoretical convergence properties and practical engineering applications.

Methods

Mathematical modelling of AUV

As shown in Fig. 5a, two coordinate systems, the inertial north-east coordinate system O_I-X_IY_IZ_I and the body-fixed coordinate system O_B-X_BY_BZ_B, are adopted to facilitate the mathematical modelling of the AUV. The body-fixed origin O_B is defined at the gravity centre of the AUV. Generally, the kinematic and kinetic model of an AUV can be expressed as³⁷:

$$\dot{{{\boldsymbol{\eta }}}}={{\bf{J}}}({{\boldsymbol{\eta }}}){{\bf{v}}}$$

(1)

$${{\bf{M}}}\dot{{{\bf{v}}}}+{{\bf{C}}}({{\bf{v}}}){{\bf{v}}}+{{\bf{D}}}({{\bf{v}}}){{\bf{v}}}+{{\bf{g}}}({{\boldsymbol{\eta }}})={{\boldsymbol{\tau }}}+{{\bf{d}}}$$

(2)

where ${{\boldsymbol{\eta }}}={[x,\,y,\,z,\,\phi ,\,\theta ,\,\psi ]}^{{{\rm{T}}}}$ represents the general position in the inertial north-east coordinate system. ${{\bf{v}}}={[u,\,\upsilon ,\,w,\,p,\,q,\,r]}^{{{\rm{T}}}}$ denotes the linear and angular velocity vector in the body-fixed coordinate system.${{\bf{J}}}({{\boldsymbol{\eta }}})\in {\Re }^{6\times 6}$ is the transformation matrix from the inertial frame to the body-fixed frame. ${{\bf{M}}}\in {\Re }^{6\times 6}$ is the mass matrix including the inertial mass of the rigid body and the added mass of hydrodynamics. ${{\bf{C}}}({{\bf{v}}}){{\bf{v}}}\in {\Re }^{6\times 1}$ contains the nonlinear Coriolis and centripetal forces and moments. ${{\bf{D}}}({{\bf{v}}}){{\bf{v}}}\in {\Re }^{6\times 1}$ provides the linear and nonlinear hydrodynamic damping forces and moments. Vector ${{\bf{G}}}({{\boldsymbol{\eta }}})\in {\Re }^{6\times 1}$ gives the restoring forces and moments induced by the vehicle’s gravity and buoyancy. Vector ${{\boldsymbol{\tau }}}\in {\Re }^{6\times 1}$ represents the control forces and moments generated by vehicle actuators. Vector ${{\bf{d}}}\in {\Re }^{6\times 1}$ denotes the forces and moments induced by external disturbances.

Fig. 5: Fundamentals of coordinate systems and line-of-sight guidance for depth tracking.

a Definition of the inertial and body-fixed coordinate systems. b Illustration of line-of-sight depth-tracking guidance.

Depth-tracking problem formulation of AUV

In this paper, we focus on the depth-tracking control problem of an underactuated AUV in the vertical plane, as shown in Fig. 5b, where only the surge, heave, and pitch motions are considered. Hence, the AUV kinematic model for depth-tracking control can be simplified as:

$${\dot{z}}_{e}=-u\,\sin (\theta )+w\,\cos (\theta )=U\,\sin (\alpha -\theta )$$

(3)

$$\dot{\theta }=q$$

(4)

where ${z}_{e}=z-{z}_{d}$ denotes the depth-tracking error. ${z}_{d}$ is the constant desired depth. $U=\sqrt{{u}^{2}+{w}^{2}}$ represents the cruise speed. The attack angle α is defined as $\alpha ={{\rm{atan2}}}(w,\,u)$. It should be noted that this paper will not adopt any rigorous assumptions for the attack angle, such as being small, constant, or at least slowly varying, which were widely used in most existing research work.

Furthermore, this paper will not address surge-speed dynamics, as the forward speed is maintained at a constant value through a constant surge propulsion force. In this context, the heave dynamic model and the pitch dynamic model of an underactuated AUV in the vertical plane can be written as¹⁶:

$$(m-{Z}_{\dot{w}})\dot{w}-({Z}_{\dot{q}}+m{x}_{g})\dot{q}=muq+(W-B)\cos (\theta )+{Z}_{w|w|}w|w|\\ +{Z}_{q|q|}q|q|+{Z}_{uq}uq+{Z}_{uw}uw+{Z}_{d}+{Z}_{uu{\delta }_{s}}{u}^{2}{\delta }_{s}$$

(5)

$$({I}_{yy}-{M}_{\dot{q}})\dot{q}-({M}_{\dot{w}}+m{x}_{g})\dot{w}={z}_{b}B\,\sin (\theta )+{M}_{w|w|}w|w|+{M}_{q|q|}q|q|\\ +{M}_{uq}uq+{M}_{uw}uw+{M}_{d}+{M}_{uu{\delta }_{s}}{u}^{2}{\delta }_{s}$$

(6)

where u is a constant surge velocity powered by the thruster. w and q denote the surge linear velocity and the pitch angular velocity, respectively. θ represents the pitch angle with its negative sign shown in Fig. 5b. W and B denote the vehicle’s gravity and buoyancy force, respectively. ${Z}_{w|w|}$, ${Z}_{q|q|}$, ${Z}_{uq}$, ${Z}_{uw}$, ${M}_{w|w|}$, ${M}_{q|q|}$, ${M}_{uq}$, and ${M}_{uw}$ are the vehicle’s hydrodynamic coefficients in its heave and pitch dynamics. ${Z}_{d}$ and ${M}_{d}$ are the corresponding external disturbance force and moment. ${Z}_{uu{\delta }_{s}}{u}^{2}{\delta }_{s}$ and ${M}_{uu{\delta }_{s}}{u}^{2}{\delta }_{s}$ denote the corresponding control input force and moment.

Depth-tracking control objectives

As shown in Fig. 2c, the depth-tracking control objectives of an underactuated AUV in the vertical plane can be summarized as follows:

• 1) Based on the depth-tracking kinematic model formulated by Eqs. (3) and (4), the guidance system should provide a desired reference of pitch angle. It aims to minimize the depth-tracking overshoot and oscillation, alleviate the integral time-delay effects, and simultaneously improve depth-tracking accuracy.

• 2) Based on the dynamic model formulated by Eq. (6), the pitch-tracking control should produce a control input of the elevator to promptly track the desired pitch angle provided by the guidance law.

Proposed guidance law design

Second-order depth-tracking kinematic model

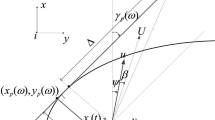
As shown in Fig. 2b, the proposed guided pitch angle can be written as:

$${\theta }_{G}=\arctan ({z}_{e}/L)+\hat{\alpha }$$

(7)

where $\hat{\alpha }$ is an estimation including the attack angle and pitch-tracking error $\theta -{\theta }_{G}$. Parameter L denotes the look-ahead distance. In this paper, we develop a depth-tracking-acceleration-based estimation, which can minimize the depth-tracking overshoot and oscillation, alleviate the integral time-delay effects, as well as improve tracking accuracy.

Inserting Eq. (7) into the depth-tracking kinematic model (3) gives

$${M}_{z}{\dot{z}}_{e}+{N}_{z}{z}_{e}=\,\sin (\hat{\alpha }-\alpha )$$

(8)

where M_z and N_z are formulated as ${M}_{z}=-\frac{\sqrt{({z}_{e}^{2}+{L}^{2})}}{UL} < 0$ and ${N}_{z}=-\frac{\cos (\alpha -\hat{\alpha })}{L} < 0$ with $|\alpha -\hat{\alpha }| < \pi /2$.

To develop the proposed depth-tracking-acceleration-based guidance method, the first-order depth-tracking system (8) should be transformed into a second-order system. In this context, we have

$${M}_{z}{\ddot{z}}_{e}+({N}_{z}+{\dot{M}}_{z}){\dot{z}}_{e}+{\dot{N}}_{z}{z}_{e}=(\dot{\hat{\alpha }}-\dot{\alpha })\cos (\hat{\alpha }-\alpha )$$

(9)

Proposed guidance law design

Inspired by the fact that the depth-tracking acceleration ${\ddot{z}}_{e}$ determines the variations of its position ${z}_{e}$ and velocity ${\dot{z}}_{e}$ over time, a desired acceleration ${\ddot{z}}_{d}$ can be developed using the state constraints of position ${z}_{e}$ and velocity ${\dot{z}}_{e}$. Hereby, a polynomial trajectory z_p(t) = a₀ + a₁t + a₂t² + a₃t³ is designed to satisfy the initial state constraints of${z}_{p}(0)={z}_{e}$ and ${\dot{z}}_{p}(0)={\dot{z}}_{e}$ and the final state constraints of ${z}_{p}({t}_{f})=0$ and ${\dot{z}}_{p}({t}_{f})=0$, for convergence purpose. Hence, the desired depth-tracking acceleration ${\ddot{z}}_{d}$ can be developed as ${\ddot{z}}_{d}={\ddot{z}}_{p}(0)=2{a}_{2}$. The update rate of the attack-angle estimation is formulated as:

$$\dot{\hat{\alpha }}={M}_{z}{\ddot{z}}_{d}=2{M}_{z}{a}_{2}={M}_{z}\left(-\frac{6{z}_{e}}{{t}_{f}^{2}}-\frac{4{\dot{z}}_{e}}{{t}_{f}}\right)$$

(10)

where the polynomial planning duration t_f determines the expected convergence time.

Overall, our proposed guidance design is summarized in Fig. 6. It should be emphasized here that the proposed attack-angle update rate in Eq. (10) outperforms the existing approaches in literature. These advantages are summarized as follows:

• 1) The existing attack-angle estimation approaches in literature only consider the integral action of the depth-tracking error and are unable to effectively handle issues such as overshoot and oscillation caused by time lag. In contrast, our proposed attack-angle update law represents a new methodology that integrates the velocity constraint into the desired acceleration profile, suppressing overshoot and oscillation in depth-tracking performance.

• 2) Existing attack-angle estimation methods rely on fine-tuned control gains without physical interpretability, often limiting their practical applications due to computational burdens or unrealistic system assumptions. Bridging this gap between theoretical research and industrial applicability remains a critical challenge. Our guidance framework addresses this by introducing a physically meaningful control gain, i.e., the polynomial planning duration t_f, which directly governs the convergence timescale of the depth-tracking system.

Fig. 6: Summary and comparative analysis of the proposed temporal-sequencing-convergent (TSC) cascaded guidance, state estimation, and control (GSC) system designs.

Hereby, the predefined planning time windows for desired accelerations are set to t_d = 2 s for the proposed differentiators, t_c = 9 s for the proposed pitch-tracking controller, and t_f = 10 s for the proposed depth-tracking guidance, which satisfies t_d <t_c <t_f to mitigate the coupling effects among them.

Proposed control law design

Second-order pitch-tracking dynamic model

Let ${\theta }_{e}=\theta -{\theta }_{G}$ denote the pitch-tracking error. The pitch-tracking dynamic system in Eq. (6) can be rewritten as:

$${M}_{\theta }{\ddot{\theta }}_{e}+{D}_{\theta }={\delta }_{s}$$

(11)

where D_θ lumps all uncertainties together including the coupling dynamics in heave motion and pitch-tracking hydrodynamics. M_θ is defined as ${M}_{\theta }=({I}_{yy}-{M}_{\dot{q}})/({M}_{uu{\delta }_{s}}{u}^{2}) < 0$ with negative hydrodynamic coefficients ${M}_{\dot{q}}$ and ${M}_{uu{\delta }_{s}}$. Alternatively, substituting the heave-tracking dynamics of Eq. (5) into the pitch-tracking dynamics of Eq. (6) to eliminate the heave acceleration term yields a formulation analogous to Eq. (11).

Proposed control law

Hereby, a similar polynomial trajectory θ_p(t) = b₀ + b₁t + b₂t² + b₃t³ for the pitch-tracking task can be planned to satisfy the initial state constraints of ${\theta }_{p}(0)={\theta }_{e}$ and ${\dot{\theta }}_{p}(0)={\dot{\theta }}_{e}$ as well as the final state constraints of ${\theta }_{p}({t}_{c})=0$ and ${\dot{\theta }}_{p}({t}_{c})=0$, for convergence purpose. In this context, the desired pitch-tracking acceleration ${\ddot{\theta }}_{d}$ can be formulated as ${\ddot{\theta }}_{d}={\ddot{\theta }}_{p}(0)=2{b}_{2}$. The elevator’s control law is then expressed as:

$${\delta }_{s}={M}_{\theta }{\ddot{\theta }}_{d}+{\hat{D}}_{\theta }={M}_{\theta }\left(-\frac{6{\theta }_{e}}{{t}_{c}^{2}}-\frac{4{\dot{\theta }}_{e}}{{t}_{c}}\right)+{\hat{D}}_{\theta }$$

(12)

where t_c denotes the polynomial planning duration, determining the finite-time convergence horizon.

Based on the pitch-tracking dynamic Eq. (6), we can observe that the uncertainty term D_θ causes the actual acceleration to deviate from its desired profile. Therefore, the uncertainty term D_θ can be updated using its desired acceleration profile, expressed as:

$${\dot{\hat{D}}}_{\theta }=\sigma {M}_{\theta }{\ddot{\theta }}_{d}=\sigma {M}_{\theta }\left(-\frac{6{\theta }_{e}}{{t}_{c}^{2}}-\frac{4{\dot{\theta }}_{e}}{{t}_{c}}\right)$$

(13)

where σ is an introduced positive gain.

Proposed second-order noise-filtering differentiator

To carry out the depth-tracking guidance and controller depicted in Fig. 5, our proposed noise-filtering differentiator should provide differential states using measurement data. Several types of differentiators have been investigated in the literature, including the sliding mode differentiator³⁸, the high-order differentiator³⁹, and the high-gain observer⁴⁰. However, these methods typically require fine-tuning and optimizing at least three control gains to accommodate time-varying working conditions. In this section, a similar polynomial planning method, as described in Eq. (10) and Eq. (12), is employed to develop a desired acceleration that is contaminated by sensor measurement noise. After applying noise reduction to the desired acceleration, the noise-filtering differential states can be updated based on the integral action of this noise-filtered acceleration.

Reconstruction of nominal states

The present nominal states $(y,\,\dot{y},\,\ddot{y})$ can be estimated from the measured signal y via a second-order polynomial curve fitting procedure with least-squares optimization. Suppose that there are k pairs of measurement collections (t₁, y₁),…, (t_i, y₂), …, (t_k = 0, y_k = y), where k ≥ 3, Δt = t_i − t_i−1, and t_k = 0 represents the present sampling time instant. To ensure filtering accuracy, the parameter k should be kept below a critical threshold. The present nominal states $(y,\,\dot{y},\,\ddot{y})$ based on least-squares-based curve fitting method are expressed as

$$A=\left[\begin{array}{ccc}1 & 0 & 0\\ 1 & -\Delta t & \Delta {t}^{2}\\ \vdots & \vdots & \vdots \\ 1 & -k\Delta t & {k}^{2}\Delta {t}^{2}\end{array}\right]$$

(14)

$$Y={({A}^{{{\rm{T}}}}A)}^{-1}{A}^{{{\rm{T}}}}{(y,\,{y}_{k-1},\,\ldots \,,\,{y}_{2},\,{y}_{1})}^{{{\rm{T}}}}$$

(15)

$$(y,\,\dot{y},\,\ddot{y})=(Y(1),\,Y(2),\,2Y(3))$$

(16)

Estimated acceleration to be executed

Then a similar polynomial planning trajectory y_p(t) = c₀ + c₁t + c₂t² + c₃t³ can be used to fulfill the initial state constraints of${y}_{p}(0)=\hat{y}-y$ and ${\dot{y}}_{p}(0)=\dot{\hat{y}}-\dot{y}$ as well as the final state constraints of ${y}_{p}({t}_{d})=0$ and ${\dot{y}}_{p}({t}_{d})=0$, for convergence purpose. Therefore, our objective is to ensure the acceleration-tracking error $\ddot{\hat{y}}-\ddot{y}$ precisely follows the desired acceleration profile ${\ddot{y}}_{p}(0)=2{c}_{2}$, and it follows that

$$\ddot{\hat{y}}=\ddot{y}-\frac{6( \, \hat{y}-y)}{{t}_{d}^{2}}-\frac{4( \, \dot{\hat{y}}-\dot{y})}{{t}_{d}}$$

(17)

where t_d denotes the polynomial planning duration, determining the finite-time convergence horizon. An initialization estimation of $( \, \hat{y},\,\dot{\hat{y}})$ can be set to $( \, y,\,0)$. Then an initial acceleration estimation can be calculated by Eq. (17).

Noise-filtering in estimated acceleration

Notably, the estimated acceleration $\ddot{\hat{y}}$ in Eq. (17) contains residual measurement noise originating from the nominal states $(y,\,\dot{y},\,\ddot{y})$ obtained in Eq. (16). We select N pairs of collections $({t}_{k-N+1},\,{\ddot{\hat{y}}}_{k-N+1})$,…, $({t}_{i},\,{\ddot{\hat{y}}}_{i})$, …, $({t}_{k}=0,\,\ddot{\hat{y}})$ computed via Eq. (17). To filter out these measurement noise from the estimated acceleration, we implement a linear regression filter expressed as:

$${\ddot{\hat{y}}}_{f}=\bar{y}-\bar{t}{\sum }_{i=k-N+1}^{k}\frac{\left(N{t}_{i}-{\sum }_{i=k-N+1}^{k}{t}_{i}\right){\ddot{\hat{y}}}_{i}}{N{\sum }_{i=k-N+1}^{k}{t}_{i}^{2}-{\left({\sum }_{i=k-N+1}^{k}{t}_{i}\right)}^{2}}$$

(18)

where ${\ddot{\hat{y}}}_{f}$ is the filtered acceleration, $\bar{y}$ and $\bar{t}$ represent the average of y_i and t_i, respectively.

State update

A second-order Taylor series expansion enables an inverse state-update procedure for the next sampling loop, formulated as:

$$\left[\begin{array}{c}{\hat{y}}_{k+1}\\ {\dot{\hat{y}}}_{k+1}\end{array}\right]=\left[\begin{array}{ccc}1 & \Delta t & \Delta {t}^{2}/2\\ 0 & 1 & \Delta t\end{array}\right]\left[\begin{array}{c}{\hat{y}}_{k}\\ {\dot{\hat{y}}}_{k}\\ {\ddot{\hat{y}}}_{f}\end{array}\right]$$

(19)

Stability analysis

In this section, we analyze the stability of the depth-tracking guidance system and the pitch-tracking control system, demonstrating that their finite-time convergence properties depend on the polynomial planning duration.

Stability analysis of depth-tracking guidance

Assuming that the attack angle varies slowly with $\dot{\alpha }\approx 0$, substitution of the attack-angle update rate derived in Eq. (10) into the second-order depth-tracking kinematic system described by Eq. (9) yields:

$${M}_{z}{\ddot{z}}_{e}+\left({N}_{z}+{\dot{M}}_{z}+\frac{4{M}_{z}\,\cos (\hat{\alpha }-\alpha )}{{t}_{f}}\right){\dot{z}}_{e}+\left({\dot{N}}_{z}+\frac{6{M}_{z}\,\cos (\hat{\alpha }-\alpha )}{{t}_{f}^{2}}\right){z}_{e}=0$$

(20)

Given that ${M}_{z} < 0$, ${N}_{z} < 0$, and $\cos (\hat{\alpha }-\alpha ) > 0$, the above depth-tracking system achieves asymptotic stability when its coefficients satisfy $|{\dot{N}}_{z}| < \frac{6|{M}_{z}|\cos (\hat{\alpha }-\alpha )}{{t}_{f}^{2}}$ and $|{\dot{M}}_{z}|\le |{N}_{z}|$. Considering the expressions of ${M}_{z}$ and ${N}_{z}$ in Eq. (8), we have $|\dot{\hat{\alpha }}| < \frac{6|{M}_{z}|L}{{t}_{f}^{2}|\tan (\alpha -\hat{\alpha })|} < \frac{6L}{U{t}_{f}^{2}}$ and $L > \frac{|{z}_{e}{\dot{z}}_{e}|}{U\,\cos (\alpha -\hat{\alpha })}$ for a constant cruise speed U. Thus, setting only upper and lower bounds for estimation $|\dot{\hat{\alpha }}|$ and look-ahead distance L respectively suffices to ensure the system’s asymptotic stability. Moreover, the system’s convergence rate is governed by the planning time duration t_f. The longer the planning time duration t_f is set, the slower the convergence rate of the depth-tracking system becomes.

Stability analysis of pitch-tracking control

For an AUV moving at constant velocity, ${M}_{\theta }$ remains constant. Differentiating Eq. (11) with respect to time and then substituting the elevator control law Eq. (12) and uncertainty estimation Eq. (13) into the resulting third-order system yields:

$${\theta }_{e}^{(3)}+\frac{4}{{t}_{c}}{\ddot{\theta }}_{e}+\left(\frac{4\sigma }{{t}_{c}}+\frac{6}{{t}_{c}^{2}}\right){\dot{\theta }}_{e}+\frac{6\sigma }{{t}_{c}^{2}}{\theta }_{e}=-\frac{{\dot{D}}_{\theta }}{{M}_{\theta }}$$

(21)

We can observe that when the uncertainty term is slowly varying (i.e., ${\dot{D}}_{\theta }\approx 0$), the system possesses asymptotic stability, with its convergence rate determined by the polynomial planning time t_c. Similarly, longer planning durations t_c lead to slower convergence rates in the pitch-tracking system. For bounded time-varying uncertainty term, the system outputs remain bounded, and the upper bound can be obtained through the following computation. Defining the state vector ${{\bf{X}}}={[{\theta }_{e},\,{\dot{\theta }}_{e},\,{\ddot{\theta }}_{e}]}^{{{\rm{T}}}}$, the above system can be expressed in state-space form as $\dot{{{\bf{X}}}}={{\bf{A}}}{{\bf{X}}}+{{\bf{B}}}F$, where

$${{\bf{A}}}=\left[\begin{array}{ccc}0 & 1 & 0\\ 0 & 0 & 1\\ -\frac{6\sigma }{{t}_{c}^{2}} & -\frac{4\sigma }{{t}_{c}}-\frac{6}{{t}_{c}^{2}} & -\frac{4}{{t}_{c}}\end{array}\right]$$

(22)

$${{\bf{B}}}=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$$

(23)

$$F=-\frac{{\dot{D}}_{\theta }}{{M}_{\theta }}$$

(24)

Consider a quadratic Lyapunov function candidate $V={{{\bf{X}}}}^{{{\rm{T}}}}{{\bf{P}}}{{\bf{X}}}$ with ${{\bf{P}}} > 0$. Its time derivative yields $\dot{V}={{{\bf{X}}}}^{{{\rm{T}}}}({{{\bf{A}}}}^{{{\rm{T}}}}{{\bf{P}}}+{{\bf{P}}}{{\bf{A}}}){{\bf{X}}}+2{{{\bf{X}}}}^{{{\rm{T}}}}{{\bf{P}}}{{\bf{B}}}F$. Given that system matrix A is negative definite, there exists $\lambda > 0$ such that ${{{\bf{X}}}}^{{{\rm{T}}}}({{{\bf{A}}}}^{{{\rm{T}}}}{{\bf{P}}}+{{\bf{P}}}{{\bf{A}}}){{\bf{X}}} < -\lambda {{{\bf{X}}}}^{{{\rm{T}}}}{{\bf{X}}}$. Consequently, we obtain $\dot{V} < -\lambda {{{\bf{X}}}}^{{{\rm{T}}}}{{\bf{X}}}+2{{{\bf{X}}}}^{{{\rm{T}}}}{{\bf{P}}}{{\bf{B}}}F$. Therefore, when $\Vert {{\bf{X}}}\Vert > \frac{2\Vert {{\bf{P}}}{{\bf{B}}}\Vert {|F|}_{\max }}{\lambda }$, the condition $\dot{V} < 0$ holds.