Non-Hermitian Casimir effect of magnons

Abstract

There has been a growing interest in non-Hermitian quantum mechanics. The key concepts of quantum mechanics are quantum fluctuations. Quantum fluctuations of quantum fields confined in a finite-size system induce the zero-point energy shift. This quantum phenomenon, the Casimir effect, is one of the most striking phenomena of quantum mechanics in the sense that there are no classical analogs and has been attracting much attention beyond the hierarchy of energy scales, ranging from elementary particle physics to condensed matter physics, together with photonics. However, the non-Hermitian extension of the Casimir effect and the application to spintronics have not yet been investigated enough, although exploring energy sources and developing energy-efficient nanodevices are its central issues. Here we fill this gap. By developing a magnonic analog of the Casimir effect into non-Hermitian systems, we show that this non-Hermitian Casimir effect of magnons is enhanced as the Gilbert damping constant (i.e., the energy dissipation rate) increases. When the damping constant exceeds a critical value, the non-Hermitian Casimir effect of magnons exhibits an oscillating behavior, including a beating one, as a function of the film thickness and is characterized by the exceptional point. Our result suggests that energy dissipation serves as a key ingredient of Casimir engineering.

Introduction

Recently, non-Hermitian quantum mechanics has been drawing considerable attention¹. The important concepts of quantum mechanics are quantum fluctuations. Quantum fluctuations of quantum fields under spatial boundary conditions realize a zero-point energy shift. This quantum effect which arises from the zero-point energy, the Casimir effect^2,3,4,5, is one of the most striking phenomena of quantum mechanics in the sense that there are no classical analogs. Although the original platform for the Casimir effect^2,3,4,5 is the photon field (See ref. ⁶, as an example, for an oscillating behavior of the Casimir effect of photons as a function of distance between two uncharged plates, where chiral material inserted between the two parallel plates plays a key role.), the concept can be extended to various fields such as scalar, tensor, and spinor fields^{7,8,9,10,11,12,13,14,15}. Thanks to this universal property, the Casimir effects have been investigated in various research areas (As an example, see refs. ^{16,17,18,19,20,21,22} for Casimir effects in magnets and ref. ²³ for a magnonic analog of the thermal Casimir effect in a Hermitian system. For details of the distinction between the thermal Casimir effect and the Casimir effect, refer to Supplemental Material. See also ref. ²⁴ for an analog of the dynamical Casimir effect with magnon excitations in a spinor Bose–Einstein condensate.) beyond the hierarchy of energy scales^{7,8,9,10,11,12,13,14,15}, ranging from elementary particle physics to condensed matter physics, together with photonics. However, the non-Hermitian extension of the Casimir effect and the application to spintronics remain missing ingredients, although exploring energy sources and developing the potential for energy-efficient nanodevices are the central issues of spintronics^{25,26,27,28,29}.

Here we fill this gap. The Casimir effects are characterized by the energy dispersion relation. We therefore incorporate the effect of energy dissipation on spins into the energy dispersion relation of magnons through the Gilbert damping constant³⁰ and thus develop a magnonic analog of the Casimir effect³¹, called the magnonic Casimir effect (see Fig. 1) (In ref. ³¹, we investigated the Casimir effect induced by quantum fields for magnons (i.e., a magnonic analog of the Casimir effect) and referred to it as the magnonic Casimir effect. See ref. ³¹ for details of the magnonic Casimir effect in dissipationless systems.), into non-Hermitian systems. We then show that this non-Hermitian extension of the magnonic Casimir effect, which we call the magnonic non-Hermitian Casimir effect, is enhanced as the Gilbert damping constant increases. When the damping constant exceeds a critical value, the magnonic non-Hermitian Casimir effect exhibits an oscillating behavior as a function of the film thickness and is characterized by the exceptional point³² (EP). We refer to this behavior as the magnonic EP-induced Casimir oscillation. We emphasize that this magnonic EP-induced Casimir oscillation is absent in the dissipationless system of magnons. The magnonic EP-induced Casimir oscillation exhibits a beating behavior in the antiferromagnets (AFMs) where the degeneracy between two kinds of magnons is lifted. Our result suggests that energy dissipation serves as a new handle on Casimir engineering³³ to control and manipulate the Casimir effect of magnons. Thus, we pave the way for magnonic Casimir engineering through the utilization of energy dissipation.

Fig. 1: Schematic of magnonic Casimir effect.

Magnonic Casimir effect arises from quantum vacuum fluctuations of magnon fields.

Results

System

We consider the insulating AFMs of two-sublattice systems in three dimensions described by the Hamiltonian,

$${{{\mathcal{H}}}}=J\mathop{\sum}\limits_{\langle i,j\rangle }{{{{\bf{S}}}}}_{i}\cdot {{{{\bf{S}}}}}_{j}-{K}_{{{{\rm{e}}}}}\mathop{\sum}\limits_{i}{({S}_{i}^{y})}^{2}+{K}_{{{{\rm{h}}}}}\mathop{\sum}\limits_{i}{({S}_{i}^{x})}^{2},$$

(1)

where ${{{{\bf{S}}}}}_{i}=({S}_{i}^{x},{S}_{i}^{y},{S}_{i}^{z})$ is the spin operator at the site i, J > 0 parametrizes the antiferromagnetic exchange interaction between the nearest-neighbor spins 〈i, j〉, K_h > 0 is the hard-axis anisotropy, and K_e > 0 is the easy-axis anisotropy. These are generally K_h/J ≪ 1 and K_e/J ≪ 1. The AFMs have the Néel magnetic order and there exists the zero-point energy^34,35. Throughout this study, we work under the assumption that the Néel phase remains stable in the presence of energy dissipation. Elementary magnetic excitations are two kinds of magnons σ = ±, acoustic mode for σ = + and optical mode for σ = −.

By incorporating the effect of energy dissipation on spins into the energy dispersion relation of magnons through the two-coupled Landau–Lifshitz–Gilbert equation where the value of the Gilbert damping constant α > 0 for each sublattice is identical to each other, we study the low-energy magnon dynamics³⁶ described by the energy dispersion relation ${\epsilon }_{\sigma ,{{{\bf{k}}}},\alpha }\in {\mathbb{C}}$ of Re(ϵ_σ,k,α) ≥ 0 and the wavenumber ${{{\bf{k}}}}=({k}_{x},{k}_{y},{k}_{z})\in {\mathbb{R}}$ (As an example, ref. ³⁷ assumes ${\epsilon }_{\sigma ,{{{\bf{k}}}},\alpha }\in {\mathbb{R}}$ and ${{{\bf{k}}}}\in {\mathbb{C}}$, which describes a spatially-decaying solution³⁸.) in the long wavelength limit as³⁷

$${\epsilon }_{\sigma ,{{{\bf{k}}}},\alpha }=\frac{2S}{1+{\alpha }^{2}}\left(-i\alpha C+\sqrt{{({E}_{\sigma ,{{{\bf{k}}}},\alpha })}^{2}}\right)$$

(2)

and

$${({E}_{\sigma ,{{{\bf{k}}}},\alpha })}^{2}:= {{A}_{\sigma ,\alpha }}^{2}{(ak)}^{2}+{{\delta }_{\sigma }}^{2}-{{{{{\mathcal{D}}}}}_{\sigma }}^{2}{\alpha }^{2},$$

(3)

where k ≔ ∣k∣, the length of a magnetic unit cell is a, the spin moment in a magnetic unit cell is S, and the others are material-dependent parameters which are independent of the wavenumber, $0 \,<\, {A}_{\sigma ,\alpha }\in {\mathbb{R}}$, $0\, < \,{\delta }_{\sigma }\in {\mathbb{R}}$, $0 \,< \,{{{{\mathcal{D}}}}}_{\sigma }\in {\mathbb{R}}$, and $0 \,<\, C\in {\mathbb{R}}$: The parameters are given as³⁷

$${A}_{\sigma ,\alpha }=\sqrt{(1+{\alpha }^{2})\left({J}^{2}+\sigma \frac{{K}_{{{{\rm{h}}}}}}{2}J\right)},$$

(4a)

$${\delta }_{\sigma }=\sqrt{{K}_{{{{\rm{e}}}}}(2J+{K}_{{{{\rm{e}}}}})+{K}_{{{{\rm{h}}}}}(J-\sigma J+{K}_{{{{\rm{e}}}}})},$$

(4b)

$${{{{\mathcal{D}}}}}_{\sigma }=\sqrt{{J}^{2}+\sigma {K}_{{{{\rm{h}}}}}J+\frac{{{K}_{{{{\rm{h}}}}}}^{2}}{4}},$$

(4c)

$$C=J+{K}_{{{{\rm{e}}}}}+\frac{{K}_{{{{\rm{h}}}}}}{2}.$$

(4d)

In the absence of the hard-axis anisotropy K_h = 0, two kinds of magnons σ = ± are in degenerate states, whereas the degeneracy is lifted by K_h > 0. Note that, in general, the effect of dipolar interactions is negligibly small in AFMs, and we neglect it throughout this study.

The Gilbert damping constant α is a dimensionless constant, and the energy dissipation rate increases as the Gilbert damping constant grows. In the dissipationless system³¹, the Gilbert damping constant is zero α = 0. The dissipative system of α > 0 described by Eq. (2) can be regarded as a non-Hermitian system for magnons in the sense that the energy dispersion takes a complex value. Note that the constant term in Eq. (2), −iαC, is independent of the wavenumber and just shifts the purely imaginary part of the magnon energy dispersion ϵ_σ,k,α. For this reason [also see Eq. (10a)], the constant term, −iαC, is not relevant to the magnonic Casimir effect. We then define the magnon energy gap of Eq. (2) as Δ_σ,α ≔ Re(ϵ_σ,k=0,α), i.e.,

$${\Delta }_{\sigma ,\alpha }=\frac{2S}{1+{\alpha }^{2}}\,{{\mbox{Re}}}\,\left(\sqrt{{({E}_{\sigma ,k = 0,\alpha })}^{2}}\right).$$

(5)

Magnonic exceptional point

When the damping constant α is small and ${({E}_{\sigma ,k = 0,\alpha })}^{2}\, > \,0$, E_σ,k=0,α takes a real value and decreases as α increases. This results in

$$\frac{d{\Delta }_{\sigma ,\alpha }}{d\alpha }\, <\, 0.$$

(6)

Thus, the magnon energy gap decreases as the damping constant increases³⁹ [compare the solid line with the dashed one in the left panel of Fig. 2(i)]. When the damping constant is large enough, the magnon energy gap vanishes Δ_σ,α = 0 at $\alpha ={\alpha }_{\sigma }^{{{{\rm{cri}}}}}$,

$${\alpha }_{\sigma }^{{{{\rm{cri}}}}}:= \frac{{\delta }_{\sigma }}{{{{{\mathcal{D}}}}}_{\sigma }},$$

(7)

where there exists the gapless magnon mode which behaves like a relativistic particle with the linear energy dispersion. From the property of Eq. (6), we call (i) $\alpha \le {\alpha }_{\sigma }^{{{{\rm{cri}}}}}$ the gap-melting regime.

Fig. 2: Plots of the magnon energy dispersion ϵ_σ,k,α, the real part of the magnonic Casimir energy Re(E_Cas), and the imaginary part Im(E_Cas) for NiO in (i) the gap-melting regime, (ii) the oscillating regime, and (iii) the beating regime.

Inset: Each magnonic Casimir coefficient ${C}_{{{{\rm{Cas}}}}}^{[b]}$.

When the damping constant exceeds the critical value ${\alpha }_{\sigma }^{{{{\rm{cri}}}}}$, i.e., $\alpha \,> \,{\alpha }_{\sigma }^{{{{\rm{cri}}}}}$, E_σ,k=0,α takes a purely imaginary value as ${({E}_{\sigma ,k = 0,\alpha })}^{2}\, < \,0$. In this regime, the real part of the magnon energy dispersion remains zero Re(ϵ_σ,k,α) = 0 for the region $0\le k\le {k}_{\sigma ,\alpha }^{{{{\rm{cri}}}}}$,

$${k}_{\sigma ,\alpha }^{{{{\rm{cri}}}}}:= \frac{1}{a}\sqrt{\frac{{{{{{\mathcal{D}}}}}_{\sigma }}^{2}{\alpha }^{2}-{{\delta }_{\sigma }}^{2}}{{{A}_{\sigma ,\alpha }}^{2}}},$$

(8)

whereas Re(ϵ_σ,k,α) > 0 for $k \,> \,{k}_{\sigma ,\alpha }^{{{{\rm{cri}}}}}$ [see the highlighted in yellow in the left panel of Fig. 2(ii) and (iii)]. The critical point ${k}_{\sigma ,\alpha }^{{{{\rm{cri}}}}}$ can be regarded as the EP³⁹ for the wavenumber k, and we refer to it as the magnonic EP. As the value of the damping constant becomes larger, that of the EP increases

$$\frac{d{k}_{\sigma ,\alpha }^{{{{\rm{cri}}}}}}{d\alpha }\, > \,0.$$

(9)

At the EP $k={k}_{\sigma ,\alpha }^{{{{\rm{cri}}}}}$, the group velocity v_σ,k,α ≔ Re[∂ϵ_σ,k,α/(∂ℏk)] becomes discontinuous [see the solid lines in the left panel of Fig. 2(ii) and (iii)]. In the vicinity of the EP, the group velocity becomes much larger than usual such as in the gap-melting regime (i) [compare the solid lines in the left panel of Fig. 2(ii) and (iii) with the one of Fig. 2(i)].

Assuming ${\alpha }_{\sigma = +}^{{{{\rm{cri}}}}}\, < \,{\alpha }_{\sigma = -}^{{{{\rm{cri}}}}}$, the non-Hermitian system for magnons described by Eq. (2) of α > 0 can be divided into three regimes (i)-(iii) in terms of the magnonic EPs as follows [see the left panel of Fig. 2(i), (ii), and (iii)]:

• (i) $\alpha \le {\alpha }_{\sigma = +}^{{{{\rm{cri}}}}}\, < \,{\alpha }_{\sigma = -}^{{{{\rm{cri}}}}}$. No magnonic EPs.

• (ii) ${\alpha }_{\sigma = +}^{{{{\rm{cri}}}}} \,< \,\alpha\, < \,{\alpha }_{\sigma = -}^{{{{\rm{cri}}}}}$. One EP, ${k}_{\sigma = +,\alpha }^{{{{\rm{cri}}}}}$.

• (iii) ${\alpha }_{\sigma = +}^{{{{\rm{cri}}}}}\, < \,{\alpha }_{\sigma = -}^{{{{\rm{cri}}}}}\le \alpha$. Two EPs, ${k}_{\sigma = +,\alpha }^{{{{\rm{cri}}}}}$ and ${k}_{\sigma = -,\alpha }^{{{{\rm{cri}}}}}$.

Magnonic Casimir energy

The magnonic analog of the Casimir energy, called the magnonic Casimir energy³¹, is characterized by the energy dispersion relation of magnons. Therefore, by incorporating the effect of energy dissipation on spins into the energy dispersion relation of magnons through the Gilbert damping constant [Eq. (2)], a non-Hermitian extension of the magnonic Casimir effect can be developed. We remark that the Casimir energy induced by quantum fields on the lattice, such as the magnonic Casimir energy³¹, can be defined by using the lattice regularization^{40,41,42,43,44,45,46}. In this study, we focus on thin films confined in the z direction (Fig. 1). In the two-sublattice systems, the wavenumber on the lattice is replaced as ${(a{k}_{j})}^{2}\to 2[1-\cos (a{k}_{j})]$ along the j axis for j = x, y, z. Here by taking into account the Brillouin zone (BZ), we set the boundary condition for the z direction in wavenumber space so that it is discretized as k_z → πn/L_z, i.e., ak_z → πn/N_z, where L_z ≔ aN_z is the film thickness, ${N}_{j}\in {\mathbb{N}}$ is the number of magnetic unit cells along the j axis, and n = 1, 2, . . . , 2N_z. Thus, the magnonic Casimir energy E_Cas³¹ per the number of magnetic unit cells on the surface for N_z is defined as the difference between the zero-point energy ${E}_{0}^{{{{\rm{sum}}}}}$ for the discrete energy ϵ_σ,k,α,n due to discrete k_z [Eq. (10b)] and the one ${E}_{0}^{{{{\rm{int}}}}}$ for the continuous energy ϵ_σ,k,α [Eqs. (10c) and (2)] as follows^{40,41,42,43,44,45,46}:

$${E}_{{{{\rm{Cas}}}}}({N}_{z}):= {E}_{0}^{{{{\rm{sum}}}}}({N}_{z})-{E}_{0}^{{{{\rm{int}}}}}({N}_{z}),$$

(10a)

$${E}_{0}^{{{{\rm{sum}}}}}({N}_{z}):= \mathop{\sum}\limits_{\sigma =\pm }{\int_{{{{\rm{BZ}}}}}}\frac{{d}^{2}(a{k}_{\perp })}{{(2\pi )}^{2}}\left[\frac{1}{2}\left(\frac{1}{2}\mathop{\sum}\limits_{n = 1}^{2{N}_{z}}{\epsilon }_{\sigma ,{{{\bf{k}}}},\alpha ,n}\right)\right],$$

(10b)

$${E}_{0}^{{{{\rm{int}}}}}({N}_{z}):= \mathop{\sum}\limits_{\sigma =\pm }{\int_{{{{\rm{BZ}}}}}}\frac{{d}^{2}(a{k}_{\perp })}{{(2\pi )}^{2}}\left[\frac{1}{2}{N}_{z}{\int_{{{{\rm{BZ}}}}}}\frac{d(a{k}_{z})}{2\pi }{\epsilon }_{\sigma ,{{{\bf{k}}}},\alpha }\right],$$

(10c)

where ${k}_{\perp }:= \sqrt{{{k}_{x}}^{2}+{{k}_{y}}^{2}}$, d²(ak_⊥) = d(ak_x)d(ak_y), the integral is over the first BZ, and the factor 1/2 in Eqs. (10b) and (10c) arises from the zero-point energy of the scalar field.

We remark that³⁶ assuming thin films of N_z ≪ N_x, N_y (Fig. 1), the zero-point energy in the thin film of the thickness N_z is ${E}_{0}^{{{{\rm{sum}}}}}({N}_{z}){N}_{x}{N}_{y}$ and consists of two parts as ${E}_{0}^{{{{\rm{sum}}}}}({N}_{z})={E}_{{{{\rm{Cas}}}}}({N}_{z})+{E}_{0}^{{{{\rm{int}}}}}({N}_{z})$ [Eq. (10a)], where ${E}_{0}^{{{{\rm{int}}}}}({N}_{z})$ exhibits the behavior of ${E}_{0}^{{{{\rm{int}}}}}({N}_{z})\propto {N}_{z}$ [Eq. (10c)]. Then, to see the film thickness dependence of E_Cas(N_z), we introduce the rescaled Casimir energy ${C}_{{{{\rm{Cas}}}}}^{[b]}$ in terms of ${{N}_{z}}^{b}$ for $b\in {\mathbb{R}}$ as

$${C}_{{{{\rm{Cas}}}}}^{[b]}({N}_{z}):= {E}_{{{{\rm{Cas}}}}}\times {{N}_{z}}^{b}$$

(11)

and call ${C}_{{{{\rm{Cas}}}}}^{[b]}$ the magnonic Casimir coefficient in the sense that ${E}_{{{{\rm{Cas}}}}}={C}_{{{{\rm{Cas}}}}}^{[b]}{{N}_{z}}^{-b}$.

Note that the zero-point energy arises from quantum fluctuations and does exist even at zero temperature. The zero-point energy defined at zero temperature does not depend on the Bose-distribution function [Eqs. (10b) and (10c)]. Throughout this work, we focus on zero temperature³⁶.

Magnonic non-Hermitian Casimir effect

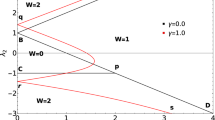
Finally, we investigate the magnonic Casimir effect in the non-Hermitian system α > 0, which we call the magnonic non-Hermitian Casimir effect, for each regime (i)–(iii). As an example, we consider NiO, an insulating AFM. From refs. ^37,47,48, we roughly estimate the model parameter values for NiO as follows [Eq. (2)]: J = 47.1 meV, K_h = 0.039 5 meV, K_e = 0.001 72 meV, S = 1.21, and a = 0.417 nm. NiO is a biaxial AFM of K_h > 0 and K_e > 0. Due to the hard-axis anisotropy K_h > 0, the degeneracy between two kinds of magnons σ = ± is lifted in NiO. These parameters provide ${\alpha }_{\sigma = +}^{{{{\rm{cri}}}}} \sim 0.008\,54 \,< \,{\alpha }_{\sigma = -}^{{{{\rm{cri}}}}} \sim 0.041\,9$. Figure 2 shows the magnon energy dispersion [Eq. (2)] and the magnonic Casimir energy [Eq. (10a)] with its Casimir coefficient [Eq. (11)] for each regime (i)-(iii).

Gap-melting regime

(i) Gap-melting regime $\alpha \le {\alpha }_{\sigma = +}^{{{{\rm{cri}}}}} \,< \,{\alpha }_{\sigma = -}^{{{{\rm{cri}}}}}$. The magnonic Casimir energy takes a real value as shown in the middle and right panels of Fig. 2(i), see also Eq. (11), and there are no magnonic EPs [see the left panel of Fig. 2(i)].

When $\alpha\, < \,{\alpha }_{\sigma = +}^{{{{\rm{cri}}}}}$, the magnon energy gap for both σ = ± is nonzero Δ_σ=±,α > 0 and both magnons σ = ± are the gapped modes. For each gapped mode, the absolute value of the magnonic Casimir coefficient ${C}_{{{{\rm{Cas}}}}}^{[3]}$ decreases and approaches asymptotically to zero as the film thickness increases. We emphasize that the magnon energy gap decreases as the damping constant α increases [Eq. (6)]. Then, the magnitude of the magnonic Casimir energy and its coefficient increase as the value of the damping constant becomes larger and approaches to the critical value $\alpha \to {\alpha }_{\sigma = +}^{{{{\rm{cri}}}}}$ [see the middle panel of Fig. 2(i)].

When $\alpha ={\alpha }_{\sigma = +}^{{{{\rm{cri}}}}}$, the magnon σ = − remains the gapped mode, whereas the magnon energy gap for σ = + vanishes Δ_σ=+,α = 0 and the magnon σ = + becomes the gapless mode which behaves like a relativistic particle with the linear energy dispersion. In the gapless mode, the magnonic Casimir coefficient ${C}_{{{{\rm{Cas}}}}}^{[3]}$ approaches asymptotically to a nonzero constant as the film thickness increases. The behavior of the gapless magnon mode is analogous to the conventional Casimir effect of a massless scalar field in continuous space⁴⁹ except for a-dependent lattice effects, whereas that of the gapped magnon modes is similar to the Casimir effect known for massive degrees of freedom^49,50.

Oscillating regime

(ii) Oscillating regime ${\alpha }_{\sigma = +}^{{{{\rm{cri}}}}}\, < \,\alpha\, < \,{\alpha }_{\sigma = -}^{{{{\rm{cri}}}}}$. The magnonic Casimir energy takes a complex value as shown in the middle and right panels of Fig. 2(ii), see also Eq. (11). There is one EP, e.g., $a{k}_{\sigma = +,\alpha = 0.04}^{{{{\rm{cri}}}}} \sim 0.039\,1$ for α = 0.04 [see the left panel of Fig. 2(ii)]. Then, the magnonic non-Hermitian Casimir effect exhibits an oscillating behavior as a function of N_z for the film thickness L_z ≔ aN_z.

An intuitive explanation for the oscillation of the magnonic non-Hermitian Casimir effect and its relation to the EP is given as follows: Through the lattice regularization, the magnonic Casimir energy is defined as the difference [Eq. (10a)] between the zero-point energy with the discrete wavenumber k_z [Eq. (10b)] and the one with the continuous wavenumber [Eq. (10c)]. On the lattice, the wavenumber k_z under the boundary condition is discretized in units of π/aN_z as k_z → (π/aN_z)n. As the film thickness N_z increases, the unit becomes smaller, and finally, it matches the EP as $\pi /a{N}_{z}={k}_{\sigma ,\alpha }^{{{{\rm{cri}}}}}$, i.e., ${N}_{z}=\pi /a{k}_{\sigma ,\alpha }^{{{{\rm{cri}}}}}$, where the magnonic non-Hermitian Casimir effect is enhanced due to the EP. Then, the magnonic non-Hermitian Casimir effect is periodically enhanced where the film thickness N_z is multiples of $\pi /a{k}_{\sigma ,\alpha }^{{{{\rm{cri}}}}}$. Thus, the oscillating behavior of the magnonic non-Hermitian Casimir effect stems from the EP, ${k}_{\sigma ,\alpha }^{{{{\rm{cri}}}}}$, and the oscillation is characterized in units of $\pi /a{k}_{\sigma ,\alpha }^{{{{\rm{cri}}}}}$. We refer to this oscillating behavior as the magnonic EP-induced Casimir oscillation. The period of this Casimir oscillation is

$${\Lambda }_{\sigma ,\alpha }^{{{{\rm{Cas}}}}}:= \frac{\pi }{a{k}_{\sigma ,\alpha }^{{{{\rm{cri}}}}}}.$$

(12)

As an example, the period is ${\Lambda }_{\sigma = +,\alpha = 0.04}^{{{{\rm{Cas}}}}} \sim 80.4$ for α = 0.04. This agrees with the numerical result in the middle and right panels of Fig. 2(ii), see the highlighted in red. We call (ii) ${\alpha }_{\sigma = +}^{{{{\rm{cri}}}}} \,<\, \alpha \,< \,{\alpha }_{\sigma = -}^{{{{\rm{cri}}}}}$ the oscillating regime. The middle and right panels of Fig. 2(ii) show that the magnonic EP-induced Casimir oscillation is characterized by its Casimir coefficient ${C}_{{{{\rm{Cas}}}}}^{[b]}$ of b = 1.5.

Beating regime

(iii) Beating regime ${\alpha }_{\sigma = +}^{{{{\rm{cri}}}}}\, < \,{\alpha }_{\sigma = -}^{{{{\rm{cri}}}}}\le \alpha$. The magnonic Casimir energy takes a complex value as shown in the middle and right panels of Fig. 2(iii), see also Eq. (11). There are two EPs, ${k}_{\sigma = +,\alpha }^{{{{\rm{cri}}}}}$ and ${k}_{\sigma = -,\alpha }^{{{{\rm{cri}}}}}$, which induce two types of the Casimir oscillations characterized by ${\Lambda }_{\sigma = +,\alpha }^{{{{\rm{Cas}}}}}$ and ${\Lambda }_{\sigma = -,\alpha }^{{{{\rm{Cas}}}}}$, respectively. As an example, $a{k}_{\sigma = +,\alpha = 0.05}^{{{{\rm{cri}}}}} \sim 0.049\,2$ and $a{k}_{\sigma = -,\alpha = 0.05}^{{{{\rm{cri}}}}} \sim 0.027\,3$ provide ${\Lambda }_{\sigma = +,\alpha = 0.05}^{{{{\rm{Cas}}}}} \sim 63.8$ and ${\Lambda }_{\sigma = -,\alpha = 0.05}^{{{{\rm{Cas}}}}} \sim 115$, respectively, for α = 0.05 [see the left panel of Fig. 2(iii)]. Due to the interference between the two Casimir oscillations, the magnonic non-Hermitian Casimir effect exhibits a beating behavior as a function of N_z for the film thickness L_z ≔ aN_z with a period of

$$\frac{1}{| 1/{\Lambda }_{\sigma = +,\alpha }^{{{{\rm{Cas}}}}}-1/{\Lambda }_{\sigma = -,\alpha }^{{{{\rm{Cas}}}}}| }.$$

(13)

As an example, the period is $| 1/{\Lambda }_{\sigma = +,\alpha = 0.05}^{{{{\rm{Cas}}}}}-1/{\Lambda }_{\sigma = -,\alpha = 0.05}^{{{{\rm{Cas}}}}}{| }^{-1} \sim 143$ for α = 0.05. This agrees with the numerical result in the middle and right panels of Fig. 2(iii), see the highlighted in blue. We call (iii) ${\alpha }_{\sigma = +}^{{{{\rm{cri}}}}} \,< \,{\alpha }_{\sigma = -}^{{{{\rm{cri}}}}}\le \alpha$ the beating regime. The middle and right panels of Fig. 2(iii) show that the beating behavior of the magnonic EP-induced Casimir oscillation is characterized by its Casimir coefficient ${C}_{{{{\rm{Cas}}}}}^{[b]}$ of b = 1.5. We remark that the beating behavior is absent in the uniaxial AFMs of K_h = 0 and K_e > 0 where two kinds of magnons σ = ± are in degenerate states³⁶.

Imaginary part of the Casimir energy

Here, we discuss the meaning of the imaginary part of the Casimir energy. The (complex) Casimir energy is defined by the zero-point energy, which is the sum of all the possible (complex) eigenvalues. The real part of the zero-point energy originates from the sum of the real parts of the eigenvalues, whereas the imaginary part of the zero-point energy is defined as the sum of imaginary parts of eigenvalues. Since the imaginary parts of eigenvalues are formally regarded as the decay width (or the inverse of a lifetime) of an unstable particle, the imaginary part of the zero-point energy is the sum of all the possible decay widths. Hence, if the decay width of an unstable particle depends on the wavenumber, and the width in the thin film and that in the bulk are different from each other, then the imaginary part of the Casimir energy can be nonzero. In this work, since we focus on magnons in the geometry of Fig. 1, the imaginary part of magnonic Casimir energy represents the L_z-dependence of the sum of magnon decay widths.

Discussion

Magnonic Casimir engineering

The Gilbert damping can be enhanced and controlled by the established experimental techniques of spintronics such as spin pumping³⁶. In addition, microfabrication technology can control the film thickness and manipulate the magnonic non-Hermitian Casimir effect. The Casimir pressure of magnons, which stems from the real part of its Casimir energy, contributes to the internal pressure of thin films. We find from the middle panel of Fig. 2(ii) and (iii) that depending on the film thickness, the sign of the real part of the magnonic Casimir coefficient changes. This means that by tuning the film thickness, we can control and manipulate the direction of the magnonic Casimir pressure as well as the magnitude thanks to the EP-induced Casimir oscillation. Thus, our study utilizing energy dissipation, the magnonic non-Hermitian Casimir effect, provides the new principles of nanoscale devices, such as highly sensitive pressure sensors and magnon transistors⁵¹, and paves the way for magnonic Casimir engineering.

Conclusion

We have shown that as the Gilbert damping constant increases, the non-Hermitian Casimir effect of magnons in antiferromagnets is enhanced and exhibits the oscillating behavior which stems from the exceptional point. This exceptional point-induced Casimir oscillation also exhibits the beating behavior when the degeneracy between two kinds of magnons is lifted. These magnonic Casimir oscillations are absent in the dissipationless system of magnons. Thus, we have shown that energy dissipation serves as a new handle on Casimir engineering.

Outlook

In this paper, following ref. ³⁷, the effect of dissipation is incorporated into the energy dispersion relation of magnons through the Landau–Lifshitz–Gilbert equation. It will be intriguing to find the quantum effect of dissipation on the magnonic non-Hermitian Casimir effect, beyond the Landau–Lifshitz–Gilbert equation, by using quantum master equation^29,52,53,54. We also remark that dipolar interactions contribute to the form of the dispersion relation⁵⁵ and play a crucial role in the magnonic Casimir effect in ferrimagnets³¹. Hence, taking dipolar interactions into account, it will be interesting to develop this study, magnonic non-Hermitian Casimir effect in antiferromagnets, into ferrimagnets. We leave these advanced studies for future works.

Methods

Numerical calculation was performed by using the software Wolfram Mathematica.