Learning design-score manifold to guide diffusion models for offline optimization

Abstract

Optimizing complex systems—from discovering therapeutic drugs to designing high-performance materials—remains a fundamental challenge across science and engineering, as the underlying rules are often unknown and costly to evaluate. Offline optimization aims to optimize designs for target scores using pre-collected datasets without system interaction. However, conventional approaches may fail beyond training data, predicting inaccurate scores and generating inferior designs. This paper introduces ManGO, a diffusion-based framework that learns the design-score manifold, capturing the design-score interdependencies holistically. Unlike existing methods that treat design and score spaces in isolation, ManGO unifies forward prediction and backward generation, attaining generalization beyond training data. Key to this is its derivative-free guidance for conditional generation, coupled with adaptive inference-time scaling that dynamically optimizes denoising paths. Extensive evaluations demonstrate that ManGO outperforms 24 single- and 10 multi-objective optimization methods across diverse domains, including synthetic tasks, robot control, material design, DNA sequence, and real-world engineering optimization.

Introduction

Across scientific and industrial domains, from drug discovery [1] to engineering superconducting materials [2], researchers face a common bottleneck: creating new designs to optimize specific property scores in complex systems where the rules governing performance are unknown or costly to evaluate. Numerous methods require either expensive trial-and-error experimentation or building system models with long-term accumulation of domain knowledge. Consider the decades-long quest for fusion reactor materials—each physical test costs millions and risks equipment damage [3] or the ethical constraints in developing neuroactive drugs where failed designs could harm patients [4, 5]. These limitations call for a general optimization framework that learns directly from historical data while eliminating the need for iterative evaluation.

Offline optimization [6], also named offline model-based optimization, has emerged as a promising solution, enabling design improvement using pre-collected datasets. This approach has proven valuable in molecule generation [7], protein properties [8], and hardware accelerators [9]. Current methods adopt a unidirectional strategy: (i) Training surrogate models to predict scores from designs. These predicted scores are then utilized by various optimizers to identify the optimal designs (forward modeling) [10, 11]; (ii) Generating designs that are conditioned on desired scores through the use of generative models (backward generation). An example of this approach is the employment of diffusion models [12], wherein small amounts of noise are incrementally added to a design sample, and a neural network is trained to reverse this noise-adding procedure. However, forward methods mislead optimizers with overconfident out-of-distribution predictions [6], while backward methods struggle with out-of-distribution generation (OOG) on unseen conditions [13]. These struggles stem from a deeper oversight: existing works operate in isolated design or score spaces, missing the underlying design-score manifold where optimal designs reside.

We propose to learn the design-score manifold to guide diffusion models for offline optimization (ManGO). As illustrated in Fig. 1, we leverage score-augmented datasets to train an unconditional diffusion model. By learning on the manifold, the model effectively captures the bidirectional relationships between designs and their corresponding scores. We then introduce a derivative-free guidance mechanism for conditional generation, which enables bidirectional guidance—generating designs based on target scores and predicting scores for given designs, thus eliminating the reliance on error-prone forward models. To further enhance generation quality, we implement adaptive inference-time scaling for ManGO, which computes model fidelity on unconditional samples. This scaling approach dynamically optimizes denoising paths through ManGO’s self-supervised rewards. Moreover, ManGO is adaptable to both single-objective optimization (SOO) and multi-objective optimization (MOO) tasks, making it a comprehensive solution for various optimization scenarios.

Fig. 1: Overview of the ManGO framework for offline optimization.

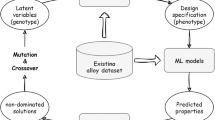
a Illustration of offline optimization: it identifies optimal designs for an unknown black-box function using an offline dataset (no environment interaction), where designs represent function inputs and scores correspond to outputs. b Training a diffusion model on score-augmented data to learn the joint design-score manifold. c Fidelity estimation via unconditional samples generated by the trained ManGO model: the fidelity metric determines whether to activate inference-time scaling during conditional generation. d Bidirectional conditional generation: it leverages preferred-score or preferred-design conditions to generate corresponding designs or scores, illustrated via the self-supervised importance sampling (self-IS) method at denoising timestep t for sample i. e Conceptual illustration of ManGO: it learns on the design-score manifold to enhance out-of-distribution generation (OOG) capability, contrasted with design-space learning that struggles with OOG issues under unseen conditions [13]. f Case study on superconductor’s temperature optimization [37]: it demonstrates the superior OOG performance via ManGO versus the design-space approach (i.e., DDOM) across varying ratios of top data removal.

The comprehensive evaluation showcases ManGO’s state-of-the-art versatility in offline optimization, consistently surpassing existing approaches across both SOO and MOO tasks. In comparison with the baselines, ManGO significantly enhances performance, attaining the top position among 24 SOO methods and 10 MOO methods. We anticipate that ManGO will serve as a valuable tool for data-driven design. By unifying optimization through learning on the design-score manifold, it offers a scalable and accessible solution for future scientific and industrial challenges.

Results

In this section, we first introduce preliminaries on offline optimization, the basics of diffusion models, baseline methods and performance metrics. Subsequently, to show the motivation and advantages of ManGO, we compare the learned versus the original design-score manifold and visualize the trajectory generation. We then conduct extensive experimental validation on offline SOO and MOO using Design-Bench [6] and Off-MOO-Bench [14]. Finally, we perform systematic ablation studies to analyze the contributions of ManGO’s core components.

Preliminaries

Offline optimization [6], also referred to as offline model-based optimization, seeks to identify an optimal design x^* within a design space ${\mathcal{X}}\subseteq {{\mathbb{R}}}^{d}$ without requiring online evaluations, where d denotes the design dimension. Based on the number of objective functions ${\boldsymbol{f}}(\cdot )=({f}_{1}({\boldsymbol{x}}),\ldots ,{f}_{m}({\boldsymbol{x}})):{\mathcal{X}}\to {{\mathbb{R}}}^{m}$, offline optimization can be classified into two types [14]: (i) offline SOO when m = 1, and (ii) offline MOO when m > 1.

Offline SOO aims to identify the optimal design ${{\boldsymbol{x}}}^{* }=\arg \mathop{\min }\limits_{{\boldsymbol{x}}\in {\mathcal{X}}}f({\boldsymbol{x}})$ using only a pre-collected offline dataset ${\mathcal{D}}={\{({{\boldsymbol{x}}}_{i},{y}_{i})\}}_{i = 1}^{N}$, where x_i denotes a specific design (also referred to as a solution) and y_i = f(x_i) represents its corresponding score (or objective value). Offline MOO aims to identify a set of designs that achieve optimal trade-offs among conflicting objectives using a pre-collected dataset ${\mathcal{D}}={\left\{({{\boldsymbol{x}}}_{i},{{\boldsymbol{y}}}_{i})\right\}}_{i = 1}^{N}$, where y_i denotes the vector of scores corresponding to design x_i. The problem is defined as [15]: $\,\text{Find}\,{{\boldsymbol{x}}}^{* }\in {\mathcal{X}}\,\text{such that}\,\nexists {\boldsymbol{x}}\in {\mathcal{X}}\,\text{with}\,{\boldsymbol{f}}({\boldsymbol{x}})\prec {\boldsymbol{f}}({{\boldsymbol{x}}}^{* }),$ where ≺ denotes Pareto dominance. A design ${{\boldsymbol{x}}}^{{\prime} }$ is said to Pareto dominate another design x, denoted as ${\boldsymbol{f}}({{\boldsymbol{x}}}^{{\prime} })\prec {\boldsymbol{f}}({\boldsymbol{x}})$, if $\exists i\in \{1,\ldots ,m\},{f}_{i}({{\boldsymbol{x}}}^{{\prime} }) < {f}_{i}({\boldsymbol{x}})$ and $\forall j\in \{1,\ldots ,m\},{f}_{j}({{\boldsymbol{x}}}^{{\prime} })\le {f}_{j}({\boldsymbol{x}}).$ Namely, ${{\boldsymbol{x}}}^{{\prime} }$ is superior to x in at least one objective while being at least as good in all others. A design x^* is Pareto optimal if no other design ${\boldsymbol{x}}\in {\mathcal{X}}$ Pareto dominates x^*. The set of all Pareto optimal designs is referred to as the Pareto set (PS), and the set of their scores {f(x^*)∣x^* ∈ PS} constitutes the Pareto front. The goal of offline MOO is to identify the PS using a pre-collected dataset, thereby achieving optimal trade-offs among conflicting objectives.

Diffusion models are a type of deep generative models that learn to reverse a gradual noising process, transforming random noise into realistic data through iterative denoising. Let x_t denote the state of a data sample x₀ at time t ∈ [0, T], where x₀ is drawn from an unknown data distribution p₀(x). Here, x_t represents a noisy version of x₀ at time t, and x_T corresponds to a point sampled from a prior noise distribution p_T(x), typically chosen as the standard normal distribution ${p}_{T}({\boldsymbol{x}})={\mathcal{N}}({\boldsymbol{0}},{\boldsymbol{I}})$.

The forward diffusion process, also known as the noise-adding process, can be modeled as a stochastic differential equation (SDE) [16]: dx = f(x, t)dt + g(t)dw, where w denotes the standard Wiener process, ${\bf{f}}:{{\mathbb{R}}}^{d}\to {{\mathbb{R}}}^{d}$ is the drift coefficient, and $g(t):{\mathbb{R}}\to {\mathbb{R}}$ is the diffusion coefficient of x_t. The denoising process is defined by the reverse-time SDE: $d{\boldsymbol{x}}=\left[{\bf{f}}({\boldsymbol{x}},t)-g{(t)}^{2}{\nabla }_{{\boldsymbol{x}}}\log {p}_{t}({\boldsymbol{x}})\right]dt+g(t)d\tilde{{\boldsymbol{w}}},$ where dt represents an infinitesimal step backward in time, and $d\tilde{{\boldsymbol{w}}}$ is the reverse-time Wiener process.

Baseline methods and performance metrics

We consider existing baseline methods for offline SOO based on three methodological paradigms: (i) Surrogate-based methods: optimizing with surrogate models, including BO-qEI [17, 18], CMA-ES [10], REINFORCE [19], Gradient Ascent and its variants of mean ensemble and min ensemble. (ii) Forward-modeling methods: employing advanced neural networks like generative models as surrogate models and integrating with surrogate-based methods, including COMs [20], RoMA [21], IOM [22], BDI [11], ICT [23], Tri-Mentoring [24], PGS [25], FGM [26], Match-OPT [27], and RaM [28]. (iii) Inverse-modeling methods: applying score as a condition to reverse design with generative models, including CbAS [29], MINs [30], DDOM [12], BONET [31], and GTG [32].

For offline MOO, existing approaches remain relatively under-explored compared to offline SOO. Our evaluation focuses on three representative approaches: (i) Multiple Models (MMs)-based NSGA-II: We implement NSGA-II with independent objective predictors and perform predictors’ ensemble as the surrogate model for evolutionary optimization, which outperforms end-to-end and multi-head variants [14]. (ii) Multi-objective Bayesian Optimization (MOBO): We adapt the canonical MOBO by substituting Gaussian Processes with the MM ensemble and employ an HV-based acquisition function, qNEHVI [33], which outperforms scalarization and information-theoretic alternatives [14]. (iii) Generative methods: ParetoFlow [34], a flow-model-based method utilizing adaptive weights for multiple predictors to guide flow sampling toward PF; MO-DDOM, a diffusion-model-based method where we extend DDOM through multi-score conditioning and adding MM-based design evaluation.

In offline optimization, where environment interaction is prohibited, it is essential to evaluate multiple candidate solutions; thus, standard benchmarks adopt k-shot evaluation with the 100th percentile (best candidate) as the performance metric [6, 14]. All results are normalized using task-specific references for comparison: For Design-Bench with maximization tasks (Table 1), we use standardization normalization for the Superconduct task and min-max normalization for other tasks based on the unobserved dataset’s highest score. For the Off-MOO-Bench with minimization tasks (Tables 2), we use min-max normalization with the best HV and IGD values of training datasets.

Table 1 The 100th percentile normalized score (k = 128) in the Design-Bench benchmark, where the best and runner-up results on each task are bold and underlined numbers

Table 2 Averaged normalized HV and IGD values of synthetic tasks (upper) and RE tasks (lower) in the Off-MOO benchmark, where the best and runner-up results on each task are highlighted by bold and underlined numbers.

Motivation and Advantages of ManGO

Compared to conventional manifold learning, our diffusion-based approach provides unique advantages for offline optimization. Unlike conventional methods like kernel-based methods that struggle with complex nonlinear geometries [35], diffusion models excel at capturing intricate manifold structures through stochastic denoising. Crucially, diffusion models inherently support conditional generation, enabling direct generation of high-performing designs conditioned on target scores-a capability absent in standard manifold learning. Furthermore, compared to GANs or VAEs, diffusion models offer superior training stability and generation fidelity [36], which are critical for reliable optimization from offline data. This combination of strong representational capacity and built-in conditional generation makes diffusion models suited for learning the design-score manifold.

Compared to existing methods for offline optimization, our proposed ManGO framework explicitly learns the design-score manifold and leverages the underlying manifold geometry to co-generate designs and scores. Specifically, ManGO learns a bidirectional generation between designs and scores: (i) Design-to-Score Prediction: Given any design configuration, ManGO predicts its corresponding score; (ii) Score-to-Design Generation: For any preferred score, ManGO generates its corresponding design. As illustrated in Figure 1e, this bidirectional mapping provides ManGO with a robust OOG capability to extrapolate beyond training distributions. Let ${\hat{{\boldsymbol{x}}}}_{t}=({{\boldsymbol{x}}}_{t},{{\boldsymbol{y}}}_{t})$ denotes a score-augmented design vector at timestep t, where x and y represent the design and its score, respectively. The denoising update can be represented as:

$$\hat{{\boldsymbol{x}}}_{t - 1} = ({{\boldsymbol{x}}}_{t},{{\boldsymbol{y}}}_{t} )+ \underbrace{({{\Delta}} {{\boldsymbol{x}}}_{t}, {{\Delta}} {{\boldsymbol{y}}}_{t})}_{{\text{Co-update}}}=\frac{1}{2}\underbrace{({{\boldsymbol{x}}}_{t}+2{{\Delta}} {{\boldsymbol{x}}}_{t}, {{\boldsymbol{y}}}_{t})}_{{\rm{Design}}\,{\rm{update}}} + \frac{1}{2}\underbrace{({{\boldsymbol{x}}}_{t}, {{\boldsymbol{y}}}_{t}+2{{\Delta}} {{\boldsymbol{y}}}_{t})}_{{\rm{Score}}\,{\rm{update}}},$$

where the co-update term indicates the denoising update based on the learned manifold geometry, the design-update term indicates the denoising update of x_t conditioned on y_t, and the score-update term indicates the denoising update of y_t conditioned on x_t. Unlike the design-space approaches that treat y_t as a fixed condition and only update x_t unidirectionally, ManGO jointly updates both x_t and y_t based on the bidirectional mapping. The design-space methods struggle with extrapolation under unseen conditions. In contrast, ManGO leverages co-updates to dynamically capture the geometric relationship between design and score: each denoising step not only pushes x_t toward the local manifold conditioned on y_t (design-update) but also refines y_t to align with the evolving x_t (score-update). This bidirectional feedback enables progressive extrapolation and converges to the conditioned points on the manifold, achieving a robust OOG capability.

We conduct a controlled experiment to elucidate the advantage of the bidirectional mapping of ManGO on a superconductor [37] task, an 86-D materials design optimization task to maximize a critical temperature, using DDOM [12] as the design-space baseline. In terms of the 128-shot evaluation, Figure 1f shows that ManGO achieves a consistent score gain of greater than 0.1 over the design-space approach across varying levels of top-data removal (from 70% to 10%). The gain grows to nearly 0.2 when only 10% of the top data are removed. Regarding the 1-shot evaluation, both methods exhibit comparable performance under severe data removal (from 70% to 30%). However, ManGO demonstrates progressively better results as data availability increases. At 10% data removal, ManGO achieves higher scores than the design-space method with 128 shots. These results confirm that: (i) ManGO captures the bidirectional design-score relationships, enabling robustness to OOG challenges; (ii) ManGO exhibits nonlinear scaling of sample efficiency with data quality, achieving superior few-shot performance.

Manifold and trajectory generation visualization

To demonstrate the bidirectional mapping capability, we visualize the performance of ManGO on two canonical minimization tasks. (i) Branin function (for SOO): A well-studied 2D function containing three global minima within x₁ ∈ [ − 5, 10], x₂ ∈ [0, 15] and ${y}_{\min }=0.398$, serving as an ideal testbed to capture multimodal landscapes. Specifically, ${f}_{{\rm{br}}}\left({x}_{1},{x}_{2}\right)=a{\left({x}_{2}-b{x}_{1}^{2}+c{x}_{1}-r\right)}^{2}-s(1-t)\cos {x}_{1}-s,$ where $a=1,b=\frac{5.1}{4{\pi }^{2}},c=\frac{5}{\pi },r=6,s=10$, and $t=\frac{1}{8\pi }$. (ii) OmniTest (for MOO): A synthetic 2D problem generating 9 disconnected Pareto-optimal points with x ∈ [0, 6]² and y ∈ [−2, 2]², challenging optimization methods in maintaining diverse designs. Specifically, ${f}_{1}({\boldsymbol{x}})=\mathop{\sum }\nolimits_{i = 1}^{2}\sin (\pi {x}_{i}),{f}_{2}({\boldsymbol{x}})=\mathop{\sum }\nolimits_{i = 1}^{2}\cos (\pi {x}_{i})$ with Pareto designs at all combinations of (x₁, x₂) ∈ {1, 3, 5} × {1, 3, 5}.

Fig. 2 shows that ManGO reconstructs the entire design-score manifold despite removing the top 40% of low-scoring data. Its generated manifold recovers the erased global minima locations and maintains the overall topographic trends in the Branin task in Figure 2a. ManGO also recovers all 9 disconnected Pareto fronts and preserves the negative correlation between f₁ and f₂ objectives in the OmniTest task in Figure 2b (visualizing two regions for ease of observation). Across both tasks, the generated manifolds exhibit only minimal deviations from the original manifolds, even in out-of-distribution regions. This demonstrates ManGO’s robust OOG capability, validating its ability to extrapolate beyond the training distribution accurately. Furthermore, both generated manifolds exhibit consistent minor elevation, with a deviation of less than 5%. For example, Figure 2c reveals a gradual score elevation between unconditional and expected scores in Branin’s training region, where higher expected scores correspond to sparser training samples. This conservative estimation under uncertainty serves as an advantage in offline optimization, where reliable performance outweighs aggressive extrapolation [20].

Fig. 2: Visualization of manifold learning, trajectory generation, and generation capabilities of ManGO.

Note that unconditional and conditional samples are generated via ManGO without guidance and with preferred-score guidance, respectively. a, b Manifold and trajectory comparisons for the Branin (SOO) and OmniTest (MOO) tasks. The generated manifold is constructed via ManGO's design-to-score prediction within the feasible region of designs. Close alignment between the ManGO-generated and original manifold, confirming the model’s proficiency in learning complex design-score relationships. Generated trajectories visualize ManGO's score-to-design mapping under minimal score and design constraints, highlighting its capacity to perform targeted denoising toward desired regions. c Branin task: Unconditional samples (green) match preferred scores from the training dataset, while conditional samples (blue) extrapolate beyond the training minimum (grey dashed line). d OmniTest task: Conditional samples better approximate preferred scores and Pareto-dominate the training data (grey) compared to unconditional samples. These results indicate that ManGO effectively reconstructs in-distribution samples during unconditional generation—reflecting well-learned manifold structure—while enabling OOG of superior samples through conditional guidance, demonstrating robust extrapolation based on the learned manifold.

Unlike design-space approaches limited to score-based guidance, ManGO’s manifold learning framework enables additional conditioning on design constraints, providing more flexible control over the generation process. Figures 2a, b present ManGO’s generated trajectories with minimal score and varying design constraints as conditional guidance. For instance, in Figure 2a with design constraints x₁ ∈ [−5, 0], x₂ ∈ [0, 15] and minimum score condition ${y}_{\min }=0.398$, ManGO successfully guides a randomly initialized point (violating the constraints) to converge to the constrained minimum. Notably, ManGO exhibits accelerated convergence as noisy samples approach preferred points. This indicates its ability to exploit favorable noise points for enhanced output quality, naturally aligning with our inference-time scaling framework. On the other hand, ManGO directly transports samples from random initializations to preferred points in the joint design-score space, simultaneously generating both designs and their scores. This eliminates two key requirements of conventional approaches: (i) iterative score evaluation on noisy designs via external forward models, and (ii) gradient computation along manifold geometry.

Figures 2 and Fig. 3 demonstrate the critical role of conditional guidance on ManGO’s OOG capability. Unconditional generation faithfully reproduces in-distribution samples (matching training score ranges in Fig. 2c, d), while conditional generation produces designs that extrapolate beyond the training distribution. This key distinction reveals that although ManGO learns the complete manifold structure, explicit guidance is essential to unlock its full OOG capabilities. The consistent results across RE21, ZDT3, DTLZ7, and RE41 benchmarks (Fig. 3) robustly confirm this fundamental behavior. Specifically, ManGO without guidance exhibits conservative behavior, remaining within the training distribution. Meanwhile, when guided by Pareto front (PF) reference points, ManGO approaches the complete PF, and our self-supervised scaling guidance achieves better precision than standard guidance.

Fig. 3: Pareto front generation under different guidance conditions.

Across all subfigures of (a) RE21, (b) ZDT3, (c) DTLZ7, and (d) RE41, columns from left to right respectively show the results of no guidance, standard guidance, and the proposed self-IS-based guidance. The progressive improvement in generation quality highlights ManGO's capability in OOG under conditional guidance. Furthermore, the enhanced performance with self-IS-based guidance illustrates the ManGO's feasibility for more delicate guidance mechanisms.

Evaluation on single-objective optimization

We employ five representative tasks from Design-Bench [6] and sample 10,000 offline design samples per task [28]: (i) Ant Morphology [38] (60-D parameter optimization for quadruped locomotion speed), (ii) D’Kitty Morphology [39] (56-D parameter optimization for movement efficiency enhancement of a quadruped robot), and (iii) Superconductor [37], (iv) TF-Bind-8 [40] and (v) TF-Bind-10 [40] (discrete DNA sequence optimization for transcription factor binding affinity with sequence lengths 8 and 10). We follow the maximization setting of Design-Bench and normalize scores based on the maximal score in the unobserved dataset [6], where higher scores indicate better performance.

As shown in Table 1, we compare ManGO with 22 baseline methods and report normalized scores of top k = 128 candidates (100th percentile). ManGO establishes a state-of-the-art performance across diverse domains (materials, robotics, bioengineering) on five datasets. ManGO with standard guidance attains a mean rank of 2.2/24 (securing the second position), while the self-supervised importance sampling (self-IS)-based variant further improves this to 1.4/24 (the first). ManGO ranks first on four tasks, including D’Kitty, Superconductor, TF-Bind-8, and TF-Bind-10, and secures second place on Ant, trailing only CMA-ES. This cross-domain advantage suggests that the effectiveness of learning the design-score manifold is general and not limited to specific problems.

The 13.6-rank leap over Mins (rank 15.0, the previous best of inverse-modeling baselines) demonstrates the superiority of the manifold-learned generation to design-space-learned methods. Meanwhile, the 2.8-rank lead over RaM (the best of forward-modeling baselines) suggests that score-conditioned diffusion can better exploit offline data than ranking-based approaches. It also outperforms the top surrogate-based methods (CMA-ES, rank 13.0) by 11.6 ranks, without the need for designing acquisition functions. On the other hand, the self-IS variant shows consistent improvements over standard ManGO: score boosts on Superconductor (+3.8%) and modest gains on Ant (+0.8%) and TF-Bind-10 (+0.9%). A deviation occurs in D’Kitty, where a slight average score reduction (−0.2%) accompanies improved peak performance (+0.3%). The marginal gains reflect that standard ManGO reaches near-optimal performance, leaving limited room for improvement.

Evaluation on multi-objective optimization

We utilize Off-MOO-Bench [14] and sample 60,000 samples per task [34]: (i) Synthetic Functions (an established collection of MOO evaluation tasks with 2 − 3 objectives exhibiting diverse PF characteristics, such as ZDT [41] and DTLZ [42]), and (ii) real-world engineering (RE) applications [43] (a suite of practical design tasks with 2−4 competing objectives, such as four-bar truss design and rocket injector design). We employ two standard evaluation metrics: (i) Hypervolume (HV)[44], which quantifies the dominated volume between candidate designs and nadir point (each dimension of which corresponds to the worst value of one objective), and (ii) Inverted Generational Distance (IGD) [45], which measures the average minimum distance between candidate designs and the ground-true PF, both metrics applied to non-dominated sorting [46] with k = 256 candidate designs (100th percentile). While generating high-quality single solutions from purely offline data remains challenging, we also report our method’s performance at k = 1 to demonstrate competitive performance. Note that while we replace the online query in MOBO/NSGA2 with a surrogate forward model for offline adaptation, performance degradation occurs versus online operation as the surrogate model cannot perfectly emulate environment feedback.

We follow the minimization setting of Off-MOO-Bench and normalize HV (IGD) values based on the best HV (IGD) of the training dataset, where higher HV (lower IGD) indicates better performance. ManGO outperforms all baseline methods across both synthetic and real-world MOO benchmarks according to Table 2. Regarding synthetic tasks, the self-IS-based ManGO achieves the best mean rankings of 2.0 (HV) and 1.3 (IGD) out of 10 competing methods, while the standard guidance version follows closely with ranks of 2.7 (HV) and 1.7 (IGD), securing the top two positions. The superiority extends to RE tasks, where self-IS-based ManGO dominates with average ranks of 1.3 (HV) and 2.0 (IGD), establishing itself as the overall leader.

As presented in the upper part of Table 2, ManGO shows consistent superiority across ZDT, OmniTest, and DTLZ series. Under the most challenging OOG scenarios where preferred designs are distant from ZDT’s training data, self-IS-based ManGO outperforms the best baselines by 60.1% in IGD (vs DDOM) and 3.9% in HV (vs NSGA-2). For 1-shot evaluation settings (i.e., k = 1), ManGO matches the performance of baseline methods requiring 256-shot evaluations. This shows that the efficient learning on the design-score manifold enables high-quality guidance generation even with minimal sampling.

As task complexity escalates with increasing objectives, the self-IS-based variant consistently achieves top performance in both HV and IGD metrics in the lower part of Table 2. This confirms its OOG capability in high-dimensional objective spaces. Compared to synthetic tasks, learning on manifolds poses greater challenges for RE tasks. Consequently, this diminishes ManGO’s performance advantage in 1-shot and standard guidance modes. However, self-IS guidance effectively offsets this by exploring more noise points, and its performance gains become more pronounced as task complexity increases.

Ablation study on robustness to preferred scores

Although we use the maximum unobserved score as a guided score (i.e., y_p = 1.0) in Table 1, practical scenarios may lack precise knowledge of optimal scores. We evaluate ManGO’s robustness to suboptimal guided scores by analyzing the best score of generated candidate designs across varying shot numbers. Fig. 4a, b reveal two key insights: (i) Increasing the shot number enhances robustness, with stable optimal designs emerging when guided scores exceed 0.7 (Ant) or 5.5 (Superconductor) at 128 shots. (ii) Decreasing the shot number to 1, peak performance occurs near but not exactly at y_p. This demonstrates that the generation diversity of diffusion models provides practical robustness for ManGO when y_p is unknown.

Fig. 4: Comprehensive ablation studies validating key components of the ManGO framework.

a, b Flexibility to guidance specification: Performance sensitivity to deviations between guided scores and true optima on Ant (a) and Superconductor (b) tasks, demonstrating ManGO's stability under suboptimal guidance conditions. c, d Fidelity-adaptive scaling: Performance gains relative to baseline fidelity thresholds in offline SOO (c) and MOO (d) tasks, with dashed lines indicating empirically optimal thresholds (τ_opt = 0.827 for SOO; τ_opt = 0.87 for MOO). e–h Inference-time scaling efficiency: HV (e, g) and IGD (f, h) versus number of function evaluations (NFE) for ZDT3 (e, f) and RE21 (g, h) task for three approaches, comparing standard denoising, self-IS scaling, and FKS scaling methods. Consistent performance improvements are achieved through adaptive noise-space exploration.

Ablation study on optimal fidelity threshold

We quantitatively evaluate the design-to-score prediction accuracy through the fidelity metric (Eq. (10)), which measures the distance between the ground-truth scores and the generated scores of unconditional samples. Figures 4c, d show that self-IS-based scaling achieves performance gains on the majority of SOO (optimal fidelity threshold τ_opt = 0.827) and MOO tasks (τ_opt = 0.87). Furthermore, MOO tasks exhibit higher fidelity than SOO tasks due to SOO’s higher-dimensional design spaces. It is more likely to increase performance gains with increasing fidelity values because diffusion models with higher fidelity generate more accurate self-reward signals during inference, enabling more effective noise-space exploration.

Ablation study on inference-time scaling

We evaluate computation-performance tradeoffs by controlling NFE on ZDT3 in Figures 4e, f and RE21 in Fig. 4g, h, comparing three approaches: (1) standard guidance with more denoising steps, (2) self-IS-based scaling, and (3) Feynman-Kac-steering (FKS)-based scaling. For ZDT3, standard guidance achieves competitive performance at NFE = 31, demonstrating ManGO’s sample efficiency. However, performance degrades at intermediate NFE before recovering, revealing instability in simple step extension. In contrast, scaling-based methods show monotonic improvement with increasing NFE, where FKS scaling temporarily outperforms IS scaling during mid-range NFEs before converging at NFE = 150. The RE21 task exhibits different characteristics: all methods display bell-shaped performance curves, peaking at NFE = 78 (FKS), NFE = 36 (IS), and NFE = 36 (standard). Scaling-based methods attain higher peak performance over standard guidance while maintaining a sustained advantage after NFE = 36. These results indicate that scaling methods yield superior computational performance compared to simple step extension.

Discussion

This work introduces ManGO, a framework that fundamentally rethinks offline optimization by learning the underlying design-score manifold through diffusion models. Unlike existing approaches that operate in isolated design or score spaces, ManGO’s bidirectional modeling unifies forward prediction and backward generation while overcoming OOG challenges. The derivative-free guidance mechanism eliminates reliance on error-prone forward models, while the adaptive inference-time scaling dynamically optimizes denoising paths. Extensive validation across synthetic tasks and real-world applications (robot control, material design, DNA optimization) demonstrates ManGO’s consistent superiority among 24 offline-SOO and 10 offline-MOO methods, establishing a new paradigm for data-driven design generation for complex system optimization.

We envision three critical future directions. First, extending ManGO to high-dimensional and discrete design spaces (e.g., 3D molecular structures) requires developing techniques for learning the latent-based manifold via encoding designs as latents to maintain computational efficiency. Recent work on latent diffusion models suggests potential pathways for improvement. Second, integrating physics-informed constraints beyond current design-clipping guidance could enhance physical plausibility in domains like metamaterial design, where conservation laws must be preserved. Preliminary experiments with physics-informed neural networks show promising results. Third, developing distributed ManGO variants would enable collaborative optimization across institutions while preserving data privacy, particularly valuable for pharmaceutical development where proprietary molecule datasets exist in isolation.

Several limitations warrant discussion. ManGO’s current implementation assumes quasi-static system environments, while gradually evolving scenarios would require incremental manifold adaptation mechanisms. While our adaptive scaling provides partial mitigation, improvement for non-stationary distributions remains an open challenge. Meanwhile, although ManGO demonstrates strong robustness to preferred scores in identifying optimal designs, it lacks an iterative refinement mechanism to further improve designs post-generation. Recent advances in post-training adaptation of diffusion models, such as controllable fine-tuning and editing, suggest promising pathways to augment ManGO with such capability.

Methods

In this section, we delve into the core components of our approach: (i) training the diffusion model to learn the design-score manifold and (ii) bidirectional guidance generation with the preferred condition. Finally, we present the training and inference settings of our proposed approach.

Unconditional training of diffusion model on score-augmented dataset

To better explore unknown design-score pairs, our method aims to capture the prior probability distribution of the design-score manifold using a diffusion model. This is a critical step to improve OOG limitation of backward methods to solve offline optimization problems. To achieve this, we train an unconditional diffusion model based on a variance-preserving (VP) SDE[16]. The model is trained on a joint design-score dataset $\hat{{\mathcal{D}}}={\{{\hat{{\boldsymbol{x}}}}_{i}:{\hat{{\boldsymbol{x}}}}_{i} = ({{\boldsymbol{x}}}_{i},{{\boldsymbol{y}}}_{i})\in {{\mathbb{R}}}^{(d+m)}\}}_{i = 1}^{N}$, where x_i denotes the design and y_i represents its corresponding score vector. Specifically, $\hat{{\mathcal{D}}}$ is constructed by augmenting the original design dataset ${{\mathcal{D}}}_{x}={\{{{\boldsymbol{x}}}_{i}\in {{\mathbb{R}}}^{d}\}}_{i = 1}^{N}$ with score information.

Unlike classifier-free diffusion models[47], which perform conditional training by incorporating score information as a condition with random dropout during training, our method directly learns the joint distribution of designs and scores. This eliminates the need to learn the design distribution under varying conditions, instead focusing on capturing the underlying structure of the design-score manifold. The diffusion process of our manifold-trained model is denoted by the following SDE:

$$d\hat{{\boldsymbol{x}}}=-\frac{1}{2}{\beta }_{t}\hat{{\boldsymbol{x}}}\,dt+\sqrt{{\beta }_{t}}\,d{\boldsymbol{w}},$$

(1)

where ${\beta }_{t}={\beta }_{\min }+({\beta }_{\max }-{\beta }_{\min })t$ with t ∈ [0, 1]. The denoising process is represented by the following reverse-time SDE:

$$d\hat{{\boldsymbol{x}}}=-{\beta }_{t}\left[\frac{\hat{{\boldsymbol{x}}}}{2}+{\nabla }_{\hat{{\boldsymbol{x}}}}\log {p}_{t}(\hat{{\boldsymbol{x}}})\right]dt+\sqrt{{\beta }_{t}}\,d\tilde{{\boldsymbol{w}}},$$

(2)

where $d\tilde{{\boldsymbol{w}}}$ denotes the reverse-time Wiener process. Using this process, the pre-trained diffusion model can transform a prior noise point ${\hat{{\boldsymbol{x}}}}_{T} \sim {p}_{T}(\hat{{\boldsymbol{x}}})$ into a design-score-joint point ${\hat{{\boldsymbol{x}}}}_{0}=({{\boldsymbol{x}}}_{0},{{\boldsymbol{y}}}_{0})$ on the design-score manifold.

Learning to reverse superior designs via score-based loss reweighting

When uniformly sampling data points from the augmented dataset $\hat{{\mathcal{D}}}$, the diffusion model learns the entire manifold. However, this does not fully align with the goal of offline optimization, which aims to find superior or optimal designs. We introduce a score-based reweighting mechanism into the loss function to steer the model toward regions of the manifold associated with lower scores (indicating better designs). This mechanism assigns higher weights to samples with lower scores, thereby encouraging the model to prioritize the generation of superior designs and reducing the learning complexity by focusing on the most promising regions of the manifold rather than learning the entire manifold.

Specifically, the weight vector for offline SOO (or MOO) tasks is obtained by applying max-min normalization to the sample scores (or the sample frontier index) based on non-dominated sorting[46] across the entire dataset. The reweighting mechanism allows the diffusion model to focus on the most promising region of the manifold, which is expressed as:

$${\boldsymbol{w}}(\hat{{\boldsymbol{x}}}:= ({\boldsymbol{x}},{\boldsymbol{y}}))=\left\{\begin{array}{rlr}\frac{{y}_{\max }-y}{{y}_{\max }-{y}_{\min }},&m=1,&\\ \frac{{l}_{{\rm{all}}}-{l}_{\text{NDS}({\boldsymbol{y}})}}{{l}_{{\rm{all}}}-1},&m > 1,\end{array}\right.$$

(3)

where ${y}_{\min }$ and ${y}_{\max }$ denote the minimum and maximum scores, respectively, and l_all and l_NDS(y) represent the total number of frontier layers and the frontier index of $\hat{{\boldsymbol{x}}}$, respectively. Equation (3) indicates that samples with lower scores (or those located on a more advanced frontier) are assigned higher weights in offline SOO (or MOO) tasks. We note that the normalization-based implementation serves as a foundational step, and future work may explore more efficient reweighting mechanisms.

The score function ${\nabla }_{\hat{{\boldsymbol{x}}}}\log {p}_{t}(\hat{{\bf{x}}})$ in Equation (2) is approximated by a time-dependent neural network ${{\boldsymbol{s}}}_{{\boldsymbol{\theta }}}\left({\hat{{\bf{x}}}}_{t},t\right)$ with parameters θ based on VP-SDE[16]. The network is optimized by minimizing the following loss function:

$${\mathcal{L}}({\boldsymbol{\theta }})=\mathop{\mathbb{E}}\limits_{t}\left[\lambda (t)\mathop{\mathbb{E}}\limits_{{\hat{{\boldsymbol{x}}}}_{0}}\left[{\boldsymbol{w}}({\hat{{\boldsymbol{x}}}}_{0})\mathop{{\mathbb{E}}}\limits_{{\hat{{\boldsymbol{x}}}}_{t}| {\hat{{\boldsymbol{x}}}}_{0}}\left[{\left\Vert {{\boldsymbol{s}}}_{{\boldsymbol{\theta }}}\left({\hat{{\boldsymbol{x}}}}_{t},t\right)-{\nabla }_{\hat{{\boldsymbol{x}}}}\log {p}_{t}\left({\hat{{\boldsymbol{x}}}}_{t}| {\hat{{\boldsymbol{x}}}}_{0}\right)\right\Vert }_{2}^{2}\right]\right]\right],$$

(4)

where λ(t) is a positive weighting function dependent on t, and ${\nabla }_{\hat{{\boldsymbol{x}}}}\log {p}_{t}\left({\hat{{\boldsymbol{x}}}}_{t}| {\hat{{\boldsymbol{x}}}}_{0}\right)$ can be obtained by the diffusion process.

Bidirectional generation on design-score samples via derivative-free guidance

Diffusion models generate data by iteratively refining random noise into preferred samples through a guided denoising process. The pre-trained diffusion model directly generates design-score samples, where each design is paired with a score predicted by the model itself, eliminating the need for an additional surrogate score model. This capability allows us to jointly guide the model on both the design and its associated score, enabling the generation of samples that align with our preferences.

In terms of score-to-design generation, the proposed method enables guided generation of preferred design-score samples through two mechanisms: (1) leveraging preferred scores y_p to guide the score component of the generated samples, ensuring alignment with desired performance; and (2) specifying a design constraint range $[{{\boldsymbol{x}}}_{{\text{c}}_{\min }},{{\boldsymbol{x}}}_{{\text{c}}_{\max }}]$ to guide the design component, ensuring design feasibility. This dual-guidance strategy generates samples that satisfy both design and score constraints without requiring an additional surrogate score model.

Concretely, during the reverse process, the guidance on the score component of the generated sample ${\hat{{\boldsymbol{x}}}}_{t}=({{\boldsymbol{x}}}_{t},{{\boldsymbol{y}}}_{t})$ is formulated as the gradient of the MSE between y_p and the current score y_t, i.e., ${\nabla }_{{{\boldsymbol{y}}}_{t}}\parallel {{\boldsymbol{y}}}_{{\rm{p}}}-{{\boldsymbol{y}}}_{t}{\parallel }_{2}^{2}$. Similarly, the guidance on the design component is formulated as the gradient of the MSE from the current design x_t to the constraint range $[{{\boldsymbol{x}}}_{{\text{c}}_{\min }},{{\boldsymbol{x}}}_{{\text{c}}_{\max }}]$, i.e., ${\nabla }_{{{\boldsymbol{x}}}_{t}}\parallel {{\boldsymbol{x}}}_{t}-\,\text{clip}\,({{\boldsymbol{x}}}_{t},{{\boldsymbol{x}}}_{{\text{c}}_{\min }},{{\boldsymbol{x}}}_{{\text{c}}_{\max }}){\parallel }_{2}^{2}$, where $\,\text{clip}\,({{\boldsymbol{x}}}_{t},{{\boldsymbol{x}}}_{{\text{c}}_{\min }},{{\boldsymbol{x}}}_{{\text{c}}_{\max }})$ ensures that x_t is projected onto the constraint range.

Since both MSE gradients can be computed analytically, our method effectively implements a derivative-free guidance scheme that operates without relying on differentiable models, avoiding the computational overhead of backpropagating (e.g., classifier guidance). Using the Euler-Maruyama method [48], the reverse process can be expressed as:

$$\begin{array}{l}{\hat{{\boldsymbol{x}}}}_{t-\Delta t}={\hat{{\boldsymbol{x}}}}_{t}+{\beta }_{t}\left[\vphantom{\frac{{\Omega }_{i1}}{2}}\frac{{\hat{{\boldsymbol{x}}}}_{t}}{2}+{{\boldsymbol{s}}}_{{\boldsymbol{\theta }}}({\hat{{\boldsymbol{x}}}}_{t},t)+{\alpha }_{x}\left({\hat{{\boldsymbol{x}}}}_{t}-\,{\text{clip}}\,({\hat{{\boldsymbol{x}}}}_{t},{\hat{{\boldsymbol{x}}}}_{{\text{c}}_{\min }},{\hat{{\boldsymbol{x}}}}_{{\text{c}}_{\max }})\right)\right.\\\qquad\quad\;\,+\,\left.{\alpha }_{y}({\hat{{\boldsymbol{y}}}}_{{\rm{p}}}-{\hat{{\boldsymbol{y}}}}_{t})\vphantom{\frac{{\Omega }_{i1}}{2}}\right]\Delta t+\sqrt{{\beta }_{t}\Delta t}\,{\mathcal{N}}({\boldsymbol{0}},{\boldsymbol{I}}),\end{array}$$

(5)

where α_x and α_y control the guidance scale on the design and score components, respectively. Here, ${\hat{{\boldsymbol{x}}}}_{t}$, ${\hat{{\boldsymbol{x}}}}_{{\text{c}}_{\min }}$, ${\hat{{\boldsymbol{x}}}}_{{\text{c}}_{\max }}$, ${\hat{{\boldsymbol{y}}}}_{{\rm{p}}}$, and ${\hat{{\boldsymbol{y}}}}_{t}$ are padded versions of their original vectors with a zero vector 0_d to match the dimensionality of ${\hat{{\boldsymbol{x}}}}_{t}$, like ${\hat{{\boldsymbol{y}}}}_{{\rm{p}}}=({{\boldsymbol{0}}}_{d},{{\boldsymbol{y}}}_{{\rm{p}}})$.

Similarly, the design-to-score prediction uses the zero-vector-augmented preferred design ${\hat{{\boldsymbol{x}}}}_{{\rm{p}}}=({{\boldsymbol{x}}}_{{\rm{p}}},{{\boldsymbol{0}}}_{m})$ as guidance:

$${\hat{{\boldsymbol{x}}}}_{t-\Delta t}={\hat{{\boldsymbol{x}}}}_{t}+{\beta }_{t}\left[\frac{{\hat{{\boldsymbol{x}}}}_{t}}{2}+{{\boldsymbol{s}}}_{{\boldsymbol{\theta }}}({\hat{{\boldsymbol{x}}}}_{t},t)+{\alpha }_{x}({\hat{{\boldsymbol{x}}}}_{{\rm{p}}}-{\hat{{\boldsymbol{x}}}}_{t})\right]\Delta t+\sqrt{{\beta }_{t}\Delta t}{\mathcal{N}}({\boldsymbol{0}},{\boldsymbol{I}}),$$

(6)

where the estimated score of the preferred design x_p is y₀ from ${\hat{{\boldsymbol{x}}}}_{0}=({{\boldsymbol{x}}}_{0},{{\boldsymbol{y}}}_{0})$.

Achieving inference-time scaling via self-supervised reward

Diffusion models have been shown to exhibit inference-time scaling behavior [49,50,51]: their generation quality can be improved by allocating additional computational budgets during inference, even without fine-tuning. This stems from a mechanism of noise space exploration, where the pre-trained model optimizes the generation trajectory by adaptively selecting high-reward noise points based on reward feedback. The reward feedback can be formulated through posterior mean approximation as:

$${\mathcal{R}}({{\boldsymbol{x}}}_{t}):= {{\mathbb{E}}}_{{{\boldsymbol{x}}}_{0} \sim {p}_{t}^{{\rm{pre}}}({{\boldsymbol{x}}}_{t})}[r({{\boldsymbol{x}}}_{0})| {{\boldsymbol{x}}}_{t}]=r({{\mathbb{E}}}_{{{\boldsymbol{x}}}_{0} \sim {p}_{t}^{{\rm{pre}}}}[{{\boldsymbol{x}}}_{0}| {{\boldsymbol{x}}}_{t}])=r({{\boldsymbol{x}}}_{0| t}),$$

(7)

where ${\mathcal{R}}({{\boldsymbol{x}}}_{t})$ evaluates the expected reward of samples generated from the noise point x_t, ${p}_{t}^{\,\text{pre}\,}$ represents the approximated distribution of the pre-trained model at t, r( ⋅ ) denotes the reward model evaluated at t = 0, and ${{\boldsymbol{x}}}_{0| t}={{\mathbb{E}}}_{{{\boldsymbol{x}}}_{0} \sim {p}_{t}^{{\rm{pre}}}}[{{\boldsymbol{x}}}_{0}| {{\boldsymbol{x}}}_{t}]$ denotes that the pre-trained model denoises the noise point from t to 0. Based on this mechanism, noise points with high rewards are retained for further refinement, while those with low rewards are discarded.

The dual-output capability (design-score generation) of our pre-trained model enables a self-supervised inference-time scaling scheme. For any intermediate noise point ${\hat{{\boldsymbol{x}}}}_{t}$, we estimate the denoised state ${\hat{{\boldsymbol{x}}}}_{0| t}$ via Tweedie’s Formula [36] as:

$${\hat{{\boldsymbol{x}}}}_{0| t}=({{\boldsymbol{x}}}_{0| t},{{\boldsymbol{y}}}_{0| t})=\left(\frac{{{\boldsymbol{x}}}_{t}+\sqrt{1-{\bar{\alpha }}_{t}}{{\boldsymbol{s}}}_{{\boldsymbol{\theta }}}^{(x)}({\hat{{\boldsymbol{x}}}}_{t},t)}{\sqrt{{\bar{\alpha }}_{t}}},\frac{{{\boldsymbol{y}}}_{t}+\sqrt{1-{\bar{\alpha }}_{t}}{{\boldsymbol{s}}}_{{\boldsymbol{\theta }}}^{(y)}({\hat{{\boldsymbol{x}}}}_{t},t)}{\sqrt{{\bar{\alpha }}_{t}}}\right),$$

(8)

where ${\bar{\alpha }}_{t}=\exp [-({\beta }_{\max }-{\beta }_{\min })\frac{{t}^{2}}{2}-{\beta }_{\min }t]$, and ${{\boldsymbol{s}}}_{{\boldsymbol{\theta }}}^{(x)}$, ${{\boldsymbol{s}}}_{{\boldsymbol{\theta }}}^{(y)}$ denote the design and score components of the model output s_θ, respectively. The estimated score y_0∣t provides self-supervised reward feedback by measuring its deviation from the preferred score:

$${\mathcal{R}}({\hat{{\boldsymbol{x}}}}_{t})=r({\hat{{\boldsymbol{x}}}}_{0| t})=\parallel {{\boldsymbol{y}}}_{{\rm{p}}}-{{\boldsymbol{y}}}_{0| t}{\parallel }_{2}.$$

(9)

This eliminates the need for external reward models, enabling the model to autonomously reject low-reward noise points and refine its generation process through self-supervised feedback.

As the effectiveness of inference-time scaling depends on the reward quality [49], the effectiveness of our self-supervised reward depends on the fidelity of the pre-trained diffusion model, denoted by ${\mathcal{F}}({{\boldsymbol{s}}}_{{\boldsymbol{\theta }}})$. We propose to quantitatively assess ${\mathcal{F}}({{\boldsymbol{s}}}_{{\boldsymbol{\theta }}})$ through the unconditional generation of s_θ. Specifically, we first generate a set of unconditional samples {x_uc = (x_uc, y_uc)} by Equation (5) without guidance. We then filter the samples that are better than training data (i.e., ${y}_{\,\text{uc}}^{(i)} < {y}_{{\rm{train}}}^{\text{(best)}\,}$ for SOO and ${{\boldsymbol{y}}}_{\,\text{uc}\,}^{(i)}\prec {{\boldsymbol{y}}}_{\,\text{train}}^{\text{(best)}\,}$ for MOO) and get the filtered set ${{\mathcal{D}}}_{{\rm{uc}}}={\{{\hat{{\boldsymbol{x}}}}_{\,\text{uc}\,}^{(i)}\}}_{i = 1}^{M}$. The fidelity metric ${\mathcal{F}}({{\boldsymbol{s}}}_{{\boldsymbol{\theta }}})$ is subsequently computed as:

$${\mathcal{F}}({{\boldsymbol{s}}}_{{\boldsymbol{\theta }}})=\exp\left(-\frac{1}{M}\mathop{\sum }\limits_{i=1}^{M}\parallel {{\boldsymbol{y}}}_{\,\text{uc}\,}^{(i)}-{{\boldsymbol{y}}}_{\,\text{train}\,}^{({j}^{* })}\parallel\right),$$

(10)

where ${\mathcal{F}}({{\boldsymbol{s}}}_{{\boldsymbol{\theta }}})\in (0,1]$, ${j}_{i}^{* }=\arg \mathop{\min }\limits_{j}\parallel {{\boldsymbol{x}}}_{\,\text{uc}\,}^{(i)}-{{\boldsymbol{x}}}_{\,\text{train}\,}^{(j)}{\parallel }_{2}$ denotes the index of the nearest training data to ${{\boldsymbol{x}}}_{\,\text{uc}\,}^{(i)}$ in ${\mathcal{D}}={\{{\hat{{\boldsymbol{x}}}}_{\,\text{train}\,}^{(j)} = ({{\boldsymbol{x}}}_{\,\text{train}\,}^{(j)},{{\boldsymbol{y}}}_{\,\text{train}\,}^{(j)})\}}_{j = 1}^{N}$. A higher value of ${\mathcal{F}}({{\boldsymbol{s}}}_{{\boldsymbol{\theta }}})$ indicates a stronger alignment between the generated and ground-truth scores. As shown in Figure 4, this metric exhibits a strong correlation with inference-time scaling performance based on the self-supervised reward mechanism. Based on this observation, we implement a conditional logic with ${\mathcal{F}}({{\boldsymbol{s}}}_{{\boldsymbol{\theta }}}) > \tau$ to activate the inference-time scaling scheme during guidance generation. In this way, we establish a general inference-time scaling framework for offline optimization by substituting external reward models in existing schemes with self-supervised rewards.

This framework is compatible with various methods, including the IS-based scaling [50] and the FKS-based scaling [51] methods. For example, we illustrate the complete process of ManGO based on IS with the self-supervised reward in Algorithm 1. Self-IS-based ManGO is designed to explore the denoising paths with higher rewards. Specifically, the algorithm first duplicates each noise point ${\hat{{\boldsymbol{x}}}}_{t}^{(i)}\,J$ times. Each copy then undergoes an independent denoising step as defined in Eq. (5), where the inherent randomness in the reverse process—introduced through the Wiener noise term. This causes the denoising paths to diverge and results in divergent candidates ${\{{\hat{{\boldsymbol{x}}}}_{t-1}^{(i,j)}\}}_{j = 1}^{J}$ at the next timestep. For each candidate, ManGO estimates its corresponding denoised state to compute self-supervised rewards ${\mathcal{R}}({\hat{{\boldsymbol{x}}}}_{t-1}^{(i,j)})$ Eq.s (8) and (9). These rewards drive an importance sampling mechanism that prioritizes higher-reward paths, effectively steering the generative process toward more promising regions of the design-score manifold. This framework leverages the innate stochasticity of diffusion models to explore the noise space dynamically, eliminating the need for explicit external perturbations or reward models. Our experiments validate the integration of the IS and FKS approaches with self-supervised rewards.

Algorithm 1

Self-IS-based ManGO

Training and inference settings

Our model architecture processes three input components: design, scores, and timestep. The timestep undergoes standard cosine embedding, while design and score are independently projected via fully connected layers, both to 128-D features. These features interact bidirectionally through cross-attention layers, with outputs fused via two multi-layer perceptron (MLP) layers (128 hidden units, Swish activation). The fused features are then combined with time embeddings and processed through a three-layer MLP (2048 hidden units, Swish) for reconstruction. We employ AdamW optimizer with a learning rate (LR) of 5 × 10⁻⁵, a weight decay coefficient of 1 × 10⁻⁴, and a one-cycle LR scheduler with cosine annealing. Training converges in 800 epochs for SOO and 400 epochs for MOO, maintaining original baseline configurations. The diffusion process uses ${\beta }_{\max },{\beta }_{\min }=1\times 1{0}^{-4},5\times 1{0}^{-2}$ for SOO and 1 × 10⁻⁴, 5 × 10⁻³ for MOO.

During inference, we configure 200 denoising steps for all MOO tasks, Ant and DKittyMorphology of Design-bench tasks, 5 for Superconduct tasks, and 250 for TF-Bind-8 and TF-Bind-10. For the guidance scaler, we set α_x = 1, α_y = 1 for design-constraint trajectory generation in Figure 2, and α_x = 0, α_y = 1 for benchmark evaluation. For the sake of comparison, we disable the fidelity-adaptive activation of the inference-time scaling, denoted as (10), in the self-supervised importance sampling-based ManGO. The scaling methods are activated every five denoising steps, where the IS-based scaling uses beam search with duplication size J = 16, and the FKS-based scaling uses accumulated maximal rewards. Complete implementation details are provided in the supplementary material.