Introduction

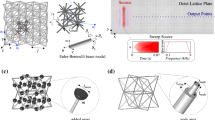
With the advancement of additive manufacturing (AM), lattice metamaterials have revolutionized structural and functional design across multiple industries1. These highly ordered cellular architectures offer lightweight solutions with tuneable mechanical, acoustic, and thermal properties, making them indispensable in fields such as aerospace, automotive, biomedical, architecture, and so on2. Lattice metamaterials can be broadly classified into strut-based, triply periodic minimal surface (TPMS), and plate-based architectures (Fig. 1). Strut-based lattices, reminiscent of traditional truss architectures, consist of struts interconnected at nodes and are the most fundamental and widely studied type of lattice architecture. TPMS lattices, with their continuous, mathematically defined curved surfaces, allow improved mechanical properties and fluid exchange and are thus often adopted for heat exchangers and biomedical scaffolds. Plate lattices, a relatively recent advancement, use planar elements instead of struts and curved surfaces and offer significantly enhanced mechanical properties. Apart from this, the unique and highly customizable architecture of plate lattices renders it the most promising candidate for achieving multifunctionality. This primarily arises from the strategic, or even designable, integration of pores or hybrid features within the closed plate cells, to overcome manufacturability limitations and to enable functional performances.

Fig. 1: Overview of lattice metamaterial types, including plate, TPMS, and truss-based architectures.
figure 1

Plate lattices are further categorized into three classes—pure plate, perforated plate, and hybrid plate—highlighting their distinct and higher number of structural features and potential for achieving multifunctionality.

Full size image

Plate lattices can be generally categorized into three main types based on design: (i) pure plate architecture associated with the closed cell, (ii) perforated plate, and (iii) hybrid plate (Fig. 1). The first category comprises entirely of solid, flat plates. Fundamental structures involve the crystal structure mimicking plate lattices based on the simple cubic (SC), body-centred cubic (BCC), and face-centred cubic (FCC)3,4. Specifically, these plate lattices are formed by replacing the family of slip planes with solid plates. However, pure plate lattices are closed-cell in nature, rendering them impossible to be manufactured using mainstream AM processes like powder-bed fusion or vat photopolymerization, as residual feedstock material would be entrapped within enclosed cells. To improve manufacturability and multifunctionality, researchers have introduced pore structures within plate lattices to form (ii) perforated plate lattices. These strategically placed pores have been shown to serve multiple functions, including tuneable mechanical properties that allow engineers to adjust stiffness, strength, and weight by varying pore size and distribution. Additionally, they enhance acoustic performance by acting as Helmholtz resonators, effectively absorbing sound and reducing noise transmission5,6,7,8. Furthermore, narrow pores induce a large pressure drop, which increases fluid velocity and subsequently enhances the Nusselt number, leading to improved convective heat transfer9. Lastly, there are also (iii) hybrid plate lattices formed by integrating plates with truss and tube features. Due to the incorporation of these elements, hybrid plate lattices inherently mitigate feedstock entrapment during AM by avoiding closed cells. Hybrid truss-plate lattices further enhance vibration isolation by exploiting the alternating high-mass and low-mass regions inherent to their architecture, creating local impedance mismatches that effectively attenuate vibrations and dissipate mechanical waves through scattering and damping mechanisms10,11. The abovementioned features, such as closed cells with perforations and cells with weakly joint features, are distinct characteristics of plate lattices and are generally not present in conventional TPMS or truss lattices (Fig. 1). Across different configurations, plate lattices consistently exhibit strong mechanical performance, largely attributed to the inherent robustness of their plate-based architecture (Fig. 2a).

Fig. 2: Overview of mechanical properties across the three classes of lattice structures.
figure 2

Comparison of the (a) relative Young’s modulus and (b) relative strength across the three classes of lattice structures. References used include: perforated SC and FCC plate14, perforated isotropic plate15, sheet gyroid, primitive, I-WP16, skeletal gyroid16, FCC + SC truss17, and BCC trusses18. c Enhanced energy absorption derived from incorporating plate features in truss lattices. Adapted with permission7.

Full size image

This perspective advocates plate lattices as versatile scaffolds for multifunctional material systems. Their inherently planar architecture, designable pores, and hybrid features provide a unique platform for integrating multiple physical phenomena within a single structure. In this perspective, we introduce the recent developments, highlight the multifunctional advantages of plate lattices, and briefly discuss the challenges and future directions that may guide their transition from promising prototypes to practical engineering solutions.

Advantages over other types of lattices

Mechanical properties

In terms of specific stiffness and strength, plate lattices unequivocally lead in this category, with some designs capable of reaching the theoretical upper limits for isotropic stiffness and strength of air-solid porous structures3,4,12. Fig. 2a, b presents a summary of the relative Young’s modulus and strength comparison for 3D-printed lattices, highlighting representative plate lattices alongside TPMS and truss lattices. The highlighted range of relative densities is kept below 40%, aligning with the commonly accepted threshold among researchers for defining cellular solids13. This includes the perforated SC and FCC plate14, perforated isotropic plate15, sheet gyroid, primitive, I-WP16, skeletal gyroid16, FCC + SC truss17, and BCC trusses18. As shown, plate lattices display higher specific stiffness across the wide range of relative densities. This is attributed to the membrane stress state introduced by the presence of plates, regardless of the specific plate type, as the fundamental characteristic of having plates inherently influences the deformation behaviour. Truss lattices are typically bending-dominated unless designed with high node connectivity, e.g., the FCC architecture, yet even these optimized structures fall short of plate lattice performance. TPMS lattices, more prominently the sheet-based, typically surpass trusses but still underperform compared to plate lattices16,19. For instance, at 40% relative density, an isotropic truss consisting of SC + FCC struts may achieve approximately 30% of the normalized stiffness of a solid material, whereas an isotropic plate lattice at the same relative density can achieve 55%, approaching the theoretical Hashin-Shtrikman upper bound4. In terms of strength, except for ultra-thin plates of below 5% relative density20, which are less commonly seen, plate lattices resist deformation (local bucking and yielding) more effectively and yield at higher loads than other lattice types owing to their load-spreading architecture4. They generally exhibit higher specific strength than the other lattice classes, as shown in Fig. 2b through comparisons of the same lattice types presented in Fig. 2a.

While it is possible that all types of lattices can deform in a controlled and gradual manner with a long and smooth plateau, plate lattices also stand out in terms of energy absorption for their high specific strength5. Given specific energy absorption (SEA) to be the mass-normalized integral under the area of the stress-strain curve, up to densification, higher specific strength would naturally result in higher SEA. Additionally, plate lattices are more likely to exhibit a smooth and stable plateau during compression deformation, primarily due to their membrane stress state under loading5. In contrast, truss lattices of comparable strength or relative density, when fabricated from the same material17, frequently display localized failure and sudden stress drops associated with strut bending, global shear deformation, or buckling. This is shown in Fig. 2c, where with the incorporation of plate features, the hybrid plate structure (termed the BMMM in the figure) architecture enhances toughness by promoting distributed damage and progressive bending, rather than localized fracture seen in hollow truss lattices7. Across different materials, plate lattices fabricated from ductile materials, such as stainless steel21, polyamide22, etc., naturally exhibit the highest toughness and specific energy absorption (SEA) due to their ability to undergo significant plastic deformation before failure. However, studies have also shown that even in less ductile materials, such as low-alloy steel, e.g., 41305, Ti-6Al-4V7, brittle plastic6, plate lattices still demonstrate a gradual plateau response during compression, contributing to high SEA. Overall, plate lattices are often observed to exhibit higher mechanical performance than TPMS and truss lattices. However, this trend may not hold when lattices of very low relative densities, e.g., <5%, are being compared20, or when structurally-weak plate lattice designs, such as plate lattices with large perforations, are being compared.

Acoustic behaviour

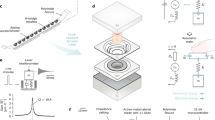
Perforated plate lattices display unparalleled sound absorption performance compared to TPMS and truss lattices. This is primarily attributed to the presence of multi-layered Helmholtz resonance (MLHR) absorption mechanisms, enabled by the incorporation of narrow pores followed by large, enclosed plate cavities within the plate architecture. An example is illustrated through a perforated FCC plate in Fig. 3a, focusing on the introduced pore and the immediate plate cell cavity. With the MLHR mechanism, perforated plate lattices display high absorption coefficients nearing unity at resonant frequencies (Fig. 3b). To enhance absorption bandwidth, geometrical heterogeneity can be introduced, allowing different resonance modes to operate in tandem23,24. This effectively produces absorption curves derived from the superposition of individual resonant components, resulting in broader and more efficient absorption (Fig. 3c). In contrast, the relatively much more open-cell nature of truss and TPMS lattices provides significantly weaker resonance and sound absorption25,26,27,28,29. While MLHR is still possible in trusses and certain TPMS lattices, it primarily occurs only at sufficiently high relative densities of around 30% or higher only. For instance, in trusses, narrow pores and wide cavities can only form if struts are sufficiently thick or the structure is sufficiently complex5,30. Low relative density trusses, without the MLHR mechanism, display poor absorption based on only general airflow resistance (Fig. 3d)27. Resonance can also occur in TPMS lattices through cavity resonance; however, it is significantly weaker than MLHR and is only effective within a specific combination of cavity width and depth, limiting its tunability and overall absorption efficiency. Due to the inherent ability to strategically introduce pores, MLHR is always present in plate lattices, regardless of their structural configuration or relative density. The closed-cell nature of plate lattices naturally forms wide cavities, inherently satisfying all the necessary conditions for MLHR. For any plate lattice in general, pores can be introduced at places such as nodes5, edges6, faces of plates8,31, leading to different critical MLHR geometrical parameters and thus enabling tailored sound absorption. A recent study on perforated plate lattices demonstrated that, while maintaining the same overall structure, sound absorption can be significantly tuned to a desired resonance range simply by adjusting solely the pore dimensions32.

Fig. 3: Overview of acoustical properties.
figure 3

Illustration of (a) how a perforated FCC plate can be modelled as a Helmholtz resonator, (b) with its corresponding sound absorption curves. Figures adapted with permission5. c A heterogeneous perforated plate lattice exhibiting a broadband absorption curve, resulting from the superposition of individual resonance peaks, and a plot of its complex plane diagram. Figures adapted with permission44. d Illustration of a low and high relative density FCC truss, signifying both poor non-resonance absorption and observable resonance absorption, respectively. FCC trusses adapted from25, and sound absorption curve adapted from26, with permission. e The sound transmission loss and corresponding bandgap plot of a hybrid perforated FCC and tube lattice. Figures adapted with permission45.

Full size image

In terms of sound insulation, plate lattices exhibit superior insulation owing to pronounced Bragg scattering and their ability to leverage local resonance. Compared to other lattice structures, particularly trusses, plate lattices exhibit a high solid surface coverage, resulting in a pronounced acoustic impedance mismatch with air. Since Bragg scattering is related to sound scattering and reflection, this pronounced mismatch enhances attenuation arising from Bragg scattering33. Apart from this, increased sound wave reflection and scattering also enhance sound insulation in general. Similar to their use of MLHR for sound absorption, plate lattices can also harness it for local resonance sound attenuation. In perforated plate lattices, MLHR provides an additional resonance mode (Fig. 3e) that complements the Bragg scattering inherent to all periodic structures, thereby broadening the sound insulation bandwidth beyond that achievable by Bragg scattering alone. This additional resonance mode significantly expands the sound insulation bandwidth beyond what is achievable with Bragg scattering alone. In contrast, without notable acoustical resonance mechanisms34, truss and TPMS lattices are speculated to rely solely on Bragg scattering and general wave reflection, limiting their effectiveness in achieving broadband sound insulation.

Thermal behaviour

Thermal behaviour generally refers to properties in terms of heat conduction and forced convection heat transfer. For thermal insulation applications, plate lattices typically create a highly tortuous pathway that hinders heat conduction, while their low permeability suppresses natural convection, together minimizing overall heat transfer. Owing to their plate-based architecture, a greater quantity of solid material, compared to trusses and TPMS, is arranged at angles that block direct lines of sight between opposing faces of the lattice. This is agreed on by Berger et al. for their closed cell plate lattices4. In contrast, truss and TPMS lattices, being open-cell structures, allow convective heat transfer and facilitate conduction through their interconnected struts or shells, making them less effective insulators35,36. Also, the smooth shell TPMS structure and trusses with struts aligned along the heat flow channel heat flow effectively. Therefore, for insulation, the general hierarchy is Plate > TPMS and Truss, as plate lattices best retain stagnant air and have torturous paths that do not channel heat flow effectively.

Compared to TPMS and trusses, perforated plate lattices excel in forced convection heat exchange via higher pressure drop and turbulence possibly induced. This is due to the incorporation of narrow pores on plate surfaces, which induces the Venturi effect. In turn, TPMS and trusses provide a balance between high surface area and moderate pressure drop. The heat transfer performance of perforated SC plate lattices has been demonstrated, particularly in a setup where the lattice array is placed between a constant-temperature base plate and a fluid flow channel (Fig. 4a)9. Heat is conducted from the base plate to the lattice and dissipated through convection as the fluid moves across the structure. Unlike SC truss structures, the perforated SC plate enhances heat dissipation by leveraging a higher pressure drop, which increases fluid velocity through the lattice. Despite having a smaller contact surface area with the heat source, this increased velocity raises the Reynolds number, promoting turbulent flow and improving the Nusselt number, which directly enhances convective heat transfer efficiency. Compared to a series of truss lattices, the perforated SC plate achieves a higher convective heat transfer coefficient, especially when normalized by its contact surface area, demonstrating the dominance of convection in forced convection setups (Fig. 4b). Although low permeability and high pressure drop are often viewed as drawbacks for engineering applications, careful tuning of pore size allows plate lattices to be strategically engineered for desired permeability levels, making fluid flow tunability more of a design parameter than a fixed limitation.

Fig. 4: Overview on thermal and vibrational properties.
figure 4

a Illustration of the convective heat transfer setup with the inset showing the perforated SC plate lattice, and (b) convection heat transfer coefficients, normalized per unit contact surface area. Figures adapted with permission9. Comparison of the bandgap diagram and modal vibration pattern for the (c) BCC truss and (d) BCC truss and plate hybrid, revealing the distinctly wider and increased number of bandgaps and vibration modes. e Schematic of the mass-spring system, and the (f) transmission loss plot of this hybrid plate. Figures adapted with permission10.

Full size image

Vibration damping

Plate lattice structures demonstrate significant advantages over truss and TPMS lattices for vibration damping due to their ability to generate broadband and low-frequency band gaps by leveraging local resonance mechanisms. Again, this is attributed to the high structural customizability of plate lattices over truss and TPMS. In hybrid truss-plate lattices, in which a central plate region is bounded by struts, the mass of the central plate unit acts as a localized resonator, and the surrounding truss struts function as elastic springs10,11. The band diagram of a BCC lattice is shown in Fig. 4c. As shown, indeed, there is only one extremely narrow bandgap being observed. Instead, for a BCC truss and plate hybrid lattice, from Fig. 4d, increase instances of bandgaps and corresponding widths is observed. The vibration mode at the lower edge of the first bandgap (0.694 kHz) in the lattice is primarily governed by the lateral resonance of its central resonator, while the vibration mode at the upper regions (3.414 kHz) are mainly driven by the bending vibrations of the surrounding connecting beams. The resulting resonance-driven bandgaps can emerge at frequencies much lower than those achievable through periodicity-based Bragg scattering alone with also higher transmission losses. Schematic of the mass-spring mechanism in the hybrid lattice is shown in Fig. 4e. As shown in the transmission loss curves in Fig. 4f, the hybrid lattice demonstrates markedly higher and broader energy attenuation than the BCC structure, with instances reaching up to even −106 dB. Another work presented hybrid plate lattices consisting of chiral plates37. Herein, local resonance is achieved through chirality, specifically the in-plane translation, rotation, and out-of-plane motion of the chiral plates. Multiple bandgaps spanning a wide frequency range (1991 – 4340 Hz) are demonstrated, with the highest transmission loss demonstrated to be nearing −80 dB. As comparison, many conventional trusses and TPMS do not display bandgap behaviour, or only small bandgap at high frequencies owing to Bragg scattering38,39. Further, transmission loss would also be low compared to that of the hybrid plate lattices of similar sizes.

Plate lattices also provide greater tunability in bandgap design compared to truss and TPMS structures. By adjusting key geometric parameters — such as plate morphology, pore size, and/or strut configuration — engineers can precisely control the frequency range and width of bandgaps without significantly affecting mechanical integrity. For instance, increasing the outer and inner strut diameter for the lattice shown in Fig. 4d allows the increase and decrease of bandgap position, respectively, without significantly influencing SEA11. This level of tunability is far superior to that of truss lattices, which require drastic changes in strut dimensions or connectivity to shift bandgap frequencies. Additionally, artificial masses are often introduced at nodes of unit cells40, or strategic regions in the repeating structures to introduce additional masses to increase the contrast in stiffness41. Similarly, TPMS lattices are defined by mathematical equations, and they offer little degree of customization, primarily through local thickness variations. For trusses and TPMS, although bandgap may be tuned by changing the relative density and unit cell sizes, they lack the fine-grained control over local resonance effects that plate lattices provide38.

Discussion

One of the most transformative aspects of plate lattices is their ability to introduce tuneable pores, which significantly enhances their functional versatility. By strategically incorporating pores of different sizes, shapes, and distributions, engineers can tailor properties beyond what is achievable with truss and TPMS lattices. Their designable pores enhance sound absorption via MLHR, providing superior sound absorption and insulation than truss and TPMS structures. In thermal applications, these pores regulate heat transfer, improving insulation in closed-cell configurations and enhancing convective heat dissipation in open designs. In a similar sense, the ability to introduce hybrid features further pushes the boundary for multifunctional design. Notably for vibration damping, the hybridization enables high-mass plate regions and low-mass truss supports that creates local resonance mechanisms for a broad elastic wave bandgap. It is worth noting that all the abovementioned properties may simultaneously co-exist along through the customized porosity (Fig. 1). This being said, plate lattices redefine multifunctionality by leveraging their designable pores and hybrid features to simultaneously achieve superior mechanical, acoustic, thermal, and vibration properties. While porosity may compromise structural integrity, plate lattices can still preserve notable stiffness and strength through their membrane stress state, and in many cases demonstrate favourable mechanical resilience and energy absorption relative to trusses and TPMS.

Despite their advantages and potential, plate lattices nonetheless face limitations and challenges. A fundamental issue is the manufacturability of fully closed-cell plate architectures using mainstream AM processes such as vat photopolymerization and laser powder-bed fusion, owing to the entrapment of feedstock materials within sealed cavities3. While perforations and hybridization are introduced to mitigate this problem, the minimum achievable pore or feature size is also constrained by the AM process. Another challenge lies in scalability. For the aforementioned functions, plate lattices generally operate at small scales, often down to the centimetre level5,8,9,10,11. Scaling their unit repetition or production for adoption in large-scale engineering solutions is not yet economical due to the inherent cost-efficiency and increased risk of build failure for larger prints in AM42. Furthermore, design optimization is inherently complex; multifunctionality might result in trade-offs between stiffness, strength, acoustic absorption, and thermal or vibrational behaviour, to name a few functions. This necessitates advanced computational approaches such as machine learning-assisted design43. Nevertheless, efforts to develop such methods are also driving the growth of more sophisticated design strategies for plate lattices.

Overall, plate lattice metamaterials offer a breakthrough in lightweight and multifunctional design. We foresee their integration into aerospace, automotive, biomedical, and energy sectors to be advanced in the near future. Further research in heterogeneous configurations, smart materials, and machine learning-driven design will expand their potential. As manufacturing capabilities evolve, plate lattices are poised to become a mainstream engineering solution, bridging the gap between strength, weight, and multifunctionality, thus fulfilling the promise of architected materials in high-performance applications.