A simplified wearable device powered by a generative EMG network for hand-gesture recognition and gait prediction

Abstract

There is an inherent trade-off between the design of comfortable wearable sensors and the need for high-resolution and large-area sensing. Here we address this challenge by introducing a generative electromyography (EMG) network (GenENet), a self-supervised generative representation learning framework combined with a wearable sensor that extrapolates limited sensor inputs to reconstruct muscle activity in unseen regions not covered by the sensor. This approach allows for gathering information equivalent to those from high-density EMG sensor networks, but using a more compact, wearable device with much reduced sensor counts, without sacrificing performance. For example, a 6-channel EMG device trained on a 32-channel dataset from low-impedance polymer electrodes shows similar performance to a 32-channel device in accuracy for predicting sign language and gait dynamics, highlighting the utility of the GenENet concept to reduce wearable-sensing-system complexity while maintaining prediction quality. Such electrophysiological data are essential for many applications, including motion detection and control, but traditionally require high-density, high-resolution sensors that can be cumbersome. This concept should be applicable to other types of electrophysiological mapping application across health monitoring, prosthetics, sports and human–machine interfaces, paving the way for more comfortable and efficient wearable devices.

Main

Accurate information extraction in many sensing applications hinges on the deployment of high-density and high-resolution sensors^1,2,3. Wearable technologies are at the forefront of this development, delivering a rich, continuous stream of data that captures a broad range of biometric details. These range from kinematic information, such as movement and vibrations^{1,2,4,5,6,7,8,9,10,11}, to physiological signals^12,13,14, including temperature^15,16 and various electrophysiological markers derived from muscle^4,17, brain^12,18,19 and cardiac^{20,21,22,23,24} activities.

Electromyography (EMG) is widely used for non-invasive monitoring of muscle activity across different body regions^3,4,5. The complex interplay between muscle groups and the corresponding body movements calls for sophisticated high-density surface EMG instruments capable of capturing intricate kinematics, such as gesture recognition^3,5 and gait analysis^25,26. Despite advancements in electrode design to reduce impedance and enhance flexibility, as well as in computational algorithms to improve signal processing and predictive accuracy, a notable challenge remains: EMG devices with a large area and high electrode count are required for accuracy, but this increases the size of the devices and limits their practicality and adoption.

To address this challenge, here we introduce a generative EMG network (GenENet) that enables predicting EMG information from a smaller set and area of sensor inputs. GenENet is an autoencoder-based self-supervised generative representation learning algorithm trained to generate unseen sensor signals, discerning generalized patterns across sensor activations from a larger body area. Leveraging this prior-learned network of associations between sparse sensory inputs and providing a latent representation approximating the corresponding full-scale sensory mapping, our approach demonstrates an enhanced capability for a simple low-channel-count device to predict a spectrum of body kinematics previously reliant on high-density sensor arrays^4,5,27. To further enhance the efficacy of our system for wearable applications, we integrated it with stretchable sensors and low-impedance electrodes. These sensors offer superior conformity to the skin and facilitate the acquisition of low-noise signals that enable high performance of the generative network by reducing motion artefacts and contact impedance.

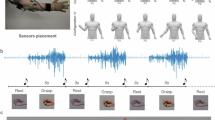
To develop GenENet, first, we designed a 32-channel soft EMG array for initial data collection to support prior learning, feeding this into our generative algorithm while omitting around 80% of the data. The model then learns to reconstruct the missing information by comparing the generated signals to the complete 32-channel signals (Fig. 1a). This pre-trained model is then integrated with a simplified 6-channel device, which, despite fewer sensing channels, generates a vector equivalent to that from a 32-channel array (Fig. 1b). The information is subsequently processed by the post-training network, which extracts crucial features of spatiotemporal muscle activities to classify static states and sequential movements, applicable to tasks such as American Sign Language (ASL) translation and gait dynamics prediction (Fig. 1c). Corresponding images of devices used for dataset collection are shown in Fig. 1d–f.

Fig. 1: GenENet for sign language and gait prediction.

a, Representation learning via GenENet using a 32-channel stretchable device, with random masking of input signals to reconstruct the original data. b, Use of a smaller 6-channel device, where the pre-trained network predicts muscle activity in unseen areas. Reference (REF) and ground (GND) electrodes are placed on the right side. c, Post-training network, enabling the transfer of the pre-trained model to different applications and users. d–f, Images showing each stage corresponding to a–c, respectively. The wireless module consists of flexible printed circuit board (FPCB).

A stretchable sensor for a high-quality dataset

The objective of the pre-training generative algorithm is to reconstruct the original temporal and spatial patterns of muscle activity signals with high fidelity using minimal sensor inputs. Achieving high accuracy from the generative model is contingent on the quality of the training dataset. To facilitate the creation of a high-quality dataset, we have engineered a fully stretchable multi-array EMG device.

The device’s layer is depicted in an exploded view in Fig. 2a. It comprises several layers: a polydimethylsiloxane (PDMS) substrate, a solvent resistant poly(acrylonitrile-co-butadiene) (NBR) protective layer, a gallium–indium eutectic (EGaIn) electrode, a poly(3,4-ethylenedioxythiophene):poly(styrenesulfonate) (PEDOT:PSS) gel and a poly(styrene–butadiene–styrene) (SBS) encapsulation. The PDMS layer provides a thin substrate with submillimetre thickness for flexible handling and easy adherence to various body contours. The NBR layer acts as a barrier to protect the PDMS from solvent-induced swelling during the fabrication of the multiple layers. The EGaIn liquid metal electrode, which is both stretchable and micro-patterned, was then applied, followed by a highly conductive PEDOT:PSS gel that serves to lower impedance when in contact with skin. The device is completed with a photo-patterned SBS layer that leaves only the electrode areas uncovered, ensuring skin contact and signal measurement. A biomedical adhesive (Skinister) is applied on the skin to ensure a conformal and secure attachment of the device before usage. Figure 2b illustrates the side view of the sensor array and the fabricated stretchable array. The device shows resilience to elongation, utilizing an intrinsically stretchable substrate along with electrodes made of EGaIn and PEDOT:PSS, as shown in Fig. 2c. It is then connected to a wireless device via a flexible flat cable, which is interfaced using anisotropic z-axis conductive tape (Fig. 2d and Extended Data Fig. 1).

Fig. 2: Stretchable sensory array for high-quality dataset generation.

a, An exploded view of the 32-channel stretchable array, showing encapsulation, sensing electrodes, interconnections and substrates. b, Side view of the 32-channel device. c, Comparison of the device in its original and stretched states. d, The 32-channel device connected via a flexible flat connector (FFC) to a custom-made wireless module (Extended Data Fig. 1). e, Electrochemical impedance spectroscopy of hydrogels with (15 mg ml⁻¹ PEDOT:PSS with 150 mg ml⁻¹ AAm and 2.5 mg ml⁻¹ N,N’-methylenebisacrylamide) and without PEDOT:PSS. f, Impedance endurance plot under 100% strain. The inset image shows PEDOT interconnects under 0% and 100% strain. Z and Z₀ denote the impedance under strain and at the unstrained state, respectively. Scale bars, 20 mm. g, Welch’s power spectral density comparing PEDOT gel with Ag/AgCl electrodes of the same size. The inset illustrates the measurement setup using a dynamometer with electrodes attached to the forearm. h,i, SNR box plot of the device fabricated on a non-stretchable polyimide substrate (h) versus the device fabricated on a stretchable substrate (i), showing higher mean SNR across the 32 channels for the stretchable substrate. Data are presented as box plots showing the median (centre line), 25th–75th percentiles (box), and whiskers extending to the most extreme data points within 1.5× the interquartile range (IQR). The red dashed line indicates the mean value of the SNRs.

Our conductive adhesive electrode is composed of an acrylamide (AAm) crosslinked gel with a PEDOT:PSS conducting polymer network. This provides both good electrical and mechanical properties, improving impedance characteristics and minimizing noise from movement. Our modifications to the AAm polymer network with the addition of PEDOT:PSS have resulted in a notable reduction in interfacial impedance when interfaced with phosphate-buffered saline (PBS), as seen in Fig. 2e. The impedance of the PEDOT-modified gel remains low at 100% strain at 50 Hz (Fig. 2f and Supplementary Fig. 1). Moreover, upon performing Welch’s power spectral density estimate, the developed sensor array shows a higher power density compared with a standard Ag/AgCl electrode of the same size under 15 kg of grasp, as depicted in Fig. 2g.

To explore the capabilities of using a stretchable device, we fabricated the PEDOT electrodes above a non-stretchable thin polyimide substrate (20 µm thickness versus 200 µm used for the stretchable array, Supplementary Fig. 2). When subjected to a 20 kg grasp, applied at the same location on the wrist, the non-stretchable array showed a lower mean signal-to-noise ratio (SNR) of 12.19 dB across the channel, as shown in Fig. 2h. In contrast, the stretchable array showed a consistently higher mean SNR (15.06 dB), as depicted in Fig. 2i.

Pre-training generalizable representations of EMG signals

The raw signals captured by the 32-channel sensory array (Fig. 3a, Supplementary Fig. 3 and Extended Data Fig. 2) were subjected to post-processing, which involved the calculation of root-mean-square (RMS) values across 32 time windows, using a sliding window with a size of 10, as depicted in Fig. 3b. The training dataset was selected from the arbitrary movement of fingers and gait movements attached to wrist (20 min; Methods) and calf (15 min walking; Methods). This large dataset allows for pre-training of the generative algorithm to capture generalized muscle signal activities during the kinematic cycles.

Fig. 3: Pre-training of the GenENet.

a, The 32-channel stretchable device captures muscle activation signals from the wrist or calf during arbitrary finger movements and walking. b,c, The signals undergo augmentation (b) and RMS processing (c) using a 32 time windows (32 time steps with 128 ms) with a sliding time (window interval; 10 time steps with 40 ms). The colour bars indicate normalized amplitude. d, Random masking (black regions) of the post-processed tensor, with GenENet trained to minimize the MSELoss between the generated and original signals. E and D denote the encoder and decoder modules of GenENet, respectively. e, Representative signal from sample 1 (S1), showing the masked, original and generated signals across the training epochs. The first row shows the generated output from an early epoch and the second row shows the output after 450 epochs. The plot on the right shows the decrease in mean squared error (MSELoss) during training. f, Detailed plot of the generated signal over the course of training. g, Results for additional samples, sample 2 (S2) and sample 3 (S3) after 450 epochs. The samples were randomly selected; an additional 100 representative samples are shown in Extended Data Fig. 3.

To mitigate the high computational demands associated with conventional spectrogram conversion, we used RMS values as a simplified representation of the EMG signals (Methods and Supplementary Video 1). Consequently, an EMG signal tensor with dimensions of 32 × 32 × 1 (32 time windows × 32 channels × 1 signal) is generated as shown in Fig. 3c. Subsequently, we deliberately masked some patches in the complete sensor data as shown in Fig. 3d. These masked data were then fed into GenENet. To strengthen the model’s resilience against varying sensor attachment positions and orientations, we randomly distributed the masking locations, and the input of the tensor is augmented through resizing, random cropping and flipping for model optimization and generalizability (Methods). The architecture of our learning model adopts an autoencoder framework, principally divided into two sections: an encoder and a decoder. The tensor is divided into 64 squared patches, with 52 patches (81%) randomly masked. The encoder translates the intentionally random masked signals into a latent representation and the decoder reconstructs the missing patches in the pixel space. The encoder–decoder layers consist of multi-head attention, normalization and linear layers. The main structure is based on generalized denoising autoencoders, a scalable self-supervised learning approach used in computer vision^28,29,30.

Figure 3e illustrates that through the training cycles, GenENet successfully reconstructed the original signals using the masked inputs. A masked input, the original unmasked signal and the generated signal for sample 1 (S1) are shown across the training epochs. As the mean squared error loss (MSELoss) between the generated signal map and the original decreases during training, the generated signal map evolves from random noise to a much clearer representation (Supplementary Fig. 4). A detailed view of the generated signal map throughout the training epochs is depicted in Fig. 3f. The application of GenENet to additional samples, S2 and S3, is shown in Fig. 3g, with a generated view of 100 additional samples presented in Extended Data Fig. 3. The fidelity of the reconstructed EMG signals is shown through signal distribution histograms over a training batch (n = 128) and uniform manifold approximation and projection visualization (Supplementary Fig. 5)

Downstream adaptation of GenENet for sign language prediction

To demonstrate practical deployment, we designed a compact six-channel wireless EMG watch, depicted in Fig. 4a, for gesture prediction (Extended Data Fig. 4). Our initial dataset consisted of EMG recordings corresponding to the 26 hand gestures representing the ASL alphabet, from A to Z. Using the pre-trained GenENet, we refined the model to enhance its predictive capabilities for ASL interpretation. Previously, achieving accurate predictions for a large number of gestures using EMG has required a dense array of electrodes, often exceeding 64 channels^5,17,27 (Supplementary Table 1). Others used non-EMG sensors, specifically capacitive and piezoelectric sensors that cover the entire finger^2,8,9. While these glove-type sensors offer easier tracking of finger movements, they are limited in terms of wearable form factor and are affected by motion artefacts. In contrast, our approach requires only a band placed above the wrist.

Fig. 4: Prediction of ASL using the GenENet device.

a, Sign language input signals captured through the six-channel device. b, Post-processing steps identical to pre-training, excluding data augmentation. c, Post-processed tensors are fed into GenENet, connected to a CNN, LSTM and dense layer. The dashed line of the decoder and CNN are only activated on regression modelling. d, Classification of sign language gestures. e, FOM measured by balancing model accuracy and total sensor area. f, FOM peaks in the six-channel region, where increasing channel count enhances accuracy but also enlarges the sensor area. g, Validation accuracy comparison between the pre-trained GenENet and the non-parameterized GenENet using six-electrode EMG array measurements for finger motion recognition. The dataset is divided into training and validation datasets with a ratio of 8:2. h, Adaptability of the device to different locations and orientations on the wrist, showing negligible accuracy differences. L1–L7 indicate the location and orientation of the electrode array attachment. i, Sign language prediction using numeric values (0–25, that is 0 for A and 25 for Z) from 6-channel EMG inputs. The red plot represents the predicted numeric values, and the corresponding alphabet labelled on top, from the EMG input signals. j, Batch attribution map for representative letters A, N and R, with corresponding EMG signals and attribution maps. ‘−1’ indicates a negative contribution to prediction and ‘1’ indicates a positive contribution to prediction. Each row in the signal corresponds to one of the six sensor channels, with channel 1 at the bottom and channel 6 at the top.

Previously, EMG and speech-recognition tasks often used attention-based encoder–decoder frameworks^31,32 or convolutional neural network (CNN)–transformer hybrids (for example, Conformer^33,34). In contrast, our method directly leverages the generalized representations learned through masked generative pre-training and feeds them into a lightweight long short-term memory (LSTM) classifier. This approach not only improves predictive performance but also exploits the masked autoencoding framework to operate effectively on intentionally masked hardware inputs, thereby reducing sensing complexity and enabling hardware-efficient deployment.

As shown in Fig. 4b, the collected channel data undergo post-processing, which includes calculating RMS values across time windows and sliding windows, as described in the generative algorithm pre-training in Fig. 3. The remaining channel information is zero-padded and fed into the encoder to generate a latent vector, which is subsequently processed through an LSTM network with a sequence length of seven (Supplementary Fig. 6), as depicted in Fig. 4c. Finally, a dense layer with an output size of 26 is used to predict the entire alphabet classes (Fig. 4d).

The selection of 6 channels and its performance collaborating with the generative algorithm was investigated next. As shown in Fig. 4e, we identified a trade-off between the number of channels and performance, which is influenced by the total electrode area (assuming each electrode is of the same size) of the EMG device versus its accuracy. We experimented with different channel numbers ranging from 2 to 16 and compared the 20-epoch accuracy using the same dataset (Supplementary Fig. 7). The figure of merit (FOM) was defined as Accuracy − λ × Form factor, where the form factor is the area (mm²) and λ = 0.0005. The parameter λ is chosen to appropriately scale the form factor (measured in mm²) to align with the accuracy range. This ensures that the units and magnitudes of both components are balanced, making the FOM meaningful and interpretable within the desired range. The results showed that the FOM peaked with a moderate number of channels. A smaller number of EMG electrodes led to a substantial drop in performance due to limited signal information, while a larger number of electrodes improved performance but substantially increased the device’s area, negatively impacting user comfort.

As shown in Fig. 4g, the pre-trained GenENet model, trained on a large dataset of random finger motions, outperformed the non-pre-trained model. The pre-trained GenENet, benefiting from unsupervised learning that captures the correlation of motion signal mappings, reached 93.6% validation accuracy within 150 transfer training epochs (Supplementary Figs. 8 and 9). In contrast, the non-pre-trained model, which shares the same architecture but is trained from scratch without access to the full 32-channel dataset, remains below 10% accuracy. The model trained directly on the full 32-channel input achieves the highest validation accuracy because it benefits from richer sensor information. In contrast, the model trained directly on the six-channel input without any pre-training shows notably lower accuracy. This clearly demonstrates that the six-channel input alone lacks sufficient information to fully support complex class prediction (Supplementary Fig. 10)

The above-described capability allowed the model to transfer pre-trained knowledge to newly attached positions, as demonstrated by placing sensors in 7 different locations within the region where the original 32-channel sensor was positioned to capture the dataset, as depicted in Fig. 4h. The real-time application of the six-channel set-up for sign language translation is illustrated in Fig. 4i. The graph shows live EMG signals from the six-channel set-up along with the predicted alphabet characters in numeric labels. During the performance of the sign language phrase ‘Hello World’, the post-trained GenENet translated the six-channel information into corresponding alphabet values (Supplementary Video 3). The red lines indicate numeric values from 0 to 25, representing the alphabet from A to Z.

An attribution map is shown during prediction in Fig. 4j, where the model interprets which muscle features contribute to specific sign language hand postures. Each row in the signal corresponds to one of the six sensor channels. Blue regions closer to 1 indicate positive contributions to the prediction and red regions closer to −1 negatively impact the prediction. Attribution maps for all 26 classes are provided in Supplementary Fig. 11. A higher attribution value in a specific channel may suggest a stronger correlation between the corresponding muscle group in the electrode’s position at each learning time frame.

Downstream adaptation of GenENet for gait dynamics prediction

To extend our system’s applicability to different body locations, we attached the device to the calf to monitor kinetic information during the gait cycles. Continuous monitoring of gait kinetics provides valuable insights into potential musculoskeletal disorders, aiding in the identification of risk factors for falls, the need for rehabilitation and optimization of athletic performance^35,36,37.

Previous work used video capture and calculation through inverse dynamics to determine knee moments and corresponding forces³³. However, this requires a specialized lab set-up, making it difficult to apply in daily life. When EMG arrays were used, 32 electrodes could be used for gait dataset capturing while a 6-electrode array was subsequently used for gait force, knee force and moment prediction. For gait kinetic prediction, a 6-electrode array was minimally required to achieve average R² value of 0.972 and relative root mean square error (RMSE) of 6.09 % (Supplementary Table 2).

For the initial pre-training dataset in gait kinetic prediction, we used the 32-channel EMG signal data collected during a normal gait cycle (15 min, ~1,700 gait cycles; experimental set-up shown in Supplementary Fig. 12). In the subsequent post-training phase, using the smaller device, we recorded six-channel EMG signals in conjunction with ground reaction forces (GRFs) captured through three force plates during a normal gait cycle, as illustrated in Fig. 5a. The measured GRF data were fed into the model, where we used MSELoss for continuous force prediction. Simultaneously, gait movements were video-captured using OpenCap³⁸, and knee moments and forces were calculated through inverse dynamics (Methods). The attached 6-channel device, shown in Fig. 5b, was then positioned within the 32-channel measurement area as the boundary.

Fig. 5: Prediction of gait dynamics using the GenENet device.

a, Experimental set-up involving walking across three force plates (FPs) with simultaneous video capture. F_z denotes the vertical ground reaction force. The post-training network is used to predict the GRF, while vertical knee force and moment are calculated through inverse dynamics based on the video data, which are incorporated into the kinetic post-training dataset. b, Schematic of the six-channel EMG device attached to the calf. c, GRF prediction during the gait cycle, showing five distinct phases where predicted values closely match the true values obtained from the video data. d, Snapshots of the real-time prediction of GRF on musculoskeletal model. The green arrow indicates the GRF and the device is attached to the right leg as shown in the red region. e, R² coefficient of 0.975 for GRF prediction. f, Adaptation to different individuals, showing a consistent R² coefficient across them. g, Illustration of GRF and KAM vector directions. h, Predicted y-axis knee joint force and KAM over specific time intervals. Muscle contributions were not included in the inverse dynamics calculation of joint forces.

We identified three key gait states—heel strike, mid-stance and toe off—using the GRF data, as shown in Fig. 5c. The GRF signals including these states were then input into the pre-trained GenENet encoder with the 32-channel stretchable EMG array for further post-training. As shown in Fig. 5d, our model successfully predicted continuous gait forces (expressed in units of body weight (BW)) throughout the gait cycle. To visualize the predicted GRF across the gait cycle, we mapped the OpenCap data to an OpenSim musculoskeletal model and associated it with the predicted GRF values over two representative gait cycles, as shown in Supplementary Video 2. The video provides two perspectives: the top panel shows a diagonal view and the bottom panel presents a side view of the motion. A green arrow represents the relative strength of the predicted GRF, with the device attached to the right leg highlighted in the red region. As depicted in Fig. 5e, the model achieved an R² coefficient of 0.975 with relative RMSE of 6.21%, and the model was able to transfer learning to different individuals, as shown for three individuals in Fig. 5f and Supplementary Figs. 13 and 14. For the gait regression task, we incorporated decoder and combined it with an additional CNN to help reconstruct and refine feature representations, capturing richer local patterns and temporal dependencies. The incorporation of the CNN-LSTM block enabled more precise reproduction of GRF signals, as shown in Supplementary Fig. 15.

To evaluate robustness under sensor placement variation, we conducted experiments involving 7 different locations on the calf, 4 placed horizontally and 3 placed vertically, each spaced 30 mm apart. As shown in Supplementary Fig. 16, the ground-truth model showed relatively high average loss across all locations. However, after applying a lightweight fine-tuning step (30 epochs) for each of the 7 locations, the overall MSE for the gait force prediction task was substantially reduced, even after just a few epochs of adaptation. These results indicate that while some performance degradation occurs due to sensor displacement, it can be effectively mitigated with minimal post-training. Inter-session and inter-individual variability are also assessed in Supplementary Fig. 17.

Understanding gait forces is essential for analysing human locomotion and assessing biomechanical health, aiding in the identification of risk factors such as fall risks, rehabilitation needs and injury prevention^{35,36,39,40,41}. The correlated EMG signals provide further predictive power for assessing these risk factors. The use of compact wearable EMG arrays enables such analysis in daily life without the requirement of specialized video set-up labs as currently used.

Through inverse dynamic simulations powered by OpenCap³⁸ (Methods), we extracted knee joint forces and the knee adduction moment (KAM) and correlated them with the corresponding EMG signals. As illustrated in Fig. 5g, KAM represents the moment acting on the joint in the frontal plane, causing medial rotation of the tibia on the femur⁴². Higher KAM is often associated with the development or progression of medial knee osteoarthritis⁴³. As shown in Fig. 5h, the GenENet combined with CNN-LSTM successfully predicted the progression of GRF and KAM during the gait cycle, particularly within the 4.5–5.5 s range depicted in Fig. 5h. The resulting peak KAM values fell within 0.5–1% BW ht (body weight × height), which is lower than previously reported values (1–3% BW ht)^44,45, without indicating deviation from expected physiological trends. This approach highlights notable advancements in KAM prediction by relying solely on EMG signals, unlike previous methods that require a combination of EMG and inertial measurement unit devices. In addition, while other systems often rely on distributed EMG arrays or with extensive sensor placements^46,47,48,49, our compact six-channel EMG array achieves comparable predictive performance, providing a clear advantage in ease of use and practicality (Supplementary Table 2). Moreover, the use of this compact, wearable EMG array shows a potential reduction in power consumption by approximately 71% compared with 32-channel systems (Methods). This power saving underscores the feasibility of deploying such systems in portable, long-term monitoring set-ups without sacrificing predictive accuracy and without the need for cumbersome large electrode arrays.

Conclusion

We have developed an approach that enables the use of compact and low-power-consumption few-electrode arrays to predict signals equivalent to those from a much larger-area and high-electrode count system. We combine a generative representation-learning algorithm with a wearable device to extrapolate limited sensor information to reconstruct muscle EMG activities in unseen regions to expand information collected, demonstrating its practical application in alphabet recognition and gait dynamics predictions. Precise gestures and gait dynamics predictions previously required increasing footprint and body coverage, such as large EMG grids with 64 to 256 electrodes, or relied on fewer electrodes combined with external sensors or distributed attachments. This approach reduced sensor count, footprint and power consumption for data transmission while maintaining performance.

In the pre-training phase, the generative representation learning network was trained on a high-quality, multichannel dataset obtained from low-impedance polymer electrodes and higher-SNR stretchable interconnections. This network was then integrated with an LSTM layer to enable sequential processing of kinetic inputs.

The successful demonstration of a compact six-channel EMG device for complex task predictions, such as individual alphabet recognition and gait dynamics predictions, highlights the potential for practical applications. Going forward, the resolution of the training array can be further enhanced to produce even more detailed information, while adapting the GenENet approach can ease the complexity of fabrication and lower the production cost of the wearable versions while maintaining performance. We anticipate that this platform could be extended to accommodate other types of input that typically require high-density sensory arrays while there are correlations between the signals, including strain, temperature, other electrophysiological sensing, such as electrocardiogram and electroencephalogram, photodiodes, ultrasonic sensors, and even chemical sensors.

While our system shows robust performance, it could be further improved by implementing on-device processing of signals, enabling reduced communication bandwidth and lower-radio-power requirements. In addition, the current model is limited to data obtained from a 32-channel area. Expanding the dataset to include a larger sensor coverage area would enhance the capabilities of the system, allowing for greater flexibility in sensor placement across more arbitrary regions of the body.

Moreover, integrating a sensor fusion strategy that combines an inertial measurement unit with EMG data alongside electrophysiological signals may enrich the dataset and improve the network’s training²⁶. In addition, proper calibration is crucial when adapting the system for multiple users, as individual variations in muscle physiology and skin impedance may require personalized adjustments to ensure optimal performance. Special attention should also be given to abnormal conditions, such as users with partial muscle dysfunction or neuromuscular disorders, where signal patterns can deviate from typical profiles. In such cases, calibration techniques such as personalized adaptive baseline subtraction and filtering may be necessary to address signal inconsistencies and enhance the system’s reliability.

This advancement paves the way for a wide range of applications with improved form factors and reduced data collection and transmission energy consumption while preserving the quality of multi-array signals. Potential applications include health monitoring (for example, blood pressure, respiration rate, pulse), prosthetics (for example, prosthetic limbs, gait analysis), sports (for example, posture monitoring) and human–machine interfaces (for example, gesture recognition, facial movement recognition, virtual reality).

Methods

Materials

The following materials were all obtained from Sigma Aldrich: dextran (product 09184), NBR (product 180912), cyclohexane (product 179191), cyclohexanone (product 398241), PEDOT:PSS (product 739332), SBS (product 182877), phenylbis(2,4,6-trimethylbenzoyl)phosphine oxide (BAPO; product 511447), pentaerythritol tetrakis(3-mercaptopropionate) (PETMP; product 381462), EGaIn (product 495425), PBS (product 806552), poly(pyromellitic dianhydride-co-4,4′-oxydianiline), amic acid solution (product 575828) and AAm (product 800830), and N,N’-methylenebisacrylamide (MBAA; product 101546). Aqueous hydrogen peroxide (30%) was obtained from Fisher Scientific. Ascorbic acid was obtained from TCI. PDMS (Slygard 184) was purchased from Dow.

Fabrication of the 32-channel dataset-generation device

Solution and substrate preparation

A 60 mg ml⁻¹ solution of NBR was prepared in cyclohexanone. This solution was left to dissolve overnight on a hotplate set to 150 °C. The fabrication process began with oxygen plasma etching (March Instruments PX-250 Plasma Asher) of a silicon wafer at 150 W and an oxygen flow rate of 2 s.c.c.m. for 100 s. Following this, a 10 wt% dextran aqueous solution was spin-coated at 800 rpm for 60 s onto the wafer and baked at 100 °C for 5 min to form a sacrificial layer. To create the flexible substrate, PDMS (1:10 weight ratio) was spin-coated onto the wafer at 800 rpm for 45 s, followed by annealing at 100 °C for 30 min. The NBR solution (60 mg ml⁻¹ in cyclohexanone solution), mixed with BAPO and PETMP (4 wt% of base polymer) for photo-crosslinking, was then spin-coated onto the PDMS substrate (oxygen plasma etched 150 W for 50 s) at 800 rpm for 60 s. Then this was ultraviolet-cured for 20 min in a nitrogen environment to complete the substrate formation with post-baking of 120 °C for 15 min.

Electrode patterning

Electrode patterning was initiated by applying photoresist (AZ 1512) at 2,000 rpm for 60 s followed by baking at 90 °C for 1 min. The desired pattern was created using masked patterning exposed in ultraviolet light for 10 s in air (Open Cure 365-nm LED UV; Supplementary Fig. 18) and developed in MF219 developer. Following patterning, chromium (3 nm) and gold (40 nm) layers were deposited via thermal evaporation. EGaIn was then applied on top of the patterned electrodes. The lift-off process was carried out by immersing the patterned device in acetone for approximately 3 h to remove the photoresist and leave the desired metal patterns.

Encapsulation preparation

For encapsulation, an 80 mg ml⁻¹ solution of SBS with BAPO and PETMP (4 wt% of base polymer) in toluene was prepared and spin-coated onto the device at 800 rpm for 60 s. A photomask was used to define the encapsulation pattern, curing with 365 nm ultraviolet lamp in 3 s, and the unexposed areas were dissolved by washing with cyclohexane.

PEDOT electrode patterning

To prepare the PEDOT electrodes, 5 ml PEDOT:PSS was combined with 1.5 g AAm and 5 mg MBAA. To initiate gel formation, 250 μl of 20% (wt/vol in water) ascorbic acid and 250 μl of 30% (v/v in water) hydrogen peroxide were added to the mixture. The solution was then dispensed onto an Ecoflex mould (4.5 mm in diameter and depth), where it formed a gel and created a defined pattern on top of the previously prepared electrodes. Then, after attaching the electrodes to the EGaIn electrodes, the Ecoflex mould was detached, where the final device was created as shown in Supplementary Fig. 19. A six-channel array was fabricated using the same method. A low-impedance, highly conductive electrode paste (Elefix V Electrode Paste, Nihon Kohden) was applied to the six-channel electrode array to enhance the signal quality. The device was then securely attached to the skin using a biomedical adhesive (Skinister). To ensure long-term stability and fully prevent oxidation, the electrode surface facing the PEDOT:PSS layer can be selectively exposed as gold, as shown in Supplementary Figs. 20 and 21. This approach requires additional fabrication steps, as illustrated in Supplementary Fig. 19. Stages a to c involve the patterning of Au for both electrode and wiring layouts. Supplementary Fig. 20g represents a faster prototyping method in which EGaIn is applied over the entire gold surface, enabling quicker data collection. In contrast, Supplementary Fig. 20d shows an additional photoresist patterning step that masks the electrode area so that EGaIn is applied only to the wiring regions.

A miniaturized wireless EMG device for dataset generation

The device integrates a flexible printed circuit board featuring an analogue-to-digital converter sensing element, a Bluetooth low energy module, a lithium polymer battery, a multiplexer, an amplifier and a 32-channel EMG module. The 32-channel EMG system is connected to the wireless module via an anisotropic conductive film, enabling reliable signal transfer. Analogue EMG signals are amplified and multiplexed through a fully integrated electrophysiology chip (Intan Technologies) before being processed by the analogue-to-digital converter. These signals are digitized and transmitted at a 250 Hz data rate via Bluetooth to the receiver. The compact wireless module, through conformal attachment to the skin, ensures accurate motion detection without compromising user comfort. The system is programmed using a system-on-chip (CC2650, Texas Instruments) in Code Composer Studio, which converts the packets of analogue sensor data into UART format for transmission.

Mould fabrication through 3D printing

To visualize and evaluate the conformability of the device, we have 3D-printed (Ender 3 V2) a corrugated surface. A detached device is placed on top of the surface as shown in Supplementary Fig. 22. Also, as shown in Supplementary Fig. 23, a 6-channel watch-type mould is created through 3D printing and poured and cured the encapsulation polymer (Elkem RTV 4420; part A and part B, mixed with 5% of silicone opaque dye).

Visualization using t-SNE

To visualize and evaluate the results of the trained dataset, we applied t-distributed stochastic neighbour embedding (t-SNE). The t-SNE visualization reveals clusters in the projected two-dimensional space, offering insights into sample relationships and the potential separability of classes in high-dimensional space. t-SNE was performed on both ASL and GRF predictions, as shown in Supplementary Figs. 9 and 14.

Dataset collection for pre-training

Dataset collection was driven by the custom-made wireless device. The dataset was collected at Stanford Human Performance Lab. Wrist movements were collected with randomly performed different finger gestures for 20 min from a single individual. Gait motions are collected while attached to the calf and with normal walking cycles with 15 min from a single individual. This protocol is approved through Stanford IRB-54795.

Inverse kinematic simulation

Post-processing of human movement kinematics collected using OpenCap were done through OpenCap processing (https://github.com/stanfordnmbl/opencap-processing). Multiple sessions of OpenCap measurements were processed to estimate kinetic information of joint force and moment.

Details on the transformer encoding and decoding block

The overall architecture is shown in Supplementary Fig. 24. The input signal is a 32 × 32 array of 32-channel EMG signals with 32 time windows (~0.12 s), for which the tensor size of input will be $x\in {{\mathbb{R}}}^{H\times W\times C}$, where H, W and C represent height (32), width (32) and channels (1), respectively. The RMS amplitude of EMG signal is shown in a one-channel array. This tensor will be augmented through resizing and random cropping into a 48 × 48 array, followed by random horizontal flipping for augmentation.

The image is then divided into patches of size P × P, resulting in N = H × W/P² patches, each with P × P × Cvalues, which defines the patch area, where the patch size P is 6.

Each patch is then embedded using a linear projection:

$${x}_{{\rm{p}}{\rm{a}}{\rm{t}}{\rm{c}}{\rm{h}}}={f}_{{\rm{p}}{\rm{r}}{\rm{o}}{\rm{j}}}({x}_{{\rm{p}}{\rm{a}}{\rm{t}}{\rm{c}}{\rm{h}}})\in {{\mathbb{R}}}^{N\times D}$$

where f_proj denotes a linear projection layer that maps each flattened patch to a D-dimensional vector (128).

Before encoding the signals into a motion feature space with the attention mechanism, we add positional embedding to the embedded vectors so that the model can understand the relative position of input sequences while encoding them in parallel. Positional embedding is one of key features of transformer architecture that allows the model to avoid iterative computation for each time frame.

For N patches, the positional embeddings are represented as:

$${{\rm{p}}{\rm{o}}{\rm{s}}}_{i}\in {{\mathbb{R}}}^{D},i\in [1,N]$$

The positional embeddings are then added to the patch embeddings to be conveyed to the transformer:

$${x}_{{\rm{p}}{\rm{a}}{\rm{t}}{\rm{c}}{\rm{h}}{\rm{\_}}{\rm{p}}{\rm{o}}{\rm{s}}}={x}_{{\rm{p}}{\rm{a}}{\rm{t}}{\rm{c}}{\rm{h}}}+{\rm{p}}{\rm{o}}{\rm{s}}$$

A subset of patches is masked before being fed into the transformer, where the randomly selected indices of patches will be masked that will be fed into the transformer decoder, where the rest of unmasked patches are passed into the transformer encoder. The transformers’ self-attention plays a crucial role in capturing long-range dependencies and global context across the EMG signals.

The encoder processes several layers of multi-head attention, layer normalization and feed-forward networks.

$${\hat{x}}_{{\rm{patch}}}={\rm{LayerNorm}}({x}_{{\rm{patch}}})$$

$${{\rm{q}}{\rm{u}}{\rm{e}}{\rm{r}}{\rm{y}}}_{ij}={W}_{{q}_{j}}{\hat{x}}_{{i}_{{\rm{p}}{\rm{a}}{\rm{t}}{\rm{c}}{\rm{h}}}},\,{{\rm{k}}{\rm{e}}{\rm{y}}}_{{t}_{ij}}={W}_{{k}_{j}}{\hat{x}}_{{i}_{{\rm{p}}{\rm{a}}{\rm{t}}{\rm{c}}{\rm{h}}}},\,{{\rm{v}}{\rm{a}}{\rm{l}}{\rm{u}}{\rm{e}}}_{{t}_{ij}}={W}_{{v}_{j}}{\hat{x}}_{{i}_{{\rm{p}}{\rm{a}}{\rm{t}}{\rm{c}}{\rm{h}}}}$$

$${\rm{a}}{\rm{t}}{\rm{t}}{\rm{n}}(i,j)={\rm{s}}{\rm{o}}{\rm{f}}{\rm{t}}{\rm{m}}{\rm{a}}{\rm{x}}\left(\frac{{\mathrm{query}}_{i}}{\sqrt{32}}\times {{\mathrm{key}}_{{t}_{kj}}}^{T}\right)$$

where i and j index the query and key tokens, respectively; W_q, W_k and W_v indicate the query, key and value projection matrices; t denotes the time step. Then the residual connection ensures the original input to be preserved:

$${x}_{{\rm{e}}{\rm{n}}{\rm{c}}}={x}_{{\rm{p}}{\rm{a}}{\rm{t}}{\rm{c}}{\rm{h}}{\rm{\_}}{\rm{p}}{\rm{o}}{\rm{s}}}+{\rm{a}}{\rm{t}}{\rm{t}}{\rm{n}}(i,j)$$

After applying residual connection, the output passes through a feed-forward layer consisting of two linear layers, a Gaussian error linear unit (GeLU) activation and dropout. The output of the encoder then further processed through the input of the decoding layer.

The decoder processes the same architecture with the encoder, but including a linear layer in the end to reconstruct the original EMG signal. The output from the encoder is first projected into the decoder space:

$${x}_{{\rm{d}}{\rm{e}}{\rm{c}}{\rm{\_}}{\rm{p}}}={W}_{{\rm{i}}{\rm{n}}}({x}_{{\rm{e}}{\rm{n}}{\rm{c}}})$$

where

$${W}_{{\rm{i}}{\rm{n}}}\in {{\mathbb{R}}}^{{D}_{{\rm{e}}{\rm{n}}{\rm{c}}}\times {D}_{{\rm{d}}{\rm{e}}{\rm{c}}}}$$

The projected input is then added with mask tokens, where mask tokens replace and represent the originally masked patches. These tokens are learnable parameters that initialized randomly from normal distribution:

$${x}_{{\rm{t}}{\rm{o}}{\rm{k}}{\rm{e}}{\rm{n}}}\sim N(0,1)\in {{\mathbb{R}}}^{P\times P\times C}$$

Positional embeddings are then applied to both of x_{dec_p} and x_token, where the final decoder input will be:

$${x}_{{\rm{d}}{\rm{e}}{\rm{c}}{\rm{\_}}{\rm{i}}{\rm{n}}}={x}_{{\rm{d}}{\rm{e}}{\rm{c}}{\rm{\_}}{\rm{p}}{\rm{\_}}{\rm{p}}{\rm{o}}{\rm{s}}}+{x}_{{\rm{t}}{\rm{o}}{\rm{k}}{\rm{e}}{\rm{n}}{\rm{\_}}{\rm{p}}{\rm{o}}{\rm{s}}}$$

As the encoder, the decoder processes layers of multi-head attention, layer normalization and feed-forward networks. The output of the decoder is flattened and passed through a linear layer to reconstruct the original EMG signal:

$${x}_{{\rm{f}}{\rm{l}}{\rm{a}}{\rm{t}}}={\rm{F}}{\rm{l}}{\rm{a}}{\rm{t}}{\rm{t}}{\rm{e}}{\rm{n}}({x}_{{\rm{d}}{\rm{e}}{\rm{c}}}),{\hat{x}}_{{\rm{r}}{\rm{e}}{\rm{c}}{\rm{o}}{\rm{n}}}={W}_{{\rm{o}}{\rm{u}}{\rm{t}}}\times {x}_{{\rm{f}}{\rm{l}}{\rm{a}}{\rm{t}}}$$

Final reshaping of ${\hat{x}}_{{\rm{r}}{\rm{e}}{\rm{c}}{\rm{o}}{\rm{n}}}$ ensures that the output matches the original dimension of multi-array EMG signal.

$${{\mathcal{L}}}_{{\rm{M}}{\rm{S}}{\rm{E}}}=\frac{1}{{N}_{{\rm{m}}{\rm{a}}{\rm{s}}{\rm{k}}}}\mathop{\sum }\limits_{i\in {\rm{m}}{\rm{a}}{\rm{s}}{\rm{k}}}{({P}_{{\rm{o}}{\rm{r}}{\rm{i}}{\rm{g}}}^{i}-{P}_{{\rm{r}}{\rm{e}}{\rm{c}}{\rm{o}}{\rm{n}}}^{i})}^{2}$$

EMG data processing with tensor generation

The raw EMG signals are filtered using a fourth-order Butterworth bandpass filter with cut-off frequencies between 1 Hz and 100 Hz. Filtering reduces noise and retains relevant frequency components. Sliding window is used to segment the EMG signal into overlapping frames. Each frame consists of 32 time steps (128 ms), corresponding to 1 sliding window. The sliding window advances with a step size of 10 (40 ms), ensuring sequential windows overlap which helps maintain temporal continuity in the data.

Within each window, the RMS of the signal is computed. The RMS features are then converted into a three-dimensional tensor via colourmap conversion. Each tensor is labelled with the corresponding gesture classes or force signal.

Gradient-based attribution visualization

To investigate the model’s interpretability across 26 classes, we utilize Gradient SHAP from Captum to generate attribution maps for representative examples from each class. This process highlights which portions of the input sequence contribute most strongly to the predictions.

Input tensors and their corresponding labels are iteratively retrieved from the dataset. For each alphabet class $c\in \{1,2,\ldots ,26\}$, a single representative sample x_c is selected from the evaluation set. Given a batch of input sequences $X=\left\{{x}_{1},{x}_{2},\ldots ,{x}_{B}\right\}$ and corresponding labels $Y=\left\{{y}_{1},{y}_{2},\ldots ,{y}_{B}\right\}$, the representative sequence is stored.

Gradient SHAP estimates feature importance by comparing the input example against a baseline tensor. The attribution values highlight the features that contribute most to the model’s decision.

The attributions are arranged in a 26 × 2 grid, where each row corresponds to a specific class. In Fig. 4j, the left panel shows the original input example, and the right panel shows the corresponding attribution map.

Details on the backend CNN-LSTM block for gesture and kinematic prediction

The CNN-LSTM network processes a sequence of EMG signals to predict target values (for example, force and finger classes). This network combines the generated information from the GenENet, where the model extracts features from individual frames and captures temporal dependencies with an LSTM.

Given a sequence $x\in {{\mathbb{R}}}^{B\times T\times C\times H\times W}$, where B is the batch size, T is the sequence length, C is the number of channels, and H × W is the signal resolution, each signal frame is processed individually. Each frame is passed through the transformer-based GenENet, resulting in tensor from the decoder z_i.

The output is passed through a CNN module to extract spatial features, which includes 3 × 3 convolution, Rectified linear unit (ReLU) activation and 2 × 2 max pooling. The output is flattened and further reduced by a fully connected compression layer. ${z}_{{\rm{c}}{\rm{o}}{\rm{m}}{\rm{p}}}\in {{\mathbb{R}}}^{B\times S}$, and S is the dimension of the compressed feature.

The sequence of compressed features is passed through an LSTM network, where the last hidden state is fed through a fully connected layer to produce the final output. Depending on the task, MSELoss or cross entropy loss is applied for force or class prediction, respectively. The final model achieves an average inference latency of 46.95 ms, with 7.7 million multiply–accumulate operations and 0.428 million parameters.

Comparative analysis of theoretical time complexity

To analyse and compare the theoretical time complexities of two signal processing techniques, RMS and spectrogram, the time complexities were calculated relative to the signal size. This offers insights into the computational demands of each method. The RMS computation requires a single pass through the signal, making its time complexity linear in n, the signal size. The time complexity for a spectrogram depends on the signal size n, the window size w, and the frequency resolution achieved through Fourier transform within each window.

A synthetic EMG signal is generated to simulate a realistic input for each processing technique. Two methods, RMS and spectrogram, are evaluated across 10,000 iterations to assess the average processing time. The average processing times across all iterations are then computed as ${\bar{t}}_{\mathrm{RMS}}=1/\mathrm{iter}{\sum }_{{\rm{n}}=1}^{\mathrm{iter}}{t}_{\mathrm{RMS}}^{(n)}$ and ${\bar{t}}_{{\rm{s}}{\rm{p}}{\rm{e}}{\rm{c}}{\rm{t}}{\rm{o}}{\rm{g}}{\rm{r}}{\rm{a}}{\rm{m}}}=1/{\rm{i}}{\rm{t}}{\rm{e}}{\rm{r}}\displaystyle {\sum }_{{\rm{n}}=1}^{\mathrm{iter}}{t}_{{\rm{s}}{\rm{p}}{\rm{e}}{\rm{c}}{\rm{t}}{\rm{o}}{\rm{g}}{\rm{r}}{\rm{a}}{\rm{m}}}^{(n)}$.

The average processing times for each method are visualized in a bar plot for direct comparison as shown in Supplementary Fig. 25, showing RMS as an efficient approach for quick signal characterization.

Power-saving estimation

The potential power savings of using a 6-channel device compared with a 32-channel device can be calculated based on their transmission characteristics:

$${P}_{{\rm{t}}{\rm{o}}{\rm{t}}{\rm{a}}{\rm{l}}}\propto {P}_{{\rm{t}}{\rm{x}}}\times {T}_{{\rm{t}}{\rm{x}}}$$

where P_tx is the power during transmission and T_tx is the transmission duration. The transmission payload for 32-channel and 6-channel devices can be determined, with each channel contributing 2 bytes to the payload:

32-channel payload: 2 × 32 + 2 = 66 bytes

6-channel payload: 2 × 6 + 2 = 14 bytes

Here, 2 bytes are used for timestamp data. The transmission duration can be expressed as:

$${T}_{{\rm{t}}{\rm{x}}}={\rm{P}}{\rm{a}}{\rm{y}}{\rm{l}}{\rm{o}}{\rm{a}}{\rm{d}}/{\rm{D}}{\rm{a}}{\rm{t}}{\rm{a}}\,{\rm{r}}{\rm{a}}{\rm{t}}{\rm{e}}$$

As ${T}_{{\rm{t}}{\rm{x}}}\propto {\rm{P}}{\rm{a}}{\rm{y}}{\rm{l}}{\rm{o}}{\rm{a}}{\rm{d}}$, the power savings can be estimated as:

$$1-{T}_{{\rm{t}}{\rm{x}},6}/{T}_{{\rm{t}}{\rm{x}},32}\approx 0.71$$

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.