Introduction

Microelectromechanical systems (MEMS) are widely utilized across diverse fields such as aerospace1,2, inertial navigation3,4, sensing5,6, and medical applications7. In non-vacuum environments, viscous damping is a major source of energy dissipation in MEMS device8, significantly influencing critical performance metrics such as sensitivity, frequency response, and bandwidth9,10. Viscous damping in MEMS devices arises from the interaction between the oscillating mechanical structures and the surrounding air. This damping effect is affected by the vibration frequency, as well as the shape and size of the structures. It becomes more significant as the device size decreases8. In applications such as micro-accelerometers11, micro-switches12, microphones13, energy harvesters14, and various micro-sensors15,16, lower damping is often desirable for enhanced performance under specific driving forces. Therefore, tuning viscous damping to meet diverse performance requirements has been a subject of continuing interest in MEMS design. Perforated structures, such as phononic crystals17,18 or photonic crystals19,20, can be utilized to manipulate energy (acoustic, electromagnetic waves, and heat). Similarly, ordered perforated structures were found to successfully control fluid flow, significantly reducing viscous damping in MEMS devices21,22,23,24,25. Understanding the tuning mechanism of perforations on viscous damping is crucial for optimizing dynamic performance across MEMS applications.

Most mechanical structures in MEMS devices can be conceptualized as two parallel plates moving relative to each other. In this scenario, the fluid behavior causing viscous damping is simplified to a manageable two-dimensional problem. The pressure experienced at any point on the plates can be accurately described using the general Reynolds equation derived from the Navier-Stokes equations26. However, the problem becomes a complex three-dimensional structure-fluid interaction for perforated MEMS devices. As a result, the general Reynolds equation is no longer sufficient for accurate modeling. Significant research efforts have been dedicated to accurately characterize the impact of perforations on damping and to derive analytical formulas for MEMS design.

Mattila27 explored the effects of perforations on viscous damping, introducing a correction term to the Reynolds equation. Following this, Bao28 derived the Reynolds equation applicable to perforated plates, enabling rapid calculations of damping; however, this approach is limited to small perforation ratios. Veijola29 then developed a formula for the viscous damping of individual perforated cells based on theoretical and simulation results. Building on Veijola’s work, Pandey30 proposed a modified Reynolds equation suitable for larger perforation ratios, incorporating a cell classification model. Jaroslaw31 developed a damping solution model for individual perforated cells based on extensive simulation results, achieving higher accuracy. However, this work did not extend to a perforated plate. Gabriele Schrag32 introduced a damping model based on a mixed-level approach that integrates well with MEMS components but requires specific applicable conditions. Although various viscous damping models for perforated plates have been proposed, they often require stringent conditions, such as applicability only to cylindrical holes33,34 or simple fluid boundary conditions35,36. In summary, research considering structural variability and complex boundary effects remains elusive, which is the subject of this paper. It is crucial for the MEMS community because actual devices may feature more complex perforation configurations.

This paper presents two complementary theoretical models for analyzing viscous damping in perforated MEMS devices. Both models treat the perforated plate as a uniformly distributed array of cells, each containing a single hole. However, the modeling of fluid behavior differs between the two models, leading to varying adaptability to different perforation ratios. The first one is the viscous damping model based on the continuity equation. This model treats the damping force as a smooth function of the position under the entire plate and assumes that the airflow within the hole is uniformly distributed across the plate area. The Reynolds equation for the perforated plate is derived under these assumptions, and the overall damping is obtained by solving the equation throughout the whole plate. The second model is the viscous damping model based on cell classification. In this model, the cells are classified according to the boundary conditions. The viscous damping of the entire perforated plate is obtained by meticulously calculating the damping coefficient of individual cells and multiplying it by the total number of cells. Both models innovatively consider various hole geometries, including cylindrical, conical, prismatic, and trapezoidal holes, and demonstrate higher computational accuracy under complex boundary conditions by thoroughly considering boundary effects. A series of simulation models are built to compare theoretical models and simulation results under different conditions, thereby validating the computational accuracy and applicability of both models. Experimental measurements based on the free-vibration decay (FVD) method further confirmed the validity of the models. Additionally, more advanced perforation configurations are developed based on the experimental findings. Overall, this work provides effective and efficient guidance for the damping design and dynamic performance optimization of MEMS devices.

Results

Viscous damping model based on the continuity equation

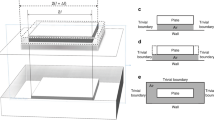
As shown in Fig. 1a, a perforated MEMS device influenced by viscous damping can be modeled as consisting of two components: a perforated plate and an oscillating plate. As illustrated in Fig. 1b, the air within the plates flows between the plates and through the holes. Take a perforated rectangular plate with cylindrical holes as an example. Such a plate can be regarded as composed of multiple perforated cells, each featuring a central hole, as shown in Fig. 1c. Given that each cell is significantly smaller than the overall plate, the pressure can be considered as a smooth function over the plate, and the airflow through the holes is assumed uniform over the cell area28. This allows the Reynolds equation to be expressed as:

$$\frac{{\partial }^{2}p}{\partial {x}^{2}}+\frac{{\partial }^{2}p}{\partial {y}^{2}}-\frac{12\mu }{{h}^{3}}{Q}_{z}=\frac{12\mu }{{h}^{3}}\frac{\partial h}{\partial t}$$
(1)

where p is the variation in surface pressure on the plate, ρ is the density of air. h is the air film thickness, which is the initial distance between the plates. μ is the viscosity coefficient of air, x and y are coordinates, and t is time. Qz is the penetration coefficient, which is closely related to the hole geometry. The following provides a detailed description of the Qz for four representative hole geometries (cylindrical, conical, prismatic, and trapezoidal), along with their corresponding Reynolds equations.

Fig. 1: Schematic of perforated MEMS structures.
figure 1

a Schematic of the perforated plate and the oscillating plate. b Cross-section of the perforated plate and the oscillating plate. c Perforated plate and cells. d Schematic of a single perforated cell. e Cell with a cylindrical hole. f Cell with a conical hole

Full size image

As shown in Fig. 1b, the geometric properties of the perforated plate with cylindrical holes are defined by the hole radius rh, the hole height (or plate thickness) H, and the hole spacing (periodicity) lc. For simplification in calculations, the cell with a cylindrical hole is modeled as an annular cell, characterized by an outer radius (cell radius) of rc, and an inner radius (hole radius) of rh, as illustrated in Fig. 1d.

The viscous damping force acting on the cell is composed of the squeeze-film damping force Fann from the airflow between the plates and the resistance FH from the airflow within the hole. As shown in Fig. 1e, assuming that the airflow at the boundary of each cell is negligible, Fann can be treated as the squeeze-film damping force acting on an annular cell. Substituting the boundary conditions into the general Reynolds equation, the squeeze-film damping force Fann acting on the cell with a cylindrical hole is obtained:

$${F}_{{\rm{ann}}-{\rm{cyl}}}=\frac{3\mu \pi {r}_{{\rm{c}}}^{4}}{2{h}^{3}}\frac{\partial h}{\partial t}k(\beta )$$
(2)

where β = rh / rc is the perforation ratio, which reflects the size of the holes relative to the cell. k(β) = 4β2 - β4 - 4lnβ - 3.

According to the Poiseuille equation, for a cylindrical hole with a radius of rh and a height of H, the volume Vc of air passing through the hole in a unit time is given by

$${V}_{{\rm{c}}-{\rm{cyl}}}=\frac{\pi {r}_{{\rm{h}}}^{4}}{8\mu }\frac{{P}_{{\rm{H}}-{\rm{cyl}}}}{H}$$
(3)

where PH-cyl is the pressure difference across the ends of the cylindrical hole. Thus, the average damping pressure of the cell is expressed as:

$$p={P}_{{\rm{H}}-{\rm{cyl}}}+\frac{{F}_{{\rm{ann}}-{\rm{cyl}}}}{\pi {r}_{{\rm{c}}}^{2}}={P}_{{\rm{H}}-{\rm{cyl}}}\left(1+\frac{3{r}_{{\rm{h}}}^{4}k(\beta)}{16H{h}^{3}}\right)={P}_{{\rm{H}}-{\rm{cyl}}}{\vartheta }_{{\rm{cyl}}}(\beta )$$
(4)

From this, the penetration coefficient Qz of the perforated plate with cylindrical holes is expressed as:

$${Q}_{{\rm{z}}-{\rm{cyl}}}=\frac{{V}_{{\rm{c}}-{\rm{cyl}}}}{\pi {r}_{{\rm{c}}}^{2}}=\frac{{\beta }^{2}{r}_{{\rm{h}}}^{2}p}{8\mu H{\vartheta }_{{\rm{cyl}}}(\beta )}$$
(5)

Substituting Eq. (5) into the Reynolds equation Eq. (1), the Reynolds equation for the perforated plate with cylindrical holes is obtained:

$$\frac{{\partial }^{2}p}{\partial {x}^{2}}+\frac{{\partial }^{2}p}{\partial {y}^{2}}-\frac{3{\beta }^{2}{r}_{{\rm{h}}}^{2}}{2{h}^{3}H}\frac{1}{{\vartheta }_{{\rm{cyl}}}(\beta )}p=\frac{12\mu }{{h}^{3}}\frac{\partial h}{\partial t}$$
(6)

It is important to emphasize that the derivation of PH-cyl in Eq. (3) relies on the assumption of fully developed Poiseuille flow. However, when the diameter of the hole is comparable to its height, significant errors can arise, known as end effects37. H is equivalently elongated to Helong to eliminate the influence of the end effects. Further details can be found in Supplementary Note 1.

As shown in Fig. 1f, the situation for conical holes is more complex. The radius varies along the height of the hole rather than remaining constant. The cross-sectional radii at both ends of the hole are denoted as rh1 (the minimum radius) and rh2 (the maximum radius). The axial position along the height of the hole is denoted as z, with the corresponding radius given by the equation r = rh1 + (rh2 - rh1) z / H. According to Eq. (3), when the airflow rate is constant, the pressure difference PH across the ends of the conical is expressed as:

$${P}_{{\rm{H}}-{\rm{con}}}={\int }_{0}^{H}\frac{8\mu {V}_{{\rm{c}}-{\rm{con}}}}{\pi {r}^{4}}{\rm{d}}z=\frac{8\mu {V}_{{\rm{c}}-{\rm{con}}}}{3\pi }\frac{H}{{r}_{{\rm{h}}2}-{r}_{{\rm{h}}1}}\left(\frac{1}{{r}_{{\rm{h}}1}^{3}}-\frac{1}{{r}_{{\rm{h}}2}^{3}}\right)$$
(7)

The squeeze-film damping force Fann-con acting on the cell with a conical hole is obtained by replacing rh in Eq. (2) with rh1. The average damping pressure within the cell is expressed as:

$$p={P}_{{\rm{H}}-{\rm{con}}}+\frac{{F}_{{\rm{ann}}-{\rm{con}}}}{\pi {r}_{{\rm{c}}}^{2}}={P}_{{\rm{H}}-{\rm{con}}}\left(1+\frac{9({r}_{{\rm{h}}2}-{r}_{{\rm{h}}1})k(\beta ){r}_{{\rm{h}}1}^{3}{r}_{{\rm{h}}2}^{3}}{16H{h}^{3}({r}_{{\rm{h}}2}^{3}-{r}_{{\rm{h}}1}^{3})}\right)={P}_{{\rm{H}}-{\rm{con}}}{\vartheta }_{{\rm{con}}}(\beta )$$
(8)

where, β = rh1/rc. The penetration coefficient Qz-con of the perforated plate with conical holes and its corresponding Reynolds equation are expressed as:

$${Q}_{{\rm{z}}-{\rm{con}}}=\frac{{V}_{{\rm{c}}-{\rm{con}}}}{\pi {r}_{{\rm{c}}}^{2}}=\frac{3\pi {r}_{{\rm{h}}1}^{3}{r}_{{\rm{h}}2}^{3}({r}_{{\rm{h}}2}-{r}_{{\rm{h}}1})}{8\mu H({r}_{{\rm{h}}2}^{3}-{r}_{{\rm{h}}1}^{3}){A}_{1}}{P}_{{\rm{H}}-{\rm{con}}}=\frac{3{r}_{{\rm{h}}1}^{3}{r}_{{\rm{h}}2}^{3}}{8\mu H{r}_{{\rm{c}}}^{2}({r}_{{\rm{h}}2}^{2}+{r}_{{\rm{h}}1}^{2}+{r}_{{\rm{h}}1}{r}_{{\rm{h}}2})}\frac{p}{{\vartheta }_{{\rm{con}}}(\beta )}$$
(9)
$$\frac{{\partial }^{2}p}{\partial {x}^{2}}+\frac{{\partial }^{2}p}{\partial {y}^{2}}-\frac{9{r}_{{\rm{h}}1}^{3}{r}_{{\rm{h}}2}^{3}}{2{h}^{3}H{r}_{{\rm{c}}}^{2}({r}_{{\rm{h}}2}^{2}+{r}_{{\rm{h}}1}^{2}+{r}_{{\rm{h}}1}{r}_{{\rm{h}}2})}\frac{p}{{\vartheta }_{{\rm{con}}}(\beta )}=\frac{12\mu }{{h}^{3}}\frac{\partial h}{\partial t}$$
(10)

The end effects of the conical hole are eliminated by equivalently shortening rh1 to rshort-h1. Further details are provided in the Supplementary Note 1.

When the cross-section of the hole is square, the cylindrical hole transforms into a prismatic hole with a side length of lh, and its penetration coefficient is denoted as Qz-pri. Similarly, a conical hole transforms into a trapezoidal hole, with the side lengths of the cross-sections at both ends being lh1 (the minimum side length) and lh2 (the maximum side length), and its penetration coefficient is denoted as Qz-tra.

Following a similar process as described previously, the penetration coefficients Qz for the plates with prismatic and trapezoidal holes can be derived separately. The Qz for four types of hole geometries are summarized as follows:

$$\left\{\begin{array}{l}{Q}_{{\rm{z}}-{\rm{cyl}}}=\frac{{\beta }^{2}{r}_{{\rm{h}}}^{2}}{8\mu H}\frac{p}{{\vartheta }_{{\rm{cyl}}}(\beta )}\\ {Q}_{{\rm{z}}-{\rm{con}}}=\frac{3{r}_{{\rm{h}}1}^{3}{r}_{{\rm{h}}2}^{3}}{8\mu H{r}_{{\rm{c}}}^{2}({r}_{{\rm{h}}2}^{2}+{r}_{{\rm{h}}1}^{2}+{r}_{{\rm{h}}1}{r}_{{\rm{h}}2})}\frac{p}{{\vartheta }_{{\rm{con}}}(\beta )}\\ {Q}_{{\rm{z}}-{\rm{pri}}}=\frac{0.035{{l}_{{\rm{h}}}}^{4}}{\pi {r}_{{\rm{c}}}^{2}\mu H}\frac{p}{{\vartheta }_{{\rm{pri}}}(\beta )}\\ {Q}_{{\rm{z}}-{\rm{tra}}}=\frac{0.105{l}_{{\rm{h}}1}^{3}{l}_{{\rm{h}}2}^{3}({l}_{{\rm{h}}2}-{l}_{{\rm{h}}1})}{\pi {r}_{{\rm{c}}}^{2}\mu H({l}_{{\rm{h}}2}^{3}-{l}_{{\rm{h}}1}^{3})}\frac{p}{{\vartheta }_{{\rm{tra}}}(\beta )}\end{array}\right.$$
(11)
$$\left\{\begin{array}{l}{\vartheta }_{{\rm{cyl}}}(\beta )=1+\frac{3{r}_{{\rm{h}}}^{4}k(\beta )}{16H{h}^{3}}\\ {\vartheta }_{{\rm{con}}}(\beta )=1+\frac{9({r}_{{\rm{h}}2}-{r}_{{\rm{h}}1})k(\beta ){r}_{{\rm{h}}1}^{3}{r}_{{\rm{h}}2}^{3}}{16H{h}^{3}({r}_{{\rm{h}}2}^{3}-{r}_{{\rm{h}}1}^{3})}\\ {\vartheta }_{{\rm{pri}}}(\beta )=1+\frac{21{{l}_{{\rm{h}}}}^{4}k(\beta )}{40\pi {h}^{3}H}\\ {\vartheta }_{{\rm{tra}}}(\beta )=1+\frac{63{l}_{{\rm{h}}1}^{3}{l}_{{\rm{h}}2}^{3}({l}_{{\rm{h}}2}-{l}_{{\rm{h}}1})k(\beta )}{400\pi H{h}^{3}({l}_{{\rm{h}}2}^{3}-{l}_{{\rm{h}}1}^{3})}\end{array}\right.$$
(12)

By substituting the specific Qz into Eq. (1), the corresponding Reynolds equations for the perforated plates can be obtained. Accordingly, the Reynolds equations for perforated plates with prismatic holes and those with trapezoidal holes are expressed as follows:

$$\frac{{\partial }^{2}p}{\partial {x}^{2}}+\frac{{\partial }^{2}p}{\partial {y}^{2}}-\frac{21{{l}_{{\rm{h}}}}^{4}}{50{h}^{3}\pi {r}_{{\rm{c}}}^{2}H}\frac{p}{{\vartheta }_{{\rm{cyl}}}(\beta )}=\frac{12\mu }{{h}^{3}}\frac{\partial h}{\partial t}$$
(13)
$$\frac{{\partial }^{2}p}{\partial {x}^{2}}+\frac{{\partial }^{2}p}{\partial {y}^{2}}-\frac{63{l}_{{\rm{h}}1}^{3}{l}_{{\rm{h}}2}^{3}({l}_{{\rm{h}}2}-{l}_{{\rm{h}}1})}{50{h}^{3}\pi {r}_{{\rm{c}}}^{2}H({l}_{{\rm{h}}2}^{3}-{l}_{{\rm{h}}1}^{3})}\frac{p}{{\vartheta }_{{\rm{tra}}}(\beta )}=\frac{12\mu }{{h}^{3}}\frac{\partial h}{\partial t}$$
(14)

Considering the solution of the Reynolds equation for the perforated plate, a unified description of the equation is established by defining \(\tau =12\mu /{h}^{3}\), \(\psi =-\tau \partial h/\partial t\), \({\varsigma }_{1}=1/\sqrt{\tau {Q}_{z}}\). Thus, Eq. (1) is rewritten as:

$$\frac{{\partial }^{2}p}{\partial {x}^{2}}+\frac{{\partial }^{2}p}{\partial {y}^{2}}-\frac{p}{{{\varsigma }_{1}}^{2}}+\psi =0$$
(15)

Equation (15) can be solved using the eigenfunction expansion method. The viscous damping force acting on the perforated plate is expressed as:

$${F}_{1}=\psi {{\varsigma }_{1}}^{2}LW\frac{{\gamma }_{1}}{3{{\alpha }_{1}}^{2}}$$
(16)
$${\gamma }_{1}=3{{\alpha }_{1}}^{2}-6{{\alpha }_{1}}^{3}\frac{{\sinh }^{2}\frac{1}{{\alpha }_{1}}}{\sinh \frac{2}{{\alpha }_{1}}}-\frac{24{{\alpha }_{1}}^{3}\kappa }{{\pi }^{2}}\mathop{\sum }\limits_{n=1,3,5,\mathrm{..}.}^{\infty }\frac{\tanh \frac{\sqrt{1+{(n\pi {\alpha }_{1}/2)}^{2}}}{{\alpha }_{1}\kappa }}{{n}^{2}{(1+{(n\pi {\alpha }_{1}/2)}^{2})}^{\frac{3}{2}}}$$
(17)

where W and L are the width and length of the rectangular plate, respectively. \({\alpha }_{1}=2{\varsigma }_{1}/W\), \(\kappa =L/W\). Dividing the damping force by the oscillation velocity of the plate yields the expression for the damping coefficient:

$${C}_{{\rm{d}}}=\frac{12\mu }{{h}^{3}}{{\varsigma }_{1}}^{2}LW\frac{{\gamma }_{1}}{3{{\alpha }_{1}}^{2}}=\frac{\mu L{W}^{3}{\gamma }_{1}}{{h}^{3}}$$
(18)

Viscous damping model based on cell classification

The perforated plate is divided into regularly arranged, uniformly sized perforated cells. These cells can be classified according to their boundary conditions, with cells of the same type considered to have equivalent damping contributions. As shown in Fig. 2a, the cells fall into three categories: internal cells, which are fully isolated from the external environment (Fig. 2b); edge cells, which have contact with the external environment on one side (Fig. 2c); and corner cells, which are in contact on two sides (Fig. 2d). Each cell type contributes differently to the overall viscous damping. The damping coefficient of edge cells and corner cells are divided by the damping coefficient of internal cells, yielding their weight coefficients A1 and A2, respectively. The total viscous damping is considered to result from the contributions of N internal cells. N is expressed as:

$$N={N}_{0}+{A}_{1}{N}_{1}+{A}_{2}{N}_{2}$$
(19)

where N0, N1, N2 represent the number of internal cells, edge cells, and corner cells, respectively.

Fig. 2: Cell classification model.
figure 2

a Schematic diagram of cell classification for the rectangular perforated plate. b Boundary conditions for internal cells. c Boundary conditions for edge cells. d Boundary conditions for corner cells. e Schematic of the viscous damping composition in the perforated cell. f Squeeze-film region. g Perforation region. h End effect region. i Flow transition region. The dashed line indicates the rotational symmetry axis of the cell, while the dotted line represents the cell boundaries

Full size image

The modified Reynolds equation is derived based on the cell classification model by equating the total mass flow rate according to the principles of mass conservation, and linear momentum conservation. The modified Reynolds equation is expressed as:

$$\frac{{\partial }^{2}p}{\partial {x}^{2}}+\frac{{\partial }^{2}p}{\partial {y}^{2}}-\frac{12\mu }{{h}^{3}}\frac{LW}{N{R}_{{\rm{p}}}}p=\frac{12\mu }{{h}^{3}}\frac{\partial h}{\partial t}$$
(20)

where, Rp is the viscous damping coefficient for a single internal cell. Clearly, the core challenge in solving the modified Reynolds equation lies in obtaining analytical expressions for N and Rp. The following presents the detailed process for obtaining the Rp for individual cells with varying hole geometries and the weight coefficients A1 and A2.

As shown in Fig. 2e, the damping coefficient of a single perforated cell is composed of four components, Rp = RG + RH + RE + RI. These components include the damping component RG, which arises from the squeeze-film effect (Fig. 2f), the damping component RH resulting from airflow within the hole (Fig. 2g), the damping component RE due to the end effects (Fig. 2h), and the damping component RI arising from flow transition between plates and holes (Fig. 2i). The expressions for RG and RH are derived using the Reynolds equation and the Poiseuille formula, respectively. The semi-analytical expressions for RE and RI are obtained through numerical regression of the simulation results against the theoretical calculations.

For the cell with a cylindrical hole, the RG and RH can be derived from Eq. (2) and Eq. (3). The RE and RI are derived using the equations proposed by Jaroslaw, which have been demonstrated to offer greater accuracy compared to previous studies31. The expressions for the damping components of the cell with a cylindrical hole are given by:

$$\left\{\begin{array}{l}{R}_{{\rm{G}}-{\rm{cyl}}}=\frac{{F}_{{\rm{ann}}-{\rm{cyl}}}}{\frac{\partial h}{\partial t}}=\frac{3\pi \mu {{r}_{{\rm{c}}}}^{4}}{2{h}^{3}}k(\beta )\\ {R}_{{\rm{H}}-{\rm{cyl}}}=\frac{{P}_{{\rm{H}}-{\rm{cyl}}}\pi {{r}_{{\rm{c}}}}^{2}}{\partial h/\partial t}=\frac{8\mu H}{\pi {{r}_{{\rm{h}}}}^{4}}{\pi }^{2}{{r}_{{\rm{c}}}}^{4}=\frac{8\pi \mu H}{{\beta }^{4}}\\ {R}_{{\rm{E}}-{\rm{cyl}}}=\frac{{\pi }^{2}{{r}_{{\rm{c}}}}^{4}\mu }{{{r}_{{\rm{h}}}}^{3}}[2.53(H/{r}_{{\rm{h}}})+2.9736-0.5009{\beta }^{2}-0.2403{\beta }^{4}-1.0415{\beta }^{6}]\\ {{\rm{R}}}_{{\rm{I}}-{\rm{cyl}}}={\pi }^{2}{r}_{{\rm{c}}}^{4}\mu \left(\frac{{b}_{1}(\beta )}{h{r}_{{\rm{h}}}^{2}}+\frac{{b}_{2}(\beta )}{{h}^{2}{r}_{{\rm{h}}}}+\frac{{b}_{3}(\beta )}{{h}^{3}}\right)\\ {b}_{1}(\beta )=-1.2279+3.9286{\beta }^{2}-8.3047{\beta }^{4}+\,10.364{\beta }^{6}-4.7769{\beta }^{8}\\ {b}_{2}(\beta )=1.8564-4.5354{\beta }^{2}+6.26363{\beta }^{4}-6.1491{\beta }^{6}+2.6235{\beta }^{8}\\ {b}_{3}(\beta )=-0.091428+0.39734{\beta }^{2}-0.89348{\beta }^{4}+\,0.97977{\beta }^{6}-0.39857{\beta }^{8}\end{array}\right.$$
(21)

For the cell with a conical hole, the RG can be directly obtained by substituting rh with rh1 in Eq. (21). The expression for the RH is derived from Eq. (7). The RE can be regarded as half of the sum of the RE-cyl of two cells, each containing a cylindrical hole with radius rh1 and rh2, respectively (see Supplementary Note 2). The empirical formula for the RI is obtained through numerical regression (see Supplementary Note 2). The expressions for the damping components of the cell with a conical hole are given by:

$$\left\{\begin{array}{l}{R}_{{\rm{G}}-{\rm{con}}}=\frac{{F}_{{\rm{ann}}-{\rm{con}}}}{\frac{\partial h}{\partial t}}=\frac{3\pi \mu {{r}_{{\rm{c}}}}^{4}}{2{h}^{3}}k(\beta )\\ {R}_{{\rm{H}}-{\rm{con}}}=\frac{8\mu}{3}\frac{H}{{r}_{{\rm{h}}2}-{r}_{{\rm{h}}1}}\left(\frac{1}{{r}_{{\rm{h}}1}^{3}}-\frac{1}{{r}_{{\rm{h}}2}^{3}}\right)\pi {r}_{{\rm{c}}}^{4}\\ {R}_{{\rm{E}}-{\rm{con}}}=\frac{{R}_{{\rm{E}}-{\rm{cyl}}}({r}_{{\rm{h1}}})+{R}_{{\rm{E}}-{\rm{cyl}}}({r}_{{\rm{h2}}})}{2}\\ {R}_{{\rm{I}}-{\rm{con}}}=\frac{\mu }{{r}_{{\rm{h}}2}^{3}}(-1.13448\frac{{r}_{{\rm{h}}2}}{{r}_{{\rm{c}}}}+1.166){(\frac{{r}_{{\rm{h}}2}}{h})}^{2.25}{(\pi {{r}_{{\rm{c}}}}^{2})}^{2}\end{array}\right.$$
(22)

For prismatic holes and trapezoidal holes, the square cross-section with a side length of l is equivalently represented as a circular cross-section with a radius of requ based on the shape function, where requ = 0.574 l. By substituting requ into the previously mentioned formula, the damping components and Rp for the cell with a prismatic hole and a trapezoidal hole can be obtained.

The weight coefficients for edge cells and corner cells are related to the perforation ratio β and the parameter γ1 = h/H. Simulation models for three different types of cells are built, and through analyzing the simulation results, expressions for A1 and A2 are derived (see Supplementary Note 3):

$$\left\{\begin{array}{c}{A}_{1}=(-0.501{\gamma }_{1}+0.912)+\frac{0.501{\gamma }_{1}-0.912}{\left(1+{(\beta /(0.176+1.755{\gamma }_{1}-0.812{{\gamma }_{1}}^{2}))}^{1.751+9.835{\gamma }_{1}-15.268{{\gamma }_{1}}^{2}+7.689{{\gamma }_{1}}^{3}}\right)}\\ {A}_{2}=(-0.489{\gamma }_{1}+0.794)+\frac{0.489{\gamma }_{1}-0.794}{\left(1+{(\beta /(0.270+1.947{\gamma }_{1}-0.873{{\gamma }_{1}}^{2}))}^{1.281+12.423{\gamma }_{1}-19.981{{\gamma }_{1}}^{2}+10.074{{\gamma }_{1}}^{3}}\right)}\end{array}\right.$$
(23)

The complete expression of the modified Reynolds equation is obtained by substituting Rp, A1, and A2 into Eq. (19) and Eq. (20). For the solution of the modified Reynolds equation, Eq. (20) can similarly be rewritten as:

$$\frac{{\partial }^{2}p}{\partial {x}^{2}}+\frac{{\partial }^{2}p}{\partial {y}^{2}}-\frac{p}{{{\varsigma }_{2}}^{2}}+\psi =0$$
(24)

where \({\varsigma }_{2}=1/\sqrt{\tau LW/N{R}_{{\rm{p}}}}\), \(\tau =12\mu /{h}^{3}\), \(N{R}_{{\rm{p}}}=({N}_{0}+{A}_{1}{N}_{1}+{A}_{2}{N}_{2})({R}_{{\rm{G}}}+{R}_{{\rm{H}}}+{R}_{{\rm{E}}}+{R}_{{\rm{I}}})\),\(\psi =-\tau \partial h/\partial t\).

Using the same solution process as described earlier, the expression for the viscous damping coefficient of the perforated plate based on the cell classification model can be obtained.

Boundary effects of the perforated plate

This work thoroughly considers the boundary effects of the perforated plate. It is essential to adopt free boundary conditions when solving the Reynolds equation. In this case, the pressure at the plate boundaries is assumed to be equal to the ambient pressure, as illustrated in Fig. 3a. However, the complete boundary conditions should account for the airflow at the plate boundaries, as shown in Fig. 3b. The computational errors resulting from this discrepancy are referred to as boundary effects. In our previous work, an equivalent elongation model has been proposed to address this issue38. As shown in Fig. 3c, the boundary effect is compensated by equivalently elongating the side lengths of the plate and substituting the adjusted lengths Lelong into our calculations. The classical elongation model is primarily applicable to non-perforated plates and still results in some computational errors when addressing the boundary effects of perforated plates.

Fig. 3: Boundary effects of the perforated plate.
figure 3

a Free boundary condition, where the pressure at the plate boundary equals the ambient pressure. b Complete boundary condition, where the pressure at the plate boundary is not equal to ambient pressure. c Equivalent elongation model, which extends the plate to simulate the fluid state under a complete boundary condition. d Schematic diagram of the simulation model. e Boundary conditions of the simulation model. The simplified simulation model adopts free boundary conditions, while the complete simulation model adopts complete boundary conditions to reflect the true motion state of the fluid and structure. f Elongation factors \(\eta\) of the perforated plate under different structural parameters. The simulation employs a square plate with a side length of 4 mm. The grey area represents the elongation factors of the perforated plate obtained through simulation, with 0.84 being the classical elongation factor

Full size image

To address the aforementioned challenges, the perforated plate under complete boundary conditions is similarly regarded as an elongated plate under free boundary conditions. The equivalent elongation model for the perforated rectangular plate is expressed as:

$$\left\{\begin{array}{l}{L}_{{\rm{elong}}-{\rm{h}}}=L(1+\eta \frac{h}{L})\\ {W}_{{\rm{elong}}-{\rm{h}}}=W(1+\eta \frac{h}{W})\end{array}\right.$$
(25)

where Lelong-h and Welong-h are the length and width of the elongated perforated plate, respectively. \(\eta\) is the elongation factor for the perforated plate.

Simulation models with free and complete boundary conditions were constructed separately to obtain reliable results for \(\eta\), as shown in Fig. 3d. In the simplified model, the plate boundaries are set as pressure outlets at ambient pressure. In comparison, the fluid domain of the complete model is set as a larger space enclosing the oscillating plate and the perforated plate. Here, the six surfaces of the fluid domain are set as pressure outlets, while all surfaces of the plates are set as walls. This configuration allows for a more realistic simulation of fluid motion, as illustrated in Fig. 3e.

Figure 3f illustrates the elongation factors \(\eta\) corresponding to various structural parameters obtained from simulations. It is evident that the \(\eta\) of the perforated plate is higher than the classical elongation factor \({\eta }_{{\rm{c}}}\). Although \(\eta\) fluctuates with variations in structural parameters, it generally remains within a stable range. For computational convenience, the \(\eta\) is set to 7/2π. The elongation model for perforated plates is obtained by substituting this value into Eq. (25). Considering Lelong and Welong as the actual length and width of the perforated plate into the aforementioned model for solving, compensates for the computational errors induced by boundary effects. Notably, the boundary effects become increasingly significant as the air film thickness increases. The proposed elongation model is particularly applicable when the air film thickness is no longer much smaller than the plate edge length. All subsequent computational results are obtained after accounting for boundary effects.

Verification of the theoretical models

Simulation verification

The computational accuracy and applicability of the two viscous damping models are validated using the complete simulation models. Table 1 summarizes the main simulation parameters, with hole geometry, hole quantity, perforation ratio, and air film thickness treated as variables. Figure 4a–h presents the computational results of two models alongside the simulation results for various hole geometries, including cylindrical holes, conical holes, prismatic holes, and trapezoidal holes. The results indicate that the viscous damping coefficients obtained from both models align well with the simulation results, with deviations generally within 10%. A smaller air film thickness results in a more pronounced damping weakening effect. Taking perforated plates with cylindrical holes as an example, damping decreases by two orders of magnitude at a 25 μm air film thickness (Fig. 4a) but only drops to one-quarter at 100 μm (Fig. 4b). This trend can be observed in perforated plates with various hole geometries, indicating that perforation produces a more pronounced damping weakening effect in highly integrated and compact MEMS devices.

Table 1 Main simulation parameters
Full size table
Fig. 4: Model calculations and simulation results.
figure 4

a–h Model calculations and simulation results of the damping coefficient, with hole geometry, perforation ratio, and air film thickness as variables. a Air film thickness of 25 μm, cylindrical hole. b Air film thickness of 100 μm, cylindrical hole. c Air film thickness of 25 μm, conical hole. d Air film thickness of 100 μm, conical hole. e Air film thickness of 25 μm, prismatic hole. f Air film thickness of 100 μm, prismatic hole. g Air film thickness of 25 μm, trapezoidal hole. h Air film thickness of 100 μm, trapezoidal hole. i Model calculations and simulation results of the damping coefficient with the number of holes as the variable. All parameters, except for the number of holes, remain constant. The schematic illustrates one-quarter of the complete perforated plate. In all figures, solid lines are the model calculations and simulation results for the damping coefficient, and the dashed lines indicate the deviations between the model calculations and the simulation results

Full size image

The calculation accuracy of the viscous damping model based on cell classification is significantly higher than that of the viscous damping model based on the continuity equation when the perforation ratio is high. Conversely, for a low perforation ratio, the situation is reversed. A transition in computational accuracy occurs around a perforation ratio of approximately 0.6, driven by varying contributions of the damping components under different structural parameters. As the perforation ratio increases, the influence of damping component RI gradually rises, while the contribution of damping component RH decreases (Supplementary Note 4, Fig. S6). The viscous damping model based on the continuity equation neglects the RI, while accounting for the RH resulting from flow within the hole and RE due to end effects. Consequently, this leads to an underestimation of the damping magnitude when the perforation ratio is high. In contrast, the viscous damping model based on cell classification divides the plate into a periodic array of perforated cells, making it better suited for scenarios with higher perforation ratios. Overall, the viscous damping model based on the continuity equation is more applicable for perforation ratios below 0.6, while the model based on the cell classification provides more reliable calculations for perforation ratios above this threshold.

For a given perforation ratio, variations in the number of holes can significantly alter hole size, thereby affecting the magnitude of damping. Taking cylindrical holes as an example, the viscous damping coefficients of the perforated plates are assessed as the number of holes increased from 25 to 625. Detailed simulation parameters are presented in Table 1. As shown in Fig. 4i, the damping coefficient increases with the number of holes. This is because a lower number of holes results in larger diameters, reducing flow resistance within the holes when other parameters remain constant. This trend is more intuitively reflected by the expressions for Qz and Rp. Both models show larger deviations with fewer holes but converge with simulation results as the number of holes increases. This inconsistency arises because the airflow within the holes cannot be modeled as Poiseuille flow when the diameter of the hole is much greater than its height, leading to substantial computational errors in both models. For example, in Fig. 4i, when the number of holes is 5 × 5, the hole diameter is 270 μm, while the hole height is only 50 μm, causing deviations of up to 20%. In summary, the proposed models are complementary to each other, enabling accurate analysis of the effect of perforations on viscous damping across various perforation configurations, particularly when the hole diameter and height are comparable.

Experimental verification

Perforated oscillators of various scales were fabricated to validate the proposed models. Our theoretical model encompasses a range of hole geometries. Among these, cylindrical and prismatic holes, as well as conical and trapezoidal holes, exhibit certain similarities. Therefore, perforated oscillators featuring trapezoidal and cylindrical holes were selected for vibrational experiments. As illustrated in Fig. 5a, d, the perforated oscillator is composed of two bonded parts: the oscillating structure and the substrate. The oscillating structure is made of a silicon-on-insulator (SOI) wafer, with a central perforated plate allowing interaction with light to obtain vibrational responses. The lower surface of the oscillating structure forms a pair of parallel surfaces with the recess in the substrate, as depicted in Fig. 5c, f. During operation, air flows in and out periodically, dissipating the mechanical energy of the oscillator. Note that although the beams differ for oscillators with two distinct hole geometries, both are categorized as cross-beams and therefore exhibit similar vibrational characteristics. Different perforated oscillators were subjected to the free-vibration decay (FVD) measurements, and the obtained vibration responses were used to fit the damping coefficients. The main parameters of the oscillators are presented in Table 2.

Fig. 5: Schematic diagrams of the perforated oscillators used in the experiments.
figure 5

a–c Schematic diagrams of perforated oscillators with cylindrical holes. d–f Schematic diagrams of perforated oscillators with trapezoidal holes. a, d Schematic diagrams of the oscillating structure and the substrate of the perforated oscillators. b, e Schematic diagrams of the complete perforated oscillators. c, f Cross-sectional views of the perforated oscillators

Full size image
Table 2 Structural parameters of perforated oscillators
Full size table

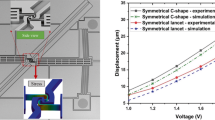
The FVD responses of the four oscillators are presented in Fig. 6a–d. It is observed that the predicted results from the theoretical models closely match the vibrational response envelopes indicated by the dashed lines for all oscillators. The deviations of the damping coefficients obtained through from fitting the response envelope and those calculated from the two models are well controlled within 10%. Both proposed models are demonstrated to provide more reliable estimates of the damping coefficient and dynamic response compared to existing models (Supplementary Table).

Fig. 6: Experimental results for perforated oscillators.
figure 6

a–d Envelopes of the free-vibration decay response of theoretical models and experimental data. a Oscillator with 25 cylindrical holes. b Oscillator with 49 cylindrical holes. c Oscillator with 25 trapezoidal holes. d Oscillator with 9 trapezoidal holes. e Envelopes of experimentally measured free-vibration decay response of perforated and non-perforated oscillators. f Impact factors f and hole images corresponding to different perforation ratios β. Red represents cylindrical holes, blue represents trapezoidal holes

Full size image

In addition, using the perforated oscillator with 49 holes as an example, the FVD curves of both the perforated and non-perforated oscillators were obtained and compared. All parameters except for the perforations were kept consistent between the two oscillators. The vibration responses were normalized by dividing by the initial amplitude. Figure 6e shows the response envelopes as the amplitude decays to 1% of the initial value. As shown in Fig. 6e, the perforated oscillator experiences a longer decay time, with its damping coefficient reduced by nearly 70% relative to the non-perforated oscillator. This finding indicates that a well-designed perforation configuration can significantly enhance and optimize the dynamic performance of MEMS devices, such as accelerometers24, ultrasonic transducers39, and vibration energy harvesters21.

We further analyzed the impact of hole geometry and structural parameters on the damping weakening effect. Figure 6f depicts holes with varying geometries and perforation ratios β within the perforated oscillator. The impact factor f is defined as the ratio of the damping coefficient of a perforated oscillator to that of a non-perforated oscillator. A smaller f implies a stronger weakening effect of the perforation on damping. As shown in Fig. 6f, f decreases significantly as the β increases for both hole geometries. Notably, trapezoidal holes with β = 0.26 exhibit a smaller f compared to cylindrical holes with β = 0.43, suggesting that trapezoidal holes achieve similar or even better damping weakening with less surface area loss (on the side of the air film). This finding is particularly promising for capacitive40, acoustic41, optical sensors42, and piezoelectric actuators43, where excessive area loss can adversely affect device performance.

Discussion

Perforated structures are critical for damping and dynamic response tuning and are widely present in various MEMS devices. However, there remains a lack of comprehensive understanding of the damping performance in perforated MEMS devices. This paper presents two comprehensive theoretical models for analyzing the damping behavior of perforated MEMS devices. Both models provide comprehensive analytical expressions, with each being applicable to low and high perforation ratios, respectively. More importantly, our models innovatively consider complex boundary conditions and various hole geometries, including cylindrical, conical, prismatic, and trapezoidal holes, thereby enhancing their applicability to more intricate MEMS devices. The proposed models are thoroughly validated through both simulation and experimentation. The results demonstrate that the two models achieve perfect complementarity, enabling accurate damping predictions for nearly all perforation configurations, including different perforation ratios, hole quantities, and geometries, with errors generally below 10%. Furthermore, trapezoidal holes are demonstrated to exhibit superior damping weakening effects compared to traditional cylindrical holes, achieving an additional damping reduction of nearly 50% at the same perforation ratio. These findings can be leveraged to enhance the performance of resonators significantly and hold potential for application in capacitive, acoustic, and optical MEMS devices. Our work provides a more accurate approach for predicting the viscous damping of perforated MEMS devices and offers effective guidance for damping design and dynamic performance optimization, which carries great significance for the community.

Perforated oscillators fabrication and experimental method

Fabrication process of perforated oscillators

The fabrication process of the oscillating structure with cylindrical holes is illustrated in Fig. 7a. We selected a 4-inch SOI wafer with a device layer thickness of 10 μm and a handle layer thickness of 300 μm (Fig. 7a1). Firstly, a 100 nm thick Cr/Au layer was sputtered onto the SOI handle layer, and spin-coated photoresist (PR) (Fig. 7a2). The patterning of the PR and Cr/Au was achieved through lithography and metal etching, respectively (Fig. 7a3, a4). The handle layer was etched using inductively coupled plasma (ICP) to a depth of 300 μm, creating the central plate (Fig. 7a5). Subsequently, the device layer was etched to form the plate with cylindrical holes and beams with a thickness of 10 μm (Fig. 7a6–a8). Finally, the oxide layer was released using Buffered Oxide Etchant (BOE) to obtain the oscillating structure (Fig. 7a9). Beam parameters were optimized through iterative design and testing to ensure high yield. The fabricated perforated oscillator structure with cylindrical holes is illustrated in Fig. 7b.

Fig. 7: Fabrication of perforated oscillators.
figure 7

a Fabrication process of oscillating structures with cylindrical holes. b Fabricated oscillating structure with cylindrical holes. c Fabrication process of oscillating structures with trapezoidal holes. d Fabricated oscillating structure with trapezoidal holes. e Fabrication process of the substrates for the perforated oscillators. f Fabricated substrate. Each substrate contains a recess with a depth of 100 μm. The dimensions of the recess are larger than that of the oscillating structure, thereby providing adequate operating space for the oscillators. g Oscillating structures and substrate bonding process

Full size image

The fabrication process of the oscillating structure with trapezoidal holes is illustrated in Fig. 7c. We utilized the same SOI wafer as described earlier (Fig. 7c1), and deposited a 1 μm thick silicon dioxide on the handle layer using low-pressure chemical vapor deposition (LPCVD) (Fig. 7c2). Silicon dioxide was patterned by employing reactive ion etching (RIE), forming windows for subsequent wet etching (Fig. 7c3, c4). Due to the significant difference in etching rates between the (100) and (111) crystal orientations of silicon, trapezoidal holes at 54.7° were formed by wet etching (Fig. 7c5). Subsequently, the device layer was patterned using ICP to create beams, a central plate, and prismatic holes with the same dimensions as trapezoidal holes (Fig. 7c6-8). Finally, we employed BOE to release the oxide layer and obtain the oscillating structure with trapezoidal holes (Fig. 7c9). Importantly, lateral etching occurs during the wet etching, resulting in additional volume loss of the plate. In order to mitigate the impact of lateral etching, we implemented convex corner compensation at the four corners of the plate (see Supplementary Note 5). This strategy ensured that the trapezoidal holes were introduced into the plates while ensuring that the shape of the plates still conforms to the intended design. The fabricated perforated oscillator structure with trapezoidal holes is illustrated in Fig. 7d.

The fabrication process for the substrates is illustrated in Fig. 7e. We selected double-sided polished single-crystal silicon wafers (Fig. 7e1) and sputtered Cr/Au on their surfaces, followed by spin-coating with PR. Subsequently, the silicon wafer was subjected to ICP etching to create a recess with a depth of 100 μm (Fig. 7e2, e3), providing operating space for the oscillating structure. The fabricated substrate is illustrated in Fig. 7f. The perforated oscillators used for experimental measurements were fabricated by bonding the substrate with the previously fabricated oscillating structures using Au–Au bonding technology, as depicted in Fig. 7g. An air film with a thickness of 100 μm is formed between the lower surface of the oscillating structure and the recess in the substrate when the oscillator is at rest. Notably, the device layer of the oscillating structure with trapezoidal holes serves as the bonding surface, which facilitates the observation of the complete trapezoidal holes but increases the susceptibility of the beams to fracture. The beam configuration was redesigned to enhance the yield, as shown in Fig. 5.

Experimental setups and analysis

All experiments were conducted in a cave laboratory maintained at ambient temperature and pressure to isolate external noise interference. The root mean square (RMS) of the velocity noise within the effective frequency band of the laboratory is less than 3.16 × 10⁻⁸ m/s, and the daily temperature variation is less than 0.03°C. A non-contact measurement system was employed to avoid additional influences on the oscillator during testing. Two IVS-500 Laser Doppler Vibrometers (LDVs) and a dual-channel data acquisition system were employed to separately collect vibration responses of the oscillating structure and the substrate. The time delay between the two channels is less than 100 ns. The LDVs sampling frequency was set to 10 kHz with a measurement range of 0 to 100 mm/s. The oscillators were horizontally placed on a fixed base, while the laser head was mounted on a three-axis rotary stage to allow for precise adjustment of the laser position. Prior to each measurement, optimal alignment was performed to ensure the effective collection of the light reflected from the oscillators by the LDVs. Mechanical excitation was applied to the oscillators for FVD measurements, with amplitudes kept below 10% of the air film thickness. Note that, as shown in Fig. 6, the instantaneous mechanical excitation causes fluctuations in the initial decay response; however, its impact on the experimental results has been proven to be negligible (see Supplementary Note 6). Multiple measurements were conducted on the same oscillator, yielding relatively stable vibration signals for subsequent analysis. The time-varying vibrations of the oscillators were recorded using vibrometers and a high-speed data acquisition system, which enabled the real-time measurement of the FVDs' response. Subsequently, the responses acquired by the two vibrometers were processed to eliminate substrate vibration noise, thereby obtaining the true vibration response of the oscillators (see Supplementary Note 6). The amplitude of the oscillators was obtained by integrating the collected velocity signals. The amplitude of the oscillator for the small damping ratio case is denoted as:

$$d={A}_{0}{e}^{-Ct/2m}\,\sin (\omega t+\varphi )$$
(26)

where d is the amplitude of the oscillator, term A0 relates to the initial amplitude, C is the damping coefficient of the oscillator, and m is the mass of the oscillating structure, ω is the vibration frequency, φ is the phase. Therefore, the damping coefficient C can be extracted from the envelope of the vibration decay response. The detailed experimental setup is provided in Supplementary Note 6.