Introduction

Two-dimensional (2D) van der Waals ferroelectric materials, which exhibit non-volatile switching with switchable polarization, have emerged as promising platforms for next-generation functional electronics, including the energy storage1,2,3,4, field-effect transistor5,6,7, ferroelectric tunneling junction8,9, bulk photovoltaic effects10,11,12, and neuromorphic computing13,14,15. Among such 2D ferroelectric materials, ferro-ionic CuInP2S6 has received considerable attention due to its phase-tunable characteristics16,17,18. The phases can be classified as (i) ferroelectric phase, (ii) ferro-ionic phase, and (iii) paraelectric phase, and correlated with interlayer Cu+ ion dynamics19. In addition, CuInP2S6 has intrinsic mechanical flexibility with a scalable 2D van der Waals structure20, which enables sensitive detection of external mechanical strain21,22. Depending on the tunable Cu+ ion dynamics and mechanical flexibility, CuInP2S6 has the potential to enable versatile advances in neuromorphic computing systems through switchable ferro-ionic conduction18,23,24,25,26.

However, 2D ferro-ionic CuInP2S6 has major challenges in terms of commercialization and practical applications. As CuInP2S6 exhibits a ferroelectric phase with insulating characteristics at room temperature16, external conditions such as temperature27,28 and electrical field29,30 are required to facilitate the CuInP2S6 phase transition. However, the external electric field and temperature inevitably induce material degradation and electrical instability of CuInP2S631. Moreover, such external conditions simultaneously facilitate the stochastic conductive filament formation with randomized Cu+ ion transport, which completely limits the device-to-device reliability and reproducibility of 2D ferro-ionic memristors32.

Recently, mechanical strain has been suggested as a reliable ferroelectric domain switching method for various ferroelectric materials33,34, which effectively hinders dielectric breakdown, leakage current, and stochastic ion migration. When a local inhomogeneous strain is applied to ferroelectric materials through the tip of an atomic force microscope (AFM), the mechanical bending induces a flexoelectric field35,36, which is derived from the net charge shift in the lattice unit cell. As the mechanical bending is inversely proportional to the length scale, the flexoelectric field exhibits dominant effects in nanoscale materials37. Nevertheless, the mechanical switching of CuInP2S6 has proved challenging owing to dimensional limitations38,39, due to the incompatibility of film thickness variation and insufficient local flexoelectric field for the CuInP2S6 phase transition38. These intrinsic physical limitations of CuInP2S6 have motivated us to develop an on-demand free-standing axial nanogap platform.

In this study, we present a programmable flexoelectric engineering platform for nanoconfined conductive filaments in free-standing 2D ferro-ionic memristor, which provides a geometrical solution for conventional stochastic limitations40,41 and structural limitations38,39. To mechanically achieve the CuInP2S6 phase transition and ultra-efficient flexoelectricity, an axial nanogap structure was fabricated to locally induce free-standing CuInP2S6 at the nanogap. Owing to the flexibility of 2D van der Waals materials, the local inhomogeneous shear strain in the free-standing area allowed for an ultra-high strain gradient, unlike conventional ionic memristors with inflexible oxide materials. As a result, 5.76 × 102-fold maximum current (Imax) enhancement and 6.25 × 102-fold increased Imax, with strain / Imax, without strain ratio was experimentally observed with vertical shear strain 720 nN with 25 nm tip radius. Since the upward polarized bottom In2Se3 suppresses the undesirable ionic conduction in the suspended junction area, a topographical Cu+ ion extraction was selectively derived within 232.42 nm width and 58.98 nm height. In conclusion, this study proposes a previously unreported flexoelectric approach for nanoscale Cu+ ion localization in free-standing 2D ferro-ionic memristor, which effectively permits reliable neuromorphic computing and ultra-low energy consumption systems.

Results and discussion

Free-standing axial nanogap platform for spatial ferro-ionic nano-manipulation

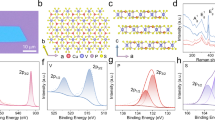
To achieve the confined growth of conductive filaments and spatial controllability of Cu+ ion transport, we adopted a free-standing 2D ferro-ionic memristor with an axial nanogap platform, as shown in Fig. 1a. As shown in Fig. 1b, the free-standing 2D ferro-ionic memristor consisted of an Au/α-In2Se3/CuInP2S6/Pt structure, which was fabricated with the dry transfer method at the axial nanogap structure (Supplementary Figs. 1 and 2). Cross-sectional transmission electron microscopy (TEM) and corresponding energy dispersive spectroscopy (EDS) element mapping (Fig. 1b) were conducted to visualize the device structure of the 2D ferro-ionic memristor, which constructed with an Au bottom electrode (20 nm), α-In2Se3 (125.37 nm), CuInP2S6 (197.91 nm), and Pt tip as the top electrode. Additionally, device construction of 2D ferro-ionic memristor was exhibited with 3D schematic illustration for structural clarification and 3D stacking order (Fig. 1c). As illustrated in Fig. 1c (top), the memristor has been organized at the crossbar arrays to enable the mechanical bending within conductive AFM tip (Pt), which can act as a top electrode and strain source, was vertically manipulated as illustrated in Fig. 1c (bottom). To achieve the spatial modulation of ferro-ionic conduction, mechanical switching has recently emerged as a versatile ferroelectric domain switching method. Nonetheless, the previous research of flexoelectric engineering was completely limited due to the geometrical substrate suspension23 and anisotropic mechanical bending38, while the axial nanogap platform (Fig. 1d) derives the local free-standing state and an efficient mechanical bending, unlike the conventional structural platform. As shown in Fig. 1e, the nanoscale mechanical bending in the free-standing state was precisely controlled with vertical shear strain. The nanoscale bending curvature was independently manipulated at the heterogeneous free-standing gap region through the tip-induced vertical shear strain. The nanoscale bending curvature radius was experimentally obtained as 97.39 nm (480 nN), 38.72 nm (600 nN), and 25.14 nm (720 nN). Following the tip-induced strain engineering, 3D topography was measured with conventional AFM imaging. Thus, the separation of tip-induced strain engineering and topography scanning enables the accurate topographical imaging in Fig. 1e. While the thickness of free-standing 2D ferroelectric heterostructure has been measured as 214.04 nm, the naturally-induced mechanical bending at the nanogap was hindered unlike monolayer and bilayer scale, which requires the external force (478.32 nN) to achieve nanoscale bending curvature at the nanogap region. The obtained mechanical bending induced downward (upward) polarization and net polarization shift in the lattice unit cell, and hence, a gradual current amplification was clearly observed under the nanoscale flexoelectric engineering, as shown in Fig. 1f.

Fig. 1: Universal axial nanogap platform for programmable flexoelectric engineering.
figure 1

a Schematic of a free-standing single 2D ferro-ionic memristor for spatial confinement of conductive filaments. b Free-standing 2D α-In2Se3/CuInP2S6 heterostructure and its corresponding TEM cross-sectional image and SAED mapping. c Schematic illustration of the 2D ferro-ionic memristor structure, constructed with an Au bottom electrode/α-In2Se3/CuInP2S6/Pt top electrode. d SEM image of the axial nanogap array with a 500 nm width and 150 nm depth. e Cross-sectional 3D line profile with tip-induced strain engineering. Flexoelectric current amplification effects in the f full I–V curve through shear strain.

Full size image

Flexoelectric domain switching behavior via nanoscale axial mechanical bending

To specifically realize flexoelectric engineering with the local strain distribution, the heterogeneous flexoelectric behavior of the downward bending and upward bending was spatially mapped within the nanogap and nanowrinkle structures through correlative electrostatic force microscopy (EFM) and piezoelectric force microscopy (PFM) imaging after the initial +7.5 V sample bias poling. Before the flexoelectric domain mapping, pre-characterization of single CuInP2S6/α-In2Se3 flake was performed with PFM imaging and XPS measurements (Supplementary Fig. 3). Figure 2a, b indicates the downward bending locally generated downward polarization in the nanogap center area and the nanowrinkle slope area. Conversely, upward polarization was localized by the upward bending occurring in the nanogap slope area and nanowrinkle center area. When the inhomogeneous strain induced the nanoscale lattice bending, which locally activates the internal flexoelectric field in the material, we observed local polarization switching and carrier redistribution. The nanoscale heterogeneity of the ferroelectric insulator CuInP2S6 and ferroelectric semiconductor α-In2Se3 were probed with their structural variations, as shown in Fig. 2c–f. As the CuInP2S6 mechanical bending caused upward and downward polarization, respectively, the ferroelectric domain was partially engineered owing to the flexoelectric polarization direction. Heterogeneous piezoresponse force microscopy (PFM) amplitude and phase at the edge and center areas were observed to be 11.37 mV / 159.89° (CuInP2S6 nanogap), 1.04 mV / 111.84° (α-In2Se3 nanogap), 55.03 mV / 103.90° (CuInP2S6 nanowrinkle), and 11.37 mV / 356.30° (α-In2Se3 nanowrinkle). To further clarify the heterogeneous electron distribution, the EFM amplitude at the edge and center area were spatially mapped as −21.70 mV (CuInP2S6 nanogap), 13.76 mV (α-In2Se3 nanogap), 6.76 mV (CuInP2S6 nanowrinkle), and −2.75 mV (α-In2Se3 nanowrinkle), which indicates the nanoconfined electron distribution within inhomogeneous strain, attributed to the down polarization. In contrast, the α-In2Se3 EFM amplitude exhibits confined hole distribution in the downward bending area, corresponding to the semiconductive properties of α-In2Se3, which can be further correlated with heterogeneous EFM phase shift (Supplementary Fig. 4). During the tip-induced strain engineering, the homogeneous strain (piezoelectricity) and the inhomogeneous strain (flexoelectricity) has been concurrently generated at the free-standing region. Hence, the coexistence of the piezoelectric effect and the flexoelectric effect should be considered. Nonetheless, the flexoelectricity is an inherently size-dependent phenomenon. When the flake thickness decreases to the nanoscale dimension, the inhomogeneous strain dominantly overwhelms the homogeneous strain, which is simultaneously induced by tip-induced vertical shear strain (Supplementary Fig. 5). Additionally, cross-sectional field calculation39 accurately correlates with the PFM image of CuInP2S6 nanowrinkle, CuInP2S6 nanogap (Fig. 2c), and free-standing flexoelectric simulation (see below). To further clarify the flexoelectric dominance in CuInP2S6 with nanoscale mechanical bending, flexoelectric field distribution in nanowrinkle has been observed in Supplementary Fig. 6a–c. As the nanowrinkle structure was generated without tip-induced vertical shear strain, internal polarization of the nanowrinkle has been dominantly generated from the local lattice bending and its corresponding flexoelectricity. As shown in Supplementary Fig. 6b, c, nanowrinkle PFM amplitude inversely correlates with the calculated surface potential of downward flexoelectricity39, while the nanowrinkle PFM phase linearly corresponds with the surface potential of downward flexoelectricity39. Moreover, tip-induced strain engineering has been conducted within substrate suspension to further minimize the flexoelectric effects. Within substrate suspension, the applied tip force exhibits linear correlation with the distance (Supplementary Fig. 6d). Therefore, the applied tip force (480 nN, 600 nN, 720 nN) is insufficient to activate the lattice bending in the suspended substrate. In this case, plastic deformation can be completely hindered, which effectively minimizes the flexoelectric field effect. The hysteresis variation was also spatially mapped in the suspended substrate with each applied tip force, resulting in the absence of hysteresis variation of suspended CuInP2S6 (Supplementary Fig. 6e). Hence, the flexoelectric dominance was clearly observed in nanoscale geometry, constructed as the nanowrinkle structure and the suspended substrate35,42,43.

Fig. 2: Local flexoelectric domain mapping with local strain distribution.
figure 2

Schematic of the local strain distribution and its corresponding flexoelectric field in the a nanowrinkle and b nanogap. Spatial domain imaging of the c nanowrinkle CuInP2S6, d nanogap CuInP2S6, e nanowrinkle In2Se3, and f nanogap In2Se3. Owing to the local flexoelectric polarization, PFM measurements indicate the downward polarization, as observed in the PFM amplitude and PFM phase. The electron distribution was correlatively obtained for the ferroelectric insulator CuInP2S6 and ferroelectric semiconductor In2Se3, which originated from the heterogeneous carrier density of the semiconductor and insulator.

Full size image

Programmable flexoelectric engineering for self-powered 2D memristor device

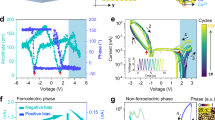
Unlike conventional geometric substrates, the axial nanogap structure permits a local free-standing state. To achieve spatial activation of ferro-ionic properties, vertical shear strain was applied to the free-standing states for efficient strain modulation, unlocking the deterministic 3D positioning of the ferro-ionic conduction. Figure 3a shows the schematic illustration of CuInP2S6 phase transition with spatial modulation of Cu+ ion dynamics. According to vertical shear strain engineering, the CuInP2S6 phase transition was controlled in the mechanical bending geometry. When the vertical shear strain was applied to the free-standing area, a downward polarization enhancement locally emerged owing to the downward net polarization shift. The downward (upward) lattice bending exhibits the compensation (attenuation) direction of Cu+ ion dynamics, which implies that the ferro-ionic conduction threshold voltage (Vth) can be reversibly controlled according to the lattice bending direction. As a result, the ferro-ionic conduction Vth was decreased considerably under downward lattice bending, whereas upward lattice bending increased the ferro-ionic conduction Vth. To observe the initial stochastic domain distribution, upward bias poling of the α-In2Se3/CuInP2S6 heterostructure was pre-characterized, which was statically clarified with the PFM domain pixel distribution (Supplementary Fig. 7). In the upward polarized α-In2Se3 / CuInP2S6 heterostructure, Cu+ and Se2− ions intrinsically generate a Cu+-Se2− dipole at the interface, which facilitates the internal upward polarization. Based on the spatial Cu+ ion transport, the non-deterministic spatial distribution is statically separated within the paraelectric and ferro-ionic phases, which is derived from the spatial dominance of Cu+ ions and Cu− vacancies. The ion-dependent spatial dominance was correlated with the stochastic PFM pixel distribution. The PFM statical phase mapping indicates the dominant distribution of Cu+ ions (−84.15°) and Cu− vacancies (89.39°), causing the discrete phase distribution. Correlatively, the PFM statical amplitude distribution was classified with the ferro-ionic Cu+ ion dominant area (6.62 mV) and paraelectric Cu− vacancy dominant area (0.44 mV). In Fig. 3b, nanoscale α-In2Se3 lattice bending was clearly observed in the cross-sectional TEM image and selected area electron diffraction (SAED) pattern, resulting in a downward net polarization shift and nanoscale flexoelectricity. Additionally, the force-distance curve and topography line profile indicate the accurate control of 3D tip positioning techniques in a three-dimensional scale (Supplementary Fig. 8a, b). Regarding the 3D tip positioning techniques, inhomogeneous mechanical strain can generate the programmable flexoelectric field, which implies the functionalized correlation of ferro-ionic current with respect to the scale of mechanical bending. To further clarify the flexoelectric enhancement of phase transition, PFM hysteresis was measured with flexoelectric energy conversion, as shown in Fig. 3c. Firstly, PFM amplitude hysteresis indicates the ferro-ionic phase transition at 5.43 V without the flexoelectric field (Supplementary Fig. 8c). In contrast, the flexoelectric field in the free-standing α-In2Se3/CuInP2S6 heterostructure reduces the ferro-ionic conduction Vth from 5.36 V to 3.24 V, regarding the polymorphicity of CuInP2S6 in the consistent voltage range. According to the flexoelectric engineering, ferro-ionic phase is exhibited with a ferroelectric hysteresis in the range −10 to 3.24 V, resulting the memristive piezoelectric response in the range 6.75–10 V. To further clarify the reproducible paraelectric Vth shift with various layer construction, exfoliated α-In2Se3/CuInP2S6 flakes were selected for heterogeneous van der Waal layer counts. As a result, fully reversible paraelectric Vth was measured with thickness-dependent layer dominance and flexoelectric energy storage. Under the flexoelectric field, paraelectric Vth was clearly reduced with α-In2Se3 dominant construction (α-In2Se3 120.70 nm / CuInP2S6 115.65 nm), while the flexoelectric field facilitates the additional paraelectric conduction Vth reduction. Nonetheless, CuInP2S6 dominant construction (α-In2Se3 33.36 nm and CuInP2S6 180.37 nm) amplifies the paraelectric Vth, resulting in the reversible paraelectric Vth reduction via downward polarization. (Supplementary Figs. 9 and 10). Additionally, the ferroelectric hysteresis loop was spatially mapped according to the axial nanogap topography to clarify the CuInP2S6 phase transition. Regardless of voltage range, the suspended region exhibited a homogeneous ferroelectric phase, whereas the nanogap region was observed to have a heterogeneous phase, exhibiting ferro-ionic and paraelectric phases within the respective ranges of −5 to 5 V and −10 to 10 V (Supplementary Fig. 11). To further validate the programmable Cu+ ion transport, spatial Imax mapping was conducted in free-standing 2D α-In2Se3/CuInP2S6 heterostructure, as shown in Fig. 3g. Since the ferro-ionic conduction was spatially generated by nanoscale mechanical bending, robust ferro-ionic current amplification can be site-selectively observed. While the current has been measured as 4.13 nA without strain, the current level is significantly increased with tip-induced shear strain as 93.26 nA (480 nN), 497.67 nA (600 nN), and 2380.84 nA (720 nN). Within 720 nN of force, a 5.76 × 102-fold maximum current enhancement was clearly observed, corresponding to the ratio of 2380.84 nA (720 nN) to 4.13 nA (W/O strain). Additionally, Imax, with strain / Imax, without strain ratio was experimentally observed as 1 (W/O strain), 23.58 (480 nN), 125.46 (600 nN), and 625.41 (720 nN), which is attributed from the nanoscale flexoelectric energy storage. Moreover, spatial Imax distribution was also mapped at the single α-In2Se3 memristor and single CuInP2S6 memristor, which correlatively indicates the programmable ferro-ionic conduction within sub-50 nm resolution (Supplementary Fig. 12). While the temperature-independency of ferro-ionic conduction is also significant for device applications, the temperature effects of ferro-ionic conduction have been further verified under 315 K, 330 K, 350 K, and 400 K conditions. According to the previous research19, the CuInP2S6 phase has been classified as four heterogeneous states, i.e., the frozen-in polarization state, ferroelectric polarization state, Cu+ ion hopping state, and conductive filament state. Because a temperature-dependent CuInP2S6 phase transition has been reported at 102 MV/m and 300 K19, the free-standing 2D nanogap device also exhibited temperature-dependent homogeneous ferro-ionic conductive behavior (Supplementary Fig. 13) under the 400 K condition. Moreover, the IV hysteresis behavior in −10 to 10 V sweep range is inhomogeneous, which is attributed to the ferro-ionic phase transition. While the −10 to 10 V range possesses the possibility of ferro-ionic phase transition within temperature variation, the −20 to 20 V sweep range clearly exceeds the ferro-ionic conduction Vth. Additionally, Cu filament formation was initiated under the 400 K condition, which is attributed to the paraelectric phase transition of CuInP2S6.

Fig. 3: Self-powered 2D ferro-ionic conduction via spatial flexoelectric nano-manipulation.
figure 3

a Ferro-ionic phase transition mechanism in the 2D α-In2Se3/CuInP2S6 heterostructure, which indicates the flexoelectric energy storage. b Cross-sectional TEM image and its corresponding SAED pattern of the bent In2Se3 lattice structure, which induces the nanoscale flexoelectricity. c PFM amplitude hysteresis behavior with nanoscale mechanical bending, indicating the conduction threshold reduction. Self-powered system in 2D ferro-ionic conduction, which was experimentally verified with d semi-log I–V curve, e Imax distribution, and f ratio of Imax, with strain to Imax, without strain. g Spatial Imax mapping in free-standing 2D α-In2Se3/CuInP2S6 heterostructure, which enables the sub-50 nm flexoelectric manipulation.

Full size image

Spatial Cu+ ion modulation via reversible ferro-ionic conduction threshold shift

According to previous ferro-ionic studies, the flexoelectric engineering of CuInP2S6 has been actively reported21,22,38,39. These previous works are only available to control its ferroelectric domain switching with mechanical switching methods. While the mechanical bending, which was reported in previous works, was completely insufficient to activate the CuInP2S6 ferro-ionic conduction, the spatial modulation of conductive filaments has been completely blocked. To achieve spatial controllability of the conductive filaments, the concept of a free-standing 2D ferro-ionic memristor is presented in Fig. 4a. As shown in Fig. 4b, programmable flexoelectric engineering at the axial nanogap array was realized with an applied force of 600 nN, confirming the robust reproducibility and reliability of tip-induced strain engineering. Regarding the geometric extensibility of the axial nanogap array, the spatial confinement of the conductive filaments can be homogeneously extended to a 6-inch wafer-scale axial nanogap structure (Supplementary Fig. 14). To unlock spatial ferro-ion controllability, an ultra-high bending curvature was selectively achieved in the axial nanogap array, allowing geometrical guidance of Cu+ ion transport. The nanoscale bending strain was measured to be 0.047 nm−1 (480 nN), 0.064 nm−1 (600 nN), and 0.071 nm−1 (720 nN) in the free-standing area, corresponding to a 4.09 × 102-fold efficient bending strain and 1.63 × 101-fold efficient mechanical energy consumption relative to the previous values for the CuInP2S6 flexoelectric engineering at the nano-hole structure38.To reversibly control the CuInP2S6 ferro-ionic conduction Vth, the initial α-In2Se3 polarization externally controlled the Cu+ ion dynamics, as illustrated in Fig. 4c, d. While the α-In2Se3 downward polarization decreased the initial ferro-ionic conduction Vth with the homogeneous field direction, α-In2Se3 upward polarization increased the initial ferro-ionic conduction Vth, owing to the heterogeneous field direction. Due to the reversible α-In2Se3 polarization, Cu+ ion dynamics were spatially controlled by ultra-high flexoelectric energy conversion efficiency. As tip-induced strain engineering only allows downward polarization, we spatially modulated the programmable shear strain 720 nN to achieve the paraelectric Vth reduction. Within α-In2Se3 downward polarization, homogeneous conductive filament growth and topographical variation (Fig. 4f) were clearly observed, which is attributed to the homogeneous paraelectric Vth shift direction in both the free-standing and suspended areas. Nonetheless, the spatial confinement of the conductive filament was experimentally observed with α-In2Se3 upward polarization, which can be attributed to the heterogeneous paraelectric Vth shift between the free-standing and suspended states. While tip-induced strain engineering permitted localized paraelectric Vth reduction with downward polarization, the paraelectric Vth of the suspended area was increased within upward polarization. As the reversible paraelectric Vth shift enabled the site-selective confinement of conductive filaments (Fig. 4g), Cu+ ion extraction was spatially nanoconfined as 36.59 nm (sample bias 5 V), 44.93 nm (sample bias 7.5 V), and 58.98 nm (sample bias 10 V), which spatially correlated with the Imax distribution as 32.81 nA (sample bias 5 V), 55.89 nA (sample bias 7.5 V), and 74.75 nA (sample bias 10 V). Moreover, nanoconfined topographical variation was further probed and clarified with cross-sectional topography line profile and conductive AFM (CAFM) current mapping, as shown in Fig. 4e, h.

Fig. 4: Deterministic Cu+ ion transport via α-In2Se3 polarization and localized flexoelectric field.
figure 4

a Schematic illustration of the free-standing 2D ferro-ionic memristor consisting of α-In2Se3/CuInP2S6 heterostructure. b Topographical line profile of mechanical bending curvature in the axial nanogap array. Reversible conduction threshold modulation through c downward polarization and d upward polarization of the bottom α-In2Se3. Conductive filaments were spatially observed within e homogeneous topographical variation with α-In2Se3 downward polarization and f inhomogeneous topographical variation with α-In2Se3 up polarization, which was correlatively verified with the g cross-sectional line profile and h CAFM current image.

Full size image

Theoretical validation of flexoelectric Cu+ ion amplification in 2D ferro-ionic memristor

To further clarify the bidirectional threshold resistive switching in the free-standing 2D ferro-ionic memristor, As shown in Fig. 5a, the semi-log I–V curve and corresponding energy band diagram were correlatively analyzed within 0 V → +10 V → −10 V → 0 V bias sweeping. The positive bias (0 V → 10 V) converts the low resistive state (LRS) to high resistive state (HRS) ([1] → [2]) at a ferro-ionic conduction Vth as 6.75 V (Fig. 5b). As the Cu+ ions drift upward in the positive-bias range, the inhomogeneous Cu+ ion distribution facilitates an internal field consisting of Cu+ ions and Cu− vacancies. Hence, the Cu+ ions near the top Pt electrode surface operate as acceptors and the Cu− vacancies near the bottom Au electrode reversibly operate as donors, allowing the formation of p-n homojunctions (Fig. 5c). Reversibly, negative bias sweep (0 V → −10 V) converts the HRS state to the LRS state ([3] → [4]) (Fig. 5d). While the Cu+ ions drift downward in the negative bias range, they are redistributed to their original position in each CuInP2S6 lattice unit cell. As the negative bias sweep derives the inversion of the spatial Cu+ ion distribution and p-n homojunction direction, bidirectional threshold resistive switching behavior is clearly observed (Fig. 5e). Additionally, single 2D memristor performance was characterized with full I–V curve measurements, resulting the conventional memristive behavior unlike 2D α-In2Se3 / CuInP2S6 heterostructure (Supplementary Fig. 15). Furthermore, a numerical simulation of ferroelectric polarization was performed to theoretically validate the observations of the flexoelectric effects. The total Gibbs free energy of the system can be calculated within the applied field configuration, as

$${G}_{{tot}}=\int\limits_{V}({G}_{{{{{\rm{bulk}}}}}}+{G}_{{{{{\rm{grad}}}}}}{+G}_{{{{{\rm{plas}}}}}}+{G}_{{{{{\rm{elec}}}}}}+{G}_{{{{{\rm{f}}}}}{{{{\rm{lexo}}}}}})\,{dV}$$
(1)

In Eq. (1), V denotes the system volume, Gbulk indicates the Gibbs free energy, Ggrad, Gelec, Gplas, and Gflexo imply the Gibbs free energy of the gradient, plasticity, electrostatic, and flexoelectricity, respectively. As shown in Fig. 5f–j, a free-standing 2D ferroelectric heterostructure was modeled with consideration of piezoelectric field and flexoelectric field to accurately quantify the flexoelectric energy conversion, which accurately matches with previous flexoelectric simulation results21,22,39,44. Within the actual bending curvature values, the polarization was numerically calculated as 0.010 µC/m2 (480 nN), 0.013 µC/m2 (600 nN), and 0.015 µC/m2 (720 nN), indicating an analogous correlation with the experimental results. Additionally, strain-polarization simulations predicted strain tensor values as 0.86 N/m2 (480 nN), 1.10 N/m2 (600 nN), and 1.28 N/m2 (720 nN), which originated from the flexoelectric energy conversion and field-dependent piezoelectric response (Supplementary Fig. 16). To further quantitatively estimate the mechanical bending dimensionality, the flexoelectric equation was derived.

$${G}_{{{{{\rm{flexo}}}}}}={\frac{1}{2}G_{{ijkl}}}\left({\frac{\partial {P}_{k}}{\partial {x}_{l}}e_{{ij}}}-\frac{\partial {e}_{{ij}}}{\partial {x}_{l}}{P}_{k}\right)$$
(2)
Fig. 5: Theoretical validation of Cu+ ion dynamics within nanoscale flexoelectric engineering.
figure 5

a Full I–V curve of a single 2D ferro-ionic memristor and b its corresponding energy band diagram of b upward α-In2Se3 / downward CuInP2S6, c downward α-In2Se3 / downward CuInP2S6, d downward α-In2Se3 / upward CuInP2S6, and e upward α-In2Se3 / upward CuInP2S6. f Strain calculation of the free-standing 2D ferroelectric heterostructures with consideration of piezoelectric field and flexoelectric field, exhibiting the cross-sectional distribution of the g domain and h strain. Theoretical evaluation of flexoelectric energy storage, resulting in the i bias-polarization hysteresis and j strain-polarization hysteresis.

Full size image

As flexoelectricity indicates the inherent scale dependence, flexoelectricity dominance emerges at nanoscale material dimensions rather than microscale material dimensions. According to Eq. (1), the strain gradients exhibited amplified polarization during downward bending. Moreover, the local polarization redistribution and amplification were theoretically supported by performing Gibbs free energy modeling. The simulation revealed that, as the bending curvature increases, the amplitude of the flexoelectric field proportionally increases, which can be further clarified by the previous nanogap research including a microscale mechanical bending that also yielded a significantly lower bending curvature than the nanoscale mechanical bending44. Furthermore, the vertical stacked 2D α-In2Se3/CuInP2S6 enhances the total ferroelectric polarization by Cu+-Se2− dipole interaction, leading to larger ferroelectric hysteresis behavior. To precisely evaluate the ferroelectric hysteresis enlargement within the 2D ferroelectric vertical stacking, Gibbs free energy modeling of the α-In2Se3/CuInP2S6 heterostructure was theoretically considered within the structural configuration as in Eq. (3)45.

$${G}_{{{{{\rm{tot}}}}}}={G}_{{{{{\rm{f}}}}}1}{t}_{{{{{\rm{f}}}}}1}+{G}_{{{{{\rm{f}}}}}2}{t}_{{{{{\rm{f}}}}}2}=\left({\alpha d}_{{{{{\rm{f}}}}}1}{+{xt}}_{{{{{\rm{f}}}}}2}\right){{P}_{{{{{\rm{s}}}}}}}^{2}+\left({\beta t}_{{{{{\rm{f}}}}}1}{+{yd}}_{{{{{\rm{f}}}}}2}\right){{P}_{{{{{\rm{s}}}}}}}^{4}-\,V{P}_{{{{{\rm{s}}}}}}$$
(3)

In Eq. (3), Gf1 is the Gibbs free energy of the ferroelectric semiconductor α-In2Se3, and Gf2 is the Gibbs free energy of the ferroelectric dielectric CuInP2S6. Α, β imply the Landau coefficient of Gf1, and (x, y) represents the Landau coefficient of Gf2. Also, the flake thicknesses are indicated as df1 and df2, while Ps represents the spontaneous polarization. Lastly, V (V = Vf1 + Vf2) denotes the voltage of α-In2Se3/CuInP2S6. To quantitatively clarify the polarization in ferroelectric heterostructures, Gibbs free energy modeling can be modified as a function of Ps and Vf1. As the df1, df2, x, and y values are consistent without the external conditions, Vf1 can be expressed as the sum of the linear function and cubic function of Ps.

$${V}_{{{{{\rm{f}}}}}2}=-2x{d}_{{{{{\rm{f}}}}}2}{P}_{{{{{\rm{s}}}}}}-4y{d}_{{{{{\rm{f}}}}}2}{{P}_{{{{{\rm{s}}}}}}}^{3}$$
(4)

From the relative combination of Eqs. (1) and (3), the Gibbs free energy can be simultaneously considered in terms of both the field and structural configuration. The Gibbs free energy has two stable Ps states, where the Gtot derivative is calculated as 0. In the initial states, one distinctive Ps state can be clearly observed, which is correlated with Cu+-Se2− dipole formation. When Vf2 gradually increases, distinctive Ps states occur sequentially as functions of the graph intersection counts. In the overlapping negative capacitance range, graph intersection counts gradually increase from one distinctive Ps state to three distinctive Ps states, similar to the reversible fashion. After negative capacitance interference, one distinctive Ps state can be derived and maintained in a high Vf2 range. As the flexoelectric field enables hopping of the overlapped negative capacitance range, the numerical validation is deterministically correlated with the experimental Ps state counts within a homogeneous Vf2 range, which theoretically supports hysteresis amplification through flexoelectricity and vertically stacked ferroelectric materials.

Discussion

In this study, we presented a free-standing axial nanogap platform for deterministic ferro-ionic modulation through nanoscale flexoelectric engineering. To spatially modulate the Cu+ ion, an ultra-high vertical shear strain was site-selectively facilitated in the free-standing area to activate the ferro-ionic conduction, which allowed local positioning of the CuInP2S6 phase transition. Moreover, we experimentally demonstrated the concept of a single 2D ferro-ionic memristor with nanoscale flexoelectric engineering. As the local flexoelectric energy storage results in a fully reversible paraelectric Vth shift, a 6.25 × 102-fold increased Imax, with strain / Imax, without strain ratio was experimentally observed owing to the vertical shear strain 720 nN, which is theoretically supported by the 3D flexoelectric simulation. Additionally, a topographical Cu+ ion extraction was locally confined within 232.42 nm width and 58.98 nm height, while the upward polarized bottom In2Se3 suppresses the undesirable ionic conduction in the suspended junction area. Therefore, we envision that our free-standing 2D ferro-ionic memristor provides an extendable geometric solution for ultra-efficient self-powered system and reliable neuromorphic computing systems.

Methods

Axial nanogap fabrication

The axial nanogap substrate was fabricated at the National Nano Fab Center (NNFC, etching team, Republic of Korea) and sequenced as a front-end-of-line poly Si etch, normal photoresist (PR) strip, followed by post-cleaning and PR coating. After fabrication, the nanogap substrate was rinsed in acetone solution for 3 min at 500 RPM to delaminate the passivation PR layer. After the PR removal, residual organic contaminants were removed using deionized water. A Ti adhesion layer (2 nm thickness) and Au film (18 nm thickness) were deposited on the nanogap structure. The deposition conditions were 0.2 A/s (deposition rate), 8 × 10−7 torr (deposition pressure), room temperature (deposition temperature), and 5 RPM (rotation rate) through the electron evaporation system (KVE-E2000L, KOREA VACUUM TECH., Republic of Korea).

Mechanical exfoliation and transfer of 2D ferroelectric materials

Prior to mechanical exfoliation and dry transfer, a polydimethylsiloxane stamp was attached to the cover glass. As the 2D ferroelectric materials (α-In2Se3/CuInP2S6) were mechanically exfoliated from the bulk crystals (HQ Graphene, Netherlands) onto polydimethylsiloxane stamps, α-In2Se3 was transferred to the nanogap. Following α-In2Se3 dry transfer, CuInP2S6 was arbitrarily transferred above the α-In2Se3 position by applying the 70 °C transfer condition, which determined the local free-standing states. Alternatively, the nanowrinkle structure was naturally generated during the dry transfer process (Supplementary Fig. 17).

Atomic force microscopy

AFM (NX-10, Park Systems, Republic of Korea) measurements were conducted using an ElectriMulti75-G cantilever, with a silver paste electrode selectively deposited at the edge of the sample to induce vertical charge transfer. The ElectriMulti75-G cantilever was calibrated with a tip radius (25 nm), length (225 µm), height (17 µm), width (28 µm), and spring constant (3.3 N/m), which resulted in 320.8 kHz contact resonance frequency. During the tip-induced strain engineering, the inhomogeneous shear strain was vertically controlled with a gradual force limitation (480, 600, and 720 nN), hold time (50 s), and speed (0.5 µm/s). After the tip-induced strain engineering, AFM topography was measured with ElectriMulti75-G cantilever, contact mode, scan rate 0.7 Hz, and set point 0.3 V.

Material characterization

To pre-characterize the 2D ferroelectric heterostructure, X-ray photoelectron spectroscopy (XPS) measurements (NEXSA, Thermo Fisher Scientific, USA) were performed with an X-ray spot size of 400 µm. XPS Peak deconvolution was performed on the Cu 2p, In 3d, P 2p, S 2p, and Se 3d spectra. The XPS profiles were aligned using the C 1 s peak at a binding energy of 285 eV. After the measurements, the data were calibrated using CASAXPS software (version 8.1). The transferred flakes were characterized using optical microscopy (U-MSSP4, Olympus, Japan) and FE-SEM (S-4800, Hitachi, Japan). A focused ion beam instrument (NX2000, Hitachi Ltd., Japan) was used to prepare the cross-sectional TEM specimens using a Ga+ ion beam from 30 to 5 keV, and a lift-off process was conducted to etch the specimens. TEM (JEM-2100F, JEOL, Japan) and X-ray diffraction (Empyrean, Malvern PANalytical, United Kingdom) were used to observe the lattice structure, EDS mapping, and SAED pattern of the layered structures of α-In2Se3 and CuInP2S6 at the atomic scale.

3D flexoelectricity simulations

To theoretically quantify the nanoscale mechanical bending, a 2D α-In2Se3/CuInP2S6 heterostructure was modeled using the commercially available 3D simulation program COMSOL Multiphysics 6.1. The experimental material characteristics, including Young’s modulus, Poisson’s ratio, domain wall density, and polarization reversibility, were extracted from previous studies38,46,47,48 and input to the 3D ferroelectric simulation model. The In2Se3/CuInP2S6 heterostructure was numerically modeled with experimental layer dimensionality at room temperature, a free-standing state, and a lateral width of 500 nm, which enabled a similar mechanical bending with experimental values. Under these conditions, the strain-polarization coupling was calculated as a function of the mechanical bending curvature (420 nN, 600 nN, 720 nN), which was experimentally obtained for a free-standing 2D ferroelectric heterostructure.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.