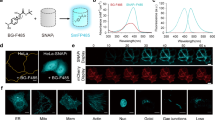
Abstract
To study biological signalling, great effort goes into designing sensors whose fluorescence follows the concentration of chemical messengers as closely as possible. However, the binding kinetics of the sensors are often overlooked when interpreting cell signals from the resulting fluorescence measurements. We propose a method to reconstruct the spatiotemporal concentration of the underlying chemical messengers in consideration of the binding process. Our method fits fluorescence data under the constraint of the corresponding chemical reactions and with the help of a deep-neural-network prior. We test it on several GCaMP calcium sensors. The recovered concentrations concur in a common temporal waveform regardless of the sensor kinetics, whereas assuming equilibrium introduces artifacts. We also show that our method can reveal distinct spatiotemporal events in the calcium distribution of single neurons. Our work augments current chemical sensors and highlights the importance of incorporating physical constraints in computational imaging.
Similar content being viewed by others
Introduction
Biological organisms transmit information by altering the spatiotemporal concentration of certain chemical species1. For instance, calcium ions (Ca2+) act as messengers in a wide range of physiological processes such as cell motility and differentiation, cardiac contraction, wound response, or brain signaling2,3. In particular, the concentration of calcium exhibits multiple temporal profiles within and across brain cells, each with a unique waveform that encodes a potentially different message4,5,6; and this is independent of whether the cells are electrically excitable4,7. For neurons, this diversity is known to play a role in the cellular mechanisms of synaptic plasticity4,5 and brain memory6. For astrocytes, it is a sign of specialization to the heterogeneity of synaptic inputs7,8,9,10. Many chemical species other than Ca2+ are involved in biological signaling. For example, hydrogen-peroxide (H2O2) waves play a key role in transmitting information within plants11,12.
To study cell signaling in living organisms, researchers use chemical sensors13. More precisely, an important subset of chemical sensors are designed to report on the presence of certain chemical species of interest (CSI) such as Ca2+14.
Their fluorescence changes upon binding to the CSI15,16, indirectly measuring its concentration. This makes it possible to follow the evolution of dynamic processes through space and time with little invasiveness13.
The ability of chemical sensors to report on cell signaling has been key to many studies17,18,19,20. However, the timescale of the binding kinetics limits the resolution of the observations and, therefore, the range of dynamic processes that can be studied21,22,23. If the concentration of the CSI varies at a similar timescale—as is often the case in neuroscience—the fluorescence might not reflect the underlying concentration accurately23,24. This has led researchers into a quest for sensors that are faster and less obscured by the chemical reaction behind the binding process. The example par excellence is the GCaMP family of calcium sensors, which has recently reached its eighth iteration (jGCaMP821) since 200116.
Overall, new generations of sensors often translate into new discoveries3,25,26,27, but experimental design still requires great care in considering the binding kinetics. The non-linearities in the binding process and the speed of its kinetics might offer a deformed picture of the underlying CSI waves and introduce time lags24,28,29. In spite of this, fluorescent signals are sometimes interpreted in place of the CSI23,24. In the few cases where the underlying chemical reaction is considered, it is presumed at equilibrium30,31,32, which is not always justified. The noise inherent to the chemical reaction, as well as that introduced by the acquisition process, are additional challenges to the interpretation of the fluorescence signals.
In this work, we aim to augment chemical sensors by separating the behavior of the CSI from that of the sensors. The final goal is to paint a more accurate picture of the behavior of the underlying CSI by attempting to recover its concentration. This entails accounting for the different kinetics of the sensors, as well as for the non-linearity and time dependency of their interactions.
We first show that overlooking the binding process—e.g., considering the reaction at equilibrium—can deform the shape of the CSI wave considerably, and introduce other artifacts such as time lags. Our main contribution is then the formulation of an inverse problem that recovers the spatiotemporal concentration of the CSI from images of the fluorescence emitted by its corresponding chemical sensor. The resulting variational framework accounts explicitly for the non-linear binding reaction outside of equilibrium and imposes a deep neural network prior to the spatiotemporal distribution of the CSI. The prior is based on a reparameterization of the concentration using our proposed adaptable latent space that does not require training. In part, this is possible because we inform the inverse problem with the ordinary differential equations (ODE) that model the binding phenomenologically.
We first validate the accuracy of our reconstructions using simulations of calcium sensors with realistic parameters and in vitro mixing experiments. We then apply our method to real calcium-imaging data of mouse neurons. The calcium concentration that we recover shows a common waveform regardless of the sensor used when the stimuli are similar. By contrast, the corresponding fluorescence signals are amorphous and vary considerably across the sensors. Moreover, our method recovers a CSI-concentration map that is regular in space and time, enabling the observation of distinct spatiotemporal events within single cells without the need for averaging. This effect translates into a denoised fluorescence signal too. Preliminary experiments on simulated hydrogen-peroxide sensors in plant leaves were also promising and can be found in our recent conference abstract33. In contrast to calcium sensors, the fluorescence of these H2O2 sensors decreases upon binding.
We would like to note that our framework is not meant to substitute careful experimental design, but to augment the information provided by chemical sensors. One should still ask whether the kinetics of the sensors are adequate for the signals under study, whether the binding model is accurate, and whether the mere presence of the sensor affects the natural physiology of the process under study. These caveats are discussed throughout the main text and the Supplementary.
Results
Principles of our framework
Physical model
We start by modeling the binding process. Our aim is to relate the concentration of the CSI with the fluorescence that is emitted from the sample. We consider a CSI such as Ca2+ or H2O2 with a concentration of c(x, t) inside the sample. The CSI binds to the chemical sensor to form a fluorescent compound. Let s(x, t) and sb(x, t) denote the concentrations of the sensor and of the fluorescent compound. The binding process can then be modeled with the reversible reaction
where nH > 0 denotes the Hill coefficient, and kf, kb are the kinetic rates of the binding and unbinding processes, respectively. We understand (1) as a phenomenological model that can potentially hide multiple reactions34 or dependent binding sites31 behind fractional Hill coefficients (see “Methods” and the Supplementary). This is a common interpretation among experimentalists and requires a measurement of nH, kf, and kb. The chemical reaction in (1) can be modeled with an ordinary differential equation (ODE) that interrelates the temporal variations in the concentrations of the three species. While the fluorescence emitted by the sensors depends mainly on the concentration of the fluorescent compound sb, we can link it to the concentration c of CSI via the ODE. Therefore, we model the predicted fluorescence as \({{\mathcal{H}}}({{\bf{x}}},t;c,{g}_{0},{q}_{e})\), where (1) is an implicit constraint, and g0(x), qe(x) are the fluorescent background and a concentration-to-fluorescence factor31 (see “Methods”). These two additional variables account for several unknown factors such as the quantum yield or the small emissions of the unbound sensor, which can vary over the field of view due to multiple factors such as the length of the optical path to each pixel (ref. 31, Section 10.3.1]. They could also act as low-order corrections for small kinetic changes, for example for those originating from surface-to-volume variations within a cell. While we chose (1) for its generality as an phenomenological model, other ODE systems tailored to specific sensors can be plugged-in seamlessly into the rest of our framework. Relatedly, the recovered concentration will be unitless unless the experiments are calibrated (see Methods).
Inverse problem
Equipped with the physical model, we now present our variational framework to recover the concentration distribution from fluorescence images (Fig. 1). To this end, we formulate the inverse problem
where one searches for the concentration c(x, t), background g0(x), and scaling qe(x) that best fit the fluorescence measurements gm(x, t). In (2), \({{\mathcal{D}}}\) is a data-fidelity term. It enforces that the predicted fluorescence \({{\mathcal{H}}}(c,{g}_{0},{q}_{e})\) (Fig. 1B) is close to the fluorescence measurements gm (Fig. 1A). The binding model in \({{\mathcal{H}}}\) ensures that the predicted fluorescence is consistent with the chemical equations. Mathematically, however, data fidelity is not enough to single out a solution: many concentration distributions can give rise to similar measurements. The addition of a regularization term \({{\mathcal{R}}}\) takes care of this so-called illposedness by enforcing additional properties that one expects from a realistic distribution of the concentration and of the background. For similar reasons, it is convenient that g0(x), qe(x) only vary spatially so that one can extract the static information from the many images in a video.
A Left: Measured fluorescence with GCaMP sensors that bind to Ca2+. Right: Predicted fluorescence with the proposed method. B DUSK recovers the spatiotemporal distribution of a chemical species. Left: Our method recovers the Ca2+ concentration by fitting the fluorescence measurements in consistency with the chemical reaction (top) and with the help of a deep-image prior (bottom). The predicted (denoised) fluorescence (A, right) is a byproduct of this. Right: Ca2+ distribution recovered by DUSK.
Deep spatiotemporal prior
In the majority of problems that are computationally similar to (2), the term \({{\mathcal{R}}}\) only enforces spatial regularity35,36,37. Imposing temporal regularity realistically with such regularization terms is complicated; it might require an accurate model of any underlying motion38,39.
To mitigate the illposedness of problem (2) in both space and time, we propose to use the framework of deep spatiotemporal priors instead40,41,42. (See Supplementary Notes 1 and 2 for a thorough comparison of the methods). In our case, we express the distribution of the concentration as the output of a neural network c(x, t) = fθ(x, z(t)) parameterized by θ, and by a latent vector z(t) that is time-dependent (Fig. 1B). This results in a model \({{\mathcal{H}}}\left({f}_{{{\boldsymbol{\theta }}}}({{\bf{x}}},{{\bf{z}}}(t)),{g}_{0},{q}_{e}\right)\) where the concentration is regularized implicitly (in space–time) by the restriction of the latent variables to a manifold, whereas g0, qe are regularized explicitly in space (see “Methods”). Note that the network is never trained.
In summary, the framework that we propose combines the information contributed by the physical model of the chemical reaction with the regularity of the neural-network parameterization. We call this approach deep-prior ODEs.
Parametric latent space
In addition, we propose a modification of deep priors so that they are better adapted to the dynamics of chemical sensors. In previous work41, the latent space of the deep prior in a Fourier-ptychography method was a straight line with equidistant samples for lack of structured motion. In ref. 40, the latent space of an MRI algorithm was a helicoidal curve to reproduce the periodicity of the sample movements. In biological signaling, however, samples may alternate between fast and slow dynamics in an unknown manner. To capture such heterogeneity, we propose to represent our latent space with a flexible parametric curve (see “Methods”).
We provide the mathematical description and implementation of our framework in the “Methods”. Find also an extended description thereof in the Supplementary Notes 1 and 2. There, we also present a more technical comparison to the state of the art. We refer to our framework as DUSK for “Deep-prior odes for Uncoupling Sensor Kinetics” (Fig. 1).
Baseline method: reaction at equilibrium
To study the effects of overlooking the sensor kinetics, we consider an alternative method where we assume that the ODE that models (1) reaches the steady state instantly (\(i.e.,\frac{{{\rm{d}}}{s}_{b}}{{{\rm{d}}}t}=0\)). This is standard practice in calcium imaging30,31. It leads to the nonlinear pointwise function
for the fluorescence of the sample.
In other words, the binding process is assumed to be much faster than the temporal variations of the CSI concentration. In our experiments, we will compare this baseline method to DUSK. For maximum fairness, we always equip the baseline method with the same deep spatiotemporal prior. We remark, however, that this already constitutes an improvement over considering (3) alone.
Calcium imaging in the brain
We developed our framework with the intention of augmenting any fluorescent chemical sensor. While other experimental models might stand more to gain from our framework, in this article, our case study is neuronal calcium imaging with GCaMP. More than for its extensive practical importance, we chose this modality because of the availability of rich datasets with accompanying electrophysiological measurements. These are useful as a pseudo groundtruth because of the “reproducibility” of action potential (AP) signals.
In principle, the study of neuronal activity is less vulnerable to misinterpreting fluorescent signals because it focuses exclusively on action potentials. Since APs are spikes, they are usually estimated directly from the fluorescence using spike-deconvolution algorithms43,44,45,46. For fast sensors, simplified spike-to-fluorescence models are sometimes enough to recover the presence of APs21,44, but the shape of the measurements is better recovered when sensor non-linearities are accounted for28,47. This is especially true in rapid successions of APs because the fluorescence does not add linearly in time. On the other hand, measurement noise is usually tackled by averaging the fluorescence signal over an entire cell21. Only recently have there been attempts to denoise the fluorescence signal, notably with the help of deep learning48,49.
While APs are admittedly the final goal of many studies in neural circuits, all these methods are not applicable to cells that are not electrically excitable such as astrocytes, or plants cells in general. Moreover, they do not consider the concentration of the CSI, which can carry information in its waveforms, even in cells that do generate APs4,6. For these reasons, some works do tackle the problem of recovering quantitative calcium signals by developing new protocols or sensors30,50,51,52,53,54,55 while being mindful of potential physiological alterations56,57. Some of these approaches estimate the concentration of calcium by experimental calibration; they often directly assume that the spatiotemporal distribution of the CSI is similar to the one of the fluorescence signal or—more rarely—presume that the chemical reactions are at equilibrium30,31, which is still only adequate for certain combinations of sensor and signal speed. We explore this with our framework.
DUSK recovers the CSI in simulations
To assess the accuracy of DUSK in realistic conditions, we developed a simulation pipeline. We used it to simulate the spatiotemporal evolution of CSI concentration in an astrocyte-like sample (Fig. 2B, Branches). The CSI binds with the sensors as it propagates through the branches of the sample by diffusion (Fig. 2A, Ground truth). We model this with a set of reaction-diffusion PDEs. The constants are taken from experimental values for the jGCaMP8s sensor. The fluorescent measurements were computed according to our physical model. We corrupted them with Poisson noise to model the emission and acquisition process (Fig. 2A, Measured). While the simulations evolve via diffusion, we remark that our reconstruction method does not assume so; DUSK is completely agnostic to the underlying transport mechanism. See “Methods” for a more detailed description of the simulations.
A Reconstruction of simulated data. Top row: XY image at frame 29. Bottom row: Maximum-intensity projection along Y. From left to right: Measured fluorescence, fluorescence denoised (predicted) by DUSK, ground-truth concentration, concentration estimated by DUSK, and concentration estimated by the baseline method (which assumes that the reaction is at equilibrium). The RSNR over the whole spatiotemporal volume is indicated at the bottom of each of the two methods. Images are saturated for the sake of visualization. B Top image: Time lag (in number of frames) of the traveling wave for the concentration recovered by DUSK. For each pixel, the time lag is defined as the frame at which the wave reaches its maximal value. Bottom image: Branches obtained by segmenting the temporal maximum projection of the concentration recovered by DUSK. C Temporal profiles of the fluorescence (top row) and of the concentration (bottom row) on the veins (left column) and over the background (right column) for different methods. The temporal profiles were temporally shifted according to the time lag of the traveling wave. The solid curve is the median, and the interquartile range (25th and 75th percentiles) is shaded. D Temporal profiles of the concentration in the veins (top row) and over the background (bottom row). The solid curve is the median, and the interquartile ranges are shaded (25th and 75th percentiles). The concentration recovered from simulated data is downsampled by the factors D = 1, 2, 4, 8.
In Fig. 2A, we show how DUSK is able to recover the CSI concentration accurately over both time and space from the measured fluorescence. The accuracy of DUSK over time is especially noticeable in the maximum intensity projection (MIP). There, we can observe how the DUSK concentration propagates through the branches similarly to how the ground-truth one does. As seen in Frame 29, DUSK also captures the heterogeneous spatial distribution of the ground-truth CSI. An additional by-product of DUSK is that it denoises the image measurements (Predicted (DUSK), Supplementary Movie 1). We also evaluated the accuracy of the reconstruction quantitatively using the regressed signal-to-noise ratio (RSNR) (see “Methods”). We found that the recovered CSI had an RSNR of 12.52 dB. To illustrate the importance of considering the binding kinetics, we then applied the baseline method to the same measured fluorescence for comparison. As seen in the MIP, the assumption of equilibrium introduces temporal artifacts that hide the astrocyte branches. Another consequence is that the CSI appears spatially homogeneous (Frame 29). The much lower RSNR of 1.31dB achieved by the baseline method is in agreement with our visual assessment.
As the CSI propagates through the sample, it creates a traveling wave. At different parts of the cell, the CSI concentration reaches its maximum value at different time points. The spatial regularity of DUSK allowed us to compute the time lag of this wave at each point in space (Fig. 2B). This kind of information is generally more difficult to obtain because most methods require averaging over the cell body. We used the computed time lags to align the CSI concentration temporally, creating a median waveform that could be representative of a stimulus-response (Fig. 2C). To avoid interferences, we split the signal into the cell and the background. We compared the waveforms resulting from the concentration recovered by DUSK and by the baseline method (with the same deep image prior). By design, both methods recover the fluorescence wave accurately. However, the assumption of equilibrium in the baseline method not only introduces a time lag in the CSI concentration but also deforms the wave significantly. Conversely, DUSK captures the behavior accurately, even for the low signal in the background. Together with Fig. 2A, these experiments suggest that, in some cases, it is important to uncouple the behavior of the CSI from that of the sensor. This is especially relevant because our simulations follow the time scale of chemical sensors that are used in practice. We reached similar conclusions with other simulations (see Supplementary Note 1), as well as with our preliminary analysis of H2O2 signaling in simulated plant leaves33. In that case, the sensors had very different kinetic coefficients and, contrarily to most sensors, their fluorescence decreased upon binding.
To further assess the influence of the kinetics on the accuracy of the reconstruction, in the Supplementary Note 4 we perform simulations with different pairs of binding rates. The results show that DUSK remains accurate across a wide range of values, while the assumption of equilibrium would require very high rates to recover a signal as fast as that in Fig. 2.
Finally, we also studied the robustness of DUSK with respect to the imaging rate. To do so, we recovered the CSI concentration using all the fluorescence measurements available (D = 1), every other image (D = 2), and every 4th image (D = 4). This D stands for the downsampling factor in the forward model (see “Methods”). We then computed the median waveform of the reconstructed CSI for each D (Fig. 2D). For reference, D = 1 is equivalent to an imaging rate with a time step that is half as small as the half-rise of the sensor. Therefore, we assessed whether for D > 1 the imaging rate would be sufficient to capture the behavior. Remarkably, we found that the waveforms recovered by DUSK remained qualitatively close to the ground truth. The RSNRs over the spatiotemporal distribution corroborated our observation quantitatively as they only decreased slightly with D, D = 1: 13.31 dB, D = 2: 12.31 dB, and D = 4: 10.91 dB. From another perspective, this reflects the ability of DUSK to interpolate between measurements.
DUSK recovers neuronal calcium activity from fluorescence measurements
Having validated our framework, we applied DUSK to the calcium imaging of neurons. We used an extensive dataset where several types of GCaMP reporters were imaged under similar conditions using a two-photon microscope21. We remark that our work does not aim at deciphering neuronal spikes, but at uncoupling the behavior of the sensors from the one of calcium. Therefore, we leveraged the richness of this neuronal dataset to compare the underlying calcium signals obtained by applying DUSK to different sensors. In particular, we considered three GCaMP sensors (jGCaMP8s, jGCaMP7f, and jGCaMP8m), each with different kinetics and sensitivity (see Extended Data Table 3 from Zhang et al.21).
Each fluorescence sequence in the dataset is paired with electrophysiological measurements that monitor the membrane voltage inside certain regions of interest (ROI). AP spikes are the main source of calcium rises in this dataset. Since our interests are not APs, we do not aim at imposing sparsity on the signal for spike deconvolution45. Instead, we have used the electrophysiological measurements as indicators of expected increases in calcium.
Before diving into the reconstruction of calcium in vivo, we tested our method under controlled conditions. In particular, DUSK was able to recover the concentration of calcium accurately in mixing and unmixing experiments with the different sensors (see Supplementary Note 3).
We then proceeded with in vivo experiments. In Fig. 3, we present an example reconstruction for each of the sensor types. Similarly to the simulations, we observe that DUSK has a strong denoising effect on the fluorescence images (two first rows in Fig. 3A–C). The fluorescent decay after a burst of action potentials is clearly observable in the MIPs. On the other hand, the concentration profiles consistently exhibit bursts that precede and are shorter than their fluorescent counterparts (Supplementary Movies 2–4).
A–C. Reconstruction of real data for jGCaMP8s (A), jGCaMP7f (B), and jGCaMP8m (C). From top to bottom in each panel: Measured fluorescence (Meas. F.), predicted fluorescence (Pred. F.), and estimated concentration (Conc.). From left to right in each panel: XY views at the indicated frame and maximum-intensity projection along Y. Images are saturated for the sake of visualization. D–F Temporal profiles for each row in A–C resulting from a spatial average over the region of interest. The curves correspond to the median trace, and the shaded regions are the interquartile ranges (25th and 75th percentiles). The golden rods indicate the occurrence of action potentials detected from the electrophysiological measurements (E Physio., olive signal). The red, dashed lines indicate the time range displayed in the maximum-intensity projections in (A–C).
We also compared the concentration with the electrophysiological measurements. To this end, we computed the temporal trace (median and interquartile) over a biological ROI (Fig. 3D–F, see AP marks in golden). The interquartile in the measured fluorescence (first row) is higher than in the predicted fluorescence (second row), which corroborates the denoising effect of DUSK. Both the fluorescence and the concentration profiles are well aligned with the APs (golden rods) detected with the electrophysiological measurements. Not only the bursts of calcium concentration are shorter than their fluorescent counterparts, we also observe a sharper rise in most cases. Spike-related concentration peaks are thus more distinguishable. For example, the concentration in the first AP burst of Fig. 3D has a higher sensitivity index (\({d}_{C}^{{\prime} }=2.578\), see “Methods”) than that of the corresponding measured fluorescence (\({d}_{M}^{{\prime} }=1.141\)), or of the predicted fluorescence (\({d}_{P}^{{\prime} }=1.407\)).
We found that the scaling qe(x) recovered by DUSK was largely homogeneous, with the typical example having a very small standard deviation across the image, e.g., 1.155 ± 0.004. This suggests that the spatial effects listed in “Physical model”, such as the difference in optical paths, play a minor role.
The spatiotemporal detail of DUSK provides rich insights
We first assessed whether DUSK does address the temporal deformation induced by the binding process. We applied DUSK to multiple samples expressing the jGCaMP8s, jGCaMP8m, or jGCaMP7f sensors. We then identified events where a single AP was recorded by the electrophysiological measurements. For each of the sensors, we computed the median temporal profile of the (normalized) concentration and of the measured fluorescence over the ROIs of the samples (Fig. 4A). We observe that the resulting fluorescence profiles of the three sensors are qualitatively different (right plot). This is in agreement with the diversity of sensor kinetics. The half-decay times reported in ref. 21 for jGCaMP8s (\({t}_{1/2}^{8{{\rm{s}}}}=188\) ms) and jGCaMP8m (\({t}_{1/2}^{8{{\rm{m}}}}=38\) ms) match well with our estimated fluorescence profiles. By contrast, the median concentration profiles that DUSK estimated for the three sensors exhibit a short, transient calcium response that is very similar across the sensors (left plot). This is in spite of the large sample variability and the three different kinetics. It is also relative to the 8.2 ms frame period of the image data. The CSI responses recovered by DUSK for a burst of two and three APs were also similar across the three sensors (see Supplementary Note 9). Overall, this experiment is further validation of the capability of DUSK to uncouple the behavior of the sensors from that of the CSI.
A Temporal median profile of the concentration and fluorescence responses to one action potential for the sensors jGCaMP8s (16 samples), jGCaMP8m (18 samples), and jGCaMP7f (12 samples). All the profiles were aligned with respect to the action potential (t = 0). Time points were plotted if there were more than 3 samples. Shaded areas indicate the interquartile (IQR) range. B Time difference between the rise times of the concentration and the duration of the corresponding n action-potential bursts. Box-and-whisker plots indicate the median and 25th–75th percentile range; bottom (top) whiskers indicate the smallest (largest) data value that is larger (smaller) than the 25th (75th) percentile ±1.5 IQR. Source data are provided as a Source Data file. C Spatially heterogeneous activity. Consecutive frames of measured (top row), predicted (middle row) fluorescence, and concentration (bottom row) for jGCaMP8s. For the sake of visualization, the concentration is displayed with the Hill coefficient (i.e., \({c}^{{n}_{{{\rm{H}}}}}\)). D Maps of time lag with two different time resolutions. The continuous temporal representation of DUSK allows us to sample the concentration at any rate. E Optimized latent vectors with L = 3. The frames with synaptic activities (golden dots) are clustered in the latent space even if they are apart in time.
Next, we evaluated the behavior of the transient response of calcium to the underlying bursts of APs. In general, if each AP elicits an increase in calcium, the last AP in a burst should occur before the calcium concentration reaches its maximum. We thus computed the difference between the rise time of the CSI response and the duration of the burst. We did this over multiple spatial ROIs and burst types (between 2 and 7 APs per burst). In Fig. 4B, we display a box plot of this time difference for each sensor. The median time difference is positive for all sensors. This confirms that calcium normally reaches its maximum concentration after the last AP. Note that this evaluation is rather conservative because a burst of APs may saturate the sensor signal, or the calcium response itself58, before the last AP occurs.
In our framework, the concentration and predicted fluorescence are denoised without averaging over a spatial area. This property allowed us to analyze the spatial behavior of the CSI in more detail. In Fig. 4C, we display time-lapse images of a burst of APs. As indicated by the arrows, spatiotemporal patterns are more evident in the concentration than in the fluorescence. In this example, an early and a late calcium rise occurs at the top and bottom of the ROI, respectively, showing spatial delays within the cell body. This type of pattern may be related to the calcium waves and sparks that are known to occur in some neurons53,59,60.
Figure 4A is a good example of the non-linear time-dependent relation between the CSI and the fluorescence: three different and rather flat fluorescence profiles lead to a very similar CSI profile with a peaked waveform. Similarly, the non-linearity and time dependency hide a lag not only over time but also over space in Fig. 4C. In Supplementary Note 5, we present three additional examples of how these effects make the fluorescence significantly different than the CSI. In one of them, two synchronized and very similar fluorescence profiles give rise to two desynchronized CSI waveforms of different magnitudes.
To visualize the interaction between the spatial and temporal heterogeneity of the concentration, we computed spatial maps of the time lag as in Fig. 2B. These maps make spatiotemporal events more evident. For the experiment in (Fig. 4D), the map outlines a distinct area with a longer time lag (red, orange). This is in line with our observations of the delays in Fig. 4C. We then leveraged the continuous representation (10) that underlies the CSI in DUSK. By sampling this function at four times (Δt = 2.05 ms) the experimental acquisition rate of Δt = 8.20 ms, this representation allowed us to explore the reconstructions in more detail. In particular, the right area of the ROI appeared constant in Fig. 4D—left, but the transition between the different high-lag regions became clearer when sampled at a higher rate in Fig. 4D—right.
We believe that the versatility of DUSK is, in part, due to the adaptability of this continuous latent space. The latent vectors seem to display a recurring behavior once optimized. In Fig. 4E, we present the latent curve (10) of some illustrative examples. There, we can see that the AP events (golden dots) tend to cluster in the latent space as much as the parameterization of the curve allows. This indicates that the latent vectors are optimized in a way that helps capture the different dynamics within the signal.
Discussion
We have proposed a variational formulation with a deep spatiotemporal prior to recovering the concentration of a CSI from noisy fluorescent images of chemical sensors.
DUSK was accurate at recovering the spatiotemporal concentration of CSI in reaction–diffusion simulations. Conversely, the assumption of equilibrium deformed the CSI and introduced artifacts such as time lags. In real data, the rise time of the CSI profiles recovered by DUSK was in agreement with the duration of the underlying AP bursts, which were measured independently. DUSK was also accurate in the mixing and unmixing experiments. Moreover, the CSI profiles recovered in response to similar stimuli were consistent across the different sensors in spite of their different fluorescence profiles. This doubles as a validation of our framework. It also highlights the importance of uncoupling the CSI from the sensor. Distinguishing whether different fluorescent responses correspond to the same underlying CSI profile could be key to deciphering the function behind the different calcium waves. Since the chemical reactions are non-linear, this uncoupling becomes even more relevant when the stimuli come in bursts. Indeed, on top of correcting for the time lags, DUSK also corrected the deformations induced by the nonlinearity of the binding process. This is perhaps most clear when comparing the fluorescence to the concentration in Fig. 4A, but is also notable in the rest of the figures (see Supplementary Notes 4, 5, 7, too). Taking into account that APs lead to CSI concentrations of similar magnitude, we expect other experimental settings might benefit even more from DUSK.
The temporal scale of the biological signals that can be studied is limited by the sensor and by the acquisition setup61. When the time scale of the signal is much faster than the binding kinetics, information is lost because any change in fluorescence becomes negligible compared to the compounding of the detector and shot noise. In principle, this loss is irreversible up to the prior. Nonetheless, it appears that accounting for the binding process might help establish these limits more clearly and—perhaps—push them (see Supplementary Note 4). That DUSK could recover similar information for sensors of different speeds is promising from this perspective. The rise time is usually the main consideration when choosing a sensor. However, a smaller decay time leads to less saturation, and a stronger signal leads to less noise. We found that these two factors were key to the well-posedness of the inversion from fluorescence to concentration, while the final temporal resolution of the CSI profiles was less affected by slower rise times upon uncoupling. Such insight might help guide the design of new sensors and suggests incorporating the inversion of the binding process as an additional consideration. One byproduct of DUSK is a denoising effect on the measurements. This might be of interest by itself and is the aim of recent works that denoise fluorescence images before further processing48,49,62,63. (See Supplementary Notes 2 and 6 for a comparison and a more thorough discussion.) In DUSK, however, this effect happens as a result of jointly considering the binding process and estimating a CSI with spatiotemporal priors. As a consequence, averaging over the cell body is not necessary to achieve a signal that is interpretable. Indeed, DUSK yields heterogeneous spatiotemporal maps of the CSI in addition to the standard temporal profiles of the fluorescence. We have found that our time-lag maps highlight how different regions in the cells might be delayed. The ability to distinguish these spatial patterns could be helpful in the study of presynaptic regions by outlining the local accumulation of calcium5. It may even be more relevant in astrocytes, where the onset of calcium signaling is less synchronized, and thus averaging is more detrimental24. Our framework also has the potential to mitigate “the oversimplification of slow Ca2+ waves” in astrocytes23,24, for example, by accounting for the long decay times.
We found that the latent space of DUSK may act similarly to a classifier by constructing a subspace where similar events, such as APs, become clustered. This could be leveraged for spike detection. It could even be more relevant for classifying the signature of different calcium waves in cells that are not electrically excitable. Exploring these subspaces could yield a succinct, low-dimensional interpretation of the distinguishing features of the waveforms.
The accuracy of DUSK is limited by the suitability of the underlying model (see Supplementary Notes 3, 7, and 8). Fortunately, the characterization of the kinetics is already a key part of the design and testing of sensors64. We did not account for the diffusion of the sensors because they are expressed constitutively, which should promote a more constant and homogeneous distribution. As in standard setups, experimental calibration is also required by DUSK if the exact concentration of CSI is of interest30,50,51,52,53. However, the spatiotemporal distribution itself does not require calibration in DUSK. We remark that DUSK should be regarded as a way to augment chemical sensors and is not meant to substitute careful experimental design. For example, one important question is whether the presence of the sensor itself perturbs the dynamics under study (other than through the chemical interaction modeled in this work).
We set out to recover the concentration of a CSI from fluorescent chemical sensors. However, the same principles of DUSK readily translate to sensors with a response signal that can be modeled with ODEs. One example is H2O2 sensors for plant imaging32,33. Another example is genetically encoded voltage indicators (GEVI)65. They are designed to report on membrane potential via fluorescent emission. Similarly to GCaMP, the design of GEVIs wrangles over low rise times, long decay, and low sensitivity because they complicate the interpretability of the voltage signal66. Accounting for the underlying kinetics could decrease the sensitivity to these parameters, facilitate signal analysis, and help guide sensor design.
Methods
Physical model
We set out from the chemical reaction (1), which models the binding process. We consider that the total number of sensors stot(x) = s(x, t) + sb(x, t) is constant over time. We also assume that the spatial diffusion of the sensor is negligible. Both assumptions are common for fluorescent sensors31,67,68. The temporal evolution of sb is then given by
Rewriting (4) in terms of sb and dividing it by stot leads to
where \({\tilde{s}}_{b}({{\bf{x}}},t)=\frac{{s}_{b}({{\bf{x}}},t)}{{s}_{{{\rm{tot}}}}({{\bf{x}}})}\) denotes the proportion of bound sensors.
We use g(x, t) to denote the fluorescence received by the imaging setup, which is emitted by the sensors. We model it as
where g0(x) and qe(x) are the fluorescent background and a concentration-to-fluorescence factor, respectively31. These variables indirectly account for several unknown factors such as the quantum yield or the small emissions of the unbound sensor.
Together, Eqs. (5) and (6) relate the CSI concentration to the fluorescence measurements. Our physical model is then
Equation (7) can be understood as the following algorithm. (i) Solve (5) for the proportion \({\tilde{s}}_{b}({{\bf{x}}},t;c)={\tilde{s}}_{b}({{\bf{x}}},t)\) of bound sensors starting from a given concentration c. (ii) Compute the fluorescence \(g({{\bf{x}}},t;{\tilde{s}}_{b},{g}_{0},{q}_{e})=g({{\bf{x}}},t)\) using (6) given the solution \({\tilde{s}}_{b}\), as well as g0(x), and qe(x). The resulting \({{\mathcal{H}}}({{\bf{x}}},t;c,{g}_{0},{q}_{e})\) is the spatiotemporal fluorescence predicted by the model given c, g0, qe.
Deep spatiotemporal prior
In the main text, we formulated our inverse problem as
Our alternative regularization strategy consists of reparameterizing the distribution of the concentration as the output of a neural network c(x, t) = fθ(x, z(t)) with the parameters θ, and the time-dependent latent vector z(t). The minimization problem (8) then becomes
Note that we apply the deep prior to the concentration alone because the background and the scaling do not have a temporal component; we only regularize these two over space with \({{{\mathcal{R}}}}_{p}\).
The benefits of this method are twofold. First, a spatial prior is enforced by an untrained deep-image prior69,70. Second, we enforce temporal regularity on the sequence by restricting the latent variables to a manifold. A single neural network generates the whole sequence, while the design of the latent vectors encodes the temporal proximity of consecutive frames.
We remark that the resulting CSI concentration is in arbitrary units. This is due to a lack of information such as the conversion efficiency or the quantum yield. If at any point in space or time the concentration can be measured, this information can be readily incorporated into DUSK for automatic calibration. Alternatively, experimental procedures of calibration may be used to recover the exact concentration afterwards30,50,51,52,53.
Parametric latent space
We propose a parameterization of deep-image priors that adapts to the fast and slow dynamics that appear in biological signaling. To this end, we represent our latent space with a flexible parametric curve
Here, the latent vector is parameterized by a number K of shifted basis functions φ( ⋅ ) with coefficients \({{{\bf{b}}}}_{k}\in {{\mathbb{R}}}^{L}\)71. We chose to use a basis of cubic B-splines with a stepsize Δt. The coefficients bk are directly optimized in place of z when solving (9). The number of basis functions (i.e., knots) determines the flexibility of the curve and, in consequence, how much temporal regularity is enforced. The possibility of this intuitive tradeoff is similar to that in more traditional regularization methods such as total variation72.
Discretization of the physical model
To discretize (5) and (6), we sample \({\tilde{s}}_{b},c\), and g on an equispaced spatial grid with Nx × Ny points and at Nt = T/Δt time points with time step Δt. Here, we assume that all the sampled functions are compactly supported in the domain \(\Omega \times \left[0,T\right)\) with \(\Omega \subset {{\mathbb{R}}}^{2}\). The samples of \({\tilde{s}}_{b},g\) and c are concatenated into the matrices \({{\bf{S}}},{{\bf{G}}},{{\bf{C}}}\in {{\mathbb{R}}}^{N\times {N}_{t}}\) with N = NxNy, respectively. Similarly, the samples of g0 and qe are concatenated into the vectors \({{{\bf{g}}}}_{0},{{{\bf{q}}}}_{e}\in {{\mathbb{R}}}_{\ge 0}^{N}\). To solve (5), we use a backward Euler scheme. We then obtain the discrete forward model \({{\bf{H}}}:{{\mathbb{R}}}^{N\times {N}_{t}}\to {{\mathbb{R}}}^{N\times {N}_{t}}\) defined as
where \({{\bf{p}}}={[{{{\bf{g}}}}_{0}^{T},{{{\bf{q}}}}_{e}^{T}]}^{T}\in {{\mathbb{R}}}_{\ge 0}^{2N}\), the symbol \({(\cdot )}^{\odot {n}_{{{\rm{H}}}}}\) denotes the Hadamard power (i.e., each matrix element is raised to the power of nH), and the entries of S are computed recursively
for n = 1, …, N and nt = 1, …, Nt.
Problem formulation in the discrete domain
Now that we are equipped with a discretized physical model, we present our variational framework to recover the concentration distribution from measured fluorescence images. In practice, we may acquire the images at a time step ΔtM = DΔt (\(D\in {\mathbb{N}}\)) larger than the one used in (11). To recover the concentration, we aim at solving the minimization problem
where \({{{\bf{M}}}}_{D}\in {{\mathbb{R}}}^{{N}_{t}\times ({N}_{t}/D)}\) encodes the downsampling operation and the matrix \({{\bf{G}}}\in {{\mathbb{R}}}^{N\times ({N}_{t}/D)}\) denotes the measurements. The ℓ1-norm is the data-fidelity term, which we found robust to the noise present in the measurements. The regularization terms \({{{\mathcal{R}}}}_{{{\bf{p}}}}:{{\mathbb{R}}}^{2N}\to {{\mathbb{R}}}_{\ge 0}\) and \({{{\mathcal{R}}}}_{{{\bf{C}}}}:{{\mathbb{R}}}^{N\times {N}_{t}}\to {{\mathbb{R}}}_{\ge 0}\) enforce some prior knowledge about the parameters p and the concentration, respectively. In this work, \({{{\mathcal{R}}}}_{{{\bf{p}}}}\) only regularizes qe with the total variation and a small trade-off parameter τp > 072.
Deep spatiotemporal priors in the discrete domain
To mitigate the illposedness of (13), we aim at enforcing some regularity along space and time on the concentration C. To that end, we reconstruct the concentration using a deep spatiotemporal prior40,41,42. In the framework of deep spatiotemporal prior, the concentration at time \(t\in \left[0,T\right)\) is the output c(θ, t) = fθ(z(t)) of a convolutional neural network \({{{\bf{f}}}}_{{{\boldsymbol{\theta }}}}:{{\mathbb{R}}}^{L}\to {{\mathbb{R}}}^{N}\) parameterized by \({{\boldsymbol{\theta }}}\in {{\mathbb{R}}}^{P}\). By design, the concentration is sampled on an equispaced spatial grid with N points, but the time can be sampled arbitrarily.
To recover the concentration, we then optimize the minimization problem
with
We represent our latent space with a parametric curve (see (10)) and optimize the coefficients bk along the coefficients θ. With a slight abuse of notation, the parameters θ will now encompass the coefficients \({\{{{{\bf{b}}}}_{k}\in {{\mathbb{R}}}^{L}\}}_{k=0}^{K-1}\) as well.
Architecture and optimization
The architecture of fθ is detailed in Table 1. The network layers are applied sequentially from the top to the bottom of the table, starting with an input of shape (1 × 3). It is noteworthy that the sequence of concentration images is represented with an underparametrized neural network. For instance, if (Nx × Ny × Nt) = (96 × 68 × 244) and K = 30, L = 3, there are 149, 925 + 90 parameters to optimize, which amounts to about 10% of the total number of recovered pixels. We do not specify validation or training sets because our framework is training-free, i.e., the network remains untrained.
We optimize all the variables in (14) using the AMSGrad algorithm73 with a constant learning rate of 0.01, tolerance ϵtol = 10−12, and a maximum number of iterations of 104. We set the tradeoff parameter τp = 10−5. The number of knots K is optimized by grid search either by maximizing a metric for simulated data or by visual inspection for real data. We enforce that \({({{{\bf{g}}}}_{0})}_{k} > 0\) and \({({{{\bf{q}}}}_{e})}_{k} > 1{0}^{-6}\) by projecting violating values to the respective bound after each gradient update.
For k = 1, …, N, we initialize \({({{{\bf{q}}}}_{e})}_{k}=Q\) and \({({{{\bf{g}}}}_{0})}_{k}=\min ({({{\bf{G}}})}_{k,\cdot })\), i.e., with the minimal value reached during the measurements for each pixel. In simulated data, Q was chosen among the values [1, 10, 100] to maximize the regressed signal-to-noise ratio (RSNR, see (18)). In real data, we set to Q = 1 for all sensors but jGCaMP7f. We observed that the DUSK results on jGCaMP7f were insufficiently fitting the measurements. This is due to the neural network inability to reach very large values of concentration that are imputable to the high Hill coefficient of jGCaMP7f (nH = 3.1).
For numerical stability, we chose to include the effect of the Hill coefficient in fθ such that \({{\bf{c}}}{({{\boldsymbol{\theta }}},t)}^{{n}_{{{\rm{H}}}}}={{{\bf{f}}}}_{{{\boldsymbol{\theta }}}}({{\bf{z}}}(t))\). Unless specified otherwise, the estimates displayed are the nHth root of the output of fθ.
In Table 2, we present the kinetic coefficients. They were measured experimentally for the sensors in the datasets that we use from ref. 21. These are the only hyper-parameters to set in our framework other than the number of knots for the latent spline.
We set the time window \(\left[0,T\right)\) to avoid cutting the signal of interest (i.e., during a burst of APs). In addition, the memory cost could limit the duration of the sequence. However, it was not detrimental to the quality of reconstruction, as past values have little impact on future values after some time. Note that the principle of DUSK is not bound to a convolutional architecture with fixed spatial discretization. There are alternatives with continuous spatial representation74. Similarly, we adopt the backward Euler scheme for temporal discretization for its efficiency and simplicity. Other adaptive schemes are possible too.
All experiments were run on a Linux workstation with an Intel Xeon Gold 6226R CPU (2.90GHz), 4 × 16 Gb, and a GPU NVIDIA RTX A6000 (48 Gb).
Temporal regularity
In this work, the basis functions \({\{\varphi (\cdot -{t}_{k})\}}_{k=0}^{K-1}\) in (10) are cubic B-splines. In Supplementary Note 10, we show the effect of our temporal regularization on the recovered concentration distribution. By increasing the number of knots K, we can see that the temporal traces over the ROI show fewer fluctuations in both the predicted fluorescence and concentration traces. This behavior corroborates well with the tradeoff parameters used in classical spatial regularization.
Simulation pipeline
Using a space colonization method75, we designed an astrocyte-like sample fully contained in the image domain \(\Omega \subset {{\mathbb{R}}}^{2}\) (see Fig. 2B, bottom). We used a 2D reaction-diffusion equation to simulate the propagation of the CSI, where the diffusion coefficient in the branches (Ωbranches ⊂ Ω) is higher than in the background. The concentration thus propagates rapidly along the branches, and slower elsewhere. Here, the signal contains two distinct traveling waves with little dispersion: One wave in the branches with higher velocity and amplitude, the other one in the background with lower velocity and amplitude. We thus solve the partial differential equation
where ∇x and ∇x ⋅ are the spatial gradients and spatial divergence, respectively. The function \(D:\Omega \to {{\mathbb{R}}}_{\ge 0}\) is the spatially varying diffusion coefficient. The quantity \(p:\Omega \times {{\mathbb{R}}}_{\ge 0}\to {{\mathbb{R}}}_{\ge 0}\) is a precursor in the autocatalytic reaction \({{\rm{p}}}+{{\rm{c}}}{\to }^{{{{\rm{k}}}}_{r}}2\,{{\rm{c}}}\) with rate kr. The chemical species is degraded at a rate \({k}_{d}:\Omega \to {{\mathbb{R}}}_{\ge 0}\). The spatially-varying decaying rate allows us to obtain different traveling waves in the branches and background. The source term s(x, t) models a stress signal that is compactly supported in both space and time. More precisely, s is only non-zeros and of value s0 = 1 in the two first frames and over a localized area at the center of the image (i.e. , in the soma of the astrocyte). We solve (16) with a backward Euler scheme and a finite element solver76 for the temporal and spatial discretization, respectively. To ensure numerical stability, we simulate with the time step ΔtEuler = 0.5Δt and downsample the computed concentration by two to get CGT.
The fluorescence images are then simulated using (11) with constant parameters \({({{{\bf{g}}}}_{0})}_{k}=0.25\) and \({({{{\bf{q}}}}_{e})}_{k}=10\) for k ∈ [1, …, N]. The sensors kinetics kf, kb correspond to the ones of the jGCaMP8s (Table 2) but the Hill coefficient is set to nH = 1. The recorded measurement images \({{\bf{G}}}\in {{\mathbb{R}}}^{N\times ({N}_{t}/D)}\) are then generated according to
where each (k, l)th entry of \({{\bf{N}}}\in {{\mathbb{R}}}^{N\times ({N}_{t}/D)}\) is a realization of a signal-dependent Gaussian random variable \({{\mathcal{N}}}(0,{\sigma }_{k,l}^{2})\). We emulate Poisson noise by setting \({\sigma }_{k,l}^{2}={({{{\bf{H}}}}_{{{\bf{p}}}}\left({{{\bf{C}}}}_{{{\rm{GT}}}}^{\odot {n}_{{{\rm{H}}}}}\right))}_{k,l}/B\) with photon budget B = 25.
The size of the astrocyte-like sample is 40 × 40 μm2, discretized with (128 × 128) pixels (corresponding to a pixel length of ~0.3 μm). We acquired 128 frames at an acquisition rate of 200 Hz (frame period of 5 ms). We set the diffusion coefficient to D(x) = 3.91 ×= 10−4 μm2/s for x ∈ Ωbranches, and to D(x) = 9.77 × 10−7 μm2/s otherwise. The reaction rate is set to kr = 1, and the decay rate is set to kd(x) = 0.03 for x ∈ Ωbranches, and to kd(x) = 0.3 otherwise. We set the initial conditions to c(x, 0) = 0 and p(x, 0) = 1 for x ∈ Ωbranches, and to p(x, 0) = 0.75 otherwise. We choose the Dirichlet boundary conditions (∂Ω = 0). The speed of the traveling wave then reaches about 31.25 μm/s, which is consistent with values measured in astrocytes77,78.
Quantitative evaluation of the performance
To measure the performance of reconstruction, we use the regressed signal-to-noise ratio (RSNR) over the whole image sequence,
where C and \(\hat{{{\bf{C}}}}\) are the ground truth and the reconstructed concentration, respectively. The RSNR adapts the standard signal-to-noise ratio—which compares the magnitude of the error of the reconstruction to the magnitude of the ground truth—to account for possible shifts and scalings of the signal. It is measured in a logarithmic scale and bigger values indicate better performance.
To quantify the detectability of a peak (i.e., fluorescence or calcium rise) within a spatial ROI, we compute a sensitivity index defined as79
where μs, μbg (σs, σbg) denote the median value (median absolute deviation) at the peak occurrence and in the background (e.g., before the rise), respectively.
Remarks about the physical model
While originally intended as an integer value, note that the Hill coefficient nH is now generally understood as an empirical indicator of cooperative binding. In this interpretation, the coefficients often take non-integer values, which can be indicative of additional (hidden) sequential reactions34 or dependent binding sites31. The coefficients kf, kb, nH in (1)—on which Hill’s equation is based—are the ones that are usually measured experimentally when designing (or using) new sensors. For example, the values in Table 2 were measured for the same GCaMP8 dataset that we use in this article.
All this suggests that the behavior of some chemical sensors can be approximated by the phenomenological reaction model (1) with the three experimental parameters. We tested the quality of our reconstruction using mixing and unmixing experiments, where the behavior of the underlying concentration is “known” (see Supplementary Note 3). In addition, we offer further comments on the suitability of model (1) in Supplementary Notes 7 and 8. When available, more complex chemical models can be plugged into the framework seamlessly by changing (5) for another set of ODEs. This might yield better estimates but requires (1) working out the model and (2) coming up with ways to measure what are often (too) many parameters (see Supplementary Note 7).
While the fluorescence of most sensors (e.g., GCaMP) increases upon binding to the corresponding CSI as per (6), a few sensors see their fluorescence decrease instead. More specifically, the light they emit is proportional to the concentration of the unbound sensor. Such sensors are readily compatible with our framework by simply replacing \({\tilde{s}}_{b}\) for s in (6). One example is the H2O2 sensors used to study signaling in plants, which we explored in33.
Statistics and reproducibility
We applied our computational framework to experimental video data of calcium sensors collected for21. These are available at80. The videos that we analyzed were randomly selected from the 1.4 TB dataset for jGCaMP8s, jGCaMP8m, and jGCaMP7f. No other data were excluded. Sample sizes are specified in the manuscript for each experiment. We did not use blinding or randomization because there were no experimental groups.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
All the data required to evaluate the conclusions of the paper can be found in the paper or in the Supplementary Materials. We took the real data of GCaMP sensors from the dataset80 of ref. 21. They consist of two-photon microscopy videos of pyramidal neurons from the mouse’s primary visual cortex. For numerical stability, each video was divided by its 99th percentile, and isolated negative values (that were due to registration) were set to 0. The mixing and unmixing experiments were also performed in the context of ref. 21 and were kindly shared by the authors thereof. Source data are provided in this paper.
Code availability
The code is available at https://doi.org/10.24433/CO.5983205.v1 and github.com/ThanhAnPham/DUSK (see81).
References
Kholodenko, B. N. Cell-signalling dynamics in time and space. Nat. Rev. Mol. Cell Biol. 7, 165–176 (2006).
Berridge, M. J., Lipp, P. & Bootman, M. D. The versatility and universality of calcium signalling. Nat. Rev. Mol. Cell Biol. 1, 11–21 (2000).
Bellandi, A. et al. Diffusion and bulk flow of amino acids mediate calcium waves in plants. Sci. Adv. 8, eabo6693 (2022).
Ismailov, I., Kalikulov, D., Inoue, T. & Friedlander, M. J. The Kinetic Profile of Intracellular Calcium Predicts Long-Term Potentiation and Long-Term Depression. J. Neurosci. 24, 9847–9861 (2004).
Evans, R. C. & Blackwell, K. T. Calcium: amplitude, duration, or location? Biol. Bull. 228, 75–83 (2015).
Kukushkin, N. V. & Carew, T. J. Memory takes time. Neuron 95, 259–279 (2017).
Durkee, C. A. & Araque, A. Diversity and specificity of astrocyte–neuron communication. Neuroscience 396, 73–78 (2019).
Badoual, A. et al. Simulation of astrocytic calcium dynamics in lattice light sheet microscopy images. In 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI), 135–139 (IEEE, Nice, France, 2021).
Denizot, A., Arizono, M., Nägerl, U. V., Soula, H. & Berry, H. Simulation of calcium signaling in fine astrocytic processes: Effect of spatial properties on spontaneous activity. PLOS Comput. Biol. 15, e1006795 (2019).
Kozachkov, L., Kastanenka, K. V. & Krotov, D. Building transformers from neurons and astrocytes. Proc. Natl Acad. Sci. USA 120, e2219150120 (2023).
Gilroy, S. et al. A tidal wave of signals: calcium and ROS at the forefront of rapid systemic signaling. Trends Plant Sci. 19, 623–630 (2014).
Tian, W., Wang, C., Gao, Q., Li, L. & Luan, S. Calcium spikes, waves and oscillations in plant development and biotic interactions. Nat. Plants 6, 750–759 (2020).
Lemke, E. A. & Schultz, C. Principles for designing fluorescent sensors and reporters. Nat. Chem. Biol. 7, 480–483 (2011).
Schäferling, M. The art of fluorescence imaging with chemical sensors. Angew. Chem. Int. Ed. 51, 3532–3554 (2012).
Tsien, R. Y. The green fluorescent protein. Annu. Rev. Biochem. 67, 509–544 (1998).
Nakai, J., Ohkura, M. & Imoto, K. A high signal-to-noise Ca2+ probe composed of a single green fluorescent protein. Nat. Biotechnol. 19, 137–141 (2001).
Chen, T.-W. et al. Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature 499, 295–300 (2013).
Petreanu, L. et al. Activity in motor–sensory projections reveals distributed coding in somatosensation. Nature 489, 299–303 (2012).
Peron, S. P., Freeman, J., Iyer, V., Guo, C. & Svoboda, K. A cellular resolution map of barrel cortex activity during tactile behavior. Neuron 86, 783–799 (2015).
Stringer, C., Pachitariu, M., Steinmetz, N., Carandini, M. & Harris, K. D. High-dimensional geometry of population responses in visual cortex. Nature 571, 361–365 (2019).
Zhang, Y. et al. Fast and sensitive GCaMP calcium indicators for imaging neural populations. Nature 615, 884–891 (2023).
Tay, L. H., Griesbeck, O. & Yue, D. T. Live-cell transforms between ca2+ transients and fret responses for a troponin-c-based ca2+ sensor. Biophys. J. 93, 4031–4040 (2007).
Rusakov, D. A. Avoiding interpretational pitfalls in fluorescence imaging of the brain. Nat. Rev. Neurosci. 23, 705–706 (2022).
Rusakov, D. A. Disentangling calcium-driven astrocyte physiology. Nat. Rev. Neurosci. 16, 226–233 (2015).
Tian, L. et al. Imaging neural activity in worms, flies and mice with improved GCaMP calcium indicators. Nat. Methods 6, 875–881 (2009).
Luo, L., Callaway, E. M. & Svoboda, K. Genetic dissection of neural circuits: a decade of progress. Neuron 98, 256–281 (2018).
Dana, H. et al. High-performance calcium sensors for imaging activity in neuronal populations and microcompartments. Nat. Methods 16, 649–657 (2019).
Wei, Z. et al. A comparison of neuronal population dynamics measured with calcium imaging and electrophysiology. PLOS Comput. Biol. 16, e1008198 (2020).
Hendel, T. et al. Fluorescence changes of genetic calcium indicators and ogb-1 correlated with neural activity and calcium in vivo and in vitro. J. Neurosci. 28, 7399–7411 (2008).
Bootman, M. D., Rietdorf, K., Collins, T., Walker, S. & Sanderson, M. Converting fluorescence data into Ca2+ concentration. Cold Spring Harb. Protoc. 2013, pdb.prot072827 (2013).
Helmchen, F. Calcium imaging. In (eds Brette, R. & Destexhe, A.) Handbook of Neural Activity Measurement, 362–409 (Cambridge University Press, 2012), 1 edn.
Lew, T. T. S. et al. Real-time detection of wound-induced H2O2 signalling waves in plants with optical nanosensors. Nat. Plants 6, 404–415 (2020).
Pham, T.-A., Mondal, S., Boquet-Pujadas, A., Unser, M. & Barbastathis, G. Chemical sensors with deep spatiotemporal priors. In Optica Imaging Congress (3D, COSI, DH, FLatOptics, IS, pcAOP) (2023), Paper CTu5B.5, CTu5B.5 (Optica Publishing Group, 2023).
Hernández-García, M. E. & Velázquez-Castro, J. Exploring the relationship between fractional hill coefficient, intermediate processes and mesoscopic fluctuations. https://doi.org/10.48550/arXiv.2312.15789 (2023).
Benning, M. & Burger, M. Modern regularization methods for inverse problems. Acta Numer. 27, 1–111 (2018).
Guo, Z. et al. Physics-assisted generative adversarial network for X-ray tomography. Opt. Express 30, 23238–23259 (2022).
Guo, Z. et al. Noise-resilient deep learning for integrated circuit tomography. Opt. Express 31, 15355–15371 (2023).
Héas, P., Drémeau, A. & Herzet, C. An efficient algorithm for video superresolution based on a sequential model. SIAM J. Imaging Sci. 9, 537–572 (2016).
Boquet-Pujadas, A. et al. 4D live imaging and computational modeling of a functional gut-on-a-chip evaluate how peristalsis facilitates enteric pathogen invasion. Sci. Adv. 8, eabo5767 (2022).
Yoo, J. et al. Time-dependent deep image prior for dynamic MRI. IEEE Trans. Med. Imaging. 40, 3337–3348 (2021).
Bohra, P., Pham, T.-a, Long, Y., Yoo, J. & Unser, M. Dynamic Fourier ptychography with deep spatiotemporal priors. Inverse Probl. 39, 064005 (2023).
Zou, Q., Ahmed, A. H., Nagpal, P., Kruger, S. & Jacob, M. Dynamic imaging using a deep generative SToRM (Gen-SToRM) model. IEEE Trans. Med. Imaging 40, 3102–3112 (2021).
Vogelstein, J. T. et al. Fast nonnegative deconvolution for spike train inference from population calcium imaging. J. Neurophysiol. 104, 3691–3704 (2010).
Pnevmatikakis, E. A. et al. Simultaneous denoising, deconvolution, and demixing of calcium imaging data. Neuron 89, 285–299 (2016).
Berens, P. et al. Community-based benchmarking improves spike rate inference from two-photon calcium imaging data. PLOS Comput. Biol. 14, e1006157 (2018).
Giovannucci, A. et al. CaImAn an open source tool for scalable calcium imaging data analysis. eLife 8, e38173 (2019).
Deneux, T. et al. Accurate spike estimation from noisy calcium signals for ultrafast three-dimensional imaging of large neuronal populations in vivo. Nat. Commun. 7, 12190 (2016).
Chaudhary, S., Moon, S. & Lu, H. Fast, efficient, and accurate neuro-imaging denoising via supervised deep learning. Nat. Commun. 13, 5165 (2022).
Lecoq, J. et al. Removing independent noise in systems neuroscience data using deepinterpolation. Nat. Methods 18, 1401–1408 (2021).
Grynkiewicz, G., Poenie, M. & Tsien, R. Y. A new generation of Ca2+ indicators with greatly improved fluorescence properties. J. Biol. Chem. 260, 3440–3450 (1985).
Maravall, M., Mainen, Z., Sabatini, B. & Svoboda, K. Estimating intracellular calcium concentrations and buffering without wavelength ratioing. Biophys. J. 78, 2655–2667 (2000).
Palmer, A. E. & Tsien, R. Y. Measuring calcium signaling using genetically targetable fluorescent indicators. Nat. Protoc. 1, 1057–1065 (2006).
Suzuki, J. et al. Imaging intraorganellar Ca2+ at subcellular resolution using CEPIA. Nat. Commun. 5, 4153 (2014).
Zheng, K., Jensen, T. P. & Rusakov, D. A. Monitoring intracellular nanomolar calcium using fluorescence lifetime imaging. Nat. Protoc. 13, 581–597 (2018).
van der Linden, F. H. et al. A turquoise fluorescence lifetime-based biosensor for quantitative imaging of intracellular calcium. Nat. Commun. 12, 7159 (2021).
Sabatini, B. L., Oertner, T. G. & Svoboda, K. The life cycle of ca2+ ions in dendritic spines. Neuron 33, 439–452 (2002).
Neher, E. The use of fura-2 for estimating ca buffers and ca fluxes. Neuropharmacology 34, 1423–1442 (1995).
Gall, D. et al. Intracellular calcium regulation by burst discharge determines bidirectional long-term synaptic plasticity at the cerebellum input stage. J. Neurosci. 25, 4813–4822 (2005).
Nakamura, T., Lasser-Ross, N., Nakamura, K. & Ross, W. N. Spatial segregation and interaction of calcium signalling mechanisms in rat hippocampal CA1 pyramidal neurons. J. Physiol. 543, 465–480 (2002).
Ross, W. N. Understanding calcium waves and sparks in central neurons. Nat. Rev. Neurosci. 13, 157–168 (2012).
Meyer, D., Hagemann, A. & Kruss, S. Kinetic requirements for spatiotemporal chemical imaging with fluorescent nanosensors. ACS Nano 11, 4017–4027 (2017).
Eom, M. et al. Statistically unbiased prediction enables accurate denoising of voltage imaging data. Nat. Methods 20, 1581–1592 (2023).
Platisa, J. et al. High-speed low-light in vivo two-photon voltage imaging of large neuronal populations. Nat. Methods 20, 1095–1103 (2023).
Jarmoskaite, I., AlSadhan, I., Vaidyanathan, P. P. & Herschlag, D. How to measure and evaluate binding affinities. eLife 9, e57264 (2020).
Bando, Y., Grimm, C., Cornejo, V. H. & Yuste, R. Genetic voltage indicators. BMC Biol. 17, 71 (2019).
Yang, H. H. & St-Pierre, F. Genetically encoded voltage indicators: opportunities and challenges. J. Neurosci. 36, 9977–9989 (2016).
Lütcke, H., Gerhard, F., Zenke, F., Gerstner, W. & Helmchen, F. Inference of neuronal network spike dynamics and topology from calcium imaging data. Front. Neural Circuits 7, 201 (2013).
Helmchen, F. & Tank, D. W. A single-compartment model of calcium dynamics in nerve terminals and dendrites. Cold Spring Harb. Protoc. 2015, pdb.top085910 (2015).
Ulyanov, D., Vedaldi, A. & Lempitsky, V. Deep image prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, June 18–22, 2018, 9446–9454.
Yang, F. et al. Robust phase unwrapping via deep image prior for quantitative phase imaging. IEEE Trans. Image Process. 30, 7025–7037 (2021).
Brigger, P., Hoeg, J. & Unser, M. B-spline snakes: a flexible tool for parametric contour detection. IEEE Trans. Image Process. 9, 1484–1496 (2000).
Rudin, L. I., Osher, S. & Fatemi, E. Nonlinear total variation based noise removal algorithms. Physica D 60, 259–268 (1992).
Reddi, S. J., Kale, S. & Kumar, S. On the Convergence of Adam and Beyond. In International Conference on Learning Representations (Vancouver, Canada, Apr 30, 2018–May 3, 2018).
Mildenhall, B. et al. NeRF: representing scenes as neural radiance fields for view synthesis. Commun. ACM 65, 99–106 (2021).
Runions, A. et al. Modeling and visualization of leaf venation patterns. In ACM SIGGRAPH 2005 Papers, SIGGRAPH ’05, 702-711 (Association for Computing Machinery, New York, NY, USA, 2005).
Logg, A., Mardal, K.-A. & Wells, G. (eds.) Automated Solution of Differential Equations by the Finite Element Method: The FEniCS Book, vol. 84 of Lecture Notes in Computational Science and Engineering (Springer Berlin Heidelberg, Berlin, Heidelberg, 2012).
Scemes, E. & Giaume, C. Astrocyte calcium waves: what they are and what they do. Glia 54, 716–725 (2006).
Kuga, N., Sasaki, T., Takahara, Y., Matsuki, N. & Ikegaya, Y. Large-scale calcium waves traveling through astrocytic networks in vivo. J. Neurosci. 31, 2607–2614 (2011).
Simpson, A. J. & Fitter, M. J. What is the best index of detectability? Psychol. Bull. 80, 481–488 (1973).
Rózsa, M. et al. Simultaneous loose seal cell-attached recordings and two-photon imaging of gcamp8 expressing mouse v1 neurons with drifting gratings visual stimuli [dataset]. DANDI archive, 000168 (2022).
Pham, T.-A., Boquet-Pujadas, A., Mondal, S., Unser, M. & Barbastathis, G. Deep-prior odes augment fluorescence imaging with chemical sensors. Code Ocean, 10.24433/CO.5983205.v1 (2024).
Ulyanov, D., Vedaldi, A. & Lempitsky, V. Improved texture networks: maximizing quality and diversity in feed-forward stylization and texture synthesis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 6924–6932 (Honolulu, HI, USA, 2017).
Acknowledgements
We are grateful to Y. Zhang, L. L. Looger, J. P. Hasseman, and A. Tsang (at Janelia, HHMI) for providing data of stopped flow experiments. We would like to thank T. Lagache for his helpful comments on the paper. This work was partly supported by the Air Force Office of Scientific Research under the Multidisciplinary University Research Initiative grant no. FA9550-23-1-0284 (T.P. and G.B.).
Author information
Authors and Affiliations
Contributions
A.B.-P. and T.P. contributed equally. They conceived the project, developed the method, and designed the experiments. T.P. implemented the method with input from A.B.-P. S.M., and T.P. implemented the code to generate astrocyte-like images. A.B.-P. wrote the manuscript with input from T.P. G.B., and M.U. revised the paper. All authors discussed the results and approved the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Karel Svoboda, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Pham, Ta., Boquet-Pujadas, A., Mondal, S. et al. Deep-prior ODEs augment fluorescence imaging with chemical sensors. Nat Commun 15, 9172 (2024). https://doi.org/10.1038/s41467-024-53232-2
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41467-024-53232-2
This article is cited by
-
Deep-prior ODEs augment fluorescence imaging with chemical sensors
Nature Communications (2024)