Parallel processing of past and future memories through reactivation and synaptic plasticity mechanisms during sleep

Ghandour, Khaled; Haga, Tatsuya; Ohkawa, Noriaki; Fung, Chi Chung Alan; Nomoto, Masanori; Fayed, Mostafa R.; Asai, Hirotaka; Sato, Masaaki; Fukai, Tomoki; Inokuchi, Kaoru

doi:10.1038/s41467-025-58860-w

Download PDF

Article
Open access
Published: 28 April 2025

Parallel processing of past and future memories through reactivation and synaptic plasticity mechanisms during sleep

Nature Communications volume 16, Article number: 3618 (2025) Cite this article

17k Accesses
1 Citations
329 Altmetric
Metrics details

Subjects

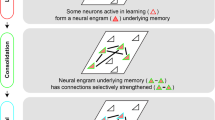
Abstract

Every day, we experience new episodes and store new memories. Although memories are stored in corresponding engram cells, how different sets of engram cells are selected for current and next episodes, and how they create their memories, remains unclear. Here we show that in male mice, hippocampal CA1 neurons show an organized synchronous activity in prelearning home cage sleep that correlates with the learning ensembles only in engram cells, termed preconfigured ensembles. Moreover, after learning, a subset of nonengram cells develops population activity, which is constructed during postlearning offline periods, and then emerges to represent engram cells for new learning. Our model suggests a potential role of synaptic depression and scaling in the reorganization of the activity of nonengram cells. Together, our findings indicate that during offline periods there are two parallel processes occurring: conserving of past memories through reactivation, and preparation for upcoming ones through offline synaptic plasticity mechanisms.

Memory engram stability and flexibility

Article Open access 18 September 2024

Dynamic and selective engrams emerge with memory consolidation

Article Open access 19 January 2024

Engram neurons: Encoding, consolidation, retrieval, and forgetting of memory

Article Open access 28 June 2023

Introduction

Our daily experiences form a myriad of memories that accrue to construct our personality. To adequately encode and retrieve these memories, the brain must always be prepared and organized for near-upcoming events and perform parallel processing of past memory. The process of determining which set of neurons is to be recruited for an upcoming event or task is known as memory allocation¹. Proper allocation of memory governs adequate retrieval of that memory whenever it is needed. Groups of neurons that represent a specific memory are called engram cells². Engram cells can be labeled and identified through the expression of immediate early genes, such as c-fos^3,4,5. Optogenetic activation or inhibition of these subsets of neurons leads to memory retrieval or silencing, respectively^6,7,8. It has been demonstrated that engram cells possess characteristic activity during learning^9,10. As previous memories affect the next event, previously formed engram cells may play some role in the selection of next engram cells^11,12,13. Several previous studies have shown that CREB and neuronal excitability could bias the competition towards the excitable neurons to be an engram^14,15,16,17, and that engram cells are quite active even before an event and their manipulation could affect this near future learning¹⁸. Moreover, hippocampal intrinsic dynamics form a repertoire of preexisting assemblies of high temporal sequential events ahead of time (known as preplay)^19,20,21 forming a network of preconfiguration^20,21. Coding principles in neuronal networks might reflect selection of remarkably excitable neurons of properly connected cells that share same birthdate and emerge together during development²². However, how engram cells dynamics orchestrate during offline pre- and postlearning stages and affect future learning and upcoming future engram cells is not well understood.

Sleep’s contribution to memory consolidation has been extensively investigated in recent decades. Brain activities occurring during offline periods when subjects are not engaged in a certain task, such as during sleep or awake rest, are defined as “idling state” activities^23,24. Neuronal reactivation and replay are responsible for the consolidation and strengthening of acquired memories^9,25,26. Artificial inhibition or disruption of theta waves or sharp wave ripples (SWRs) during either rapid-eye-movement (REM)²⁷ or non-REM (NREM)²⁸ sleep, respectively, disrupts the retrieval of recent memories. However, sleep is now thought of as an active process that is required for more than just consolidation of past memories, rather than a passive process²⁶. Sleep and awake rest reactivations are linked with many behavioral outcomes like learning²⁹, creativity^30,31,32, and planning, either toward a reward³³ or away from an expected averse outcome³⁴. Although the concept of sleep has recently expanded, with sleep now being considered a more dynamic process of diverse functions, the physiological role of sleep in memory acquisition and encoding is not well understood.

Episodic memories do not merely reflect past experiences but are also important for thinking about the future². Several functional magnetic resonance imaging (fMRI) studies provide evidence^35,36 that denotable activity associated with the past occurs in the brain when thinking about the future, mimicking mental time travel³⁷. This high overlap between past and future events is in agreement with findings where hippocampal lesions or damages lead to an inability in thinking and imagining about the past and future, respectively^38,39. Nonetheless, how and when our brains prepare and modify our existing memories to accommodate our new experiences remains unclear. In this study, we addressed the questions of whether and how sleep plays a role in the selection of engram cells.

In this work, we show that coactivities of subsets of nonengram cells emerge in parallel with the consolidation during sleep. These newly coactive neurons, which we call engram-to-be cells, will later encode future learning. Notably, engram-to-be cells show increased coactivity with existing engram cells during sleep, suggesting that this interaction helps shape new memory networks. A neural network model shows sleep-related synaptic scaling mechanisms are crucial for the engram-to-be cells emergence. This highlights the importance of sleep in the emergence of engram-to-be cells. This process occurs only during postlearning sleep, not before or during wakefulness. Together, these data indicate that a dual process takes place in the brain during sleep, preserving the past (consolidation) and preparing for the future (engram-to-be emergence).

Results

Active ensembles during prelearning sleep are recruited into upcoming engram

To understand how a specific set of neurons are chosen to represent a particular event as a memory trace, we need to track the activity of engram cells across different memory processing stages. We recently established a Ca²⁺ imaging system using a miniature microscope⁹ that is suitable for visualizing both engram and nonengram cells across memory processing stages in freely moving mice^40,41 (Fig. 1A, Supplementary Fig. 1). We used double transgenic Thy1-G-CaMP7 mice crossed with c-fos-tTA mice and the miniature microscope to track and label the activity of both engram and nonengram cells. Lentivirus (LV), harboring KikGR (coding for Kikume Green Red fluorescent protein)⁴² under the control of the tetracycline responsive element (TRE), was injected into the hippocampal CA1 region to label the engram CA1 cells, with the result that activated cells express KikGR protein in the absence of doxycycline (DOX; Fig. 1A). We previously showed that cells labeled by this system represent contextual engram cells⁹. KikGR is irreversibly photoconverted from green to red fluorescent protein by exposure to UV light of 365 nm (Fig. 1B), which allows simultaneous Ca²⁺ imaging with G-CaMP7. EEG and EMG electrodes were implanted along with the microscope to allow different sleep stages to be differentiated (Supplementary Fig. 2a and see Methods). Imaging on day 1 was performed in prelearning NREM (N1) and REM (R1) sleep, during learning (A), and in postlearning NREM (N2) and REM (R2) sleep. This was followed by imaging sessions during retrieval (A’) and in a different context (B) on day 2 (Fig. 1A). Calcium transients were detected automatically using a HOTARU online sorting system⁴³. All detected cells were categorized into engram and nonengram cells according to a snapshot image taken 24 h after the context exposure (Supplementary Fig. 2b–e). Engram cells constituted 7% ( ± 1.5 standard error) of the total cells recorded while nonengram cells constituted 93% (± 1.5 standard error) (Supplementary Fig. 2f and Supplementary Table 1). We have confirmed that sleep recorded sessions show a comparable detected number of cells to awake sessions (Supplementary Fig. 2h).

**Fig. 1: Ensembles activated during prelearning sleep are recruited into the upcoming engram.**

Previously, we demonstrated that engram cells possess a characteristic repetitive activity through correlation matrix repetition analysis during contextual learning⁹. Engram cells still maintain the characteristically high repetitive correlation during contextual learning (Supplementary Fig. 2g). We previously described a method that is well suited for picking neurons that are activated together and their activity patterns⁹, non-negative matrix factorization (NMF) analysis^44,45. In brief, the population activity ensembles were selected on the basis of the Akaike information criterion with a second-order correction (AICc), in which the data matrix was approximated by two non-negative factors (the pattern matrix and the intensity of that pattern activity) to calculate an error function (Supplementary Fig. 3a). Collectively, NMF analysis decomposed the total complex pattern activity into a series of group activated neurons (termed ensembles) and their temporal activity patterns (Supplementary Fig. 3b and see Methods). Each ensemble is constituted of different individual cells’ contributions and their grouped synchronous activity across different time points; therefore, several ensembles have different cell compositions and temporal activity. A given cell can be identified in several ensembles based on their activity and time course of its activity compared to shuffled data. To track the activity of the detected ensembles across other sessions, we applied the normalized dot product (cosine similarity) to compare the similarity between all pairs of pattern vectors of ensembles across two different sessions. If two ensemble vectors completely share the cell identities and activity, the normalized dot product score is 1. However, if there is no similarity, the score is 0. In this study, an ensemble was considered active in another session if it had a normalized dot product equal to or above 0.6⁹. We calculated the similarities between session A and other sessions at different thresholds (0.1-0.9) (Supplementary Fig. 3c). Thresholds below 0.6 displayed comparable activity across all sessions, which appeared less stringent and above 0.6 maintained similar trends (Supplementary Fig. 3c). NMF analysis was applied to all recorded sessions (session N1 to session B) for all cells, and separately to engrams and nonengrams (Supplementary Fig. 3d–g). Then, to estimate the reoccurrence of the ensembles across the sessions, we calculated the matching score (MS), which shows the fraction of ensembles from session X that is similar to any of the ensembles from session Y (see Methods; Fig. 1C). The normalized MS results from session (A) were quantified and compared with those of all other sessions in both engram and nonengram cells. Both engram and nonengram ensembles were normalized to their shuffled engram and nonengram ensembles, respectively. Collectively, similar neuronal ensembles were repeated more often across different sessions in engram cells. By contrast, very few ensembles detected in nonengram cells were repeated (Fig. 1D). Engram cells showed significantly higher normalized MS than nonengram cells across all sessions, exhibiting around 40–60% resemblance, even before the learning in prelearning sleep sessions (N1 and R1). Given the fact that engram cells constitute only a small proportion of the total recorded cells, it is important to make sure that the difference found in MS activity was not attributed to the difference in cell size number. We re-performed the dot product and MS analysis using the same number of cells for both nonengram and engram. Engram cells still show higher MS values, and the same conclusion is maintained (Supplementary Fig. 4a and see Methods). This is consistent with our previous finding that the high MS of engram cells was maintained in replay (N2 and R2) retrieval (A’) sessions⁹, and that MS discrimination ratio of the engram ensembles decreased significantly from the retrieval session (A’) to a different context (B; Supplementary Fig. 4b).

To check the necessity of sleep in this process, on another cohort of mice, we added awake (Aw) and sleep (S) sessions 1 day before learning (Day 0; Supplementary Fig. 4c). Remarkably, engram cells show highly correlated ensemble activity in prelearning periods only during sleep (S1), but not awake (Aw), sessions when compared to learning session A (Supplementary Fig. 4d). Moreover, engram cells show highly correlated activity even 1 day prior to learning, only during sleep session (S0). To further support the results, we have employed the population vector distance (PVD) to track the activity of the engram and non-engram ensembles across sessions (Supplementary Fig. 4e). Engram cells show smaller distances across sessions in reference to session A showing that the activity of engram cells remained stable and similar before and after learning. In contrast, the activity of non-engram cells was more variable overall, with a decreased similarity in response to the learning session (A). This result further supports the conclusions driven from the NMF analysis (Fig. 1D). These results indicate that a group of preconfigured neuronal ensembles that are prominent during sleep, but not awake, sessions are recruited into an upcoming engram upon exposure to contextual learning, and such activity is specific to engram cells.

Preconfigured ensembles constitute around half of engram ensembles

Then, to know the fate and lifetime of each ensemble detected, we tracked the activity of all ensembles detected in A across sessions (Fig. 2A). All ensembles detected in learning were then named and classified based on their activity in other sessions. Briefly, ensembles activated before and continued their activity after learning were termed ‘preconfigured aligned,’ while ensembles activated before and during learning but were not correlated with any of the ensembles after the learning were termed ‘stand-by’ ensembles. Alternatively, ensembles active during and after learning but were not correlated with any of the ensembles active before the learning were termed ‘online emerging’ ensembles. Finally, ensembles that were not active either before or after learning were termed ‘isolated’ ensembles (Fig. 2A). To simplify the analysis, ensembles that did not match any of the previously mentioned patterns of activity were termed as ‘others’. We applied this tracking to all detected engram and nonengram. The preconfigured-aligned ensembles comprised around 40% of all engram ensembles when NREM sleep (N1 and N2) was used for activation during pre- and post-learning sleep (Fig. 2B), whereas isolated ensembles were most abundant in nonengram ensembles (around 60% of ensembles). Similar results were obtained when REM sleep (R1 and R2) was considered (Fig. 2C). This shows that neuronal ensembles that are activated together, even before a certain event, constitute a hippocampal engram and are later activated in postlearning sleep and retrieval sessions. This offline reactivation, especially in engram ensembles, maybe representing what is known as the consolidation process for this event.

**Fig. 2: Preconfigured ensembles are aligned across both pre- and postlearning sleep in engram cells.**

Recent studies have supported the concept of dynamic memory engram^46,47, as suggested by previous research. Building on this idea, we explored the dynamism of the engram by calculating the fraction of drop-in and drop-out engram ensembles. Drop-in ensembles refer to those not activated during the learning session (A) but become active during the retrieval session (A’), whereas drop-out ensembles are active during learning but not during retrieval. Stable ensembles, in contrast, are those activated in both learning and retrieval sessions. Our findings revealed that drop-in and drop-out ensembles each constituted approximately 25% of the total engram population, while stable ensembles accounted for roughly 50% (Supplementary Fig. 5a). This suggests that while individual ensembles may vary, the total engram population remains consistent, with a similar proportion of ensembles dropping in and out. Additionally, we tracked the activity of these ensembles during both prelearning and postlearning sleep. Drop-in ensembles displayed higher activity during prelearning sleep compared to postlearning sleep, whereas drop-out ensembles exhibited similar activity levels across both sleep sessions (Supplementary Fig. 5b).

Engram-to-be ensembles arise from nonengram population to represent future memory

Memory allocation theory holds that neurons having relatively higher excitability would be the memory bearers and the winners of the allocation competition¹. However, it remains unclear what happens to the neurons that do not allocate the memory (losing neurons) in upcoming events, in this case the nonengram cells. Consequently, we investigated whether there is a temporal shift from random to coordinated pattern activities in these nonengram cells across the memory processing stages. We searched the pool of nonengram cells for a group of neurons that could possibly become engram cells in the upcoming event (B) (Fig. 3A).

**Fig. 3: Engram-to-be cells, chosen from the nonengram pool, act as future engram cells for upcoming events.**

We sorted all the nonengram cells. First, on the basis of the characteristic features of the engram cells showing preconfigured aligned ensemble activity in the sleep sessions before learning, we searched for ensembles in session (B) that showed high cosine similarity with ensembles in postlearning sleep (N2 and R2) but not prelearning sleep (N1 and R1) sessions (Fig. 3B and Supplementary Fig. 6a). These candidate ensembles were picked up as engram-to-be ensembles (Supplementary Fig. 6b, c). Next, we picked up actively participating cells in these ensembles and termed them “engram-to-be cells”. In principle, engram-to-be cells are cells that are active as an ensemble in session B and show correlated activity in sleep sessions N2 and R2, but not in sleep sessions N1 and R1 before the first learning exposure.

To ensure that the engram-to-be ensembles represented the majority of the potential engram ensembles of the next event, we applied these criteria to the engram ensembles of session A (Supplementary Fig. 6d, e). The majority of engram ensembles that were active before learning continued to be active in postlearning sleep and retrieval sessions (Fig. 2, Supplementary Fig. 4d). Given that the engram ensemble is defined as those activated during both learning and retrieval, true engram-to-be ensembles (patterns 1 and 3) formed the majority of the predicted engram-to-be ensembles that were identified by the above criteria, whereas pseudopositive engram ensembles (patterns 2 and 4) formed only a small percentage (Supplementary Fig. 6d). Similarly, the true engram-to-be ensembles that were missed by the criteria (false-negative engram-to-be ensembles, patterns 5 and 7) comprised only a small proportion (Supplementary Fig. 6e). This indicates that the criteria applied to pick up the engram-to-be ensembles did indeed capture the majority of meaningful ensembles.

Next, we calculated the correlation repetition analysis for the engram-to-be cells compared with the other nonengram cells, to check if they have the same feature of engram cells during learning⁹. The engram-to-be cells showed higher correlated matrix activity compared to other nonengram cells, denoted by their synchronous repetitive activity and recurring temporal pattern of activity across different time points within a session (session B; Fig. 3C). When the repetitive correlated activity was quantified, only the contextual learning in session B in the engram-to-be cells was significantly higher than in the other nonengram cells (Fig. 3D), while other sessions were comparable. This activity is similar to how the engram cells were behaving in session A (Supplementary Fig. 2g). However, both engram-to-be and other nonengram showed lower correlated activities in session A’ compared to engram cells (Fig. 3E), indicating that the temporal shift and increase in engram-to-be cells activity was specific to new learning (B). The engram-to-be cells showed higher basal activity than the other nonengram cells in session B (Supplementary Fig. 7a). In terms of population size, engram and engram-to-be populations both had comparable numbers of cells, and both were considerably smaller than other nonengram populations (Supplementary Fig. 7b and Supplementary Table 1). On the cellular level, around half (44%) the engram-to-be cells had significantly increased activities in session B compared with session A (Supplementary Fig. 7c, e), while only 37% of the other nonengram population showed a significant increase activity in session B (Supplementary Fig. 7d, e).

To assess the necessity of the postlearning sleep (N2 and R2) ensembles activation, we have picked up cells constituting ensemble patterns that are active during pre-learning sleep and session B, but not in N2 and R2 sleep, which were termed as pre-learning ensembles (Supplementary Fig. 8a). Then, we compared the activity of engram-to-be and pre-learning cells during session B. Correlated activity of engram-to-be cells were significantly higher than the pre-learning cells (Supplementary Fig. 8b). Since the preN1/R1 and postN2/R2 sleeps were recordings from the same day with learning A in between, this result indicates that the difference in engram-to-be and pre-learning ensembles in learning B is due to the experience (learning A). This further denotes the importance of the post experience sleep activation for the engram-to-be preparation and next learning. In accordance with our argument, post-experience sleep, rather than sleep in general, is correlated with new ensembles emergence.

In addition, we have analyzed an awake and sleep home cage activity of engram-to-be cells one day before (Day0; Aw0 and S0), immediately before (Day1; Aw1 and S1), and after (Day1; Aw2 and S2) the learning. Those three time points track engram-to-be awake and sleep home cage activity as a function of time with and without learning experience (A). In accordance with our argument, engram-to-be cells show comparable activity across the three time points in awake sessions (Supplementary Fig. 8c, d), while only postlearning sleep (S2) exhibits higher correlations compared to both awake and other sleep sessions (S0 and S1), this suggests that the learning experience specifically influences the activity of engram-to-be cells during postlearning sleep, but not during wakefulness. Overall, these results indicate that there is a subset of nonengram cells that have drastically altered their activity after the 1^st learning session to suit the next upcoming learning.

Furthermore, we aimed to investigate whether there was a shift in the overall activity of the nonengram cell population through an unsupervised analysis (Supplementary Fig. 9). We conducted a PCA-ICA analysis on the entire nonengram cell population and monitored activities of the ensembles identified during the postlearning sleep session (N2 and R2) in relation to other sessions, prelearning sleep, A, A’, and B. Notably, the ensembles from the postlearning sleep session exhibited a significantly higher level of activities during session B when compared to their activities during the prelearning period. This observation further confirms a notable alteration in the overall population activity patterns during postlearning sleep, patterns that were absent during the prelearning sleep.

To check if engram-to-be cells show postlearning reactivation, we recorded NREM and REM sleep sessions after session B (Fig. 3f). By utilizing PVD, we were able to demonstrate that engram-to-be cells also maintained stable activity during post-learning sleep sessions. This consistency suggests that, like engram cells, engram-to-be cells preserve their activity across sessions. PVD showed smaller distances in both NREM and REM sleep compared to other nonengram cells, using session B as a reference. The NMF analysis of engram-to-be cells during post-learning sleep revealed that, as expected, these cells exhibited higher matching scores across sleep sessions in reference to session B (Supplementary Fig. 8e), suggesting that the engram-to-be ensembles were reactivated during subsequent sleep. These findings highlight the role of post-learning sleep in reinforcing and stabilizing engram-to-be cell activity, further supporting their involvement in memory processes. This activity could be representing engram-to-be offline reactivations or replay of session B and behaving similarly as engram cells⁹. To recapitulate, the engram-to-be population behaved in a similar manner during contextual learning for session B but not A’, reactivating at subsequent sleep sessions as a form of consolidation. These implications may designate that this population is the upcoming engram or “engram-to-be” cells for session B.

Engram and engram-to-be cells show high cooccurrences during postlearning sleep

We next investigated whether there was any interaction between engram cells representing session A and engram-to-be cells representing session B in terms of the coactivity between the two populations within a certain time window. We first tracked the activity of all engram ensembles throughout the sessions. Some ensembles of session A engram cells showed high cosine similarity (> 0.6) with session B (common engram ensemble), whereas some ensembles did not (< 0.6; (specific engram ensemble, Supplementary Fig. 10a and f). Accordingly, the engram cells were subcategorized according to their activity in session (B) into common engram and specific engram cells (see Methods, Supplementary Fig. 10). To investigate whether there was any functional difference between the two subgroups of the engram population, the neuronal activities were binarized, and all co-occurrences between the different subgroups were counted over a short time window (see Methods; Fig. 4A). The co-occurrences between common engram and engram-to-be cells, and between specific engram and engram-to-be cells, were measured in sessions N1&R1, A, N2&R2, A’, and B (Fig. 4B). Comparisons revealed that the co-occurrences between common engram and engram-to-be cells were significantly higher than the co-occurrences between specific engram and engram-to-be cells only during the postlearning sleep (N2&R2) session, with there being no significant difference detected in the other sessions (Fig. 4C and Supplementary Fig. 11c, d). Importantly, in retrieval session A’ just prior new learning B, there was no significant difference in co-occurrences. This suggests that retrieval of previous experience does not affect the emergence of engram-to-be cells. The differences in the co-occurrences between the subgroups were not due to a difference in the rate of single occurrences of either the common engram or specific cells (Fig. 4D), nor the number of cells (Fig. 4E) in each subgroup. Moreover, there was no significant difference in comparisons of the co-occurrences between common engrams vs. other nonengram cells, and specific engrams vs. other nonengram cells (Fig. 4F). This excludes that the difference in co-occurrences detected during post learning sleep is due to any individual differences of each subgroup in terms of group size or basal activity level. Each of the common and specific engram population represented around 30% of the total engram population (Supplementary Fig. 11a). The maximum number of coactive neurons in a single frame was approximately 3% of the total population, with no frame exceeding 10% of the total population (Supplementary Fig. 11b). Taken together, these results demonstrate that different subgroups in a single engram population might play different functions in the processing of memory.

**Fig. 4: Common engram cells are coactivated with engram-to-be cells during postlearning sleep.**

Synaptic plasticity mechanisms during offline periods govern engram-to-be cells emergence

To understand the plasticity mechanism behind the temporal shift of engram assemblies, we created a neural network model to simulate how the engram-to-be cells might emerge. Specifically, we hypothesized that synaptic plasticity during offline periods supports the emergence of engram-to-be cells. In this model, we simulated the responses of CA1 neurons receiving context-dependent inputs from CA3 during four sessions: prelearning sleep, context A, postlearning sleep, and context B (Fig. 5A). During the context exposure, highly activated CA1 neurons become engram cells, and synapses connected to engram cells are potentiated^12,48,49. With this learning rule (see Methods “Simulation model and procedure” for details of the learning rule), pre-existing assemblies that are active before learning are prone to become engram cells, and after learning, they strongly respond to input patterns of context A (Fig. 5B). During the postlearning sleep, we applied offline synaptic plasticity mechanisms that have been experimentally observed in CA1: synaptic depression in nonengram cells caused by sharp-wave ripples (SWRs)²⁹ and homeostatic synaptic scaling^50,51,52. After this offline synaptic tuning, nonengram cells in CA1 stopped responding to CA3 patterns of context A, which are frequently replayed during SWRs. Instead, the nonengram cells respond strongly to different CA3 patterns (nonreplay patterns), which results in the emergence of novel assemblies in CA1 (Fig. 5B). These novel assemblies are supposed to be recruited as engram cells if the next experience is different from the previous one, and part of these assemblies are observed as engram-to-be cells. Actually, a previous report showed that such synaptic depotentiation and synaptic scaling during sleep is critical for learning of future memories²⁹.

**Fig. 5: A neural network model reproduces emergence of engram-to-be cells and coactivity with common engram cells.**

We checked whether the proposed model captured the key features of the experimental data through statistical analyses of simulation results. First, we classified simulated CA1 neurons into engram cells and nonengram cells according to context A, and then nonengram cells were further subdivided into engram-to-be and other nonengram cells based on their activity in context B (see Methods). We subdivided the engram cells of context A into common engram and specific engram types according to their activity in context B (Supplementary Fig. 12a; see Methods). The ratio of the cell types in our model matched that in the experimental data (Supplementary Fig. 12b). We analyzed the matching between activity patterns in context A and those in pre and postlearning sleep sessions and found that the engram cells showed higher matching with context A than the nonengram cells (Fig. 5C), whose matching scores resembled those observed in our in-vivo Ca²⁺ recordings (Fig. 1D). We repeated the same analysis for populations of engram and engram-to-be cells in context B and compared the score against other nonengram cells. The activity patterns of engram and engram-to-be cells showed high matching (compared with other nonengram cells) with context B only during postlearning sleep (Fig. 5D), indicating that the assembly activated in context B was formed after learning of context A. We obtained the qualitatively same result when we separately analyzed engram and engram-to-be cells, although the matching ratio became unstable due to limited population sizes (Supplementary Fig. 12c), repeating the same analysis using a higher threshold (0.7) showed same tendency (Supplementary Fig. 12d), further confirming that the new ensembles activated in context B emerged after the first learning (context A). Furthermore, we also simulated a sleep session after context B and evaluated the matching between activity patterns in context B and the following sleep. We confirmed that the matching of engram-to-be cells was higher than that of non-engram cells (Supplementary Fig. 12e), which corresponds to experimental results in Fig. 3F. To provide further evidence of the temporal shift in the activity of the engram-to-be cells, we calculated the average pairwise correlation within each cell type (engram, engram-to-be, and other nonengram) in either pre or postlearning sleep sessions. Engram cells showed higher correlations than nonengram cells in both pre and postlearning sleep sessions (Fig. 5E), mimicking the synchronous correlated activity experimentally observed both before and after learning (Fig. 1D). Engram-to-be cells showed high correlated activity only during postlearning sleep, not in the prelearning sleep session, which further validates the temporal shift in the activity of the nonengram cells and the emergence of the engram-to-be cells only after the first learning (Fig. 5E). Next, following subclassification of the engram cells in the experimental data (Fig. 4B), the coincidences of the activities of common engram cells and engram-to-be cells were found to be significantly higher than those of specific engram and engram-to-be cells, and all other combinations, during the postlearning sleep (Fig. 5F), which matches with the experimental result (Fig. 4C). We also confirmed that this difference between common engram and specific engram emerged in postlearning sleep but not in prelearning sleep (Supplementary Fig. 12f), which qualitatively reproduces the experimental results in Fig. 4C. Overall, these results suggest that the hypothesized plasticity mechanism can explain the experimentally observed reformulation of engram assemblies in CA1.

To confirm that offline plasticity is critical for the emergence of engram-to-be cells, we simulated the network model without offline synaptic plasticity in the postlearning sleep period (synaptic depression caused by SWRs and homeostatic synaptic scaling) (Fig. 5B). This manipulation significantly decreased the number of engram-to-be cells and increased the other nonengram cells, while the number of engram cells remained the same (Fig. 6A), indicating that blocking offline sleep plasticity hindered the emergence of the engram-to-be cells. Moreover, the correlation of the activities of engram-to-be cells in postlearning sleep was significantly reduced compared with normal model conditions, while the correlation of activities of engram and other nonengram cells remained the same (Fig. 6B). Comparisons of the correlations of activities between prelearning and postlearning sleep revealed that engram cells increased significantly, engram-to-be cells decreased significantly, and other nonengram cells remained the same. Thus, blocking the offline sleep plasticity affected the engram-to-be cells in the postlearning sleep (Supplementary Fig. 12g). We also measured the difference in the coincidence of activities between common engram and engram-to-be cells, and between specific engram and engram-to-be cells. There was a significant decrease in the model without offline synaptic plasticity (Fig. 6C, D). Moreover, we tested the effects of shutting off synaptic depression and homeostatic plasticity individually. Disabling homeostatic plasticity during sleep directly impaired the formation of engram-to-be assemblies (Supplementary Fig. 13a). When synaptic depression was turned off, all cells were typically more active in all sessions, nonspecifically increasing the coincidence ratio (Supplementary Fig. 13b). Both models, with either synaptic depression or homeostatic plasticity off, displayed low engram-to-be correlations during post-sleep sessions (Supplementary Fig. 13c). This suggests that both mechanisms are essential for the emergence of specific ensembles and highlights the importance of sleep-related plasticity for the formation of engram-to-be cells.

**Fig. 6: Abolishing sleep plasticity in the network model hinders emergence of engram-to-be cells.**

Discussion

Artificially increasing or decreasing the excitability of certain neurons can bias the memory allocation process toward or against them, respectively, thereby generating engram cells¹². Over the past decade, a consensus has been steadily building regarding the preexisting configuration of the hippocampal network as basis for memory and cognition in rodents^{19,20,21,53,54,55} and recently in humans⁵⁶. The intrinsic dynamic activity occurring in the hippocampus is organized into synchronous assemblies, even with minimal external sensory input⁵⁴. This process might act as a physiological equivalent to the artificially activated subsets of neurons, and act as a building block for the upcoming experience⁵⁷. Unique pattern coactivity and hardwiring of the hippocampal preconfigured network were attributed to their birthdate and neurogenesis⁵⁸. A recent study showed that tagging cells while mice are in their home cage immediately before learning, but not 1 day earlier, is sufficient to diminish fear memory if these cells are inhibited during retrieval¹⁸. However, because of the technical challenges involved, it is difficult to directly relate the activity of engram cells to preconfigured assemblies in freely behaving mice.

Using an imaging system that combines live Ca²⁺ imaging and engram cell labeling allowed us to preemptively monitor the activity of engram cells even before their emergence. Engram ensembles formed during learning showed high correlations during sleep before learning and continued their correlated activities during postlearning sleep. We termed these ensembles ‘preconfigured’ ensembles, which denotes that the brain prepares new ‘slots’ for the next upcoming task. This is in accordance with previous findings showing that engram cells are picked up from a pool of particularly excitable and connected neurons even before learning¹⁸. Although initial engram cells might have won the competition to encode the first learning experience, it should be possible to recruit a new group of neurons to represent the upcoming experience. Based on previous literature¹¹, introducing mice to novel contexts within a 5-h interval leads to the formation of a single engram for both events. To avoid this overlap, we introduced a 24-h interval between the first and second contexts and added a retrieval session to reinforce the initial memory. Without this approach, it is likely that we wouldn’t observe distinct engram and engram-to-be populations for contexts A and B, respectively. Hippocampal neurons are in a continuous dynamic state in which internally generated representations allow new sets of correlated and properly connected cells to fit the requirements of the near future task^39,59. During postlearning idling periods reactivations take place to consolidate and stabilize previous events⁶⁰. Our results show that, parallel to consolidation a temporal shift in activity occurs in a subpopulation of nonengram to prepare them to the next future event, which we term engram-to-be. Engram-to-be cells developed a temporal shift from a random to a highly correlated pattern of activity by the second learning event during session B, indicating that they were still immature during session A on the first day. The synaptic plasticity mechanisms that occur during idling periods maybe the underlying mechanism for the emergence of these engram-to-be cells. The synchronous activity of engram-to-be cells during new learning signifies the continuous pattern turnover and dynamism in the hippocampal repertoire for future scenarios while the original engram cells preserve the previous memory identity.

Furthermore, we show that engram cells can be further apportioned into two subpopulations: common and specific engrams, each playing a different role. Common engram cells could correspond to general features that can be shared in the future with similar situations, while specific engram cells are tuned to the precise features of the experience that govern its uniqueness. This is in line with previous reports suggesting that within a single engram population there are several subensembles that could represent different features⁹ or have different functions^61,62.

Sleep and its role in consolidating acquired memories is thoroughly demonstrated^25,27,28. Both NREM and REM sleep showed comparable results regarding the reappearance of ensembles across sessions. This resemblance in their function could be due to the fact that NREM and REM sleep share several roles in memory processing, such as replay for consolidation^27,28, or the fact that only a small proportion of the entire sleep was recorded to prevent photobleaching of cells. Majority of engram ensembles were preconfigured aligned, showing high correlated activity from prelearning till postlearning and retrieval periods, whereas stand-by ensembles, were very low (~ 5% in REM and 0% in NREM). This indicates that most engram cell ensembles that were active before learning were integrated into the upcoming engram population and maintained their activity after learning for the consolidation process. Another noticeable point is that REM sleep shows a tendency of high ensemble percentage in online emerging and stand-by patterns, this could be related to the nature of REM sleep in the emergence of new ensembles^24,63,64. Sleep is also believed to be of importance for future events²⁶. In our network model, we showed that synaptic plasticity in postlearning sleep is crucial for the emergence of engram-to-be that are important for the upcoming event, and also guides the coactivity between engram-to-be and common engram cells. This coupling of the two populations may enhance the basal activity of the engram-to-be cells. This is in agreement with a previous study that showed that optically increasing the excitability of a group of cells unmasks preexisting cell assemblies that were initially non-place cells²¹. Conceptually, this is similar to our engram-to-be cells that were initially masked within the pool of non-engram cells but after the initial learning emerged through synaptic plasticity mechanisms. Collectively, during offline periods and idling moments, two processes occur, consolidating previous memories and preparing for future ones.

Our neural network model not only explains how offline plasticity mechanisms support the emergence of engram-to-be cells, but also suggests an important functional role of the offline state of the brain. Because highly activated cells tend to become engram cells, and engram cells become more excitable^12,48, the differentiation of engram assemblies for independent memories would require active rebalancing of activity levels. In the offline state, the hippocampal neural network needs to undergo reformulation to prepare novel assemblies for the novel experience while keeping previous engram assemblies stable. Our model provides a specific learning mechanism for such offline tradeoff between assemblies.

We built a minimal model that incorporates key offline plasticity mechanisms to reproduce the experimental data. However, we cannot exclude the possible contribution of other factors. For example, we implemented homeostatic synaptic scaling in our model but tuning of the excitability of each neuron^12,48 may substitute for this scaling effect. Furthermore, we took into account the plasticity of excitatory synapses from CA3 to CA1 but did not include the plasticity of entorhinal cortex-to-CA1 synapses and inhibitory circuits in CA1⁶⁵. Our model explained the emergence of the coactivity between common engram and engram-to-be cells mainly. It is also possible that the common engram cells directly recruit engram-to-be cells through internal connections in CA1. Previous reports suggest that the internal circuit structure in CA1 significantly affects the formation of place coding^66,67, and that the deactivation of preexisting engram cells results in the rapid recruitment of new engram cells, possibly through internal circuits in CA1¹². As all the model manipulations were performed solely in silico, additional biological evidences are needed to validate these findings.

Recently, neural network models have been proposed for the formation and the drift of memory engrams in hippocampus^46,68,69. Those models employed a recurrent network model, the modulation of neuronal excitability and plasticity of inhibitory circuits, by which the model successfully explained how common and specific engrams emerge and evolve during learning and offline periods. However, the emergence of engram-to-be cells has not been reported in the previous models because those models do not have offline mechanisms to actively recruit non-engram cells for next memory formation. Furthermore, the offline learning mechanisms (synaptic downregulation and scaling during offline periods) in our model are different from those in the previous models, although functions may be partly similar (e.g. potentiation of inhibitory synapses and downregulation of excitatory synapses). These multiple mechanisms may work independently or cooperatively. Otherwise, different mechanisms may correspond to the difference of brain regions such as dentate gyrus⁴⁶ and CA1 (our model). The proposed model suggests that synaptic depression and scaling may play a key role in reorganizing the activity patterns of non-engram cells, allowing for flexibility and efficient network adaptation, essential for encoding new memories.

We propose that during offline periods after learning, two simultaneous processes commence: consolidation of past memories through reactivation of engram ensembles, and emergence of an engram-to-be population through synaptic mechanisms to act as encoders for future memories (Supplementary Fig. 14). Together, offline period dynamics fix the past and prepare for the future.

Methods

Animals

All procedures involving animals complied with the guidelines of the National Institutes of Health, were approved by the Animal Care and Use Committee of the University of Toyama (Approval number: A2022MED-8), and were conducted in accordance with the Institutional Animal Experiment Handling Rules of the University of Toyama. Thy1-G-CaMP7-T2A-DsRed2 mice have been described previously⁷⁰. All surgery was conducted on male c-fos-tTA × Thy1-G-CaMP7 mice with a C57BL/6 J background. Mice were maintained on food containing 40 mg/kg doxycycline (Dox) after weaning.

The progeny of the c-fos-tTA × Thy1-G-CaMP7 line were generated by in-vitro fertilization (IVF) of eggs from C57BL/6 J mice and embryo transfer techniques to produce a sufficient number of mice for behavioral analysis^3,9. Genotyping of genomic DNA isolated from the tails of the pups was performed by polymerase chain reaction^71,72. All mice were maintained on a 12 h light-dark cycle (lights on at 8:00 am) at 24 °C ± 3 °C and 55% ± 5% humidity, given food and water ad libitum, and housed with littermates until 5 days before surgery.

Viral vectors

The pLenti-TRE-hKiKGR plasmid has been described previously⁹. pLenti-TRE-hKiKGR plasmid was prepared using an EndoFree Plasmid Maxi kit (Qiagen). The lentivirus (LV) was prepared as described previously³, according to the protocol adopted from that of the laboratory of K. Deisseroth (https://dlab.stanford.edu/resources/optogenetics/expression-systems).

Stereotactic surgery for Ca²⁺ imaging and EEG/EMG recording

All surgery was conducted on male c-fos-tTA × Thy1-G-CaMP7 mice (aged around 12–20 weeks) with a C57BL/6 J background, as described previously⁹. Briefly, mice were anesthetized by intraperitoneal (i.p.) injection of pentobarbital solution (80 mg/kg of body weight) and placed in a stereotactic apparatus (Narishige, Japan). The craniotomy for injecting TRE-hKikGR lentivirus (LV) was ~1.0 mm in diameter. TRE-hKiKGR-LV (1 μl/injection site) was injected using an injection cannula connected to a Hamilton microsyringe through a water-filled polyethylene tube. The injection cannula (Unique Medical Co., Ltd., Japan) was targeted to the right CA1 (AP -2.0 mm, ML 1.4 mm, DV -1.5 mm from bregma). LV was injected at 0.1 μl/minute with a microsyringe pump (CMA 400, Harvard Apparatus). After injection, the injection cannula was kept in position for 10 minutes and then slowly withdrawn to prevent any damage to the tissues. The craniotomy was then sealed with dental cement, and the skin was closed.

To ensure complete recovery of the mice, the next surgery to implant a gradient refractive index (GRIN) relay lens over the hippocampus, as reported previously^9,41,73,74, was performed 4 weeks after the LV injection surgery. Similarly, mice were anesthetized by i.p. injection of pentobarbital solution (80 mg/kg of body weight) and placed in a stereotactic apparatus (Narishige, Japan). A 2.0-mm-diameter craniotomy was made in the skull to set the cannula lens sleeve (1.8 mm outer diameter and 3.6 mm in length; Inscopix, CA). To set the lens over the hippocampus, a cylindrical column of neocortex and corpus callosum above the alveus covering the dorsal hippocampus was carefully and gently aspirated with saline using a 27 gauge blunt drawing-up needle. Phosphate buffered saline (PBS) solution was added frequently to prevent tissue drying up. The cannula lens sleeve was gently placed on the alveus. To fix and straighten the cannula lens sleeve to the edge of the burr hole, bone wax was melted, and the sleeve lens was straightened using low-temperature cautery. The cannula lens sleeve targeted the center of the right hemisphere (AP, 2.0 mm, ML, 1.5 mm). At the frontal part of the skull, two anchor screws linked to a recording connector were fixed to serve as an anchor to the sleeve lens and electrodes for recording the cortical electroencephalogram (EEG). Then, stainless wire electrodes were inserted into the neck muscle to record the electromyogram (EMG). Another set of anchor screws was fixed on the lateral part to act as a body earth for noise reduction. A final set of two screws was fixed on the other side of the skull as an extra anchor for the whole setting. Finally, the visible parts of the skull and electrodes were covered with dental cement to attach the cannula lens sleeve to the skull and anchor screws.

Two weeks after from the sleeve lens and EEG and EMG electrodes setting, mice were anesthetized with pentobarbital solution (80 mg/kg of body weight; intraperitoneal injection), and a GRIN lens (1.0 mm outer diameter and 4.0 mm length; Inscopix, CA) was inserted into the fixed cannula lens sleeve and fixed in place with ultraviolet-curing adhesive (Norland, NOA 81). An integrated miniature microscope (nVista HD, Inscopix, CA)⁴¹ with a microscope baseplate (Inscopix, CA) was placed above the GRIN lens, allowing observation of G-CaMP7 fluorescence and blood vessels in CA1. The microscope baseplate was fixed to the head of the previously fixed anchor screws using dental cement so that the GRIN lens was covered, and then the integrated microscope was detached from the baseplate. The GRIN lens was covered by attaching the microscope baseplate cover to the baseplate until it was time for Ca²⁺ imaging.

Microscopy and EEG/EMG recording of freely moving mice

All behavioral analyses and recordings were performed during the light cycle. Ca²⁺ transients were recorded using nVista HD acquisition software (Inscopix, CA) at 20 frames/s frequency, maximum gain, and 60% LED power. To differentiate between different sleep stages, EEG/EMG traces at a sampling rate of 1 kHz with bandpass filtering (low cut-off frequency of 0.5 Hz and high cut-off frequency of 300 Hz for EEG; low cut-off frequency of 5 Hz and high cut-off frequency of 3000 Hz for EMG) were amplified and collected using a Unique Acquisition system (Unique Medical). Using fast Fourier transform analysis, sleep scoring was performed on the EEG and EMG traces for all 16 s consecutive epochs. In this scoring, high EMG and low EEG voltages with high frequency were labeled as wakefulness, low EMG and high EEG voltages with dominant δ (0.5–4 Hz) frequency components were labeled as non-rapid-eye-movement (NREM) sleep, and low EMG (indicating muscle atonia) and low EEG voltages with dominant θ (6–9 Hz) frequency components were labeled as REM sleep⁹. The contexts used for learning session A and session B were located in the same behavioral room but in different locations. Context A was a cylindrical chamber (300 mm diameter, 450 mm height) with white acrylic walls and a floor covered with brown tissues. Context B was a square chamber with a Plexiglass front, gray sides, back walls (width × depth × height: 175 × 165 × 300 mm), and a floor consisting of 26 stainless steel rods (diameter, 2 mm) placed 5 mm apart. Before starting the experiment, the c-fos-tTA × Thy1-G-CaMP7 mice injected with TRE-KikGR-LV were moved to an isolation box (FRP BIO2000, CLEA Japan) located in a Faraday cage (Narishige, Japan). Mice were first habituated to the weight of the miniature microscope and the EEG/EMG wires for 30 minutes on each of 3 consecutive days. On the next day, DOX pellets were removed from the food and replaced with normal pellets. Two days later, the mice were anesthetized with around 2% isoflurane for about 5 minutes. Then, 15 second pulses of 365 nm light were delivered to the GRIN lens from an LED light source (BL-LED-365, OPTO-LINE, Inc., Japan) through an optic fiber (SH4001 Super Eska, NA: 0.5, Mitsubishi Rayon Co., Ltd., Japan). This procedure was repeated three times with 1-minute intervals between each repetition, to remove any nonspecific KikGR expressed before the learning. Then, a snapshot of the CA1 was captured using the nVista HD acquisition software (Inscopix, CA). Mice with the microscope attached to their head were returned to their home cage in the Faraday cage; the EEG/EMG electrodes were attached, and the mice were allowed to rest. After 1–2 h, the Ca²⁺ activities of the first stable-appearing NREM sleep were recorded (N1). Around 1 h later, the first-appearing REM sleep that lasted for at least 1 minute was also recorded (R1). Mice were then introduced to the cylindrical chamber for the first time, and the Ca²⁺ activities were recorded for 6 minutes (session A). After this, the mice were returned to their home cage with the miniature microscope still attached to their head and were allowed to sleep. Around 1 h later, Ca²⁺ activities of stable NREM (N2) and REM (R2) were recorded, as previously described⁹. The EEG/EMG electrodes and miniature microscope were detached upon waking from the REM sleep. Across the sleep stage recording (N1, R1, N2, and R2), the nVista LED was shut off between NREM and REM for both prelearning and postlearning sleep stages to prevent any photobleaching. Sleep recording duration was recorded for 1 minute for each NREM or REM session and was increased to 3-4 minutes in NREM and 2 minutes REM in a sperate group of mice; both groups showed the same offline reactivation activity (Fig. 1D and Supplementary Fig. 4d). The mice were returned to DOX food from the 2^nd day. Twenty-four h after the first context exposure, a snapshot of KikGR expression was captured using the nVista HD acquisition software (Inscopix, CA) under 2% isoflurane anesthesia for 5 minutes, to prevent the capture of any nonspecific spontaneous calcium activity as a KikGR⁺ cell. This was followed by exposure to 15 s pulses of 365 nm light from an LED light source, with each pulse occurring three times with a 1 minute interval between pulses, as mentioned previously. After 1.5–2 h, Ca²⁺ activities were recorded when the mice were reintroduced into context A for 3 minutes (session A’). Following the re-exposure, the mice with the nVista HD microscope attached were returned immediately to their home cage. Then, after 1.5–2 h, the mice were introduced into the square context for 3 minutes (session B), and their Ca²⁺ activities were recorded.

In another set of double transgenic mice after injecting the TRE-KikGR LV, setting the EEG/EMG electrodes and fixing the lens and the baseplate for the miniature microscope. Calcium transients were recorded one day earlier (Day 0) before exposure to the learning session during both awake (Aw0) and sleep sessions (S0). Next day (Day 1) both awake (Aw1) and sleep sessions (S1) were captured before session (A) followed by awake (Aw2) and sleep (S2) sessions. Next day (Day 2), KikGR snapshot capturing and photoconversion were performed in the same manner as mentioned earlier, then both awake (Aw3) and sleep sessions (S3) were captured, as well (Supplementary Fig. 4c). Later, sleep sessions were recorded (both NREM and REM) after session B (Fig. 3F).

Ca²⁺ imaging data acquisition, processing, and cell sorting

All Ca²⁺ transients were captured using nVista acquisition software (Inscopix, CA). The captured images were processed in a similar manner to that described in our previous report⁹. Briefly, using Mosaic software (Inscopix, CA), each session movie was spatially binned using a factor of 2. To maintain the same field of view (FOV) and correct for motion artifacts, motion correction was performed (correction type: translation only, spatial mean [r = 20 pixels] subtracted, and spatial mean applied [r = 5 pixels]) using blood vessels as landmarks. The binned movie was then further processed using ImageJ software (NIH). Each session movie was divided (pixel by pixel) by a low-pass filtered (r = 20 pixels) version. Then, the single session movies were concatenated into one total movie containing all the recording sessions to allow tracking of the same neurons across sessions and days. Motion correction was applied to the total movie, using a single frame as a reference frame, to ensure that the XY translation was adjusted across all recording sessions (Supplementary Fig. 1a), similar to the method used in a previous report⁷⁵. The motion correction efficiency was assessed by checking the activity of several cells in the total movie across 2 days to ensure that cells maintained both their spatial location and morphology across days (Supplementary Fig. 1b–d). To measure changes in the fluorescence of each frame, the ΔF(t)/F0 = (F(t) − F0)/F0 value was calculated for each movie session (where F0 is the mean image obtained by averaging the entire movie for that session). Finally, using Mosaic software, all movie sessions were once again combined into a single movie comprising the entire behavior. Once the Ca²⁺ movie was finalized, a HOTARU fully automated Ca²⁺ sorting algorithm system (high performance optimizer for spike timing and cell location via linear impulse)^43,72 was used to extract the spatial and temporal dynamics of active cells.

Identifying engram cells through KikGR expression

Engram cells were identified using the snapshot taken 24 h after the novel context exposure (session A). The snapshot was first spatially binned by a factor of 2 and then manually realigned to a reference frame to maintain the same FOV, using blood vessels as landmarks. These procedures were performed using Image J software (NIH). Following the procedure used for the Ca²⁺ movies, the snapshot was divided (pixel by pixel) by a low-pass (r = 20 pixels) filtered version. Then, to maintain the top ~10% signal intensity, a threshold was applied to remove the background. The output image was further processed by binarization (binary options: Iterations, 1; Counts, 2; Close [fill small holes between pixels], and Watershed). Finally, the remaining contours in the resulting image were analyzed automatically using Image J. The successfully detected ROIs represented the locations of KikGR⁺ cells (Supplementary Fig. 2b–d). Then, the spatial contours generated by the HOTARU system were compared with the spatial locations of the KikGR⁺ cells identified from the Image J ROIs. Some ROIs for gene-expressing cells did not fully overlap with the detected calcium transients and were discarded (Supplementary Fig. 2e). Only ROIs that showed complete overlap with active cells on visual inspection were recognized as engram cells. The engram cells constituted 8% of all automatically detected cells (Supplementary Fig. 2f).

Selection criteria for engram-to-be cells

Engram-to-be cells were chosen from the nonengram pool of cells by screening all session B ensembles that showed high cosine similarity (> 0.6) with any of the postsleep learning (N2, R2) ensembles, while at the same time showing low cosine similarity (< 0.6) with all presleep learning (N1, R1). Active neurons participating in these ensembles were further filtered by choosing neurons having activity higher than double the median of the nonzero activity of that ensemble. These selected neurons were later termed engram-to-be cells. Those cells that did not meet these criteria were excluded from the engram-to-be population and added to the other nonengram pool. To identify engram-to-be and other nonengram cells that significantly increased or decreased their activity during session B on day 2, we compared their Ca²⁺ signals for session B with those in session A (Wilcoxon rank-sum test, using a significance threshold of p < 0.01).

Subcategorization criteria for engram cells

In the screening of the engram ensembles of session A, there were some ensembles that were activated in the prelearning sleep, context A, postlearning sleep, and session B, and other ensembles that were activated in prelearning sleep, context A, and postlearning sleep but not in session B. Engram ensembles that showed activity including session B were termed common engram ensembles, and ensembles that did not show activity in session B were termed specific engram ensembles. The active participating cells (higher than double the median of nonzero activity) of these ensembles were termed common engram and specific engram cells, respectively (Supplementary Fig. 10).

Dynamic engram

Dynamic engram calculated by quantifying the fraction of drop-in and drop-out from the total engram ensembles of both the learning (A) and retrieval (A’). Drop-out ensembles are those active during learning but not showing overlap with any of the retrieval ensembles (dot product >0.6). In contrast drop-in ensembles are those active during retrieval but not showing overlap with any of the learning ensembles (dot product >0.6), whereas. Stable ensembles are those showing high overlap (dot product > 0.6) in the learning and retrieval sessions. Then, to determine their activity in pre and postlearning sleep, drop-in and drop-out ensembles that are showing high overlap (dot product > 0.6) with any of pre and postlearning sleep ensembles are considered active in pre and postlearning sleep sessions, respectively.

Ca²⁺ event co-occurrences

The Ca²⁺ transients of each subpopulation of both engram cells (common engram and specific engram) and nonengram cells (engram-to-be and other nonengram) were binarized using a threshold of >3 standard deviations of the ΔF/F signal, and then downsampled from 20 HZ to 4 HZ (250 ms temporal binning) using a custom-made MATLAB code²³. Consequently, the total co-occurrences between two subpopulations (in a 250 ms time window) were counted for the prelearning sleep (N1&R1), context A, postlearning sleep (N2&R2), and context B sessions (Fig. 4A), and then normalized according to

$${Total}\; {co}-{occurrences}=\frac{{Co}-{occurrences}\,\left(A+B\right)\,{neurons}}{T\times \left({n}_{A}+{n}_{B}\right)}\times 100$$

(1)

where A is either of the engram subpopulation cells, B is either of the nonengram subpopulation cells, n is the total number of cells active in A or B, and T is the total number of bins. The total co-occurrences were then normalized to the total score of the co-occurrences of specific engrams and engrams-to-be in each calculated session to allow absolute comparisons of co-occurrences across sessions (Fig. 4C). The normalized single occurrences of a certain subpopulation were calculated in a similar manner,

$${Total}\; {occurrences}=\frac{{occurrences}\,\left(A\right)\,{neurons}}{T\times ({n}_{A})}\times 100$$

(2)

in which A is one of the engram subpopulation cells, n is the total number of cells active in A, and T is the total number of bins. Subjects that did not show at least a single co-occurrence in any or all the sessions were excluded from this analysis (4 of the 9 mice who underwent this analysis were excluded).

Correlation matrix overlaps

Temporal correlations between pairs of engram cells, engram-to-be cells, other nonengrams, or nonengram cells were calculated using a 1 s sliding time window with time steps of 200 ms. The correlation matrix calculated at time $t$ is denoted by $\hat{C}\left(t\right)\equiv ({C}_{{ij}}^{t})$, where $i$ and $j$ are neuron indices, and $t$ refers to the midpoint of the time window. Note that if either neuron $i$ or $j$ was silent, ${C}_{{ij}}^{t}=0$. The similarity between the two correlation matrixes at $t$ and $t^{\prime}$ was calculated as $M\left(t,t ^{\prime} \right)\equiv \frac{1}{N\left(N-1\right)}{\sum }_{i\ne j}{C}_{{ij}}^{t}{C}_{{ij}}^{{t}^{{\prime} }}$⁷⁶, where $N$ is the number of cells of interest. To compare engram cells, engram-to-be cells, other nonengram cells, and nonengram cells, the MS with respect to $t^{\prime}$ was calculated as$\,{M}_{{{\rm{total}}}}\left(t\right)\equiv {\sum }_{t^{\prime} }M\left(t,{t}^{{\prime} }\right)$, which measures the degree to which the correlation pattern of the population activity at $t$ is repeated at different times within the whole dataset. The larger the value, the more often the correlation pattern looks similar to that obtained at ${t}$.

Since the numbers of engram cells, engram-to-be cells, other nonengrams, and nonengram cells were different, if the correlation matrixes for different groups of cells were calculated using all cells, the comparison would not be fair. Therefore, we took $N$ to be the number of cells in the smallest neuronal group. For those neuronal groups having a size larger than $N$, we took the ensemble average of ${M}_{{{\rm{total}}}}\left(t\right)$ to be the representative sum of the correlation matrixes. Each ensemble consisted of randomly sampled $N$ cells from the group. For comparing across sessions with different number of frames recorded, we normalized their sum of correlations to their respective frame number (Fig. 3D and Supplementary Fig. 8d).

Cell ensemble analysis

Non-negative matrix factorization (NMF)

NMF was used to extract population activity patterns from the calcium signal dataset⁹. More specifically, NMF finds an optimal factorization of the data matrix $\hat{D}$, with a pattern matrix $\hat{B}$ and the corresponding intensity matrix $\hat{C}$, i.e., $\hat{D}\approx \hat{B}\hat{C}$. Here, the rows of $\hat{D}$ represent the time series of the signals from individual neurons, each column vector of $\hat{B}$ represents a synchronously activated neuron ensemble (population activity pattern), and each row of $\hat{C}$ represents the time series of the activation intensity of the corresponding pattern. To search for such a factorization, the cost function defined by $E\equiv {\sum }_{{ij}}{({D}_{{ij}}-{\sum }_{k}{B}_{{ik}}{C}_{{kj}})}^{2}$ was minimized using both multiplicative and additive algorithms⁴⁵. Random initial entries from matrixes $\hat{B}$ and $\hat{C}$ were used for 1000 minimization attempts, and the pair of pattern and intensity matrixes that minimized the cost function were chosen to be the best factorization. The cost function becomes smaller if more patterns are introduced, but the model (i.e., the right-hand side of the cost function) becomes more complex. This trade-off between cost minimization and model complexity was optimized using the Akaike information criterion with second-order correction (AICc)⁴⁴ to determine the optimal number of patterns (i.e., the number of columns in the pattern matrix). Both the neuron indices and the timestamps of the original data were shuffled independently to obtain a shuffled dataset. Ten shuffled datasets were constructed for each sample in each session. Because the ratio of the standard deviation to the mean was small (~ 0.03), this number of samples should be sufficient. Neuron (i) identified in an ensemble (k) if the i-th neuron in k-th ensemble’ peak activity or average activity is strong relative to those in other patterns, if not it would be discarded. Then, if the time course of the i-th neuron in the k-th ensemble significant enough compared to shuffles of the original data, will be considered as a participating neuron in the ensemble. If the i-th neuron did not pass any of these filters, it would be discarded.

Matching score (MS)

The overall similarity between pattern vectors in sessions X and Y was measured according to the normalized dot product ${\vec{v}}_{i}^{{{\rm{X}}}}\cdot {\vec{v}}_{j}^{{{\rm{Y}}}}$ for all possible pattern pairs across the two sessions, noting that the dot product is equivalent to the cosine of the angle between the pattern vectors^77,78. To this end, the MS between sessions X and Y was defined as ${{\rm{MS}}}\left({{\rm{X}}},{{\rm{Y}}}\right)\equiv \frac{1}{{N}_{{{\rm{X}}}}}{\sum }_{i\in X}\Theta \left[{\sum }_{j\in Y}\Theta \left({\vec{v}}_{i}^{{{\rm{X}}}}\cdot {\vec{v}}_{j}^{{{\rm{Y}}}}-c\right)-d\right]$, where ${\vec{v}}_{i}^{{{\rm{X}}}}\,$(${\vec{v}}_{j}^{{{\rm{Y}}}}$) is the $i$-th ($j$-th) pattern vector in session X (Y), ${N}_{{{\rm{X}}}}$ is the number of patterns in session X, and $\Theta (\cdot )$ is a step function. In Supplementary Fig. 4a and d, to make the comparison between engram and nonengram cells fair, the number of those major principal components is the same as the number of engram cells in the concerned sample. the MS between sessions X and Y was defined as ${{\rm{MS}}}\left({{\rm{X}}},{{\rm{Y}}}\right)\equiv \frac{1}{{N}_{{{\rm{X}}}}}{\sum }_{i\in X}\Theta \left[{\sum }_{j\in Y}\Theta \left[{T}_{X}\left({\vec{v}}_{i}^{{{\rm{X}}}}\right)\cdot {T}_{Y}\left({\vec{v}}_{j}^{{{\rm{Y}}}}\right)-c\right]-d\right]$, where ${\vec{v}}_{i}^{{{\rm{X}}}}\,$(${\vec{v}}_{j}^{{{\rm{Y}}}}$) is the $i$-th ($j$-th) pattern vector in session X (Y), ${N}_{{{\rm{X}}}}$ is the number of patterns in session X and $\Theta (\cdot )$ is a step function. ${T}_{X}$ (${T}_{Y}$) is a vector-valued mapping projecting vector ${\vec{v}}_{i}^{{{\rm{X}}}}\,$(${\vec{v}}_{j}^{{{\rm{Y}}}}$) onto major eigen vectors of session X (Y). The constant $d$ is an arbitrary positive number smaller than unity. This scoring function yields the portion of patterns in session X that have a normalized dot product larger than $c$ with any of the patterns in session Y. A threshold of $c$ = 0.6 was used throughout the study. Monte Carlo resampling was conducted for the MSs of engram cells. In the resampling, the MSs of datasets with shuffled timestamps and neuronal indices were calculated to assess significance. For each session-pair comparison, the mean of the MS for the shuffled data was compared with that calculated from the original data. To calculate the Mean of the MS for the shuffled data, 40 shuffled samples were used. Since the resampling was not for the purpose of constructing a random-number distribution, the calculation of the mean value converged, and the number of samples was sufficient. Normalized data were calculated by subtracting shuffled data of engram and nonengram cells from their corresponding MS data.

Principal component analysis

To detect coactivity patterns among calcium transients of the total nonengram population (engram-to-be and other nonengram), an unsupervised analysis combining Principal Component Analysis (PCA) and Independent Component Analysis (ICA) was employed, as described previously^79,80. Briefly, neuronal activities were binned in 20 ms time bins and normalized (z scored, in which the activity of every neuron was adjusted to have an average value of zero and a standard deviation of one) to prevent any bias by neurons having a higher firing rate. We derived ensembles of coactive neurons through a two-step process. Initially, we estimated the quantity of meaningful coactivation ensembles present within a certain population of neurons by identifying the number of principal components from the activity matrix. Subsequently, we employed an independent component analysis to extract the coactivity patterns defined by these principal components (Supplementary Fig. 9), as described in previous reports^79,80.

Population vector distance (PVD)

PVD quantifies the difference in calcium signals obtained from a group of neurons during two distinct sessions. Calcium signals from two distinct sessions, X and Y, of the same neuron group were compared using the restricted Mahalanobis distance, which is defined on the basis of the Mahalanobis distance⁸¹. The restricted Mahalanobis distance is defined as ${{\rm{PVD}}}\left({{\rm{X}}},{{\rm{Y}}}\right)\equiv \sqrt{{\max }_{\varphi }{\sum }_{i=1}^{10}\left[{v}_{\varphi \left(i\right)}^{T}\left({\mu }_{{{\rm{X}}}}-{\mu }_{{{\rm{Y}}}}\right)\right]/{\lambda }_{\varphi \left(i\right)}}$, where ${\mu }_{{{\rm{X}}}}$ and ${\mu }_{{{\rm{Y}}}}$ are the means of X and Y, respectively, ${\lambda }_{\varphi \left(i\right)}$ s are eigenvalues of the covariance matrix of the union of X and Y, ${v}_{\varphi (i)}$ is the corresponding eigenvector, and $\varphi$ is a bijective mapping reordering indices of eigenvalues and eigenvectors. Intuitively, this equation calculates the maximum distance within a restricted number of dimensions. This definition enables us to compare the PVD across different groups of neurons, i.e., engram-to-be cells and other nonengram cells, that contain different numbers of neurons.

Simulation model and procedure

In our network model, we set the activities of CA3 neurons ${r}_{i}\,\left(i={{\mathrm{1,2}}},\ldots,{N}_{{{\rm{CA}}}3}\right)$ as inputs, and simulated the responses of excitatory neurons ${x}_{i}\,\left(i={{\mathrm{1,2}}},\ldots,{N}_{{{\rm{CA}}}1}\right)$ and inhibitory neurons ${y}_{i}\,\left(i={{\mathrm{1,2}}},\ldots,{N}_{{{\rm{inh}}}}\right)$ in CA1. Inhibitory neurons provided recurrent inhibitory feedback in CA1. The simulations were performed by solving dynamical equations:

$$\tau {\dot{x}}_{i}\left(t\right)=-{x}_{i}\left(t\right)+{{\rm{\sigma }}}\left({\sum}_{j=1}^{{N}_{{CA}3}}{w}_{{ij}}^{{{\rm{EE}}}}{r}_{j}-{\sum}_{j=1}^{{N}_{{{\rm{inh}}}}}{w}_{{ij}}^{{{\rm{EI}}}}{y}_{j}\left(t\right)+{\epsilon }_{i}\right)\,$$

(3)

$$\tau {\dot{y}}_{i}\left(t\right)=-{y}_{i}\left(t\right)+{{\upsigma }}\left({\sum}_{j=1}^{{N}_{{CA}1}}{w}_{{ij}}^{{{\rm{IE}}}}{x}_{j}\,\right)$$

(4)

where ${{\rm{\sigma }}}\left(x\right)$ is a logistic sigmoid function:

$${{\rm{\sigma }}}\left(x\right)=\frac{1}{1+\exp \left(-\beta \left(x-\theta \right)\right)}\,$$

(5)

and ${\epsilon }_{i}$ is a random external input sampled from a Gaussian distribution with a standard deviation of 0.5. The number of neurons was ${N}_{{{\rm{CA}}}3}={N}_{{{\rm{CA}}}1}=400$ and ${N}_{{{\rm{inh}}}}=100$. The time constant was $\tau$ = 2 ms. The parameters of the sigmoid function were $\beta=5$ and $\theta=1$. For each CA3 activity pattern, we initialized ${x}_{i}\left(t\right)=0$ and ${y}_{i}\left(t\right)=0$ and sampled ${\epsilon }_{i}$, then simulated time evolution of the dynamics for 20 ms, and recorded the activity patterns of CA1 excitatory neurons at the final state as a response. Below, we specify a CA3 activity pattern as a ${N}_{{{\rm{CA}}}3}$-dimensional vector ${{\bf{r}}}$ and a CA1 response pattern as a ${N}_{{{\rm{CA}}}1}$-dimensional vector ${{\bf{x}}}$.

In each CA3 pattern ${{\bf{r}}}$, each neuron took a value of 1 (active) with a 10% probability and was otherwise zero (inactive). In simulations of sleep sessions, the values of active neurons were randomly fluctuated within the range of 0.5–1.5.

Before each simulation, we initially sampled the excitatory synaptic weights ${w}_{{ij}}^{{{\rm{EE}}}}$ from a uniform distribution [0, 0.125]. We set the I-to-E weight ${w}_{{ij}}^{{{\rm{EI}}}}$ to 1.6 with a 5% probability, with it being zero otherwise, and the E-to-I weight ${w}_{{ij}}^{{{\rm{IE}}}}$ to 0.4 with a 10% probability and zero otherwise. We fixed I-to-E and E-to-I weights throughout the simulation. We applied synaptic plasticity to only E-to-E synaptic weights ${w}_{{ij}}^{{{\rm{EE}}}}$.

The simulation consisted of four sessions: presleep, context A, postsleep, and context B. First, we performed a prelearning sleep session in which we recorded CA1 responses ${{{\bf{x}}}}_{{{\rm{pre}}}}^{\left(n\right)}$ to 1000 random CA3 patterns ${{{\bf{r}}}}_{{{\rm{pre}}}}^{\left(n\right)}$ $(n={\mathrm{1,2}},\ldots,1000)$. Next, we simulated a CA1 response ${{{\bf{x}}}}_{{{\rm{A}}}}$ in the context A by setting a CA3 pattern ${{{\bf{r}}}}_{{{\rm{A}}}}$ (${{{\bf{r}}}}_{{{\rm{A}}}}$ was randomly sampled and fixed throughout the simulation). After the first simulation, active CA1 neurons (${x}_{i} \, > \, 0.5$ in ${{{\bf{x}}}}_{{{\rm{A}}}}$) were labeled as engram cells. We defined an engram label ${e}_{i}^{{{\rm{A}}}}$ that takes 1 for engram cells and 0 for nonengram cells. Using these labels, we potentiated ${w}_{{ij}}^{{{\rm{EE}}}}$ as

$${w}_{{ij}}^{{{\rm{EE}}}}\leftarrow {w}_{{ij}}^{{{\rm{EE}}}}+\eta {e}_{i}^{{{\rm{A}}}}{r}_{j}^{{{\rm{A}}}}$$

(6)

Here, ${r}_{j}^{{{\rm{A}}}}$ represents CA3 activities in the context A (${{{\bf{r}}}}_{{{\rm{A}}}}$) and $\eta=0.05$. We performed a second simulation using updated weights and recorded a CA1 response ${{{\bf{x}}}}_{{{\rm{A}}}}$ in the second simulation for data analyses (${{{\bf{x}}}}_{{{\rm{A}}}}$ in the first simulation was discarded).

In the postlearning sleep session, we first applied synaptic depression caused by SWR and synaptic scaling. The synaptic depression caused by SWR is defined by

$${w}_{{ij}}^{{{\rm{EE}}}}\leftarrow {w}_{{ij}}^{{{\rm{EE}}}}-\eta \left(1-{e}_{i}^{{{\rm{A}}}}\right){r}_{j}^{{{\rm{A}}}}$$

(7)

The weight updates resulting from the synaptic scaling were

$${w}_{{ij}}^{{{\rm{EE}}}}\leftarrow {w}_{{ij}}^{{{\rm{EE}}}}-\eta {e}_{i}^{{{\rm{A}}}}\left(1-{r}_{j}^{{{\rm{A}}}}\right)$$

(8)

$${w}_{{ij}}^{{{\rm{EE}}}}\leftarrow {w}_{{ij}}^{{{\rm{EE}}}}+\eta \left(1-{e}_{i}^{{{\rm{A}}}}\right)\left(1-{r}_{j}^{{{\rm{A}}}}\right)$$

(9)

After updating the weights, we obtained CA1 responses ${{{\bf{x}}}}_{{{\rm{post}}}}^{\left(n\right)}$ to 1000 CA3 activity patterns ${{{\bf{r}}}}_{{{\rm{post}}}}^{\left(n\right)}$. Eighty percent of ${{{\bf{r}}}}_{{{\rm{post}}}}^{\left(n\right)}$ was the same as ${{{\bf{r}}}}_{{{\rm{A}}}}$ (replay), and the remaining 20% were independent random patterns.

Finally, we simulated a CA1 response ${{{\bf{x}}}}_{{{\rm{B}}}}$ in the context B by setting a CA3 pattern ${{{\bf{r}}}}_{{{\rm{B}}}}$. We used the same procedure as used for context A. We determined engram cells for the context B first, potentiated synapses, and recorded a CA1 response ${{{\bf{x}}}}_{{{\rm{B}}}}$ with updated weights.

Furthermore, we also simulated an additional sleep session after the context B to check replay of the context B. We simulated synaptic plasticity and activity patterns in the same way with the postlearning sleep, replacing ${e}_{i}^{{{\rm{A}}}}$ and ${{{\bf{r}}}}_{{{\rm{A}}}}$ with ${e}_{i}^{{{\rm{B}}}}$ (the engram label in the session B) and ${{{\bf{r}}}}_{{{\rm{B}}}}$.

We repeated this simulation procedure five times with different random seeds and analyzed data from each trial independently. In the control simulations presented in Fig. 6, we did not apply synaptic changes in postsleep sessions (synaptic depression by SWR and synaptic scaling) while keeping synaptic potentiation in context A and B.

Analysis of simulated data

We separated engram cells and nonengram cells by engram labels determined from the first simulation in context A. Furthermore, we separated active and inactive cells in context B by thresholding the activity (a neuron was active if ${x}_{i} \, > \, 0.5$). Accordingly, we defined four subtypes of CA1 neurons: common engram cells (engram in context A and active in context B), specific engram cells (engram in context A and inactive in B), engram-to-be cells (nonengram in context A and active in B), and other nonengram cells (nonengram in context A and inactive in B). The activity patterns below (${{{\bf{x}}}}_{{{\rm{pre}}}}^{\left(n\right)}$, ${{{\bf{x}}}}_{{{\rm{A}}}}$, ${{{\bf{x}}}}_{{{\rm{post}}}}^{\left(n\right)}$, and ${{{\bf{x}}}}_{{{\rm{B}}}}$) indicate divided parts of patterns based on cell types.

The matching ratio between presleep and context A was calculated as

$${MR}=\frac{1}{1000}{\sum}_{n=1}^{1000}\Theta \left({{\rm{g}}}\left({{{\bf{x}}}}_{{{\rm{pre}}}}^{\left(n\right)},\,{{{\bf{x}}}}_{{{\rm{A}}}}\right)-0.6\right)$$

(10)

where $\Theta \left(x\right)$ is a Heaviside step function, and ${{\rm{g}}}\left({{\bf{x}}},{{\bf{y}}}\right)$ is the cosine similarity between vectors ${{\bf{x}}}$ and ${{\bf{y}}}$. Matching ratios for other combinations (such as postlearning sleep and context B) were also calculated using the same procedure.

To calculate pairwise correlations and coincidence ratios, we artificially generated the augmented CA1 activity patterns ${{{\bf{x}}}}_{{{\rm{pre}}}-{{\rm{mix}}}}^{\left(n\right)}$ and ${{{\bf{x}}}}_{{{\rm{post}}}-{{\rm{mix}}}}^{\left(n\right)}\,(n={\mathrm{1,2}},\ldots,\,5000)$ by mixing 1000 simulated activity patterns and 4000 “silent” activity patterns in which the activity of each CA1 neuron was sampled from the range [0, 0.01]. These silent activity patterns corresponded to activity-silent periods between burst activities in CA1. The correlation within each cell type was calculated as follows. The activities of each CA1 neuron in a sleep session were expressed as ${x}_{i}^{\left(n\right)}\,\left(i={{\mathrm{1,2}}},\ldots,{N}_{{{\rm{CA}}}1},{{\rm{n}}}={\mathrm{1,2}},\ldots,5000\right)$. The correlation coefficient between neuron $i$ and $j$ was calculated using Pearson correlation between two sets of observations ${\left\{{x}_{i}^{\left(n\right)}\right\}}_{n=1}^{5000}$ and ${\left\{{x}_{j}^{\left(n\right)}\right\}}_{n=1}^{5000}$. We averaged the correlation over all cell pairs within each cell type (engram, nonengram, or one of the four subtypes). The coincidence ratio was calculated using the mean population activity in a cell type C ${\bar{x}}_{C}^{\left(n\right)}=\frac{1}{{N}_{C}}{\sum }_{i\in C}{x}_{i}^{\left(n\right)}$ (C is common engram, specific engram, engram-to-be, or other nonengram), where ${N}_{C}$ is the number of neurons in cell-type C. The coincidence ratio between two cell types C1 and C2 was calculated as

$${CR}=\frac{{T}^{-1}{\sum }_{n=1}^{T}{\bar{x}}_{C1}^{\left(n\right)}{\bar{x}}_{C2}^{\left(n\right)}}{\left({T}^{-1}{\sum }_{n=1}^{T}{\bar{x}}_{C1}^{\left(n\right)}\right)\left({T}^{-1}{\sum }_{n=1}^{T}{\bar{x}}_{C2}^{\left(n\right)}\right)}\,$$

(11)

where $T=5000$. Values of CR were normalized by CR between specific engram cells and non-engram cells, following the analyses of experimental data.

Statistical analysis

Statistical analyses were performed in GraphPad Prism 6 (GraphPad Software). Comparisons of data between three groups were performed using one-way ANOVA. Comparisons of data between two groups at multiple time points were performed using two-way repeated-measures ANOVA followed by Bonferroni’s multiple comparisons test, unless otherwise specified. Comparisons of data between two paired groups were performed using paired t-tests (no assumption was made that data were normally distributed). One-tailed comparisons were used whenever the difference between the two groups was expected to be in a single direction. Quantitative data are expressed as the mean ± standard error of the mean (s.e.m.).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

All data and resources that supported the findings of this study are available upon request. The datasets supporting this study will be deposited to a public repository when the ongoing studies using the same dataset are published. Source data are provided with this paper.

Code availability

The code that supports the findings of this study are all available at https://github.com/fccaa/NMF_custom, https://github.com/oist-ncbc/engramtobe_simulation and https://github.com/IdlingBrainUT/Ghandour2025_NatureCommunications.git. Additionally all codes are available at Zenodo https://doi.org/10.5281/zenodo.14963950⁸² and https://doi.org/10.5281/zenodo.14978317⁸³.

References

Silva, A. J., Zhou, Y., Rogerson, T., Shobe, J. & Balaji, J. Molecular and cellular approaches to memory allocation in neural circuits. Science 326, 391–395 (2009).
Article PubMed PubMed Central CAS Google Scholar
Josselyn, S. A. & Tonegawa, S. Memory engrams: Recalling the past and imagining the future. Science 367, eaaw4325 (2020).
Article PubMed PubMed Central CAS Google Scholar
Ohkawa, N. et al. Artificial association of pre-stored information to generate a qualitatively new memory. Cell Rep. 11, 261–269 (2015).
Article PubMed CAS Google Scholar
Reijmers, L. G., Perkins, B. L., Matsuo, N. & Mayford, M. Localization of a stable neural correlate of associative memory. Science 317, 1230–1233 (2007).
Article ADS PubMed CAS Google Scholar
Liu, X. et al. Optogenetic stimulation of a hippocampal engram activates fear memory recall. Nature 484, 381 https://www.nature.com/articles/nature11028#supplementary-information (2012).
Article ADS PubMed PubMed Central CAS Google Scholar
Abdou, K. et al. Synapse-specific representation of the identity of overlapping memory engrams. Sci. (N. Y., N. Y.) 360, 1227–1231 (2018).
Article ADS CAS Google Scholar
Nomoto, M. et al. Cellular tagging as a neural network mechanism for behavioural tagging. Nat. Commun. 7, 12319 (2016).
Article ADS PubMed PubMed Central CAS Google Scholar
Goode, T. D., Tanaka, K. Z., Sahay, A. & McHugh, T. J. An Integrated Index: Engrams, place cells, and hippocampal memory. Neuron 107, 805–820 (2020).
Article PubMed PubMed Central CAS Google Scholar
Ghandour, K. et al. Orchestrated ensemble activities constitute a hippocampal memory engram. Nat. Commun. 10, 2637 (2019).
Article ADS PubMed PubMed Central Google Scholar
Tanaka, K. Z. et al. The hippocampal engram maps experience but not place. Sci. (N. Y., N. Y.) 361, 392–397 (2018).
Article ADS CAS Google Scholar
Cai, D. J. et al. A shared neural ensemble links distinct contextual memories encoded close in time. Nature 534, 115 (2016).
Article ADS PubMed PubMed Central CAS Google Scholar
Rashid, A. J. et al. Competition between engrams influences fear memory formation and recall. Sci. (N. Y., N. Y.) 353, 383–387 (2016).
Article ADS CAS Google Scholar
Sharpe, M. J., Batchelor, H. M., Mueller, L. E., Gardner, M. P. H. & Schoenbaum, G. Past experience shapes the neural circuits recruited for future learning. Nat. Neurosci. 24, 391–400 (2021).
Article PubMed PubMed Central CAS Google Scholar
Yiu, A. P. et al. Neurons are recruited to a memory trace based on relative neuronal excitability immediately before training. Neuron 83, 722–735 (2014).
Article PubMed CAS Google Scholar
Han, J. H. et al. Neuronal competition and selection during memory formation. Sci. (N. Y., N. Y.) 316, 457–460 (2007).
Article ADS CAS Google Scholar
Park, S. et al. Neuronal allocation to a hippocampal engram. Neuropsychopharmacology 41, 2987–2993 (2016).
Article PubMed PubMed Central CAS Google Scholar
Gouty-Colomer, L. A. et al. Arc expression identifies the lateral amygdala fear memory trace. Mol. Psychiatry 21, 364–375 (2016).
Article PubMed CAS Google Scholar
Mocle, A. J. et al. Excitability mediates allocation of pre-configured ensembles to a hippocampal engram supporting contextual conditioned threat in mice. Neuron 112, 1487–1497.e1486 (2024).
Article PubMed CAS Google Scholar
Dragoi, G. & Tonegawa, S. Preplay of future place cell sequences by hippocampal cellular assemblies. Nature 469, 397–401 (2011).
Article ADS PubMed CAS Google Scholar
McKenzie, S. et al. Preexisting hippocampal network dynamics constrain optogenetically induced place fields. Neuron 109, 1040–1054.e1047 (2021).
Article PubMed PubMed Central CAS Google Scholar
Valero, M., Zutshi, I., Yoon, E. & Buzsáki, G. Probing subthreshold dynamics of hippocampal neurons by pulsed optogenetics. Sci. (N.Y., N.Y.) 375, 570–574 (2022).
Article ADS CAS Google Scholar
Farooq, U. & Dragoi, G. Emergence of preconfigured and plastic time-compressed sequences in early postnatal development. Sci. (N.Y., N.Y.) 363, 168–173 (2019).
Article ADS CAS Google Scholar
Aly, M. H., Abdou, K., Okubo-Suzuki, R., Nomoto, M. & Inokuchi, K. Selective engram coreactivation in idling brain inspires implicit learning. Proc. Natl Acad. Sci. USA 119, e2201578119 (2022).
Article PubMed PubMed Central CAS Google Scholar
Abdou, K. et al. Prefrontal coding of learned and inferred knowledge during REM and NREM sleep. Nat. Commun. 15, 4566 (2024).
Article ADS PubMed PubMed Central CAS Google Scholar
Huff, M. L., Miller, R. L., Deisseroth, K., Moorman, D. E. & LaLumiere, R. T. Posttraining optogenetic manipulations of basolateral amygdala activity modulate consolidation of inhibitory avoidance memory in rats. Proc. Natl Acad. Sci. USA 110, 3597–3602 (2013).
Article ADS PubMed PubMed Central CAS Google Scholar
Findlay, G., Tononi, G. & Cirelli, C. The evolving view of replay and its functions in wake and sleep. Sleep. Adv.: a J. Sleep. Res. Soc. 1, zpab002 (2020).
Article Google Scholar
Boyce, R., Glasgow, S. D., Williams, S. & Adamantidis, A. Causal evidence for the role of REM sleep theta rhythm in contextual memory consolidation. Science 352, 812 (2016).
Article ADS PubMed CAS Google Scholar
Girardeau, G., Benchenane, K., Wiener, S. I., Buzsáki, G. & Zugaro, M. B. Selective suppression of hippocampal ripples impairs spatial memory. Nat. Neurosci. 12, 1222 https://www.nature.com/articles/nn.2384#supplementary-information (2009).
Article PubMed CAS Google Scholar
Norimoto, H. et al. Hippocampal ripples down-regulate synapses. Science 359, 1524–1527 (2018).
Article ADS PubMed CAS Google Scholar
Wagner, U., Gais, S., Haider, H., Verleger, R. & Born, J. Sleep inspires insight. Nature 427, 352–355 (2004).
Article ADS PubMed CAS Google Scholar
Lewis, P. A., Knoblich, G. & Poe, G. How memory replay in sleep boosts creative problem-solving. Trends Cogn. Sci. 22, 491–503 (2018).
Article PubMed PubMed Central Google Scholar
Lacaux, C. et al. Sleep onset is a creative sweet spot. Sci. Adv. 7, eabj5866 (2021).
Article ADS PubMed PubMed Central Google Scholar
Pfeiffer, B. E. & Foster, D. J. Hippocampal place-cell sequences depict future paths to remembered goals. Nature 497, 74–79 (2013).
Article ADS PubMed PubMed Central CAS Google Scholar
Wu, C.-T., Haggerty, D., Kemere, C. & Ji, D. Hippocampal awake replay in fear memory retrieval. Nat. Neurosci. 20, 571–580 (2017).
Article PubMed PubMed Central CAS Google Scholar
Addis, D. R., Wong, A. T. & Schacter, D. L. Remembering the past and imagining the future: Common and distinct neural substrates during event construction and elaboration. Neuropsychologia 45, 1363–1377 (2007).
Article PubMed Google Scholar
Szpunar, K. K., Watson, J. M. & McDermott, K. B. Neural substrates of envisioning the future. Proc. Natl Acad. Sci. USA 104, 642 (2007).
Article ADS PubMed PubMed Central CAS Google Scholar
Schacter, D. L., Addis, D. R. & Buckner, R. L. Remembering the past to imagine the future: the prospective brain. Nat. Rev. Neurosci. 8, 657–661 (2007).
Article PubMed CAS Google Scholar
Hassabis, D., Kumaran, D., Vann, S. D. & Maguire, E. A. Patients with hippocampal amnesia cannot imagine new experiences. Proc. Natl Acad. Sci. 104, 1726 (2007).
Article ADS PubMed PubMed Central CAS Google Scholar
Dragoi, G. & Tonegawa, S. Selection of preconfigured cell assemblies for representation of novel spatial experiences. Philos. Trans. R. Soc. Lond. Ser. B, Biol. Sci. 369, 20120522 (2014).
Article Google Scholar
Asai, H. et al. Pcdhβ deficiency affects hippocampal CA1 ensemble activity and contextual fear discrimination. Mol. Brain 13, 7 (2020).
Article PubMed PubMed Central CAS Google Scholar
Ghosh, K. K. et al. Miniaturized integration of a fluorescence microscope. Nat. Methods 8, 871–878 (2011).
Article PubMed PubMed Central CAS Google Scholar
Tsutsui, H., Karasawa, S., Shimizu, H., Nukina, N. & Miyawaki, A. Semi-rational engineering of a coral fluorescent protein into an efficient highlighter. EMBO Rep. 6, 233–238 (2005).
Article PubMed PubMed Central CAS Google Scholar
Takekawa, T. et al. Automatic sorting system for large calcium imaging data. bioRxiv, https://doi.org/10.1101/215145 (2017).
Burnham, K. P. & Anderson, D. R. Model selection and multimodel inference: a practical information-theoretic approach. (Springer Science & Business Media, 2003).
Lee, D. D. & Seung, H. S. in Advances in neural information processing systems. 556-562.
Tomé, D. F. et al. Dynamic and selective engrams emerge with memory consolidation. Nat. Neurosci. 27, 561–572 (2024).
Article PubMed PubMed Central Google Scholar
DeNardo, L. A. et al. Temporal evolution of cortical ensembles promoting remote memory retrieval. Nat. Neurosci. 22, 460–469 (2019).
Article PubMed PubMed Central CAS Google Scholar
Sehgal, M. et al. Memory allocation mechanisms underlie memory linking across time. Neurobiol. Learn. Mem. 153, 21–25 (2018).
Article PubMed PubMed Central CAS Google Scholar
Choi, S. H. et al. Combined adult neurogenesis and BDNF mimic exercise effects on cognition in an Alzheimer’s mouse model. Science (New York, N.Y.) 361, https://doi.org/10.1126/science.aan8821 (2018).
Shepherd, J. D. et al. Arc/Arg3.1 Mediates homeostatic synaptic scaling of AMPA receptors. Neuron 52, 475–484 (2006).
Article PubMed PubMed Central CAS Google Scholar
Béïque, J.-C., Na, Y., Kuhl, D., Worley, P. F. & Huganir, R. L. Arc-dependent synapse-specific homeostatic plasticity. Proc. Natl Acad. Sci. 108, 816–821 (2011).
Article ADS PubMed Google Scholar
Okuno, H. et al. Inverse synaptic tagging of inactive synapses via dynamic interaction of Arc/Arg3.1 with CaMKIIβ. Cell 149, 886–898 (2012).
Article PubMed PubMed Central CAS Google Scholar
Grosmark, A. D. & Buzsáki, G. Diversity in neural firing dynamics supports both rigid and learned hippocampal sequences. Science 351, 1440–1443 (2016).
Article ADS PubMed PubMed Central CAS Google Scholar
Malvache, A., Reichinnek, S., Villette, V., Haimerl, C. & Cossart, R. Awake hippocampal reactivations project onto orthogonal neuronal assemblies. Sci. (N. Y., N. Y.) 353, 1280–1283 (2016).
Article ADS CAS Google Scholar
Miyawaki, H. & Mizuseki, K. De novo inter-regional coactivations of preconfigured local ensembles support memory. Nat. Commun. 13, 1272 (2022).
Article ADS PubMed PubMed Central CAS Google Scholar
Vaz, A. P., Wittig, J. H., Inati, S. K. & Zaghloul, K. A. Backbone spiking sequence as a basis for preplay, replay, and default states in human cortex. Nat. Commun. 14, https://doi.org/10.1038/s41467-023-40440-5 (2023).
Holtmaat, A. & Caroni, P. Functional and structural underpinnings of neuronal assembly formation in learning. Nat. Neurosci. 19, 1553–1562 (2016).
Article PubMed CAS Google Scholar
Huszár, R., Zhang, Y., Blockus, H. & Buzsáki, G. Preconfigured dynamics in the hippocampus are guided by embryonic birthdate and rate of neurogenesis. Nat. Neurosci. 25, 1201–1212 (2022).
Article PubMed PubMed Central Google Scholar
Buzsáki, G. The Brain from Inside Out. (Oxford University Press, 2019).
van de Ven, G. M., Trouche, S., McNamara, C. G., Allen, K. & Dupret, D. Hippocampal offline reactivation consolidates recently formed cell assembly patterns during sharp wave-ripples. Neuron 92, 968–974 (2016).
Article PubMed PubMed Central Google Scholar
Sun, X. et al. Functionally distinct neuronal ensembles within the memory engram. Cell 181, 410–423.e417 (2020).
Article PubMed PubMed Central CAS Google Scholar
Nambu, M. F., Lin, Y.-J., Reuschenbach, J. & Tanaka, K. Z. What does engram encode?: Heterogeneous memory engrams for different aspects of experience. Curr. Opin. Neurobiol. 75, 102568 (2022).
Article PubMed CAS Google Scholar
Cai, D. J., Mednick, S. A., Harrison, E. M., Kanady, J. C. & Mednick, S. C. REM, not incubation, improves creativity by priming associative networks. Proc. Natl Acad. Sci. USA 106, 10130–10134 (2009).
Article ADS PubMed PubMed Central CAS Google Scholar
Fayed, M. R., Ghandour, K. & Inokuchi, K. Sleep and quiet wakefulness signify an idling brain hub for creative insights. Philos. Trans. R. Soc. Lond. B Biol. Sci. 379, 20230226 (2024).
Article PubMed Google Scholar
Udakis, M., Pedrosa, V., Chamberlain, S. E. L., Clopath, C. & Mellor, J. R. Interneuron-specific plasticity at parvalbumin and somatostatin inhibitory synapses onto CA1 pyramidal neurons shapes hippocampal output. Nat. Commun. 11, 4395 (2020).
Article ADS PubMed PubMed Central CAS Google Scholar
Geiller, T. et al. Local circuit amplification of spatial selectivity in the hippocampus. Nature 601, 105–109 (2022).
Article ADS PubMed CAS Google Scholar
Rolotti, S. V. et al. Local feedback inhibition tightly controls rapid formation of hippocampal place fields. Neuron 110, 783–794.e786 (2022).
Article PubMed PubMed Central CAS Google Scholar
Delamare, G., Zaki, Y., Cai, D. J. & Clopath, C. Drift of neural ensembles driven by slow fluctuations of intrinsic excitability. eLife 12, RP88053 (2024).
Article PubMed PubMed Central Google Scholar
Delamare, G., Tomé, D. F. & Clopath, C. Intrinsic neural excitability biases allocation and overlap of memory engrams. J. Neurosci. 44, e0846232024 (2024).
Article PubMed PubMed Central CAS Google Scholar
Sato, M. et al. Distinct mechanisms of over-representation of landmarks and rewards in the hippocampus. Cell Rep. 32, 107864 (2020).
Article PubMed PubMed Central CAS Google Scholar
Matsuo, N., Reijmers, L. & Mayford, M. Spine-type-specific recruitment of newly synthesized ampa receptors with learning. Science 319, 1104 (2008).
Article ADS PubMed PubMed Central CAS Google Scholar
Sato, M. et al. Dynamic embedding of salience coding in hippocampal spatial maps. bioRxiv, (2018).
Barretto, R. P. et al. Time-lapse imaging of disease progression in deep brain areas using fluorescence microendoscopy. Nat. Med 17, 223–228 (2011).
Article PubMed PubMed Central CAS Google Scholar
Ziv, Y. et al. Long-term dynamics of CA1 hippocampal place codes. Nat. Neurosci. 16, 264–266 (2013).
Article PubMed PubMed Central CAS Google Scholar
Jimenez, J. C. et al. Anxiety cells in a hippocampal-hypothalamic circuit. Neuron 97, 670–683.e676 (2018).
Article PubMed PubMed Central CAS Google Scholar
Peyrache, A., Benchenane, K., Khamassi, M., Wiener, S. I. & Battaglia, F. P. Principal component analysis of ensemble recordings reveals cell assemblies at high temporal resolution. J. Comput Neurosci. 29, 309–325 (2010).
Article PubMed Google Scholar
Sasaki, T., Kimura, R., Tsukamoto, M., Matsuki, N. & Ikegaya, Y. Integrative spike dynamics of rat CA1 neurons: a multineuronal imaging study. J. Physiol. 574, 195–208 (2006).
Article PubMed PubMed Central CAS Google Scholar
Carrillo-Reid, L., Miller, J. E., Hamm, J. P., Jackson, J. & Yuste, R. Endogenous sequential cortical activity evoked by visual stimuli. J. Neurosci. 35, 8813–8828 (2015).
Article PubMed PubMed Central CAS Google Scholar
Middleton, S. J. et al. Altered hippocampal replay is associated with memory impairment in mice heterozygous for the Scn2a gene. Nat. Neurosci. 21, 996–1003 (2018).
Article PubMed PubMed Central CAS Google Scholar
Trouche, S. et al. Recoding a cocaine-place memory engram to a neutral engram in the hippocampus. Nat. Neurosci. 19, 564–567 (2016).
Article PubMed PubMed Central CAS Google Scholar
Mahalanobis, P. On tests and measures of group divergence I. Theoretical formulae. J. Asiatic Soc. Bengal 26, 541–588 (1930).
Google Scholar
Ghandour, K. et al. Parallel processing of past and future memories through reactivation and synaptic mechanisms during sleep, Ghandour2025_NatureCommunications, Zenodo. https://doi.org/10.5281/zenodo.14963950 (2025).
Ghandour, K. et al. Parallel processing of past and future memories through reactivation and synaptic mechanisms during sleep. oist-ncbc/engramtobe_simulation: v1.0.0. Zenodo. https://doi.org/10.5281/zenodo.14978317 (2025).

Download references

Acknowledgements

The authors thank S. Tsujimura and M. Matsuo for genotyping the transgenic mice, Y. Saitoh for helping in the mice surgeries, M. H. Aly for helping in Ca²⁺ imaging data analysis, T. Takekawa for helping with the automatic calcium sorting system (HOTARU), K. Abdou and A. Choucry for their valuable discussion and advice, and all members of the Inokuchi laboratory at the University of Toyama for advice and technical support. Japan Society for the Promotion of Science KAKENHI (grant numbers JP23H05476 and JP18H05213 [K.I.], JP21K15611 [T.H], JP23H02789 [N.O.], JP19K16885 [C.F.], JP20H03554 and JP23H02785 [M.N], JP24H02315 [M.S], JP18H05213, JP19H04994, JP20H03554, JP23H05476 and JP23H02785 [T.F]), JST CREST program JPMJCR13W1, JPMJCR23N2 (K.I.), JST PRESTO program JPMJPR1684 (N.O.), Grant-in-Aid for Scientific Research on Innovative Areas “Memory dynamism” (JP25115002 [K.I.]), the AMED PRIME (JP23gm6510021h0001 [N.O] and JP23gm6510028h0001 [M.N]), the Naito Foundation (N.O. and M.N.), the Takeda Science Foundation (N.O., M.N., and K.I.), City University of Hong Kong project No. 9610591 (C.F.), the Uehara Memorial Foundation (M.N), the Inamori Foundation, the FIRSTBANK OF TOYAMA SCHOLARSHIP FOUNDATION RESEARCH GRANT (M.N), the HOKURIKU BANK Grant-in-Aid for Young Scientists (M.N), and the Tamura Science and Technology Foundation support (M.N).

Author information

Hirotaka Asai
Present address: Graduate School of Medicine, The University of Tokyo, Tokyo, Japan
These authors contributed equally: Khaled Ghandour, Tatsuya Haga, Noriaki Ohkawa.

Authors and Affiliations

Graduate School of Medicine and Pharmaceutical Sciences, University of Toyama, Toyama, Japan
Khaled Ghandour, Masanori Nomoto, Mostafa R. Fayed, Hirotaka Asai & Kaoru Inokuchi
Research Center for Idling Brain Science, University of Toyama, Toyama, Japan
Khaled Ghandour, Masanori Nomoto, Mostafa R. Fayed, Hirotaka Asai & Kaoru Inokuchi
Center initiative for training international researchers (CITIR), University of Toyama, Toyama, Japan
Khaled Ghandour
Department of Biochemistry, Faculty of Pharmacy, Cairo University, Cairo, Egypt
Khaled Ghandour
Neural Coding and Brain Computing unit, OIST, Okinawa, Japan
Tatsuya Haga, Chi Chung Alan Fung & Tomoki Fukai
Center for Information and Neural Networks (CiNet), National Institute of Information and Communications Technology, Osaka, Japan
Tatsuya Haga
Research Center for Advanced Medical Science, Dokkyo Medical University, Tochigi, Japan
Noriaki Ohkawa
Department of Neuroscience, City University of Hong Kong, Tat Chee Avenue, Kowloon, Hong Kong, Hong Kong
Chi Chung Alan Fung
Department of Pharmacology and Toxicology, Kafrelsheikh University, Kafr El Sheikh, Egypt
Mostafa R. Fayed
Department of Neuropharmacology, Hokkaido University Graduate School of Medicine, Sapporo, Japan
Masaaki Sato

Authors

Khaled Ghandour
View author publications
Search author on:PubMed Google Scholar
Tatsuya Haga
View author publications
Search author on:PubMed Google Scholar
Noriaki Ohkawa
View author publications
Search author on:PubMed Google Scholar
Chi Chung Alan Fung
View author publications
Search author on:PubMed Google Scholar
Masanori Nomoto
View author publications
Search author on:PubMed Google Scholar
Mostafa R. Fayed
View author publications
Search author on:PubMed Google Scholar
Hirotaka Asai
View author publications
Search author on:PubMed Google Scholar
Masaaki Sato
View author publications
Search author on:PubMed Google Scholar
Tomoki Fukai
View author publications
Search author on:PubMed Google Scholar
Kaoru Inokuchi
View author publications
Search author on:PubMed Google Scholar

Contributions

K.G., N.O., T.F., and K.I. designed the study. N.O. prepared the lentiviruses. K.G. performed the behavioral experiments. K.G. and H. A analyzed the Ca²⁺ imaging data. K.G. and M.R.F. performed animal surgery. M.S. established the Thy1-G-CaMP7 transgenic mice. C.C.A.F. performed the mathematical analyses. T.H. constructed the neural model and performed its manipulation. M.N. wrote the code to calculate coactivities and the PCA-ICA analysis. K.G., N.O., T.H., T.F., and K.I. wrote the manuscript. K.I. supervised the entire project.

Corresponding author

Correspondence to Kaoru Inokuchi.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks Ying Zhang, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Description of Additional Supplementary Information

Supplementary Data 1

Reporting Summary

Transparent Peer Review file

Source data

Source Data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Ghandour, K., Haga, T., Ohkawa, N. et al. Parallel processing of past and future memories through reactivation and synaptic plasticity mechanisms during sleep. Nat Commun 16, 3618 (2025). https://doi.org/10.1038/s41467-025-58860-w

Download citation

Received: 17 June 2024
Accepted: 03 April 2025
Published: 28 April 2025
DOI: https://doi.org/10.1038/s41467-025-58860-w