Abstract
Conducting disentanglement learning on single-cell omics data offers a promising alternative to traditional black-box representation learning by separating the semantic concepts embedded in a biological process. We present CausCell, which incorporates the factual information about causal relationships among disentangled concepts within a diffusion model to generate more reliable disentangled cellular representations, with the aim of increasing the explainability, generalizability and controllability of single-cell data, including spatial-temporal omics data, relative to those of the existing black-box representation learning models. Two quantitative evaluation scenarios, i.e., disentanglement and reconstruction, are presented to conduct the first comprehensive single-cell disentanglement learning benchmark, which demonstrates that CausCell outperforms the state-of-the-art methods in both scenarios. Additionally, CausCell can implement controllable generation by intervening with the concepts of single-cell data when given a causal structure. It also has the potential to uncover biological insights by generating counterfactuals from small and noisy single-cell datasets.
Similar content being viewed by others
Introduction
Single-cell technologies have revolutionised the field of biology by enabling analyses to be conducted at the individual cell resolution1. This granular perspective has revealed the vast heterogeneity within cell populations, leading to new insights into cellular functions, development processes, and diseases2. Single-cell omics data, such as gene expression data obtained by technologies like scRNA-seq, is commonly used to represent the state of individual cells. In addition, each cell also contains information about its properties, such as cell type, batch effects, and other biological factors. In this study, we refer to these properties as concepts. Although single-cell data can measure gene expression levels, important concept information often remains hidden within the data. Therefore, the complexity of single-cell omics data, which is characterised by high dimensionality and the presence of entangled concepts (interdependent biological factors embedded in the data), poses great challenges for data interpretation tasks. The process of disentangling these data, i.e., separating complex, intertwined signals into distinct, interpretable components, has therefore emerged as a critical task3. It also presented to be an alternative path to build the virtual cell4, which is advocating for the use of artificial intelligence (AI) technology to build computational cell models that can simulate, predict and steer cell behaviour, ultimately providing deeper insights into cellular processes.
Disentangled representation learning seeks to capture and separate the underlying concepts embedded in intertwined data, such as images5. Unlike traditional end-to-end black-box representation learning methods, which often directly learn to predict human-annotated labels or reconstruct observable data, disentangled representation learning mimics the human understanding process by leveraging hidden semantic concepts to guide predictions or data generation6. However, this is very challenging for single-cell data, as sequencing technology often introduces noise, such as dropout effects, and the underlying biological concepts cannot be directly observed, unlike in image data. In addition, these latent concepts – such as parasite infection and cell status - in single-cell data are often causally connected, making it hard to clearly separate them with existing disentanglement methods. It requires more advanced techniques to capture latent concepts with causal structure and subsequently establish accurate mappings between the data and concepts in single-cell data.
Several studies have attempted to apply disentangled representation learning to obtain interpretable and manipulable representations of single-cell data. These methods can be categorised into two main groups. (1) Statistical methods: Methods such as factor analysis or nonnegative matrix factorisation are used to identify various biological programmes on the basis of statistical patterns7,8. However, these methods operate purely at a correlational level and do not account for causal relationships between biological concepts. In addition, they cannot support controlled manipulation of these concepts or perform counterfactual generation. (2) Learning-based methods: These approaches are generative and often utilise variational autoencoder (VAE)-based methods to learn hidden concepts by reconstructing single-cell data3,9,10,11. For example, CPA decouples perturbation responses11, scDisInFact removes batch effects9, and Biolord disentangles the concepts contained in single-cell data3. However, these methods operate under the assumption of independence between concepts and cannot guarantee the causality of concepts. In addition, most methods rely on latent optimisation12, which can result in a loss of fine-grained concept representations at the single-cell resolution level. Notably, prior studies have failed to design and implement comprehensive quantitative benchmarking to rigorously evaluate these disentanglement methods. Collectively, a comprehensive benchmarking of existing disentanglement methods, along with the development of a causal disentanglement technique for single-cell omics data, is lacking and urgently needed.
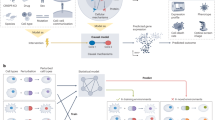
Herein, we introduce CausCell, the first deep generative framework for conducting causal disentanglement and counterfactual generation on single-cell omics data (Fig. 1a). By leveraging factual information about causal structures, CausCell generates more reliable disentangled cellular representations. Specifically, CausCell combines a structural causal model13,14 (SCM) with a diffusion model, offering unprecedented advantages in three aspects for obtaining disentangled single-cell data representations, including for spatial-temporal omics data: (1) Explainability: CausCell leverages an SCM to recover latent concepts with semantic meanings and their causal relationships via a causal directed acyclic graph (cDAG), substantially enhancing the interpretability of the model. (2) Generalisability: Unlike previously developed VAE-based methods, CausCell uses a diffusion model as its backbone, which provides strong generative and generalisation capabilities, ensuring a high-quality sample generation process15. (3) Controllability: CausCell enables controllable generation by manipulating disentangled representations in the latent space while preserving their consistency with the underlying causal structure. In addition, to disentangle single-cell data into various concepts, we assume that each cell is generated by two types of concepts, i.e., observed and unexplained concepts. For example, observed concepts may involve the cancer type related to single-cell tumour omics data or spatial-domain loci derived from spatial single-cell data, while unexplained concepts are the potential unknown concepts contained in the given data, such as noise residual and unobserved biological variation, enabling control over individual information for each cell during generation. Therefore, such a framework enables us to effectively distinguish and explore the concepts hidden in the latent space. To train our model, we propose a new loss function that incorporates a new evidence lower bound (ELBO) loss and an independence constraint for the unexplained concepts. As a result, two quantitative evaluation scenarios, i.e., disentanglement and reconstruction, are presented to conduct the first comprehensive single-cell disentanglement learning benchmark, which demonstrates that CausCell outperforms the state-of-the-art tools in both scenarios. Furthermore, we validate the effectiveness of the cDAG in our model, showing that it can generate gene expression profiles for cells that are consistent with the underlying causal structure when performing interventions on concepts. In this study, we refer to this process as generating cells for brevity. Finally, we show that CausCell can uncover biological insights when the input experimental single-cell omics dataset is small and noisy. Collectively, CausCell presents an unprecedented perspective and method for obtaining causal disentanglement representations of single-cell data compared with traditional black-box representation learning, and it can uncover interpretable biological insights from single-cell data by controllable counterfactual generation.
a The framework of CausCell, which consists of a causal disentanglement module and a diffusion-based generative module. In the causal disentanglement module, encoding gene expression data into exogenous embeddings, processed through an SCM layer to learn causal relationships, yielding endogenous embeddings. Concept labels are predicted via supervised constraints. In the diffusion-based generative model, employing a denoising diffusion model to generate realistic gene expression profiles, conditioned on latent concepts via cross-attention mechanisms at each step. b The schematic diagram of the disentanglement representation for the cells in CausCell. Each cell can be represented as multi-concept embeddings. c The schematic diagram of counterfactual generation in CausCell. CausCell can generate new single-cell omics data for the unseen concept combinations. Credit: all of these concept-related icons in (b, c), except for cell icons, https://smart.servier.com/.
Results
Overview of CausCell
CausCell is a novel deep generative framework designed to perform causal disentanglement and counterfactual generation on single-cell omics data. In this framework, CausCell combines a structural causal model (SCM) with a diffusion model to achieve a high level of explainability, generalisability, and controllability for analysing complex, high-dimensional biological data. It assumes that each cell’s data is generated by two types of concepts: observed concepts (e.g., cancer types or spatial domain loci) and unexplained concepts, which may represent unknown biological factors. Given gene expression data, factual information of causal structure between different biological concepts and these biological concepts labels, CausCell outputs disentangled concept embeddings for each cell and enables the counterfactual generation of cells by interventions on these concepts.
CausCell consists of two main modules: a causal disentanglement module and a diffusion-based generative module (Fig. 1a). The causal disentanglement module is central to the framework and learns latent concept representation from gene expression data. Specifically, it encodes input gene expression profiles into a set of exogenous embeddings, which are subsequently passed through an SCM layer. This layer models the causal relationships between various concepts, producing the endogenous embeddings that capture biological concepts in a causally structured latent space. These endogenous embeddings are then mapped to predict concept labels using separate predictors for each concept, enforced by supervised constraints (see “Methods” section). In the generative module, CausCell employed a diffusion model to progressively transform random noise to a realistic gene expression profile through a series of denoising steps. Each step is conditioned on learned latent concept embeddings via a cross-attention mechanism, ensuring that the generative process is guided by meaningful biological concepts. Previous study has showed that the cross-attention mechanism serves as an effective inductive bias for disentangling complex data in the diffusion model. To train CausCell, we propose a novel loss function that integrates a new evidence lower bound (ELBO) with an independence constraint to ensure that the separation of observed concepts and unexplained concepts, as well as a supervised constraint to ensure the biological interpretability of learned concept embeddings. Therefore, by combining the interpretable latent space from the causal disentanglement module with the powerful sample generation capabilities of the diffusion model, CausCell allows the disentanglement of complex biological concepts and makes controllable generation by manipulating specific latent concepts (Fig. 1b, c).
Evaluation of CausCell on disentanglement performance
A comprehensive quantitative disentanglement model benchmark is critical for establishing the reliability of such models, and this step was overlooked in previous studies. Evaluating the effectiveness of a disentanglement model involves the evaluation of two key aspects: (1) concept disentanglement and (2) reconstruction. The first aspect reflects the ability of the tested model to accurately capture and separate underlying semantic concepts, whereas the second aspect determines the quality and fidelity of the generated counterfactual samples by manipulating concepts for further biological analysis. Properly evaluating these aspects is essential for ensuring the practical applicability and robustness of the developed model.
To conduct comprehensive benchmarking, we collected five distinct single-cell datasets spanning different biological domains16,17,18,19,20, each with various causal relationships among different concepts, including ICI_response dataset19, Immune_atlas dataset16, MERFISH_Brain dataset17, Spatiotemporally_Liver dataset18, Limb_development dataset20 (Fig. 2a, Supplementary Note 1 and 2, Supplementary Fig. 1 and Supplementary Table 1). We also included two experimental settings, in-distribution (ID) and out-of-distribution (OOD) settings, on the basis of whether the different combinations of concept labels were presented during training (Fig. 2b and Supplementary Note 3). In the ID setting, the model had seen all possible combinations of concept labels during training, providing a direct assessment of its ability to operate within the same data distribution. The more challenging OOD setting involved cases where the model encountered unseen combinations of concept labels, and this task aimed to assess the ability of the model to transfer complex relationships among concept representations and examine its generalisability. Furthermore, we defined five types of metrics to evaluate various aspects of disentanglement and reconstruction performance (Supplementary Note 4). Disentanglement performance was evaluated by determining whether the learned concept representation contained sufficient information for predicting the concept labels. Therefore, we defined (1) the predictive ability of the concept embeddings and (2) the clustering consistency of the embeddings when the label granularity was varied (Supplementary Note 5).
a. The causal structure of various concepts in the ICI_Response dataset. b The two experimental settings for benchmarking the disentanglement and reconstruction capabilities of the tested model. c The results of a disentanglement performance comparison conducted under experimental setting 1 (ID) for each concept contained in the ICI_response dataset. d The results of a disentanglement performance comparison conducted under experimental setting 2 (OOD) for each concept contained in the ICI_response dataset. e UMAPs of the cell type embeddings produced with coarse-grained and fine-grained cell type annotations across the two experimental settings. Here, each cell was represented by its cell type-associated concept embedding. f NMI and ARI metrics attained by different models for evaluating their fine-grained geometric property preservation capabilities across the two experimental settings. For all the bar charts, the data are presented as mean values, with each error bar representing the standard deviation based on n = 5 (fivefold cross-validation). Source data are provided as a Source Data file. Credit: all of these concept-related icons in (b), except for cell icons, https://smart.servier.com/.
To evaluate the disentanglement performance of the proposed approach, scDisInFact was selected as the baseline model because it uniquely maintains a single-cell resolution in concept representation tasks. Most existing disentanglement models rely on latent optimisation, wherein cells sharing the same concept label are represented by identical concept representations12. These approaches compromise the single-cell resolution, thereby hindering the disentanglement performance assessment. Preserving concept representations at the single-cell level is crucial, as doing so captures the heterogeneity inherent within cell populations. For example, within the T-cell lineage, distinct subtypes, such as exhausted T cells and effector T cells, exhibit unique functional states. Utilising a uniform representation for all T cells would obscure these subtle biological distinctions. Our results showed that CausCell outperformed scDisInFact in terms of various predictive metrics, including accuracy, precision, weighted F1 scores and weighted recall scores (Fig. 2c, d and Supplementary Figs. 2–5). In addition, we benchmarked CausCell against a multi-task baseline model. For a fair comparison, we used the same multi-classifier architecture employed in CausCell. In this baseline model, each cell’s gene expression was the input, and each cell was represented by a single compressed embedding, which was then fed into the multi-task classifier. Our results show that CausCell also outperforms this baseline model, highlighting the effectiveness of representing cell with multi-concept embeddings (Supplementary Figs. 6 and 7).
To evaluate the concept embedding generalisation capabilities of the models, we varied the granularity of their concept labels by training the models on coarse-grained cell type information and subsequently assessing their performance in terms of fine-grained cell subtype consistency (Supplementary Note 6). This task is challenging because it requires the model to preserve the underlying fine-grained geometry of the cells, despite being trained only on coarse labels. This test assesses the model’s ability to retain subtle biological distinctions and ensure meaningful separations between cell subtypes. CausCell also demonstrated superior performance across several clustering consistency metrics, such as the normalised mutual information (NMI) and adjusted Rand index (ARI) scores (Fig. 2e, f and Supplementary Note 7). This result highlights the potential of CausCell in capturing fine-grained structures in the concept embedding space, even when trained with coarse-grained labels.
To evaluate CausCell’s ability to preserve biological signals while mitigating batch effects – modelled as an independent concept in our causal framework – we quantified performance using two key metrics: biological conservation and batch correction scores (calculated via the scIB21 benchmarking toolkit). We tested the model on three datasets (Immune_atlas, ICI_response and Limb_development dataset), all of which include explicit batch annotations. When benchmarked against scDisInFact, CausCell’s concept embedding demonstrated superior biological signal preservation and stronger batch effect separation (Supplementary Figs. 8–13). Our results suggest that CausCell’s concept embeddings can preserve more biological signals while more effectively separating batch effects compared to the existing disentanglement model.
Evaluation of CausCell on reconstruction performance
To evaluate the reconstruction performance of the models, we defined three key metric categories to assess the consistency between the generated single-cell data with the realistic single-cell data distribution: (1) Trend matching, (2) Geometric structure consistency, and (3) Fine-grained score. These metrics were selected to capture different aspects of the quality of the generated data. Specifically, for the trend matching category, we used the Pearson correlation coefficient (PCC) and mean squared error (MSE) to measure the consistency of the overall trends between the generated data and the original data, which are commonly used in single-cell data evaluation. PCC quantifies the linear relationship between trends, while MSE provides a measure of the average squared difference. In the geometric structure consistency category, Normalised mutual information (NMI) and the Adjusted rand index (ARI) were employed to assess the preservation of geometric structures. These two metrics evaluate how well the clusters of the generated cells align with the clusters of the realistic cells, which are essential for ensuring that the generated data preserves the inherent grouping structures that is vital in single-cell analysis. Then, we introduced a fine-grained score to evaluate the maintenance of marker genes in the generated cells. This score is critical for assessing the biological relevance of the generated data, as marker genes are key indicators of cell identity and functional state. Ensuring that these genes are preserved in the generated data helps validate the biological accuracy and utility of the model in representing real cellular behaviours.
Then, CausCell was benchmarked against six baseline models, including four mainstream disentanglement-based models (Biolord3, scDisInFact9, CPA11 and MichiGAN10) and two generative models without disentanglement (scVI22 and scGen23) across all the above evaluation metrics (Fig. 3a). Theoretically, a trade-off exists between disentanglement and reconstruction performance in VAE-based models24,25. The regularisation term in its loss function, such as the KL divergence, promotes latent concept independence but can reduce reconstruction accuracy, as it forces the model to separate factors that are often dependent in real data. CausCell can mitigate this trade-off through three strategies: (1) causal structure constraints, which ensure dependencies between concepts, (2) supervised constraints, which guide the model to learn meaningful, biologically relevant concept embeddings, and (3) cross-attention mechanism, which provides an effective inductive bias for disentanglement in the diffusion model26. Benefit from these strategies, our results demonstrated that CausCell not only surpassed all disentanglement-based models but also achieved reconstruction performance that was on par with or superior to that of the mainstream generative models (Fig. 3b and Supplementary Figs. 2–5). The exceptional performance of CausCell in both disentanglement and reconstruction tasks provided a solid foundation for various downstream analyses. These included generating cells that adhered to causal structures and producing reliable cell data, thereby facilitating the discovery of biological insights.
a Schematic illustration of differences between the disentanglement model and the generative model. b Comparison among different models in terms of their reconstruction performance across two experimental settings. This is created by the funcky heatmap (version 0.5.0), so the lengths of the bars are proportional to the min-max normalised mean values. Source data are provided as a Source Data file. Credit: all of these concept-related icons in (a), except for cell icons, https://smart.servier.com/.
Counterfactual generation and causal consistency in CausCell
Counterfactual generation plays a critical role in generating simulated versions of single-cell data by intervening in one or several concepts, and it aims to investigate how scientific conclusions change and explore the reasons behind these changes, presenting to be an important task to build a virtual cell4 (Fig. 4a). However, the existing disentanglement models exhibit a critical limitation because they intervene in concepts without considering their causal relationships with other concepts, resulting in the generation of unrealistic or erroneous samples. To illustrate this point, we compared the quality of the samples generated by CausCell and a modified version, CausCell_IND, which lacks the causal structure and treats concept relationships as independent by removing the SCM layer from the model (Fig. 4b). We used the Spatiotemporally_liver dataset18, which comes from a study which investigate the host and parasite temporal expression programmes after injection of Plasmodium at single-cell resolution. This dataset includes the “Time” concept, indicating the time elapsed after injection with Plasmodium; the “Inject” concept, indicating whether the host were injected with Plasmodium; and the “Infect” concept, indicating whether the host cells were infected. In addition, the PBAGenesScore, proposed in the original study, was used to quantify the infection status of cells.
a The detailed schematic framework of counterfactual generation in CausCell. b The differences between CausCell_IND and CausCell when performing the counterfactual generation. c PBAGenesScore values obtained for various intervention-associated cells generated by CausCell without incorporating a causal structure (CausCell_IND). d PBAGenesScore values produced for various intervention-associated cells generated by the CausCell version incorporating the causal structure. Source data are provided as a Source Data file. Credit: all of these concept-related icons in (a), except for cell icons, https://smart.servier.com/. The hammer icon in (b), https://www.flaticon.com/.
We applied both CausCell and CausCell_IND to this dataset and using the “Control” cells (i.e., those without Plasmodium injection) as the basis for counterfactual generation. Specifically, we performed interventions on the “Inject,” “Time,” and “Infect” concepts by modifying their concept labels and generating cells. We then assessed the infection status of these generated cells, quantified by their PBAGenesScore18 values (Supplementary Note 8). In the case of CausCell_IND, which lacks causal structure, we observed that the cells generated with the “Inject” intervention presented the highest PBAGenesScore values across all time points, regardless of whether the cells were infected, even when the time value was set to 0 (Fig. 4c and Supplementary Fig. 14). This unrealistic behaviour highlighted the limitation of ignoring causal dependencies among concepts. In contrast, CausCell by incorporating the causal structure mitigate this phenomenon, allowing the model to generate more realistic samples that were consistent with the underlying causal relationships, where the injected and infected cells presented higher scores than other conditions did (Fig. 4d and Supplementary Fig. 14). These results demonstrate the CausCell can enhance the plausibility and consistency of the counterfactual generation process by aligning with the underlying causal structure.
Revealing biological insights from small data by counterfactual generation with CausCell
Single-cell data are often confounded by latent concepts, which may obscure critical biological signals, especially when the sample size is small. As a result, wet-lab experiments typically require large sample sizes and significant costs for high-throughput sequencing. The controllable counterfactual generation process conducted by CausCell offers a promising solution for augmenting data when the number of data samples is small. To illustrate this point, we analysed another spatial-temporal dataset, i.e., the mouse ageing dataset (MERFISH_brain)17, which includes 3 mice aged 4 weeks (4wk), 3 mice aged 24 weeks (24wk), and 5 mice aged 90 weeks (90wk). A previous study17 revealed that the expressions of 3 genes in oligodendrocytes (Oligo), 2 genes in microglia (Micro), 2 genes in astrocytes (Astro), and 1 gene in endothelial cells (Endo) increased with age, whereas the expression of one gene (Gpc5) in Astro decreased. However, when the sample sizes were reduced (by selecting only 2 mice with the highest cell counts from each age group), these gene expression trends were no longer observed (Fig. 5a and Supplementary Fig. 15).
a Gene expression differences among different ages in the original dataset, where C4b in Oligo (n = 6717 cells), Xdh in Endo (n = 5220 cells) and Gpc5 in Astro (n = 6675 cells). b Gene expression differences among different ages in the counterfactually generated dataset, where C4b in Oligo (n = 6717 cells), Xdh in Endo (n = 5220 cells) and Gpc5 in Astro (n = 6675 cells). c GO enrichment analysis of the differentially expressed upregulated genes in microglia enriched in the striatum domain, performed using the hypergeometric test. d Age-related Lilrb4a gene expression differences across all cell types, including Astro (n = 6675 cells), Endo (n = 5220 cells), ExN (n = 17307 cells), InN (n = 4149 cells), MSN (n = 17205 cells), Micro (n = 1725 cells), Olig (n = 6717 cells) and Peri (n = 333 cells). e Lilrb4a expression differences among different ages in the original dataset. f Spatial segmentation results concerning the anatomical regions of the mouse brain. g The spatial distribution characteristics of Lilrb4a expression across all ages. In the GO enrichment analysis, a hypergeometric test was performed. In each boxplot, the box boundaries represent the interquartile range, the whiskers extend to the most extreme data points within 1.5 times the interquartile range, the value indicated above the box represents the mean value, and the black line inside the box represents the median. In subfigures (a, b), statistical tests were conducted via a two-sided t test with significance levels of ns: p > 0.05; *: p ≤ 0.05; **: p ≤ 0.01; ***: p ≤ 0.001; ****: p ≤ 0.0001). In subfigure (d), an analysis of variance (ANOVA) test was used. The exact p-values are provided in Source data. Source data are provided as a Source Data file.
We subsequently used this smaller dataset to train CausCell and performed controllable counterfactual generation on the 4-week-old mice by intervening in the age concept to simulate mice at 24 and 90 weeks of age. By using these generated cells, we replicated the analysis and found that 6 out of the 9 genes presented the same expression trends as previous study17 (Fig. 5b and Supplementary Fig. 15). In addition, the abundance of cells with high degrees of expression for 2 of the remaining 3 genes also increased (Supplementary Fig. 16). To further illustrate the robustness of model to individual differences, we repeated the analysis using 2 mice with lowest cell counts from each group – a more challenging scenario. Despite the further reduced sample size, 5 out of 9 genes retained consistent expression trends with the previous study (Supplementary Fig. 17).
Furthermore, we statistically analysed the number of age-related differential genes contained in different cell types across various spatial domains, which yielded results similar to those of a previous study17 (Supplementary Fig. 18 and Supplementary Note 9). Notably, we obtained a new finding: the age-upregulated genes in Micro were enriched in the striatum domain, which has never been reported in previous studies17. A GO enrichment analysis27 revealed that these age-related, upregulated genes were predominantly involved in the regulation of adaptive immunity, particularly pathways related to T cell activation, differentiation, and cell–cell adhesion (Fig. 5c and Supplementary Note 10). Notably, genes such as Apln, C4b, Cd47, Cd74, Il2ra, Gata3, and Lilrb4a were elevated with age, indicating that aging Micro in the striatum adopt a complex, mixed phenotype. This phenotype is characterised by enhanced capacity to recruit and activate peripheral T cells, drive neuroinflammatory responses, and simultaneously suppress protective Type 2 immune response28,29,30,31. Given that neuroinflammation increases risks to neurodegenerative diseases32,33, and the Type 2 immunity plays a crucial role in mitigating aging-related decline34, these findings suggest that striatal Micro may contribute to brain aging through a multifaceted and region-specific immune remodelling.
We then counted the number of enriched pathways for each gene and identified Lilrb4a as the gene with the most enriched pathways, including T-cell activation, leucocyte adhesion and type 2 immune response. Further analysis showed its expression increases with age in almost all glial cells, which were not highlighted in earlier work and could not be identified in the original data (Fig. 5d, e). Although LILRB4, the homologue of Lilrb4a, is widely studied as an immunosuppressive receptor in cancer research35, recent study36 have shown that ApoE protein within amyloid plaques can bind to LILRB4 on Micro, leading to Micro inactivation. Targeting LILRB4 has been shown to reduce the extracellular amyloid plaque burden and alleviate neuronal dystrophy. In addition, its family gene LilrB3 can specifically bind to APOE4 and activate microglia into a proinflammatory state37. This finding suggests the potential role of Lilrb4a in influencing brain ageing by regulating the immune states of glial cells and participating in processes such as binding to amyloid plaques. Finally, we assessed the expression of Lilrb4a across different cell types and spatial domains and found that its expression increased with age in both neuronal and nonneuronal cells, with spatial specificity (Fig. 5f, g). These findings suggest that Lilrb4a may be a common regulator of ageing across various cell types in the brains of mice. These results show the potential of CausCell on revealing biological insights even from small and noisy single-cell datasets via controllable counterfactual generation.
Discussion
In conclusion, we presented comprehensive evaluation metrics that demonstrate the superior disentanglement and reconstruction performance of CausCell in single-cell disentanglement representation tasks. In addition, by leveraging causal structures and diffusion models, CausCell has the potential to generate more realistic samples and uncover meaningful biological insights through the generation of counterfactuals, particularly when the given sample size is small. The primary contribution of this work lies in the first proposal to efficient integration of causal structures in single-cell representation learning.
The current version of CausCell is that it relies on a predefined causal structure to guide the disentanglement process and demonstrate the benefits of incorporating causality into single-cell representation learning. However, in practical scenarios, the true causal relationships between biological concepts are often unknown. As the number of concepts increases, manually constructing a causal graph becomes increasingly time-consuming. To address this, causal discovery algorithms, which aim to learn causal structure directly from data, offer a potential solution. For example, the Peter-Clark (PC) algorithm38, one of the most classical approaches, begins with observational data, constructs a fully connected undirected graph, and iteratively removes edges based on conditional independence tests to produce a sparse causal graph. However, the PC algorithm cannot always determine the direction of causal links, often resulting in partially oriented edges. Other advanced causal discovery approaches, such as Greedy Equivalence Search39 or Bayesian network-based approaches40,41, may suffer from local optima, while models like the Linear Non-Gaussian Acyclic Model (LiNGAM)42 require strong assumptions, such as linearity and non-Gaussian distribution. Given these challenges, a promising future direction of CausCell is to adopt a hybrid approach: integrating automated causal discovery with domain expert refinement, where learned causal graphs are further reviewed and adjusted by biological experts to ensure alignment with real-world knowledge. This would allow CausCell to remain both data-driven and biologically grounded, enhancing its robustness and applicability across different single-cell omics datasets.
In addition, other future extensions of CausCell are expected: (1) While our focus was on evaluating the performance of the disentanglement model and demonstrating the benefits of the causal prior in the counterfactual generation task, many potential applications of this model remain to be explored. The current CausCell framework can be naturally extended to model more modalities in single-cell data, even a foundational disentanglement model in the future. (2) Although CausCell exhibited superior performance in preserving the underlying fine-grained geometry of the cells, its overall performance remains relatively low. Achieving more effective disentanglement still further dedicated model design to address this challenging task.
Methods
Overview of CausCell
Consider the input data a single-cell sequencing dataset of \(N\) cells \(D={\{\left({x}^{i},{y}^{i}\right)\}}_{i=1}^{N}\), where \({x}^{i}\) represents the gene expression vector for cell \(i\) and \({y}^{i}\) consists of \(M\) observed concept labels for that cell. The disentanglement process involves learning a series of latent concept embeddings \({z}^{i}=\left({o}_{1}^{i},{o}_{2}^{i},\ldots,{o}_{m}^{i},{u}^{i}\right)\), where each \({o}_{j}^{i}\) is a low-dimensional vector corresponding to the label \({y}_{j}^{i}\), and \({u}^{i}\) serves as an extra captured embedding of the unobserved concepts. These embeddings \({z}^{i}\) are then employed during the generative process to achieve a better reconstruction effect. Previously, VAEs were implemented as generative modules, but they tend to produce lower-quality samples, especially when addressing high-dimensional data such as high-resolution image data43. In contrast, diffusion models have been demonstrated to produce high-quality samples by generating samples in a step-by-step manner. However, their lack of an interpretable latent space makes them less suitable for disentanglement and explainability purposes. To address these issues, we propose CausCell to learn a causal disentanglement module \(F\) for concept embeddings and then integrate them into the diffusion process \(G\). Both modules are incorporated into a unified network, which is end-to-end trained via a newly derived ELBO loss.
Causal disentanglement module F
The goal is to learn causal representations of concepts \({z}^{i}\). The disentanglement learning methods used in previous single-cell studies were constrained by the assumption of concept independence. However, concepts are not necessarily independent in practice. Instead, an underlying causal structure is present and renders these concepts dependent. Therefore, we introduce an SCM layer to construct causal relationships among the concepts. In this study, the causal structure between concepts is predefined. Specifically, the observed concepts \({o}_{j}^{i}\) are connected through a DAG, which is represented by an adjacency matrix \(A\). We apply a linear version of the SCM, which satisfies the following equation:
where ε represents the exogenous variables and \(z\) denotes the endogenous variables for capturing the latent concepts. We first learn a function (a multilayer perceptron (MLP)) for extracting the exogenous concept embeddings ε from the gene expression \({x}_{0}\) and then leverage ε to transform it into \(z\) via a closed-form solution.
To ensure the semantic meanings of the concept embeddings and to enforce causal disentanglement, we employ m discriminators \(D=\{{D}_{1},{D}_{2},\ldots,{D}_{m}\}\), each of which corresponds to an observed concept. These discriminators are trained to predict the observed concept labels from the embeddings \({o}_{j}^{i}\) via the cross-entropy loss (supervised constraints), while encouraging independence between the observed concepts \(o\) and the unexplained concept \(u\):
where \(L\) is the cross-entropy loss function.
Generative module G
We use a diffusion model as our generative backbone in CausCell because of its powerful generative capabilities. A diffusion model defines a latent variable distribution \(p\left({x}_{0:T}\right)\) over a gene expression vector \({{\rm{x}}}_{0}\) sampled from a single-cell distribution, as well as noisy gene expression vectors \({x}_{1:T}:={x}_{1},{x}_{2},\ldots,{x}_{T}\) that represent a gradual transformation of \({x}_{0}\) into random Gaussian noise \({x}_{T}\). The reverse diffusion process is modelled as a Markov chain:
where \({p}_{\theta }\) is a learned denoising distribution parameterised by a neural network with a parameter \(\theta \).
The forward diffusion process \(q\) adds Gaussian noise to \({x}_{0}\) at each step:
with a predefined noise schedule \({\{{\alpha }_{t}\}}_{{\rm{t}}=1}^{{\rm{T}}}\). The marginal distribution can be directly computed as shown below:
where \(\bar{\alpha }={\varPi }_{t=1}^{T}{\alpha }_{t}\).
The denoising network \({g}_{\theta }\) in the diffusion model is an \(\epsilon \) predictor in most cases. However, single-cell data often exhibit extreme sparsity, and the corrupted input at a time step \(t\) is mostly pure noise. Under this setting, the model is likely to learn to reverse the noise schedule instead of the true data posterior. Therefore, we adopt the \({x}_{0}\)-predictor44 in this study, and a simplified training loss for the generative module is defined as follows:
where \(\xi \) is the noise sampled from \(N\sim \left(0,I\right)\) and \(t\) is the time step.
Integration causal disentanglement module F with a diffusion process G
The causal disentanglement module takes a single-cell expression profile as its input to obtain a set of concept embeddings \({z}^{i}\) under the guarantee of a causal structure. We then use these concept embeddings as the condition information for the generative module. Specifically, we incorporate these concept embeddings into the reverse diffusion process of the generative model through a cross-attention mechanism. By conditioning this process on the concept embeddings, the model can generate gene expression profiles that are consistent with specific biological concepts, allowing for a controlled and interpretable data generation procedure. The cross-attention mechanism45 facilitates this conditioning task by enabling the model to focus on the relevant parts of the concept embeddings during the generation phase. The noisy input \({x}_{t}\in {R}^{{d}_{x}}\) (i.e., corrupted gene expression at timestep t) is projected to a query vector Q, and the concept embedding \(z\in {R}^{n\times {d}_{z}}\) (i.e., concept embeddings of size n) are projected to key and value matrices K and V, respectively:
The attention output is then computed as:
In multi-head attention, this is extended over multiple parallel attention heads and followed by a feed-forward projection \({W}^{o}\in {R}^{H\times {d}_{x}}\) (\(H=m\times {d}_{h}\)):
Each head is computed as above, with different learned projection weights. \({d}_{h}\) is the scaling vector, which is used to ensure numerical stability in the softmax function, and its value is set as the dimensionality of the head. Then, this multi-head attention output is used to guide the denoising step, allowing the model to generate gene expression profiles that are consistent with the specific concept embeddings.
Evidence lower bound of CausCell
We formulate the training objective via a variational inference approach to derive the ELBO for optimising the model parameters. We treat both z and ϵ as latent variables. Consider the following conditional generative model:
We define \({p}_{\epsilon }\left(\epsilon \right)=N\left(0,I\right)\) and the joint prior \(p\left(\epsilon,z,|,y\right)\) for latent variables \(z\) and \(\epsilon \) as follows14:
We define CausCell as a causal disentanglement-based diffusion model represented by the conditional probability distribution \(p\left({x}_{0:T},z,\epsilon {|y}\right)\), which can be factorised as follows:
This model implements a reverse diffusion process \({p}_{\theta }\left({x}_{t-1}|{x}_{t},z,\epsilon,y\right)\) over \({x}_{0:T}\), which is conditioned on the endogenous variables z, the exogenous variables ϵ and the concept labels y. All of these variables are independent of the diffusion process because these variables are properties of the input, not control variables of the diffusion process.
To optimise the model parameters, we apply variational inference twice to impose a variational lower bound on the conditional log-likelihood of the concept labels \(\log {p}\left({x}_{o},|,y\right)\):
Proposition 1: The ELBO of CausCell can be derived as follows (Proof: Supplementary Note 11):
The above equation is intractable in general. Given an SCM with latent exogenous independent variables \(\epsilon \) and the latent endogenous variables \(z\), we have \(z={A}^{T}z+\epsilon={(I-{A}^{T})}^{-1}\epsilon \). For simplicity, we denote \(C={(I-{A}^{T})}^{-1}\). Leveraging the one-to-one correspondence between \(\epsilon \) and \(z\), we can simplify the variational posterior as follows:
where \(\delta \left(\cdot \right)\) is the Dirac delta function. According to the model assumptions introduced above, we can further simplify the ELBO as follows:
Proposition 2: The ELBO of CausCell can be rewritten as follows (Proof: Supplementary Note 12):
In practical scenarios, the latent factors \(z\) consist of observed variables \(o\) and unobserved variables u such that \(z=\left[o,u\right]\). Assuming independence between o and u, we augment the ELBO with a term \(-\gamma {\sum }_{i}^{m}{\rm{KL}}\left({q}_{\phi }\left({o}_{i},u\right){||}{q}_{\phi }\left({o}_{i}\right){q}_{\phi }\left(u\right)\right)\) that encourages this independence, and it is implemented via an adversarial debiasing strategy46 using discriminators. Therefore, the overall training objective is to maximise the ELBO, leading to the following combined loss function (Supplementary Note 14):
Benefit of disentanglement in the diffusion model
We show that the reverse diffusion process introduces an information bottleneck effect, promoting disentanglement by dynamically allocating information to the latent concepts as the time steps increases26. This is reflected in the ELBO term for the reverse diffusion process, which can be formulated as follows.
Proposition 3: The reverse diffusion process term in the ELBO can be rewritten as shown below (Proof: Supplementary Note 13):
where \({C}_{t}\) denotes the Kullback-Leibler (KL) divergence between the determined distribution \(q\left({x}_{t-1}|{x}_{t},{x}_{0}\right)\) and the standard Gaussian distribution \(p\left({x}_{t-1}\right):=N\left(0,I\right)\).
Therefore, optimising the model encourages the KL divergence \({\rm{KL}}\left(p\left({x}_{t-1}|{x}_{t},o,u\right)|{|p}\left({x}_{t-1}\right)\right)\) to approximate a constant \({C}_{t}\), effectively regulating the information content of \({x}_{t-1}\). The larger the KL divergence is, the more information \({x}_{t-1}\) carries. By promoting \({\rm{KL}}\left(p\left({x}_{t-1}|{x}_{t},o,u\right)|{|p}\left({x}_{t-1}\right)\right)\) to approximate \({C}_{t}\), an information bottleneck effect is added to it and thus transferred to the latent factors \(o,u\). Therefore, the diffusion model has a natural information bottleneck and is a good inductive bias for disentanglement representation purposes26. As different concepts to be disentangled may contain different amounts of information, the diffusion model can dynamically allocate this information to the latent concepts in the reverse diffusion step, where the information decreases as the number of time steps increases. This optimisation objective is then similar to that of AnnealVAE47.
Single-cell counterfactual generation via the do operator
CausCell performs interventions on individual cells by modifying their associated concepts, enabling the generation of counterfactual gene expression profiles. The causal disentanglement module of CausCell maps the concept representations of all \(N\) cells to a concept representation space \(\varOmega \). In this space, each concept \({o}_{i}\) has a representation for every cell, resulting in a total of \(N\) representations per concept. For each concept \({o}_{i}\), there exist \(m\) distinct concept labels labelled \({a}_{1},{a}_{2},\ldots,{a}_{m}\), each of which is associated with a subset of cells such that the total number of cells across all concept labels equals \(N\).
To perform a concept intervention on a specific cell \(c\) that originally had a concept label of \({a}_{1}\) for concept \({o}_{i}\), we apply the do operator to set the concept to a new value \({a}_{k}\), which is denoted as \({do}\left({o}_{i}={a}_{k}\right)\). This intervention is implemented in three steps. (1) Randomly select a concept representation from the set of representations associated with the concept label \({a}_{k}\) for the concept \({o}_{i}\). (2) Replace the original concept representation of the cell \(c\) with the selected representation. (3) Keep the representations of all other concepts \({o}_{j\ne i}\), including any unexplained concepts, unchanged for the cell \(c\). The postintervention distribution is formally represented as follows:
where \({o}_{j\ne i}={a}_{j}^{c}\) denotes that all other concepts \({o}_{j}\) (for \(j\ne i\)) retain their original concept labels \({a}_{j}^{c}\), as in the original cell \(c\). Utilising these intervened concept representations, the generative diffusion module of CausCell generates a counterfactual gene expression profile \(\hat{c}\) by sampling from the postintervention distribution:
This process allows us to simulate how the gene expression profile of a cell \(c\) would appear under an intervention \({do}\left({o}_{i}={a}_{k}\right)\), isolating the causal effect of changing concept \({o}_{i}\) from \({a}_{1}\) to \({a}_{k}\) while controlling for all other concepts.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
All datasets utilised by CausCell for training, testing, and application examples were obtained from publicly accessible databases. Specifically, the Immun_atlas dataset16 is available at [https://www.tissueimmunecellatlas.org], the MERFISH_Brain dataset17 at [https://cellxgene.cziscience.com/collections/31937775-0602-4e52-a799-b6acdd2bac2e], and the Spatiotemporally_Liver dataset18 at [https://zenodo.org/records/7081863]. The ICI_Response dataset19 is available in the Gene Expression Omnibus (GEO) under accession number GSE123814, while the Limb_development dataset20 is available from ArrayExpress under accession ID E-MTAB−10514. These benchmark datasets can also be obtained from Zenodo [https://zenodo.org/records/15242547]48. Source data are provided in this paper.
Code availability
CausCell is publicly available on GitHub [https://github.com/bm2-lab/CausCell], under the GPL-3.0 license, together with a usage documentation and comprehensive example testing datasets. The specific version of the code associated with the publication is archived in Zenodo and is accessible via [https://zenodo.org/records/15242547]48.
Change history
12 September 2025
A Correction to this paper has been published: https://doi.org/10.1038/s41467-025-63728-0
References
Shapiro, E., Biezuner, T. & Linnarsson, S. Single-cell sequencing-based technologies will revolutionize whole-organism science. Nat. Rev. Genet. 14, 618–630 (2013).
Papalexi, E. & Satija, R. Single-cell RNA sequencing to explore immune cell heterogeneity. Nat. Rev. Immunol. 18, 35–45 (2018).
Piran, Z., Cohen, N., Hoshen, Y. & Nitzan, M. Disentanglement of single-cell data with biolord. Nat. Biotechnol. 42, 1678–1683 (2024).
Bunne, C. et al. How to build the virtual cell with artificial intelligence: Priorities and opportunities. Cell 187, 7045–7063 (2024).
Higgins, I. et al. Towards a definition of disentangled representations. Preprint at https://doi.org/10.48550/arXiv.1812.02230 (2018).
Bengio, Y., Courville, A. & Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 35, 1798–1828 (2013).
Buettner, F. et al. Computational analysis of cell-to-cell heterogeneity in single-cell RNA-sequencing data reveals hidden subpopulations of cells. Nat. Biotechnol. 33, 155–160 (2015).
Buettner, F., Pratanwanich, N., McCarthy, D. J., Marioni, J. C. & Stegle, O. f-scLVM: scalable and versatile factor analysis for single-cell RNA-seq. Genome Biol. 18, 1–13 (2017).
Zhang, Z., Zhao, X., Bindra, M., Qiu, P. & Zhang, X. scDisInFact: disentangled learning for integration and prediction of multi-batch multi-condition single-cell RNA-sequencing data. Nat. Commun. 15, 912 (2024).
Yu, H. & Welch, J. D. MichiGAN: sampling from disentangled representations of single-cell data using generative adversarial networks. Genome Biol. 22, 158 (2021).
Lotfollahi, M. et al. Predicting cellular responses to complex perturbations in high‐throughput screens. Mol. Syst. Biol. 19, e11517 (2023).
Gabbay, A. & Hoshen, Y. Demystifying inter-class disentanglement. In International Conference on Learning Representations (2020).
Pawlowski, N., Coelho de Castro, D. & Glocker, B. Deep structural causal models for tractable counterfactual inference. Adv. Neural Inf. Process. Syst. 33, 857–869 (2020).
Yang, M. et al. CausalVAE: Disentangled representation learning via neural structural causal models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (2021).
Croitoru, F.-A., Hondru, V., Ionescu, R. T. & Shah, M. Diffusion models in vision: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 45, 10850–10869 (2023).
Domínguez Conde, C. et al. Cross-tissue immune cell analysis reveals tissue-specific features in humans. Science 376, eabl5197 (2022).
Allen, W. E., Blosser, T. R., Sullivan, Z. A., Dulac, C. & Zhuang, X. Molecular and spatial signatures of mouse brain aging at single-cell resolution. Cell 186, 194–208 (2023).
Afriat, A. et al. A spatiotemporally resolved single-cell atlas of the Plasmodium liver stage. Nature 611, 563–569 (2022).
Yost, K. E. et al. Clonal replacement of tumor-specific T cells following PD−1 blockade. Nat. Med. 25, 1251–1259 (2019).
Zhang, B. et al. A human embryonic limb cell atlas resolved in space and time. Nature 635, 668–678 (2023).
Luecken, M. D. et al. Benchmarking atlas-level data integration in single-cell genomics. Nat. Methods 19, 41–50 (2022).
Lopez, R., Regier, J., Cole, M. B., Jordan, M. I. & Yosef, N. Deep generative modeling for single-cell transcriptomics. Nat. Methods 15, 1053–1058 (2018).
Lotfollahi, M., Wolf, F. A. & Theis, F. J. scGen predicts single-cell perturbation responses. Nat. Methods 16, 715–721 (2019).
Kim, H. & Mnih, A. Disentangling by Factorising. In International Conference on Machine Learning 2649-2658 (PMLR, 2018).
Higgins, I. et al. beta-vae: Learning basic visual concepts with a constrained variational framework. ICLR (Poster) 3 (2017).
Yang, T., Lan, C., Lu, Y. & Zheng, N. Diffusion Model with Cross Attention as an Inductive Bias for Disentanglement. In The Thirty-eighth Annual Conference on Neural Information Processing Systems (2024).
Ashburner, M. et al. Gene ontology: tool for the unification of biology. Nat. Genet. 25, 25–29 (2000).
Zhang, L. et al. CD74 is a functional MIF receptor on activated CD4+ T cells. Cell. Mol. Life Sci. 81, 296 (2024).
Kanmogne, M. & Klein, R. S. Neuroprotective versus neuroinflammatory roles of complement: from development to disease. Trends Neurosci. 44, 97–109 (2021).
Wang, H. et al. CD47 antibody blockade suppresses microglia-dependent phagocytosis and monocyte transition to macrophages, impairing recovery in EAE. JCI Insight 6, e148719 (2021).
Shouse, A. N., LaPorte, K. M. & Malek, T. R. Interleukin-2 signaling in the regulation of T cell biology in autoimmunity and cancer. Immunity 57, 414–428 (2024).
Zhang, X. et al. Aged microglia promote peripheral T cell infiltration by reprogramming the microenvironment of neurogenic niches. Immunity Ageing 19, 34 (2022).
Grabert, K. et al. Microglial brain region− dependent diversity and selective regional sensitivities to aging. Nat. Neurosci. 19, 504–516 (2016).
Finlay, C. M. & Allen, J. E. IL-4-ever young: Type 2 cytokine signaling in macrophages slows aging. Immunity 57, 403–406 (2024).
Deng, M. et al. LILRB4 signalling in leukaemia cells mediates T cell suppression and tumour infiltration. Nature 562, 605–609 (2018).
Hou, J. et al. Antibody-mediated targeting of human microglial leukocyte Ig-like receptor B4 attenuates amyloid pathology in a mouse model. Sci. Transl. Med. 16, eadj9052 (2024).
Zhou, J. et al. LilrB3 is a putative cell surface receptor of APOE4. Cell Res. 33, 116–130 (2023).
Spirtes, P., Glymour, C. N. & Scheines, R. Causation, Prediction, and Search. (MIT press, 2000).
Chickering, D. M. Optimal structure identification with greedy search. J. Mach. Learn. Res. 3, 507–554 (2002).
Heckerman, D., Meek, C. & Cooper, G. in Innovations in Machine Learning: Theory and Applications (2006).
Kitson, N. K., Constantinou, A. C., Guo, Z., Liu, Y. & Chobtham, K. A survey of Bayesian network structure learning. Artif. Intell. Rev. 56, 8721–8814 (2023).
Shimizu, S., Hoyer, P. O., Hyvärinen, A., Kerminen, A. & Jordan, M. A linear non-Gaussian acyclic model for causal discovery. J. Mach. Learn. Res. 7, 2003–2030 (2006).
Song, Y. & Ermon, S. Generative modeling by estimating gradients of the data distribution. In Advances in Neural Information Processing Systems, 32 (2019).
Tang, W. et al. A general single-cell analysis framework via conditional diffusion generative models. Preprint at https://doi.org/10.1101/2023.10.13.562243 (2023).
Hou, R., Chang, H., Ma, B., Shan, S. & Chen, X. Cross attention network for few-shot classification. In Advances in Neural Information Processing Systems, 32 (2019).
Savani, Y., White, C. & Govindarajulu, N. S. Intra-processing methods for debiasing neural networks. Adv. Neural Inf. Process. Syst. 33, 2798–2810 (2020).
Burgess, C. P. et al. Understanding disentangling in $\beta $-VAE. Preprint at https://doi.org/10.48550/arXiv.1804.03599 (2018).
Gao, Y. et al. Causal disentanglement for single-cell representations and controllable counterfactual generation (v0.1.0). Zenodo https://zenodo.org/records/15242547 (2025).
Acknowledgements
Q.L. was supported by National Natural Science Foundation of China (Grant No. T2425019, 32341008, 62088101), the National Key Research and Development Programme of China (Grant No. 2021YFF1201200, No. 2021YFF1200900), Shanghai Pilot Program for Basic Research, Shanghai Science and Technology Innovation Action Plan-Key Specialisation in Computational Biology, Shanghai Shuguang Scholars Project, Shanghai Excellent Academic Leader Project, Shanghai Municipal Science and Technology Major Project (Grant No. 2021SHZDZX0100) and Fundamental Research Funds for the Central Universities. Y.G. was supported by the National Natural Science Foundation of China (Grant No. 324B2013). Y.G. finished this work during an internship at Microsoft Research Asia and received partial funding from Microsoft Research Asia.
Author information
Authors and Affiliations
Contributions
Q.L., Y.G. and K.D. designed the framework of this work. D.L. and C.S. provided technical support. Y.G. and K.D. performed the analyses. Y.G., K.D., C.S. and Q.L. wrote the manuscript with the help of other authors. All authors read and approved the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Zheng Xia, who co-reviewed with Tao Ren, and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Gao, Y., Dong, K., Shan, C. et al. Causal disentanglement for single-cell representations and controllable counterfactual generation. Nat Commun 16, 6775 (2025). https://doi.org/10.1038/s41467-025-62008-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-62008-1
This article is cited by
-
Causal disentanglement for single-cell representations and controllable counterfactual generation
Nature Communications (2025)