Introduction

The autumn date of foliar senescence (DFS, i.e., autumn phenology) plays a crucial role in controlling the length of the growing season in the carbon (C) uptake of terrestrial ecosystems1,2,3,4. It is widely acknowledged that global warming delays autumn phenology by reducing the rate of accumulation of chilling units in autumn trees5,6,7,8. However, some studies also suggest that global warming has a lower explanatory power for delayed autumn phenology9,10. Warmer autumns may sometimes be associated with an earlier DFS11. This might be caused by the fact that water availability contributes more substantially to interannual variation in DFS than warming12, particularly in arid and semi-arid ecosystems13,14. Under drought conditions, vegetation may modify its strategies for allocating C by prioritizing essential physiological processes over growth, thereby accelerating the senescence of leaves15. Moreover, hydraulic strategies, including adjustments in stomatal conductance and xylem structure, play a crucial role in alleviating water stress; they can also affect the timing of DFS16.

Vegetation is resistant to short-term water deficiencies because of the buffering effect of soil moisture and the fertilization effect of carbon dioxide (CO₂), which can alleviate the impact of droughts on DFS. This resistance safeguards vegetation until it experiences maximum drought stress17. Once this threshold is exceeded, vegetation transitions from highly resistant to highly vulnerable18,19, thus potentially initiating an earlier DFS. However, the spatial distributions and dynamic changes of these critical pre-season drought thresholds triggering an earlier DFS (PDT-DFS) remain unclear despite their significant implications for understanding, simulating, and predicting responses to droughts owing to autumn phenology.

Pre-season droughts related to warming may be crucial causes of an earlier DFS5,6. This process is initiated by the accumulation of abscisic acid and is accompanied by the breakdown of chlorophyll and other pigments, such as β-carotene and lutein, along with the remobilization of nutrients20. This process is also regulated by temperature, solar radiation, water availability, and spring leaf-out dates11,21,22. This suggests that a nonlinear and complex response exists between autumn phenology and drought events.

For example, the compound effects of heatwaves and droughts further influence vegetation23 because heatwaves can lead to soil and hydrological droughts by propagating meteorological droughts into soil and hydrological systems24,25. This can potentially lead to a more pronounced and earlier DFS, owing to an increase in water stress and the acceleration of physiological responses in vegetation.

However, the asymmetric effects in daytime and nighttime warming may have different impacts on the earlier DFS caused by droughts26. Daytime warming, which generally leads to an increase in the diurnal temperature range, amplifies the adverse effects of drought stress on vegetation growth by decreasing stomatal conductance and photosynthesis27. However, nighttime warming, which generally leads to a lower diurnal temperature range, has a more nuanced relationship with vegetation growth and droughts. For example, studies conducted in growth chambers have observed heightened drought stress during nighttime warming28, whereas field studies have indicated that nighttime warming may reduce the impact of drought stress on vegetation growth29. Thus, the physiological impacts of nighttime warming are still ambiguous. Nighttime warming may elevate respiration rates, which causes a net loss in C over a diurnal period30. However, it might also induce compensatory photosynthesis the following day, thereby enhancing C uptake. It is not clear whether and how pre-season warming and its asymmetric changes intensify changes in the critical drought state (drought thresholds) that result in an earlier DFS.

We construct a framework to identify the PDT-DFS based on copula functions. The advantage of copula functions lies in their ability to capture the nonlinear relationships between pre-season droughts and an earlier DFS, and they can identify drought thresholds that trigger varying degrees of advancement in DFS. We focus on terrestrial ecosystems across the Northern Hemisphere (>30°N) where vegetation dynamics exhibit distinct seasonal variations, with the goal of addressing the following three questions: (1) What are the spatial patterns in the PDT-DFS? (2) How do pre-season heatwaves alter the PDT-DFS? and (3) What are the drivers of the PDT-DFS? First, we use copula functions to construct a joint distribution function between pre-season meteorological drought indices (unless otherwise specified, drought thresholds refer to meteorological drought thresholds calculated by the Standard Precipitation-Evapotranspiration Index [SPEI]) and an earlier DFS to identify the joint probability. We then iterate the joint probability distribution to determine the PDT-DFS (see Methods). Secondly, by establishing the joint probability distribution for drought thresholds and heatwaves, we evaluate how pre-season heatwaves enhance the PDT-DFS (see Methods). We then evaluate the propagation mechanisms among the pre-season heatwaves and droughts, and an earlier DFS based on a copula-based Bayesian framework (see Methods). Finally, we analyze the drivers of the PDT-DFS by incorporating the propagation mechanism and other potential drivers into a random forest model (see Methods).

Results

Pre-season drought thresholds triggering an earlier DFS

The results of the copula-based Bayesian framework indicated that an earlier DFS is associated with higher drought thresholds based on both satellite-derived and site-level ground datasets. When the PDT-DFS approaches −0.5, a lower drought intensity is required to trigger an earlier DFS. Conversely, when the PDT-DFS approaches −5.0, a higher drought intensity is needed to trigger an earlier DFS.

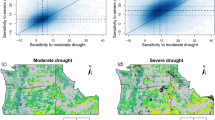
For example, the DFS for the <10%, <20%, <30%, and <40% quantiles (a lower quantile indicates that the DFS will occur earlier under the same drought conditions) resulted in PDT-DFS values of −2.59, −2.30, −1.80, and −1.63, respectively (Fig. 1a–d). The deserts and xeric shrubland biomes (DXS) had a higher PDT-DFS compared to other biomes, with PDT-DFS values of −1.75, −1.46, −1.56, and −1.60, respectively, for quantiles <10% to <40% (Fig. 1e). This indicates that the earlier DFS in these biomes is the most sensitive to pre-season droughts.

Fig. 1: Pre-season drought thresholds triggering an earlier DFS (PDT-DFS) based on both satellite-derived and site-level ground datasets.
figure 1

a–d Spatial patterns of the PDT-DFS based on the satellite-derived dataset for DFS from the <10% quantile to the <40% quantile, respectively. Bar charts in a–d represent the density distribution of the spatial data, with the vertical dashed line indicating the median value of the threshold range. P in a–d represents the percentage of land area occupied by the regions with an identified PDT-DFS. M in a–d represents the mean value of the PDT-DFS. e Mean value of the PDT-DFS across different biomes based on the satellite-derived dataset. Letters on the vertical axis in e represent abbreviations of different biome names, with their full names provided in Supplementary Table S1. The longitudinal axes of ≤ DFS10th, ≤ DFS20th, ≤ DFS30th, and ≤ DFS40th in e represent DFS from the <10% to <40% quantiles, respectively. e The statistical significance across different DFS quantiles was determined using a one-way ANOVA. “Not Diff” indicates no statistically significant difference in PDT-DFS between any two biomes (p  >  0.01). f PDT-DFS based on site-level ground dataset. The lower dashed line in the box plot represents the 25th percentile; upper dashed line represents the 75th percentile; black line inside the box indicates the median value; the points on the box represent the PDT-DFS of each site-level ground dataset. M represents the average value in each box plot, and N represents the number of points in each box plot. The longitudinal axes of SPEI10th, SPEI20th, SPEI30th, and SPEI40th in f represent DFS from the <10% to <40% quantiles, respectively. The statistical significance across different DFS quantiles was determined using a one-way ANOVA. g Pearson correlation coefficients of PDT-DFS between satellite-derived and site-level ground datasets were calculated. The statistical significance of the correlation coefficients was assessed using a two-tailed t-test. No adjustments for multiple comparisons were made. Source data are provided as a Source Data file.

Full size image

Moreover, we also found that with the spatial transition of vegetation from isohydric to anisohydric biomes, the PDT-DFS increased (tending toward −0.5) (Supplementary Figs. S1, S2). This indicates that, compared to isohydric biomes characterized by stomatal closure during drought periods, anisohydric biomes can keep their stomata relatively open to maintain photosynthesis, which may exhibit a strong response to droughts.

The DFS based on the site-level ground datasets was less sensitive to droughts compared to the satellite-derived dataset. For example, for the DFS from the quantiles <10%, <20%, <30%, and <40%, the PDT-DFS values were −2.81, −2.58, −2.25, and −1.64, respectively (Fig. 1f). Despite this difference in their sensitivity, the PDT-DFS identified from the satellite-derived data and site-level ground datasets were highly consistent (r = 0.92, p < 0.01) (Fig. 1g). These results suggest that while satellite-derived data may overestimate the sensitivity of the earlier DFS to droughts, the overall patterns of drought thresholds are consistent between the two datasets.

The PDT-DFS was not identified in regions where droughts are unlikely to be the dominant factor controlling earlier DFS (joint probability between drought and earlier DFS < 0.5), or where more intense drought conditions (i.e., SPEI<−5) may be necessary to trigger an earlier DFS. For the DFS from quantiles <10% to <40%, the PDT-DFS were identified in 55.15%, 58.51%, 64.28%, and 66.20% of the regions, respectively (Fig. 1a–d). In central North America, Mediterranean regions of Europe, and north-eastern regions of China, the PDT-DFS was higher (closer to −0.5), which indicated that the earlier DFS in these regions is the most sensitive to pre-season droughts.

In contrast, the PDT-DFS were not observed in most regions of northwestern North America, the central northern part of Siberia, and northern East Siberia (Fig. 1a–d). Similarly, heatwave thresholds triggering an earlier DFS were also not observed in most of these regions (Supplementary Figs. S6, S7a–d). However, in areas where the drought thresholds caused an earlier DFS, the daytime heatwave thresholds were a contributing factor in 66.8–84.7% of the regions (Supplementary Fig. S8), and the nighttime heatwave thresholds were also influential in 61.1–78.4% of the regions (Supplementary Fig. S9). This suggests a potential association between pre-season drought thresholds and pre-season heatwave thresholds in triggering an earlier DFS.

Pre-season heatwaves increase the drought thresholds triggering an earlier DFS

A correlation analysis indicated that pre-season heatwaves amplified the PDT-DFS based on both satellite-derived and site-level ground datasets (Fig. 2c and Supplementary Fig. S10). However, daytime heatwaves had a stronger amplifying effect on the PDT-DFS compared nighttime heatwaves. For example, for DFS from the <10% to <40% quantiles, the correlation coefficients between the drought thresholds and the compound event probability calculated by the standardized maximum temperature index (STImax) and SPEI were 0.76 (p < 0.01), 0.74 (p < 0.01), 0.70 (p < 0.01), and 0.62 (p < 0.01) (Fig. 2a, c). In contrast, such correlation coefficients between the drought thresholds and the compound event probability calculated by the standardized minimum temperature index (STTmin) and SPEI were 0.64 (p < 0.01), 0.62 (p < 0.01), 0.59 (p < 0.01), and 0.51 (p < 0.01) (Fig. 2b, c).

Fig. 2: Pre-season heatwaves alter the PDT-DFS based on the satellite-derived datasets.
figure 2

a Spatial patterns of probabilities between daytime heatwaves and the PDT-DFS. b Spatial patterns of probabilities between nighttime heatwaves and the PDT-DFS. Bar charts in a, b represent the density distribution of spatial data. Vertical dashed lines of bar charts in a, b represent median values of the probability range. c Pearson correlation coefficients between drought thresholds and the compound event probability were calculated. STImax of the transverse axis in (c) represents the compound event probability calculated by STImax and the drought indices. STImin of the transverse axis in c represents the compound event probability calculated by STImin and the drought indices. 10th to 40th on the longitudinal axis in c represent the PDT-DFS for <10% to <40% quantiles. “** ” in c represents the correlation coefficient was significant at p < 0.01. The statistical significance of the correlation coefficients was assessed using a two-tailed t-test. No adjustments for multiple comparisons were made. Source data are provided as a Source Data file.

Full size image

Mechanisms of pre-season drought thresholds triggering an earlier DFS

To explore how the pre-season heatwaves amplify the PDT-DFS, we established propagation mechanisms among the pre-season heatwaves, pre-season droughts, and earlier DFS based on a copula-based Bayesian framework (see Methods). Pre-season heatwaves mediate droughts and thereby lead to an earlier DFS, which is primarily achieved through 14 potential propagation pathways (Fig. 3e). They are divided into three categories. First, pre-season heatwaves trigger an earlier DFS by propagating into meteorological droughts; second, pre-season heatwaves directly induce soil and hydrological droughts, which cause an earlier DFS; and third, pre-season heatwaves propagate into meteorological droughts, which then trigger soil or hydrological droughts, thus resulting in an earlier DFS.

Fig. 3: Propagation mechanisms among the pre-season heatwaves, pre-season droughts, and earlier DFS using a copula-based Bayesian framework based on satellite-derived datasets.
figure 3

Black and red arrows in a–d represent the thresholds required for different types of droughts caused by heatwaves, or the thresholds for an earlier DFS triggered by heatwaves, or the thresholds for an earlier DFS caused by different types of droughts. Numbers in a–d represent average thresholds of potential propagation pathways. In a–d, we multiplied STImax and STImin by −1 to correlate their directions with drought indices. That is, the larger the negative value, the greater the severity of the heatwaves. e All the potential propagation pathways triggering an earlier DFS in a–d.

Full size image

Comparing the propagation thresholds of 14 potential propagation pathways showed that an earlier DFS was the most sensitive to the pathway in which the pre-season heatwaves cause meteorological droughts, thus subsequently causing soil droughts. Satellite-derived and site-level ground datasets both showed that thresholds for this propagation pathway were closer to −0.5 (Fig. 3a–d and Supplementary Figs. S11–S21).

Furthermore, we found that the PDT-DFS, identified using the standardized runoff index (SRI) and total water storage anomaly-drought severity index (TWSA-DSI) based on both satellite-derived and site-level ground datasets, were more dependent on daytime heatwaves (Fig. 2c and Supplementary Fig. S8). Conversely, the PDT-DFS, identified using the standardized soil index (SSI) derived from both satellite-derived and site-level ground datasets, depended less on daytime heatwaves (Fig. 2c and Supplementary Fig. S10). The results of the propagation mechanisms also showed that thresholds for soil droughts (measured by SSI) triggered by daytime heatwaves were generally higher than those triggered by nighttime heatwaves (Fig. 3a–d and Supplementary Figs. S22–S24). This indicates that respiration may adapt to a higher STImin and partially offset C losses caused by nighttime heatwaves31,32.

Drivers of the pre-season drought thresholds triggering an earlier DFS

To further analyze PDT-DFS drivers, we incorporated 72 potential drivers, including 14 propagation mechanism drivers and 58 environmental drivers (Supplementary Table S3), into the random forest model (see Methods). Recursive feature elimination methods were used to select a subset of 16 influential drivers, which explained 0.81–0.86 of the spatial variation in the PDT-DFS (see Methods). The drivers primarily included five categories: propagation mechanism drivers, climatic drivers, vegetation drivers, hydraulic characteristics of vegetation, and topographic drivers.

The PDT-DFS were predominantly governed by propagation thresholds from the SPEI to SSI, which accounted for more than 0.55 of their importance (average values of 100 cross-validations) (Fig. 4a–d). Secondly, the PDT-DFS were governed by propagation thresholds from the SPEI to TWSA-DSI, which accounted for more than 0.19 of their importance (Fig. 4a–d). Partial dependence plots further revealed that the PDT-DFS also increased as propagation thresholds from the SPEI to SSI and TWSA-DSI increased (close to −0.5), (Fig. 4e, f). This suggests that stronger mediation of soil and hydrological droughts by meteorological droughts results in higher drought thresholds (close to -0.5) triggering an earlier DFS.

Fig. 4: Drivers of the PDT-DFS.
figure 4

a–d The importance of drivers in controlling the PDT-DFS. DFS ≤ DFS10th (n = 125,488), DFS ≤ DFS20th (n = 125,918), DFS ≤ DFS30th (n = 126,428), and DFS ≤ DFS40th (n = 126,957) in a–d represent DFS from the <10% quantile to the <40% quantile, respectively. Numbers in the parenthese are the sample size for each group. The box plots in panels (a–d) represent the range of each variable across 100 cross-validation runs. The lower dashed line indicates the 25th percentile, while the upper dashed line indicates the 75th percentile. The black line within each box denotes the median, and the dots on the boxes show the mean absolute SHAP value from each random forest iteration. The x-axes in (a–d) are uniformly truncated to the range [0.23, 0.52] to better display the data distribution. The tags on the y axis in a–d represent the drivers (Supplementary Table S3). R² in a–d represents the coefficient of determination; RMSE in a–d represents the root mean square error. e–h Partial dependence plots of the top 3 drivers. The shaded area of the partial dependence plots represents the mean velues ±SD of SHAP values for DFS ≤ DFS10th–DFS ≤ DFS40th. Source data are provided as a Source Data file.

Full size image

Furthermore, after excluding the 14 propagation mechanism drivers in the random forest model, the recursive feature elimination method was applied to select a subset of 12 influential predictor drivers from 58 environmental drivers (Supplementary Table S3). These 12 drivers explained 0.72–0.79 of the spatial variation in the PDT-DFS, which were predominantly governed by resilience, and accounted for more than 0.69 of the importance (Supplementary Fig. S25a–d and Supplementary Fig. S26a–d). As resilience increased, the Shapley values (SHAP) tended toward lower negative values, which indicated that a higher ecosystem resilience would hinder the sensitivity of DFS to droughts (Supplementary Figs. S25e and S26e).

Resilience and leaf area index (LAI) served as the primary mechanisms buffering ecosystem sensitivity to droughts based on structural equation modeling (SEM) results. This finding aligned with the results derived from the random forest model after removing the 14 propagation mechanism drivers. For example, we found positive effects of precipitation (PPT, path coefficients ranging from 0.54 to 0.55) and aridity index (AI; higher AI values indicate more humid conditions with path coefficients ranging from 0.77 to 0.78) on resilience that subsequently delayed the occurrence of an earlier DFS (path coefficient approximately −0.05 to −0.06) (Supplementary Fig. S28). Increased precipitation positively enhanced LAI (path coefficients 0.54–0.56), which in turn significantly delayed an earlier DFS (path coefficient around −0.02 to −0.03). These findings indicate that sufficient precipitation enhances vegetation growth potential and effectively mitigates ecosystem sensitivities to droughts (Supplementary Fig. S28).

Some variation existed in the buffering effects of resilience and LAI on ecosystem sensitivity to droughts across different biomes. For example, in temperate broadleaf mixed forests (TBMF), AI notably delayed earlier DFS through enhanced LAI (Supplementary Figs. S29–S30). In contrast, Boreal forests/taiga (BF) and tundra ecosystems (TUN) showed stronger delayed earlier DFS through enhanced resilience. Moreover, in deserts and xeric shrublands (DXS), both AI and PPT significantly delayed earlier DFS through enhanced resilience and LAI, thus reflecting the crucial role of water availability in drought-prone ecosystems.

Projected future changes in pre-season drought thresholds triggering an earlier DFS

Based on the Inter-Sectoral Impact Model Intercomparison Project Phase 3b (ISIMIP3b) datasets from the averages of five global climate models (GCMs) (for the dataset details, see Supplementary Notes S1 and Supplementary Tables S5–S6), we found that the PDT-DFS increased significantly (p < 0.01) (Fig. 5a–d) under most of the climatic scenarios over the Northern Hemisphere. This indicates that there will be an increased sensitivity of DFS to pre-season droughts in the future. Compared with the estimates for 1982–2021, more than 51.09% of the areas had higher drought thresholds in 2061–2100 (Supplementary Fig. S31). This indicates that the future DFS would be more sensitive to pre-season droughts in most areas of the Northern Hemisphere. Higher drought thresholds were primarily concentrated in the northern part of the Eurasian continent under the three climate scenarios of SSP1-2.6, SSP3-7.0, and SSP5-8.5 (Supplementary Fig. S31).

Fig. 5: Projected future changes in the PDT-DFS.
figure 5

a–d Trends in the PDT-DFS for 1982–2100 under the SSP1-2.6, SSP3-7.0 and SSP5-8.5 climate scenarios. The horizontal axis label of End Year represents the last year of the 15-year sliding window. The each shaded area in (a–d) of the trends represent the mean velues ± 0.5 SD of five global climate models. 10th–40th in (a–d) represent DFS for the <10% quantile to the <40% quantile, respectively. Source data are provided as a Source Data file.

Full size image

Moreover, correlation coefficients between the compound drought and heatwave events (CDHWs) and the PDT-DFS tended to increase under most of the climatic scenarios (Supplementary Notes S3 and Supplementary Figs. S38–S39). Furthermore, correlation coefficients between the sensitivity of vegetation to extreme climate events, including heatwaves, droughts, and CDHWs, and the PDT-DFS also tended to increase under most of the climatic scenarios (Supplementary Notes S3 and Supplementary Figs. S40–S44). These results highlight the roles of CDHWs in enhancing PDT-DFS trends. However, the adaptability of vegetation to extreme climates, including heatwaves, droughts, and CDHWs, hindered increases in PDT-DFS.

Discussion

Implications of pre-season drought thresholds triggering an earlier DFS

Water conditions are known to be crucial in the response of autumn phenology to climate change33,34. This can be attributed to the typical evolutionary response of vegetation to limited resources34. For example, water availability serves as a limiting factor in arid and semiarid ecosystems where vegetation is more sensitive to changes in water availability than to changes in other factors35. However, vegetation has evolved various strategies to maximize resource use, such as water, CO2, and nitrogen, and to adapt to changes in availability36. This may buffer the impact of droughts on DFS. Therefore, identifying the PDT-DFS can reveal ecological deviations between drought characteristics and actual DFS responses for different regions and species.

Asymmetric impacts of pre-season heatwaves on pre-season drought thresholds triggering an earlier DFS

Heatwaves and droughts are strongly correlated, and their joint occurrence often results in a greater negative impact on terrestrial ecosystems than when they occur separately23,37. Moreover, increases in both daytime and nighttime temperatures commonly occur simultaneously rather than as mutually exclusive phenomena26,38. Their relative magnitudes and temporal patterns can differ, which leads to distinct impacts on vegetation. For example, in warm autumns, the climate responses triggered by nighttime warming are stronger, which causes delayed leaf senescence6,26,33. However, daytime warming, particularly in warm autumns, imposes drought stress, thus, accelerating leaf senescence6.

We used a random forest model to predict differences in the drivers of daytime and nighttime heatwave thresholds triggering an earlier DFS. Among these drivers, LAI emerged as a consistently important factor for both daytime and nighttime heatwave thresholds triggering an earlier DFS (Supplementary Fig. S45a–h). Moreover, compared to daytime heatwaves, partial dependence plots revealed that increased LAI more strongly inhibits nighttime heatwave thresholds triggering an earlier DFS (Supplementary Fig. S45i).

During the daytime, elevated temperatures increase stomatal conductance and transpiration rates39, which increases water loss and accelerates soil moisture depletion. This heightened water demand under high temperatures imposes substantial drought stress on the vegetation40, thereby lowering the drought intensity required to trigger an earlier DFS. In contrast, nighttime heatwaves exert a less immediate impact on soil moisture levels even though they still contribute to overall temperature stress. This is primarily because the stomata are nearly closed during the cooler nighttime periods, which reduces the amount of transpiration and conserves soil moisture41,42.

Potential links among pre-season heatwaves, pre-season droughts, and an earlier DFS

Firstly, we found that the propagation of pre-season heatwaves into meteorological droughts triggers an earlier DFS. On a temporal scale, the periodic oscillations of El Niño and the Southern Oscillation (ENSO), which lead to tropospheric warming and atmospheric blocking, are key processes that cause atmospheric droughts and heatwaves43. Pre-season heatwaves intensify deficits in atmospheric moisture, which thereby propagate into meteorological droughts.

Secondly, owing to the transferable risk, atmospheric droughts can transition into hydrological and soil moisture droughts44,45, which trigger an earlier DFS. Pre-season heatwaves can directly reduce soil moisture and disrupt hydrological balances, thus causing soil and hydrological droughts23,46. This direct pathway underscores the immediate impact of heatwaves on soil water content and groundwater levels, which are crucial for sustaining the physiological processes of vegetation. The reduction in soil moisture hampers the uptake of nutrients and activity of photosynthesis, which triggers an earlier DFS34.

Thirdly, the propagation of pre-season heatwaves into meteorological droughts, which then trigger soil and hydrological droughts, results in an earlier DFS. This combined pathway involves pre-season heatwaves that first exacerbate meteorological droughts and then subsequently induce soil and hydrological droughts, thus culminating in an earlier DFS. The cumulative effect of this sequential propagation highlights the compounded stress on vegetation47,48.

Physiological responses of pre-season drought thresholds triggering an earlier DFS

Our results further revealed that increases in LAI, resilience, and hydraulic resistance hinder the PDT-DFS (Fig. 4f, g and Supplementary Fig. S46). This indicates that the impacts of droughts and/or heatwaves on vegetation phenology result from physiological responses49. For example, the physiological responses of vegetation to drought across space are primarily controlled by aridity and are additionally modulated by abnormal hydro-meteorological conditions and vegetation types49.

For example, ecosystems with a higher LAI possess enhanced water-use capacity and transpiration efficiency50,51, thus enabling the vegetation to maintain physiological functions longer under drought conditions before they initiate senescence. Furthermore, higher resilience reflects robust physiological and structural traits, such as deep rooting systems and efficient strategies of water use52,53, which enable vegetation to maintain its physiological functions under prolonged drought stress. Moreover, higher hydraulic resistance can impede water flow16, which mitigates drought stress by reducing excessive water loss and lowers the drought thresholds, which can hinder the triggering of an earlier DFS. This highlights the importance of efficient water transport mechanisms in sustaining the vegetative physiological processes during drought conditions54.

We mapped the PDT-DFS over the Northern Hemisphere (>30°N). We found that 61.1–84.7% of the regions had a potential association between the PDT-DFS and pre-season heatwaves. Furthermore, daytime heatwaves were more effective at amplifying the PDT-DFS. The propagation mechanisms indicated that the PDT-DFS is primarily realized by pre-season heatwaves leading to meteorological droughts, thereby causing soil droughts. The random forest model further indicated that the propagation thresholds from the meteorological droughts to the soil droughts determine the PDT-DFS. However, the increase in LAI and resilience hinders the sensitivity of earlier DFS to droughts. Simulations using ISIMIP3b datasets further suggest that the PDT-DFS would increase significantly (p < 0.01) in the future. Compared with the estimates in 1982–2021, more than 51.09% of the areas showed higher drought thresholds in 2061–2100. This indicates that the future DFS will be more sensitive to pre-season droughts in most of the areas over the Northern Hemisphere. These results offer a perspective for decision-makers to address the nonlinear relationship between water deficiency and vegetation growth with warming.

Methods

Satellite-derived DFS datasets

The satellite-derived DFS datasets for 1982–2021 were developed using the normalized difference vegetation index (NDVI). The NDVI data were sourced from the third-generation V1.2 (GIMMS-3G + ) dataset, with a 0.0833° × 0.0833° spatial resolution at the global level from 1982 to 2022. NDVI values are reported twice per month. This dataset was assembled from various AVHRR sensors and accounted for various problematic issues, such as calibration loss, orbital drift, and volcanic eruptions.

First, we excluded areas with a multi-year average NDVI of <0.1. Secondly, we excluded farmland and areas that lacked vegetation based on the moderate-resolution imaging spectrometer Land Cover Version 6 data product (MCD12C1 v006). Third, we applied the Savitzky-Golay smoothing method to the NDVI time series data to reduce noise, while preserving seasonal trends in vegetation dynamics55. In particular, we used a 5 × 5 moving window, where the window size represented a temporal span of five observations that were centered on each point, with a polynomial order of 3 for the optimal fit. This approach has been widely used in phenological studies because it effectively reduces high-frequency noise, while retaining the signal of vegetation growth and patterns of senescence34,55.

Based on the reconstructed NDVI time series, we extracted the DFS dataset for 1982–2021 over the Northern Hemisphere (>30°N) by applying the Hants-Maximum56, Polyfit-Maximum57, double logistic58, and piecewise logistic methods59. These methods utilize different mathematical models to describe the NDVI time series, which enabled us to identify the critical transition point where the vegetation activity shifts from peak growth into the rapid decline phase, which denotes the acceleration of senescence (Supplementary Notes S2). To reduce the uncertainty of DFS extracted from a single method, we calculated the annual arithmetic average DFS based on these four methods34,60 (Supplementary Fig. S47a).

Additionally, we chose the MidGreendown band from MCD12Q2, which represents the date when EVI2 last crossed 50% of the segment EVI2 amplitude (MODIS-derived DFS). Since the MODIS-derived DFS reflects the acceleration phase of senescence, it serves as a valuable indicator to validate the consistency and robustness of our DFS dataset. We found that the DFS derived from AVHRR GIMMS-3G+ and MODIS-derived DFS are highly correlated (r = 0.73, p < 0.01) (Supplementary Fig. S49). Furthermore, we found that calculating the PDT-DFS using AVHRR GIMMS-3G + -derived DFS and MODIS-derived DFS results in similar values (Supplementary Figs. S50, S51). This indicated that the PDT-DFS driven by AVHRR GIMMS-3G + -derived DFS and drought indices were highly robust.

Site-level ground DFS datasets

Site-level ground DFS datasets were sourced from the Pan European Phenology project (PEP725). The site-level ground DFS datasets for PEP725 were based on the autumnal foliar senescence (50%) (BBCH = 94). We selected four temperate tree species, including Aesculus hippocastanum, Fagus sylvatica, Betula pendula, and Quercus robur, and each site had at least 30 years of continuous observational data. Moreover, based on the median absolute deviation (MAD) method, we excluded outliers that deviated from the median by more than 2.5 times61. The results included 283, 203 sites of DFS recorded from 1951–2015 (Supplementary Fig. S52c). The mean number of sites for 1951–2015 for each species was 1203, 1156, 1001, and 996 (Supplementary Table S7).

Drought and heatwave indicators

We used the SPEI function in R to calculate the monthly SPEI values at 1- to 12-month scales using the potential evapotranspiration (PET, mm) and precipitation (Pre, mm) for 1951–2021. The monthly PET and Pre were sourced from CRU-TS 4.08 of the Climatic Research Unit Time Series (CRU) with a spatial resolution of 0.5°.

The monthly soil moisture values (m3·m−3) for 1951–2021 were sourced from the ERA5-Land reanalysis dataset. The soil moisture data consisted of four layers (0–7 cm, 7–28 cm, 28–100 cm, and 100–289 cm) with an original spatial resolution of 0.1° × 0.1°. We used a weighted average method to calculate the soil moisture for the top 100 cm in depth based on the first three layers62. Based on the methods for equiprobability transformation, we standardized the soil moisture as SSI at 1- to 12-month scales63.

Terrestrial water storage anomalies (TWSA) were obtained from Yin et al.64. These data provide a longer time series compared with the terrestrial water storage data measured by the Gravity Recovery and Climate Experiment (GRACE) satellite mission. TWSA-DSIi,j was defined as follows:

$${TWSA}{{\_}}{DS}{I}_{i,j}=\frac{{TWS}{A}_{i,j}-\overline{{TWS}{A}_{j}}}{{\delta }_{j}}$$
(1)

where SPEI and SSI indicate meteorological droughts and soil droughts, respectively. We acknowledge that soil droughts are not a formal drought type. However, they are often used to represent agricultural droughts. We referred to the SSI as soil droughts rather than agricultural droughts because our analysis excluded areas affected by humans, such as farmlands and urban zones. We also used SRI and TWSA-DSI to represent hydrological droughts (Supplementary Table S8).

Furthermore, we collected monthly maximum temperature (Tmax, °C) and monthly minimum temperature (Tmin, °C) data from CRU-TS 4.08 with a spatial resolution of 0.5°. Based on the methods for equiprobability transformation, we first converted Tmax and Tmin to standardized temperature indices at 1–12-month scales (STImax, and STImin, respectively). We then multiplied STImax, and STImin by −1, to conform to the same direction as the drought indices; i.e., larger negative values indicate more severe heatwaves (Supplementary Table S8).

To match the spatial resolution of the DFS, we used an area-weighted mean approach to adjust the drought indices to a 0.083° × 0.083° spatial resolution65. Moreover, to verify the impact of the differences in resolution on the drought thresholds that trigger a DFS, we also resampled the climate indices to a 0.5° × 0.5° spatial resolution using an area-weighted mean approach. We generated spatial distribution maps of the PDT-DFS at 0.083° × 0.083° and 0.5° × 0.5°, respectively (Supplementary Figs. S53–S56 and Tables S9–S12). We found that the PDT-DFS is not sensitive to resolution (Supplementary Notes S5).

Auxiliary dataset

The auxiliary dataset included global land use datasets (Supplementary Fig. S52b and Table S2) and global biomes (Supplementary Fig. S52a and Table S1). Based on the MCD12C1 v006 dataset, land use pixels that remained constant between 2001 and 2020 were analyzed, while excluding regions classified as barren, terrain, ice formations, and urban areas. The Earth was divided into eight biomes based on the Terrestrial Ecoregions of the World (TEOW) dataset66. We analyzed the PDT-DFS in different biomes.

Quantifying the joint probability distribution of the pre-season drought indices and an earlier DFS

First, we used copula functions to construct a joint distribution function between the pre-season drought indices and DFS. The copula functions can overcome the shortcomings of counting the cooccurrence rate between pre-season drought indices and an earlier DFS with few samples44,67.

We performed linear detrending of the DFS dataset. The detrended DFS dataset was then converted to a percentile dataset to represent varying degrees of the advancement of DFS68. Lower percentiles of DFS represent earlier advancements of DFS, while higher percentiles of DFS indicate delayed DFS. We used DFS ≤ 10th percentile, DFS ≤ 20th percentile, DFS ≤ 30th percentile, and DFS ≤ 40th percentile to represent the advancement of DFS.

To account for the pre-season drought legacy effects on DFS34,69, we identified the optimal response months of DFS to pre-season drought indices (SPEI, SSI, SRI, and TWSA-DSI) by calculating the absolute correlation coefficients between the DFS and drought indices for each pre-season month (1–12) during the period from 1982 to 2021 (Supplementary Figs. S57, S58(a)–(d)).

Furthermore, we aggregated daily DFS values into months. The optimal response months of DFS to pre-season drought indices for each pixel were then calculated based on the 1–12 months that preceded the DFS month (Supplementary Fig. S47(d), (e)). For example, if a DFS pixel is located in August, the length of its pre-season 1–12 period will start from July and move backwards.

Moreover, owing to the limited efficiency of parametric distributions caused by uncertainties in the estimation of parameters and their inapplicability to random variables <070, a kernel distribution was utilized to fit the marginal distributions and in subsequent calculations24. A copula function was used to construct the joint probability distribution between the DFS (x) and SPEI (y) as Formula (2) where FX and FY are the marginal distributions of x, y. C is the cumulative distribution function of copula as shown below:

$${F}_{{XY}}(X,Y)=C\left[{F}_{X}(X),{F}_{Y}(Y)\right]$$
(2)

The kernel density estimator is defined by Formula (3) where xi, random samples; n, sample size; K, kernel smoothing function; h, bandwidth as shown below68.

$${\hat{f}}_{h}(x)=\frac{1}{{nh}}{\sum}_{i=1}^{n}\left(\frac{x-{x}_{i}}{h}\right)$$
(3)

The bivariate copula function was applied to establish the joint distribution function of DFS and pre-season drought indices. Taking SPEI as an example, it was described as Formula (4) shown below:

$${F}_{{DFS}|{SPEI}}({DFS}\le {{\rm{dfs}}}| {spe}{i}_{u1}\le {SPEI}\le {spe}{i}_{u2}) \\ =\frac{F({DFS}\le {{\mbox{dfs}}},{spe}{i}_{u1}\le {SPEI}\le {spe}{i}_{u2})}{F({spe}{i}_{u1}\le {SPEI}\le {spe}{i}_{u2})} \\ =\frac{{F}_{{SPEI},{DFS}}({spe}{i}_{u2},{dfs})-{F}_{{SPEI},{DFS}}({spe}{i}_{u1},{dfs})}{{F}_{{SPEI}}({spe}{i}_{u2})-{F}_{{SPEI}}({spe}{i}_{u1})}$$
(4)

where \({F}_{DFS|SPEI}(DFS\le {{\rm{dfs}}}|SPEI\le spei)\) represents the joint cumulative probability distribution function (CDF) between DFS below a certain threshold (DFS ≤ dfs) and SPEI within a certain range (speiu1 ≤ SPEI ≤ speiu2). The ranges of SPEI are defined as follows when calculating the joint distribution (all drought, [−0.5, −5), mild drought, [−0.5, −1), moderate drought [−1, −1.5), severe drought [−1.5, −2), extreme drought [−2, −5)). F represents the CDF.

The specific implementation of the bivariate copula function for DFS and pre-season drought indices was as follows

First, we performed normal fitting for the DFS and pre-season drought indices. For the DFS and, SPEI, SSI, and TWSA-DSI, we used the normal distribution and generalized extreme value distribution for fitting, and then selected the optimal marginal distribution based on the Kolmogorov-Smirnov (K-S) test and root mean square error (RMSE). We then used five copulas—Clayton function, Frank function, Gumbel function, Joe function, and t function—as potential joint distribution functions (F) for the DFS and pre-season drought indices. The optimal fitting function for each grid was selected based on the Akaike Information Content (AIC)25,44. This represents the optimal joint probability distribution between the DFS and different pre-season drought indices.

The joint probability distribution between the DFS and different pre-season drought indices ranges from [0,1]. A higher joint distribution probability indicates a greater likelihood of the simultaneous occurrence of DFS and drought, while a lower joint distribution probability indicates a lower likelihood of the simultaneous occurrence of DFS and droughts.

Based on the four scenarios (i.e., earlier DFS—DFS <40th percentile, DFS <30th percentile, DFS <20th percentile, and DFS <10th percentile) and four drought intervals (mild drought, moderate drought, severe drought, and extreme drought), we established the possible spatial distribution characteristics of 16 joint probability distributions between an earlier DFS and droughts. As drought severity increased, the probability of triggering an earlier DFS also increased. This implies that more severe pre-season droughts are more likely to trigger an earlier DFS (Supplementary Figs. S63–S66).

Quantifying the pre-season drought thresholds triggering an earlier DFS

Based on the copula function, we iteratively applied the joint probability distribution between the pre-season drought indices and DFS to establish a copula-based Bayesian framework to identify the PDT-DFS as described in Formula (5) (Fig. 6) shown below:

$${F}_{{DFS}|{SPEI}}({DFS}\le {{\rm{dfs}}}|{spe}{i}_{{xi}-0.1}\le {SPEI}\le {spe}{i}_{{xi}}) \\=\frac{{F}_{{SPEI},{DFS}}({x}_{i},{dfs})-{F}_{{SPEI},{DFS}}({x}_{i-0.1},{dfs})}{{F}_{{SPEI}}({x}_{i})-{F}_{{SPEI}}({x}_{i-0.1})}$$
(5)

Based on the optimal response months for the DFS and pre-season drought indices for each grid, we constructed the joint distribution of DFS and pre-season drought indices at the maximum time scale, pixel by pixel. Taking DFS ≤ 40% and pre-season SPEI as an example, the SPEI was iterated from −0.5 with intervals of −0.1 until it equated to −5.0. The joint probability of SPEI and DFS was calculated at each iteration. When the joint probability ≥ 0.5, the iterative process was terminated, and the corresponding SPEI interval was returned. The left side of the interval was taken as the triggering thresholds, which is the SPEI that corresponds to the induction of earlier DFS. A lower triggering threshold (SPEI close to −5.0) indicates that more extreme drought is needed to trigger an earlier DFS. A higher triggering threshold (SPEI close to −0.5) indicates that a milder drought can trigger an earlier DFS. If the entire iterative process ends, and we do not retrieve the corresponding drought thresholds, then no drought threshold exists that triggers an earlier DFS for that pixel.

Fig. 6: Copula-based Bayesian framework for identifying the PDT-DFS.
figure 6

a Diagram of pre-season heatwaves enhancing the PDT-DFS. This figure was created by utilizing resources from the Integration and Application Network (IAN) of the University of Maryland Center for Environmental Science. These resources are made available under a Creative Commons CC BY-SA 4.0 license. b Flowchart of the copula-based Bayesian framework for identifying the PDT-DFS.

Full size image

For the analysis of each pixel, we utilized a 3 × 3 moving window to execute a copula-based Bayesian framework to identify the PDT-DFS. In particular, we aggregated the values from the adjacent 3 × 3 pixels to increase the sample size by a factor of 971. Moreover, we also utilized 1 × 1 and 5 × 5 moving windows to execute a copula-based Bayesian framework to identify the PDT-DFS. We found little difference between using 1 × 1, 3 × 3, and 5 × 5 moving windows to execute a copula-based Bayesian framework to identify the PDT-DFS (Supplementary Fig. S67). Additionally, executing the copula-based Bayesian framework with a 3 × 3 moving window to identify the PDT-DFS resulted in good marginal distribution characteristics, which suggested a robust copula-based Bayesian framework (Supplementary Figs. S68–S75). Considering the trade-off between the computational cost and sample size of executing a copula-based Bayesian framework, we ultimately used a 3×3 moving window to identify the PDT-DFS. Moreover, we also assessed the robustness and uncertainty of the copula-based Bayesian framework (Supplementary Notes S4–S5).

Quantifying the pre-season heatwaves that amplify drought thresholds triggering an earlier DFS

We established a joint distribution function for the drought thresholds and corresponding monthly STI using Formula (6) as shown below:

$${F}_{{SPEI}|{STI}}({SPEI}\le {{\rm{spei}}}|{STI}\le {sti})=\frac{F({SPEI}\le {sPEI},{STI}\le {sti})}{F({STI}\le {sti})}=\frac{F({spei},{sti})}{F({sti})}$$
(6)

where \({F}_{{SPEI}|{STI}}({SPEI}\le {spei}|{STI}\le {sti})\), CDF of drought (SPEI ≤ spei) and heatwave (STI ≤ sti) conditions. SPEI ≤ spei represents drought thresholds at each location; STI ≤ sti represents STI ≥ to a certain heatwave threshold. In this study, we selected STI ≤ -2 to establish the joint probability distribution of pre-season heatwaves and drought thresholds. If no PDT-DFS were detected in the region, STI ≤ -2 and SPEI ≤ -2 were used to represent the joint probability distribution of pre-season heatwaves and drought thresholds for that region. This represented relatively extreme compound heatwave and drought events in the region.

Quantifying the mechanisms of propagation from the pre-season heatwaves to an earlier DFS

Previous studies suggest that warming-related droughts, which lead to water resource limitations, may in turn stimulate an earlier DFS9,69. Moreover, meteorological droughts can propagate into soil and hydrological systems24,25,47, thus causing soil and hydrological droughts. Therefore, based on a copula-based Bayesian framework, we established potential relationships among the pre-season heatwaves and pre-season droughts, including SPEI, SSI, SRI, and TWSA-DSI, and an earlier DFS.

Based on Formula (3), we calculated 15 sets of propagation thresholds (Fig. 1a–d, Supplementary Figs. S3–S5a–d, and Supplementary Figs. S11–S21). These included the following: SPEI thresholds triggering an earlier DFS; SSI thresholds triggering an earlier DFS; SRI thresholds triggering an earlier DFS; TWSA-DSI thresholds triggering an earlier DFS; STImax thresholds triggering meteorological droughts (SPEI as a proxy for meteorological drought); STImax thresholds triggering soil droughts (SSI as a proxy for soil droughts); STImax thresholds triggering hydrological droughts (SRI and TWSA-DSI as a proxy for hydrological droughts); STImin thresholds triggering meteorological droughts; STImin thresholds triggering soil droughts; STImin thresholds triggering hydrological droughts; SPEI thresholds triggering soil droughts, and SPEI thresholds triggering hydrological droughts.

These form 14 potential pathways that could lead to an earlier DFS, which are divided into three categories (Fig. 3h). We calculated drought triggering thresholds for an earlier DFS under different scenarios (quantiles <10%, <20%, <30%, and <40%) and different drought indices (SPEI, SSI, SRI, and TWSA-DSI). We also calculated the drought and heatwaves triggering thresholds for other types of droughts under different scenarios (quantiles < −0.5, < −1.0, < −1.5, and < −2.0) different drought indices (SPEI, SSI, SRI, and TWSA-DSI). When the average thresholds of a potential pathway are closer to −0.5, it is more likely that the heatwaves cause an earlier DFS by influencing droughts along that pathway.

Quantifying the drivers of pre-season drought thresholds triggering an earlier DFS

This study used the random forest method to identify the drivers of the PDT-DFS. A total of 72 potential drivers were selected (Supplementary Table S3), and they are categorized into six main groups, including soil, topography, climate, vegetation, vegetation hydraulic characteristics, and propagation mechanism drivers (14 propagation thresholds). As described by Green et al.72 and Deng et al.73, the recursive feature elimination method was used to select the variable combination with the highest coefficient of determination (R²). The number of drivers used for splitting each node was set to 2, and the model contained 500 trees with the goal of maximizing the R².

SHAP values assessed the contribution of each predictor combination to the outcome. Partial dependence plots of the SHAP values can be used to determine the impact of a single variable on the response, independent of the interference of other drivers. A SHAP value > 0 indicates that the driving variable promotes the dependent variable; conversely, a SHAP value < 0 indicates that the driving variable obstructs the dependent variable.

Based on the SEM, we estimated and examined causal relationships between PDT-DFS and influential environmental factors. We selected five influential environmental factors to discern their mechanisms influencing the PDT-DFS. These five factors were selected according to the random forest model after removing the 14 propagation mechanism drivers. The relative importance of these five variables was consistently ranked in the top five across different DFS percentiles ( < 10%, <20%, <30%, and <40%), and their ranking remained unchanged, demonstrating that these indicators have an important and stable influence on the PDT-DFS. We used the lavaan package74 in R 4.2.0 to compute standardized path coefficients for the predefined path diagram, calculating them as the product of the standardized coefficients along each path.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.