Introduction

The increase in CdTe solar cell efficiency from 22.1% (2015) to 23.1% (2024) is attributed to improvement in open-circuit voltage (VOC)1,2, which now exceeds 900 mV in polycrystalline devices3. Single crystal CdTe solar cells reached VOC > 1 V with both p-type4 and n-type5 doping. It was proposed that smaller bandgap and recombination are the primary reasons for lower VOC in polycrystalline CdSeTe6 and it was suggested that contact selectivity can limit voltage7. Landmark studies guided focus on recombination6,8,9 and advanced contacts7,10,11,12; approaches also used for perovskite (in 2015–25 small area cell efficiency increased from 20.1% to 27.0%) and silicon photovoltaics (in 2015–23 efficiency increased from 25.1% to 27.3%)1.

We recently showed that (unlike for perovskites and silicon) electronic disorder can have a large effect on CdSeTe solar cells13,14. Disorder can lead to carrier trapping14, reduce mobility13, and can create band tails15,16, with cumulative impacts comparable or larger than that for recombination or contact selectivity. This makes it imperative to control electronic defects in CdSeTe, including band tails13,17,18, electrostatic potential fluctuations14,15,16, and point defects19,20,21. Radiative emission spectra measured with photoluminescence (PL)13,14,17,18,22,23 or cathodoluminescence24 indicate complex sub-bandgap defect states, and such measurements can be used as contactless optical probes of electronic disorder. Complex CdSeTe emission spectra also require critical evaluation of thermodynamic solar cell metrics typically derived from PL—implied and radiative voltages, iVOC and VOC,rad25. Thus, defect characterization is also essential for material and device metrology18,25,26.

Unlike perovskites or Cu(In,Ga)Se2, high-efficiency Cd(Se)Te solar cells are intentionally doped27. Transition from cation-site doping with Cu to anion-site doping with As increased efficiency6 and reliability28 but created electrostatic potential fluctuations even in binary CdTe (no Se) absorbers16. Such fluctuations can impact many characteristics, from temperature coefficients15 to voltage entitlement15,16. In addition to As3,6, other group-V dopants were investigated, including Sb29, P2,4,30, and Bi31. Modeling predicted improvements with increased hole density32 and efforts were applied to increase dopant activation in polycrystalline devices6,15 and in single crystals33. It was found that dopants improve performance even when carrier density introduced by doping31 does not exceed background carrier density17, suggesting that additional effects, such as grain growth, halide incorporation, and others, might be important. Correlation between dopant activation and performance is complex, and voltage appears to saturate at ≈900 mV, ≥200 mV below the detailed balance limit15. Clearly, doping impact in CdSeTe is more complex than space charge field control to enable faster minority carrier collection32.

Here, we report electronic property analysis for polycrystalline CdSeTe doped with N, P, As, and Sb. As and P are used in the record efficiency solar cells1,2,3, while Sb and N enable comparison where dopant covalent radii are smaller (N, radius 70 pm) and larger (Sb, 140 pm) in comparison to As (120 pm) and P (106 pm). We differentiate dopant interactions with hole trap states and dopant-induced changes in the electronic band tails. Doping with As increases band tails13,14,15,16 and reduces mobility to μ < 1 cm2V−1s−1 due to carrier scattering and/or trapping13. Doping with P improves both aspects: it reduces band tails (in comparison to As) and decreases trap defect density. Reduction in trapping with P-doping is shown even in comparison to CdSeTe without intentional doping14,17,18,23. Phosphorus-doped CdSeTe reaches the radiative recombination regime at low temperatures, to our knowledge the first such result for polycrystalline semiconductors. Our results reveal a different approach for improving device performance—using dopants to control not only the space charge field of the pn junction, but also electronic defect states.

Using device simulations, we consider CdSeTe solar cells with large electronic disorder (no intentional doping, N, As, and Sb doping) and with reduced electronic disorder (P doping). We show that As-doped solar cells with low hole mobility, Urbach energies EU ≈ 30 meV, and hole density p ≈ 1016 cm−3 have reached their limiting efficiency of ≈23%13, while P-doped solar cells with Eu ≈ 20 meV, comparable doping, and charge carrier mobility ≥50 cm2/(Vs) can reach 25%; a long-sought target27. These semiconductor characteristics (doping, mobility, Urbach energy) are demonstrated in P-doped samples, indicating that the next steps are integration of such absorbers to advanced device architectures.

As proof-of-principle for approaches described in this paper, we demonstrate increase in fill factor (FF, from 76.2% to 79.2%), voltage (from 836 mV to 852 mV), and efficiency (from 19.3% to 20.2%) when P-doped heterostructures were completed to devices.

Results and discussion

Samples and methodology

Figure 1 illustrates heterostructures with graded Se composition fabricated by vapor transport deposition (VTD) of CdSe and CdTe on TCO (transparent conductive oxide) substrates and doped with N, As, P, and Sb (see Methods)3,6,15,28,30. Table 1 summarizes electro-optical (EO) properties, where column titles indicate dopant and chlorine heat treatment (CHT) time when this time was varied (15 min. or 45 min., see Methods).

Fig. 1: CdSeTe heterostructures used in this study.
figure 1

Absorbers were graded and doped as shown in the figure.

Full size image
Table 1 Electro-optical characteristics for undoped and doped (as indicated in column headings) CdSeTe heterostructures
Full size table

Radiative emission spectra for our samples are similar to corresponding data for CdSeTe fabricated using close-space sublimation with controllable CdSe to CdTe ratios18, co-evaporation of CdSe and CdTe22, deep pocket sublimation from a ternary source followed by annealing in Se and Cd3As2 vapor23, and evaporation from a ternary CdSeTe17,24. Substrates used in earlier studies include Corning glass22, MgZnO on TEC12 glass24, and Al2O3 on TEC12 glass17. Arsenic dopant incorporation in-situ (during absorber growth) and ex-situ (after absorber deposition) resulted in similar defect PL14. This comparison suggests that defects with complex emission signatures are intrinsic to CdSeTe or are due to the most common impurities, such as O and/or Cl. It is likely that defects analyzed here impact performance of many if not all polycrystalline CdSeTe solar cells.

Electronic defects in CdSeTe without intentional doping

First, we analyze CdSeTe without intentional doping. Emission peak at 298 K has maximum at 1.397 eV (Fig. 2a) and absorptance a(E) calculated from this data is described by the Urbach energy Eu = 14.4±0.1 meV (Table 1). Exciton emission at low temperature (Eg (4 K)) and sub-Eg emission are distinct, indicating that broad emission at 0.8–1.4 eV is due to the defect states13,14,17,18,22,23,24. Temperature dependence is shown in Fig. 2b, where D1 indicates 1.24 eV emission and D2 indicates ≈1.0 eV emission, best resolved at 250 K. D1 and D2 defect states distinctly interact with dopants (next Section).

Fig. 2: Electronic defects in undoped CdSeTe.
figure 2

a PL emission spectra at 298 K (black) and at 4 K. Inset shows D1 peak shift with injection. b Temperature-dependent PL emission spectra. c Analysis to determine activation energies EA,D1 and EA,D2; solid lines are fits to Eq. (1). d Configuration energy diagram for excited states (D + e + h and D + e) and the ground state (D). Red arrows indicate PL emission bands, ℏω is phonon energy, q is configuration coordinate. e TRPL decays at emission energies indicated in the legend. f Temperature-dependent TRPL decays measured at 1.24 eV. Inset shows lifetimes determined using single exponential fits to the decay tails, fit at 4 K is shown. g Band diagram summarizing results in this Figure.

Full size image

Activation energies EA,D1 and EA,D2 for D1 and D2 were determined using34:

$${PL}\left(T\right)=\frac{{I}_{0}}{1+{a}_{1}{T}^{3/2}+{a}_{2}{T}^{3/2}\exp \left(-{E}_{A}/{kT}\right)}$$
(1)

Where PL(T) is PL intensity at temperature T, I0, a1, a2 are constants, and k is Boltzmann’s constant. Such quenching models apply to both thermally activated and tunneling multi-phonon nonradiative recombination, as analyzed next. Integration ranges 1.23–1.26 eV (for EA,D1) and 0.78–1.1 eV (for EA,D2) were used for all samples, best resolved for Sb-doping (next Section). Figure 2c shows that without doping EA,D1 = 100 ± 10 meV and EA,D2 = 130 ± 20 meV. While defect emissions are well-below the bandgap, such relatively shallow defects can allow carrier detrapping, potentially impacting charge transport.

Figure 2d illustrates configuration energy diagram (which accounts for relaxation in the excited states), consistent with earlier results for CdSeTe13, ZnSeTe35, CdSe36, and first-principles models for CdSe20 and CdSeTe19,21. D1 and D2 defect states can be related to anion vacancies19,20,36, interstitials19, or common impurities, such as oxygen36. D1 and D2 can be two configurations of the same defect states, or they can be distinct defects. In binary CdSe, carrier traps with D1 emission signatures were attributed to selenium vacancies37.

As shown in Fig. S1, inhomogeneous spectral broadening at <50 K is \({\Gamma }_{0}\) = 276 ± 4 meV. Spectral broadening is high (e.g., \({\Gamma }_{0}\) = 19 – 32 meV for hybrid lead halide perovskites38, \({\Gamma }_{0}\) = 6.0 – 6.5 meV for ZnSe and Zn0.56Cd0.44Se39, and \({\Gamma }_{0}\) = 2.3–13.4 meV for CdxZn1-xSe40) due to electronic disorder in CdSeTe. Similar electronic disorder (\({\Gamma }_{0}\) > 75 meV) was observed in polycrystalline CdSeTe fabricated by evaporation17 and close space sublimation14.

To learn about carrier lifetimes and defect capture and emission rates, Fig. 2e, f shows time resolved PL (TRPL) decays at different temperatures, emission energies, and time scales. Data clearly indicates trapping, where trap emission at 1.18–1.24 eV increases with the same rate as bandgap PL quenching (ktrapping = (τtrapping)−1 = (0.5 ns)−1 = 2 × 109 s−1). Since TRPL is measured at low injection, trapping dynamics is due to minority carriers. McGott et al. showed that CdSeTe has n-type background carrier density17, which is also known for CdSe20. Thus, minority carriers in samples without doping are holes, and defects D1 and D2 with picosecond-time-scale carrier capture are hole traps close to the valence band (VB). Doping type changes with group-V doping6,27,29, and defects D1/D2 near VB become majority carrier traps.

Heterostructures are grown on TCOs and have pn junction space charge fields, requiring numerical modeling of TRPL data to infer minority carrier lifetimes τB41. According to modeling for similar dopant density, the slower component of the TRPL decay is a good approximation for τB41. To estimate τB we fit the slower component of the TRPL decay τ2,TRPL corresponding to ≈10% of the total amplitude. Figure 2f shows such fit for the 4 K data, and the inset indicates that τ2,TRPL increases 175 times, from 24 ns at 285 K to 4.2 ± 0.5 μs at 4–50 K. Such strong temperature dependence is not consistent with Shockley-Read-Hall (SRH) recombination, where expected temperature dependence is ∝T−0.542,43, and SRH lifetimes are expected to increase only 3 to 8 times in this temperature range. Microsecond lifetimes that are temperature-independent <50 K indicate tunneling recombination14, which is attributed to electronic disorder in CdSeTe.

As shown in Fig. S2, applying the tunneling rate model44 to low-temperature TRPL data implies defect density (1–2) × 1018 cm−3. Majority and minority carrier localization to the defect states is required for tunneling recombination44. Activation energies for defects near VB were already determined. To estimate activation energy for defects near the conduction band (CB), we analyze blue shift (to higher energy) with injection in PL spectra, Fig. 2a. This shift (of +32.8 meV) is a signature of donor-acceptor-pair (DAP) emission44, and it indicates the binding energy for the shallower impurity45. We use DAP shift as an estimate for the compensating donor binding energy, ED ≈ 33 meV. Compensation due to such defects leads to Eu = 14.4 meV for undoped heterostructures.

Figure 2g summarizes all data in a band diagram. As shown next, the defect model for doped CdSeTe remains essentially the same. Doping, however, modifies defect properties, and with P-doping defect impact is reduced, transitioning from DAP tunneling to radiative recombination thus overcoming trapping limitations.

Band tails, compensating defects, and carrier traps in doped CdSeTe

Figure S3 shows that PL emission for doped CdSeTe becomes asymmetric and broader, which is also evident in the absorptance spectra. Urbach energies are (Table 1): EU = 14.1 ± 0.1 meV without doping, EU = 16.1 ± 0.1 meV for N-doping, EU = 20.1–21.1 meV for P-doping, and EU = 24.5–25.6 meV for As-doping. In comparison to single crystal CdTe (EU ≈ 8 meV)14, silicon (EU ≈ 9 meV)46, perovskites (EU ≈ 13 meV47, EU ≈ 18 meV for larger bandgaps)48, and Cu(In,Ga)Se2 (EU ≥ 15 meV)47, EU values in doped CdSeTe are higher.

Spectral broadening in doped semiconductors with low dopant activation is usually attributed to compensation15,16. As explained earlier and shown in Fig. 3a, activation energies of compensating defects were estimated from DAP spectral shifts.

Fig. 3: Compensation and carrier traps in doped heterostructures.
figure 3

a Injection-dependent donor-acceptor pair (DAP) spectral shifts at 5 K. Lines are fits to the model from ref. 45. Insets show spectra measured with the lowest (black) and the highest (red) injection. b Defect energy diagrams. Values are also listed in Table 1. c Temperature-dependent PL emission spectra used to determine D1/D2 activation energies. Excitation fluence was the same and intensities can be compared. (Gray shaded areas indicate scattering from glass substrates).

Full size image

In addition, potential fluctuations are commonly evaluated for disordered semiconductors49. Since the CdSeyTe1-y composition y is close to the Eg bowing minimum50, amplitude of bandgap fluctuations is low15. Electrostatic potential fluctuation amplitude, γ, can be estimated using analytical models51. Using dopant density measured with SIMS (secondary ion mass spectrometry, Fig. S4a and Fig. S14) and carrier density measured with CV (capacitance voltage, Fig. S4b), γ = 111–255 meV for As-doping, γ = 92–189 meV for P-doping, and γ = 37–89 meV for N-doping (Table S1).

Finally, Stokes shifts between absorption and emission spectra are also listed in Table 1. These four sets of metrics (Eu, energy of compensating defects, γ, and Stokes shift) can correlate with radiative voltage Voc,rad15,16,18,46,47. However, majority carrier traps (D1/D2) are the most critical CdSeTe defects because such traps can reduce mobility and thus FF of solar cells13,14,25.

Activation energies EA,D1/EA,D2 for traps D1/D2 were determined from PL(temperature) data in Fig. 3c as shown in Fig. S5 and illustrated in band diagrams in Fig. 3b. In comparison to CdSeTe without doping, As-45, P-45, and P-15 heterostructures have shallower traps and N, As-15, and Sb-doped heterostructures have deeper traps. D1 and D2 activation energies are within 30 meV in all cases except Sb, where EA,D1 is low and EA,D2 has the highest value. Using P-doping decreases EA,D1/EA,D2 even in comparison to undoped CdSeTe, while band tails (compensation) increase less with P than with As. In addition, inhomogeneous broadening (Fig. S1) is the lowest for P-doped heterostructures.

As is the case for undoped CdSeTe, first principles studies suggest possible defects in group-V doped CdSeTe21,52,53. Such defects can include Cdi + AsTe21 and AX centers52,53. It was suggested that P can be a more efficient dopant than As due to reduced compensation21, in agreement with lower EU values for P-doping. Experimental defect identification is challenging because of broadening and potential overlap of spectroscopic signatures.

Scanning Spreading Resistance Microscopy (SSRM) data in Fig. 4 shows nm-to-μm-scale variation of electrical resistance taken at the delaminated front Cd(Se)Te interface, where the measured resistance is dominated by the local resistivity below the AFM probe30. The resistance of P-45, As-45, and Sb-45 samples show similar nonuniformity with relative standard deviation Rq/R ≈ 0.5 and amplitude variation of one order of magnitude. For the N-45, P-15, and As-15 samples the nonuniformity is larger with Rq/R > 0.75 and amplitude variation of about 3 orders of magnitude. These resistance nonuniformity trends are not consistent with the amount of the electronic disorder, illustrating that the electronic disorder did not result from the doping nonuniformity, but is attributed to defects and their complexes originating at the CdSeTe anion sublattice.

Fig. 4: Scanning spreading resistance microscopy (SSRM) data and analysis.
figure 4

a–f SSRM images taken with positive sample bias voltage Vs = +10 V at the CdSeTe front interface for all dopants in this study, as indicated in the legends. Dashed lines indicate directions of representative resistance line profiles shown in panels below images. Resistance is shown using logarithmic scales.

Full size image

Contrasting carrier dynamics in doped CdSeTe: from tunnelling to radiative recombination

Emission spectra identified dopant-dependent defects D1/D2 and compensating centers, resulting in complex energy diagrams. We used TRPL, Light-Induced Transient Grating (LITG), and pump-probe (PP) measurements to analyze how defects impact carrier dynamics13. First, we consider P-45 heterostructure. Figure 5a shows TRPL decays (measured at 1.24 eV) at 285 K, 35 K, and 6 K. We used the TRPL tail fitting model41 described earlier to determine τB ≈ τ2,TRPL = 45 ns at 285 K, 300 ns at 35 K, and 175 ns at 6 K. Increase in recombination rate τ2,TRPL−1 between 35 K (3.3 × 106 s−1) and 6 K (5.7 × 106 s−1) is a reliable signature of radiative recombination42. A similar trend is observed for the P-15 heterostructure, Fig. S6.

Fig. 5: Carrier dynamics.
figure 5

a–c Data for P-45 heterostructure. a TRPL decays at 285 K (red), 35 K (dark red), and 6 K (brown). b Recombination rate analysis using Eq. (2). c Injection dependence for lateral ambipolar diffusivity and mobility, with and without light bias, when the grating period was 1.2–6.8 μm. d Recombination rates for all samples. Insets indicate that radiative recombination dominates with P-doping and tunneling recombination due to trapping is observed for other samples.

Full size image

As shown in Fig. 5b, rates τ2,TRPL-1 were fit to42,43:

$$\frac{1}{{\tau }_{2}}=\frac{1}{{\tau }_{{rad}}}+\frac{1}{{\tau }_{{SRH}}}+\frac{1}{{\tau }_{{act}}}\propto {C}_{{rad}}{T}^{-1.5}+{C}_{{SRH}}{T}^{0.5}+{C}_{{act}}{T}^{0.5}\exp \left(-\frac{{E}_{A,{TRPL}}}{{kT}}\right)$$
(2)

Where \({{\tau }_{{rad}}}^{-1}\), \({{\tau }_{{SRH}}}^{-1}\), \({{\tau }_{{act}}}^{-1}\) are radiative, SRH, and activated rates, Crad, CSRH, and Cact are constants, and EA,TRPL = 80 ± 20 meV is activation energy (measured from the Fermi level). Analysis identifies that at 6 K radiative recombination makes the largest contribution, at 35 K radiative and SRH rates are comparable, and above 200 K activated process has the highest rate.

Minimal or no trapping with P-doping is also suggested by \({\tau }_{{rad}}\) values. The temperature dependence of the radiative constant is \(B={B}_{o}{\left(300/T\right)}^{3/2}\)42, where B0 = (1–2) × 10−10 cm3s−154. If hole density at 6 K is p ≈ 1 × 1015 cm-3, \({\tau }_{{rad}}=1/{Bp}\) = 15–30 ns at 6 K. Estimated \({\tau }_{{rad}}\) is similar to τ2,TRPL, indicating that free carrier density at 6 K is not much lower than 1015 cm−3.

Next, we directly measured charge carrier mobility with LITG spectroscopy, where laser excitation modulates carrier density and an optical beam diffracted from the carrier grating probes lateral diffusion and recombination. By using several grating periods, diffusion and recombination processes can be separated13. Figure S7 shows LITG data and analysis, and Fig. 5c shows injection-dependent ambipolar diffusivity D and mobility μ. At the lowest fluence, D = 1.8 ± 0.2 cm2s-1 corresponding to μ = 69 ± 8 cm2V−1s−1. Because hole effective mass is ≈ 4 times higher, hole mobility μp = 35 ± 4 cm2V−1s−1 and electron mobility μe = 140 ± 16 cm2V−1s−1, excellent values for polycrystalline semiconductors. In addition to diffusivity and mobility measurements shown in Fig. 5c, we analyzed absolute LITG diffraction intensities (Fig. S8) and found carrier effective masses consistent with literature values, further supporting increased mobility in P-doped CdSeTe.

Increase of D with injection identifies ionized impurity scattering and/or random alloy scattering as possible mechanisms limiting mobility from single-crystal values.55 The same mechanisms lead to PL broadening (Fig. S1). Hall mobilities in As-doped single-crystal CdTe with similar dopant activation are comparable33,56, further indicating that compensation (resulting in ionized impurity scattering) limits mobilities in P-doped heterostructure, rather than grain boundary or extended defect scattering, which would presumably differ in polycrystalline and single crystal absorbers.

While inhomogeneous broadening in CdSeTe:P is larger than that for hybrid lead halide perovskites (\({\Gamma }_{0}\) = 132 meV vs. \({\Gamma }_{0}\) = 19–32 meV38), mobility in CdSeTe:P is higher (35 cm2V−1s−1 vs. 0.1–2.2 cm2V−1s−1 for FAPbI357), indicating that scattering mechanisms in solar semiconductors need further studies.

Because LITG measurements were performed using pulsed excitation and trap occupancy might differ with continuous-wave excitation, we repeated LITG experiments with light bias, where bias light fluence was approximately 1 Sun. As shown Fig. 5c, diffusivities and mobilities with and without light bias were approximately the same.

To further show that carrier trapping is reduced with P-doping, transient absorption (TA) measurements were applied. TA probes carrier dynamics for radiative and non-radiative states, and is especially useful for monitoring states with low radiative efficiency56. As shown in Fig. S9, TA lifetimes are in good agreement with TRPL data.

In summary, P-doped heterostructures in this study no longer have trapping limitations as probed by TRPL lifetime temperature dependence, LITG diffusivity injection dependence with and without light bias, and TA data.

Trapping persists for other samples. Figure S10 shows temperature-dependent TRPL decays and Fig. 5d contrasts TRPL(temperature) data for all heterostructures. For As-45 and N-doping τ2,TRPL = 5.0–5.6 μs and lifetimes are temperature-independent at ≤40 K, indicating trapping followed by tunneling recombination. Tunneling center density is comparable, (1–2) × 1018 cm−3 with and without doping, Fig. S2.

As-15 and Sb-doped heterostructures have the deepest traps, and as shown in Fig. S11, trapping is already impacting carrier dynamics at room temperature, with ktrapping ≈ (0.5 ns)−1 = 2 × 109 s−1. For Sb-doping lifetimes of the D1 and D2 states can be differentiated from PL emission at 1.24 eV (D1) and 0.83 eV (D2).

Taken together, data indicates that using anion-site doping it is possible to change electronic disorder in CdSeTe. Defect D1 inhomogeneous broadening can range from \({\Gamma }_{0}\) = 132 meV (P-15) to 344 meV (As-15), hole trap activation energies can range from 70 meV (P-15) to 420 meV (Sb), carrier lifetimes can range from radiative (P-15) to limited by trapping at the room temperature (As-15, Sb). To evaluate impacts on solar cells, we included extended range of electronic characteristics to solar cell device models.

Device modeling in the radiative limit with the shallow defect states

Device modeling was conducted to quantify the effects of shallow defects and transport characteristics on device performance relative to the radiative limit. Shallow defect states can affect device performance in various ways, including (i) increasing Voc when acting as dopants, (ii) reduction of mobility due to charge carrier scattering, (iii) interactions with dopant species thereby impacting the junction electric field, and (iv) creation of band tails (characterized by Eu). The latter can lead to lower Voc due to a reduced recombination activation energy, but higher Jsc due to enhanced absorption of lower energy photons46,58.

To capture shallow defect features, simulations were performed in the parameter space μp = 0.1–50 cm2V−1s−1, NA = 1014–1017 cm−3, and Eu = 0–30 meV. The minority carrier mobility was kept fixed at 320 cm2V−1s−159, while the majority carrier mobility μp was varied to consider the effects of hole traps (varying μn is explored later). Eu was used to calculate both the Voc loss and the absorption coefficient, α(E), as described in the Supplementary Information. Voc loss was captured with a reduced bandgap46,60,61,62. To simulate the radiative limit, non-radiative recombination was omitted, contacts were assumed Ohmic, and interfaces had no surface recombination or detrimental band offsets. Se grading (y in CdSeyTe1-y) as a function of depth, x, was set to an erfc(x) dependence with y = 0.3 at the SnO2/Cd(Se,Te) interface and y = 0 at 1.5 μm distance from that interface41. Eg and electron affinity gradings were determined from the published bowing functions50. A list of simulation parameters is provided in the Supplementary Information and methodology is described in Methods.

Figure 6a–c shows how the efficiency varies with μp and doping for Eu = 0, 20, and 30 meV. Increased doping tends to improve efficiency, especially when mobility is low. For all Eu values, hole mobility μp \(\le\) 1 cm2V−1s−1 is very detrimental to device performance due to FF and Voc loss when NA < 5 × 1016 cm−3. Band tails reduce the maximum radiative efficiency, with values of 28.3%, 27.7%, and 26.2% when Eu = 0, 20, and 30 meV, respectively. The efficiency for Eu = 10 meV (not shown) is nearly identical to that of Eu = 0 meV, indicating that small tails of Eu \(\approx\) 10–20 meV can be tolerated. There is significant qualitative change near NA = 1016 cm−3. Hence, Fig. 6d–f shows the performance metrics for NA = 1015 cm−3 and NA = 1017 cm−3 as functions of mobility and Eu. All metrics are independent of mobility at NA = 1017 cm−3. At NA = 1015 cm−3, however, the negative impact of low mobility on FF is evident, in addition to some Voc loss. At higher doping, there is a slight loss in Jsc due to the decreased extent of the junction electric field. That loss is more than compensated for by increases in Voc and FF with doping. Oddly, Jsc increases slightly at low doping as Urbach energy increases and mobility decreases. At low doping and low mobility, injected charge (greater with band tails) is sufficient to reduce the net space charge in the depletion region, resulting in a larger depletion width and better carrier collection under short circuit conditions. Band tails cause a slight increase in Jsc while significantly reducing Voc with losses of 13, 25, and 108 mV for Eu = 10, 20, and 30 meV, respectively (see Table S3).

Fig. 6: Simulated performance metrics in the radiative limit with shallow defect effects.
figure 6

Efficiency as a function of hole mobility (μp) and acceptor doping (NA) for Urbach energies of (a) Eu = 0 meV, (b) Eu = 20 meV, and (c) Eu = 30 meV. Common color legend on the right. Performance metrics for (d) short-circuit current (Jsc), (e) open-circuit voltage (Voc), and (f) fill factor (FF) as functions of μp for Eu = 0–30 meV and doping levels of NA = 1015 cm−3 (solid lines) and NA = 1017 cm−3 (dashed lines). The SQ limit for each metric is the horizontal dashed line.

Full size image

The Shockley–Queisser (SQ) limits for each metric (assuming Eg = 1.42 eV and interpolated from ref. 63 are shown as the horizontal dashed lines in Fig. 6d–f. Without band tails (Eu = 0 meV) and at the highest doping, the best values of Jsc and Voc are below the SQ limit by 4.7% (1.5 mA/cm2) and 8.6% (98 mV). Jsc increases beyond the SQ limit when Eu = 30 meV because the detailed balance calculation assumes an abrupt absorption edge, which neglects some band-tail-induced photocurrent enhancement. Despite the device models being set to the radiative limit, the metrics fall short of the SQ values mostly due to the lack of photon recycling64, but also because of a constant reflectivity of 2% and absorption losses in the buffer layer. For the same reasons, the highest simulated efficiency is 28.3%, while the SQ limit is 32.66%. Even higher absorber doping of 1018 cm−3 increases efficiency to 28.8% (not shown), but surpassing 29% would require meticulous optical management.

Device results

Spectroscopy indicated potential advantages of P-doping by reducing band tails and hole traps, and device modeling benchmarked performance in the radiative limit due to such improvements. To test these predictions, we completed P- and As-doped heterostructures to solar cell devices, see Methods.

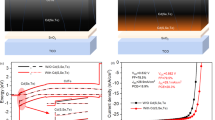
Figure 7 shows JV and EQE data for the best As- and P-doped devices selected from a set of 12 for each doping type. The inset table indicates statistics for efficiency, JSC, Voc, and FF. Simulated JV and EQE curves, in good correspondence with the data, are also shown in Fig. 7. The device models are the same as the idealized case in Fig. 6, except that the P-doped model assumed μp = 10 cm2V−1s−1 and Eu = 20 meV (Stokes shift = 20 meV). Values for the As-doped model were μp = 0.35 cm2V−1s−1, Eu = 25 meV (Stokes shift = 50 meV). The low mobility for As-doped CdSeTe was previously reported13, and Eu and Stokes shift were based on the values in Table 1. Both models assumed NA = 2 × 1016 cm−3 (from typical CV measurements for these devices), bulk nonradiative lifetime τB = 2 ns (devices had similar PLQY, Table 1), and contact series resistance Rs = 0.3 Ω cm2. Increases in Voc and FF for the P-doped device are due to lower Eu and higher μp, respectively. As expected, JSC remains approximately the same, with slightly higher current with As-doping likely due to band tail effects (see Device modeling section). The P-doped JV curve is insensitive to further increases in μp, so the actual value could be ≥ 10 cm2V−1s−1. The effects of varying μn on the JV characteristics for this device are shown in Fig. S13. Comparison to device data suggests that μn > 100 cm2V−1s−1. Voltage for both models is very sensitive to τB. For example, increasing τB from 2 ns to 100 ns results in a 25.6%-efficient device with Voc = 976 mV, suggesting that further improvements could be gained by reducing nonradiative recombination. The corresponding radiative limit in Fig. 7b is 26.4%. Overall, device efficiency for P-doping increases by 0.9% absolute, with 0.3% from higher Voc (lower Eu) and 0.6% from higher FF (higher μp). This indicates significant potential to increase CdSeTe solar cell performance with tailored defect control using dopants.

Fig. 7: Solar cell device results and comparison with device models.
figure 7

a JV and (b) EQE data (points) for As- and P-doped devices compared to simulation results (solid curves). Performance metrics are provided in the inset table (for 12 devices) with simulation results in parenthesis. The JV curves pertain to the best devices with efficiencies of 19.7% and 20.7% for As and P doping, respectively. a Increasing τB from 2 to 100 ns increases efficiency to 25.6% (dashed). b Omitting band tails in the P-doped device model results in an abrupt long wavelength EQE cutoff (dashed).

Full size image

The EQE simulations in Fig. 7b account for the observed broadening at long wavelengths when band tails with Eu = 20 and 25 meV are included for P-doped and As-doped devices, respectively. Omitting band tails results in the abrupt cutoff shown by the dashed line. Discrepancies at wavelengths less than 850 nm are due to the simple optical model that does not include wavelength-dependent reflection or thin film interference effects.

Summary

CdSeTe PV has reached over 50 GWpp (peak power) cumulative installations and 20 GWpp annual manufacturing capacity15, making understanding of efficiency potential and limitations of this material system highly pertinent. To make progress towards this goal, we developed defect models for group-V doped CdSeTe and applied these models to state-of-the-art thin film solar cells. Defects in CdSeTe are complex, making it necessary to consider not only solar cell thermodynamics46,47,58, but also charge transport. Mobility is a critical parameter for CdSeTe solar cells due to majority carrier (hole) trapping13,14,25. Complex near-Eg defects also increase band tails. Although numerous forms of disorder can cause band tails, in this case, it appears that anion disorder and, possibly, a high degree of nonuniform dopant compensation result in band tails that reduce the activation energy for electron-hole pair generation, as indicated in the EQE results. The same activation energy reduction affects recombination according to the Stoke’s shift in the PL data. We hope results reported here clarify multiple impacts that doping on anion sites can have in CdSeTe solar cells, largely due to anion disorder in this semiconductor.

We show that doping polycrystalline CdSeTe with phosphorus overcomes trapping limitations and increases mobilities to values equal to those of compensated CdTe single crystals, μp ≥ 50 cm2V−1s−133,55,56. With P-doping, electronic disorder (inhomogeneous broadening, Eu, trap activation energy) is reduced, and low temperature charge carrier lifetimes reach the radiative limit. Device modeling identified that solar cells with EO characteristics demonstrated in the study have the potential to reach 25% efficiency, which would be a breakthrough for CdTe PV27. In addition to seeking higher radiative efficiency6 for energies at or above absorbed photons energies and better contact selectivity7, reducing electronic disorder becomes an important research direction for CdTe PV. Corroborating results from characterization and modeling, we demonstrate device FF increase from 76% to 79% and efficiency improvement +0.9% absolute with P-doping, which is primarily attributed to increased μp due to reduced trapping.

To our knowledge, this is the first demonstration of decreasing electronic disorder by doping in inorganic semiconductors. Such results were reported for conjugated organic polymers65, which are more tunable due to conformational, structural, and other flexibility inherent in organic materials. In addition to doping, other processes could improve charge transport in CdSeTe. For example, polycrystalline CdSeTe where several high temperature anneals were used to increase crystalline grain sizes to  ≥ 10 μm had high mobility (≈ 100 cm2V−1s−1) and diffusion length (≈ 10 μm)66. Combining doping with thermal treatments might reduce passivation requirements and improve device contacts. Using additives, such as dopants, to change defect properties can also be a promising method for understanding and reducing defects in other polycrystalline semiconductors.

Methods

Fabrication of heterostructures and solar cells

Polycrystalline CdSeyTe1-y semiconductors were grown by vapor transport deposition (VTD) of CdSe and CdTe on glass substrates coated with fluorine-doped tin oxide as the transparent conductive oxide (TCO)3,6,15,30. The CdSeyTe1−y layers have graded Se content with y = 0.20–0.30 near the TCO with the bandgap Eg ≈ 1.4 eV and y < 0.05 at the back with Eg ≈ 1.5 eV. The analytical model for the grading profile was described41, and it was also used in device simulations. Dopants were incorporated into the CdSeTe absorber after the VTD step, followed by a chlorine heat treatment (CHT) where annealing is carried out in the presence of CdCl2 at temperatures between 400 and 500 °C, introducing Cl at levels on the order of 1018 cm−3. During the CHT step, dopant activation occurs in addition to Se diffusion, chlorination, and grain growth3,6,15,30. For As- and P-doping CHT treatment times were 15 min. and 45 min., and it was 45 min. for Sb and N-doping. Samples where CdCl2 treatment time was varied are identified as As-15/As-45 and P-15/P-45. P- and As-doped heterostructures were completed to devices by depositing a ZnTe layer that was capped with a metal stack10,28.

Characterization of solar cells

Selenium grading and dopant incorporation were measured by SIMS (secondary-ion mass spectrometry) and carrier density was measured by CV (capacitance voltage). CV characteristics were measured with an Agilent E4980A impedance analyzer. Voltage was scanned from −2 to +0.5 V in 0.1 V steps in the dark, with a measurement frequency of 40 kHz. SIMS data were collected using a TOF-SIMS-5 instrument with O2-negative profiling. Arsenic-doped samples without metal back contact, including graded-Eg and uniform-Eg compositions, were studied in ref. 13.

Current-voltage measurements were performed using a Newport Model SP94061A-SR1 solar simulator at 1 sun with sample air cooling to maintain 25 °C and scanning from −0.75 to 1.25 V at a rate of 0.93 V/s with 6.5 mV steps. Efficiency, JSC, VOC, and FF are summarized in Fig. 7, where uncertainties indicate standard deviations of these parameters for 12 devices.

Photoluminescence spectroscopy

Absolute PL emission spectra were measured with 1 Sun equivalent excitation (1.98 × 1022 photons cm−2s−1) at 632.8 nm using 300 mm spectrograph equipped with Si CCD and InGaAs array detectors14. Spectral response was corrected using calibration sources provided by the manufacturer (Princeton Instruments), and absolute photon numbers were obtained using reflectance standards (Lab Sphere). TRPL was measured using excitation at 640 nm (300 fs pulses, Pharos/Orpheus OPA system, Light Conversion) and time-correlated single photon counting with Si and gated InGaAs/InP detectors (Picoquant and Micro Photon Devices). For low temperature measurements closed loop He cryostats were used.

Light induced transient grating and pump probe spectroscopy

For light induced transient grating (LITG) and pump-probe (PP) spectroscopy, 10 ps excitation pulses at 527 nm were used. Probe wavelengths were 1056 nm (LITG) and 1550 nm (PP) and the measurements were performed in transmission geometry, as described earlier13. The LITG grating period was varied from Λ = 1.2 μm to 6.8 μm. Light bias in LITG and PP measurements utilized 532 nm continuous-wave laser and fluence of 70 mWcm−2.

Scanning spreading resistance microscopy

SSRM is based on the contact mode of AFM (Bruker Dimension Icon and Nanoscope V) and set in an Ar-glovebox with a logarithm-scale amplifier (Bruker SSRM module) to measure a wide range of resistance (103 − 1014 Ω)30. The probe (Bruker DDESP-V2) is a highly doped diamond-coated Si tip. SSRM is a two-terminal resistance measurement with a bias voltage applied to the sample (Vs), and the probe is floating-grounded. The contact resistance is suppressed sufficiently below the spreading resistance by applying a large probe/sample contact force (≈1 mN) and a large forward sample bias voltage (Vs = +10 V). For sample preparation, the front interface was delaminated by thermomechanical stressing in liquid nitrogen.

Device modeling

Device simulations were conducted using COMSOL Multiphysics® software. The Poisson and current continuity equations were solved numerically by the finite-element method. Simulations of current density versus voltage (JV) were conducted at a temperature of 298 K in the dark and at 1-sun intensity illumination with the AM1.5 G spectrum. Absorber doping density, hole mobility, and Urbach energy were independently varied for this study. Graded CdSeTe band gap, \({E}_{g}(x)\), and electron affinity were included as described in the text. Due to band-gap grading, a depth-dependent absorption coefficient was used in the CdSeTe layer, \(\alpha \left(E,x\right)=A\sqrt{E-{E}_{g}(x)}\), where \(A=\) 105 cm−1 eV-1/2 and \(E\ge {E}_{g}(x)\) is photon energy. For cases with band tails, \(\alpha (E,x)\) was convoluted with an exponential function with decay energy \({E}_{u}\). Further details and parameter values, largely based on refs. 32 and 41, are provided in the Supplementary Information.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.