Introduction

Large Language Models (LLMs)1,2 have become widely accepted as highly capable generalist systems with a surprising range of emergent capacities3,4,5. They have also sparked broad controversy, with some suggesting that they are approaching general intelligence6, and others noting a number of significant deficiencies7. A particularly notable shortcoming is their poor ability to plan or perform faithful multi-step reasoning8,9. Recent work10 has evaluated the extent to which LLMs might possess an emergent capacity for planning and exploiting cognitive maps, the relational structures that humans and other animals utilize to perform planning11,12,13. This work found that LLMs displayed systematic shortcomings in planning tasks that suggested an inability to reason about cognitive maps. Common failure modes included a tendency to hallucinate (e.g., to use non-existent transitions and paths), and to fall into loops. This work raises the question of how LLMs can be improved so as to enable a capacity for planning. This is especially important given the ubiquity of sequential decision-making, reasoning, and planning problems across the wide application of generative AI and LLMs.

In the present work, we take a step toward improving planning in LLMs, by taking inspiration from the planning mechanisms employed by the human brain. Planning is generally thought to depend on the prefrontal cortex (PFC)14,15,16,17,18,19, a region in the frontal lobe that is broadly involved in executive function, decision-making, and reasoning20. Research in cognitive neuroscience has identified specific component processes that are predominantly associated with specific PFC subregions. These include functions such as conflict monitoring21; state prediction and state evaluation22,23; and task decomposition and task coordination24,25,26. Although there is debate over whether the PFC is truly modular, and the specific computational function of each PFC subregion is still a matter of debate27,28,29,30, the identified component processes may nevertheless suggest a useful factorization of the planning process, and may guide the development of modular AI systems with improved planning capabilities.

An interesting observation is that LLMs often seem to display some of these capacities when probed in isolation, even though they are unable to reliably integrate and deploy these capacities in the service of a goal. For instance Momennejad et al.10 noted that LLMs often attempt to traverse invalid or hallucinated paths in planning problems (e.g., to move between rooms that are not connected), even though they can correctly identify these paths as invalid when probed separately. This suggests the possibility of a brain-inspired approach, in which planning is carried out through the coordinated activity of multiple LLM modules, each of which is specialized to perform a distinct process.

With this goal in mind, we propose the Modular Agentic Planner (MAP), an agentic architecture composed of modules that are specialized to perform specific PFC-inspired functions within the planning process. Specifically, we have identified and implemented the following key modules: error monitoring, action proposal, state prediction, state evaluation, task decomposition, and task coordination. Action proposal, state prediction, and state evaluation are further combined to perform tree search. All modules are implemented using an LLM, which receives instructions describing the module’s role via prompting and few-shot in-context learning (ICL). The resulting MAP algorithm solves reasoning and planning problems via the recurrent interaction of these modules, combining the strengths of classical planning and search algorithms with the use of LLMs as general-purpose world models and planning functions.

We evaluate MAP on four challenging decision-making tasks that require planning and multi-step reasoning. First, we investigate Tower of Hanoi (ToH), a classic problem-solving task that requires multi-step planning31, and for which performance is known to be heavily dependent on PFC function32,33. Second, we performed controlled experiments on a set of graph traversal tasks according to the CogEval protocol10. These tasks require goal-directed navigation in novel environments (MDPs) described in natural language, of which we selected an environment that was most challenging for LLMs, including GPT-4. Third, we investigate the two most challenging tasks in the PlanBench benchmark: Mystery BlocksWorld and Logistics8. Finally, we investigate a challenging NLP task that requires multi-step reasoning, StrategyQA34. We find that, when implemented with GPT-4, MAP significantly improves performance on all four tasks, and that the algorithm can also be effectively implemented with a smaller and more cost-efficient LLM (Llama3-70B). Transfer experiments further indicate that MAP displays an improved ability to generalize between tasks, and ablation experiments indicate that each of the individual modules plays an important role in the overall architecture’s performance. Taken together, these results indicate the potential of a brain-inspired approach to improve the reasoning and planning capabilities of LLMs.

Results

Problem formulation

We define a planning task \({{{\mathcal{T}}}}\) as a tuple:

$${{{\mathcal{T}}}}=({{{\mathcal{S}}}},{{{\mathcal{A}}}},T,{s}_{0},{s}_{goal})$$
(1)

where \({{{\mathcal{S}}}}\) is the set of all possible states in an environment, \({{{\mathcal{A}}}}\) is the set of available actions, \(T:{{{\mathcal{S}}}}\times {{{\mathcal{A}}}}\to {{{\mathcal{S}}}}\) is the transition function, s0 is the starting state at the beginning of the task, and sgoal is the goal state. A plan P is a sequence of actions:

$$P=({a}_{1},{a}_{2},\ldots,{a}_{N}),\quad {a}_{i}\in {{{\mathcal{A}}}}$$
(2)

such that applying P to s0 under T results in transitioning to sgoal (Fig. 1). We are interested in the setting in which an agent is not allowed to interact with the external environment to iteratively refine a plan, but instead must generate a plan internally based on knowledge of the structure of the environment (given in the task description provided to the model). Importantly, we investigate problems in which the planning task (e.g., the set of all possible states \({{{\mathcal{S}}}}\) and the transition function T) is not formally specified, but is instead informally described in natural language. Rather than receiving the transition function directly, the components of the model must infer from this natural language description which state will result from a particular action, whether a particular action is valid or invalid, etc., meaning that classical planning algorithms cannot be directly applied to these problems.

Fig. 1: Modular agentic planner (MAP).
figure 1

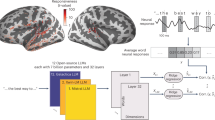
The agent receives states from the environment and high-level goals. These are processed by a set of specialized LLM modules. The Task Decomposer receives the current state and a high-level goal and generates a series of subgoals. The Actor generates proposed actions given a state and a subgoal. The Monitor gates these proposed actions based on whether they violate certain constraints (e.g., task rules) and provides feedback to the Actor. The Predictor predicts the next state given the current state and a proposed action. The Evaluator is used to estimate the value of a predicted state. The Predictor and Evaluator are used together to perform tree search. The Orchestrator determines when each subgoal has been achieved, and when the final goal has been achieved, at which point the plan is emitted to the environment as a series of actions.

Full size image

Architecture and approach

Figure 1 depicts the MAP architecture. MAP consists of a set of modules, each of which is implemented by an LLM, and a set of algorithms through which they interact to generate a plan. The modules and algorithms employed by MAP are inspired by the factorization of planning in the human PFC. In the following sections, we first describe each of the modules, highlighting the specific ways in which they are inspired by specific brain regions involved in planning, and then provide a formal specification of the algorithms that employ these modules to perform planning. Throughout our description of the architecture and algorithm, we refer to the Tower of Hanoi task shown in Fig. 2A as an illustrative example.

Fig. 2: Tower of hanoi task and results.
figure 2

A Depiction of Tower of Hanoi (ToH) task. Original formulation involves disks of different sizes stacked on a set of pegs. Disks must be moved from initial state to goal state while avoiding invalid moves. To test LLMs, an alternative formulation was created involving lists of digits, ensuring that the task could not be solved based on standard solutions that may be found in the LLMs' training data. B ToH results. `% solved' indicates the percentage of problems solved without proposing invalid actions (↑ better). `% invalid' indicates the percentage of moves that are invalid (↓ better). Note that 4-disk problems are out-of-distribution (OOD). ICL: in-context learning; CoT: chain-of-thought; MAD: multi-agent debate; ToT: tree-of-thought. GPT-4 Zero-shot, ICL, CoT, and MAD baselines are deterministic and reflect a single run. Gray error bars reflect 95% binomial confidence intervals. Black dots indicate performance for individual runs. Colored dots reflect values of 0%. Dark bars indicate average performance over multiple plans/runs. Light bars indicate best performance. MAP results for 3-disk problems reflect the average over 5 runs  ± the standard error of the mean (black error bars). MAP results for 4-disk problems reflect a single run, due to the high computational cost of multiple runs. See Supplementary Section S3 for results in tabular form.

Full size image

MAP employs a set of brain-inspired modules, each constructed from a separate LLM instance. For each module, the LLM is provided with a description of the environment and task, along with a description of the role that the module is supposed to play, and in-context examples (≤3 examples) that illustrate this role. More details on the specific prompts can be found in Supplementary Section S4. The modules are described below:

  • TaskDecomposer. The TaskDecomposer receives the start state s0 and a goal sgoal and generates a set of subgoals SZ that will allow the agent to gradually work toward its final goal:

    $$\,{\mbox{TaskDecomposer}}\,({s}_{0},{s}_{goal})\to {S}_{Z}=({s}_{{z}_{1}},\ldots,{s}_{{z}_{K}})$$
    (3)

    For example, in the ToH task (Fig. 2A), the number 0 must be moved from list A to list C, but in order to do so, the larger numbers must first be moved out of list A. In this case, a subgoal might be to move the larger numbers into list B. To implement this module, the in-context examples included chain-of-thought reasoning that illustrated how to identify effective subgoals for a given task (see Supplementary Section S4). This module is inspired by the anterior PFC (aPFC), which is known to play a key role in task decomposition (among other functions) through the generation and maintenance of subgoals24.

  • Actor. The Actor receives the current state st and a subgoal \({s}_{{z}_{k}}\) and proposes B potential actions:

    $$\,{\mbox{Actor}}\,({s}_{t},{s}_{{z}_{k}},\epsilon )\to \{{a}_{1},\ldots,{a}_{B}\}\in {{{\mathcal{A}}}}$$
    (4)

    The Actor can also receive feedback ϵ from the Monitor about its proposed actions. This module can be viewed as being analogous to the dorsolateral PFC (dlPFC), which plays a role in decision-making through top-down control and guidance of lower-order premotor and motor regions20.

  • Monitor. The Monitor assesses the actions proposed by the Actor to determine whether they are valid (e.g., whether they violate the rules of a task). Invalid actions are any actions not contained in the transition function T for the current state st. The Monitor emits an assessment of validity σ, and also feedback ϵ in the event the action is deemed invalid:

    $$\,{\mbox{Monitor}}\,({s}_{t},a)\to (\sigma \in \{0,1\},\epsilon )$$
    (5)

    For example, in the ToH task, this module is responsible for determining whether any of the proposed actions are invalid moves (see Fig. 2A). This module is inspired by the Anterior Cingulate Cortex (ACC), which is known to play a role in conflict monitoring21, i.e., detecting errors or instances of ambiguity.

  • Predictor. The Predictor receives the current state st, and a proposed action a, and predicts the resulting next state \({\tilde{s}}_{t+1}\):

    $$\,{\mbox{Predictor}}\,({s}_{t},a)\to {\tilde{s}}_{t+1}\in {{{\mathcal{S}}}}$$
    (6)

    The Predictor is inspired by the Orbitofrontal cortex (OFC), which plays a role in estimating and predicting task states. In particular, it has been proposed that the OFC plays a key role in encoding cognitive maps: representations of task-relevant states and their relationships to one another23.

  • Evaluator. The Evaluator receives a next-state prediction \({\tilde{s}}_{t+1}\) and produces an estimate of its value v in the context of goal sgoal. This is accomplished by prompting the Evaluator (and demonstrating via a few in-context examples) to estimate the minimum number of steps required to reach the goal (or subgoal) from the current state:

    $$\,{\mbox{Evaluator}}\,({\tilde{s}}_{t+1},{s}_{goal})\to v\in {{\mathbb{R}}}_{\ge 0}$$
    (7)

    The Evaluator is also inspired by the OFC, which, in addition to predicting task states, plays a key role in estimating the motivational value of those states22.

  • Orchestrator. The Orchestrator receives the current state st, and a subgoal \({s}_{{z}_{k}}\) and emits an assessment Ω of whether the subgoal has been achieved:

    $$\,{\mbox{Orchestrator}}\,({s}_{t},{s}_{{z}_{k}})\to \varOmega \in \{0,1\}$$
    (8)

    When the Orchestrator determines that all subgoals (including the final goal) have been achieved, the plan is emitted to the environment as a series of actions. This module is also inspired by the aPFC, which is thought to both identify subgoals and coordinate their sequential execution24.

MAP’s modules interact via the following algorithms to generate a plan:

  • Action Proposal Loop. The Actor and Monitor interact via the ProposeAction function (Algorithm 1). The Actor proposes a set of potential actions, which are then gated by the Monitor. If the Monitor determines that the actions are invalid (e.g., they violate the rules of a task), feedback is provided to the Actor, which then proposes an alternative action. The output of the ProposeAction function is a set of potential actions, one of which will be selected as the action at the next time step (as described in the following section).

  • Tree Search. ProposeAction is embedded in a Search loop (Algorithm 2). The actions emitted by ProposeAction are passed to the Predictor, which predicts the states that will result from these actions. A limited tree search is then performed, starting from the current state, and then exploring B branches recursively to a depth of L layers. Values are assigned to the terminal states of this search by the Evaluator, and the action leading to the most valuable predicted state is selected. In the brain, this search process is thought to be coordinated by the aPFC, which enables the parallel consideration of multiple plans (i.e., cognitive branching)35. This process is known to be significantly capacity-limited (i.e., the breadth and depth of the search process are severely constrained). This is in line with the limited search performed by our model.

  • Plan Generation. Algorithm 3 describes the complete MAP algorithm. To generate a plan, the TaskDecomposer component of MAP first generates a set of subgoals based on the final goal and current state. These subgoals guide the search and are internally pursued one at a time, utilizing the Search loop to generate actions until the Orchestrator determines that the subgoal has been achieved. For some simpler tasks, we do not employ the TaskDecomposer, and only the final goal is pursued (though this is only for simpler tasks - for more complex tasks, ablating the TaskDecomposer significantly impairs performance). The actions are accumulated in a plan buffer P until either the Orchestrator determines that the final goal has been reached, or the maximum allowable number of actions N is accumulated.

Benchmarks

We investigate several benchmarks that instantiate this problem. First, we investigated a classic multi-step problem-solving task, the Tower of Hanoi (ToH). ToH was a popular testbed for the development of early symbolic planning methods31, but it exemplifies the type of complex, multi-step planning tasks that are still challenging for LLMs. The task is illustrated in Fig. 2A. In the original task, there are three pegs and a set of disks of different sizes. The disks must be moved into a particular goal configuration, while observing a set of constraints that prevent simple solutions. In our experiments, we designed an alternative (but isomorphic) formulation of this task in which the inputs are text-based rather than visual. This text-based formulation made it possible to evaluate language models on the task, but it also resulted in a task that does not share any surface features with the original task, making it unlikely that GPT-4 could rely on exposure to descriptions of ToH in its training data to solve the problem.

We also investigated a set of graph traversal tasks from the CogEval benchmark10, which was recently proposed to study the navigation and planning capabilities of LLMs. For each task, a complete description of a graph was first provided, consisting of nodes and pairwise edges. Figure 3A depicts some of the tasks, including the Steppath task, involving navigation from a start state to a goal state, and the Valuepath task, involving navigation from a start state to the location with the highest reward.

Fig. 3: Graph traversal tasks and results.
figure 3

A Graph traversal tasks. Steppath: Agent must identify the shortest path from a start state to a goal state. Valuepath: Agent must identify the shortest path from a start state to the state with the largest reward, while avoiding the state with the smaller reward. B Graph traversal results. `% solved' indicates the percentage of problems solved without proposing invalid actions (↑ better). GPT-4 Zero-shot, ICL, COT, and MAD baselines are deterministic, and therefore, a single run was performed on all problems. Note that MAP did not employ tree search on the Steppath task, and did not employ task decomposition on any of the graph traversal tasks. Without tree search, MAP's performance is deterministic, and therefore only a single run was performed on the Steppath task, whereas we performed 5 runs with ToT. Gray error bars reflect 95% binomial confidence intervals (for models evaluated on a single run). Black dots indicate performance for individual runs. Colored dots reflect values of 0%. Dark bars indicate average performance over multiple plans/runs. Light bars indicate best performance. For Valuepath, Detour, and Reward Revaluation, we performed 10, 10, and 5 runs, respectively, with MAP and ToT, and present average performance  ± the standard error of the mean (black error bars). See Supplementary Section S3 for results in tabular form.

Full size image

We also evaluated our approach on tasks from PlanBench, a large-scale benchmark consisting of planning tasks in various domains8. Planning problems in this task consist of a set of initial configurations, a goal configuration, and a set of constraints that are specific to each domain. We investigate two of the most challenging domains: Logistics, featuring problems involving the transportation of goods with different forms of transportation (airplanes, trucks, etc); and the ‘Mystery Blocksworld’ (MBW) domain, which is structurally isomorphic to Blocksworld (an easier domain that involves stacking blocks), but involves objects and actions with meaningless or confusing names (thus requiring a greater degree of abstraction).

Finally, to evaluate the extent to which the proposed approach can be useful in more real-world settings, we investigated the StrategyQA dataset34, a task that consists of unusual questions that require multi-step reasoning and retrieval of general knowledge. For example, the task involves questions such as ‘Did Aristotle use a laptop?’, which require the reasoner to first generate and answer a series of intermediate questions (e.g., ‘When did Aristotle live?’, ‘When was the laptop invented?’), and then integrate the results of these intermediate inferences to generate an answer.

Problem solving: Tower of Hanoi

Figure 2B shows the results for the ToH task. As expected, the alternative, text-based formulation of the task was very difficult for LLMs, with GPT-4 zero-shot only solving 11% of standard 3-disk problems. This is in contrast to MAP, which achieved an average performance of 74% solved problems, and solved every problem at least once out of five attempts. MAP also outperformed a number of baseline methods, including: a version of GPT-4 that was given access to in-context examples of successful solutions (GPT-4 ICL); a version of GPT-4 that was also given access to detailed explanations of those solutions, sometimes referred to as chain-of-thought36 (GPT-4 CoT); Tree-of-Thought (ToT)37, a method that combines LLMs with tree search, similar to the search performed by MAP; and Multi-Agent Debate (MAD)38. These results illustrate several important points. First, the comparison between MAP and GPT-4 ICL indicates that MAP’s improved performance cannot be explained purely as a consequence of the in-context examples that are used to specialize the modules. Second, the comparison between MAP and GPT-4 CoT indicates that planning cannot be comparably improved simply through additional inference-time computation (i.e., chain-of-thought), but that it is important to modularize this inference-time computation as in MAP. Third, the comparison between MAP and ToT indicates that MAP’s improved performance is not due solely to the use of tree search, but also depends on the other modules (though, as shown in the ablation results presented below, tree search does play an important role). Finally, the comparison between MAP and MAD indicates that is not sufficient to use several LLM instances to perform planning (as is done with multi-agent debate), but that it is important to also give specialized roles to each of the LLM instances.

To study the robustness and generalizability of MAP’s planning abilities, we also investigated a set of out-of-distribution (OOD) problems involving 4 disks (the prompts and in-context examples used for each of the modules involved only 3-disk problems). We found that MAP demonstrated some capacity for OOD generalization (solving 24% of problems correctly), whereas the baseline methods solved very few problems in this setting (GPT-4 CoT, the best performing baseline, solved only 5% of OOD problems). Importantly, we also found that MAP’s performance in this OOD setting was on par with its performance in a comparable in-distribution setting (Supplementary Table S3). Specifically, MAP performed similarly when presented with in-context examples that were also from 4-disk problems, whereas the GPT-4 ICL baseline showed significantly worse performance in the OOD vs. in-distribution setting (and worse performance than MAP in both settings). This suggests that the lower performance observed for MAP on 4-disk problems is driven primarily by their greater complexity, rather than the use of out-of-distribution in-context examples.

We also carried out an ablation study to determine the relative importance of each of MAP’s major components, focusing on the 3-disk ToH problems. Table 1 shows the results. We found that the Monitor was the most important component, as ablating this module resulted in significantly fewer solved problems, due primarily to an increased tendency to propose invalid moves (31% invalid moves vs. 0% for other ablation models). This highlights the importance of having a separate, modularized monitoring process, which prevented MAP from proposing any invalid actions, even in the OOD setting (Fig. 2B), whereas all of the baseline methods proposed some number of invalid actions. Ablating the tree search and TaskDecomposer module also resulted in significantly fewer solved problems, indicating the importance of these components. Furthermore, a version of MAP in which the TaskDecomposer generated two subgoals outperformed the default version that used only a single subgoal, further underscoring the usefulness of subgoals. Overall, these results suggest that all major components played an important role in MAP’s performance, with the Monitor playing an especially important role.

Table 1 Ablation study on ToH (3-disk problems)
Full size table

One concern with the proposed approach is that it incurs substantially greater computational costs than simpler LLM methods (see Supplementary Section S1). We addressed this in two ways. First, we developed a more efficient version of MAP that cached and reused module outputs for redundant prompts, reducing computational costs by a factor of 3 (while retaining the same level of performance, Table S6). Second, we investigated the extent to which MAP could be combined with smaller, less costly LLMs by implementing a version that used the open-source model Llama3-70b for all modules instead of GPT-4. In experiments on 3-disk ToH problems, we found that MAP still outperformed other baselines that employed the same Llama3-70b language model, and even outperformed the best GPT-4 baseline, GPT-4 ICL (Table 2), suggesting that smaller LLMs may enable a more cost-efficient version of the proposed approach.

Table 2 Results on ToH (3-disk problems) using a smaller LLM (Llama3-70B)
Full size table

Navigation: CogEval

Figure 3B shows the results for the graph traversal tasks from the CogEval benchmark10. On Steppath, MAP outperformed all baselines, achieving perfect performance for 2-step and 3-step paths. The discrepancy was especially pronounced for 4-step paths, where MAP still achieved nearly perfect performance (95% of problems solved), while all baselines showed a dramatic drop in performance (with the best performing baseline, ToT, only solving 50% of problems). MAP also achieved perfect performance on the Valuepath task, again outperforming all baselines. Notably, the ToT baseline was able to solve each of the Valuepath problems on at least one attempt (i.e., best performance of 100%), but was not able to do so reliably, whereas MAP reliably solved these problems on every attempt. This indicates that, although the tree search process enabled ToT to occasionally identify a correct solution, the model had no method for reliably determining when a goal had been achieved. This is in contrast to MAP, which uses the Orchestrator module to determine when the tree search process has converged on a correct solution, enabling MAP to reliably solve these problems.

We also investigated two tasks that probe the flexibility of MAP’s planning capabilities by altering the task following the initial problem description. In one task, Detour, an edge is removed from the graph. In the other task, Reward Revaluation, the value associated with the two reward locations is changed, such that the higher reward location becomes the lower reward location, and vice versa. We found that MAP outperformed all baselines on the Detour task, and performed on par with the baselines on the Reward Revaluation task (while still outperforming GPT-4 zero-shot), demonstrating that MAP can flexibly adjust to new circumstances when generating plans. Additionally, we found that, aross all four graph traversal tasks, MAP proposed very few ( < 1%) invalid actions (i.e., actions that involved traversal of non-existent edges), whereas many baselines proposed a significant number of invalid actions (Fig. 4). This further emphasizes the importance of having a separate Monitor module, which filtered invalid actions proposed by the Actor. Overall, our experiments with graph traversal tasks indicated that MAP can improve the robustness and flexibility of goal-directed navigation in LLMs.

Fig. 4: Invalid actions in graph traversal tasks.
figure 4

`% invalid' indicates the percentage of moves that are invalid (↓ better). GPT-4 Zero-shot, ICL, CoT, and MAD baselines are deterministic, and therefore, a single run was performed on all problems. Note that MAP did not employ tree search on the Steppath task, and did not employ task decomposition on any of the graph traversal tasks. Without tree search, MAP's performance is deterministic, and therefore only a single run was performed on the Steppath task, whereas we performed 5 runs with ToT. Gray error bars reflect 95% binomial confidence intervals (for models evaluated on a single run). Colored dots reflect values of 0%. For Valuepath, Detour, and Reward Revaluation we performed 10, 10, and 5 runs respectively with MAP and ToT, and present average performance  ± the standard error of the mean (black error bars).

Full size image

Planning: PlanBench

Table 3 shows the results for the PlanBench dataset, where MAP outperformed all of the baselines that we considered. Notably, due to the complexity of the problems in this dataset, it was very costly to perform tree search (Supplementary Table S3), so we evaluated a minimal version of MAP that did not involve tree search. For this same reason, we were unable to evaluate a ToT baseline on the full set of problems. However, we performed an evaluation on a smaller subset of problems, finding that MAP substantially outperformed ToT (Table 4). Overall, these results indicate that MAP can provide significant performance benefits even when tree search is not feasible, and can even outperform methods that employ tree search, such as ToT. Note also that we did not apply the TaskDecomposer for the Mystery BW domain, since MAP already significantly outperformed all baselines, whereas the TaskDecomposer was applied to the Logistics domain, where it improved performance (24% accuracy with TaskDecomposer vs. 20.5% accuracy without TaskDecomposer).

Table 3 PlanBench results
Full size table
Table 4 PlanBench results for a smaller subset of problems (the first 30/200 problems for Logistics, and the first 100/500 problems for Mystery BW) comparing MAP with ToT
Full size table

Real-world reasoning: StrategyQA

Table 5 shows the results for the StrategyQA dataset34. We found that MAP outperformed both the GPT-4 CoT and ToT baselines, and performed on par with human participants. These results indicate that MAP can also yield benefits in more real-world settings, such as multi-step reasoning with natural language.

Table 5 StrategyQA results
Full size table

Transfer experiments

Finally, we performed transfer experiments to study whether few-shot in-context learning would support generalization to different planning tasks. For ToH, we studied whether in-context learning on 3-disk problems could be generalized out-of-distribution to 4-disk problems. Here, we extend these results to study out-of-distribution generalization between tasks. Table 6 shows the results for these experiments, including results for transfer from planning on a smaller graph to planning on a larger graph (n7tree → n15star, using the CogEval dataset10), transfer to a semantically distinct but structurally isomorphic task (blocksworld (BW) → mystery blocksworld (mystery BW), using the PlanBench dataset8), and transfer between completely different tasks (ToH  → Mystery BW). We found that MAP outperformed both GPT-4 ICL and CoT in each of these settings, indicating that MAP can improve the generalizability and robustness of planning in LLMs.

Table 6 Transfer between different planning tasks
Full size table

Discussion

In this work, we have proposed the MAP architecture, a modular agentic approach aimed at improving planning with LLMs. In experiments on four challenging domains, we found that MAP significantly improved multi-step planning and decision-making performance over other LLM methods (e.g., Chain of Thought, Multi-Agent Debate, Tree of Thought). We also found that MAP could be effectively combined with a smaller, less costly LLM (Llama3-70b), supports improved (albeit imperfect) transfer and generalization between different planning tasks, and, through a series of ablation experiments, established that each of MAP’s components makes an important contribution to overall performance.

Related work

Early work in AI formalized planning as a problem of search through a combinatorial state space, typically utilizing various heuristic methods to make this search tractable39,40. Problems such as ToH figured prominently in this early research31, as it affords the opportunity to explore ideas based on hierarchical or recursive planning (in which a larger problem is decomposed into a set of smaller problems). Our proposed architecture adopts some of the key ideas from this early work, including tree search and hierarchical planning.

A few recent studies have investigated planning and multi-step decision-making in LLMs. These studies suggest that, although LLMs can perform relatively simple planning tasks41, and can learn to make more complex plans given extensive domain-specific fine-tuning42,43, they struggle on tasks that require zero-shot or few-shot generation of multi-step plans8,10. These results also align with studies that have found poor performance in tasks that involve other forms of extended multi-step reasoning, such as arithmetic9. Our approach is in large part motivated by the poor planning and reasoning performance exhibited by LLMs in these settings.

Our approach is similar to other recently proposed black-box approaches in which ‘thoughts’ – meaningful chunks of natural language – are utilized as intermediate computations to solve more complex problems. These approaches include ‘scratchpads’ or chain-of-thought36,44, methods that incorporate explicit tree search37,45, ‘least-to-most’ prompting (incorporating task decomposition)46, and methods for combining planning with external tools47,48 or external model-based verifiers49. All of these approaches can be viewed as implementing a form of controlled, or ‘system 2’, processing (as contrasted with automatic, or ‘system 1’, processing)50,51,52. Our approach has a similar high-level motivation, and shares some components with other black box approaches (e.g., tree search37 and task decomposition46), but also introduces a number of new components. These include our LLM-based Monitor (which is distinct from the use of domain-specifc model-based verifiers in previous work49, and distinct from the use of LLM-verification at the level of entire plans53), and the Orchestrator (responsible for determining whether a goal or subgoal has been achieved). We also combine these components in a novel manner and provide a collective framework that allows them to autonomously interact to generate a plan. Importantly, we find that the combined architecture substantially outperforms the most competitive variants of these approaches (e.g., tree-of-thought) across all of the experiments that we performed.

Our approach is also related to a classic line of work in cognitive science on the topic of cognitive architectures54,55,56. The aim of that work was to develop systems of interacting cognitive components, including processes for perception, memory, and decision-making, typically instantiated with symbolic components. More recently, the rise of language model agents–integrated systems consisting of multiple interacting language models performing specialized roles–can be viewed as an instantiation of cognitive architectures, albeit with components formed from pretrained language models instead of symbolic programs57. In this work, we have proposed a specific cognitive architecture for reasoning and decision-making. In future work, it will be useful to integrate this with components that carry out other processes, such as perception or memory.

There have also been a number of proposals for incorporating modularity into deep learning systems, including neural module networks58, and recurrent independent mechanisms59. Our approach is distinguished from these approaches by the proposal of modules that perform specific high-level component processes, based on knowledge of specific subregions within the PFC. This approach is also closely related to a recent proposal to augment deep learning systems with PFC-inspired mechanisms17. MAP can be viewed as a concrete framework for accomplishing this goal.

Our proposal is also related to reinforcement learning (RL)60, which has a close connection to the PFC18,61,62,63,64,65. In particular, many of the modules in the MAP algorithm are closely related to aspects of traditional RL algorithms. Specifically, the Actor and Evaluator modules bear some resemblance to the actor and the critic in the popular actor-critic framework66, and the TaskDecomposer is related to hierarchical RL67,68,69, in which temporal abstractions are learned to achieve subgoals. The Predictor is also closely related to the world model that can substitute for direct interaction with the environment in model-based RL60,70. An important difference in each of these cases is that the modules in MAP only receive a task description and a couple of examples, relying on the general-purpose knowledge of the LLM to effectively perform the task, rather than being trained through RL. This also distinguishes the approach from other recent efforts to combine LLMs and RL71,72,73, and to train LLMs to perform search74,75,76,77, both of which involve training LLMs directly on decision-making and planning tasks, whereas MAP generates plans internally. Finally, there are also some modules that have no obvious analog in previous RL algorithms, but which were necessitated by weaknesses that LLMs display in the planning domain. These include the Monitor, which was necessitated by the tendency of LLMs to hallucinate or violate task constraints, and the Orchestrator, which allows MAP to autonomously determine when a goal has been achieved (without ground truth evaluation) and thus terminate planning.

Limitations and future directions

It is worth emphasizing a few limitations of the proposed approach. First, in this work, we only considered problems in which the environment is fully observable and deterministic. Although even this setting is challenging for LLMs, it will be important in future work to investigate how the proposed approach can be extended to more complex open-ended environments. This will likely necessitate the incorporation of additional components, including memory mechanisms for storing knowledge about the environment as it is accumulated in partially observable settings. Additionally, the model still has less than optimal performance in some tasks, including Tower of Hanoi, the Reward Revaluation graph traversal task, and the PlanBench benchmark (see Supplementary Section S2), and although it improves transfer performance and out-of-distribution generalization, these settings are still very challenging for the model. This may be due in part to the inherent limitations of prompting and in-context learning as methods for the specialization of MAP’s modules. This limitation is particularly pronounced for the TaskDecomposer module, which currently requires carefully designed chain-of-thought prompts to identify effective subgoals. More work is needed to develop an effective general-purpose approach to task decomposition.

One promising avenue for further improvement may be to jointly fine-tune smaller open-source LLMs to serve as modules across a range of diverse tasks, rather than relying only on black box methods (as with GPT-4). This approach would also eliminate the need for task-specific prompts and may further improve zero-shot planning on novel tasks. Finally, the proposed approach incurs substantially greater computational costs than simpler LLM methods. Although this aligns well with the deliberative nature of controlled (i.e., system 2) processes52, it would nevertheless be desirable to find ways to reduce these costs. In this work, we found that costs can be partially mitigated through the use of a smaller LLM (Llama3-70B), though performance was not as strong as the version that used GPT-4. A fine-tuning approach would thus also likely reduce costs by enabling smaller models to more effectively perform the specialized roles of each module.

Finally, it should be noted that MAP does not constitute a detailed computational model of the prefrontal cortex. Instead, our goal in the present work was to take high-level inspiration from what is known about planning in the prefrontal cortex—including both the general modular organization, as well as the specific component processes and the ways in which they interact—and to leverage these insights to improve planning with LLMs. However, it may be beneficial in future work to more directly apply the MAP framework as a neuroscientific model of PFC function. In particular, though much previous work has characterized the function of individual PFC subregions21,22,23,24, there has been less emphasis on the development of integrative models in which these functions interact to carry out coordinated behavior. The present work represents a first step in that direction. An important next step will be to directly evaluate MAP as a model of neural data, which may then lead to further refinements of the model. We look forward to investigating these possibilities in future work.

Methods

Experiment details

We implemented each of the modules using a separate instance of GPT-4 (32K context, ‘2023-03-15-preview’ model index for ToH and cogeval tasks, and 128K context, ‘0125-preview‘ model index for strategyQA and planbench tasks from Microsoft Azure openAI service) through a combination of prompting and few-shot in-context examples. We set Top-p to 0 and temperature to 0, except for the Actor (as detailed in Supplementary Section S4). The Search loop explored B = 2 branches recursively for a depth L = 2.

For ToH, we used two randomly selected in-context examples of three-disk problems and a description of the problem in the prompts for all the modules. For the graph traversal tasks, we used two in-context examples for all modules, except for the Actor and Evaluator in the Steppath task, where we used three in-context examples, one each for 2-, 3-, and 4-step paths. For strategyQA, we didn’t use any in-context examples. For the logistics task from Planbench, we used two incontext examples for all modules except for Actor which used three in-context examples. For the mystery blocksworld (deceptive) task from Planbench, we used two in-context examples for all modules except for Actor and Predictor, which used three in-context examples. For both the tasks from Planbench, we extracted the goal from the initial state conditions, and the state and the goal was separately fed as input to the modules as required. The prompt also described the specific task that was to be performed by each module (e.g., monitoring, task decomposition). For more details about the prompts and specific procedures used for each module, see Supplementary Section S4.

For three-disk ToH problems, we allowed a maximum of N = 10 actions per problem, and evaluated on 24 out of 26 possible problems (leaving out the two problems that were used as in-context examples for the Actor). We also evaluated on four-disk ToH problems, for which we allowed a maximum of N = 20 actions per problem. The same three-disk problems were used as in-context examples, meaning that the four-disk problems tested for out-of-distribution (OOD) generalization. For the graph traversal tasks, we allowed a maximum of N = 6 actions per problem. For strategyQA, we allowed N = 1 action per problem. For the Planbench tasks, we allowed a maximum of N = 4 + number of actions in the optimal plan.

For ToH, the TaskDecomposer generated only a single subgoal by default, but we also evaluated a version of the model in which the TaskDecomposer generated two subgoals. For the graph traversal tasks, we didn’t use a separate Predictor, since the action proposed by the Actor directly specifies the next state. We also did not include the TaskDecomposer for these tasks, and did not use the Search loop for the Steppath task, as the model’s performance was already at ceiling without the use of these components. For strategyQA, we didn’t use the Evaluator or the Orchestrator. For the Planbench tasks we didn’t use tree search, and for mystery blocksworld task we didn’t use the TaskDecomposer. To compare MAP with ToT on a smaller subset of PlanBench problems, we used the first 30 (out of 200) problems from the logistics domain, and the first 100 (out of 500) problems from the mystery blocksworld domain.

For the ToT baseline in StrategyQA, Yao et al.37 reported a performance of 83%, but since the subset of 100 questions they used for evaluation is unknown, we ran ToT using the publicly released code on a fixed subset of 100 questions for fair comparison with MAP. Human performance on this task reflects a random subset of 100 questions, as reported by Geva et al.34.

Algorithms

Algorithm 1

Action proposal loop. ProposeAction takes a state st and a goal sgoal and generates B potential actions A = ab=1…ab=B. This is implemented via a loop, in which the Actor first proposes potential actions, and the Monitor then assesses those actions according to certain constraints (e.g., task rules), providing feedback if any of the actions are deemed to be invalid. This continues until the proposed actions are considered valid.

Algorithm 2

Search loop. Tree search with a depth of L layers, with B branches at each layer l. For each branch, a proposed action is sampled, and the Predictor predicts the next state \({\tilde{s}}_{t+1}\). This process continues recursively until the terminal layer L, at which point the value vl= L of the terminal states is estimated by the Evaluator. The values are backpropagated to their parent states in the first layer, and the action that leads to the most valuable state is selected. In our implementation, we accelerate this process by caching the actions and predicted states from deeper search layers and then reusing them in subsequent searches. We also employ the Orchestrator to prematurely terminate the search if the goal state is achieved.

Algorithm 3

Modular Agentic Planner (MAP). MAP takes a state s0 and a goal sgoal and generates a plan P, a series of actions with a maximum length of N. The TaskDecomposer first generates a set of subgoals SZ. The agent then pursues each individual subgoal sz in sequence, followed by the final goal sgoal. At each time step, Search (Algorithm 2) is called to generate an action and a predicted next state. Actions are added to the plan until the Orchestrator determines that the goal has been achieved, or the plan reaches the maximum length N.