High-throughput screening of 2D materials identifies p-type monolayer WS₂ as potential ultra-high mobility semiconductor

Abstract

2D semiconductors offer a promising pathway to replace silicon in next-generation electronics. Among their many advantages, 2D materials possess atomically-sharp surfaces and enable scaling the channel thickness down to the monolayer limit. However, these materials exhibit comparatively lower charge carrier mobility and higher contact resistance than 3D semiconductors, making it challenging to realize high-performance devices at scale. In this work, we search for high-mobility 2D materials by combining a high-throughput screening strategy with state-of-the-art calculations based on the ab initio Boltzmann transport equation. Our analysis singles out a known transition metal dichalcogenide, monolayer WS₂, as the most promising 2D semiconductor, with the potential to reach ultra-high room-temperature hole mobilities in excess of 1300 cm²/Vs should Ohmic contacts and low defect densities be achieved. Our work also highlights the importance of performing full-blown ab initio transport calculations to achieve predictive accuracy, including spin–orbital couplings, quasiparticle corrections, dipole and quadrupole long-range electron–phonon interactions, as well as scattering by point defects and extended defects.

Introduction

Ever since the early days of integrated circuits, the number of transistors per chip has nearly doubled every two years, a trend that is known as Moore’s law¹. For this trend to continue beyond the current 5 nm technology node, it will be necessary to develop GAAFETs (gate-all-around field-effect transistors) and ribbonFETs with sub-nanometer channel thickness². In this ultra-scaled regime, the carrier mobility of silicon is severely degraded by quantum confinement, surface roughness, and dangling bonds, falling below 50 cm²/Vs at room temperature^3,4. To mitigate this effect, van der Waals 2D materials are being investigated as potential transistor channels. The main appeal of 2D materials is that they possess atomically sharp surfaces and can be scaled down to the monolayer limit^5,6,7. Additionally, the use of 2D materials enables the reduction of the gate length as compared to silicon finFETs, leading to lower switching capacitance and reduced power consumption⁸.

Despite their unique promise, the use of 2D materials in transistor channels faces significant challenges. For one, reduced dimensionality leads to intrinsically high density of electronic states at the band edges, which leads to high carrier scattering rates and low phonon-limited mobilities^9,10,11,12. Furthermore, the very lack of surface dangling bonds makes it harder to form Ohmic contacts, leading to high contact resistance². On top of these difficulties, native defects in 2D materials and the lack of suitable dopants make it challenging to avoid Fermi-level pinning. As a result, most 2D materials exhibit low field-effect mobilities, typically in the range of 50–100 cm²/Vs^5,6.

Advanced ab initio computational methods can play an important role in this area by shedding light on the microscopic mechanisms that hinder carrier transport in 2D materials, and by helping to identify high-mobility compounds via computational screening. Several groups have embarked in the computational search for high-mobility 2D materials^{9,11,12,13,14,15}. For example, in ref. ¹⁴, the authors have performed mobility calculations for two dozen putative binary borides, nitrides, and oxides in the monolayer hexagonal lattice, as well as III–V and II–VI semiconductors in the bilayer hexagonal lattice. They identified several candidates with very high mobility, in excess of 1000 cm²/Vs. However, these calculations are based on the relaxation time approximation and do not include spin-orbit coupling except for BSb. In ref. ¹³, the authors considered electron-doped MoS₂, WS₂, WSe₂, phosphorene, and arsenene, as well as hole-doped phosphorene, but spin-orbit coupling was not accounted for. They identified phosphorene as the most promising n-type channel, however this compound tends to be unstable toward oxidation under ambient conditions. In ref. ¹¹, the authors investigated elemental pnictogen compounds in their hexagonal monolayer form (Sb, As, P, Bi), and predicted a very high hole mobility for antimonene, in excess of 1300 cm²/Vs at room temperature. In this case, calculations were performed within the relaxation time approximation, which may not be as accurate as full Boltzmann transport calculations¹⁶.

Large-scale high-throughput (HT) searches for high-mobility 2D materials have recently been made possible by the development of 2D materials repositories such as the Materials Cloud 2D Database (MC2D)^17,18 and the Computational 2D materials database (C2DB)^19,20. The MC2D database was generated by considering all 3D bulk inorganic compounds experimentally synthesized, and by identifying the subset of layered compounds that are amenable to exfoliation. The C2DB database was generated by considering known 2D structure polytypes and decorating these lattices combinatorially with every element of the periodic table. These libraries provide us with thousands of promising 2D materials to screen in search of high-mobility compounds. For example, the authors of ref. ¹⁵ recently analyzed over 4000 putative compounds from the C2DB dataset in search of high-mobility semiconductors; they identified several candidates with room-temperature mobilities in excess of 1400 cm²/Vs, including BSb monolayer, which was also identified in ref. ¹⁴.

In this broad context, the aim of the present work is threefold: (i) To establish a systematic HT screening approach for identifying high-mobility 2D materials; (ii) To report reproducible ab initio data on the carrier mobilities of top materials candidates; (iii) To explain why real 2D materials exhibit carrier mobilities that are far below their theoretical intrinsic limit. In order to complement existing studies, we here focus on the MC2D database whose practical advantage is that all 3D parent compounds are experimentally available; therefore, the likelihood of realizing the corresponding 2D monolayers is high. This database was also screened in the previous work²¹ but using different criteria. In particular, in ref. ²¹ SOC was not considered in the band structure screening and in the calculation of transport properties (except for WSe₂). As we show in this manuscript, SOC plays an important role in mobility calculations and in the determination of the hole effective masses in most cases.

The distinctive feature of the present study is that, for the most promising compounds, we do not limit ourselves to the relaxation time approximation, but we perform full-blown ab initio Boltzmann transport calculations (including spin-orbit couplings and recent development for Fröhlich electron–phonon interactions in 2D²²) in order to provide best theoretical estimates for the carrier mobility. For the case of WS₂, which emerges from the present unbiased search as the most promising p-type compound, we also perform GW quasiparticle calculations and include quadrupole corrections as well as scattering by ionized impurities and extended defects in order to obtain the most accurate estimate of the carrier mobility reported thus far.

Results

We present our findings in three steps. First, we outline our procedure for pre-selecting high-mobility candidate materials from the MC2D database (see Fig. 1). Second, we report high-precision calculations of carrier mobility for sixteen top candidates based on the ab initio Boltzmann transport equation (aiBTE). Third, we proceed to an in-depth analysis of WS₂, which emerges from the present search as the highest-mobility 2D compound within the MC2D database. For this latter case, we report on high-level many-body calculations and investigate the role of carrier concentration, spin–orbital couplings (SOC), quadrupole corrections, impurity scattering, and scattering by extended defects. Full details on the methodology and calculation parameters are reported in the “Methods” section.

Fig. 1: High-throughput screening workflow.

Schematic of the down-selection procedure employed to identify high-mobility 2D materials within the MC2D database¹⁷. Starting from this database, we perform structure optimization for 258 compounds; we compute band structures and identify a subset of 166 compounds with finite band gap (Set A); we calculate conductivity effective masses without SOC and down-select 95 compounds (Set B); for this set, we re-calculate effective masses with SOC and down-select to 50 compounds (Set C); we estimate mobilities via Emin’s formula and down-select 12 compounds for high-accuracy ab initio Boltzmann transport calculations (Set D).

High-throughput screening

Figure 1 shows a schematic of the HT screening workflow employed in this work. The workflow starts from the MC2D database, which reports 2D materials that can be obtained from exfoliation of 3D compounds already synthesized¹⁷. Parent 3D compounds were sourced from the inorganic crystal structure database (ICSD)²³ and the crystallographic open database (COD)²⁴. The database contains 5619 layered materials, and a subset of 1036 compounds are labeled as “easily exfoliable” based on their computed exfoliation energy (<30 meV/Ų). From this subset, phonon dispersion relations were computed, and 258 compounds were found to exhibit no soft phonons, i.e., to be dynamically stable. 166 compounds of this set are non-metallic at the density-functional theory (DFT) level. We name this collection of 166 non-metallic compounds “Set A” (Supplementary Table 1).

We perform DFT calculations for all 2D materials in Set A; in particular, we compute ground-state structure, band structures, and conductivity effective masses. ref. ¹⁷ reports the magnetic order for 25 compounds of this set. In these cases, we tested both ferro- and antiferromagnetic order; these compounds are indicated in Supplementary Table 1. The conductivity effective masses of electrons and holes computed for compounds in Set A are shown in Fig. 2, as a function of the DFT band gap. Masses are evaluated for a carrier concentration of 10¹⁰ cm⁻² and a temperature of 300 K. We have checked that these masses do not change significantly when considering a higher carrier concentration of 10¹² cm⁻². At this stage we do not include SOC in order to contain computational cost. Calculated masses span a very broad range, from 0.05 m_e to ~ 300 m_e, where m_e is the free electron mass. For clarity, only compounds with masses smaller than 20 m_e are shown in the figure, and all data are reported in Supplementary Table 1. As in the case of 3D bulk semiconductors²⁵, hole masses are typically heavier than electron masses: the average electron mass in Set A is 2.0 m_e, while the average hole mass is 4.1 m_e. Conversely, unlike in simple k ⋅ p models, which predict a monotonic dependence of the effective mass on the band gap, Fig. 2 shows that the correlation between masses and band gap is relatively weak for the compounds investigated here.

Fig. 2: Conductivity effective masses without SOC.

Computed conductivity effective masses for the 165 compounds of Set A. a Electron masses, b hole masses. Effective masses are calculated at 300 K and for a carrier concentration of 10¹⁰ cm⁻². In the case of anisotropic effective mass tensors, we report the isotropic average. These calculations do not include SOC.

In the next step of the down-selection process, we retain compounds that exhibit low effective masses and narrow or intermediate band gaps. Specifically, we retain compounds with either the electron or the hole mass < 1 m_e based on typical values for conventional 3D semiconductors, and band gaps in the range 0.1 < E_g < 3 eV. Given the band gap underestimation in DFT, this lower bound ensures that we only retain compounds with an (expected) experimental band gap ≳ 0.5 eV. These criteria narrow down the collection to 95 compounds; we call this reduced subset “Set B” (Supplementary Table 2).

Starting from Set B, we re-calculate the conductivity effective masses of 95 compounds, this time by taking into account SOC, which is considerably more demanding computationally. The computed effective masses are shown in Fig. 3 and reported in full in Supplementary Table 2. As expected, SOC modifies the effective masses significantly in most materials containing heavy elements, as shown in Fig. 4. In this figure, we see that the modification of the effective masses induced by SOC ranges from a reduction of 50% to an enhancement of up to 200%. On average, this effect is most pronounced in the case of the hole effective masses, for which the mean absolute relative error (MARE) between non-SOC and SOC calculations over Set B is 27.6%; in comparison, the MARE is 10.5% for electrons. Furthermore, several compounds such as CdI₂, BiTeCl, CuI, MoS₂, and Bi₂TeSe₂ show an anomalously large reduction of the hole mass upon including SOC, in the range 2× to 4× (Supplementary Table 2). From this dataset, we retain compounds exhibiting both electron and hole-effective masses, including SOC below 1 m_e. Upon application of this filter, we obtain 50 compounds, which we denote as “Set C” (compounds marked in bold font in Supplementary Table 2). We note that this dataset does not contain any magnetic compounds.

Fig. 3: Conductivity effective masses including SOC.

Computed conductivity effective masses for the 95 compounds of Set B. a Electron masses, b hole masses. Effective masses are calculated at 300 K and for a carrier concentration of 10¹⁰ cm⁻². In the case of anisotropic effective mass tensors, we report the isotropic average. SOC is included in these calculations. Supplementary Table 2 reports directional masses for each compound.

Fig. 4: Effect of SOC on the conductivity effective masses.

Comparison between the conductivity effective masses computed for the 95 compounds of Set B, without SOC (horizontal axis) and with SOC (vertical axis). a Electron masses; b hole masses. If SOC and non-SOC masses were identical, all data points would fall on the diagonal line at 45°. For compounds with anisotropic mass tensors, we report the isotropic average. The shaded areas bounded by the dashed lines indicate the region where the ratio of non-SOC and SOC effective masses is between 50% and 200%. All effective masses are evaluated at 300 K for a carrier concentration of 10¹⁰ cm⁻². The complete data set is reported in Supplementary Table 2.

For compounds in Set C, we estimate the carrier mobilities using simple analytical formulas. We start from a 2D Fröhlich model, which assumes the scattering of carriers by polar phonons in 2D and corresponds to Eqs. (6–8) of the Methods. The parameters necessary for this model are the highest phonon frequency, the high-frequency and static dielectric constants of the 2D materials, and the layer thickness. These quantities are computed by performing Γ-point phonon calculations and by extracting the thickness and dielectric constants using the same procedure as in ref. ²⁶. All calculated parameters are reported in full in Supplementary Table 3. Figure 5 shows that the room-temperature mobilities estimated with this model extend up to unrealistically high values (>10,000 cm²/Vs) for well-known transition metal dichalcogenides (TMDs). Therefore this simple model is insufficient to describe carrier lifetimes and mobilities in these materials.

Fig. 5: Estimates of carrier mobilities using the 2D Fröhlich model.

a Electron mobilities of 48 compounds in Set C, estimated using the polar phonon scattering model given by Eqs. (6, 8) of the “Methods”, at room temperature. The dataset contains 50 compounds, but antimonene and bismuthene are excluded as they are non-polar. b Estimated hole mobilities for the same dataset. The 2D Fröhlich model yields unrealistically high mobilities. The parameters used to generate these data are given in Supplementary Table 3.

As an alternative model to estimate mobilities, we employ the simple Emin formula shown in Eq. (9) of the Methods. Estimates based on this model are reported in Supplementary Table 3. Figure 6 shows that room-temperature mobilities estimated with the Emin model for TMDs fall in the expected range^5,6. Electron mobilities are generally higher than hole mobilities, reflecting the corresponding effective masses shown in Fig. 3. We also note that, for this subset of compounds, higher mobilities are found for materials with narrower band gaps, in line with expectations. Based on these observations, we use Fig. 6 as a 0th-order approximation to the mobility of Set C. We can now down-select compounds with both the electron and the hole mobility above the threshold μ_th = 100 cm²/Vs. This threshold is chosen so that 2D materials will be competitive with ultrathin-body Si MOSFETs scaled down to a thickness of 2.5 nm, which exhibit mobilities near μ_th³. Compounds that fulfill this criterion are highlighted in color in Fig. 6. After this selection, we are left with 12 candidates for 2D materials with the potential for balanced ambipolar transport, namely: Sb, GeSe, SnTe, ZrSe₂, HfSe₂, WS₂, WTe₂, SiH, Tl₂O, Bi₂TeSe₂, TiNCl, and TiNBr. We note that skippenite Bi₂TeSe₂ is the only candidate identified in this work that overlaps with the selection of ref. ²¹. The difference between our lists originates from our choice of including SOC in the screening of band effective masses. These compounds constitute Set D. The band structures of these compounds, both with and without SOC, are reported in Supplementary Fig. 1. For these materials candidates, we perform full-blown aiBTE calculations. For comparative purposes, we also perform aiBTE calculations for monolayer MoS₂, Bi, GeS, and WSe₂, as discussed below.

Fig. 6: Estimates of carrier mobilities using Emin’s formula.

a Electron mobilities of 50 compounds in Set C, stimulated using Emin’s formula [Eq. (9) of the Methods], at room temperature. b Estimated hole mobilities for the same dataset. These estimates fall within the expected range for TMDs, lending support to this simple model. The shaded regions mark the mobility threshold for identifying potential high-mobility candidates. 2D materials with both electron and hole mobility > 100 cm²/Vs are highlighted in color and constitute Set D. The effective masses used to generate these data are given in Supplementary Table 3.

Carrier mobilities via the ab initio Boltzmann transport equation

In this section, we first report on calculations for MoS₂, for which there are many experimental data available. This comparison serves as a validation test and allows us to gauge the predictive accuracy of our methodology. Then, we discuss, in turn, our aiBTE calculations for all materials in Set D. SOC is included in all calculations.

Molybdenum disulfide

Figure 7 shows the structure, electronic band structure, phonon dispersions, scattering rate, and carrier mobilities of monolayer MoS₂. For a very low carrier concentration of 10¹⁰ cm⁻², we obtain room-temperature hole and electron mobilities of 104 and 165 cm²/Vs, respectively. These values are consistent with hole mobilities around 70 cm²/Vs and electron mobilities in the range 130–180 cm²/Vs reported in previous theoretical works^12,15,27. In addition, we note that our calculated electron mobility is significantly lower than the value of 410 cm²/Vs obtained in the first ab initio calculation of carrier mobility in 2D MoS₂²⁸. This difference originates from the fact that in ref. ²⁸, SOC was not taken into account, and various approximations for the electron–phonon matrix elements and the solution of the BTE were employed. Our results fall in the middle of the range of reported experimental mobilities for holes, from 40 to 200 cm²/Vs^29,30,31; and slightly above the range of reported mobilities for electrons, from 44 to 148 cm²/Vs^{29,30,32,33,34}. The comparatively lower mobility of holes with respect to electrons is primarily due to the heavier masses (0.87 m_e for holes vs. 0.50 m_e for electrons, Supplementary Table 2), while the scattering rates are comparable up to 50 meV from the band edges [Fig. 7d]. SOC plays an important role in the hole mobility, since it splits the K-valleys by 148 meV and lowers the Γ valley by 51 meV [Supplementary Fig. 2a]; these values are comparable to the highest phonon energy [Fig. 7c], therefore intervalley scattering is partly suppressed by SOC. A spectral analysis of the scattering rates shows that acoustic phonons are primarily responsible electron scattering (90%) while optical optical phonons dominate hole scattering (82%), Supplementary Fig. 2b, c. Overall, our calculations are in very good agreement with existing experimental and theoretical values, thus showing the reliability of the present methodology. Further improvements on our calculations can be obtained by using GW band structures, as discussed in Supplementary Fig. 15.

Fig. 7: Carrier mobility of monolayer MoS₂.

a Side view and top view of a ball-stick model of MoS₂. Mo is in pink, and S is in yellow. b DFT electronic band structure. c Phonon dispersion relations. d Carrier scattering rates from electron–phonon coupling. The left panel shows the scattering rates of holes (orange), and the right panel is for electrons (blue). e BTE phonon-limited hole mobility (orange) and electron mobility (blue) of MoS₂. Scattering rates and mobilities are evaluated at 300 K for a carrier concentration of 10¹⁰ cm⁻². The gray bars in e indicate the range of experimental values reported for monolayer MoS₂, from refs. ^{29,30,31,32,33,34}.

Antimonene

Antimonene, or monolayer h-Sb, was predicted to exist in both a tetragonal α phase and a hexagonal β phase³⁵. Both phases have successfully been synthesized³⁶. The structure of the hexagonal phase, which is identified by our screening as a potential high-mobility material, is shown in Fig. 8a. This phase was successfully synthesized in few-layer as well as monolayer form^{37,38,39,40,41,42}, and has been investigated for diverse applications ranging from optoelectronics to energy storage^43,44,45. To the best of our knowledge, experimental mobility data on this compound have not been reported yet. Our calculated room-temperature phonon-limited mobilities are 1258 and 47 cm²/Vs for holes and electrons, respectively [Fig. 8e]. Both hole and electron effective masses are very low (0.16 m_e and 0.23 m_e, respectively, Supplementary Table 2); the hole scattering rates are unusually low, in the range of 10 ps⁻¹ [Fig. 8d], contributing to exceptionally high hole mobility. The low hole–phonon scattering rates can be attributed to the SOC splitting the valence band maximum at Γ by more than 300 meV, causing a suppression of intravalley interband scattering. In contrast, interval scattering between the six degenerate conduction band minima located halfway along the ΓM line is allowed, leading to poor electron mobility. Spectral analysis of the scattering rates [Supplementary Fig. 3a, b] reveals that holes are primarily scattered by the highest-energy optical phonons [78%, Fig. 8c], while both acoustic and optical phonons contribute equally to electron scattering. We note that h-Sb was already recognized as a potential high-mobility 2D material in a previous computational study^11,15, which reported a hole mobility of 1100–1330 cm²/Vs, in good agreement with our value.

Fig. 8: Carrier mobility of antimonene.

a Side and top views of antimonene. b DFT electronic band structure. c Phonon dispersion relations. d Carrier-phonon scattering rates of holes (orange) and electrons (blue). e Phonon-limited carrier mobility of antimonene from the aiBTE solution: holes (orange) and electrons (blue). Scattering rates and mobilities are evaluated at 300 K and a carrier density of 10¹⁰ cm⁻². The confirmation of electronic band structure near band edges using the HSE hybrid functional^206,207 is provided in Supplementary Fig. 14a.

A related compound, bismuthene h-Bi, was filtered out by Emin’s estimate for the hole mobility [Fig. 6b] and is discussed for completeness in Supplementary Figs. 9, 12, and 13.

Silicane

Silicane (SiH) is a hydrated monolayer of silicon, as shown in Fig. 9a. This compound has been investigated extensively from the computational standpoint^{46,47,48,49,50}, but only partially-hydrogenated layers^51,52,53,54 and Ge_0.5Si_0.5H alloys⁵⁵ have been synthesized. In silicane, Si atoms maintain tetrahedral coordination as in bulk Si, but two out of four neighbors are H atoms. As all bonds are saturated, this compound exhibits a band gap⁵⁶, as seen in Fig. 9b. The gap is indirect, between the VBM at Γ and the CBM at M. Figure 9c shows the phonon dispersion relations, which consist of three sets of modes: Si–Si vibrations in the range up to 60 meV, H wagging modes between 60 and 100 meV, and Si–H stretching modes near 260 meV with dominant H displacements, as expected from the mass difference. These latter modes do not contribute to the scattering of carriers [Supplementary Fig. 3c, d]. The predominant scattering channel is from acoustic phonons for electrons (89%) and from optical phonons for holes (67%). Our calculated room-temperature mobilities (for 10¹⁰ carriers/cm⁻²) are 107 cm²/Vs for holes and 27 cm²/Vs for electrons [Fig. 9d]. These values are in good agreement with previous calculations which reported 109 and 53 cm²/Vs for holes and electrons, respectively⁴⁸. Given the relatively low phonon-limited theoretical mobilities, silicane does not constitute a promising 2D semiconductor.

Fig. 9: Carrier mobility of silicane.

a Side and top views of silicane. Si is blue, H is white. b DFT electronic band structure. c Phonon dispersion relations. d Carrier-phonon scattering rates of holes (orange) and electrons (blue). e Phonon-limited carrier mobility of silicane from the aiBTE: holes (orange) and electrons (blue), evaluated at 300 K and a carrier density of 10¹⁰ cm⁻².

Thallium monoxide

Tl₂O represents the first 2D semiconductor that was predicted to be stable with metal cations located on the outer layers (hence dubbed “metal-shrouded”)⁵⁷. The structure is the same as that of 1T-MoS₂, with O and Tl replacing Mo and S, respectively [Fig. 10a]. It has been investigated intensively from the theoretical standpoint, to assess its potential for applications in thermoelectrics and spintronics^{58,59,60,61,62,63,64,65,66,67}. However, we are unaware of any synthesis attempts, which may be due to the toxicity of thallium. Figure 10b shows that Tl₂O exhibits a direct band gap at M, and that electrons are lighter than holes (Supplementary Table 2). The main source of carrier scattering is the optical phonons near 21 meV [Supplementary Fig. 4a, b], which correspond to in-plane longitudinal-optical (LO) vibrations of the O sublattice. Our calculated mobilities at room temperature are 11 cm²/Vs for holes and 45 cm²/Vs for electrons. Based on these aiBTE data, our assessment is that Tl₂O does not constitute a promising 2D semiconductor. We also note that prior work predicted very high carrier mobilities for this compound, in the order of 4000 cm²/Vs at room temperature⁵⁷; this prior work was based on the acoustic deformation potential model, which misses the dominant contribution from optical phonons to the scattering rates and leads to a significant overestimation of the mobility.

Fig. 10: Carrier mobility of monolayer thallium oxide.

a Side and top views of monolayer Tl₂O. Tl is in gold, and O is in red. b DFT electronic band structure. c Phonon dispersion relations. d Carrier-phonon scattering rates of holes (orange) and electrons (blue). e Phonon-limited carrier mobility of monolayer Tl₂O from the aiBTE: holes (orange) and electrons (blue), evaluated at 300 K and a carrier density of 10¹⁰ cm⁻².

Skippenite

The monolayer form of skippenite, Bi₂TeSe₂, consists of a single layer of Te sandwiched between two hexagonal BiSe bilayers, as shown in Fig. 11a. This compound attracted interest for its predicted transport and thermoelectric properties^68,69,70,71, but only multi-layer films have been synthesized thus far^72,73. Our calculations indicate that SOC is especially important in this system, as expected from the presence of Bi. For example, upon including SOC, the band gap decreases from 1.5 to 0.2 eV, and the hole mass decreases concomitantly from 1.49 m_e to 0.39 m_e [Supplementary Fig. 1d]. Both holes and electrons are primarily scattered by two optical phonons near 10 and 15 meV, which correspond to the in-plane LO vibrations of the Te and Se layers, respectively [Supplementary Fig. 4c, d]. Our predicted hole and electron mobilities are 95 and 361 cm²/Vs, respectively. These values are significantly lower than previously reported theoretical mobilities in the range 754–1329 cm²/Vs for holes and 1983–2510 cm²/Vs for electrons^68,69,71. We ascribe this discrepancy to the fact that previous work employed the acoustic deformation potential model, which neglects the key role of optical phonons in this compound. Based on our calculations, n-type Bi₂TeSe₂ should be a promising 2D semiconductor.

Fig. 11: Carrier mobility of monolayer skippenite.

a Side and top views of monolayer Bi₂TeSe₂. Bi is pink, Se is green, and Te is brown. b DFT electronic band structure. c Phonon dispersion relations. d Carrier-phonon scattering rates of holes (orange) and electrons (blue). e Phonon-limited carrier mobility of monolayer Bi₂TeSe₂ from the aiBTE: holes (orange) and electrons (blue), evaluated at 300 K and for a carrier concentration of 10¹⁰ cm⁻². The confirmation of electronic band structure near band edges using the HSE hybrid functional^206,207 is provided in Supplementary Fig. 14b.

Germanium selenide and tin telluride

These materials belong to the broader family of IV–VI 2D semiconductors. Material Set C (Supplementary Table 3) contains three candidates from this family: GeS, GeSe, and SnTe. Of these candidates, GeS is filtered out based on Emin’s estimate for the hole mobility [Fig. 6b]; for completeness, we discuss its properties in Supplementary Figs. 10, 12, and 13. 3D parent compounds of these materials have been investigated extensively owing to potential applications as photodetectors and ferroelectrics⁷⁴. In their bulk form, GeSe and SnTe crystallize in layered orthorhombic structures with Cmcm or Pnma space groups⁷⁴. The 2D versions are obtained by exfoliation of the Pnma phase, and the resulting structures are shown in Fig. 12a, f, respectively. Synthesis of few-layer and thin-film GeSe is well established^{75,76,77,78,79,80,81,82,83,84}, while monolayer crystals are far less common⁸⁵. Conversely, several studies reported the synthesis of monolayer SnTe^{86,87,88,89,90,91,92}, which attracted considerable interest in the field of 2D ferroelectrics.

Fig. 12: Carrier mobilities of GeSe and SnTe monolayers.

a Side and top views of monolayer GeSe. Ge is purple, and Se is green. b DFT band structure. c Phonon dispersion relations. d Carrier-phonon scattering rates of holes (orange) and electrons (blue). e Phonon-limited carrier mobility of monolayer GeSe from the aiBTE: holes (orange) and electrons (blue), evaluated at 300 K and for a carrier concentration of 10¹⁰ cm⁻². x and y denote the armchair and zigzag directions, respectively. f Side and top views of monolayer SnTe. Sn is gray, Te is dark green. g–j Same as b–e but for SnTe.

Electron–phonon coupling in GeSe is dominated by LO stretching vibrations near 20 meV, leading to unusually high scattering rates near the band edges [Supplementary Fig. 5a, b]. Thus, despite the relatively light carrier masses (Supplementary Table 1), this compound exhibits an unimpressive room-temperature phonon-limited hole mobility of 44 cm²/Vs (isotropic average value) and electron mobility of 37 cm²/Vs, as shown in Fig. 12e. Our results agree with recent computational studies which reported 45 and 18 cm²/Vs, respectively⁹³. To the best of our knowledge, measured mobilities have been reported only for few-layer GeSe, and the values are very low, in the range 0.9–5 cm²/Vs^79,94,95,96; we are unaware of mobility measurements for monolayer GeSe.

In the case of SnTe, SOC induces significant band splitting both in the valence and in the conduction bands (70–80 meV), as seen in Fig. 12g; since the highest phonon energy is 18 meV [Fig. 12h], SOC splitting suppresses inter-valley scattering by phonons. LO stretching phonons around 11 meV couple most strongly with both electrons and holes, leading once again to unusually high scattering rates as for GeSe [Supplementary Fig. 5(c) and (d)]. We calculate directionally-averaged room-temperature mobilities of 180 cm²/Vs for holes, and 160 cm²/Vs for electrons, in reasonable agreement with a very recent computational study which reported 220 cm²/Vs and 120 cm²/Vs, respectively¹⁵. We are unaware of experimentally-measured mobilities for monolayer SnTe. Overall, among IV–VI monolayer semiconductors, SnTe offers the highest promise as a 2D channel material owing to its moderately high ambipolar carrier mobilities at room temperature.

Zirconium and hafnium diselenides

ZrSe₂ and HfSe₂ crystallize in the 1T-CdI₂ structure, as seen in Fig. 13a, f. Both compounds have been synthesized as few-layer or nano-sheets (ZrSe₂^97,98,99,100 and HfSe₂^{98,101,102,103,104,105}). Despite having relatively light effective masses, as well as significant SOC splitting in the valence bands [Fig. 13b, g], the calculated mobilities of both materials remain low due to a very strong electron–phonon coupling which causes exceptionally high scattering rates [Fig. 13d, i]. In particular, the coupling is dominated by Fröhlich interactions with modes at 26 and 22 meV for ZrSe₂ and HfSe₂, respectively (Supplementary Fig. 6). The same coupling mechanism has also been shown to lead to the formation of large polarons in these materials¹⁰⁶. Our calculated room-temperature hole mobilities are 45 and 35 cm²/Vs for ZrSe₂ and HfSe₂, respectively, while the corresponding electron mobilities are 15 and 13 cm²/Vs [Fig. 13e, j]. We are not aware of experimental measurements or previous calculations for ZrSe₂. Conversely, in the case of HfSe₂, measured mobilities in the range 0.2–6 cm²/Vs have been reported for nanosheets and few-layer systems^101,104. Furthermore, a previous theoretical study of HfSe₂ obtained carrier mobilities below 2 cm²/Vs¹⁰⁷; this prior work employed the relaxation time approximation, which might explain the small discrepancy in our calculations.

Fig. 13: Carrier mobilities of ZrSe₂ and HfSe₂ monolayers.

a Side and top views of monolayer ZrSe₂. Zr is blue, and Se is green. b DFT band structure. c Phonon dispersion relations. d Carrier-phonon scattering rates of holes (orange) and electrons (blue). e Phonon-limited carrier mobility of monolayer ZrSe₂ from the aiBTE: holes (orange) and electrons (blue), evaluated at 300 K and for a carrier concentration of 10¹⁰ cm⁻². f Ball-stick models of HfSe₂, with Hf and Se in brown and green, respectively. g–j Same as b–e but for HfSe₂.

Titanium nitride chloride and bromide

TiNCl and TiNBr consist of TiN bilayers decorated with two halogen layers, as shown in Fig. 14a, f. The parent 3D compounds are well known for their superconducting properties¹⁰⁸, but the synthesis of individual monolayers has not been reported yet. These 2D materials have been investigated theoretically for a number of applications, spanning photovoltaics, thermoelectrics, and electronics^109,110,111. One interesting feature of TiNCl and TiNBr is that they possess parabolic bands with a direct gap at Γ, unlike all the other compounds considered in the present work [Fig. 14(b, g)]. The electron–phonon coupling is very strong in both cases and is dominated by LO stretching modes at 20 and 18 meV for TiNCl and TiNBr, respectively (Supplementary Fig. 7). As a result, the carrier scattering rates are very high, as seen in Fig. 14(d, i). The directionally-averaged mobilities at room temperature are all in the order of 100 cm²/Vs, namely 98 and 74 cm²/Vs for holes and electrons in TiNCl, and 97 cm²/Vs for both holes and electrons in TiNBr. Our calculations are at odds with recent theoretical predictions placing the mobilities of these materials in the range 600–1500 cm²/Vs¹¹⁰. This discrepancy can be traced back to the use of an acoustic deformation potential scattering model in prior work, which misses the key contribution of optical phonons as seen in Supplementary Fig. 7.

Fig. 14: Carrier mobilities of TiNCl and TiNBr monolayers.

a Side and top views of monolayer TiNCl. Ti is in blue, N is in white, and Cl is in green. b DFT electronic band structure. c Phonon dispersion relations. d Carrier-phonon scattering rates of holes (orange) and electrons (blue). e Phonon-limited carrier mobility of monolayer TiNCl from the aiBTE: holes (orange) and electrons (blue), evaluated at 300 K and for a carrier density of 10¹⁰ cm⁻². The x direction is aligned with the rows of Cl atoms. f Ball-stick models of TiNBr, with Br in brown. g–j Same as b–e but for TiNBr.

Tungsten disulfide and ditelluride

WS₂ and WTe₂ are common TMDs and are isostructural with the prototypical compound MoS₂, as shown in Fig. 15a, f, respectively. SOC does not affect the phonon dispersions of these compounds but plays an important role in the electronic band structures, especially the valence bands. In fact, Fig. 15b, g shows large splittings at the K-valleys, of 440 and 490 meV for WS₂ and WTe₂, respectively. These values are an order of magnitude larger than the highest phonon energy, therefore the incorporation of SOC completely suppresses intravalley interband scattering at K. This effects results in very low hole scattering rates, as shown in Fig. 15d, i. It is worth noting that the spin-splitting at the K-valleys has been confirmed by angle-resolved photoemission spectroscopy (ARPES) measurements¹¹². Supplementary Fig. 8a, b shows that both holes and electrons in WS₂ are primarily scattered by acoustic phonons (holes: 65%; electrons: 88%) since Fröhlich coupling is very small in this material (see Supplementary Table 3). Conversely, transport in WTe₂ is dominated by polar phonon scattering, as seen in Supplementary Fig. 8c, d. Our calculated room-temperature hole mobilities are 3021 cm²/Vs for WS₂, and 424 cm²/Vs for WTe₂.

Fig. 15: Carrier mobilities of WS₂ and WTe₂ monolayers.

a Side and top views of monolayer WS₂. W is gray, and S is yellow. b DFT band structure. c Phonon dispersions. d Carrier-phonon scattering rates of holes (orange) and electrons (blue). e Phonon-limited carrier mobility of monolayer WS₂ from the aiBTE: holes (orange) and electrons (blue), evaluated at 300 K and for 10¹⁰ cm⁻² carriers. f Ball-stick models of WTe₂, with Te in olive. g–j Same as b–e but for WTe₂.

The very high mobility of holes in WS₂ will be analyzed in detail in the next section. In comparison, prior theoretical work reported much lower values, namely 988 cm²/Vs for WS₂ in ref. ¹¹² and 900 and 200 cm²/Vs for WS₂ and WSe₂, respectively, in ref. ¹⁵. These discrepancies can be ascribed to the fact that the authors of refs. ¹⁵ and ¹¹² used the relaxation time approximation and a high carrier concentration of 10¹³ cm⁻². Using similar settings, we obtain a hole mobility of 1549 cm²/Vs for WS₂; the residual discrepancy is likely a numerical convergence issue. Recently, the authors of ref. ¹¹³ investigated the implications of SOC and valley degeneracy in the transport properties of 2D TMDs. In the case of WS₂, they reported an extremely high room-temperature hole mobility of around 5000 cm²/Vs, which is much higher than in our calculations. We suspect that this high mobility results from the choice made in ref. ¹¹³ to compute electron–phonon matrix elements in the presence of free carriers already at the density-functional perturbation theory (DFPT) level. This choice tends to suppress electron–phonon couplings and favors very high mobilities. It is unclear to us whether this choice is the most realistic since DFPT screening is static in nature (while carrier screening of electron–phonon coupling is a dynamic process), and since at such high carrier concentrations, one might also need to consider scattering by carrier plasmons. SOC also plays a smaller but non-negligible role in electron transport: from Supplementary Fig. 1k, l we see that SOC induces K-valley splittings of the order of 50 meV for both compounds, which is comparable to the optical phonon energies and leads to a partial suppression of interband scattering. Our calculated electron mobilities for WS₂ and WTe₂ are 225 and 145 cm²/Vs, respectively, and are in good agreement with the values reported in ref. ¹⁵ (200 and 150 cm²/Vs, respectively).

For completeness, in Supplementary Fig. 11, we also analyze the carrier mobility of WSe₂, which belongs to the same group as WS₂ and WTe₂, but does not appear in Set D since its estimated electron mobility via Emin’s formula is slightly below 100 cm²/Vs [Fig. 9b]. Supplementary Figs. 11, 12c, and 13e, f report our results for this additional compound. We find a very high hole mobility of 967 cm²/Vs at room temperature, making this system a very promising p-type channel material, comparable to h-Sb.

In-depth analysis for p-type WS₂

Our systematic and unbiased screening singles out monolayer WS₂ as a potential ultra-high mobility semiconductor with μ_h = 1549–3021 cm²/Vs at room temperature, depending on carrier concentration. If experimentally realized, this exceptional mobility could open the way to ground-breaking new applications in ultra-scaled electronics, therefore our data call for a more in-depth analysis and higher-level calculations.

One might ask what is the origin of such a high hole mobility. In Fig. 16b, we show that the calculated mobility without including SOC is dramatically lower, 99 cm²/Vs at 300 K and for a low carrier concentration of 10¹⁰ cm⁻². This result indicates that SOC plays an essential role in achieving high mobility. To understand this effect, in Fig. 16a, we show a schematic of the valence band valleys of WS₂ in the presence of SOC. Without SOC, the Γ-valley and the K-valleys are at nearly the same energy, and the K-valleys are doubly degenerate. Upon including SOC, the Γ-valley is pushed down by 235 meV below the top of the K-valleys, rendering hole–phonon scattering from K to Γ forbidden. Furthermore, the degeneracy of the K-valley is lifted by a SOC splitting of 428 meV, making intravalley interband hole–phonon scattering forbidden as well. Lastly, the spin–momentum locking that is common to all TMDs induces opposed spin textures on the K and ${{\rm{K}}}^{{\prime} }$ valleys, therefore intervalley K–${{\rm{K}}}^{{\prime} }$ hole–phonon scattering also becomes forbidden. These three SOC-related mechanisms contribute to propelling the hole mobility of WS₂ to very high values. A similar mechanism is operational also in WSe₂, where SOC induces a K-valley splitting of 465 meV; however, in this case the higher ionic contribution to the dielectric constant (Supplementary Table 3) makes the Fröhlich coupling stronger than in WS₂, leading to a still-impressive but lower intrinsic mobility (see Supplementary Figs. 11 and 13).

Fig. 16: In-depth analysis of the carrier mobility in WS₂.

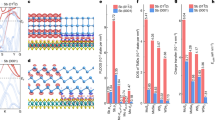
a Schematic representation of the effect of SOC on the valence band valleys of monolayer WS₂. The hexagon denotes the first Brillouin zone, the blue and red paraboloids represent K/${{\rm{K}}}^{{\prime} }$ valleys with opposite spin orientation, green denotes the Γ valley. Crossed arrows indicate hole–phonon scattering processes that are forbidden by either energy or spin conservation. b Calculated hole mobility of monolayer WS₂ under different scenarios and levels of theory. From left to right: DFT calculation without including SOC and low carrier concentration (10¹⁰ cm⁻²); SOC included on top of the previous result; GW corrections included; As in the previous bar, but this time for a high density of carriers (10¹³ cm⁻²); As previous bar, but with quadrupole corrections; Ionized impurity scattering added to the previous result; Scattering by extended defects (e.g., grain boundaries or ripples) added to the previous result, with large defect size of 500 nm; As in the previous bar, but with small defect size of 30 nm. The horizontal gray bar indicates the range of experimental data from refs. ^{122,123,124,125,126,127}. The striped bar with the star on top indicates our best estimate for the intrinsic hole mobility. c Same notation as in b, but for the electron mobility in monolayer WS₂. The horizontal gray bar indicates the range of experimental data from refs. ^{114,115,116,117,118,119,120,121}.

There exists abundant experimental literature on the electron mobility of WS₂, with room-temperature values ranging between 20 and 213 cm²/Vs^{114,115,116,117,118,119,120,121}. The record-high electron mobility of 214 cm²/Vs was obtained for exfoliated monolayer WS₂ and Ohmic contacts to Al/Au electrodes¹¹⁸. This experimental value is remarkably close to our calculated mobility of 225 cm²/Vs, suggesting that the samples of ref. ¹¹⁸ have a relatively low defect density.

Unlike electron mobilities, experimental studies reported measurements of hole mobility in WS₂ with low values ranging between 4 and 105 cm²/Vs^{122,123,124,125,126,127}. Possible sources of discrepancy between our very high predicted mobility and these experimental data are: (i) inaccuracy of DFT band structure, (ii) difference in carrier concentration, (iii) effect of quadrupolar couplings, (iv) scattering by defects, (v) scattering by extended defects such as grain boundaries or ripples, (vi) contact resistance in devices, and (vii) gate dielectric and substrate effects. In the following we analyze each of these effects in turn.

Inaccuracy of DFT band structure

As discussed above, the high hole mobility of WS₂ is closely related to the energetics of the Γ and K valleys in this compound. Since these energies are all evaluated at the DFT level, it is important to check band structures with a higher level theory. To this end, we perform GW calculations and obtain the band structures shown in Supplementary Fig. 15b. With the incorporation of GW quasiparticle corrections in the calculations, we obtain a room-temperature mobility of 3309 cm²/Vs, which is 10% higher than our DFT value owing to a slightly lighter hole mass (0.36 m_e with GW vs. 0.39 m_e in DFT).

Difference in carrier concentration

Our calculations are performed using a carrier concentration of 10¹⁰ cm⁻², while the experimental data reported in refs. ^122,123 correspond to the much higher carrier density of 10¹³ cm⁻². At this high density, the quasi-Fermi level lies 69 meV below VBM at K, therefore the carrier distribution function extends beyond the threshold for polar phonon emission around 50 meV [Fig. 15d], leading to a significant increase in the scattering rates. At this higher concentration, and including GW quasiparticle corrections, we calculate a hole mobility of 2087 cm²/Vs. This result represents a 37% reduction over the mobility at low carrier concentration, see Fig. 16b.

Effect of quadrupolar couplings

Long-range electron–phonon couplings such as the Fröhlich interaction introduce non-analyticities in the electron–phonon coupling matrix elements that necessitate a specialized treatment (see “Methods”). In most cases, the Fröhlich electron–phonon interaction dominates over other non-analytic terms, but in materials with weak polar couplings the next-to-leading-order contribution can play a significant role^128,129. This contribution results from dynamical quadrupoles and relates to piezoelectric effects¹³⁰. WS₂ stands out among the materials in Set D for having a very small ionic contribution to the dielectric constant (ϵ_ion = 0.05, Supplementary Table 2), which implies weak Fröhlich couplings, as confirmed by the frequency-resolved scattering rates in Supplementary Fig. 8a. In order to check for the effect of dynamical quadrupoles, we recompute the room-temperature hole mobility for a carrier concentration of 10¹³ cm⁻². Upon including quadrupole correction, we observe a 36% reduction of the mobility, from 2087 to 1342 cm²/Vs with quadrupoles [see Fig. 16b]. This result can be rationalized by noting that piezoacoustic scattering increases the intra-valley scattering rates in the energy range where polar phonon scattering is very weak (see Supplementary Fig. 16).

We point out that these calculations do not take into account screening of piezoacoustic and polar optical phonon scattering by free carriers, therefore it is possible that these effects be somewhat overestimated.

Scattering by defects

Real WS₂ samples contain a variety of intrinsic and extrinsic point defects such as S vacancies, W vacancies, W/S antisite defects, and substitutional O defects^{131,132,133,134,135}. To estimate the impact of defects on the mobility, we incorporate ionized-impurity scattering as an upper bound to the defect-induced scattering rates. When we consider a typical defect concentration of 10¹¹ cm^{−2 136,137}, we obtain a defect-limited hole mobility of 819 cm²/Vs. By combining this value with the intrinsic, phonon-limited mobility of 1342 cm²/Vs via Matthiessen’s rule, we obtain 509 cm²/Vs. Therefore, the inclusion of defect scattering reduces the intrinsic mobility by a factor 2.6 [see Fig. 16b]. This finding indicates that reducing the defect density will be essential to enable high-mobility p-type WS₂.

Scattering by extended defects

Another important source of scattering in TMDs is provided by one-dimensional and two-dimensional extended defects such as grain boundaries and ripples¹³⁸. Since grain sizes in CVD-grown WS₂ range from 30 to 500 nm^139,140, and ripples range from 100 to 600 nm^141,142,143, in Fig. 17 we show calculations of the hole mobility for extended defect sizes in the range 10–500 nm. It is seen that this scattering channel reduces the hole mobility by almost an order of magnitude over the range considered. In Fig. 16b we show the hole mobilities obtained by considering phonons, defects, and extended defects altogether. We see that, for an average size of extended defects of 30 nm, the hole mobility drops from 509 cm²/Vs (without such defects) to 240 cm²/Vs, therefore the presence of small grains or ripples causes a twofold reduction of the mobility. This latter value is close the highest reported experimental value of 105 cm²/Vs¹²³. We point out that this experimental value is for an exfoliated WS₂ sample with liquid electrolyte gate, therefore a precise comparison is not possible at present. However, it is clear from the present analysis that the incorporation of phonons, SOC, GW band structures, carrier concentration, quadrupoles, defects, and extended defects all contribute to bringing the theoretical value very close to experiments.

Fig. 17: Scattering by extended defects in WS₂.

Calculated hole mobility of WS₂ as a function of extended defect size (discs). The calculations are performed at room temperature and for a carrier concentration of 10¹³ cm⁻². We include SOC, GW quasiparticle corrections, and electron–phonon scattering. The horizontal dashed line is the intrinsic, phonon-limited mobility without extended defects.

A summary view of the relative importance of each of the above effects is provided in Fig. 16b. In the same panel, we highlight with stripes our best theoretical estimate for the intrinsic (defect-free) hole mobility of suspended singe-crystal WS₂, i.e., 1342 cm²/Vs at 300 K, for a carrier density of 10¹³ cm⁻².

Unlike the hole mobility, in the case of the electron mobility electron–phonon scattering is strong enough to dominate over all other effects, as shown in Fig. 16c. In this case, our calculations fall within the range of experimentally measured mobilities.

Contact resistance in devices

A significant obstacle toward using TMDs in p-type transistor channels is to realize Ohmic metal–semiconductor contacts. For example, in ref. ¹²² the authors fabricated transistors with Schottky-type WS₂/Au contacts, carrying a high contact resistance in the range of 50 kΩ. When extracting the channel mobility from these device measurements, contact resistance often introduces an additional spurious contribution that tends to lower the apparent mobility¹⁴⁴. Realizing Ohmic p-contacts with WS₂ is particularly challenging owing to its high ionization energy of 5.74 eV^145,146,147, which exceeds the work function of most elemental metals¹⁴⁸.

The importance of contacts can be gauged by considering the related example of MoS₂, for which the realization of Ohmic contacts using degenerately p-doped 2D Mo_0.995Nb_0.005S₂ led to a reduced contact resistance of 0.3 kΩ and a record hole mobility of 200 cm²/Vs³¹, far exceeding the mobilities measured in prior work, which are in the range of 40–86 cm²/Vs^29,30. Since MoS₂ has an even higher ionization energy than WS₂ (5.77 eV vs. 5.74 eV¹⁴⁵), it is possible that the use of 2D Mo_0.995Nb_0.005S₂ contact to WS₂ will make it possible to observe values more representative of the intrinsic hole mobility of WS₂. More generally, the use of doped TMDs as metal contacs is a promising strategy to realize p-type Ohmic junctions^149,150, and could be key to reach the theoretical mobility limit of WS₂ predicted here.

Gate dielectric and substrate

Our calculations describe a scenario where monolayer WS₂ is suspended in vacuum. In practical field-effect devices the 2D layer sits on top of a dielectric substrate, and is insulated from the gate electrode by an oxide, for example HfO₂¹⁵¹. The dielectric environment that surrounds the 2D channel may have beneficial effects in terms of screening the scattering potential of ionized impurities. However, it was pointed out early on that such a dielectric medium can also degrade mobility by introducing remote phonon scattering^152,153. This scattering mechanism originates from the long-range electrostatic field generated by plasmon-phonon polaritons; these hybrid excitations result from the hybridization of free-carrier plasmons in the channel and polaron optical phonons in the insulator.

The coupling matrix elements for remote phonon scattering scales as ${g}_{{\rm{RP}}}=\hslash \omega [{({\epsilon }_{\infty }+{\epsilon }_{\infty }^{{\rm{ins}}})}^{-1}-{({\epsilon }_{\infty }+{\epsilon }_{0}^{{\rm{ins}}})}^{-1}]$, where ϵ_∞ is the high-frequency dielectric constant of the 2D channel and ${\epsilon }_{\infty }^{{\rm{ins}}}$, ${\epsilon }_{0}^{{\rm{ins}}}$ are the static and high-frequency dielectric constants of the insulator, respectively¹⁵³. Taking HfO₂ as a representative example (${\epsilon }_{\infty }^{{\rm{ins}}}=5.03$, ${\epsilon }_{0}^{{\rm{ins}}}=22.0$, ℏω = 12.4 meV, ref. ¹⁵⁴), and using the parameters for WS₂ in Supplementary Table 3, we find g_RP = 0.21 meV. This energy scale is significantly larger than the characteristic energy of the Fröhlich coupling included in our calculations, g_F = ℏω(1/ϵ_∞ − 1/ϵ₀) ≃ 0.02 meV (using parameters from Supplementary Table 3).

The above order-of-magnitude comparison suggests that remote phonon scattering may play a significant role in the mobility of WS₂. This conclusion is supported by recent calculations of the hole mobility of WS₂ embedded in a model dielectric environment describing a HfO₂/WS₂/SiO₂ stack, which reported a nearly fivefold mobility reduction by remote phonon scattering¹⁵⁴.

Discussion

Starting from the 5619 layered compounds collected in the MC2D database, we performed a first-principles HT screening of potential high-mobility 2D materials using the tiered approach illustrated in Fig. 1. We filtered putative 2D semiconductors by combining ab initio data reported in MC2D and a large number of new first-principles calculations. This analysis led to down-selection of 16 compounds (12 in Set D plus 4 closely-related compounds) for which we proceeded to perform state-of-the-art transport calculations using the aiBTE approach implemented in the EPW code. Our three main findings are as follows:

(i) Even though we started from a very large library of putative as well as existing materials, only a handful of compounds exhibit very high mobilities. In particular, considering a temperature or 300 K and a low carrier concentration of 10¹⁰ cm⁻², we found very high intrinsic hole mobilities in antimonene h-Sb (1258 cm²/Vs), WSe₂ (with 967 cm²/Vs), and WS₂ (3021 cm²/Vs); in the case of electron mobilities, the top candidates are bismuthene h-Bi (361 cm²/Vs) and skippenite Bi₂TeSe₂ (361 cm²/Vs). These data are summarized in Fig. 18. That the highest hole mobility exceeds the best electron mobility by almost 10× is unexpected, and is ground for optimism in view of realizing p-channel 2D devices.

Fig. 18: Summary view of ab initio mobilities.

Hole and electron mobilities of the 12 2D compounds in Set D (left) plus the additional compounds MoS₂, h-Bi, GeS, WSe₂ (right). Calculations are performed using the aiBTE, they include only electron–phonon scattering and 2D Fröhlich corrections, and are performed at 300 K for a low carrier concentration of 10⁻¹⁰ cm⁻². Note the logarithmic scale. The gray bar in the case of WS₂ indicates that its mobility decreases to 1342 cm²/Vs upon taking into account GW corrections, high-carrier density, and quadrupole effects. Similar reductions of mobility are expected for WSe₂ and h-Sb.

(ii) The intrinsic theoretical hole mobility of WS₂ is exceptionally high. To be confident about this surprising result, we have performed an extensive range of validation tests. For example, we showed that our calculations for MoS₂ are very close to available experimental data; furthermore, our calculations for the elecron mobility of WS₂ are also in the same range as experimental data. To rationalize the large discrepancy between the intrinsic hole mobility predicted here and measured data for p-type WS₂, we extended our calculations to include the effects of spin–orbital coupings, quasiparticle band structures, carrier concentration, quadrupole corrections, impurity scattering, and scattering by extended defects. We find that each of these effects can significantly reduce the hole mobility, and that calculations including all these effects simultaneously are close to available experimental estimates. Our best theoretical estimate for the intrinsic hole mobility of WS₂ including SOC, GW bands, and quadrupoles is 1342 cm²/Vs at 300 K and for 10¹³ cm⁻² carriers. This value should constitute the ultimate mobility limit for the ideal, suspended single-crystal and defect-free monolayer.

We also pointed out that the hole mobility is especially prone to underestimation due to the contact resistance and the scarcity of high-workfunction metals suitable for WS₂. Another important mechanism that is not included in the present study is the effect of gate dielectric and substrate, and in particular remote phonon scattering. Similarly, higher-order phonon scattering processes, such as electron-two-phonon scattering^155,156, could also play a role and deserve a detailed investigation.

Overall, the present analysis suggests that extrinsic effects and interfaces could play a major role in the observed hole mobility of WS₂, and that by controlling these effects it might be possible to unlock unprecedented performance. Therefore, the present work calls for renewed efforts in the experimental synthesis and processing of WS₂ for p-type transistor channels.

(iii) This study shows that reliable predictions of carrier mobilities in 2D materials ultimately require full-blown ab initio calculations. In particular, we find that the scattering rates are extremely sensitive to materials structure and chemistry, and show significant variations between compounds of the same family and even between electron and holes of the same compound (see Fig. 19). Therefore, simplified approaches based on constant relaxation-time approximations and related simplifications may not be sufficient in quantitative studies. Furthermore, our in-depth analysis of WS₂ reveals that focusing on intrinsic phonon-limited carrier mobilities may not be fully representative of the experimental reality, especially in the case of compounds with weak electron–phonon couplings where extrinsic effects might ultimately dominate. The lesson for future HT searches is that a blanket approach might be too coarse to identify promising materials, and deep-dives into the specifics of individual compounds and their interfaces with contacts and substrates will be necessary going forward.

Fig. 19: Relaxation times for compounds in Set D.

Computed average relaxation times of electrons and holes for the 12 compounds in Set D. For completeness, we also show data for the 4 additional compounds included in Fig. 18. The average relaxation time τ is obtained from Drude’s formula via the computed aiBTE mobilities μ and conductivity effective masses m^*, τ = μm^*/e (e is the electron charge). For comparison, we also show the simple estimate via Emin’s formula (thick horizontal line).

In summary, our findings indicate that WS₂ is inherently an ultra-high mobility semiconductor, but its true potential is hindered by defects and interfaces. Hence, our study suggests that the the key to high-mobility transistors based on 2D materials may not lie in the discovery of entirely new compounds, but rather in managing defect density and co-optimizing channel, contacts, and dielectrics. We propose that this approach may hold greater promise for achieving groundbreaking advances in ultra-scaled electronics based on 2D materials.

Methods

Computational setup

In this section we describe the computational setup employed for performing calculations of the electronic structure, lattice dynamics, electron–phonon couplings, and carrier transport coefficients in the present study.

We perform DFT^157,158 and DFPT^{159,160,161,162,163} calculations using planwaves basis sets and pseudopotentials, as implemented in the Quantum ESPRESSO suite¹⁶⁴. We describe exchange and correlation effects using the PBE functional¹⁶⁵. For HT calculations of band structures and effective masses without SOC, we employ pseudopotentials from the Standard Solid-State Pseudopotentials (SSSP) library¹⁶⁶, which afford a low planewaves kinetic energy cutoff and are advantageous for calculations at scale. For HT calculations of effective masses, phonon dispersion relations, electron–phonon couplings, and carrier transport coefficients including SOC, we employ optimized norm-conserving pseudopotentials (ONCV)¹⁶⁷ from the PseudoDojo library^168,169 to achieve higher accuracy at the price of higher computational cost. In all cases, we use the planewaves kinetic energy cutoffs recommended in these libraries, which have been determined via extensive testing^166,169. For structural optimization, we set the energy threshold to 10⁻⁵ Ry, and the force threshold to 10⁻⁴ Ry/bohr when performing HT calculations. These thresholds are reduced by one order of magnitude for calculations of phonons and transport coefficients. To eliminate spurious Coulomb interactions among periodic slab replicas along the z direction, we apply 2D truncation in all DFT and DFPT calculations using the approach of ref. ¹⁷⁰.

We calculate conductivity effective masses [see Eq. (5)] using the BoltzTrap code¹⁷¹. The advantage of this approach is that BoltzTrap does not require Wannier–Fourier interpolation, therefore it can be used for HT calculations on large materials libraries¹⁷². To validate our results, we collected effective masses in the literature for 16 compounds (see Table 1) and presented a comparison with our data in Supplementary Table 4. Our conductivity effective masses are generally consistent with previous works.

Table 1 Brillouin zone sampling

We compute electrical transport properties by solving the aiBTE^173,174 as implemented in the EPW code¹⁷⁵. EPW employs Wannier–Fourier interpolation by calling the Wannier90 code in library mode^{176,177,178,179,180,181}. The calculations involve determining electron wavefunctions, vibrational eigenmodes, and their couplings on coarse Brillouin zone grids, and interpolating these quantities onto ultra-dense grids by means of maximally-localized Wannier functions^179,182. The interpolation accuracy and reliablity is thoroughly checked in all cases¹⁶. Owing to their Fermi-Dirac occupation factors and the energy selection rule for electron–phonon scattering [see Eqs. (2, 3) below], only electronic states in the vicinity of the band edges contribute to the carrier mobility. Accordingly, we consider states within a 300 meV energy window from either the conduction band minimum (CBM) or the valence band maximum (VBM) for electron and hole mobility calculations, respectively. We have performed convergence tests to verify that this choice yields accurate mobility values. To ensure convergence of calculated mobilities with respect to the Brillouin zone sampling, we systematically increase the number of points in the fine grid and repeat the calculations until the mobility changes by less than 1 cm²/Vs. The grid sizes obtained using this criterion and employed throughout this study are reported in Table 1 for reproducibility purposes. Brillouin-zone integrals are evaluated using the adaptive smearing of refs. ^16,183 which has been shown to provide the most reliable results. Long-range Fröhlich electron–phonon couplings^{26,28,184,185} are included by using the method of ref. ²², which fully takes into account the dipolar fields generated by out-of-plane vibrations unlike earlier approaches. For a few test cases, we confirmed that the alternative approach of refs. ^27,186 yields very similar results. Long-range quadrupole corrections^128,129 are not included except for WS₂; for this compound we included quadrupoles using the method of ref. ²⁷, with quadrupole tensors computed via the Abinit code¹⁸⁷. All calculations of carrier mobility are performed by including spin-orbit coupling (SOC).

Quasiparticle GW calculations for WS₂ are performed using the BerkeleyGW code^188,189. We employ a dielectric matrix kinetic energy cutoff of 25 Ry, 390 empty bands for the summation over states, and the Hybertsen–Louie plasmon-pole model. GW band structures are used to obtain more accurate values for the effective masses, and to solve aiBTE equations with the highest precision in the case of WS₂.

Ab initio Boltzmann transport equation

In this section, we briefly summarize the methodology underlying the aiBTE approach, as well as its simplified version provided by the relaxation time approximation for comparison with previous work. A detailed derivation of the aiBTE formalism can be found in refs. ^174,190. The carrier mobility tensor in the weak-field limit is computed as:

$${\mu }_{\alpha \beta }=\frac{1}{{n}_{{\rm{c}}}\,\Omega }\frac{1}{{N}_{{\bf{k}}}}\sum _{n{\bf{k}}}{v}_{n{\bf{k}},\alpha }{\partial }_{{E}_{\beta }}{f}_{n{\bf{k}}},$$

(1)

where Greek indices indicate Cartesian directions, n_c is the carrier density, Ω is the volume of the crystal unit cell, and N_k is the number of electron wavevectors k in a uniform Brillouin zone grid; v_nk,α denotes the electron group velocity along the Cartesian direction α for the electronic state with band n and wavevector k; ${\partial }_{{E}_{\beta }}{f}_{n{\bf{k}}}$ is the derivative of the electron occupation function with respect to the β-component of the electric field, evaluated at vanishing field. In the case of calculations without SOC, an additional factor of 2 is needed in Eq. (1) to account for spin degeneracy.

The variation ${\partial }_{{E}_{\beta }}{f}_{n{\bf{k}}}$ is obtained from the self-consistent solution of the equation:

$$-e{v}_{n{\bf{k}}}^{\beta }\frac{\partial {f}_{n{\bf{k}}}^{0}}{\partial {\varepsilon }_{n{\bf{k}}}}=\frac{1}{{N}_{{\bf{q}}}}\sum _{m{\bf{q}}}\left({\Gamma }_{m{\bf{k}}+{\bf{q}}\to n{\bf{k}}}\,{\partial }_{{E}_{\beta }}{f}_{m{\bf{k}}+{\bf{q}}}-{\Gamma }_{n{\bf{k}}\to m{\bf{k}}+{\bf{q}}}\,{\partial }_{{E}_{\beta }}{f}_{n{\bf{k}}}\right),$$

(2)

where e is the electron charge, ${f}_{n{\bf{k}}}^{0}$ denotes the Fermi-Dirac occupation of the state nk, and Γ_nk→mk+q denotes the transition rate from the state nk to the state mk + q. The electron–phonon scattering rate is written as:

$$\begin{array}{rcl}{\Gamma }_{n{\bf{k}}\to m{\bf{k}}+{\bf{q}}}^{{\rm{(ph)}}}&=&\sum\limits_{\nu }\frac{2\pi }{\hslash }{\left\vert {g}_{mn\nu }({\bf{k}},{\bf{q}})\right\vert }^{2}\\ &&\times \left[({n}_{{\bf{q}}\nu }+1-{f}_{m{\bf{k}}+{\bf{q}}}^{0})\delta ({\varepsilon }_{n{\bf{k}}}-{\varepsilon }_{m{\bf{k}}+{\bf{q}}}-\hslash {\omega }_{{\bf{q}}\nu })\right.\\ &&+\left.({n}_{{\bf{q}}\nu }+{f}_{m{\bf{k}}+{\bf{q}}}^{0})\delta ({\varepsilon }_{n{\bf{k}}}-{\varepsilon }_{m{\bf{k}}+{\bf{q}}}+\hslash {\omega }_{{\bf{q}}\nu })\right],\end{array}$$

(3)

where ℏ is the reduced Planck constant, and g_mnν(k, q) is the electron–phonon matrix element for the scattering between Kohn-Sham states nk and mk + q via the phonon of wavevector q in branch ν¹⁹¹, n_qν denotes the Bose–Einstein occupation of this mode, and ω_qν is the corresponding vibrational frequency; ε_nk and ε_mk+q denote DFT or GW eigenvalues.

The evaluation of the electron–phonon matrix elements g_mnν(k, q) using Wannier–Fourier interpolation requires some caution in polar materials. In fact, in 3D materials this matrix element diverges as 1/∣q∣ for q → 0 in the case of longitudinal-optical (LO) phonons^184,185. This effect is a consequence of the long-range electric field established by a LO phonon at long wavelength. In 2D materials, there is no such singularity, by the matrix element exhibits a discontinuity in the long-wavelength limit^22,26,27,192. To handle these non-analyticities, the matrix element is separated into a short-range and a long-range component, $g={g}_{{\mathcal{S}}}+{g}_{{\mathcal{L}}}$¹⁸⁴. The short-range component is dealt with via standard Wannier–Fourier interpolation¹⁸², while the long-range component is evaluated using an exact formula that contains the LO phonon frequency, Born effective charges, and electronic dielectric permittivity tensor for the dipole term^184,185, and additionally the Born dynamical quadrupole tensors for the quadrupole component^16,128,129.

The evaluation of the long-range component of the matrix element, ${g}_{{\mathcal{L}}}$, in 2D polar materials is made challenging by the presence of a dielectric interface between the 2D material and vacuum (or another dielectric substrate). This problem has been addressed by resorting to various approximations, e.g., using an infinitesimally-thin 2D later¹⁹³, a square-well potential along the direction perpendicular to the slab^194,195, and a uniform macroscopic polarization within the 2D slab²⁶. More recent work included the effect of out-of-plane dipoles^27,192,196, and a unified approach to both 3D and 2D polaron electron–phonon interactions²². In this work, we evaluate ${g}_{{\mathcal{L}}}$ using Eq. (34) of ref. ²², as implemented in EPW v5.8¹⁷⁵.

As for Fröhlich interactions, long-range quadrupole corrections also exhibit non-analiticities at long wavelenght, which can be captured in 2D materials using the method of ref. ²⁷. These effects are not expected to play a significant role for the low-mobility compounds of Set D, but are important in the case of WS₂ where long-range Fröhlich couplings are weak and low-energy acoustic modes dominate. The computed tensors of dynamical quadrupoles for WS₂ are reported in Supplementary Table 5. We expect corrections of similar magnitude for the related high-mobility compound WSe₂, which also exhibits weak Fröhlich couplings. The present calculations of long-range electron–phonon couplings do not take into account free-carrier screening. Screening is expected to play a role for carrier densities of 10¹³ cm⁻², for which the Fermi level lies within the bands, and will likely weaken long-range electron–phonon scattering.

In order to check for scattering mechanisms beyond electron–phonon processes, we also perform calculations of scattering by ionized impurities in selected cases. Ionized impurities lead to strong carrier scattering due to the long-range nature of their associated Coulomb potential^197,198. In ref. ¹⁹⁸ the following ionized-impurity scattering rate was derived starting from the Kohn–Luttinger ensamble average procedure¹⁹⁹:

$$\begin{array}{l}{\Gamma }_{n{\bf{k}}\to m{\bf{k}}+{\bf{q}}}^{({\rm{ii}})}={n}_{{\rm{imp}}}\frac{2\pi {e}^{4}{Z}^{2}}{\hslash \,{\epsilon }_{0}^{2}\,\Omega }\\ \times \sum\limits_{{\bf{G}}\ne -{\bf{q}}}\frac{| \langle {u}_{m{\bf{k}}+{\bf{q}}}| {e}^{i{\bf{G}}\cdot {\bf{r}}}| {u}_{n{\bf{k}}}\rangle {| }^{2}}{| ({\bf{q}}+{\bf{G}})\cdot {{\boldsymbol{\epsilon }}}^{0}\cdot ({\bf{q}}+{\bf{G}}){| }^{2}}\,\delta ({\varepsilon }_{n{\bf{k}}}-{\varepsilon }_{m{\bf{k}}+{\bf{q}}}),\end{array}$$

(4)

where n_imp is the impurity concentration, ϵ₀ and ϵ⁰ are vacuum permittivity and the electronic dielectric permittivity tensor, respectively. G denote reciprocal lattice vectors, and u_nk is the lattice-periodic part of the Kohn-Sham state. Equation (4) was derived for bulk crystals; a generalization of this equation for 2D materials should proceed along the same lines as for the Fröhlich matrix element in ref. ²², but is not available yet. Therefore, here we compute ionized-impurity scattering in the bulk parent compounds, and we estimate the effect of impurity scattering in 2D by using Matthiessen’s rule rule¹⁹⁸.

We take into account scattering by extended defects using the simplest possible model, whereby the relaxation time is given by the time needed for the carrier to traverse the entire defect length L. Given the carrier velocity v_nk, the scattering rate in this model is ${\Gamma }_{n{\bf{k}}}^{({\rm{e}}d)}=| {{\bf{v}}}_{n{\bf{k}}}| /L$. This model is popular in the study of thermal transport^{200,201,202,203}. To obtain electron velocities, we employ Wannier–Fourier interpolation within the EPW code. The defect size L is an external parameter of the model.

Transport descriptors for HT screening

Accurate mobility calculations using Eq. (2) are too expensive for HT approaches. In order to perform a rapid screening large materials libraries, it is necessary to down-select the most promising materials via descriptors that are computationally affordable. In the simplest approximation, the mobility is expressed by Drude’s law as μ = eτ/m^*, where τ and m^* are an effective relaxation time and an average effective mass. The effective mass can in principle be obtained from the band curvature at the VBM or CBM edges; however, this textbook approach does not take into account possible band degeneracy and multi-valley band extrema. A more useful definition which automatically includes these effects is provided by the conductivity effective mass^171,204:

$${\left[{m}^{* }\right]}_{\alpha \beta }^{-1}=-{\left(\sum _{n{\bf{k}}}{f}_{n{\bf{k}}}^{0}\right)}^{-1}\sum _{n{\bf{k}}}{v}_{n{\bf{k}}}^{\alpha }{v}_{n{\bf{k}}}^{\beta }\,\frac{\partial {f}_{n{\bf{k}}}^{0}}{\partial {\varepsilon }_{n{\bf{k}}}}.$$

(5)

This expression reduces to the textbook definition of effective mass in the case of a single parabolic band, and provide an averaged quantity in more complex scenarios. Formally, this definition can be obtained from Eqs. (1, 2) by neglecting the ${\partial }_{{E}_{\beta }}{f}_{m{\bf{k}}+{\bf{q}}}$ term in the latter equation, replacing Γ_nk→mk+q by a constant rate, and assuming Drude’s formula to hold. We note that, by definition, the conductivity effective mass depends on temperature and carrier concentration.

For the average relaxation time τ to be used for HT screening, we test two possible approximations: (i) We evaluate the relaxation time corresponding to polar phonon scattering in 2D, using a model electron–phonon matrix element derived in ref. ²²; (ii) We use the much simpler Emin’s formula²⁰⁵.

The scattering rate for polar phonon scattering in 2D can be derived from Fermi’s Golden Rule by assuming a dispersionless polar phonon of frequency ω and an electron in a parabolic band of mass m^*. Using the matrix element in Eqs. (62) and (63) of ref. ²², the rate for carriers at the energy ε above the CBM reads:

$$\begin{array}{rcl}{\tau }^{-1}(\varepsilon )&=&\frac{{e}^{2}{m}^{* }\omega d}{8\pi {\epsilon }_{0}{\hslash }^{2}}{\epsilon }^{{\rm{ion}}}\left\{\theta (\varepsilon -\hslash \omega )[1-f(\varepsilon -\hslash \omega )+n(\hslash \omega )]\right.\\ &\times &\left.g(\varepsilon ,\hslash \omega )+[f(\varepsilon +\hslash \omega )+n(\hslash \omega )]g(\varepsilon ,-\hslash \omega )\right\},\end{array}$$

(6)

where d is the effective thickness of the 2D material, ϵ^ion is the lattice contribution to the dielectric constant, and f, n, θ are Fermi-Dirac, Bose–Einstein, and Heaviside functions, respectively. The two terms in the square brackets in Eq. (6) correspond to phonon emission and absorption, respectively. The auxiliary function g is:

$$g(x,y)={\int_{2x-y-2\sqrt{x}\sqrt{x-y}}^{2x-y+2\sqrt{x}\sqrt{x-y}}}\frac{{[4xu-{(y+u)}^{2}]}^{-1/2}}{{(1+\sqrt{u/\eta })}^{2}}du,$$

(7)

where $\eta ={\hslash }^{2}{[4{\epsilon }^{\infty }/(2{\epsilon }^{\infty ,2}-1)d]}^{2}/2{m}^{* }$²². The quadrature in Eq. (7) is performed numerically. The average scattering rate needed in Drude’s formula is obtained from τ(ε) in Eq. (6) via:

$$\tau ={\int_{0}}^{\infty }dx\,x\,{e}^{-x}\,\tau (x{k}_{{\rm{B}}}T).$$

(8)

Mobility estimates using this model only require the knowledge of the effective mass, slab thickness, dielectric constants, and phonon frequency.

Emin’s formula for the relaxation time is considerably simpler, as it does not take into account any materials parameters. It is given by²⁰⁵:

$$\tau =\hslash /{k}_{{\rm{B}}}T.$$

(9)

The advantages of this expression are that (i) it establishes a simple conversion formula between effective mass and mobility, μ = eℏ/m^*k_BT, (ii) it exhibits a reasonable dependence on temperature, and (iii) it does not require any materials data other than band structures. In this manuscript we use both Eqs. (6, 9) for the initial HT screening of 2D materials.