Introduction

Scanning transmission electron microscopy (STEM) has proven highly successful and versatile for characterising material structure from the micron down to the atomic scale. For every byte of data generated by traditional monolithic STEM detectors, developments in fast readout electron pixel detectors (e.g. refs. 1,2) now mean we can collect millions of bytes with the added benefit of momentum resolution. Recording the detailed electron scattering distribution has enabled a range of imaging strategies. In four-dimensional (4D) STEM, at each probe position in a two-dimensional scan across a sample a two-dimensional convergent beam electron diffraction (CBED) pattern is acquired (Fig. 1a). Described by the umbrella term of 4D STEM, these imaging strategies include mapping crystal orientation, strain and electromagnetic fields, and phase contrast techniques for determining the crystal structure (see Ref. 3 for a review). While in some cases the known scattering physics leads to constructive processing algorithms to determine the quantity of interest4,5,6, in many cases machine learning, optimisation and other statistical methods are used to efficiently identify patterns or determine quantities of interest from the data7,8,9,10,11,12,13. In most cases, the reliability of the analysis depends on the quality of the data.

Fig. 1: Overview of 4D STEM.
figure 1

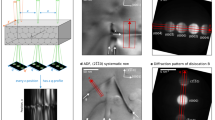
a Schematic 4D STEM set-up. At each probe position a convergent electron beam scatters through a material and forms a convergent beam electron diffraction (CBED) pattern. b Experimental CBED patterns from aluminium ([001] zone axis, 300 keV electrons, 15 mrad convergence semiangle, 0.2 Å probe spacing and 8 × 106 e−. Å−2 dose). Visual features in the patterns change smoothly in position, intensity and shape across adjacent probe positions, a kind of geometric flow, with prominent examples indicated by white and orange arrows. c STEM imaging of the total number of electrons in each pattern in the 4D STEM data. The red box indicates the region from which the patterns in (b) are taken. d The probe-position averaged CBED (PACBED) pattern for data in (c), with the bright and dark field regions indicated.

Full size image

In contrast to traditional STEM imaging modes such as annular dark field imaging that use only a fraction of the electrons incident upon the sample or recorded by the detector, 4D STEM modes are often considered dose efficient because they make use of the majority of such electrons14,15. Nevertheless, spreading the dose over many detector pixels reduces the signal-to-noise ratio per pixel. The CBED patterns may therefore appear noisy, which can impact forms of 4D STEM analysis that depend on detailed structure in the patterns.

In principle, signal-to-noise can only be improved by increasing the number of counts in each pattern, by counting longer (dwell time) and/or increasing count rate (beam current), both of which may be undesirable in practice. First, increasing dwell time increases susceptibility to time-dependent variables like sample drift, heating and electric charging, while also increasing dose (number of electrons per probe position). Second, many materials of interest for high resolution characterisation are electron-beam-sensitive, for which the dose must necessarily be kept very low16. This then poses the challenge of whether and which 4D STEM methods remain reliable for analyzing noisy data obtained at low dose for beam sensitive applications17,18. While some materials admit material-specific strategies (such as using assumed periodicity to distribute dose widely and solve for an average structure19), this work will focus on denoising as a preprocessing step as a more general strategy.

Various denoising strategies have been applied to 2D STEM images20,21,22,23 and might be adapted for application to individual CBED patterns, but are not designed to take advantage of the connection between probe position and diffraction coordinate inherent in 4D STEM. One approach that uses the 4D nature of the dataset is the tensor-SVD (TSVD) method of Zhang et al.24. Linear models used in TSVD (also used during compressive sensing25) are efficient and, depending as they do on repetitions in diffraction patterns to provide reliable statistics, are particularly effective for periodic samples. However, many samples of interest are not perfectly periodic, and to handle this larger class of materials we take a different approach. Figure 1b shows several adjacent experimental CBED patterns, a subset of a larger 4D STEM dataset taken from the region indicated by the red box in the STEM image in Fig. 1c. At this 0.2 Å probe spacing, the position, intensity and shape of visual features in the CBED patterns change smoothly between adjacent probe positions, with specific examples indicated by the white and orange arrows. We will use this geometric flow26 connection between adjacent CBED patterns as the basis for denoising 4D STEM data.

A useful analogy for our general strategy comes from language models: having learned relationships between words as they occur in the context of sentences27, a language model can predict a missing word in an incomplete sentence28. Similarly, in the 4D STEM example in Fig. 1b, if one can learn the 2D language, as it were, of the geometric flow connections between nearby CBED patterns then one could predict a missing pattern. Further, in the presence of noise, a learning model of appropriate complexity may be able to learn the geometric flow connections that derive from the common structural information between adjacent patterns but not the noise (which is independent between patterns) and so predict denoised patterns.

Our approach is also reminiscent of the J-invariant denoisers introduced in noise2self29 and noise2noise30. Those methods target denoising of 2D static images through the addition and subsequent removal of additive noise, and the selection of pixels to contaminate in these techniques is simply random. Another method that typically uses a Gaussian noise is diffusion mapping in a long and careful training process31. Instead of noise addition and removal, we propose a strategy of data completion by assuming a relationship between CBED images.

While it may be possible to use models originally designed for language learning such as Transformers27, they are large and so have the drawback that the careful training is slow. We instead use a fully convolutional neural network (CNN) named U-Net32. This model can learn the intricate relationships between adjacent patterns and individual pixel values by optimizing learnable kernels that describe many complex features of different sizes in images33. Such models can utilize and optimize many parameters at once, granting them the capacity to identify and learn more complex visual features than linear models34. So that it can be used for denoising 4D STEM data from any given specimen or area of interest, we use unsupervised training35 based solely on the specific 4D STEM dataset of interest, disregarding any other dataset from the past.

In this paper, we explain how to structure the 4D STEM data into a training dataset that resembles 2D sentences to be learned, present the mathematical objectives used for unsupervised training of a CNN over this dataset, and show the effectiveness of the resultant network as a denoiser on experimental data. Since simple visualisation of 4D STEM data provides limited insight, denoising is not an end in itself. Using real experimental and simulated data, we therefore show how some prominent analysis methods can struggle in the presence of high levels of noise but are improved if the 4D STEM data are denoised as a preprocessing step. It is thus anticipated that denoising the raw data may boost the effectiveness of post-processing analysis of 4D STEM data and thereby aid the detailed study of dose-sensitive specimens. Key for diverse 4D STEM applications, it is of prime importance that characteristic features in every individual CBED pattern are preserved by the denoising algorithm. We test this in simulation and experiment.

Results and discussion

The network denoiser

CNNs are particularly proficient in identifying and representing visual features in input-image-to-output-image tasks. The first part is usually an encoder where CNNs employ multiple kernels to transform the input images’ features into a latent space representation. The second part of the network, called a decoder, then utilizes additional convolutional layers to reconstruct a new image from this latent representation.

To learn the relationship between any given CBED pattern and the CBED patterns from adjacent probe positions in the 4D STEM dataset, we form a series of training entries based on all subsets of 3 × 3 adjacent CBED patterns. As shown in Fig. 2a, we separate the central pattern from its eight neighbouring CBED patterns. The latter is reformatted into a single image with multiple channels (Fig. 2b), with the arrangement of patterns within the channels remaining consistent throughout the training process. These form the input to a CNN with encoder/decoder structure, Fig. 2c, the output of which is a single CBED pattern. The network is trained via back-propagation using the original central CBED pattern as the conventional label in the loss function.

Fig. 2: Data structuring and network training for denoising 4D STEM data.
figure 2

a Each 3 × 3 set of adjacent CBED patterns is divided into (b) the central “label” pattern and the eight outside patterns. The latter form a single training input for (c) the CNN, which is trained to output/predict the label pattern via back-propagation of a reconstruction error between the network output and the actual label pattern. The process is repeated on all 3 × 3 sets of adjacent CBED patterns in (d) the input noisy experimental data, and for multiple epochs, until convergence. e A high dose dataset from a comparable region of the same material agrees well with (f) the output denoised dataset.

Full size image

By feeding the network with patterns adjacent to a target CBED pattern and setting the desired output as the label CBED pattern itself, the network’s output becomes an approximation of that label CBED pattern. This is necessarily an approximation due to the limited capacity of the network. A layered neural network comprises an ensemble of many parameters to be learned. Changing the total number of parameters of a network changes its capacity to learn details, leading to under-fitting or over-fitting36. Intentionally limiting the network’s capacity leads to under-fitting, resulting in a denoised version of the data. This occurs as the network retains only essential visual features of the CBED patterns to minimize the loss, discarding less structured features typically associated with noise. While it is possible to achieve a similar under-fitting effect by training a larger network for fewer epochs37, where one epoch is defined as using all data points once for training, larger networks are slower to train. In our study, we train a model much smaller than the original U-Net for a sufficient number of epochs to stabilize the loss, highlighting the significance of the hyper-parameter that governs the network’s complexity. The effect of this hyper-parameter on the denoiser is evaluated in the Methods section.

The network is trained using stochastic gradient descent to minimize a loss function that quantifies the discrepancy between the network’s output and label CBED pattern. We take as our loss function the negative log-likelihood function associated with the Poisson distribution38:

$${{\mathcal{L}}}=-\sum\limits_{j}^{J}\sum\limits_{h}\left\{{I}_{{{\rm{r}}}}(j,h)\log \left[{I}_{{{\rm{D}}}}(j,h)\right]-{I}_{{{\rm{D}}}}(j,h)-\log \left[{I}_{{{\rm{r}}}}(j,h)!\right]\right\},$$
(1)

where j is the multi-channel input image index in a mini-batch of size J, h is the pixel index in the CBED pattern, Ir(j, h) is the j-th label CBED pattern all composed of integer values, and ID(j, h) = fN(Iin(j, h)) is the neural network output for j-th input, in which fN is the neural network as a single differentiable operator and Iin(j, h) is the network input comprised of adjacent CBED patterns of the j-th label CBED pattern in the form of a multi-channel image. The final term involving the factorial may be neglected since it does not contribute to the gradient with respect to the model parameters. This loss function is suited to data where the limiting form of noise is that of shot (or counting) noise. Such noise can make the recorded CBED patterns sparse, and in extreme cases only a few pixels may have nonzero electron counts. Combined with the limited network complexity, this loss function facilitates denoising by not overly penalising pixel-by-pixel fluctuations that are consistent with Poisson distributions.

By way of example, Fig. 2d shows a portion of a relatively low dose experimental 4D STEM dataset taken from SrTiO3 (details in Methods section) with about 140 electrons per CBED pattern (about 2.2 × 103 e−.Å−2). The sparsity of these patterns is evident, and very little clear structure can be perceived by eye. Figure 2f shows the corresponding output of the network denoiser trained on the full low dose dataset, in which structure within the CBED patterns is now clearly visible. Note that the denoiser was only trained on the bright field region—see Fig. 1d—since at the present noise level the count rate in the dark field region was too low to reliably denoise. To validate the denoised results, Fig. 2e shows a portion of a relatively high dose dataset (about 22,000 electrons per diffraction pattern, or 3.5 × 105 e−.Å−2) from an equivalent region of the same sample, and is seen to be in good visual agreement with the denoised results, which we quantify by noting that the Pearson cross correlation coefficient between the two data subsets is 0.96 (i.e. very close to 1).

Technical details of the network denoiser training and complexity are given in the Methods section, but two further aspects of our implementation are worth noting here. First, the dominance of higher angle electron scattering when the probe is on or near columns reduces the number of electrons within the bright field disk. This disparity produces an imbalance of information among the entries of a 4D STEM dataset. The features of most interest in atomic resolution STEM are the atomic columns, yet the CBED patterns in the close vicinity of columns convey less information (fewer counts) for the CNN to learn visual features. Any fitting method, regardless of the chosen model, must account for and regulate this imbalance, and approaches to overcome the challenge of such an imbalance for various representation learning methods have been much studied by the machine learning community39,40. We therefore found it advantageous to segment the 4D STEM data into two groups according to their average total intensity in the bright field region. The network was trained on patterns with lower average intensities twice as often as those with high intensities.

Second, we have found that the denoising performance can be enhanced through an iterative technique. Specifically, we take a weighted sum of the noisy initial 4D STEM dataset and the denoised 4D STEM output from the preceding iteration as the input for the next iteration of training according to the simple rule:

$${I}_{{{\rm{in}}}}^{(c)}=(1-\beta ){I}_{{{\rm{m}}}}+\beta {I}_{{{\rm{D}}}}^{(c-1)},\quad \beta =\frac{c-1}{C},\quad c=\{1,\cdots \,,C\}$$
(2)

where c is the iteration number, \({I}_{{{\rm{in}}}}^{(c)}\) is the c-th input dataset constructed by a weighted sum of the input dataset formed via measurement, Im, and the denoised dataset of the previous iteration, \({I}_{{{\rm{D}}}}^{(c-1)}\). The total number of iterations, C, is set to 10 when such refinement is used in our experiments (when used, this is noted). Following each cycle, the input dataset is updated and the training process is continued. Increasing the weight assigned to the denoised data at each step allows the quality of denoised dataset to incrementally improve. We stress that this refinement process solely relies on the original noisy data, without any other priors, which ensures the fidelity of the information throughout the denoising process. Although this method consistently produced enhanced results in our studies, it also increases computational time linearly with each additional iteration.

Dependency on geometric flow

Since our approach is motivated by the notion of geometric flow, i.e. smooth variation in CBED patterns between adjacent probe positions, we expect its effectiveness to depend on the how the width of the probe compares to the step size between probe positions. To explore this, we simulated a series of 4D STEM datasets for perovskite SrTiO3 viewed along the [001] zone axis, with a 3.9 Å × 3.9 Å (projected) repeat unit, and pyrochlore Y2Ti2O7 viewed along the [011] zone axis, with a 10.1 Å × 7.1 Å (projected) repeat unit. All calculations assumed 200 Å thick samples, 300 keV electrons and Poisson noise (specific values for the different explorations are detailed below). Following denoising, we assessed the reconstruction errors by evaluating the Frobenius norm ∣∣I* − ID∣∣F between the noise-free, ground truth simulated 4D STEM data I* and the denoised 4D STEM data ID. (Though formally the Frobenius norm is defined on (2D) matrices, we follow its loose generalisation in machine learning as the square root of the sum of the squares of all entries in any n-dimensional array.)

Figure 3a plots the reconstruction error as a function of probe spacing, assuming 64 probe positions, a 21.4 mrad convergence semiangle, and noise resulting from 256 electrons per CBED pattern (though this means dose varies with probe spacing, keeping the counts per probe position fixed is the fairer comparison here). In all cases, the reconstruction error initially increases with probe spacing, as decreasing similarity between adjacent CBED patterns makes the geometric flow less evident and so less learnable by the network. A strong decrease in reconstruction error is observed for the SrTiO3 examples at probe spacings of 1/4, 1/2, 3/4 and 1 times the length of the SrTiO3 repeating unit (i.e. probe spacings of approximately 1, 2, 3 and 4 Å), meaning the 4D STEM dataset comprises CBED patterns that repeat themselves over the field of view. This repetition, also amenable to denoising via linear approaches like TSVD, is learnable by the network though it does not constitute geometric flow per se. By contrast, few such sharp dips are evident in the reconstruction error for Y2Ti2O7, where the larger, rectangular unit cell means no probe spacing produces high repetition. Figure 4 provides some sample patterns for these step sizes.

Fig. 3: Reconstruction error plots varying probe spacing and convergence semiangle.
figure 3

Reconstruction errors for denoising simulated 4D STEM datasets from SrTiO3 and Y2Ti2O7 as a function of (a) probe spacing (assuming a 21.4 mrad convergence semiangle) and (b) convergence semiangle (assuming a 0.75 Å probe spacing). In (a) results are shown both for probes focused at the surface, and for probes with a probe-spacing-dependent defocus (labelled “df”) equal to ps/α (where ps is the probe spacing and α is the convergence semiangle). The added noise level in (a, b) differ.

Full size image
Fig. 4: Reconstruction error of patterns with varying probe spacing.
figure 4

For five probe spacings for each material, sample patterns of synthetic noise-free datasets, their denoised version and the absolute difference between these two is shown in the first, second and third rows respectively. Since the reconstruction error was already quantified in Fig. 3a, in order to visualise the structure in the patterns here we scale each row to have maximum value equal to one. This includes the last row, which thus shows the reconstruction error to be noticeably less for lower probe spacing values.

Full size image

In the popular phase reconstruction method of ptychography, using a defocused probe above the sample is an established way to reduce the dose by allowing a larger probe spacing while producing a wider probe on the sample, thereby preserving the degree of overlap (and thus information in common) on which that reconstruction method depends41,42. In Fig. 3a, the plots labelled “df” result from a probe-spacing-dependent defocus value equal to ps/α (where ps is the probe spacing and α is the convergence semiangle), which increases the width of the probe on the surface in proportion to the increased probe spacing. The reconstruction error shown in Fig. 3a suggests that increasing the defocus does not significantly enhance geometric flow.

We also expect geometric flow to depend on convergence semiangle, since at smaller semiangles the structure in the bright field disk changes more slowly with probe position because the probe is wider on the surface of the sample. (In a perfect crystal, if the probe-forming aperture diameter is such that the probe convergence semiangle is less than half the Bragg angle, then the CBED pattern becomes independent of probe position43, trivially guaranteeing geometric flow.) Using a fixed probe spacing of 0.75 Å, which in Fig. 3a caused the denoiser to struggle with a 21.4 mrad convergence semiangle, Fig. 3b shows that the reconstruction error decreases with decreasing convergence semiangle. What constitutes equivalent noise when comparing different convergence semiangles is contestable, but we choose to fix the flux of electrons within the bright field disk by scaling the number of electrons per diffraction pattern with bright field disk area: Ne = 40α2 (giving 128 electron per diffraction pattern when α = 1.8 mrad and 1.9 × 104 electrons per diffraction pattern when α = 21.4 mrad). Figure 5 provides some sample patterns showing the denoiser to be more effective at smaller convergence semiangles.

Fig. 5: Reconstruction error of individual CBED patterns with varying convergence semiangle.
figure 5

For each convergence semiangle, sample patterns of synthetic noise-free datasets, their denoised version and the absolute difference between these two is shown in the first, second and third rows respectively. Since the reconstruction error was already quantified in Fig. 3b, in order to visualise the structure in the patterns here we scale each row to have maximum value equal to one. This includes the last row, which thus shows the reconstruction error to be noticeably less for lower convergence semiangles.

Full size image

We can further compare the advantages of geometric flow with that of repetition by restricting the field of view. Assuming a 21.4 mrad convergence semiangle and a 0.125 Å probe spacing, Fig. 6 shows violin plots depicting the distribution of reconstruction errors for the individual CBED patterns using the Frobenius norm (a for SrTiO3 and b for Y2Ti2O7) and also the Pearson correlation coefficient (c for SrTiO3 and d for Y2Ti2O7), and compares results from the current network to those from TSVD. The Frobenius norm describes absolute difference of patterns, while the correlation coefficient considers the similarity of denoised and noise-free patterns after a normalization step (subtraction of mean and division by standard deviation) and so describes their relative similarity in location of peaks and troughs. The field of view is denoted by the number of patterns: for SrTiO3, 128 patterns corresponds to almost three unit cells and so gives some pattern repetition, whereas for Y2Ti2O7 it corresponds to just over one unit cell and so almost eliminates pattern repetition. For the larger field of view in SrTiO3, where there is appreciable repetition of CBED patterns, both the network and TSVD methods give comparable reconstruction errors. However, in cases with less repetition—especially when analysing smaller fields of view, but even for the larger fields of view considered here for Y2Ti2O7—the network has lower reconstruction errors. For large fields of view in periodic structures, linear multivariate statistical methods like TSVD will perform well, and their speed and relative simplicity are attractive. However, utilizing geometric flow in 4D STEM datasets can assist in the more accurate denoising for smaller fields of view and structures where periodicity is broken, such as may be appropriate to studying localised defects. To demonstrate this, we created a synthetic SrTiO3 sample with a wedge-shaped variation in thickness along the [100] direction, utilizing a 21.4 mrad convergence semiangle. We then introduced Poisson noise by adding 128 electrons to each pattern and applied denoising with both methods (where the iterative technique of Eq. (2) was used). The outcomes of this evaluation are displayed in Fig. 7. Figure 7a shows little difference between our CNN method and the TSVD method when assessed by error and cross correlation metrics across the full 4D data set. However, such single-number comparisons conceal some significant differences. Figure 7b shows that both methods proficiently denoise the patterns from regions between atoms, which are highly repetitive across the dataset. However, Fig. 7c shows that the CNN method outperforms the TSVD method when denoising patterns adjacent to heavy atoms, since the nonlinear network has the capacity to more accurately learn these patterns which are few in number but vary significantly across the field of view.

Fig. 6: Reconstruction error with varying field of view.
figure 6

Violin plots of the histogram of reconstruction errors for the Frobenius norm (the lower the better) for (a) SrTiO3 and (b) Y2Ti2O7 and for the Pearson cross correlation coefficient (the higher the better) for (c) SrTiO3 and (d) Y2Ti2O7. Results are compared for different fields of view as indicated by the number of patterns, and between the TSVD and CNN approaches to denoising. The vertical blue lines indicate the correspondence between the number of patterns and the field of view, with the first blue line from the left corresponding to a single unit cell field of view, the second to two unit cells, and so forth. The reconstruction errors are lower in the network approach for the smaller fields of view, demonstrating its efficacy in exploiting geometric flow for signal recovery.

Full size image
Fig. 7: Comparison of denoising approaches for a wedge-shaped sample.
figure 7

a The blue structure inset shows a side view of the sample geometry with varying thickness from 80 Å to 120 Å along [100] direction (the electron beam is in the vertical direction). The yellow image above the structure shows the STEM image. The vertical axis, EI, gives the Frobenius norm (FN) and cross-correlation coefficient (CC) metrics for both denoising methods to compare the denoised ID and noise free I* datasets. The black arrows show the two rows (horizontal) and four columns (vertical) of where the diffraction patterns in (b, c) are sampled from. CBED patterns from locations (b) in between atoms (from the upper row in the yellow image in (a)) and (c) closest to heavy atoms (from the lower row in the yellow image in (a)), for noise-free, noisy and denoised datasets using both methods. The noisy data has integer values. The overall electron counts are less for locations on heavy atoms due to absorption (i.e. thermal scattering to high angles).

Full size image

Moreover, we incorporate a final layer for the network that produces squared values which ensures that the output is always positive, as measured intensities must be, something TSVD does not guarantee.

Applications

Figure 2d–f showed that the network denoiser improves the visual quality of 4D STEM data. However, 4D STEM data is rarely analysed by visual inspection. Therefore, we further explore how applying the denoiser to various simulated and experimental 4D STEM datasets as a preprocessing step can improve subsequent 4D STEM analysis.

One approach to analysing 4D STEM data is to generate STEM images which map some quantity evaluated for each CBED pattern as a function of probe position. Two examples that take advantage of the detailed scattering distribution in 4D STEM data are centre-of-mass (CoM) and Symmetry STEM imaging. CoM imaging evaluates the first moment, or centre-of-mass of the CBED patterns, which in samples thin enough for the phase object approximation to hold is proportional to the (projected) electric field in the sample (convolved with the probe intensity)4,14,44. By using all the measured electrons, CoM imaging is dose efficient and quite robust to shot noise14, but nevertheless its accuracy diminishes under sufficiently low-dose conditions. Symmetry STEM45 plots some measure of whether a particular symmetry is present in the CBED pattern at each probe position, for example the cross-correlation of each CBED pattern with its own 90∘ rotation. Symmetry is a defining property of crystal structures and is very sensitive to small deviations. Consequently, Symmetry STEM images often display finer features than conventional STEM imaging modes. However, this sensitivity can make Symmetry STEM images susceptible to noise, particularly when the dose is sufficiently low that the electrons in the CBED patterns are sparsely distributed. For related reasons, in disordered solids such as glasses, the same symmetry analysis from 4D STEM cross-correlation must be further analysed to extract statistical estimates of Fourier coefficients for various symmetry orders46.

Figure 8 explores CoM and Symmetry STEM images on simulated noisy, denoised and noise-free 4D STEM datasets for CeB6, assuming a 300 keV, 16 electrons per pattern (256 e−. Å−2), an aberration-free probe with 21.4 mrad convergence semiangle and a probe spacing of 0.25 Å, for both a 28 Å thick sample (Fig. 8a, b) and a 240 Å thick sample (Fig. 8f, g). We have only applied the denoiser to the bright field region, and so only that region is used in evaluating the CoM and Symmetry STEM images. This does not appear to be overly restrictive, with the images in Fig. 8 showing the qualitative features expected of these imaging modes. The results chosen for visualisation in Fig. 8a, b, f, g were refined (where the iterative technique of Eq. (2) was used).

Fig. 8: Denoiser preprocessing for centre-of-mass and symmetry STEM imaging.
figure 8

Comparison of noisy, denoised and noise-free 4D STEM simulations for 28 Å thick CeB6, at 16 electrons in each CBED pattern, used to generate (a) centre-of-mass (CoM) STEM images (with colour denoting CoM direction and brightness denoting CoM magnitude) and (b) Symmetry STEM images for 90∘ rotational symmetry. Plots of the (c) intensities reconstruction error EI = ∣∣I* − ID∣∣F, (d) CoM error ECoM = ∣∣CoM(I*) − CoM(ID)∣∣F where CoM(I) is comprised of two images for any dataset I (one for the first moment in each of the x and y directions), and (e) symmetries error ESymm = ∣∣Symm(I*) − Symm(ID)∣∣F where Symm(I) is comprised of 360 images for any dataset I (i.e. all rotational symmetries at 1∘ increments), all compared to true data. f–j As per (a–e) but at 240 Å thickness.

Full size image

For the thinner sample, Fig. 8a shows that the Ce columns are visible in the CoM STEM image from the noisy data, but there is little clear structure around the B6 cluster. In the CoM image from denoised data there is clearly perceptible contrast around the B6 cluster, albeit less clearly resolved than in the noise-free data and its contrast is larger, relative to the Ce column, than in the noise-free case. For the thicker sample, Fig. 8f shows that there is little perceptible structure in the CoM STEM image from the noisy data, but that from the denoised data shows the same qualitative structure as that from the noise-free data. Similarly, in Fig. 8b and g, there is little perceptible structure in the Symmetry STEM images at either thicknesses, whereas there is much clearer structure in the Symmetry STEM images from the denoised data—they are not in exact agreement with the noise-free data, but denoising has clearly benefited the analysis.

Figure 8c, h seek to quantify the advantage of denoising with respect to dose, measuring the deviation via the Frobenius norm error of both 4D STEM datasets with respect to the noise free data. Figure 8d and i show the error of the calculated CoM and Fig. 8e, j show it for Symmetry STEM with respect to CoM and Symmetry STEM of noise free data, respectively. The denoised results are consistently in better agreement with the noise-free results, and this relative advantage grows as dose reduces, though denoising ultimately fails at extremely low dose.

Another increasingly popular strategy for analysing 4D STEM data is ptychography, a family of algorithms for reconstructing the specimen potential47,48,49. Ptychography is even more dose efficient than CoM imaging50,51, yet is increasingly impacted by noise at lower doses (less than 512 e−. Å−2). In that regime, denoising may improve the reconstructions.

We first consider a phase object, replicating the approach of Wen et al.52 in using single-slice, iterative ptychography to determine the structure (specifically, the projected electrostatic potential) of single layer MoS2. We use a simulated dataset, assuming a 300 keV, aberration-free probe with 21.4 mrad convergence semiangle and a probe spacing of 0.25 Å. Figure 9a compares the reconstructed complex objects from noisy and denoised data against that from the noise-free dataset via the Frobenius norm difference measure, while varying the dose from 16 to 512 e− per pattern (equivalent to the range of 256 to 8192 e−. Å−2). At the low doses considered here, the results depend on the noise realisation, and results from five different noise realisations are shown for each dose in Fig. 9a, with the solid line a guide-to-the-eye average. While the iterative ptychography algorithm (which seeks to optimise the structure for best agreement with all CBED patterns) is quite robust to noise at the higher dose of 512 e−. Å−2, at the lower doses, denoising is seen to offer some benefit. Figure 9b–d show a concrete example for the case of 1024 e−. Å−2 and the noise realisation indicated by the arrows in Fig. 9a. The ptychographic reconstruction fails on this noisy data as seen in Fig. 9c. In contrast, the ptychographic reconstruction on the denoised data, Fig. 9d, yields a projected potential that qualitatively resembles the structure, albeit with some evident distortions.

Fig. 9: Denoiser preprocessing for single-slice ptychography.
figure 9

a Plot of the Frobenius norm comparing the ptychographic reconstruction (P) from noisy (crosses) and denoised (circles) data with that from noise-free data (P*), all simulated for MoS2, as a function of dose. The results for five different noise realizations are given by the symbols at each dose, with the solid line giving the guide-to-the-eye average. b The reconstructed potential from noise-free data, for comparison against that from (c) noisy and (d) denoised data for the dose and noise realisations indicated by the arrows in (a).

Full size image

We next consider a thick object. Among various approaches to solving for the potential of thick samples53,54,55,56,57, multislice ptychography has shown the most success to date48,58,59,60,61,62,63,64. In a similar vein to Gilgenbach et al.49, Fig. 10a explores the impact of defocus, dose and probe spacing on multislice ptychographic reconstruction on simulated 4D STEM datasets of 240 Å thick SrTiO3, assuming 300 keV electrons and a 19 mrad convergence semiangle. The probe spacing was varied from 0.125 Å to 1 Å in increments of 0.125 Å, and defocus values ranged from −150 Å to 150 Å in increments of 25 Å (negative defocus indicates focusing of the probe into the sample). Again, five different Poisson noise realizations were generated for each of the dose cases, which range from 2 to 128 electrons per probe position. After performing multislice ptychography as detailed in the Methods section, the reconstruction error was quantified using the Frobenius norm of the difference between the complex objects produced for noisy and noise-free datasets. The results, summarised in Fig. 10a, show a rapid increase in reconstruction error with reduced dose, where the dose on the horizontal axis incorporates the effect of both number of electrons per pattern and the probe spacing. For 16 e−. Å−2 and using the iterative technique of Eq. (2), the reconstructions based on the denoised dataset (Fig. 10d) clearly agree better with those from the noise-free dataset (Fig. 10b) than with those from the noisy dataset (Fig. 10c). We stress that this simulation is in many ways ideal — with other experimental limitations (e.g. scan distortion, spatial incoherence), somewhat higher doses may be needed for accurate reconstruction.

Fig. 10: Denoiser preprocessing for multislice ptychography.
figure 10

a Reconstruction errors from multislice ptychography of simulated 4D STEM datasets of SrTiO3 for different dose levels, corresponding to ranges of probe spacing values, defocus values and number of electrons in patterns. We only show those with lower errors and electron counts, and for simplicity do not convey the defocus values. b The reconstructed potential from noise-free data, for comparison against that from (c) noisy and (d) denoised data for the parameter combination indicated by the arrow in (a). Calculations assume 16 e−. Å−2, 1 Å probe spacing, and 50 Å defocus (which as per Fig. 3 does allow successful denoising of SrTiO3 at 1 Å).

Full size image

Let us now consider a few examples applied to experimental data that further show when the geometric flow can and cannot aid in denoising 4D STEM analysis. Figure 11 shows total intensity STEM images formed from 4D STEM datasets taken over a large field of view (1.5 μm × 1.5 μm) of SrTiO3. Using a 300 keV electron beam, the data in the top row used a low convergence semiangle of 1.5 mrad (corresponding to a beam waist of ~7 Å full-width-half-maximum) while that in the bottom row used a high convergence semiangle of 21.4 mrad (corresponding to a beam waist of ~0.5 Å full-width-half-maximum). Average dose is not very meaningful when the probe spacing is much larger than the probe width, but in the low convergence semiangle data there are around 50 e− per CBED pattern in the low dose case and 500 e− per CBED pattern in the high dose case. Since the probe spacing is around 60 Å, we might initially expect that geometric flow would not apply in either case. However, the 1.5 mrad probe does not lead to diffraction disk overlap, which can be seen in the PACBED inset in Fig. 11a, meaning that for a perfect crystal the CBED pattern will be independent of probe position relative to the unit cell. Consequently, geometric flow will apply provided that any structural defects and variations in thickness or sample orientation occur on a longer length scale than the 60 Å probe spacing. Thus the denoised low dose result (Fig. 11c) resembles the high dose result (Fig. 11a) more than the raw low dose result (Fig. 11b). To further confirm that the network denoiser preserves the structure but reduces the noise in local regions, Fig. 11d–f show the locally averaged CBED patterns for the three distinct regions shown by white boxes in Fig. 11b. In contrast, the 21.4 mrad probe case does not satisfy conditions for geometric flow. One manifestation of this is the Moiré fringes clearly evident in the high dose data (Fig. 11g) and still perceptible in the low dose data (Fig. 11h). Geometric flow is absent because there is no consistent relationship between adjacent CBED patterns, with the consequence that the denoised result (Fig. 11i) has not enhanced the fringes as (predictable) signal but instead eliminated them as (unpredictable) noise.

Fig. 11: Experimental images from SrTiO3 after denoiser preprocessing.
figure 11

Virtual dark field STEM images from experimental 4D STEM data acquired using a 1.5 mrad convergence semiangle at (a) high dose and (b) low dose, and c the denoised low dose data. d–f PACBEDs of three small areas for each dataset (the areas indicated with number 1, 2 and 3 correspond to subsets of size 5 × 5 patterns at the location of numbers shown by text in (b), visualising that the denoiser can consistently denoise different structures in the field of view, independently. g–i Similar to (a–c) but now virtual bright field STEM images acquired using a 21.4 mrad convergence semiangle. In both cases the sample is SrTiO3 and the probe spacing is about 60 Å. The denoiser fails in the bottom row due to the absence of geometric flow among patterns, but does reasonably well in the top row. The inset images for (a) and (g) are the corresponding PACBEDs, with the virtual dark field detector locations for (a–c) shown by the red disks in the PACBED inset in (a).

Full size image

Figure 12 a shows a STEM image from a single detector pixel within the bright field disk of a 4D STEM dataset from an MgO smoke sample. The data was acquired on a Titan3 80-300 FEGTEM, operating at 80 keV, with a 15 mrad convergence semiangle, 3.9 Å probe spacing and 1.7 × 103 e−. Å−2 dose, using an EMPAD detector. The cubes were carefully rotated to an orientation that minimised apparent channelling conditions by actively diminishing intensities in Bragg beams, using a combination of diffraction pattern monitoring and live 4D STEM phase contrast imaging on the EMPAD. Figure 12b shows the corresponding image after the 4D STEM data has been denoised, with the structure much more clearly evident. Denoising was not necessary to get a clear STEM image here: the dose is high enough that it can be done by including more detector pixels in the STEM image (incoherent bright field, CoM imaging or similar). The denoiser reduces the variability in the data, as seen in the histograms of standard deviation (Fig. 12c) and average (Fig. 12d) of the pixels in the bright field region of each CBED pattern taken from a line scan along the red line in Fig. 12b (where the expected cubic geometry of the nanoparticle should have uniform thickness). The point of interest, however, is that the denoising leads to clear structure even though we expect the geometric flow in the data to be low, i.e. visual features change noticeably from one image to the next. This is visible among the patterns from the orange line in Fig. 12a, as shown in Fig. 12e. While there is a considerable disk overlap in the CBED patterns, the probe spacing of 3.9 Å is such that we do not expect much consistency in the nominal unit cell position between adjacent CBED patterns (this can be confirmed when comparing patterns of Fig. 12e with patterns in Fig. 1b where the probe spacing was significantly smaller and the geometric flow more pronounced). Our tentative interpretation is that the network is learning features in the CBED pattern deriving from the long-range structure (here the thickness gradients in different areas of the cube) but not the pattern-to-pattern variability from channelling within the unit cell. This is a tantalising result, with potential applications in electrostatic field mapping65, though further work is needed to determine whether this finding is robust and quantitative.

Fig. 12: Experimental images from MgO after denoiser preprocessing.
figure 12

a Raw data from an on-axis point detector (0.4 mrad collection angle; indicated by the red mark on the inset PACBED pattern), synthesised from experimental 4D STEM data from an MgO smoke sample. b Equivalent image after denoising of the 4D STEM data, in which more detailed structure (an example of which is indicated by the black arrow) is clearly evident. c Standard deviation and (d) average value of the pixels in the bright field region of each CBED pattern displayed as a histograms of the distribution across the probe positions along the red line scan region in (b). The average values are seen to be largely unchanged upon denoising, whereas the standard deviation has reduced significantly. e CBED patterns from the orange line scan in (a) show local visual features become distinguishable in the denoised dataset.

Full size image

We round out our discussion with a few comments on limitations and possible further directions. An assumption made here is that the raster scan is evenly spaced. Some tolerance to moderate probe jitter is expected—the scan noise visible in Fig. 1c did not overly hinder the denoising result in Fig. 2f—but large scan distortions would break the geometric flow on which this method is based. Further work is required to better understand the tolerance of the method to such scan distortions. Another potential limitation, as discussed in the Methods section, is the time requirement of training a network denoiser for every different dataset. When seeking to improve a dataset of interest for detailed analysis, this is good time investment. However, for rapid preliminary assessment of multiple datasets, training time might be limiting. TSVD, being faster and simpler, may be better suited to such cases, and will give comparably good results for large fields of view in periodic structures, though as discussed earlier it may be less accurate than the present approach in structures where periodicity is broken (regions with localised defects, or simply varying thickness) or for very small fields of view. The need to train afresh on every data set is the price of the unsupervised approach. Supervised approaches shift the cost of training to the outset. For example, Lobato et al.23 have shown supervised learning to be highly effective for reducing noise and other distortions for 2D S/TEM images. In principle, a 4D STEM dataset might be treated as a set of ‘independent’ 2D STEM images. However, this would forfeit the ability to use the physics-based dependence between the 2D STEM images (the geometric flow property of 4D STEM), which helps the present method handle lower doses. It is also unclear what training would be sufficient to handle 2D STEM images from all detector pixels as well as a wide diversity of materials and imaging conditions66—we therefore favour the unsupervised approach for its generality.

In conclusion, we developed a technique for denoising 4D STEM datasets using CNNs with an unsupervised training approach. The effectiveness of our method relies on a geometric flow relationship between the diffraction patterns in adjacent probe positions, and structuring the dataset and cost loss function to make use of it. The denoiser reliably reduces reconstruction errors across multiple imaging and analysis approaches on both experimental and simulated data, demonstrating its ability to accumulate and re-project information across the dataset and thereby enhance 4D STEM diffraction patterns. This enhancement was particularly evident in improving the reliability of statistics from, and symmetries in, the data. With experimental 4D STEM data we have shown the denoiser reliably improves its visual appearance and consistency. On simulated 4D STEM data we have shown that preprocessing via denoising improves the reliability of various 4D STEM data analysis approaches, including CoM, Symmetry STEM and ptychographic reconstruction, down to lower doses than those methods currently handle. This approach shows promise for enabling more advanced material analyses in experiments where low electron doses previously limited data quality.

Methods

4D STEM experiments

The experimental data in Figs. 2, 11 were acquired using the Thermo Scientific Spectra-φ FEGTEM at the Monash Centre for Electron Microscopy (MCEM) with a 128 × 128 pixel EMPAD detector, and a 300 keV electron beam. To ensure mechanical stability, the samples were allowed to stabilize before data collection. The data in these images were acquired from a SrTiO3 sample viewed along the [001] zone axis. In Fig. 2 the probe-forming aperture semiangle was 21.4 mrad and the probe spacing was about 0.25 Å. The scan regions comprised 256 × 256 probe positions. Two distinct datasets were obtained: a high-dose dataset with approximately 22,000 electrons per probe position and a low-dose dataset with about 140 electrons per probe position. The low-dose dataset was then processed through our deep learning-based denoiser. Due to the sample damage caused by the electron beam and changes in settings to reduce the dose, the areas captured in the high-dose and low-dose datasets were not identical. To be able to compare the denoised and the high dose datasets, we identified areas with the highest cross-correlation in between low dose and high dose datasets. In Fig. 11 a probe-forming aperture semiangle of 1.5 mrad was used for the low convergence semiangle (with around 50 e− per CBED pattern for low dose and around 500 e− per CBED pattern at high dose), 21.4 mrad was used for the high convergence semiangle (with around 250 e− per CBED pattern for low dose and around 2.3 × 104 e− per CBED pattern at high dose), and the probe spacing was about 60 Å for both.

The experimental data in Figs. 1, 12 were acquired using the Titan3 80-300 FEGTEM at MCEM. The data in Fig. 1 were acquired from aluminium viewed along the [001] zone axis, using 300 keV electrons, a 15 mrad convergence semiangle, a 0.2 Å probe spacing and an approximately 8 × 106 e−. Å−2 dose. The experimental data in Fig. 12 were acquired from an MgO smoke sample using 80 keV electrons, a 15 mrad convergence semiangle, and a probe spacing of 10.4 Å with 256 × 256 probe positions. In the vacuum region, the number of electrons per diffraction pattern was 9.7 × 104, corresponding to around 900 e−. Å−2.

Network initialization and training procedure

From a 4D STEM dataset, two 2D images can be synthesised that help with network training: one is the PACBED pattern generated by averaging the CBED patterns within a specific region of the probe scan, and the other is the virtual STEM image generated by summing electron counts within a specific region of the CBED patterns. PACBED patterns are not strongly affected by noise and can be used to help the denoising algorithm produce a denoised 4D STEM dataset with a PACBED pattern similar to that of the original dataset. The STEM image of the total counts within the bright field region can also guide the optimization, especially if it is denoised as a 2D image prior to denoising the 4D STEM dataset. This is particularly important at very low doses where the number of electrons per CBED pattern can fluctuate not because of the scattering processes taking place but purely due to counting statistics. Thus, in addition to the loss function in Eq. (1), in the final cost function we include two additional terms that compel the output to have similar PACBED and total count STEM image, with weight factors of 0.02 and 0.01 respectively (with the remaining 0.97 weighting coming from the Poisson loss). In our experience, larger values for the weight of noisy PACBED and total STEM images bias the model to fit more to noise, whereas the recommended values have a sufficient regularization effect on the learning processes. Moreover, we use the PACBED of the input dataset to define the bright field area (as per Fig. 1d) and we crop around it, leaving a few pixels of the dark field (such that the image size is divisible by 16).

We have used the original U-Net67, with its parameters initialized with random values. In the last layer of the network we incorporate a multiplying constant such that, initially, the output of the network produces the same total count STEM image and PACBED as the noisy dataset. This constant is not learnable. During the initial 8 epochs, we employ a Gaussian loss function, represented as the mean-square error MSE(ID − Ir), in place of the Poisson loss in Eq. (1). This is because the higher derivatives of the Poisson loss for pixels whose estimated values are lower than the true solution were found to hinder early training phases. However, after utilizing the Gaussian loss (which has symmetric derivatives, regardless of the sign of the error) for a few epochs, pixel value estimates predicted by the network approaching the actual values and we can switch to the Poisson loss (which enhances result accuracy since it better accounts for the fluctuations due to shot noise than does a Gaussian loss at very low doses). To ensure training stability, we train the network with a learning rate of 1e–3. When using iterative refinement, the learning rate is decayed every iteration by multiplying to 0.8 to become almost 1e-4 after 10 iterations.

By increasing the size of the local window around a pattern from 3 × 3 to 5 × 5, or even larger, the network can learn more about the data and produce more accurate results. However, from our explorations we deemed the advantage did not generally warrant the increased training time needed for the larger input data size, nor the loss of more than one layer of CBED patterns: using 3 × 3 subsets means that the CBED patterns at the edge of the probe scan field of view can never be a central pattern since they do not have a full set of adjacent patterns.

All tests were carried out on a DELL Precision 7920 desktop PC with an NVIDIA RTX-3090 GPU with 24GB of dedicated memory. The entire algorithm is implemented in PyTorch68 using float32 data type. A single epoch of training of a network of size 38 million parameters (64 kernels in the first layer of U-Net), takes about 5.6 ms for a single 16 × 16 CBED pattern and takes about 10 ms for a 64 × 64 pixel CBED pattern. The number of epochs and number of patterns in the dataset linearly determine the required time to obtain the final solution. The denoising task of the real dataset in Fig. 2 took almost 8 hours by 10 refinement steps.

Model complexity

To evaluate the role of model complexity on the reliability of our denoising algorithm, we trained multiple neural networks while varying the number of parameters by setting the number of kernels of U-Net. We used two simulated 4D STEM datasets, one for the wedge-shaped SrTiO3 sample as shown in Fig. 7 with 21.4 mrad convergence semiangle and one for a 28 Å CeB6 sample, assuming a 15 mrad convergence semiangle, both with 300 keV electron beam and a probe spacing of 0.25 Å. We introduced Poisson noise of 16, 32, 64, 128 and 256 electrons per diffraction pattern (equivalent to 64, 128, 256, 512, 1024 and 2048 e−. Å−2). To quantify the reconstruction error, we evaluate the Frobenius norm of the difference between denoised and original noise-free data, with low error meaning denoising has been effective. However, since under such strong noise it is possible to minimize the algebraic norm without necessarily preserving the overall shape of the diffraction pattern, we have also calculated the cross-correlation (CC) of the denoised and noise free datasets to provide a statistical distance (where values close to one mean denoising has been effective). While minimizing CC does not guarantee proper average and variance, it provides a reliable metric for the similarity in locations of peaks and troughs in patterns across the two datasets.

Figure 13 plots these reconstruction errors against the complexity of the neural network model. The number of parameters in the network corresponding to factors of 2, 4, 8, 16, 32, 64 and 128 kernels would be almost 35k, 140k, 0.5M, 2.2M, 8M, 34M and 138M (the factors change the number of kernels of all layers linearly based on the original design in Ronneberger et al.67). The trend observed reveals that models with very low complexity tend to under-fit the data, failing to capture essential details and the error value increases (CC decreases) for networks that are too small. Conversely, an overly complex model with 128 size factor exhibits over-fitting, capturing noise as if it were part of the intended signal and so produces larger errors (lower CC) with networks that are too large making them unsuitable for low dose data analysis. Moreover, a large network with size factor of 128 is impractical due to long training time. This analysis underscores the critical balance needed in model complexity to achieve optimal denoising performance. There is no guarantee that the optimum value seen here is optimum for every case, but, based on our observations during evaluations for the results presented in this paper, we recommend a network that is not too small and not too large, with size factor around 16 and no more than 64.

Fig. 13: Reconstruction error with varying network size.
figure 13

The effect of changing the size of the neural network by multiples of number of kernels of the network on the reconstruction error (comparing the noise-free against the denoised, scaled by Ne to allow direct comparison, such that low error means the denoising has been effective) and cross-correlation, CC, is shown for (a) the wedge-shaped SrTiO3 sample (as considered in Fig. 7) and (b) 28 Å CeB6 (as considered in Fig. 8a–e), for five different dose levels, shown by colour and measured by the number of electrons per diffraction pattern Ne.

Full size image

4D STEM simulations and analysis methods

Simulated datasets were synthesized using the py_multislice suite69, with thermal scattering approximated using an absorptive model. Ptychographic reconstructions were carried out using the py4DSTEM suite70, with default values used for the majority of hyperparameters for this proof-of-principle demonstration on simulated data. All multislice ptychography analysis assumed all slices are identical to each other and the defocus value and the thickness was known. For our calculations on 240 Å thick SrTiO3 we assumed 6 identical slices of 40 Å thickness.