Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Minute-scale Schrödinger-cat state of spin-5/2 atoms

Nature Photonics volume 19, pages 89–94 (2025)Cite this article

Subjects

Abstract

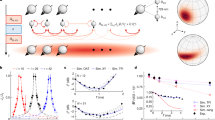
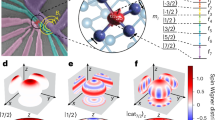
Quantum metrology with non-classical states offers a promising route to improved precision in physical measurements. The quantum effects of Schrödinger-cat superpositions or entanglements enable measurement uncertainties to reach below the standard quantum limit. However, the challenge of maintaining a long coherence time for such non-classical states often prevents full exploitation of the quantum advantage in metrology. Here we demonstrate a long-lived Schrödinger-cat state of optically trapped 173Yb (I = 5/2) atoms. The cat state, a superposition of two oppositely directed and furthest-apart spin states, is generated by a nonlinear spin rotation. Protected in a decoherence-free subspace against inhomogeneous light shifts of an optical lattice, the cat state persists for a coherence time of 1.4(1) × 103 s. A magnetic field is measured using Ramsey interferometry, demonstrating a scheme of Heisenberg-limited metrology for atomic magnetometry, quantum information processing and searching for new physics beyond the Standard Model.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Principle of the method.
Fig. 2: Set-up and spin dynamics.
Fig. 3: Ramsey interference.
Fig. 4: Sensitivity to a magnetic field.
Fig. 5: The reconstructed Wigner function distribution on the sphere divided into 100 regions along the longitudinal and latitudinal directions.

Similar content being viewed by others

Data availability

Source data for Figs. 2–4 are available via Figshare at https://doi.org/10.6084/m9.figshare.24151038 (ref. 58).

References

  1. Haroche, S. & Raimond, J.-M. Exploring the Quantum: Atoms, Cavities, and Photons (Oxford Univ. Press, 2006); https://doi.org/10.1093/acprof:oso/9780198509141.001.0001

  2. Monroe, C., Meekhof, D. M., King, B. E. & Wineland, D. J. A “Schrödinger cat" superposition state of an atom. Science 272, 1131–1136 (1996).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  3. Facon, A. et al. A sensitive electrometer based on a Rydberg atom in a Schrödinger-cat state. Nature 535, 262–265 (2016).

    Article  ADS  MATH  Google Scholar 

  4. Chalopin, T. et al. Quantum-enhanced sensing using non-classical spin states of a highly magnetic atom. Nat. Commun. 9, 4955 (2018).

    Article  ADS  MATH  Google Scholar 

  5. Dietsche, E. K. et al. High-sensitivity magnetometry with a single atom in a superposition of two circular Rydberg states. Nat. Phys. 15, 326–329 (2019).

    Article  MATH  Google Scholar 

  6. Bild, M. et al. Schrödinger cat states of a 16-microgram mechanical oscillator. Science 380, 274–278 (2023).

    Article  ADS  Google Scholar 

  7. Pezzè, L., Smerzi, A., Oberthaler, M. K., Schmied, R. & Treutlein, P. Quantum metrology with nonclassical states of atomic ensembles. Rev. Mod. Phys. 90, 035005 (2018).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  8. Gross, C., Zibold, T., Nicklas, E., Estève, J. & Oberthaler, M. K. Nonlinear atom interferometer surpasses classical precision limit. Nature 464, 1165–1169 (2010).

    Article  ADS  Google Scholar 

  9. Strobel, H. et al. Fisher information and entanglement of non-Gaussian spin states. Science 345, 424–427 (2014).

    Article  ADS  MATH  Google Scholar 

  10. Hosten, O., Engelsen, N. J., Krishnakumar, R. & Kasevich, M. A. Measurement noise 100 times lower than the quantum-projection limit using entangled atoms. Nature 529, 505–508 (2016).

    Article  ADS  MATH  Google Scholar 

  11. Bao, H. et al. Spin squeezing of 1011 atoms by prediction and retrodiction measurements. Nature 581, 159–163 (2020).

    Article  ADS  MATH  Google Scholar 

  12. Pedrozo-Peñafiel, E. et al. Entanglement on an optical atomic-clock transition. Nature 588, 414–418 (2020).

    Article  ADS  MATH  Google Scholar 

  13. Erhard, M., Krenn, M. & Zeilinger, A. Advances in high-dimensional quantum entanglement. Nat. Rev. Phys. 2, 365–381 (2020).

    Article  MATH  Google Scholar 

  14. Liu, Q. et al. Nonlinear interferometry beyond classical limit enabled by cyclic dynamics. Nat. Phys. 18, 167–171 (2022).

    Article  ADS  MATH  Google Scholar 

  15. Greve, G. P., Luo, C., Wu, B. & Thompson, J. K. Entanglement-enhanced matter-wave interferometry in a high-finesse cavity. Nature 610, 472–477 (2022).

    Article  ADS  Google Scholar 

  16. Caves, C. M., Thorne, K. S., Drever, R. W. P., Sandberg, V. D. & Zimmermann, M. On the measurement of a weak classical force coupled to a quantum-mechanical oscillator. I. Issues of principle. Rev. Mod. Phys. 52, 341–392 (1980).

    Article  ADS  Google Scholar 

  17. Raimond, J. M., Brune, M. & Haroche, S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 73, 565–582 (2001).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  18. Zurek, W. H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 75, 715–775 (2003).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  19. Fröwis, F., Sekatski, P., Dür, W., Gisin, N. & Sangouard, N. Macroscopic quantum states: measures, fragility, and implementations. Rev. Mod. Phys. 90, 025004 (2018).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  20. Walther, P. et al. De Broglie wavelength of a non-local four-photon state. Nature 429, 158–161 (2004).

    Article  ADS  MATH  Google Scholar 

  21. Mitchell, M. W., Lundeen, J. S. & Steinberg, A. M. Super-resolving phase measurements with a multiphoton entangled state. Nature 429, 161–164 (2004).

    Article  ADS  MATH  Google Scholar 

  22. Hald, J., Sørensen, J. L., Schori, C. & Polzik, E. S. Spin squeezed atoms: a macroscopic entangled ensemble created by light. Phys. Rev. Lett. 83, 1319–1322 (1999).

    Article  ADS  MATH  Google Scholar 

  23. Orzel, C., Tuchman, A. K., Fenselau, M. L., Yasuda, M. & Kasevich, M. A. Squeezed states in a Bose–Einstein condensate. Science 291, 2386–2389 (2001).

    Article  ADS  Google Scholar 

  24. Zurek, W. Decoherence and the transition from quantum to classical. Phys. Today 44, 36–44 (1991).

    Article  MATH  Google Scholar 

  25. Myatt, C. J. et al. Decoherence of quantum superpositions through coupling to engineered reservoirs. Nature 403, 269–273 (2000).

    Article  ADS  MATH  Google Scholar 

  26. Deléglise, S. et al. Reconstruction of non-classical cavity field states with snapshots of their decoherence. Nature 455, 510–514 (2008).

    Article  ADS  MATH  Google Scholar 

  27. Lidar, D. A., Chuang, I. L. & Whaley, K. B. Decoherence-free subspaces for quantum computation. Phys. Rev. Lett. 81, 2594–2597 (1998).

    Article  ADS  MATH  Google Scholar 

  28. Haroche, S. Nobel Lecture: Controlling photons in a box and exploring the quantum to classical boundary. Rev. Mod. Phys. 85, 1083–1102 (2013).

    Article  ADS  MATH  Google Scholar 

  29. Wang, Y. et al. Single-qubit quantum memory exceeding ten-minute coherence time. Nat. Photonics 11, 646–650 (2017).

    Article  ADS  MATH  Google Scholar 

  30. Wang, P. et al. Single ion qubit with estimated coherence time exceeding one hour. Nat. Commun. 12, 233 (2021).

    Article  ADS  MATH  Google Scholar 

  31. Lidar, D.A. in Quantum Information and Computation for Chemistry (ed. Kais, S.) 295–354 (Wiley, 2014); https://doi.org/10.1002/9781118742631.ch11

  32. Kielpinski, D. et al. A decoherence-free quantum memory using trapped ions. Science 291, 1013–1015 (2001).

    Article  ADS  MATH  Google Scholar 

  33. Roos, C. F., Chwalla, M., Kim, K., Riebe, M. & Blatt, R. ‘Designer atoms’ for quantum metrology. Nature 443, 316–319 (2006).

    Article  ADS  Google Scholar 

  34. Safronova, M. S. et al. Search for new physics with atoms and molecules. Rev. Mod. Phys. 90, 025008 (2018).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  35. Chupp, T. E., Fierlinger, P., Ramsey-Musolf, M. J. & Singh, J. T. Electric dipole moments of the atoms, molecules, nuclei and particles. Rev. Mod. Phys. 91, 015001 (2019).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  36. Jenkins, A., Lis, J. W., Senoo, A., McGrew, W. F. & Kaufman, A. M. Ytterbium nuclear-spin qubits in an optical tweezer array. Phys. Rev. X 12, 021027 (2021).

    Google Scholar 

  37. Ma, S. et al. Universal gate operations on nuclear spin qubits in an optical tweezer array of 171Yb atoms. Phys. Rev. X 12, 021028 (2022).

    Google Scholar 

  38. Huie, W. et al. Repetitive readout and real-time control of nuclear spin qubits in 171Yb atoms. Phys. Rev. X Quantum 4, 030337 (2023).

    ADS  MATH  Google Scholar 

  39. Arecchi, F. T., Courtens, E., Gilmore, R. & Thomas, H. Atomic coherent states in quantum optics. Phys. Rev. A 6, 2211–2237 (1972).

    Article  ADS  MATH  Google Scholar 

  40. Kwon, H., Tan, K. C., Volkoff, T. & Jeong, H. Nonclassicality as a quantifiable resource for quantum metrology. Phys. Rev. Lett. 122, 040503 (2019).

    Article  ADS  Google Scholar 

  41. Dowling, J. P., Agarwal, G. S. & Schleich, W. P. Wigner distribution of a general angular-momentum state: applications to a collection of two-level atoms. Phys. Rev. A 49, 4101–4109 (1994).

    Article  ADS  MATH  Google Scholar 

  42. Zheng, T. A. et al. Magic wavelengths of the Yb (6s2 1S0–6s6p 3P1) intercombination transition. Phys. Rev. A 102, 062805 (2020).

    Article  ADS  Google Scholar 

  43. Yurke, B. & Stoler, D. Generating quantum mechanical superpositions of macroscopically distinguishable states via amplitude dispersion. Phys. Rev. Lett. 57, 13–16 (1986).

    Article  ADS  MATH  Google Scholar 

  44. Sanders, B. C. Quantum dynamics of the nonlinear rotator and the effects of continual spin measurement. Phys. Rev. A 40, 2417–2427 (1989).

    Article  ADS  MATH  Google Scholar 

  45. Smith, G. A., Chaudhury, S., Silberfarb, A., Deutsch, I. H. & Jessen, P. S. Continuous weak measurement and nonlinear dynamics in a cold spin ensemble. Phys. Rev. Lett. 93, 163602 (2004).

    Article  ADS  MATH  Google Scholar 

  46. Zheng, T. A. et al. Measurement of the electric dipole moment of 171Yb atoms in an optical dipole trap. Phys. Rev. Lett. 129, 083001 (2022).

    Article  ADS  MATH  Google Scholar 

  47. Ye, J., Kimble, H. J. & Katori, H. Quantum state engineering and precision metrology using state-insensitive light traps. Science 320, 1734–1738 (2008).

    Article  ADS  MATH  Google Scholar 

  48. Neyenhuis, B. et al. Anisotropic polarizability of ultracold polar 40K87Rb molecules. Phys. Rev. Lett. 109, 230403 (2012).

    Article  ADS  Google Scholar 

  49. Ramsey, N. F. A molecular beam resonance method with separated oscillating fields. Phys. Rev. 78, 695–699 (1950).

    Article  ADS  MATH  Google Scholar 

  50. McConnell, R., Zhang, H., Hu, J., Ćuk, S. & Vuletić, V. Entanglement with negative Wigner function of almost 3,000 atoms heralded by one photon. Nature 519, 439–442 (2015).

    Article  ADS  Google Scholar 

  51. Ringbauer, M. et al. A universal qudit quantum processor with trapped ions. Nat. Phys. 18, 1053–1057 (2021).

    Article  MATH  Google Scholar 

  52. Rosenbusch, P. et al. ac Stark shift of the Cs microwave atomic clock transitions. Phys. Rev. A 79, 013404 (2009).

    Article  ADS  MATH  Google Scholar 

  53. Le Kien, F., Schneeweiss, P. & Rauschenbeutel, A. Dynamical polarizability of atoms in arbitrary light fields: general theory and application to cesium. Eur. Phys. J. D 67, 92 (2013).

    Article  ADS  MATH  Google Scholar 

  54. Stone, N. J. Table of nuclear magnetic dipole and electric quadrupole moments. At. Data Nucl. Data Tables 90, 75–176 (2005).

    Article  ADS  MATH  Google Scholar 

  55. Chen, S. Ultra-low noise magnetic field for quantum gases. Rev. Sci. Instrum. 90, 054708 (2019).

    Article  ADS  Google Scholar 

  56. Schmied, R. & Treutlein, P. Tomographic reconstruction of the Wigner function on the Bloch sphere. New J. Phys. 13, 065019 (2011).

    Article  ADS  MATH  Google Scholar 

  57. Everett, J. E. & Osemeikhian, J. E. Spherical coils for uniform magnetic fields. J. Sci. Instrum. 43, 470–474 (1966).

    Article  ADS  MATH  Google Scholar 

  58. Yang, Y. et al. Minutes-scale Schrödinger-cat state of spin-5/2 atoms. Figshare https://doi.org/10.6084/m9.figshare.24151038 (2024).

Download references

Acknowledgements

We thank D. Sheng and M. Krstají for fruitful discussions, M.-D. Li and W.-K. Hu for contribution to the apparatus during the early stages. This work is supported by the National Natural Science Foundation of China (NSFC) through grant no. 12174371 and the Innovation Program for Quantum Science and Technology through grant no. 2021ZD0303100. C.-L.Z. was supported by the NSFC through grant no. 11922411 and by the Innovation Program for Quantum Science and Technology through grant no. 2021ZD0300203.

Author information

Author notes

  1. Y. A. Yang

    Present address: JILA, National Institute of Standards and Technology and University of Colorado, Department of Physics, University of Colorado, Boulder, CO, USA

Authors and Affiliations

  1. Hefei National Research Center for Physical Sciences at the Microscale, School of Physical Sciences, University of Science and Technology of China, Hefei, China

    Y. A. Yang, W.-T. Luo, J.-L. Zhang, S.-Z. Wang, Chang-Ling Zou, T. Xia & Z.-T. Lu

  2. Hefei National Laboratory, University of Science and Technology of China, Hefei, China

    Chang-Ling Zou, T. Xia & Z.-T. Lu

  3. CAS Key Laboratory of Quantum Information, University of Science and Technology of China, Hefei, China

    Chang-Ling Zou

Authors
  1. Y. A. Yang
    View author publications

    Search author on:PubMed Google Scholar

  2. W.-T. Luo
    View author publications

    Search author on:PubMed Google Scholar

  3. J.-L. Zhang
    View author publications

    Search author on:PubMed Google Scholar

  4. S.-Z. Wang
    View author publications

    Search author on:PubMed Google Scholar

  5. Chang-Ling Zou
    View author publications

    Search author on:PubMed Google Scholar

  6. T. Xia
    View author publications

    Search author on:PubMed Google Scholar

  7. Z.-T. Lu
    View author publications

    Search author on:PubMed Google Scholar

Contributions

Y.A.Y., W.-T.L. and J.-L.Z. constructed the experimental apparatus and performed the experiments and simulations. C.-L.Z. made contributions to the theory part. Y.A.Y., W.-T.L., J.-L.Z., S.-Z.W., C.-L.Z., T.X. and Z.-T.L. carried out data analysis and wrote the manuscript.

Corresponding authors

Correspondence to T. Xia or Z.-T. Lu.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Photonics thanks Adam Miranowicz and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Polarizabilities and effective Rabi frequencies.

a, the dynamical vector and tensor polarizabilities \({\alpha }_{F}^{\{{\rm{V}},{\rm{T}}\}}\) of 1S0 are plotted as a function of the laser frequency, whose value is relative to the \(6{{\rm{s}}{}^{2}}^{1}{{\rm{S}}}_{0}\to 6{\rm{s}}6{{\rm{p}}}^{3}{{\rm{P}}}_{1},F=5/2\to F=3/2\) hyperfine transition. For polarizabilities 1a. u. = 1.648773 × 10−41 C m2 V−1. b, The generalized Rabi frequencies \({\Omega }_{x}^{(1)}\) and \({\Omega }_{x,x}^{(2)}\) are plotted as a function of the laser frequency, where \({\Omega }_{x}^{(1)}=-\frac{{\alpha }_{F}^{V}}{8F}{| {\mathcal{E}}| }^{2}\) and \({\Omega }_{x,x}^{(2)}=\frac{3{\alpha }_{F}^{T}}{8F(2F-1)}{| {\mathcal{E}}| }^{2}\). The Rabi frequencies are normalized assuming a light intensity I of = 1W/cm2, and \({| {\mathcal{E}}| }^{2}=\frac{2I}{{\epsilon }_{0}c}\). The inset shows the frequency ratio \(| {\Omega }_{x}^{(1)}/{\Omega }_{x,x}^{(2)}|\).

Extended Data Fig. 2 Principal of state-selective measurement.

The tensor light shift induced by the trap laser distinctly separates Zeeman sublevels of the upper state 3P1, effectively preventing photon absorption by the \(\left\vert -5/2\right\rangle\) state. Following the measurement of the population of the \(\left\vert +5/2\right\rangle\) state, a π pulse generated by the control laser swaps the populations of the \(\left\vert +5/2\right\rangle\) and \(\left\vert -5/2\right\rangle\) states. Subsequently, the same probe pulse is applied to detect the population of the original \(\left\vert -5/2\right\rangle\) state.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, Y.A., Luo, WT., Zhang, JL. et al. Minute-scale Schrödinger-cat state of spin-5/2 atoms. Nat. Photon. 19, 89–94 (2025). https://doi.org/10.1038/s41566-024-01555-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41566-024-01555-3

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing