Abstract
Motor skill repertoire can be stably retained over long periods, but the neural mechanism that underlies stable memory storage remains poorly understood1,2,3,4,5,6,7,8. Moreover, it is unknown how existing motor memories are maintained as new motor skills are continuously acquired. Here we tracked neural representation of learned actions throughout a significant portion of the lifespan of a mouse and show that learned actions are stably retained in combination with context, which protects existing memories from erasure during new motor learning. We established a continual learning paradigm in which mice learned to perform directional licking in different task contexts while we tracked motor cortex activity for up to six months using two-photon imaging. Within the same task context, activity driving directional licking was stable over time with little representational drift. When learning new task contexts, new preparatory activity emerged to drive the same licking actions. Learning created parallel new motor memories instead of modifying existing representations. Re-learning to make the same actions in the previous task context re-activated the previous preparatory activity, even months later. Continual learning of new task contexts kept creating new preparatory activity patterns. Context-specific memories, as we observed in the motor system, may provide a solution for stable memory storage throughout continual learning.
Similar content being viewed by others
Main
In our lifetime we stably retain a myriad of motor skills. How learned actions are stored in motor memory remains poorly understood. In the motor cortex, specific learned actions are evoked by distinct patterns of preparatory activity7,9,10,11 (Fig. 1a). Preparatory activity is thought to provide the initial conditions for the ensuing dynamics dictating movement execution12,13,14,15,16, but its relationship to subsequent action remains obscure17,18,19. For example, it remains unknown whether preparatory activity states are linked to subsequent movement execution and therefore fixed for actions with identical kinematics; alternatively, preparatory activity might encode other cognitive variables associated with learned actions beyond the movement itself4,5,7,8,20.
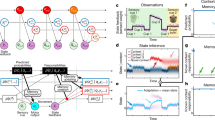
a, Preparatory states for different actions in activity space. b, Possible outcomes of preparatory states across time and new task learning. c, Top, mice living in the home-cage system voluntarily engage in head fixation and learn directional lick tasks. Bottom, behavioural data from an example mouse. Dark bands represent epochs of voluntary head fixation; grey bands represent rest. d, Mice report pole position using lick left or lick right after a delay epoch. Sensorimotor contingency is reversed across task contexts. e, Behaviour performance of an example mouse. Contingency reversals are introduced when performance is above 75%. Averaging window, 100 trials. f, Number of trials to reach 75% correct performance (mean ± s.e.m.). Individual lines show data from individual mice. Mice used for in-cage optogenetic (5 mice), imaging (13 mice) and behaviour testing only (5 mice) are combined. Learning task context 1 versus 2, *P = 0.0286 (23 mice); learning task context 2 versus 1′, *P = 0.0431 (19 mice); learning task context 1′ versus 2′, P = 0.3425 (13 mice), not significant (NS). Two-tailed paired t-test. g, Top, optogenetic approach to silence ALM activity in the home cage. Bottom, task and photoinhibition timelines. Photostimulation during the sample (S), delay (D) and response (R) epochs; power 0.35, 1.77 and 3.54 mW mm−2 for each epoch. h, Behaviour performance of an example mouse during ALM photoinhibition. Black, control trials. Red, photoinhibition during the delay epoch (3.54 mW mm−2). Red shaded area, photoinhibition blocks. Photostim., photostimulation. i, Behaviour performance during ALM photoinhibition (mean ± s.e.m.). Trial types by instructed lick direction. Left ALM photostimulation. Sample epoch, instructed lick right, *P = 0.0248, F = 0.7574 (1.77 mW mm−2), *P = 0.0349, F = 0.8402 (3.54 mW mm−2); instructed lick left, *P = 0.0360, F = 1.0334 (0.35 mW mm−2). Delay epoch, instructed lick right, **P = 0.0054, F = 0.7212 (1.77 mW mm−2), **P = 0.0012, F = 0.3909 (3.54 mW mm−2). Response epoch, instructed lick right, *P = 0.0249, F = 0.4940 (0.35 mW mm−2), **P = 0.0093, F = 0.6863 (3.54 mW mm−2); instructed lick left, *P = 0.0423, F = 1.0702 (3.54 mW mm−2). Two-tailed t-test against control.
A related question is how learned actions are maintained by motor circuits over time. Motor cortex circuits exhibit considerable plasticity during motor learning7,21,22,23,24,25,26,27,28,29,30,31,32. Given this plasticity, the neural mechanism underlying motor memory storage is unclear. Recent studies propose memory storage mechanisms based on unstable representations3,33: in a redundant neural network in which multiple network configurations produce the same output, activity patterns leading to the same motor output can change over time34,35. For example, if a pattern of activity drives our speech of the word ‘cat’, a different pattern of activity may occur when we utter the word ‘cat’ a year later (Fig. 1b, left). This question remains under-explored as motor cortical activity has rarely been tracked over periods of more than one month36,37,38,39,40.
Moreover, it is unknown how existing motor memories are protected from modifications by continual learning of new motor skills. Theories of learning posit a modular approach, in which multiple parallel motor memories are formed for distinct contexts1,4,5,6, thus new learning takes place in separate modules. Neurophysiological studies of motor learning mostly examine single tasks. It remains poorly understood how neural representation of an action is formed and maintained when we learn to utilize the same action in different contexts—for example, learning to speak the word ‘cat’ in different sentences (Fig. 1b, right).
To address these questions, we developed an automated home-cage training paradigm in which mice learned to perform directional licking in different task contexts. Learned directional licking is dependent on preparatory activity in anterior lateral motor cortex14,41,42 (ALM). We tracked ALM activity across continual learning for multiple months using two-photon calcium imaging. We found that learned directional licking was stably encoded in preparatory activity with little representational drift. Across learning multiple task contexts, multiple preparatory states were created to encode the same licking action in a context-dependent manner. Our results show that motor memories encode learned actions in combination with their context, which we call a combinatorial code. A feedforward network that stored sensorimotor combinations in high-dimensional hidden layers was able to explain multiple aspects of the results. Context-specific motor memories may help reduce interference of new learning to previously learned representations6,8, thus protecting existing motor repertoire from erasure in the face of continual learning.
A continual learning paradigm
To track neural representation of the same movement across continual learning of new motor skills, we studied a stereotyped and yet cortex-dependent movement: goal-directed directional licking in mice. We developed a home-cage system in which mice voluntarily engaged in head fixation and learned multiple licking tasks without human supervision43 (Fig. 1c). In a tactile-instructed licking task, mice discriminated the location of a pole during a sample epoch and reported decision using ‘lick left’ or ‘lick right’ after a delay epoch (Fig. 1d). Mice initially learned to lick left for anterior pole position and lick right for posterior pole position (task context 1; Fig. 1d). After achieving more than 75% correct (Methods), the home-cage system automatically reversed the contingency between pole locations and lick directions (task context 2; Fig. 1d). The delay epoch separated sensory stimuli from motor response. Thus in the two tasks, mice made identical actions under identical external environment after the delay epoch, but with different stimulus history and task rules. We therefore refer to these conditions as different ‘task context’.
Mice learned many rounds of reversals over several months (Fig. 1e). High-speed videography showed that tongue and jaw movements were consistent over time and across contingency reversals (Extended Data Fig. 1a,b). Mice were faster to reach criterion performance (>75% correct) for subsequent reversals (Fig. 1f and Methods). Faster reversal was observed when mice re-learned the previously learned sensorimotor contingency, but less correlated with overall amount of prior training (Extended Data Fig. 1c), consistent with a saving effect typically associated with motor skill learning2.
The ALM is critical for planning and execution of directional licking14,41,44,45. To test whether ALM is required for learned directional licking after extended training, we optogenetically silenced ALM activity during task performance in home cage43 (Fig. 1g and Methods). We virally expressed a red-shifted channelrhodopsin46 (ChRmine) in ALM GABA (γ-aminobutyric acid)-expressing (GABAergic) neurons and photostimulated ALM through a clear skull implant during voluntary head fixation (Fig. 1g). ALM photoinhibition during the delay epoch disrupted behavioural performance, even after multiple rounds of contingency reversal (Fig. 1h). Left ALM photoinhibition biased future licking to the ipsilateral direction (lick left) in a light dose-dependent manner (Fig. 1i and Extended Data Fig. 1d). These results show that directional licking consistently depends on ALM preparatory activity over time, thus enabling us to chronically track neural activity that is causally driving the learned licking actions.
Stable representation of action
To examine whether neural representations of learned actions drift over time (Fig. 2a), we performed longitudinal two-photon calcium imaging of ALM (GP4.3 mice; Extended Data Fig. 1e–g; imaging duration, 26–233 days). After mice attained high performance under task context 1 in the home cage, we transferred them to a two-photon microscope where they performed the same task in daily sessions (Methods). After brief acclimatization, mice maintained stable performance (Fig. 2b), with little performance change within session (Extended Data Fig. 1j). We imaged the same field of view across multiple days (Fig. 2c and Extended Data Fig. 2a; referred to as ‘expert-early’ or ‘expert-late’ sessions), covering different fields of view on interleaved days (Extended Data Fig. 2b). The imaged fields of view were remarkably stable. We identified 42,739 neurons that could be confidently matched across days based on their shapes and centroid locations47 (Extended Data Fig. 2c–i; 50 fields of view, 8 mice; Methods).
a, Left, possible outcomes of preparatory states over time. Right, task context 1. b, Behaviour performance during imaging sessions. Each data point shows average performance in one imaging session. Colours indicate individual mice. c, Example field of view. Scale bar, 50 μm. d, Top, dF/F0 from two example neurons. Thick lines are the mean and thin lines show individual trials. Bottom, mean deconvolved activities from an example field of view (n = 386 neurons). Neurons are sorted based on their peak activities from different days. e, Selectivity index in expert-early and expert-late sessions for neurons showing significant selectivity (P < 0.001, two-tailed t-test) during the sample (top), delay (middle) and response epoch (bottom). Green, neurons preferring anterior pole position. Purple, neurons preferring posterior pole position. Red, neurons preferring lick left; blue, neurons preferring lick right. Significant selectivity and trial-type preferences are determined in expert-early session. f, Schematic of movement-specific activity trajectories in activity space. Coding direction (CDDelay) is estimated using activities during the late delay epoch (inset, yellow shade). Red and blue shading indicates preparatory states for lick left and lick right, respectively. g, Decoding scheme. Non-overlapping trials for training and testing within (solid arrows) and across sessions (dashed arrows). h, ALM activities from an example field of view projected on the CDDelay from day 1 (top) or day 16 (bottom). Thick lines are the mean and thin lines show single trials. a.u., arbitrary units. i, Lick direction decoding using the CDDelay as a function of delta days between imaging sessions. Colours represent different mice. Within session decoding shows the mean of two conditions (train expert-early and test expert-early, train expert-late and test expert-late). Across sessions decoding shows the mean of two conditions (train expert-early and test expert-late, train expert-late and test expert-early). Dashed lines are linear regressions of individual mouse data. Inset graph shows R values of linear regressions. FOVs, fields of view. j, Decoding accuracy within and across imaging sessions. n = 113 pairs of sessions, 10 mice. Data are mean ± s.e.m. k, Weight contributions of individual neurons to the CDDelay vectors from expert-early and expert-late sessions (35,420 neurons from 8 mice).
ALM neurons exhibited task-related activity (dF/F0; Fig. 2d, top). We deconvolved dF/F0 to avoid the spillover of slow-decaying calcium dynamics across task epochs48 (Extended Data Fig. 2j and Methods). Sorting neurons by their peak activities revealed similar task-related activity across days (Fig. 2d, bottom). We computed selectivity as the difference in activity between trial types divided by their sum (anterior versus posterior pole position for the sample epoch; lick left versus lick right for the delay and response epochs; correct trials; Methods). On error trials, when mice licked in the opposite direction to the instruction provided by pole location, ALM activity during the delay epoch predicted the licking direction (Extended Data Fig. 2k,l). Neurons showing significant trial-type selectivity (P < 0.001, two-tailed t-test) in expert-early sessions largely maintained their selectivity in expert-late sessions (Fig. 2e; Pearson’s correlation, sample epoch: R = 0.9404, P = 0; delay epoch: R = 0.8861, P = 0; response epoch: R = 0.9001, P = 0). A subset of ALM neurons exhibited altered activity across days, but these changes mainly occurred in non-selective neurons (Extended Data Fig. 3a–c). This suggests that lick direction encoding is selectively maintained.
To investigate lick direction encoding at the population level, we analysed ALM activity in an activity space, where each dimension corresponds to activity of one neuron14,49. We estimated a ‘coding direction’ (CDDelay) along which activity maximally discriminated future lick direction at the end of the delay epoch (‘preparatory state’; Methods). To examine population encoding over time (Fig. 2f), we estimated the CDDelay using 50% of the trials in a session (training dataset) and projected activity in non-overlapping trials from the same session or across sessions (testing dataset; Fig. 2g). ALM activity along the CDDelay was maintained over time (Fig. 2h), despite moderate changes in population activity vector (Extended Data Fig. 3d–f). We used a decision boundary on the CDDelay to predict lick direction from ALM activity (Methods). A decoder defined in one session could accurately predict lick direction in other sessions regardless of the timespan between sessions, even up to 2 months apart (Fig. 2i; linear regression: −0.08 ± 0.11, mean ± s.e.m. across mice; P = 0.4870, t-test against 0). A decoder from expert-early or late sessions could similarly predict lick direction in expert-late or early sessions, respectively (Fig. 2j). Individual neurons contributing to the CDDelay were highly correlated across sessions (Fig. 2k; Pearson’s correlation, R = 0.6053, P = 0).
We analysed ALM activity during the sample and response epochs and found similarly stable selectivity along the coding directions (Extended Data Fig. 4). These results show that ALM activity is selectively maintained along coding directions that encode learned directional licking for at least two months.
New representation emerges with learning
We next explored how motor memories form when new motor skills are acquired. A key question here is whether existing activity states are reused11,31 or whether entirely new activity states are formed (Fig. 3a). To address this question, we monitored ALM activity across two different task contexts. After imaging in task context 1, we returned mice to the home cage to learn reversed sensorimotor contingency then imaged them again in task context 2 (Fig. 3b; task context 1→2). Performance was similar in the two task contexts (85.59 ± 1.00% versus 84.06 ± 0.99% correct rate, mean ± s.e.m.; P = 0.1862, paired t-test), and video analysis showed that mice made the same tongue and jaw movements (Extended Data Fig. 1a,b, bottom). We identified 1,118 ± 500 matched neurons in each field of view (58 fields of view, 10 mice; 31.88 ± 13.88 days between imaging sessions, mean ± s.d. across sessions).
a, Possible outcomes of preparatory states across different task contexts. b, Task contexts 1 and 2. Time interval between imaging sessions, 31.88 ± 13.88 days, mean ± s.d. across fields of view. c, Mean deconvolved activities from an example field of view (n = 1,112 neurons). Neurons are sorted on the basis of their selectivity during the delay epoch in either task context 1 (top) or 2 (bottom). d, Selectivity index in task context 1 (left) and 2 (right) for neurons showing significant trial-type selectivity (P < 0.001, two-tailed t-test) during the delay epoch. Red, neurons preferring lick left; blue, neurons preferring lick right. Significant selectivity and trial-type preferences are determined in task context 1. e, Schematic of movement-specific activity trajectories in activity space and CDDelay vectors across task contexts. Red and blue shading indicates preparatory states for lick left and lick right, respectively. f, ALM activities from an example field of view projected on the CDDelay from task context 1 (top) or 2 (bottom). Thick lines are the mean and thin lines show single trials. g, Decoding accuracy of the CDDelay within and across task contexts. n = 58 pairs of sessions, 10 mice. Data are mean ± s.e.m. Circles represent individual fields of view. h, Weight contribution of individual neurons to the CDDelay vectors from task contexts 1 and 2 (44,409 neurons from 10 mice).
We observed a profound reorganization of ALM preparatory activity in new task context. Many ALM neurons lost or even reversed their lick direction selectivity in task context 2 (Fig. 3c, top), whereas other neurons retained their selectivity. Also, new selective neurons emerged in task context 2 (Fig. 3c, bottom). Across the population, neuronal selectivity across the two task contexts were not correlated (Fig. 3d and Extended Data Fig. 5e; Pearson’s correlation, R = −0.0057, P = 0.6774).
We examined population encoding of future lick direction by calculating the CDDelay in each task context (Fig. 3e). Activity projected on the CDDelay reliably differentiated lick direction within task context, but this activity collapsed when projected on the CDDelay across task contexts (Fig. 3f). Across all fields of view, a CDDelay decoder predicted lick direction at near chance level on average in the other task context (Fig. 3g). Individual neurons supporting the CDDelay vectors in the two task contexts were weakly correlated (Fig. 3h; Pearson’s correlation, R = 0.3; significantly less than the correlation within task context over time in Fig. 2k, P = 0, bootstrap). Thus, different task contexts yielded distinct CDDelay vectors. In contrast to the reorganization of ALM preparatory activity, selectivity during the sample and response epochs remained remarkably stable across task contexts (Extended Data Fig. 5). This ruled out the possibility that the change in preparatory activity was due to unstable imaging or changes in motor behaviour.
Although ALM preparatory activity was reorganized across task contexts on average, we found substantial individual variability across mice (Fig. 3g and Extended Data Fig. 6a–c). In some mice, the CDDelay vectors in the two task contexts were nearly orthogonal (Fig. 3f). But in other mice, preparatory activity maintained along the same CDDelay (Extended Data Fig. 6d), or even reversed direction along the CDDelay (Extended Data Fig. 6e). Within each mouse, similar pattern of reorganization was consistently observed across different fields of view (Extended Data Fig. 6a–c), indicating that the variability was not due to heterogeneous sampling of neurons or location of imaging (Extended Data Fig. 6g). Task performance, uninstructed movements, task learning speed or the time interval between imaging sessions did not explain this individual variability (Extended Data Fig. 6f,g). Individual variability may result from differences in the underlying circuits (see later modelling).
Thus, new preparatory states form when mice learn to make the same licking actions under new task contexts. These results also show that distinct preparatory states in motor cortex can drive the same subsequent movement execution. Preparatory states could therefore encode a learned action in multiple representations that index distinct contexts.
Stable retention of learned representations
Encoding learned actions in combination with context could enable stable retention of motor memories over continual learning, because learning in different contexts forms parallel new representations without altering previously learned representations. To test this notion, we examined whether learned preparatory states in previous contexts were retained after intervening learning (Fig. 4a).
a, Possible outcomes of preparatory states for re-learning. b, Task contexts 1, 2 and 1′. Task contexts 1 and 1′ are identical. Time interval, 30.65 ± 8.73 days between task contexts 1 and 2, 57.19 ± 12.89 days between task contexts 1 and 1′; mean ± s.d. across fields of view. c, Mean deconvolved activities from an example field of view (n = 608 neurons). Neurons are sorted on the basis of their selectivity during the delay epoch in task context 1. d, Selectivity index in task context 1 (left), 2 (middle) and 1′ (right) for neurons showing significant trial-type selectivity (P < 0.001, two-tailed t-test) during the delay epoch. Red, neurons preferring lick left; blue, neurons preferring lick right. Significant selectivity and trial-type preferences are determined in task context 1. e, Schematic of movement-specific activity trajectories in activity space and CDDelay vectors across task contexts. Red and blue shades, preparatory states for lick left and lick right, respectively. f, ALM activities from an example field of view projected on the CDDelay from task context 1. Thick lines are the mean and thin lines show single trials. g, Same as f, but for the CDDelay from task context 2. h, Decoding accuracy of the CDDelay from task context 1 tested on task contexts 1, 2, 1′ and 2′. Grey circles and lines indicate fields of views imaged across task contexts 1, 2 and 1′ (n = 26 fields of view, 5 mice). Black circles and lines indicate fields of views imaged across task contexts 1, 2, 1′, and 2′ (n = 7 fields of view, 3 mice). Task context 1 versus 2, ***P = 1.12 × 10−10; task context 2 versus 1′, ***P = 3.46 × 10−7; task context 1′ versus 2′, **P = 0.0091. Two-tailed paired t-test. Data are mean ± s.e.m. i, Same as h, but for the CDDelay from task context 2. Task context 1 versus 2, ***P = 4.87 × 10−10; task context 2 versus 1′, ***P = 7.40 × 10−9; task context 1′ versus 2′, *P = 0.0496. Two-tailed paired t-test.
After imaging ALM activity in task contexts 1 and 2, mice were re-trained in task context 1 (notated as 1′ for re-learning) in the automated home cage (Extended Data Fig. 1f). We then imaged the same neuronal populations again (Fig. 4b; task context 1→2→1′). We observed a re-activation of the previous preparatory activity pattern, even though task contexts 1 and 1′ were tested 2 months apart on average (32–78 days; Fig. 4b and Extended Data Fig. 1f,g). Individual neurons showing lick direction selectivity in task context 1 were reconfigured in task context 2 but reappeared in task context 1′ (Fig. 4c,d and Extended Data Fig. 7h; Pearson’s correlation, task context 1 versus 1′, R = 0.7675, P = 0).
We examined whether ALM preparatory activity was re-activated along similar coding directions in activity space (Fig. 4e). Activity trajectories in lick left and lick right trials were well separated in task context 1′ when projected on the CDDelay from task context 1 (Fig. 4f). By contrast, the activity trajectories were poorly separated when projected on the CDDelay from task context 2 (Fig. 4g). Across all fields of view, a CDDelay decoder trained on task context 1 predicted lick direction at near chance level in task context 2, but performance recovered in task context 1′ (Fig. 4h). Together, these data indicate a re-activation of the previously learned preparatory states under task context 1′.
We also observed a similar re-activation of ALM preparatory states associated with task context 2. In a subset of mice (n = 3), we further imaged the same ALM populations across task context 1→2→1′→2′, spanning up to 3 months (59–97 days across mice; Extended Data Fig. 1f,g). We found consistent reorganization and re-activation of CDDelay vectors across the reversals (Fig. 4i). Thus, stable retention of preparatory states was not limited to any specific task context. Unlike preparatory activity, selectivity during the sample and response epochs were stably maintained across all task contexts (Extended Data Fig. 7).
In addition to the reorganization and re-activation of coding directions (CDDelay), we also observed activity changes along other dimensions of activity space across task contexts (Extended Data Fig. 8). Activity along these dimensions did not discriminate lick direction (Extended Data Fig. 8e; ‘movement-irrelevant subspace’), and activity did not recover in previous task contexts (Extended Data Fig. 8c,d). Therefore, preparatory activity is selectively maintained along coding directions encoding behaviour-related information, but activity drifts over time along other non-informative directions7,14,50.
Learning creates parallel representations
We next tested whether continual learning in new task contexts will keep creating new preparatory states. Experiments so far only tested two task contexts. Now we tested whether yet new preparatory states would emerge if mice learned to perform directional licking instructed by a novel stimulus (Fig. 5a).
a, Possible outcomes of preparatory states over continual learning. b, Task structure of task context 1, 2 and 3. In task context 3, mice report frequency of a pure tone using directional licking after a delay epoch. Time interval, 31.50 ± 9.65 days between task contexts 1 and 2, 66.75 ± 26.36 days between task contexts 1 and 3; mean ± s.d. across fields of view. c, Selectivity index in task contexts 1, 2 and 3 for neurons with significant trial-type selectivity (P < 0.001, two-tailed t-test) during the delay epoch. Red, neurons preferring lick left; blue, neurons preferring lick right. Significant selectivity and trial-type preferences are determined in task context 1. d, Schematic of movement-specific activity trajectories in activity space and CDDelay vectors across task contexts. Red and blue shades, preparatory states for lick left and lick right, respectively. e, ALM activities from an example field of view projected on the CDDelay from task context 1. Thick lines are the mean and thin lines show single trials. f, Decoding accuracy of the CDDelay from task context 1 tested on task contexts 1, 2 and 3 (n = 8 fields of view, 3 mice). Task context 1 versus 3, ***P = 5.56 × 10−5. Decoding accuracy of the CDDelay from task context 2 (n = 8 fields of view, 3 mice). Task context 2 versus 3, ***P = 6.08 × 10−4. Decoding accuracy of the CDDelay from task context 3 (n = 8 fields of view, 3 mice). Comparing to task context 1 decoder, **P = 0.0022; comparing to task context 2 decoder, **P = 0.002. Two-tailed paired t-test. Data are mean ± s.e.m.
We trained mice to perform an auditory-instructed licking task in the automated home cage after imaging ALM activity in the tactile tasks (Fig. 5b; task context 1→2→3; 40–118 days). Mice discriminated frequency of a pure tone, and licked left for 2 kHz and licked right for 10 kHz. We then imaged the same ALM populations in auditory task. Individual neurons with significant lick direction selectivity during the delay epoch in tactile task showed distinct pattern of selectivity in auditory task (Fig. 5c; Pearson’s correlation, task context 1 versus 3, R = 0.3435; significantly less than the correlation within task context over time in Fig. 2e, P = 0, bootstrap).
We further examined whether ALM preparatory activity encoded tactile- and auditory-instructed lickings along different coding directions (Fig. 5d). Indeed, we found poor separation between activity trajectories in lick left and lick right trials when activities in the auditory task were projected on the CDDelay from the tactile task (Fig. 5e). Across all fields of view, the CDDelay decoders trained on the tactile tasks predicted lick direction poorly when tested on the auditory task (Fig. 5f). By contrast, a decoder trained within the auditory task could decode lick direction significantly better than the decoders from tactile task 1 and 2 (P = 0.0022 and P = 0.002, two-tailed paired t-test), indicating that their poor decoding performances in the auditory task were not due to a lack of neuronal selectivity.
Finally, ALM activity during the sample epoch was distinct across tactile and auditory tasks (Extended Data Fig. 9a,b). Lick direction selectivity during the response epoch remained stable across all task contexts (Extended Data Fig. 9e,f), which probably reflected conserved licking movement execution across tasks and ruled out the possibility of unstable imaging over time.
Together, these results show that motor learning produces context-specific preparatory states. Once learned, these activity states are stably stored and can be recalled after several months, despite intervening motor learning involving the same actions in other contexts. At the same time, activity related to movement execution remains the same across contexts. Preparatory states thus reflect context-specific motor memories that are stably retained over continual learning.
Preparatory activity reflects motor memory
We next explored how a context-specific neural code could support motor memory behaviour. Mice exhibited faster re-learning in the previously learned sensorimotor contingency (Extended Data Fig. 1c). We examined whether preparatory states retained a memory trace that could facilitate faster re-learning8.
We re-analysed the imaging data from tactile task 1→2→1′ in which we imaged ALM activity in the same task context before and after an intervening learning. If learning of task context 2 left a memory trace, we should observe an activity change in task context 1′ compared with task context 1, and this change should support the performance of task 2. We calculated the CDDelay for task context 2 and projected ALM activity at the end of the delay epoch on the CDDelay (Extended Data Fig. 10a). ALM activity in task context 1′ exhibited increased lick direction selectivity along the CDDelay compared with task context 1 (Extended Data Fig. 10b; P = 0.005, paired t-test). To examine whether this activity change could support the performance of task 2, we performed decoding of lick direction using activity projected on the CDDelay from task context 2. Decoding was near chance level in task context 1 (52.75 ± 5.24%, mean ± s.e.m. across sessions) but significantly increased to 58.66 ± 4.63% in task context 1′ (Extended Data Fig. 10c; P = 0.0199, paired t-test). Thus learning of task context 2 left a subtle but persistent alteration of ALM preparatory activity along the CDDelay8.
If each task-specific CDDelay retains a memory trace of previous learning, distinct CDDelay vectors could provide a place to store task-specific motor memories while protecting them from interference. We tested this notion by taking advantage of the individual variability that some mice exhibited distinct CDDelay vectors across task contexts, whereas others exhibited fixed CDDelay vectors (Extended Data Fig. 6a–c). Remarkably, mice with distinct CDDelay vectors in different task contexts (lower dot product) re-learned the previously learned task faster (Extended Data Fig. 10d; P = 0.0002, Pearson’s correlation).
These results suggest that task-specific motor memories are stored along distinct coding directions in activity space, which could help protect the memories from new learning and support faster re-learning of previously learned tasks.
A feedforward network for stable memory storage
We used network modelling to explore network architectures that might support the observed memory storage. Preparatory activity is mediated by interactions between ALM and multiple brain regions51. Our goal was to be agnostic to how models map onto brain regions but explore what networks could explain reorganization of preparatory activity by learning, specifically: (1) formation of new preparatory activity across contingency reversal; and (2) re-activation of learned preparatory activity patterns after intervening task learning.
We started with recurrent neural networks52 (RNNs) (Fig. 6a). RNNs were trained to generate linear ramps along the correct readout dimension and no activity along the incorrect readout dimension (Fig. 6b, task context 1; Methods). For contingency reversal, we trained the internal connections of learned RNNs to generate the opposite responses while keeping the input and output connections fixed (Methods). Contrary to the neural data in which a new pattern of selectivity emerged after contingency reversal (Fig. 3), RNN activity mostly followed the network output (that is, lick direction; Fig. 6b). Network units similarly contributed to the CDDelay defined by lick direction in both task contexts (Fig. 6c). We also tested RNNs in which only two internal units contributed to the output, yielding similar results (Extended Data Fig. 11a–c). RNN dynamics were therefore constrained to the previously learned CDDelay and the networks solved the contingency reversal by re-association (Fig. 6d).
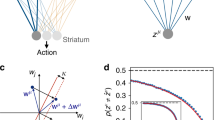
a, The RNN model. b, Activity of a RNN projected on the CDDelay from task context 1. The CDDelay is defined by lick direction. Blue, lick right; red, lick left. c, Weight contribution of the RNN units to the CDDelay vectors from task contexts 1 and 2 (left) or task contexts 1 and 1′ (right). d, Dot product between the CDDelay vectors from task contexts 1 and 2. Data from 50 randomly initialized RNNs. e, Schematic of the AFF network. f–h, Same as b–d, except for the AFF networks. Data from 50 randomly initialized AFF networks.
We next explored a class of amplifying feedforward (AFF) networks that generate persistent activity by passing activity through a chain of network states53,54 (Fig. 6e and Extended Data Fig. 11d), which can be modelled as a series of layers with feedforward connections. AFF networks learned feedforward amplifications to generate choice-specific persistent activity in response to transient inputs to the early layer (Fig. 6f). Feedback connections conveyed output signals to early layers and allowed the network to learn (Methods). In the hidden layers, AFF networks maintained persistent activity along multiple dimensions (Extended Data Fig. 11e,f). AFF networks readily captured both features of the neural data: (1) upon contingency reversal, the network learned a new CDDelay; (2) re-training in the previous sensorimotor contingency re-activated the previous CDDelay (Fig. 6f,g). Resetting the weights of the hidden layers before re-training prevented the CDDelay re-activation (Extended Data Fig. 11g,h). Thus, AFF networks stored sensorimotor mappings in hidden layers.
We next examined the features that allowed AFF networks to create new CDDelay vectors upon contingency reversal learning while retaining previously learned CDDelay vectors. Owing to feedforward and feedback connections, intermediate layers contained mixtures of input and output representations. We decompose AFF network activity into distinct modes. AFF networks learned a persistent stimulus mode and an output mode along orthogonal dimensions that together established the CDDelay (Extended Data Fig. 12a). Upon contingency reversal, the output mode combined with the new stimulus mode to form a new CDDelay (Extended Data Fig. 12a). Reversion to the previous contingency re-activated the original stimulus and output modes, which re-activated the previously CDDelay (Fig. 6g). By contrast, we found that the persistent stimulus mode was absent in RNNs, which resulted in CDDelay vectors that were aligned to only the output mode (Extended Data Fig. 12b). This suggests that a high-dimensional circuit that can maintain multiple persistent activity modes is critical to support context-dependent CDDelay reorganization.
This feature of AFF networks could also explain individual variability across mice (Extended Data Fig. 6a–c). Individual networks could exhibit a range of CDDelay reorganization depending on the relative strength of input and output representations in the intermediate layers (Extended Data Fig. 12a). Networks with strong stimulus modes (due to weak feedback connections) exhibited reorganized CDDelay vectors; networks with strong output modes exhibited stable CDDelay vectors aligned to the network output (Fig. 6h and Extended Data Fig. 12c). This suggests an unexpected role of stimulus activity in the formation of motor memory. We tested whether ALM stimulus activity could explain the individual variability across mice in our data. Remarkably, stimulus activity strength measured in task context 1 predicted whether a mouse would exhibit context-dependent reorganization of CDDelay across task contexts (Extended Data Fig. 12d). This suggests individual differences in their underlying neural circuits.
In summary, an AFF network architecture that maintained multiple persistent activity modes to encode sensorimotor combinations in high-dimensional hidden layers could explain multiple aspects of the neural data. These results suggest that stable motor memory is rooted in high-dimensional representations. AFF network is a subclass of RNNs. There may be other architectures that could also produce these neural dynamics.
Discussion
Our study reveals a combinatorial neural code that stores learned actions in combination with their contexts. Within a task context, preparatory activity encoding lick direction is stably maintained over multiple months (Fig. 2), and even across intervening motor learning (Fig. 4). Across task contexts, the same action is preceded by distinct preparatory activity (Fig. 3), whereas selectivity related to sensory stimulus and movement execution remains remarkably stable over time and across task contexts (Extended Data Figs. 4, 5, 7 and 9). These results suggest that the same action can be encoded by multiple preparatory states. This afforded degree of freedom may allow the motor circuits to create parallel representations for the same actions while indexing their contexts. Indeed, we find that new task learning continually creates new preparatory states for learned actions in a context-dependent manner (Fig. 5). Motor learning thus forms modular motor memories for each context.
Preparatory states in different task contexts are arranged along distinct coding directions in activity space. Each coding direction retains a memory trace of the previous learning in specific tasks (Extended Data Fig. 10a–c). Context-specific coding directions could help protect existing memories from interference by new learning: mice with distinct coding directions across task contexts were faster to re-learn previously learned tasks—that is, greater saving (Extended Data Fig. 10d). These properties of ALM preparatory activity indicate that it reflects motor memory and reveal the underlying neural code for stable motor skill retention. Context-specific memory, as we observed in the motor system, may provide a solution for stable memory storage throughout continual learning. Learning in new contexts produces parallel new representations instead of modifying existing representations, thus protecting existing motor memories from erasure6,8.
Motor cortical preparatory activity is thought to provide the initial conditions for subsequent movement execution16. Our results show that preparatory activity is not directly linked to the movement itself but reflects motor memories of learned actions and contexts5. Reorganization of preparatory activity across task contexts shares similarities with place cells of hippocampus, which encode space and experience within specific context and undergo global remapping across distinct contexts55. Context-specific code may be a general feature for learning cognitive representations.
Our findings suggest that when movement parameters and task context are controlled, neural representation of actions in motor cortex shows surprisingly little representational drift. Interestingly, preparatory activity is selectively maintained along coding directions, but activity drifts over time along other non-informative directions (Extended Data Figs. 3 and 8). Preparatory activity is maintained by recurrent networks in motor cortex and connected brain areas16,51. Our findings suggest that motor memories are stored in stable network configurations. Previous studies have reported representational drift in sensory, association, and memory-related brain regions34,56,57. However, little representational drift has been reported in motor areas38,39,40. Differences in brain areas and behavioural paradigms may explain some differences in these findings.
It was recently reported that motor learning induces a persistent change in preparatory activity7,8. Notably, this persistent change occurs outside of the activity subspace encoding specific movements (coding directions), whereas the geometry of activity states encoding specific movements is mostly preserved. These studies examine activity change within a session or across a few days, thus the stability of the reorganized activity remains to be determined. By tracking activity over long-term, here we find that learning new task context induces a dramatic reorganization of the coding directions (Figs. 3 and 5), along with changes in movement-irrelevant subspace (Extended Data Fig. 8). We also find that, once learned, the preparatory states are stably retained and can be recalled after multiple months (Fig. 4). Thus multiple concerted changes, along both coding directions and movement-irrelevant subspaces, accompany motor skill learning and may work collectively to differentiate motor memories.
A combinatorial code requires high-capacity storage for motor memories owing to potentially many combinations of actions and contexts. Standard RNNs mostly reused output activity states in different tasks. The delay epoch separating sensory input and network output in time and the network training to generate ramping output dynamics during the delay epoch might have made it difficult for the RNNs to learn sensorimotor combinations. Our network modelling suggests that stable motor memory is rooted in high-dimensional representations and requires a network architecture that can readily acquire and store sensorimotor combinations (Fig. 6e–h). It remains to be determined how such high-dimensional representations map onto neural circuits. Preparatory activity is maintained by recurrent loops between ALM and subcortical regions51,58, including thalamus59, midbrain60, and cerebellum61. The storage locus for such motor memories is unknown. We propose the cerebellum as a potential candidate. Cerebellar granule cells integrate inputs from the neocortex and form the basis for cerebellar output that influences preparatory activity62. Cerebellar granule cells are the most numerous cell type in the brain, which could provide a substrate for high-dimensional representations with minimal interference between motor memories63,64. Future work probing mechanisms of memory storage in the cerebellum may be of interest.
Methods
Mice
This study was based on data from 36 mice (age more than postnatal day 60, both male and female mice). Fifteen GP4.3 mice (Thy1-GCaMP6s; Jackson laboratory, JAX 024275) were used for longitudinal two-photon calcium imaging. Among them, one mouse was removed from subsequent neuronal data analyses due to the low number of matched neurons across days (see ‘Preprocessing of two-photon imaging data’). Five GAD2-IRES-Cre mice (JAX 010802) were used for ALM photoinhibition in home cage. Five additional GAD2-IRES-Cre mice were used only for behaviour training in home cage. Eleven Slc17a7-Cre mice (JAX 023527) crossed to Cre-dependent GCaMP6f reporter Ai148 mice (JAX 030328) were used for behaviour training but were not used for calcium imaging due to poor behavioural performance (Extended Data Fig. 1i).
All procedures were in accordance with protocols approved by the Institutional Animal Care and Use Committees at Baylor College of Medicine. Mice were housed in a 12:12 reversed light:dark cycle and tested during the dark phase. On days not tested, mice received 0.5–1 ml of water. On other days, mice were tested in experimental sessions lasting 1–2 h where they received all their water (0.5–1 ml). If mice did not maintain a stable body weight, they received supplementary water65. All surgical procedures were carried out aseptically under 1–2% isoflurane anaesthesia. Buprenorphine Sustained Release (1 mg kg−1) and Meloxicam Sustained Release (4 mg kg−1) were used for preoperative and postoperative analgesia. A mixture of bupivacaine and lidocaine was administered topically before scalp removal. After surgery, mice were allowed to recover for at least 3 days with free access to water before water restriction.
Surgery
Mice were prepared with a clear skull cap and a headpost41,65. The scalp and periosteum over the dorsal skull were removed. For ALM photoinhibition in GAD2-ires-cre mice, AAV8-Ef1a-DIO-ChRmine-mScarlet46 (Stanford Gene Vector and Virus Core; titre 8.44 × 1012 viral genomes (vg) per ml) was injected in the left ALM (anterior 2.5 mm from bregma, lateral 1.5 mm, depth 0.5 and 0.8 mm, 200 nl at each depth) using a Nanoliter 2010 injector (World Precision Instruments) with glass pipettes (20–30 µm diameter tip and beveled). A layer of cyanoacrylate adhesive was applied to the skull. A custom headpost was placed on the skull and cemented in place with clear dental acrylic. A thin layer of clear dental acrylic was applied over the cyanoacrylate adhesive covering the entire exposed skull.
For two-photon calcium imaging in GP4.3 mice, a glass window was additionally implanted over ALM. A circular craniotomy with diameter 3.2 mm was made over the left ALM (anterior 2.5 mm from bregma, lateral 1.5 mm). Dura inside craniotomy was removed. A glass assembly consisting of a single 4 mm diameter coverslip (Warner Instruments; CS-4R) on the top of two 3 mm diameter coverslips (Warner Instruments; CS-3R) was combined using optical adhesive (Norland Products; NOA 61) and UV light (Kinetic instruments Inc.; SpotCure-B6). The glass window was affixed to the surrounding skull of craniotomy using cyanoacrylate adhesive (Elmer; Krazy Glue) and dental acrylic (Lang Dental Jet Repair Acrylic; 1223-clear).
Behaviour tasks and training in home cage
Details of behaviour task and training in the autonomous home-cage system have been described previously43. In brief, a headport (~20 × 20 mm) was in the frontal side of the home cage. The two sides of the headport were fitted with widened tracks that guided a custom headpost (26.5 mm long, 3.2 mm wide) into a narrow spacing where the headpost could trigger two snap action switches (D429-R1ML-G2, Mouser) mounted on both sides of the headport. Upon switch trigger, two air pistons (McMaster; 6604K11) were pneumatically driven (Festo; 557773) to clamp the headpost. A custom 3D-printed platform was placed inside the home cage in front of the headport. The stage was embedded with a load cell (Phidgets; CZL639HD) to record mouse body weight. This body weight-sensing stage was also used to detect struggles during head fixations and triggered self-release. A lickport with two lickspouts (5 mm apart) was placed in front of the headport. Each of the lickspout was electrically coupled to the custom circuit board that detected licks via completion of an electrical circuit upon licking contacts41,66. Water rewards were dispensed by two solenoid valves (The Lee Company; LHDA1233215H). The sensory stimulus for the tactile-instructed licking task was a mechanical pole (1.5 mm diameter) on the right side of the headport. The pole was motorized by a linear motor (Actuonix; L12-30-50-12-I) and presented at different locations to stimulate the whiskers. The sensory stimuli for the auditory-instructed licking task were pure tones (2 kHz or 10 kHz) provided by a piezo buzzer (CUI Devices; CPE-163) placed in front of the headport. The auditory ‘go’ cue (3.5 kHz) in both tactile and auditory tasks was provided by the same piezo buzzer.
Protocols stored on microcontrollers (Arduino; A000062) operated the home-cage system and autonomously trained mice in voluntary head fixation and behavioural tasks, as well as carrying out optogenetic testing. In brief, mice were placed inside the home cage and could freely lick both lickspouts that were placed inside the home cage through the headport. The rewarded lickspout alternated between the left and right lickspouts (3 times each) to encourage licking on both lickspouts. This phase of the training acclimatized mice to the lickport and the lickport was gradually retracted into the headport away from the home cage. The lickport retraction continued until the tip of the lickspouts was approximately 14 mm away from the headport. At this point, mice could only reach the lickspouts by entering the headport with the headpost triggering the head-fixation switches. After 30 successful voluntary head-fixation switch triggers, the pneumatic pistons were activated to clamp the headpost upon the switch trigger (‘voluntary head fixation’; Fig. 1c). The head-fixation training protocol continuously increased the pneumatic clamping duration (from 3 s to 30 s). This clamping was self-released when the body weight readings from the load-sensing platform exceeded either an upper (30 g) or lower (−1 g) threshold. Overt movements of the mice during the head fixation typically produced large fluctuations in weight readings exceeding the thresholds. These thresholds were dynamically adjusted during the training process.
When mice successfully performed head-fixation training protocol by reaching 30 s head-fixation duration, the next training protocol for the tactile-instructed licking task began. In the tactile-instructed licking task, mice used their whiskers to discriminate the location of a pole and reported choice using directional licking for a water reward41,65 (Fig. 1d). The pole was presented at one of two positions that were 6 mm apart along the anterior–posterior axis. The posterior pole position was approximately 5 mm from the right whisker pad. The sample epoch was defined as the time between the pole movement onset to 0.1 s after the pole retraction onset (sample epoch, 1.3 s). A delay epoch followed during which the mice must keep the information in short-term memory (delay epoch, 1.3 s). An auditory ‘go’ cue (0.1 s duration) signalled the beginning of response epoch and mice reported choice by licking one of the two lickspouts. Task training had three subprotocols that shaped mice behaviour in stages. First, a ‘directional licking’ subprotocol trained mice to lick both lickspouts and switch between the two. Then, a ‘discrimination’ subprotocol taught mice to report pole position with directional licking. Finally, a ‘delay’ subprotocol taught mice to withhold licking during the delay epoch and initiate licking upon the ‘go’ cue by gradually (in 0.2 s steps) increasing the delay epoch duration up to 1.3 s. At the end of the delay subprotocol, the head-fixation duration was further increased from 30 s to 60 s. The head-fixation duration was increased by 2 s after every 20 successful head fixations. This was done to obtain more behavioural trials in each head fixation. The program also adjusted the probability of each trial type to correct biased licking of the mice.
Mice were first trained in one sensorimotor contingency (Fig. 1b, task context 1; anterior pole position→lick left, posterior pole position→lick right). Then, the correspondence between pole locations and lick directions was reversed (task context 2; anterior pole position→lick right, posterior pole position→lick left). Over multiple months, mice could learn multiple rounds of sensorimotor contingency reversal depending on experiment (see ‘Performance criteria for contingency reversals and acclimatization to imaging setup’).
For auditory-instructed licking task, mice were trained to perform directional licking to report the frequency of a pure tone presented during the sample epoch (Fig. 5b, task context 3; 2 kHz (low tone)→lick left, 10 kHz (high tone)→lick right). Task structures such as the delay epoch (1.3 s) and auditory go cue (3.5 kHz, 0.1 s) were the same as the tactile-instructed licking task.
Performance criteria for contingency reversals and acclimatization to imaging setup
For mice that underwent optogenetic experiment in home cage, contingency reversal was automatically introduced when mice reached performance criteria of >75% correct and <50% early lick for 100 trials in a given task contingency (Fig. 1e,h). Mice learned multiple rounds of contingency reversals before optogenetic experiment initiated. Optogenetic experiment was manually initiated based on inspections of behavioural performance (Fig. 1h).
Mice for two-photon imaging were over-trained in each task context to reach performance criteria of >80–85% correct for 100 trials. Over-training facilitated faster habituation after transferring to the two-photon setup. After mice acquired this high level of task performance in home-cage training, we transferred the mice to the imaging setup where they performed the same task in daily sessions under the two-photon microscope. During this period, mice were singly housed outside of the automated home-cage system. A brief acclimatization period lasting for a few days was required to habituate the mice to perform the task under the microscope (Extended Data Fig. 1e–g). We started imaging sessions once mice recovered their task performance (typically >75%). After imaging across multiple sessions, mice were returned to the automated home cage again in which they learned other tasks. In this manner, we repeatedly transferred mice between the automated home cage and two-photon setup for as long as possible (Extended Data Fig. 1f,g).
For tactile-instructed licking task, mice were first trained and imaged in one sensorimotor contingency (Fig. 3b, task context 1). After imaging under the two-photon microscope, we transferred the mice back to the home cage and reversed the sensorimotor contingency (Fig. 3b, task context 2). The mice were over-trained in the new task contingency before transferring to the two-photon setup to re-image the same ALM populations across task contexts (task context 1→2; 10 mice). In a subset of mice, after imaging, we re-trained the mice in the previous contingency in the home cage (Fig. 4b, task context 1′). After achieving proficient task performance, we translocated the mice to the two-photon setup and imaged the same ALM populations again (task context 1→2→1′; 5 mice). In a subset of mice, we further repeated the contingency reversal one more time and imaged across four task contexts (task context 1→2→1′→2′; 3 mice).
For auditory-instructed licking task, mice were imaged first in the tactile task contexts 1 and 2 before training in the auditory task to image the same ALM populations across task contexts (task context 1→2→3; 8 mice).
ALM photoinhibition in home cage
The procedure for ALM photoinhibition in home cage has been described previously43. Light from a 633 nm laser (Ultralaser; MRL-III-633L-50 mW) was delivered via an optical fibre (Thorlabs; M79L005) placed above the headport (Fig. 1g). Photostimulation of the virus injection site was through a clear skull. The photostimulus was a 40 Hz sinusoid lasting for 1.3 s, including a 100 ms linear ramp during photostimulus offset to reduce rebound neuronal activity67. Photostimulation was delivered in a random subset of trials (18%) during either the sample, delay, or response epoch. Photostimulation started at the beginning of the task epoch. Photostimulation power was 2.5, 12.5, or 25 mW, randomly selected in each trial. Therefore, the probability of each photostimulation condition was 2% (total of 9 conditions). The size of the light beam on the skull surface was 7.07 mm2 (3.0 mm diameter). 2.5, 12.5, and 25.0 mW power corresponded to 0.35, 1.77, and 3.54 mW mm−2 in light intensity. This range of the light intensity was much lower than the previous studies41,42 (typically 1.5 mW with a light beam diameter of 0.4 mm, corresponding to 11.9 mW mm−2). To prevent the mice from distinguishing photostimulation trials from control trials using visual cues, a masking flash was delivered using a 627 nm LED on all trials near the eyes of the mice. The masking flash began at the start of the sample epoch and continued through the end of the response epoch in which photostimulation could occur.
Videography
Two CMOS cameras (Teledyne FLIR; Blackfly BFS-U3-04S2M) were used to measure orofacial movements of the mouse from the bottom and side views (Extended Data Figs. 1a,b and 5e). Both the bottom and side views were acquired at 224 × 192 pixels and 400 frames per second. Mice performed the task in complete darkness, and videos were recorded under infrared 940 nm LED illumination (Luxeon Star; SM-01-R9). A custom written software controlled the video acquisition68.
Two-photon imaging
A Thorlabs Bergamo II two-photon microscope equipped with a tunable femtosecond laser (Coherent; Chameleon Discovery) is controlled by ScanImage 2016a (Vidrio). GCaMP6s was excited at 920 nm. Images were collected with a 16× water immersion lens (Nikon, 0.8 NA, 3 mm working distance) at 2× zoom (512 × 512 pixels, 600 × 600 µm). For all imaging sessions, we performed volumetric imaging by serially scanning five planes (30 or 40 μm equally spaced along the z axis) at 6 Hz each. The range of depth from all imaging planes was 120–500 μm below the pial surface, and the range of laser power was 80–225 mW, measured below the objective. To identify the spatial locations of individual field of view (FOV), we imaged at the pial surface before imaging during the task (Extended Data Fig. 2b). To monitor the same ALM neurons across days, we saved 6 reference images with 10 µm interval around the most superficial imaging plane for all imaging sessions and identified the most similar imaging plane based on visual inspection across sessions.
Multiple FOVs were imaged across multiple days in each task context. The same set of FOVs were imaged across multiple task contexts. Across all experiments, the total duration from the first imaging session to the last imaging session was 26–233 days (Extended Data Fig. 1g; 95.86 ± 71.95 days, mean ± s.d. across mice).
Behaviour data analysis
Performance was computed as the fraction of correct choices, excluding early lick trials and no lick trials. Mice whose performance never exceeded 70% after 35–40 days of training were considered unsuccessful in task learning (Extended Data Fig. 1h,i). Chance performance was 50%. Behavioural effects of photoinhibition were quantified by comparing the performance under photoinhibition with control trials using paired two-tailed t-test (Fig. 1i). To quantify the speed of task learning in a given task context (Fig. 1f and Extended Data Figs. 1c, 6g and 10d), we calculated the number of trials to reach performance criteria of >75% correct and <50% early lick for 100 trials. We excluded the trials in the head-fixation training protocol from the initial task learning for a fair comparison.
Video data analysis
We used DeepLabCut69 to track manually defined body parts. Separate models were used to track tongue and jaw movements (Extended Data Fig. 1a,b). The development dataset for model training and validation contained manually labelled videos from multiple mice and multiple sessions (correct trials only). For tongue network model, 6 markers were manually labelled in 500 video frames. For jaw network model, 5 markers were manually labelled in 300 video frames. The frames for labelling were automatically and uniformly selected by the program at different timepoints within trials. The labelled frames of the training dataset were split randomly into a training dataset (95%) and a test dataset (5%). Training was performed using the default settings of DeepLabCut. All models were trained up to 500,000 iterations with a batch size of one. The trained models tracked the body features in the test data with an average tracking error of less than 2.5 pixels68.
To analyse tongue and jaw movements during the response epoch, we defined single lick events based on continuous presence of the tongue volume in each frame44. Tongue volume was determined from the internal area of the four tongue markers (Extended Data Fig. 1a, left), which were located at the corners of tongue. Lick events were separately grouped based on the lick duration for further time-bin-matched correlation analysis. x and y pixel positions of the tongue tip trajectories were calculated by averaging the frontal tongue markers in each frame. x and y pixel positions of the jaw tip trajectories were calculated by averaging the three frontal jaw markers in each frame. For each lick event, we obtained four time series (x position, y position, x velocity and y velocity) for the tongue (or jaw) tip trajectories (Extended Data Fig. 1a,b, middle). To calculate the similarity between the tongue (or jaw) tip trajectories across lick events (within lick left or lick right), we computed Pearson correlation on the time series for all pairwise lick events within and across sessions. We then calculated the average correlation for the four parameters (x position, y position, x velocity and y velocity) and compared them within session and across sessions (Extended Data Fig. 1a,b, right).
To examine jaw movements during the delay epoch across task contexts, we calculated the x and y displacement jaw tip position by subtracting the average jaw position in a baseline period (1.57 s) before the sample epoch (Extended Data Fig. 6f).
Preprocessing of two-photon imaging data
Imaging data were preprocessed using Suite2p package70 to perform motion correction and extract raw fluorescence signals (F) from automatically identified regions of interest (ROIs). ROIs with >1 skewness were used for further analyses. Neuropil corrected trace was estimated as Fneuropil_corrected(t) = F(t) – 0.7 × Fneuropil(t). To visualize activity (Fig. 1d, top and Extended Data Fig. 2j, left), ΔF/F0 (type 1) was separately calculated in each trial as (F − F0)/F0, where F0 is the baseline fluorescence signal averaged over a 1.57 s period immediately before the start of each trial. For all other analyses, we calculated deconvolved activity to avoid the spillover influence of slow-decaying calcium dynamics across task epochs (Extended Data Fig. 2j). To calculate deconvolved activity, Fneuropil_corrected from all trials were concatenated and ΔF/F0 (type 2) was calculated as (F − F0)/F0, where F0 is a running baseline calculated as the median fluorescence within a sliding window of 60 s. Subsequently, ΔF/F0 (type 2) was deconvolved using the OASIS algorithm48 (Extended Data Fig. 2j) after estimating the time constant by auto-regressive model with order p = 1. Deconvolved activities were used for all the analyses in this study, except in Fig. 2d (top) and Extended Data Fig. 2j (left) where ΔF/F0 (type 1) traces were shown. Type 1 and type 2 ΔF/F0 only differed in their F0 calculation.
To track the activity of the same neurons across days, spatial footprints of individual ROIs from the same FOVs were aligned across different imaging days using the CellReg pipeline47. This probabilistic algorithm computes the distributions of centroid distance and spatial correlation between neuronal pairs of the nearest neighbour and all other neighbours within a 10 μm distance (Extended Data Fig. 2g,h). Based on the bimodality between distributions (nearest neighbours versus other neighbours), CellReg algorithm calculates the estimated false positive and false negative probabilities. By minimizing both estimated error rates for each pair of ROIs, this probabilistic algorithm identifies co-registered neurons and quantifies registration scores for these co-registered neurons (Extended Data Fig. 2i). If the mean squared errors of both centroid distance and spatial correlation model are above 0.1 (a pre-determined hyperparameter), CellReg algorithm generates an error and the FOV is considered as a failure to find co-registered neurons across days. One mouse was removed from all subsequent neuronal data analyses due to failures to find matched neurons across days from all imaging sessions, primarily due to poor imaging window quality. Among co-registered neurons, only neurons with reliable responses in at least one imaging session (i.e., Pearson correlation between trial-averaged and trial-type-concatenated ΔF/F0 (type 1) peristimulus time histograms (PSTHs) calculated using the first versus second halves of the trials >0.5) were used for further analyses.
In the experiment where we imaged the same FOV across multiple sessions in the same task context, we define the sessions as expert-early and expert-late sessions (Fig. 2). In cases where we imaged the same FOV twice over time, the 2 sessions were defined as expert-early and expert-late sessions accordingly. In cases where we imaged more than 2 sessions from the same FOV over time, the expert-early and expert-late sessions were defined for pairs of sessions. Specifically, for single neuron analyses (for example, Fig. 2e,k), we only compared the first and second imaging sessions to avoid inclusion of duplicate data points from the same session. These two sessions are defined as expert-early and expert-late sessions, respectively. For population level activity projection and decoding analyses (Fig. 2i,j), we included all the possible pairwise comparisons. For each pair, the two sessions used are defined as expert-early and expert-late sessions, respectively.
Two-photon imaging data analysis
Neurons were tested for significant trial-type selectivity during the sample, delay, and response epochs, using deconvolved activities from different trial types (non-paired two-tailed t-test, P < 0.001; correct trials only). We used the early sample epoch (first 0.83 s, 5 imaging frames), late delay epoch (last 0.67 s, 4 frames), and early response epoch (first 1.33 s, 8 frames) as the respective time windows for the statistical comparisons and all the following analyses (Extended Data Fig. 4a–c). To examine the stability of single neuron selectivity index, we first identified significantly selective neurons in each task epoch. We then determined each neuron’s preferred trial type (‘lick left’ versus ‘lick right’) using the earlier imaging session in task context 1. Next, selectivity index was calculated as the difference in activity between trial types divided by their sum (anterior versus posterior pole position for sample epoch selectivity; lick left versus lick right for delay and response epoch selectivity; correct trials only). To define preferred trial types in earlier sessions, a portion of the trials were used for statistical tests to determine significant selectivity and the preferred trial type, then independent trials were used to calculate selectivity index within the same session. We then calculated selectivity for the defined neurons in later sessions or across different task contexts.
For error trial analysis (Extended Data Fig. 2k,l), only the imaging sessions with more than ten error trials for each trial type were analysed. Selectivity was calculated as the difference in trial-averaged activity (deconvolved calcium activity) between instructed lick right and lick left trials, using correct and error trials separately. Selectivity was calculated during the early sample epoch, late delay epoch, and response epoch.
To analyse the encoding of trial types in ALM population activity, we built linear decoders that were weighted sums of ALM neuron activities to best differentiate trial types. We examined the encoding of four kinds of trial types: (1) anterior versus posterior pole position trials for stimulus encoding during the sample epoch in the tactile-instructed lick task; (2) low tone (2 kHz) versus high tone (10 kHz) for stimulus encoding during the sample epoch in the auditory-instructed lick task; (3) lick left versus lick right for lick direction encoding during the delay epoch; and (4) lick left versus lick right for lick direction encoding during the response epoch.
To build the linear decoder for a population of n ALM neurons, we found a n × 1 vector coding direction (CD) in the n dimensional activity space that maximally separates response vectors in different trial types during defined task epochs—that is, CDSample for stimulus encoding during the sample epoch, CDDelay for lick direction encoding during the delay epoch, and CDResponse for lick direction encoding during the response epoch. To estimate the CD vectors, we first computed CDt at different time points as:
where \(\bar{{\bf{x}}}\) are n × 1 trial-averaged response vectors that described the population response for each trial type at each time point, t, during the defined task epochs. Next, we averaged the CDt vectors within the defined task epoch to separately estimate the CDSample, CDDelay, and CDResponse. CDSample, CDDelay, and CDResponse were computed using 50% of trials and the remaining trials from the same session or from different sessions were used for activity projections and decoding (Fig. 2g; correct trials only).
To project the ALM population activity along the CDSample, CDDelay, and CDResponse, we computed the deconvolved activity for individual neurons and assembled their single-trial activity at each time point into population response vectors, x (n × 1 vectors for n neurons). The activity projection in Figs. 2–5 and Extended Data Figs. 3–5, 7 and 9 were obtained as CDSampleTx, CDDelayTx, and CDResponseTx.
To decode trial types using ALM population activity projected onto the CDSample, CDDelay and CDResponse (Figs. 2–5 and Extended Data Figs. 4, 5, 7 and 9), we calculated ALM activity projections (CDSampleTx, CDDelayTx and CDResponseTx) within defined time windows and we computed a decision boundary (DB) to best separate different trial types:
σ2 is the variance of the activity projection \({{\bf{CD}}}^{{\rm{T}}}{\bf{x}}\) within each trial types. Decision boundaries were computed using the same trials used to compute the CD vectors and independent trials were used to predict trial types. To examine decoding performance across task contexts, we restricted the analysis to decoders with accuracy of >0.7 within the session it was trained in (cross-validated performance). This is because if a decoder exhibited low decoding performance to begin with, its decoding performance will be generally low in other sessions due to poor training of the decoder.
To analyse activity changes along other dimensions of activity space across task contexts, we defined a ‘uniform shift (US) axis7’ using trial-type-averaged activity:
where \(\bar{{\bf{R}}}\) and \(\bar{{\bf{L}}}\) are n × 1 response vectors that described the trial-averaged population response for lick left and lick right trials at the end of the delay epoch. We separately calculated US axes for each task context change—that is, US1→2 for task context 1→2, US2→1′ for task context 2→1′, US1′→2′ for task context 1′→2′ (Extended Data Fig. 8b). For activity projections (Extended Data Fig. 8c), the US axes are further orthogonalized to the CD vectors using the Gram–Schmidt process to capture activity changes along dimensions of activity space that were not selective for lick direction (‘movement-irrelevant subspace’). We computed the US vectors using 50% of the trials and the remaining 50% of the trials were used for activity projections (Extended Data Fig. 8c). The dot products in Extended Data Fig. 8d were calculated without any orthogonalization.
Modelling
The instructed directional licking task with a delay epoch was modelled with simulations lasting for two seconds. The first second of the simulation was the sample epoch during which time trial-specific external inputs were provided and the last second was the delay epoch in which the inputs were removed. The coding direction, \({{\bf{CD}}}_{{\bf{Delay}}}\) was calculated as the difference between network activity on lick left and lick right trials at the end of the delay epoch (\(t=0\)), similar to the neural data. The trial type was always defined by instructed lick direction in different task contexts (across contingency reversals).
Recurrent neural networks
RNNs consisted of 50 units with dynamics governed by the equations
where \({r}_{i}(t)\) is the spike rate of neuron i, the synaptic time constant \(\tau \) was set equal to 200 ms, \({W}_{i,j}\) is the synaptic strength from neuron j to neuron i, \({I}_{i}^{{\rm{TT}}}(t)\) is the trial-type (TT)-dependent external input to neuron i, and \(f(x)=\tanh (x)\) is the neural activation function.
The connection matrix W was randomly initialized from a Gaussian distribution. The network was scaled to have a maximum eigenvalue equal to 0.9. To generate persistent activity, networks must have an eigenvalue greater than or equal to one. Networks initialized with eigenvalues greater than one tended to learn the task with high-dimensional persistent activity, inconsistent with ALM dynamics14. Initializing with eigenvalues less than one tended to produce lower dimensional persistent activity.
External input strengths \({I}_{i}^{{\rm{TT}}}\) were drawn from a Gaussian distribution with mean equal to zero and s.d. of 0.3. Two distinct input vectors were used for anterior \({I}_{i}^{A}\) and posterior \({I}_{i}^{P}\) pole position trials.
Behavioural readout B was given by the linear projections \(B={\sum }_{i}{r}_{i}(t=0){W}_{{\rm{out}}}^{R}-{\sum }_{i}{r}_{i}(t=0){W}_{{\rm{out}}}^{L}\), where \(t=0\) is the time at the end of the delay epoch, \({W}_{{\rm{out}}}^{R}\) and \({W}_{{\rm{out}}}^{L}\) are Gaussian random readout vectors corresponding to rightward and leftward movements, respectively.
RNNs were trained using backpropagation through time (BPTT). The input (\({I}_{i}^{{\rm{TT}}}\)) and readout weights (\({W}_{{\rm{out}}}^{R}\) and \({W}_{{\rm{out}}}^{L}\)) were fixed and only the recurrent weights \({W}_{i,j}\) internal to the RNN were trained. For each trial type, activity along the correct readout direction was trained to match a linear ramp of activity starting at the beginning of the sample epoch and the incorrect readout direction was trained to have zero activation. For task context 1, presentation of \({I}_{i}^{A}\) was associated with ramping along \({W}_{{\rm{out}}}^{L}\) and zero activation along \({W}_{{\rm{out}}}^{R}\), presentation of \({I}_{i}^{P}\) was associated with the opposite behaviour. These associations were reversed for task context 2. Networks were trained for 100 iterations.
In the RNNs, the behaviour readout relied on many units (dense \({W}_{{\rm{out}}}^{R}\) and \({W}_{{\rm{out}}}^{L}\)). Because only 2 units in the AFF networks contributed to behaviour output, this difference in readout may affect how these networks learned to produce reversed output. We therefore also tested RNNs in which we fixed the behaviour readout to only 2 units like the AFF network (sparse \({W}_{{\rm{out}}}^{R}\) and \({W}_{{\rm{out}}}^{L}\)), but all results remained unchanged.
Amplifying feedforward network
ALM circuitry contains an AFF circuit motif54. The AFF network is a recurrent circuit in which preparatory activity during the delay epoch flows through a sequence of activity states. Each activity state can be modelled as a layer within a feedforward network. In addition, the late layers in the network are connected to early layers through feedback connections. Here we develop a framework for training AFF networks to generate choice-selective persistent activity.
Before detailing the learning rules used for training AFF networks, we first introduce several features that make AFF networks advantageous for training. Training neural networks require pathways linking input units to output units for computation, and pathways linking outputs to inputs for learning. In the simplest cases, output to input feedback may interfere with the input to output computations. AFF networks, and non-normal networks in general, do not generate reverberating feedback. For this reason, it is possible to construct AFF networks that bidirectionally link inputs to outputs through separate channels that do not interfere with each other.
AFF (also commonly referred to as non-normal) networks are constructed by applying orthonormal transformations to purely feedforward networks. Orthonormal transformations to feedforward networks serve two useful anatomical purposes: (1) they form feedback connections from late layers to early layers; and (2) they form stabilizing excitatory/inhibitory connections to eliminate any reverberation that may result from the newly formed feedback connections. In this model, we use the feedback connections from late layers to early layers to convey performance feedback signals allowing the AFF network to learn via error backpropagation.
We first constructed a purely feedforward network with 4 layers referred to as input (n; 30 units), hidden layer 1 (h1; 200 units), hidden layer 2 (h2; 5 units) and output (o; 2 units) (Extended Data Fig. 11). Trial-type (TT)-dependent external inputs, \({I}_{i}^{{\rm{TT}}}(t)\), were provided only to the input layer. Feedforward connection matrices (\({W}_{i,j}^{n,{\rm{h1}}},{W}_{i,j}^{{\rm{h1,h2}}}\) and \({W}_{i,j}^{{\rm{h2}},o}\)) conveyed these inputs to downstream layers and were initialized from a uniform positive distribution. Next, we added feedback connections from o to h2 (\({W}_{j,i}^{o,{\rm{h2}}}\)) and from h2 to h1 (\({W}_{j,i}^{{\rm{h2,h1}}}\)) to provide performance feedback for training the feedforward connections. Feedback connections were matched to feedforward connections so that \({W}_{j,i}^{o,{\rm{h2}}}={W}_{i,j}^{{\rm{h2}},o}\). These feedback connections provide scaffolding to precisely implement error backpropagation to train feedforward connections. However, the presence of feedback connections in the circuit will introduce feedback to the network that will interfere with its feedforward computations.
To cancel out the reverberations caused by this feedback we incorporated additional stabilization hidden layers s1 (200 units) and s2 (5 units) (Extended Data Fig. 11). Each hidden unit in layer h1 is matched with a stabilizing neuron in the stabilization layer s1 which receives the same feedback connections as its paired excitatory neuron and projects inhibitory connections of the same strength as its excitatory partner. Similarly, each neuron in h2 has a corresponding unit in s2. Mathematically this relationship is written as
and
Because of the precisely balanced excitation and inhibition, this recurrent network is non-normal; all eigenvalues are equal to zero. This non-normal network has two independent pathways, one linking the input layer to the output layer, useful for computation; and the other linking the output layer to the input layer, useful for learning.
The network is trained using error backpropagation; an error signal is computed and then sent back into each unit in the output layer. This error signal is conveyed to the early layers by the feedback connections. The stabilizing network ensures that this error signal does not reverberate. The backpropagated signal in neuron \(i\) in the hidden layers h1 and h2 are thus given by the equations
As in error backpropagation, feedforward weights (that is, \({W}_{i,j}^{{\rm{h1,h2}}}\)) are updated by taking the product of the forward pass activity and the backward pass activity. For example, connections from neuron i in layer h1 onto neuron j in layer h2 are updated according to the rule
This rule is applied to all feedforward connections (that is, \(n\to {\rm{h1}}\), \({\rm{h1}}\to {\rm{h2}}\) and \({\rm{h2}}\to o\)). Changing the feedforward weights will necessarily disrupt the precise balance in the network. To maintain stability, the stabilizing weights must be updated to precisely cancel the changes to the feedforward weights
Compensatory weight changes based on this equation are applied to all connections in the stabilization layers (that is, \({\rm{s1}}\to {\rm{h2}}\) and \({\rm{s2}}\to o\)).
The AFF network was trained to form the same associations as the RNN. Unlike the RNN, the AFF utilized a linear neuronal activation (\(f(x)=x\)) so that dynamics are governed by the equation
Additionally, because the AFF naturally generates ramping signals54, the output units were not trained to match a ramping signal at all time points, but rather trained to be activated at a specific level at the end of the delay. For example, the target for the lick right output unit (TR) on posterior trials was TR(t = 0) = 6 and TR(t = 0) = 0 on anterior trials.
Analysis of neural dynamics within RNN and AFF networks
For each network, we calculated the selectivity of each unit as the activity difference between the lick right and lick left trials in each task context. We calculated eigenvectors of the network selectivity matrix using singular value decomposition (SVD). The data for the SVD were an n × t matrix containing the selectivity of n units over t time bins (selectivity from task contexts 1 and 2 were concatenated). Three vectors usually captured most of the network activity variance across both task contexts (Extended Data Fig. 11f). We then rotated the 3 eigenvectors so that the first vector was aligned to the dimension that maximized the difference in network selectivity matrix between task contexts 1 and 2. Network activity projected on the first vector was correlated with the network input across task contexts, thus referred to as the stimulus mode (Extended Data Fig. 12a,b). Network activity projected on the second vector was correlated with the network output across task contexts and exhibited ramping activity during the delay epoch, thus referred to as the output mode (Extended Data Fig. 12a,b).
To examine the CDDelay reorganization across task contexts as a function of stimulus mode strength (Extended Data Fig. 12c), we summed the network activity projected on the stimulus mode across time. This activity strength was normalized to the mean activity of each network to enable comparisons across different networks.
Statistics and reproducibility
The sample sizes were similar to sample sizes used in the field: for behaviour and two-photon calcium imaging, three mice or more per condition. No statistical methods were used to determine sample size. All key results were replicated in multiple mice. Mice were allocated into experimental groups according to their strain or by experimenter. Unless stated otherwise, the investigators were not blinded to mouse group allocation during experiments and outcome assessment. Trial types were randomly determined by a computer program. Statistical comparisons using t-tests and other statistical tests are described above. All statistics are two-sided unless otherwise noted. We used Pearson’s correlation for the linear regression. Error bars indicate mean ± s.e.m. unless noted otherwise. Representative images in Fig. 2c and Extended Data Fig. 2a,c,d were reproduced across all FOVs (n = 78 fields of view, 14 mice).
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
Processed data have been deposited on the DANDI (Distributed Archives for Neurophysiology Data Integration) archive and can be accessed at https://doi.org/10.48324/dandi.001188/0.240912.1925. Source data are provided with this paper.
Code availability
All analyses and statistics were performed with MATLAB R2020b using custom written code. Code used for data analysis is available at https://github.com/NuoLiLabBCM/KimEtAl2024.
References
Wolpert, D. M. & Kawato, M. Multiple paired forward and inverse models for motor control. Neural Netw. 11, 1317–1329 (1998).
Smith, M. A., Ghazizadeh, A. & Shadmehr, R. Interacting adaptive processes with different timescales underlie short-term motor learning. PLoS Biol 4, e179 (2006).
Rokni, U., Richardson, A. G., Bizzi, E. & Seung, H. S. Motor learning with unstable neural representations. Neuron 54, 653–666 (2007).
Herzfeld, D. J., Vaswani, P. A., Marko, M. K. & Shadmehr, R. A memory of errors in sensorimotor learning. Science 345, 1349–1353 (2014).
Sheahan, H. R., Franklin, D. W. & Wolpert, D. M. Motor planning, not execution, separates motor memories. Neuron 92, 773–779 (2016).
Heald, J. B., Lengyel, M. & Wolpert, D. M. Contextual inference underlies the learning of sensorimotor repertoires. Nature 600, 489–493 (2021).
Sun, X. et al. Cortical preparatory activity indexes learned motor memories. Nature 602, 274–279 (2022).
Losey, D. M. et al. Learning leaves a memory trace in motor cortex. Curr. Biol. 34, 1519–1531.e1514 (2024).
Mitz, A. R., Godschalk, M. & Wise, S. P. Learning-dependent neuronal activity in the premotor cortex: activity during the acquisition of conditional motor associations. J. Neurosci. 11, 1855–1872 (1991).
Paz, R., Boraud, T., Natan, C., Bergman, H. & Vaadia, E. Preparatory activity in motor cortex reflects learning of local visuomotor skills. Nat. Neurosci. 6, 882–890 (2003).
Vyas, S. et al. Neural population dynamics underlying motor learning transfer. Neuron 97, 1177–1186.e1173 (2018).
Tanji, J. & Evarts, E. V. Anticipatory activity of motor cortex neurons in relation to direction of an intended movement. J. Neurophysiol. 39, 1062–1068 (1976).
Kubota, K. & Hamada, I. Preparatory activity of monkey pyramidal tract neurons related to quick movement onset during visual tracking performance. Brain Res. 168, 435–439 (1979).
Li, N., Daie, K., Svoboda, K. & Druckmann, S. Robust neuronal dynamics in premotor cortex during motor planning. Nature 532, 459–464 (2016).
Gallego, J. A., Perich, M. G., Miller, L. E. & Solla, S. A. Neural manifolds for the control of movement. Neuron 94, 978–984 (2017).
Vyas, S., Golub, M. D., Sussillo, D. & Shenoy, K. V. Computation through neural population dynamics. Annu. Rev. Neurosci. 43, 249–275 (2020).
Kaufman, M. T., Churchland, M. M., Ryu, S. I. & Shenoy, K. V. Cortical activity in the null space: permitting preparation without movement. Nat. Neurosci. 17, 440–448 (2014).
Sussillo, D., Churchland, M. M., Kaufman, M. T. & Shenoy, K. V. A neural network that finds a naturalistic solution for the production of muscle activity. Nat. Neurosci. 18, 1025–1033 (2015).
Darlington, T. R. & Lisgerger, S. G. Mechanisms that allow cortical preparatory activity without inappropriate movement. eLife 9, e50962 (2020).
Vyas, S., O'Shea, D. J., Ryu, S. I. & Shenoy, K. V. Causal role of motor preparation during error-driven learning. Neuron 106, 329–339.e4 (2020).
Nudo, R. J., Milliken, G. W., Jenkins, W. M. & Merzenich, M. M. Use-dependent alterations of movement representations in primary motor cortex of adult squirrel monkeys. J. Neurosci. 16, 785–807 (1996).
Xu, T. et al. Rapid formation and selective stabilization of synapses for enduring motor memories. Nature 462, 915–919 (2009).
Yang, G., Pan, F. & Gan, W. B. Stably maintained dendritic spines are associated with lifelong memories. Nature 462, 920–924 (2009).
Peters, A. J., Chen, S. X. & Komiyama, T. Emergence of reproducible spatiotemporal activity during motor learning. Nature 510, 263–267 (2014).
Chen, S. X., Kim, A. N., Peters, A. J. & Komiyama, T. Subtype-specific plasticity of inhibitory circuits in motor cortex during motor learning. Nat. Neurosci. 18, 1109–1115 (2015).
Costa, R. M., Cohen, D. & Nicolelis, M. A. Differential corticostriatal plasticity during fast and slow motor skill learning in mice. Curr. Biol. 14, 1124–1134 (2004).
Huber, D. et al. Multiple dynamic representations in the motor cortex during sensorimotor learning. Nature 484, 473–478 (2012).
Li, C. S., Padoa-Schioppa, C. & Bizzi, E. Neuronal correlates of motor performance and motor learning in the primary motor cortex of monkeys adapting to an external force field. Neuron 30, 593–607 (2001).
Padoa-Schioppa, C., Li, C. S. & Bizzi, E. Neuronal activity in the supplementary motor area of monkeys adapting to a new dynamic environment. J. Neurophysiol. 91, 449–473 (2004).
Sadtler, P. T. et al. Neural constraints on learning. Nature 512, 423–426 (2014).
Golub, M. D. et al. Learning by neural reassociation. Nat. Neurosci. 21, 607–616 (2018).
Clancy, K. B., Koralek, A. C., Costa, R. M., Feldman, D. E. & Carmena, J. M. Volitional modulation of optically recorded calcium signals during neuroprosthetic learning. Nat. Neurosci. 17, 807–809 (2014).
Driscoll, L. N., Duncker, L. & Harvey, C. D. Representational drift: emerging theories for continual learning and experimental future directions. Curr. Opin. Neurobiol. 76, 102609 (2022).
Driscoll, L. N., Pettit, N. L., Minderer, M., Chettih, S. N. & Harvey, C. D. Dynamic reorganization of neuronal activity patterns in parietal cortex. Cell 170, 986–999.e916 (2017).
Rule, M. E., O’Leary, T. & Harvey, C. D. Causes and consequences of representational drift. Curr. Opin. Neurobiol. 58, 141–147 (2019).
Chestek, C. A. et al. Single-neuron stability during repeated reaching in macaque premotor cortex. J. Neurosci. 27, 10742–10750 (2007).
Ganguly, K. & Carmena, J. M. Emergence of a stable cortical map for neuroprosthetic control. PLoS Biol. 7, e1000153 (2009).
Katlowitz, K. A., Picardo, M. A. & Long, M. A. Stable sequential activity underlying the maintenance of a precisely executed skilled behavior. Neuron 98, 1133–1140.e1133 (2018).
Jensen, K. T., Kadmon Harpaz, N., Dhawale, A. K., Wolff, S. B. E. & Olveczky, B. P. Long-term stability of single neuron activity in the motor system. Nat. Neurosci. 25, 1664–1674 (2022).
Gallego, J. A., Perich, M. G., Chowdhury, R. H., Solla, S. A. & Miller, L. E. Long-term stability of cortical population dynamics underlying consistent behavior. Nat. Neurosci. 23, 260–270 (2020).
Guo, Z. V. et al. Flow of cortical activity underlying a tactile decision in mice. Neuron 81, 179–194 (2014).
Li, N., Chen, T. W., Guo, Z. V., Gerfen, C. R. & Svoboda, K. A motor cortex circuit for motor planning and movement. Nature 519, 51–56 (2015).
Hao, Y., Thomas, A. N. & Li, N. Fully autonomous mouse behavioral and optogenetic experiments in home-cage. eLife 10, e66112 (2021).
Bollu, T. et al. Cortex-dependent corrections as the tongue reaches for and misses targets. Nature 594, 82–87 (2021).
Xu, D. et al. Cortical processing of flexible and context-dependent sensorimotor sequences. Nature 603, 464–469 (2022).
Marshel, J. H. et al. Cortical layer-specific critical dynamics triggering perception. Science 365, eaaw5202 (2019).
Sheintuch, L. et al. Tracking the same neurons across multiple days in Ca2+ imaging data. Cell Rep. 21, 1102–1115 (2017).
Friedrich, J., Zhou, P. & Paninski, L. Fast online deconvolution of calcium imaging data. PLoS Comput Biol. 13, e1005423 (2017).
Cunningham, J. P. & Yu, B. M. Dimensionality reduction for large-scale neural recordings. Nat. Neurosci. 17, 1500–1509 (2014).
Druckmann, S. & Chklovskii, D. B. Neuronal circuits underlying persistent representations despite time varying activity. Curr. Biol. 22, 2095–2103 (2012).
Svoboda, K. & Li, N. Neural mechanisms of movement planning: motor cortex and beyond. Curr. Opin. Neurobiol. 49, 33–41 (2018).
Sussillo, D. & Abbott, L. F. Generating coherent patterns of activity from chaotic neural networks. Neuron 63, 544–557 (2009).
Goldman, M. S. Memory without feedback in a neural network. Neuron 61, 621–634 (2009).
Daie, K., Fontolan, L., Druckmann, S. & Svoboda, K. Feedforward amplification in recurrent networks underlies paradoxical neural coding. Preprint at bioRxiv https://doi.org/10.1101/2023.08.04.552026 (2023).
Colgin, L. L., Moser, E. I. & Moser, M. B. Understanding memory through hippocampal remapping. Trends Neurosci. 31, 469–477 (2008).
Ziv, Y. et al. Long-term dynamics of CA1 hippocampal place codes. Nat. Neurosci. 16, 264–266 (2013).
Schoonover, C. E., Ohashi, S. N., Axel, R. & Fink, A. J. P. Representational drift in primary olfactory cortex. Nature 594, 541–546 (2021).
Chen, S. et al. Brain-wide neural activity underlying memory-guided movement. Cell 187, 676–691.e16 (2024).
Guo, Z. V. et al. Maintenance of persistent activity in a frontal thalamocortical loop. Nature 545, 181–186 (2017).
Thomas, A. et al. Superior colliculus bidirectionally modulates choice activity in frontal cortex. Nat. Commun. 14, 7358 (2023).
Zhu, J., Hasanbegovic, H., Liu, L., Gao, Z. & Li, N. Activity map of a cortico-cerebellar loop underlying motor planning. Nat. Neurosci. 26, 1916–1928 (2023).
Li, N. & Mrsic-Flogel, T. D. Cortico-cerebellar interactions during goal-directed behavior. Curr. Opin. Neurobiol. 65, 27–37 (2020).
Albus, J. S. A theory of cerebellar function. Math. Biosci. 10, 25–61 (1971).
Marr, D. A theory of cerebellar cortex. J. Physiol. 202, 437–470 (1969).
Guo, Z. V. et al. Procedures for behavioral experiments in head-fixed mice. PloS ONE 9, e88678 (2014).
Slotnick, B. A simple 2-transistor touch or lick detector circuit. J. Exp. Anal. Behav. 91, 253–255 (2009).
Li, N. et al. Spatiotemporal constraints on optogenetic inactivation in cortical circuits. eLife 8, e48622 (2019).
Mangin, E. N., Chen, J., Lin, J. & Li, N. Behavioral measurements of motor readiness in mice. Curr. Biol. 33, 3610–3624.e3614 (2023).
Mathis, A. et al. DeepLabCut: markerless pose estimation of user-defined body parts with deep learning. Nat. Neurosci. 21, 1281–1289 (2018).
Pachitariu, M. et al. Suite2p: beyond 10,000 neurons with standard two-photon microscopy. Preprint at bioRxiv https://doi.org/10.1101/061507 (2016).
Chen, T. W., Li, N., Daie, K. & Svoboda, K. A map of anticipatory activity in mouse motor cortex. Neuron 94, 866–879.e864 (2017).
Acknowledgements
The authors thank S. Lisberger, J. Yau, D. Herzfeld, H. Inagaki, M. Economo, D. Lipshutz, D. Ji and members of the Li laboratory for comments on the manuscript and insightful discussions. This work was funded by the Pew Scholars Program, NIH NS112312, NS113110, NS131229, NS132025, McKnight Foundation, and Simons Collaboration on the Global Brain. J.-H.K. is supported by National Research Foundation of Korea (RS-2023-00238217). K.D. is supported by Allen Institute for Neural Dynamics. Diagrams in Fig. 1 were created with BioRender.com.
Author information
Authors and Affiliations
Contributions
J.-H.K. and N.L. conceived and designed the experiments. J.-H.K. performed the experiments. J.-H.K. analysed data. K.D. performed modelling. J.-H.K., K.D. and N.L. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Chunyu Duan, Reza Shadmehr and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer review reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Behavioral analysis, behavioral training, and experimental timeline.
a. Top left, representative video frame with automatically labeled tongue markers using DeepLabCut. Top middle, superimposed tongue tip trajectories and x and y velocities of individual lick events during lick left (red) and lick right (blue). Data from an example mouse across sessions within the same task context. Tongue tip trajectory scale bar, 4 pixels (x) and 6 pixels (y). X velocity scale bar, 12 ms and 2 pixels/s. Y velocity scale bar, 12 ms and 1.5 pixels/s. Top right, scatter of averaged pairwise similarity of single lick events (Pearson’s correlation) calculated within session versus across sessions. Data from two mice. Bottom, same as top but for data across task contexts 1 and 2. b. Same as a, but for jaw marker analysis. Jaw tip trajectory scale bar, 4 pixels (x) and 4 pixels (y). X velocity scale bar, 12 ms and 1 pixels/s. Y velocity scale bar, 12 ms and 1.5 pixels/s. c. Left, schematics of learning speed under two models. Context-specific saving effect (top): faster re-learning only for previously learned tasks. Context non-specific saving effect (bottom): faster learning each time. Right, faster reversal learning is consistent with a context-specific saving effect. Re-learning of task context 2’ is significantly faster than initial learning of task context 2 (top). P = 0.0487, paired t-test. Circles indicate individual mice (N = 13 mice). Crosses indicate mean ± s.e.m. We examine task context 2 because the initial learning of task context 1 is confounded by the exposure to home-cage training. To examine context non-specific saving effect, we compare the speed of re-learning task context 1’ versus re-learning task context 2’ (bottom). The two conditions have similar task-specific prior training. No significant difference is observed. P = 0.3425, two-tailed paired t-test. d. Same as Fig. 1i, but separately plotting photoinhibition results for task context 1 (left) and task context 2 (right). e. Experimental timeline of an example mouse imaged within the same task context over extended time. Black, behavior training in automated home-cage. Gray, habituation in two-photon setup. Red, calcium imaging in two-photon setup. All the trials are concatenated. Black triangle indicates the end of learning voluntary head-fixation and start of learning in tactile instructed licking task. Averaging window, 100 trials. f. Same as e, but for two mice imaged across different task contexts. g. Summary plot of experimental timeline from all GP4.3 mice used for imaging in this study. h-i. Behavior performance curves for the initial learning from GP4.3 mice (h, n = 15 mice, all were trained in automated home-cage) and Slc17a7-Cre x Ai148 mice (i, n = 11 mice, 7 mice were trained in automated home-cage and 4 mice were manually trained). Different colors represent individual mice. Circles indicate end of the learning curves for GP4.3 mice and termination of training for Slc17a7-Cre x Ai148 mice. j. Behavior performance within imaging sessions across 4 segments of trials. Thin gray lines indicate individual sessions. Thick black lines indicate mean ± s.e.m. Data from Fig. 2b.
Extended Data Fig. 2 Preprocessing of imaging data and ALM preparatory activity.
a. Mean two-photon fluorescence images from the same field of view (FOV) across 3 imaging sessions (Day 1, 17, and 60). b. Left, cranial windows from two example mice. Each black box indicates one imaging FOV (600 × 600 µm). Right, all imaging FOVs (n = 50 from 8 mice). Imaging FOVs cover ALM, defined as the area where photoinhibition during the delay epoch impairs behavior performance (dotted red line41) and exhibiting enriched choice selectivity (gray71). c. Spatial footprints of individual neurons from the same FOV across 3 imaging sessions, which are the output of Suite2p (Methods). d. Identified co-registered neurons (green) across 3 imaging sessions, which are computed by CellReg (Methods). e. The number of neurons from the expert-early session (n = 1,690 ± 758, mean ± SD), expert-late session (n = 1,704 ± 777), and matched neurons in both expert-early and expert-late sessions (n = 855 ± 402). 12.80 ± 8.90 (mean ± SD) days between imaging sessions. Data from Fig. 2. f. Fraction of match neurons across individual mice. Dots, individual FOVs. Error bars, mean ± SD. g. Distribution of centroid distance (left) and spatial footprint correlation (right) from nearest neighboring neuronal pairs (green) and other neighboring neuronal pairs within 10 µm (red). Centroid distance and spatial footprint correlation are parameters used to define co-registered neurons across imaging sessions used by CellReg package. Data from the same FOV in a, c, d. h. Density map between centroid distance and spatial footprint correlation from all co-registered neurons (n = 42,739 from 8 mice). Data from Fig. 2. i. Distribution of registration score from all co-registered neurons (n = 42,739 from 8 mice). j. dF/F0 activity (left), deconvolved activity (middle), and heatmap of single trial deconvolved activity (right) from two example neurons. Thick lines represent the mean; thin lines represent single trials. k. Single trial deconvolved activity (top) and peristimulus time histograms (PSTH, bottom) for correct and error trials are shown for three example ALM neurons. Trial types are based on instructed lick direction (blue, lick right; red, lick left). Correct trials, solid lines. Error trials, dotted lines. mean ± s.e.m. l. Top, comparison of individual neuron trial-type selectivity between correct and error trials. Neurons with significant trial-type selectivity (P < 0.001, two-tailed t-test). Selectivity is the difference in deconvolved activity between instructed lick right and lick left trials during the early sample epoch (left), late delay epoch (middle), and response epoch (right). On error trials, when mice licked in the opposite direction to the instruction provided by object location (Fig. 2a), a majority of ALM neurons switched their trial type preference to predict the licking direction during the delay and response epochs, as indicated by the negative correlations (R, Pearson’s correlation). Bottom, histogram of selectivity angle between correct and error trials. A negative angle indicates neuron switching selectivity on error trials. Bin size: 2°.
Extended Data Fig. 3 Activity drift in individual neurons and population activity.
a. Quantification of PSTH stability. Pearson’s correlation between PSTHs of individual neurons from different imaging sessions (expert-early and expert-late). b. Relationship between PSTH stability and weight contribution to the CDDelay. Dots, individual neurons. Red neurons (n = 3,542) are the top 10% weight contributors to the CDDelay. Black neurons (n = 31,878) are the remaining 90% of neurons. c. Probability density functions of PSTH correlation for the top 10% weight contributors (red) and the other neurons (black). P = 2.85 × 10−114, two-sample Kolmogorov-Smirnov test, two-tailed test. d. Pearson’s correlation between vectors of concatenated PSTHs across the whole population as a function of delta days between expert-early and expert-late imaging sessions. Different colors represent different mice. Dotted lines indicated linear regressions of individual mice across days. e. Same as d, but for population activity vectors projected onto the CDDelay. f. R values of linear regressions of individual mice in panels d and e. P = 0.0156, two-tailed paired t-test. Data from Fig. 2 (50 fields of view from 8 mice); mean ± s.e.m.
Extended Data Fig. 4 Task-related activity during the sample, delay, and response epochs within the same task context.
a-c. Analysis time window to estimate coding direction in different task epochs. Early sample epoch (a, CDSample), late delay epoch (b, CDDelay), and early response epoch (c, CDResponse) were used, respectively. d-f. Scatter plots and histograms of individual neuron selectivity index during the sample (d), delay (e), and response epoch (f) comparing expert-early and expert-late sessions. Colors indicate neurons with significant trial-type selectivity (P < 0.001, two-tailed t-test) during specific epochs in expert-early sessions. Neurons are colored based on their preferred trial-type in expert-early sessions. Green, neurons preferring anterior pole position. Purple, neurons preferring posterior pole position. Red, neurons preferring lick left. Blue, neurons preferring lick right. Gray, no preference neurons. Pearson’s correlation, sample epoch, R = 0.9404, P = 0 (d); delay epoch, R = 0.8861, P = 0 (e); response epoch, R = 0.9001, P = 0 (f). g. Same as Fig. 2h, but from the example FOV projected on the CDSample trained on day 1 (top) or day 23 (bottom) and tested on day 1 (left) or day 23 (right). h. Same as Fig. 2h (for CDDelay) replotted here for comparison. i. Same as Fig. 2h, but for CDResponse. j-l. Trial-averaged ALM activities projected on the CDSample (j), CDDelay (k), and CDResponse (l) from the same session (left) and across different sessions (right). Thin lines represent individual sessions. Thick lines represent the mean. m-o. Same as Fig. 2i, but for CDSample (m), CDDelay (n), and CDResponse (o). P = 0.4203 (o), P = 0.4870 (n), P = 0.0886 (o), R values of linear regression, two-tailed t-test against 0. p-r. Same as Fig. 2j, but for CDSample (p, n = 111 pairs of sessions, 8 mice), CDDelay (q, n = 113 pairs of sessions, 8 mice), and CDResponse (r, n = 123 pairs of sessions, 8 mice).
Extended Data Fig. 5 Task-related activity during the sample, delay, and response epochs across different tasks contexts.
a-c. Same as Fig. 3c, but sorting the same neuronal population based on their selectivity during the sample epoch (a, n = 1,043), delay epoch (b, n = 1,112), and response epoch (c, n = 654) in task context 1 (top) or task context 2 (bottom). a, b, and c contain different fields of views. d-f. Scatter plots and histograms of individual neuron selectivity index during the sample (d), delay (e), and response epoch (f) comparing task contexts 1 and 2. Colors indicate neurons with significant trial-type selectivity (P < 0.001, two-tailed t-test) during specific epochs in task context 1. Neurons are colored based on their preferred trial-type in task context 1. Green, neurons preferring anterior pole position. Purple, neurons preferring posterior pole position. Red, neurons preferring lick left. Blue, neurons preferring lick right. Gray, no preference neurons. Pearson’s correlation, sample epoch, R = 0.8707, P = 0 (d); delay epoch, R = −0.0057, P = 0.6774 (e); response epoch R = 0.6804, P = 0 (f). g-i. Same as Fig. 3f, but for CDSample (g), CDDelay (h), and CDResponse (i). j-l. Trial-averaged ALM activities projected on the CDSample (j), CDDelay (k), and CDResponse (l) within the same task context (left) and across different task contexts. m-o. Same as Fig. 3g, but for CDSample (m, n = 55 pairs of sessions, 10 mice), CDDelay (n, n = 58 pairs of sessions, 10 mice), and CDResponse (o, n = 58 pairs of sessions, 10 mice). p. Schematic of calculating Euclidean distance between selectivity index vectors. q. Euclidean distance between the delay epoch selectivity vectors calculated within task context (1 vs. 1) and across task contexts (1 vs. 2). Selectivity vectors within task context are calculated using split-half trials from the same session. ***P = 4.03 × 10−20, two-tailed paired t-test. Mean ± s.e.m. r. Euclidean distance of sample, delay, and response epoch selectivity vectors across task contexts (1 vs. 2). Sample vs. delay epoch, ***P = 9.21 × 10−13; delay vs. response epoch, ***P = 1.71 × 10−12, two-tailed paired t-test. Mean ± s.e.m.
Extended Data Fig. 6 Individual variability across mice in the degree of CDDelay reorganization across task contexts.
a. Data from Fig. 3g, but broken out by individual mice, sorted by mean decoding accuracy across task contexts (train context 1 and test context 2). Individual mice are plotted separately in different colors. b. Dot product between CDDelay within the same task context (left) and across different task contexts (right). Individual mice are sorted by mean dot product of CDDelay across task contexts. Same color scheme as a. Note that variability across mice is much higher than variability across FOVs within the same mouse. Numbers in brackets indicate pairs of sessions for each mouse. c. Left, decoding accuracy of the CDDelay, CDSample, and CDResponse across task contexts. Right, decoding accuracy of the CDDelay, normalized by that of CDSample and CDResponse. Arrows indicate two outlier data points (y-axis values, 1.93 and 2.23). d-e. Same as Fig. 3f (top), but data from an example FOV of a mouse with stable CDDelay across task contexts (c, JH118; see a-b) and a mouse with reversed CDDelay (d, JH123; see a-b). f. Displacement of x and y jaw positions in task contexts 1 and 2 from two example mice. Mean ± SD across trials. g. No relationship between decoding accuracy of CDDelay across task contexts (x axis) versus 7 parameters (y axis) as follows: delta days between imaging sessions; matched number of neurons co-registered across imaging sessions; number of correct trials from task context 1; behavior performance from task context 1; relative learning speed to reach 75% behavior performance (number of trials to reach criterion performance in task context 2 relative to task context 1); relative AP location of imaging FOVs after subtracting mean AP location of each mouse; relative ML location of imaging FOVs after subtracting mean ML location of each mouse.
Extended Data Fig. 7 Task-related activity during the sample, delay, and response epochs across task context 1, 2, and 1’.
a. Mean deconvolved activities from an example field of view across three task contexts (n = 781 neurons). b. Scatter plots and histograms of individual neuron selectivity index during the sample epoch comparing task contexts 1 and 2 (left) or task contexts 1 and 1’ (right). Colors indicate neurons with significant trial-type selectivity (P < 0.001, two-tailed t-test) during specific epochs in expert-early sessions. Neurons are colored based on their preferred trial-type in task context 1. Green, neurons preferring anterior pole position. Purple, neurons preferring posterior pole position. Gray, no preference neurons. Pearson’s correlation, task context 1 vs. 2, R = 0.8912, P = 0; task context 1 vs. 1’, R = 0.8290, P = 0. c-f. Same as Fig. 4f–i, but for activity during the sample epoch. In d and f, gray circles and lines indicate FOVs imaged across task contexts 1, 2, and 1’ (n = 24 FOVs, 5 mice); black circles and lines indicate subset of FOVs imaged across task contexts 1, 2, 1’, and 2’ (n = 5 FOVs, 2 mice). Bar/errorbar, mean/s.e.m. g-l. Same as a-f, but for activity during the delay epoch. h, red indicates neurons preferring lick left and blue indicates neurons preferring lick right in task context 1. Pearson’s correlation, task context 1 vs. 2, R = −0.1224, P = 1.38 × 10−8; task context 1 vs. 1’, R = 0.7675, P = 0. In j and l, FOVs imaged across task contexts 1, 2, and 1’ (n = 26 FOVs, 5 mice); FOVs imaged across task contexts 1, 2, 1’, and 2’ (n = 7 FOVs, 3 mice). Data from Fig. 4, replotted here for comparison. Bar/errorbar, mean/s.e.m. m-r. Same as g-l, but for activity during the response epoch. n, Pearson’s correlation, task context 1 vs. 2, R = 0.6220, P = 0; task context 1 vs. 1’, R = 0.7624, P = 0. In p and r, FOVs imaged across task contexts 1, 2, and 1’ (n = 26 FOVs, 5 mice); FOVs imaged across task contexts 1, 2, 1’, and 2’ (n = 5 FOVs, 3 mice). Bar/errorbar, mean/s.e.m.
Extended Data Fig. 8 Neural activity change in movement-irrelevant activity subspace across task contexts.
a. Schematic of activity changes across task contexts along coding directions (top, CDDelay, estimated from task contexts 1 and 2) and movement-irrelevant subspace (bottom, USDelay, estimated from task context 1→2 and 2→1’). b. Formula to calculate the CDDelay’s and the USDelay’s. CDDelay’s are calculated separately for each task context. USDelay’s are calculated separately for each task context change. c. Activity of an example FOV across 4 task contexts (1, 2, 1’, and 2’). Top, activity projections on the CDDelay’s. The CDDelay of task context 2 is orthogonalized to the CDDelay of task context 1 here for visualization purposes. Similar patterns of activity are re-activated in the same task context (1 vs. 1’ and 2 vs. 2’). Big solid circles represent the mean; small transparent circles represent activity in single trials. Bottom, activity projections on the USDelay’s. In contrast to the activity along the CDDelay’s, activity along the USDelay’s does not show reliable re-activation in the same context. d. Dot products (mean ± s.e.m.) between the CDDelay’s and USDelay’s (n = 9 fields of view, 3 mice). Activity along the coding directions shows reliable re-activation (consistent CDDelay’s for task context 1 vs. 1’ and 2 vs. 2’). Activity in the movement-irrelevant subspace does not show consistent changes across re-learning of previous task contexts (1→2 vs. 2→1’ and 1→2 vs. 1’→2’). e. Decoding accuracy of the CDDelay and USDelay to predict lick directions (58 pairs of imaging sessions, 10 mice). Bar/errorbar, mean/s.d. ***P = 5.64 × 10−39, two-tailed paired t-test. Activity projection on the USDelay does not predict lick direction.
Extended Data Fig. 9 Task-related activity during the sample, delay, and response epochs across task context 1, 2, and 3.
a-b. Same as Fig. 5e,f, but for activity during the sample epoch (n = 4 fields of view, 2 mice). Bar/errorbar, mean/s.e.m. c-d. Same as Fig. 5e,f, replotted here for comparison. Bar/errorbar, mean/s.e.m. e-f. Same as Fig. 5e,f, but for activity during the response epoch (n = 8 fields of view, 3 mice). Bar/errorbar, mean/s.e.m.
Extended Data Fig. 10 Context-specific preparatory activity retains memory trace of previous learning and reduces interference.
a. Schematic of the memory trace. ALM preparatory activity from task contexts 1, 2, and 1’ is projected onto the CDDelay from task context 2. Memory trace is defined as a selectivity increase along the CDDelay for task context 2 during performance of task context 1’, as shown in black arrows combining blue and red arrows. b. Memory trace. Change in delay epoch selectivity along the CDDelay for task context 2 from task context 1 to 1’. Bar/errorbar, mean/s.e.m. **P = 0.005, two-tailed paired t-test. c. Decoding accuracy of the CDDelay for task context 2 tested on task contexts 1 (52.75 ± 5.24%) and 1’ (58.66 ± 4.63%). Cross, mean ± s.e.m. *P = 0.0199, two-tailed paired t-test. 26 fields of view from 5 mice. d. Speed of re-learning task context 1’ as a function of the CDDelay reorganization across task contexts 1 and 2. Number of trials to reach criterion performance in task context 1’ relative to number of trials during the initial learning of task context 1. Mice exhibiting more distinct CDDelay’s across task contexts (i.e. lower dot product) re-learned the previously learned task context 1’ faster (i.e. fewer trials to reach 75% performance criterion). Each dot shows one field of view from one mouse. Dotted line, linear regression; R, Pearson’s correlation.
Extended Data Fig. 11 Recurrent neural network (RNN) and amplifying feedforward (AFF) network models.
a. A schematic of RNN model with sparse readout. Only two internal units directly contribute to the output. b-c. Same as Fig. 6c,d, but for RNNs with sparse readout. d. A schematic of the AFF networks and governing equations. e. Analysis of the AFF network similar to Daie et al.54. We identified directions in activity space at different time points that influence network activity along the CDDelay at the end of the delay epoch (t = 0 s). We refer to these as transitional directions. The plot shows correlation between transitional directions at time point t vs time point t’ for all sample and delay epoch time points. AFF networks generate persistent activity by passing activity through a chain of network states, where early layers influence activity in the late layers. This results in network activity sequentially traversing multiple directions in activity space, as indicated by the low correlation values off diagonal. f. Dimensionality of trial-type selectivity in the AFF networks. 3 dimensions captured most of the network selectivity. g. Resetting AFF network hidden layer weights to random values before re-learning task context 1’. h. Resetting synaptic weights before re-learning task context 1’ prevented the re-activation of the CDDelay. Weight contribution of the AFF units to the CDDelay’s from task contexts 1 and 1’.
Extended Data Fig. 12 Neural dynamics within RNN and AFF networks.
a. AFF network activity projected on the stimulus mode (top), output mode (middle), and in state space (bottom). Trial types are defined by lick direction. Blue, lick right. Red, lick left. See Methods for decomposition of network activity modes. AFF networks exhibit persistent activity along the stimulus mode, which combines with the ramping output mode to produce distinct CDDelay’s in each task context (yellow arrows). b. Same as a, but for RNN. RNNs do not maintain persistent activity along the stimulus mode, which results in stable CDDelay’s across task contexts that are aligned to the output mode. c. The strength of network activity along the stimulus mode predicts the degree of CDDelay reorganization across task contexts (dot product of the CDDelay’s from task contexts 1 and 2). Dots, individual randomly initialized AFFs. R and P values, Pearson’s correlation. d. Neural data. Individual variability of CDDelay reorganization across task contexts is predicted by the strength of stimulus activity in ALM. The strength of ALM stimulus activity is quantified as the decoding accuracy of the CDSample in task context 1 (trained and tested within task context), or the fraction of neurons with significant trial-type selectivity during the sample epoch in task context 1. Dots, individual FOVs. Individual mice are plotted separately in different colors. R and P values, Pearson’s correlation.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Kim, JH., Daie, K. & Li, N. A combinatorial neural code for long-term motor memory. Nature 637, 663–672 (2025). https://doi.org/10.1038/s41586-024-08193-3
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41586-024-08193-3