Main

Natural enzymes are exceptionally versatile, selective and highly efficient catalysts. Yet, computational design of enzymes that match this proficiency, particularly for non-natural reactions, remains elusive11. Recent advances in computational design have enabled rapid and effective optimization of natural enzyme stability, expressibility, catalytic rate and selectivity through fully computational workflows12,13. Furthermore, advances in fold design enabled the grafting of natural or engineered active sites into idealized de novo backbones14,15. By contrast, enzymes designed de novo, that is, without recourse to naturally occurring enzymes that catalyse the same reaction, were orders of magnitude less active relative to comparable natural ones1,2,3,4,5,11. Previous studies have therefore used repeated cycles of laboratory evolution, involving high-throughput screening of mutants, to reach effective enzymes5,6,7,8,9. Such cycles are inefficient and are restricted to reactions that can be assayed in medium-to-high-throughput fashion11. Critically, continuing to rely on large-library screening of random mutants suggests that our understanding and control of the fundamentals of biocatalysis are far from complete.

The Kemp elimination (KE) reaction (Fig. 1a), a prototype for natural base-catalysed proton abstraction, has long served as a model for studying de novo enzyme design, as no natural enzyme is known to have been evolved for this reaction. Despite increasing sophistication in protein design methods, computationally designed Kemp eliminases exhibited low catalytic efficiencies and rates (kcat/KM 1–420 M−1 s−1 and kcat 0.006–0.7 s−1, respectively)1,3 and required further optimization by iterative mutational library screening to achieve catalytic parameters comparable to7 or above6 the median values of enzymes in nature (kcat/KM 105 M−1 s−1, kcat 10 s−1)16.

Fig. 1: Key steps in the design workflow.
figure 1

a, KE of 5-nitrobenzisoxazole. ‘B’ is a base, implemented as the sidechain of Asp or Glu. b, Thousands of backbones are generated through combinatorial backbone assembly (step 1) and stabilized using PROSS29 (step 2, red spheres). Geometric matching43 and active-site (purple spheres) optimization with Rosetta yield millions of designs that are filtered by balancing energy terms that contribute to stability and activity (step 3). A few dozen top designs are chosen for further core (green spheres) and active-site stabilization (step 4). Following experimental screening (step 5), we apply FuncLib28 to the active sites of select functional designs (step 6). Illustrations in b (step 5) were created using BioRender (https://biorender.com).

Full size image

The underlying reasons for the low efficiencies of de novo designed enzymes have been intensely studied10,17,18,19. These analyses revealed that the designed active sites exhibited significant structural distortions relative to the design conception17,19. Notably, catalysis is extremely sensitive to molecular details, and shifts of the catalytic constellation by a few degrees or tenths of an Ångstrom from optimality may translate into orders of magnitude decreases in efficiency20. Furthermore, designs often exhibited low stability and expressibility7, limiting their ability to accommodate activity-enhancing mutations7,21. Further concerns were that fixed-backbone design methods fail to precisely position non-native catalytic groups1; the molecular details of the designed transition state (theozyme) were uncertain6,22; and that protein dynamics23 and long-range electrostatic interactions may be necessary to achieve high catalytic efficiency but are unaccounted for in the design process6,24,25.

Recent analyses suggested that overcoming the shortcomings of de novo enzyme design methodology may require artificial intelligence-based approaches, more accurate physics-based energetics and data from high-throughput screening11,26. Here, we test whether recent developments in atomistic protein design that allow accurate backbone27 and sequence28,29 design in natural protein folds address the limitations of de novo enzyme design methodology without resorting to experimental optimization or big-data analyses. To directly compare with previous design approaches, we apply the strategy to the KE reaction and generate enzymes that rival laboratory-evolved eliminases without recourse to high-throughput screening or iterative mutagenesis.

Designing stability, foldability and activity

Our working hypothesis is that effective enzyme design demands control over all protein degrees of freedom to establish stability, foldability and accurate positioning of the theozyme. Foldability, the ability of the protein to fold uniquely into the design conception, has been a long-standing challenge for de novo enzyme design. Over the past decade, foldability has been partly addressed through de novo fold design, enabling the generation of numerous stable and accurately designed proteins30,31,32,33. These design methods, however, maximize foldability, generating backbones that are dominated by ideal secondary structure elements that lack the non-ideal elements that may lower foldability but are nonetheless needed for sophisticated functions12,34. Until now, functionalizing de novo generated folds has produced enzymes that exhibited rates (kcat) well below 1 s−1. In certain cases, de novo designs exhibited high catalytic efficiencies (104 to 105 M−1 s−1)15,35 but only through very low KM values (0.3–30 µM). Low KM values indicate tight binding of the substrate in its ground state, suggesting that the designs optimize molecular recognition of their substrates before the catalytic step. By contrast, turnover numbers (kcat) reflect the chemical transformation following substrate binding and are a more stringent test of the ability to design high-efficiency catalysts rather than effective binders36. The persistently low kcat values, including in recent studies15,35, highlight the challenge of achieving catalytic control in enzyme design.

Given these limitations, we focused on the TIM-barrel fold, which is one of the most prevalent protein folds found among enzymes37,38. In this fold, the residues of the central β barrel are oriented towards the active-site cavity, providing many opportunities for optimally placing the catalytic and substrate-binding groups. We reasoned that despite the challenges in designing accurate and functional TIM barrels39,40, this fold provides an attractive framework for engineering new enzymatic functions.

We developed a computational method that can be applied, in principle, to any reaction, given a precomputed theozyme. The workflow starts by generating thousands of backbones using combinatorial assembly and design (Fig. 1b, step 1), which combines fragments from homologous proteins to generate new backbones27,41,42. Subsequently, Protein Repair One Stop Shop (PROSS) design calculations are applied to stabilize the designed conformation29 (Fig. 1b, step 2). The resulting structures show backbone variations within the active-site pocket, increasing the likelihood of obtaining foldable backbones that position the theozyme and supporting residues in a catalytically competent and energetically relaxed constellation. Following backbone generation, we implement geometric matching43 to position the KE theozyme in each of the designed structures and optimize the remainder of the active site using Rosetta atomistic calculations44, in effect mutating all active-site positions, including the vestigial catalytic residues of the natural enzyme (Fig. 1b, step 3). The workflow results in millions of designs which are filtered using a ‘fuzzy-logic’ optimization objective function45. This approach balances potentially conflicting objectives that are critical for design of function, such as low system energy and high desolvation of the catalytic base. Selecting a few dozen top-scoring designs, we next stabilize the active site and positions in the protein core46 (Fig. 1b, step 4), resulting in designs with more than 100 mutations from any natural protein. Unlike previous approaches, this workflow emphasizes stability across the entire protein. It capitalizes on the ability to generate thousands of stable, natural-like TIM barrels that exhibit backbone diversity in the active site27 and on automated scaffold29 and active-site28 sequence design methods that have been validated on dozens of natural enzymes12.

Efficient, stable and accurate Kemp eliminases

We applied our pipeline to the indole-3-glycerol-phosphate synthase (IGPS) enzyme family, which can sterically accommodate the 5-nitrobenzisoxazole substrate and was previously used to design Kemp eliminases1,7. The theozyme builds on a catalytic constellation derived from quantum-mechanical calculations47,48. It includes a nucleophile, such as Asp or Glu, which serves as a base for proton abstraction from the substrate, and an aromatic sidechain that forms π-stacking interactions with the substrate in the transition state (Fig. 1b, step 3). The latter interaction has been used in all previous computational Kemp eliminase design studies to promote binding to the aromatic benzisoxazole rings1,3. Typical design studies also introduced a polar interaction with the isoxazole oxygen to stabilize the developing negative charge in the transition state1,3. We excluded this requirement from our theozyme because a water molecule can satisfy it, and a misplaced polar group could reduce reactivity by lowering the pKa of the catalytic base.

We selected 73 designs for experimental testing. The designs ranged from 245 to 268 amino acids and were diverse, with 30–93% sequence identity to one another and 41–59% identity to any natural protein. In total, 66 designs were solubly expressed and 14 showed cooperative thermal denaturation (Extended Data Fig. 1). Three designs showed measurable KE activity in an initial screen, with the top two designs, Des27 and Des61, exhibiting kcat/KM values of 130 and 210 M−1 s−1, respectively, and kcat < 1 s−1 (Extended Data Fig. 2, Extended Data Table 1 and Supplementary Table 1).

The catalytic rate and efficiency of these designs are on a par with previously designed enzymes1,3, falling short by several orders of magnitude from comparable natural eliminases and from designed Kemp eliminases that were optimized through laboratory-evolution campaigns6,7. To optimize these designs computationally, we applied FuncLib to active-site positions, excluding the theozyme residues. The FuncLib method restricts amino acid mutations to those likely to appear in the natural diversity of homologous proteins28. To develop an optimization strategy for a de novo reaction, we removed all homology-based restrictions in the active site, thus using atomistic energy as the sole optimization objective function. We selected 6 and 12 low-energy designs for experimental testing for Des61 and Des27, respectively, each comprising 5–8 specific mutations relative to their origin. All designs exhibited high expression yields and showed cooperative denaturation (Extended Data Fig. 1 and Supplementary Table 1). One design derived from Des61 showed catalytic efficiency of 3,600 M−1 s−1 and kcat of 0.85 s−1. Remarkably, eight designs on the basis of Des27 showed increased catalytic rates by 10–70-fold (Extended Data Table 1 and Supplementary Table 1), with Des27.7, harbouring seven mutations relative to Des27, reaching kcat/KM 12,700 M−1 s−1 and kcat 2.85 s−1, a rate that is an order of magnitude greater than that of any previously reported computational design3 (Fig. 2a,b). This design diverges significantly from natural IGPSs, and a pairwise sequence alignment to the closest protein in the non-redundant sequence database reveals 141 mutations and multiple insertions and deletions (Extended Data Fig. 3). It also diverges in sequence and backbone from previously designed Kemp eliminases in natural IGPS scaffolds1 and features a different active-site constellation and position.

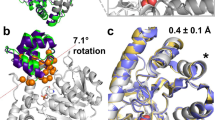
Fig. 2: Improving catalytic efficiency through low-throughput screening of FuncLib designs.
figure 2

a, Catalytic efficiencies of 12 FuncLib designs encoding 5–8 active-site mutations relative to Des27. Data represent mean ± s.d. of 2–5 biological replicates, except for Des27.2 and Des27.3 (n = 1). b, Michaelis–Menten analysis of Des27.7. Data are the mean of two technical repeats. c, The crystal structure of the ligand-unbound Des27.7 (grey, PDB entry 9HVB) verifies the accuracy of the designed active site (blue) with r.m.s.d. < 0.5 Å.

Full size image

We analysed the structural models of Des27 and its FuncLib-derived variants to understand the mechanistic basis for the differences in catalytic efficiency, which span three orders of magnitude, using the Rosetta force field and molecular dynamics (MD) simulations. A sequence alignment of the FuncLib designs shows that Ile136Val, Ile216Val and Val183Ile are associated with high catalytic efficiency (Fig. 3a). Contrasting the structure models of Des27 and Des27.7 reveals that these mutations may increase hydrophobic packing around the catalytic Asp162, probably improving its preorganization and desolvation and increasing its reactivity (Fig. 3a,b, top). Indeed, the Rosetta-computed van der Waals (vdW) energy of Asp162 is highly correlated with catalytic efficiency among the FuncLib designs (Spearman ρ = −0.88, P = 6 × 10−5; Fig. 3a). As further support, MD simulations show that Asp162 is conformationally dynamic in the ligand-unbound models, sampling multiple metastable conformations, and that the fraction of non-productive conformations decreases in Des27.7 relative to Des27 (Extended Data Fig. 4a). Furthermore, the Des27 model suggests that Leu236 may partly overlap with the substrate (Fig. 3b, middle), and that the mutation to Val in Des27.7 would alleviate this unfavourable interaction while increasing the volume of the pocket from 717 to 829 Å3 (Extended Data Fig. 4b,c). Finally, Ile54Val, Phe92His and Leu183Val may improve the solvation of the polar nitro moiety of the substrate (Fig. 3b, bottom), and Phe92His may enable water-mediated polar interactions with the nitro group. Thus, although the seven mutations in Des27.7 are mostly conservative, their aggregate markedly improves the catalytic parameters by reshaping the active-site pocket for better substrate recognition and optimizing the preorganization and reactivity of the catalytic base.

Fig. 3: Structural, energetic and dynamic contributions to the improved catalytic rate of Des27.7.
figure 3

a, Mutations (grey background) at positions 136, 216 and 236 trend with increasing catalytic efficiency, which also trends with Rosetta-computed vdW energy of the catalytic Asp162. Spearman ρ = −0.88, P = 6 × 10−5. b, Analysis of the structural basis of increased KE activity by comparing substrate-bound models of Des27 (left) and Des27.7 (right). c, Percentage of MD simulation time in which the substrate is within the active site for Des27 and Des27.7 (less than or equal to 4 Å between the substrate and the active site centre of mass; blue) or distant from the active site (wheat). For 24% of the time spent in the bound conformation the substrate adopts a reactive donor-acceptor geometry (highlighted arc). The bars on the right of each pie chart show the distribution of conformations (in, out and other) in the reactive mode. d, In MD simulations, 5-nitrobenzisoxazole (sticks) can assume two catalytically competent conformations: one in which the nitro group is buried inside the TIM barrel (in, blue) and another in which it is solvent exposed (out, orange). Shown are two representative conformations from the MD simulations. e, Activation free energy for the proton abstraction of 5-nitrobenzisoxazole, comparing ΔG‡ computed from the experimentally determined kcat values (mean ± s.d. of 2 and 5 biological replicates for Des27 and Des27.7, respectively) using the Eyring rate equation, assuming T = 298 K (experiment), and the corresponding values calculated for ‘in’ and ‘out’ substrate conformations (mean ± s.d. over 30 independent EVB trajectories per system). A two-sample Wilcoxon rank-sum test (two-sided) indicated statistically significant differences in the calculated activation free energies between the ‘in’ and ‘out’ conformations for Des27.7 (P = 7.7 × 10−9) but not for Des27 (P = 0.088). R.e.u., Rosetta energy units.

Full size image

To analyse the stability of the substrate within the active site, we conducted microsecond MD simulations of Des27 and Des27.7, starting from their ligand-bound design models. In both cases and across all replicas, the substrate exited and re-entered the active-site pocket multiple times (Extended Data Fig. 5), with Des27.7 showing five times more substrate retention (Fig. 3c and Supplementary Table 2). This contrasts with the typical scenario in MD simulations in which unbinding events are terminal49,50. Thus, the MD simulations indicate that our designs exhibit high affinity for the substrate, and that Des27.7 improves it further. We also noticed that the substrate may enter the pocket in two reactive conformations that are inverted: one that closely matches the design model, with the nitro substituent occupying the entrance to the active site, and one in which it is inverted by approximately 180° (Fig. 3d). Empirical valence bond (EVB) calculations of reaction free energies51 show similar energy profiles for both conformations, indicating that both are catalytically competent (Fig. 3e and Supplementary Table 3). Taken together, the MD and EVB calculations suggest that the experimentally measured results reflect the sum of both reaction modes, with the ‘out’ conformation (Fig. 3c) being occupied a greater fraction of MD simulation time than the ‘in’ conformation, but with EVB predicting the in conformation as being slightly more reactive in the optimized Des27.7 variant (Fig. 3e). Further, although such desolvated nitro group (‘in’) conformations were observed in previous de novo designed Kemp eliminases6,49,50, in those studies only one conformation was catalytically competent50. Thus, the high efficiency of Des27.7 may be partly due to the high preorganization of the active-site pocket and its ability to accommodate productive substrate interactions through distinct conformations.

To verify the molecular accuracy of the design process, we determined the structure of Des27.7 in the unbound form by crystallographic analysis (Extended Data Table 2; PDB 9HVB). All active-site positions aligned well with the design conception (less than 0.7 Å all-atom root mean squared deviation (r.m.s.d.) across 20 residues), including the catalytic Asp162, although a slight shift (r.m.s.d. 0.78 Å) was observed in the orientation of Phe113. Outside the active-site pocket, 180 of 257 positions aligned with backbone r.m.s.d. < 0.6 Å, but 65 amino acids either deviated or did not exhibit significant electron density, probably due to backbone flexibility in this region (Extended Data Fig. 6a,b). This fragment is known to be dynamic in the IGPS protein family52, but it lies outside the active-site pocket and probably does not contribute directly to reactivity and substrate recognition. Taken together, our results verify a fully computational pipeline that designs an accurate de novo active site and generates a stable and high-efficiency new-to-nature enzyme.

Necessary and sufficient conditions for design

Our computational workflow is based on the combination of several design components, each of which introduces multiple mutations that address aspects that are critical for efficient biocatalysis, such as backbone diversity, stability, foldability and activity. We next probed whether each of these components contributes to the intended property and whether all are essential.

We started by examining whether modular assembly and design is essential for generating diverse backbones. Instead of applying modular assembly and design, we applied the subsequent steps of the workflow to 1,072 representative IGPSs that were modelled using AlphaFold2 (Methods). We tested 55 designs (design round 2), of which 49 were solubly expressed (89%) and 28 (50%) exhibited apparent cooperative unfolding with apparent melting temperature (Tm) values 47–88 °C. In total, 70% of the cooperatively folded designs (20 designs) showed measurable KE activity with kcat/KM in the range of 0.5–155 M−1 s−1, demonstrating that the workflow can design stable and functional Kemp eliminases in a wide range of different starting points. As expected, designs that did not show cooperative unfolding lacked KE activity. We applied FuncLib to the active sites of six designs and tested 9–14 variants for each starting point. In five cases, catalytic efficiencies improved by 3–10-fold (Supplementary Table 1), with the highest catalytic efficiency reaching 300 M−1 s−1 (R2.Des39.2). We determined the crystallographic structure of two designs, R2.Des39 (kcat/KM 100 M−1 s−1) and Des49 (kcat/KM 150 M−1 s−1) (Extended Data Fig. 6c–i, PDB IDs 9HVH and 9HVG and Extended Data Table 2). The active sites were close to their design conceptions (r.m.s.d. < 0.6 Å and r.m.s.d. < 0.82 Å, respectively), but, in both cases, several loops either lacked electron density or exhibited significant conformational changes compared with the designs, which could impede substrate entry to the active site53. To explore whether the foldability of these loops could be improved, we applied FuncLib to stabilize these regions according to the design models. Three of 16 FuncLib variants of Des39.2 showed a significant increase in catalytic efficiency, with improvements up to 20-fold compared with the original design, reaching kcat/KM 2,000 M−1 s−1 (Extended Data Table 1 and Supplementary Table 1), but none surpassed the performance of Des27.7. These results demonstrate that large-scale artificial intelligence-based structure prediction of natural enzymes provides a valuable resource for de novo enzyme design, and that the computational workflow reproducibly generates efficient enzymes. In this case, however, optimization with FuncLib reached superior catalytic parameters in the designs derived from modular assembly, which may reflect the greater structural diversity in these designs.

As a next step to understanding the necessary and sufficient conditions for design of high-efficiency enzymes, we deconvoluted the contributions of each design component to the high stability and activity of Des27.7. As a baseline, we tested the outcome of combinatorial assembly and design alone (with 92 mutations relative to any natural protein), excluding both the PROSS-based stability mutations and the active-site design. This variant exhibited an apparent melting temperature of 57 °C and no detectable KE activity. Adding the 11 PROSS-designed mutations substantially improved both bacterial expression and thermal stability (69 °C) (Fig. 4 and Supplementary Fig. 1). Separately, grafting the active site from Des27.7 (15 mutations) onto the combinatorial assembly starting point (without PROSS stabilizing mutations) conferred high activity levels (2,900 M−1 s−1) but fourfold lower than in Des27.7. Combining the modular assembly, PROSS and the designed active site yielded a synergistic, higher-than-expected improvement in both stability and reactivity beyond the contribution of the individual components. Thus, despite the large number of mutations introduced by each computational component, resulting designs did not exhibit the trade-offs between stability and activity that were often reported in laboratory-evolution campaigns7,21,54. Furthermore, although active-site mutations are often assumed to compromise stability21, in our case, the designed active site contributed positively to stability. Collectively, these findings emphasize the importance of stabilizing the entire protein to obtain efficient enzymes and the potential for synergy between stability and activity-promoting mutations when using reliable sequence design methods21.

Fig. 4: Deconvoluting the contributions of the mutations in Des27.7 reveals necessary and sufficient components for effective de novo enzyme design.
figure 4

Apparent melting temperature and catalytic efficiency of Des27.7 (top row) are compared with variants in which design components are ablated (X symbols). The number of mutations relative to the modular assembly baseline is indicated in parentheses. Data represent the mean ± s.d. of 2–5 biological replicates. Muts, number of mutations; ND, not detected.

Full size image

Finally, we evaluated the contribution of the theozyme to the activity of Des27.7. Mutating the catalytic base Asp162 to Ala completely abolished activity, verifying that the designed base is essential. Remarkably, this single-point mutation also markedly increased protein stability, with the apparent melting temperature rising from 85 °C in Des27.7 to above boiling point (Fig. 4). This significant increase in stability underscores the strong destabilization induced by desolvating a charged group in the core of the active site and the importance of effective stability design methods.

We then tested whether the second theozyme residue, Phe113, was essential by replacing it with point mutations suggested by atomistic design. Replacement with Met and Leu exhibited similar Rosetta energies to the original Phe, and we subjected these point mutants to experimental analysis. The Met mutation showed similar catalytic parameters to Phe (Extended Data Table 1), suggesting that an aromatic identity is not essential at this position. Strikingly, Phe113Leu led to an order of magnitude increase in catalytic efficiency and rate to kcat/KM of 123,000 M−1 s−1 and kcat of 30 s−1, surpassing by two orders of magnitude recently designed enzymes in artificial intelligence-generated proteins (kcat = 0.03–0.7 s−1)14,15,35. To understand the reasons for this large gain in efficiency, we compared Leu113 in models of the unbound and transition states. Unlike the reorientation observed for Phe113 between the ligand-bound model and unbound experimental structure of Des27.7 (Extended Data Fig. 7a), Leu113 exhibits almost no sidechain conformation changes (Extended Data Fig. 7b), suggesting that this mutation improves active-site preorganization.

We note that the aromatic theozyme residue was forced in all our design steps and was based on previous Kemp eliminase design studies1,3. The fact that a completely aliphatic active-site pocket effectively accelerates the KE reaction is in line with the observation that London dispersion forces are sufficient for transition-state stabilization55. This finding challenges a two-decade assumption in computational Kemp eliminase design that an aromatic residue is important for ligand binding1,3, demonstrating how de novo design of function can expose shortcomings in our understanding of fundamental aspects in biocatalysis.

Conclusions

De novo enzyme design has until now resulted in rudimentary catalytic rates and required iterative random mutagenesis to close the gap with enzymes found in nature. Our strategy uses recent approaches for reliable backbone and sequence design in natural folds to generate diverse TIM-barrel backbones, stabilize the protein and design preorganized active-site constellations. This comprehensive design approach allowed us to explore the principles underlying high stability and activity in KE biocatalysis. In a single step, we generated a dozen designs with activities that spanned three orders of magnitude and gained insights into the determinants of high-efficiency catalysis. The best variant showed high stability and remarkable catalytic efficiency for a fully designed enzyme (greater than 85 °C and 12,700 M−1 s−1, respectively), which was increased to over 105 M−1 s−1 with a single designed mutation. Active-site preorganization combined with the ability to adopt multiple catalytically competent substrate-bound modes distinguishes this design from previously generated ones. Importantly, our best design exhibited a catalytic rate (30 s−1) and efficiency on par with the median values of natural enzymes16. Thus, the ability to design large sets of diverse backbones and encode high protein stability and active-site preorganization is necessary and sufficient for generating high-efficiency enzymes of model reactions. Furthermore, contrary to recent suggestions11, the results confirm that current atomistic methods are already sufficiently reliable to generate efficient enzymes in natural folds without extensive experimental screening, big-data analyses or artificial intelligence-generated scaffolds. Future improvements in modelling theozymes may enable fully programmable biocatalysis.

Methods

Backbone generation and stabilization

Modular assembly and design was applied as described in ref. 42. In brief, five different IGPS structures (PDB entries 1LBF, 1I4A, 1JCM, 1VC4 and 4FB7) were aligned and segmented into five fragments according to points of maximum structure conservation at positions 44, 105, 154 and 206 (numbering relative to PDB entry 1I4N). The fragments were then computationally combined all against all, and Rosetta sequence design was applied to optimize the stability and compatibility between the segments, resulting in 2,500 backbones. Design calculations were constrained using a position-specific scoring matrix (PSSM) that was generated for each structure using PROSS29. For designs 37–73, a further stabilization protocol was applied. This protocol, based on mutational scanning with PSSM constraints, identifies the most beneficial mutations across the protein. These mutations are combined and threaded onto the input structure. These backbones were then evaluated by an activity predictor27 and the top 1,000 designs were chosen.

To implement the workflow without recourse to modular assembly and design (design round 2), we used BLAST to search the non-redundant sequence database with the sequence of the Thermotoga maritima IGPS (PDB entry 1I4N), identifying 4,381 IGPS homologues. These were clustered with CD-HIT56 by 30–90% sequence identity to one another and 1,200 were selected for further analysis. The structures of these sequences were modelled using ColabFold AlphaFold2 (refs. 57,58). Models with average local confidence in predicted structures (predicted local distance difference test (pLDDT)) scores below 90 were discarded, leaving 1,072 backbones. All structures were subjected to PROSS stability design calculations29 and Design 8 for each was selected for further calculations. For models generated using AlphaFold2, PROSS design was disabled in amino acids that exhibited low predicted confidence (pLDDT < 90%) and those that were 5 Å from these residues59.

Catalytic site generation

Theozyme geometries (Supplementary Table 4) were based on previous calculations1. Geometric parameters that define the catalytic placements, such as tolerance, penalty coefficient, periodicity and number of matching samples to test, were manually adjusted60. The interaction between the catalytic base and the acidic carbon on the ligand was defined as covalent to mimic transition-state geometry. Theozyme placement was carried out using the Rosetta Matcher algorithm43. All positions inside or in the opening of the active site were allowed for theozyme matching (Fig. 1, step 3).

Initial active-site design and filtering

After matching, Rosetta sequence design was performed in an 8 Å shell around the ligand and catalytic residues. The design was performed under theozyme and PSSM constraints. To constrain the sequence space, the catalytic residues of the IGPS family, as described by the M-CSA database61, underwent Rosetta computational mutation scanning, and all mutations with ΔΔGsystem < +1 R.e.u. compared with the starting identity were included as allowed for design. The Rosetta Match and design steps generated 105 to 106 designs for each starting structure. Designs were filtered on the basis of a ‘fuzzy’-logic objective function45 that balanced potentially conflicting criteria: energy density (system energy divided by the protein length), energy rank relative to other designs in the same backbone, active-site vdW energy, catalytic base vdW, ligand solvation and accuracy of theozyme geometry. vdW energy is defined as the sum of the Rosetta atomistic energy terms fa_atr and fa_rep (as weighted in Rosetta scoring function62).

Active-site and core stabilization

To enhance active-site stability, we performed an enumeration of all low-energy mutations in the active site with ΔΔGsystem < +3 R.e.u. and chose the top variant. To ensure amino acid optimality throughout the protein, a pSUFER46 scan was performed on the whole protein excluding the active site. Flagged positions, those with at least five favourable amino acid substitutions (ΔΔGsystem < 0), were redesigned using FuncLib calculations28. The lowest-energy design was selected.

Computational validation

Active-site preorganization was analysed by performing extensive rigid-body minimization in the absence of the ligand. Structures in which the catalytic base exhibited an r.m.s.d. > 1.2 Å relative to the ligand-unbound model were discarded. For the R2 series the workflow included an extra validation step comparing the bound model and the AlphaFold2-predicted model. Designs were accepted if the r.m.s.d. between the AlphaFold2 model and the Rosetta model was less than 1 Å.

Active-site optimization

All functional variants identified through experimental screening were optimized by identifying diverse and stable active-site constellations using FuncLib28. FuncLib uses two filters to constrain the enumerated sequence space: a filter based on homologous sequences and exclusion of destabilizing point mutations. However, in de novo design of function, the homologous sequence filter is irrelevant and was omitted. For experimental screening, the 10–15 lowest-energy designs were selected.

Protein expression

The designed genes were ordered from Twist Bioscience, cloned into pET28 plasmid with an N-terminal His-tag, followed by a bdSUMO tag. Plasmids were transformed into Escherichia coli BL21 (DE3) cells. For expression, 50 ml of 2YT medium supplemented with 50 μg ml−1 kanamycin was inoculated with 500 μl of overnight culture produced from a single colony and grown at 37 °C until optical density (OD)600 0.6–0.8. Overexpression was induced by adding 1 mM IPTG and the cultures were grown for 20 h at 16 °C and collected, and the pellet was frozen at −20 °C. The cells were resuspended in basic buffer (50 mM Tris-Cl pH 7.25, 200 mM NaCl) supplemented with 10 µg ml−1 lysozyme, protease-inhibitor cocktail (Sigma) and benzonase, lysed by sonication and centrifuged at 20,000g for 30 min at 4 °C. The soluble fraction was loaded onto an Ni-NTA (nitrilotriacetic acid) column and washed twice with basic buffer and 20 mM imidazole. The protein was subjected to overnight on-column Sumo protease cleavage at 4 °C (5 μg ml−1 in basic buffer). Protein purity was assessed by SDS–PAGE. Protein concentration was determined using Pierce BCA protein assay kit. For crystallography, large-scale expression was performed in 1,500 ml of culture. After Ni-NTA purification and bdSUMO cleavage, the protein was purified by gel filtration (HiLoad 26/600 Superdex75 preparative grade column, GE).

Activity assay and determination of kinetic parameters

Product formation was monitored spectrophotometrically at 380 nm in 200-μl reaction volumes using 96-well plates. For initial screening, the reactions were started by adding 150 μl of 1 mM 5-nitrobenzisoxazole in basic buffer to 50 μl of purified protein. 5-Nitrobenzisoxazole was used from 0.1 M stock in acetonitrile. For the kinetic characterization, 150 μl of 5-nitrobenzisoxazole at various concentrations (final 0.05–0.75 mM in basic buffer with 1 mM acetonitrile) was mixed with 50 μl of purified protein. Kinetic parameters were obtained by fitting the data to the Michaelis–Menten equation v0 = kcat[E]0[S]0/([S]0 + KM). At low substrate concentrations the data were fitted to the linear regime of the Michaelis–Menten model v0 = [S]0[E]0kcat/KM, and kcat/KM values were inferred from the slope. All measurements in the main text were performed in biological duplicates or triplicates.

Thermal stability

Apparent Tm measurements were performed using nanoscale differential scanning fluorimetry (nanoDSF) experiments (Prometheus NT.Plex instrument, NanoTemper Technologies). The temperature ramp was 20–95 °C with 1.0 °C min−1 slope.

Crystallization, data collection and structure determination

Crystals were grown at 19 °C using the sitting-drop vapour diffusion method. Diffraction data were collected from a single crystal flash-cooled to 100 K, using a wavelength of 1.34 Å. Data were collected using an in-house Rigaku liquid-metal-jet X-ray Synergy System with a HyPix Arc 150° detector. AlphaFold2 (ref. 57) was used to generate all three models for molecular replacement (Extended Data Table 2). Initial models were iteratively rebuilt and refined using COOT63 and PHENIX64. Model geometry was evaluated using MOLPROBITY65. Atomic coordinates and structure factors for Des27.7, R2.Des39 and R2.Des49 are deposited in the PDB database under accession numbers 9HVB, 9HVH and 9HVG, respectively.

Specific crystallization conditions

Des27.7: the well solution contained 0.15 M lithium sulfate monohydrate, 0.1 M citric acid (pH 3.5) and 18% polyethylene glycol (PEG) 6000. Diffraction data were collected to 2.0 Å. Des27.7 crystallized in the P61 space group, with one subunit in the asymmetric unit.

R2.Des39: the well solution contained 0.07 M citric acid, 0.03 M Bis-Tris propane (pH 3.4) and 14% PEG 3350. Diffraction data were collected to 2.1 Å resolution. R2.Des39 crystallized in the P21 space group, with two subunits in the asymmetric unit.

R2.Des49: the well solution contained 8% Tacsimate (pH 7.0) and 20% PEG 3350. Diffraction data were collected to 1.9 Å resolution. R2.Des49 crystallized in the C2221 space group, with one subunit in the asymmetric unit.

MD and EVB simulations

System setup

Two designed Kemp eliminases, Des27 and Des27.7, were simulated in both their ligand-bound and unbound forms, using MD simulations to model dynamics, and EVB simulations51. All simulations were initiated from the FuncLib design models for each variant. Ligand-bound simulations were performed in complex with the substrate 5-nitrobenzisoxazole. The partial charges for the substrate were calculated using restrained electrostatic potential66 fitting at the HF/6-31 G(d) level of theory with Antechamber67, on the basis of gas-phase geometries optimized at the B3LYP/6-31 G(d) level of theory in Gaussian 16 Rev. B.01 (ref. 68). All other force field parameters for the substrate were obtained from the General AMBER Force Field (GAFF2)69. Residue protonation states were checked using PROPKA 3.0 (refs. 70,71) to estimate sidechain pKas, coupled with visual examination using PyMOL, on the basis of which all residues were kept in their standard protonation states at physiological pH. For simulations of the unbound system, the catalytic residue Asp162 was modelled in its protonated form. All systems were solvated in a truncated octahedral water box containing OPC water molecules72, extending 11.0 Å from the protein in all directions. Neutralization was achieved using 12 Mg2+ and 12 Cl− counterions for the three variants. Protonation patterns of histidine residues for each system are collected in Supplementary Table 5. Non-standard substrate parameters are provided in Supplementary Table 6 and in the Zenodo data package available at https://doi.org/10.5281/zenodo.14563437 (ref. 73).

Classical MD simulations

All MD simulations in this work were performed using the HIP-accelerated version of Amber24 (ref. 74) using the ff19SB force field75 and the OPC water model72. MD simulations for all systems followed the same protocol, used also in previous work modelling designed Kemp eliminases50. For a detailed description, see ref. 50. In brief, each trajectory was first energy minimized with 100 steps of the steepest-descent algorithm, followed by 900 steps of conjugate gradient minimization, applying a 100-kcal mol−1 Å−2 restraint to all solute (protein and substrate) atoms. The system was then heated from 50 to 300 K in an NVT ensemble using simulated annealing, reaching 300 K within the first 100 ps and continuing for a total of 1 ns with a 1-fs time step. Langevin temperature control76 was used with a collision frequency of 1 ps−1. During this stage, the 100-kcal mol−1 Å−2 solute restraints were maintained and subsequently reduced to 10 kcal mol−1 Å−2 in later equilibration steps. A second energy minimization and heating step followed, with positional restraints applied to solute heavy atoms. During subsequent equilibration, the restraints were progressively reduced from 10 to 1 to 0.1 kcal mol−1 Å−2 before being fully removed. The systems, now with no restraints applied, underwent final equilibration for 1 ns in an NPT ensemble (300 K, 1 atm) using a Berendsen barostat77 with a 1-ps pressure relaxation time and Langevin temperature control (collision frequency of 1 ps−1). The SHAKE algorithm78 was applied to constrain all bonds involving hydrogen atoms, and all equilibration simulations used a 1-fs time step. Production MD runs were performed using a 4-fs time step, enabled by hydrogen mass repartitioning79 and the SHAKE algorithm78, with an 8 Å direct space non-bonded cutoff, Langevin temperature control (collision frequency of 1 ps−1) and a Berendsen barostat (pressure relaxation time of 1 ps). Equilibration of these trajectories is shown in Extended Data Fig. 4d,e. The final production trajectories were 1-µs long for each system, with 5 independent replicas per system, resulting in a total of 5 µs of simulation time per system and 15 µs across all systems.

EVB simulations

EVB simulations were performed on the Des27 and Des27.7 variants, using both substrate conformers (‘in’ and ‘out’; Fig. 3c) observed as being dominant in the MD simulations, and following the same protocol described in detail in ref. 50. Reactive in and out conformers were extracted from our MD simulations and overlaid onto the FuncLib predicted structures of Des27 and Des27.7 as starting coordinates for the EVB simulations. Before the EVB simulations, in all cases, the enzyme–substrate complex was minimized with Amber24 (ref. 74) in vacuum, with 2,500 steps of the steepest-descent algorithm, followed by 2,500 steps of conjugate gradient minimization, applying 10-kcal mol−1 Å−2 positional restraints on all heavy (non-hydrogen) atoms. The minimization was repeated with the same steps, with 5-kcal mol−1 Å−2 positional restraint on protein Cα-atoms, and substrate heavy atoms, and with twice as many steps, keeping the restraint only on the substrate heavy atoms.

All EVB simulations were performed using the Q6 simulation package80, the OPLS-AA force field81, the TIP3P water model82 and the surface constrained all atom solvent (SCAAS) model83 to describe solvent. Long-range interactions were described using the local reaction field approach84. Protonation states of ionizable residues within the explicit simulation sphere, as well as histidine protonation patterns (both of which were validated by PROPKA 3.0 (refs. 70,71) and visual inspection), can be found in Supplementary Table 7. Each system was simulated in 30 replicas of 30-ns equilibration, with 5-kcal mol−1 Å−2 distance-based harmonic restraints applied between the substrate hydrogen donor carbon and the acceptor oxygen of Asp162. Each equilibration was followed by 10.2 ns of EVB simulations (200-ps window over 51 discrete EVB windows), carried out without the distance restraint applied, leading to a cumulative 612 ns of EVB simulation time per system (including ‘in’ and ‘out’ substrate conformations), and 3.6 µs of EVB equilibration time and 1.2 µs of EVB simulation time across all systems studied in this work (4.8 µs of simulation time in total). The corresponding r.m.s.d. values of the equilibration phase (calculated with the QCalc6 module of Q6) are shown in Extended Data Fig. 8a,b. We note that in one of the initial 30 EVB trajectories for Des27.7 with the substrate in the out conformation, we observed active-site distortion with the catalytic Asp moving into a non-reactive conformation. This trajectory was excluded from further analysis, with an extra trajectory being run to create a full set of 30 replicas.

Representative stationary points for the KE reaction catalysed by Des27, extracted from EVB simulations of this system, are shown in Extended Data Fig. 8c,d. To extract the conformations representing each stationary point, all 30 replicas were evaluated together. The MDTraj software (version 1.10.0)85 was applied to convert the trajectories to a CPPTRAJ compatible format, and clustering was performed based on the r.m.s.d. of the substrate heavy atoms, using the average linkage clustering method, with an ε value of 0.75. We note that the key stationary points for Des27.7 are visually similar to those for Des27. Sample input files, parameter files, starting structures and simulation snapshots have all been made available on Zenodo at https://doi.org/10.5281/zenodo.14563437 (ref. 73).

Simulation analysis

Unless otherwise stated, all MD analyses were performed using the CPPTRAJ module86 of AmberTools24 (ref. 87). Trajectory frames were extracted every 400 ps, and results (where applicable) are reported as averages and standard deviations over 5 × 1-µs trajectories per system. The fractions of unbound and bound modes during the simulations were determined by counting trajectory frames. A bound mode was defined on the basis of the distance between the ligand and the centre of mass of the active site, including residues 54, 84, 86, 92, 136, 162, 183 and 236. A threshold of 4 Å was defined to classify the frames into unbound or bound. Unbound modes have left the active-site pocket, but not necessarily dissociated from the protein itself (sampling non-productive conformations out of the active site). The substrate orientation was defined using the distance between the Cα-atom of residue Leu41 and the N1 and N2 atoms of the substrate. Conformations with a Leu41–N1 distance between 0 and 15 Å and L41–N2 distance between 15 and 20 Å were classified as ‘out’, and otherwise as ‘in’. Pocket volumes of Des27 and Des27.7 systems were calculated using MDPocket88,89, with snapshots taken every 4 ns of the simulations for unbound systems. Additionally, the volume of the ligand was calculated using the mol_volume package in VMD90. Finally, PyMOL was used for all visualization analyses.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.