A computational pipeline for spatial mechano-transcriptomics

Abstract

Advances in spatial profiling technologies are providing insights into how molecular programs are influenced by local signaling and environmental cues. However, cell fate specification and tissue patterning involve the interplay of biochemical and mechanical feedback. Here we develop a computational framework that enables the joint statistical analysis of transcriptional and mechanical signals in the context of spatial transcriptomics. To illustrate the application and utility of the approach, we use spatial transcriptomics data from the developing mouse embryo to infer the forces acting on individual cells, and use these results to identify mechanical, morphometric and gene expression signatures that are predictive of tissue compartment boundaries. In addition, we use geoadditive structural equation modeling to identify gene modules that predict the mechanical behavior of cells in an unbiased manner. This computational framework is easily generalized to other spatial profiling contexts, providing a generic scheme for exploring the interplay of biomolecular and mechanical cues in tissues.

Main

The advent of single-cell profiling technologies has transformed our understanding of the mechanisms that control cell state transitions and lineage hierarchies. Through the development of computational and statistical methods, these approaches provide a window into the transcriptional and epigenetic programs that control cell fate under normal and perturbed conditions. However, these programs do not act in isolation, but respond to environmental cues and collective cell behaviors, mediated by reciprocal signaling networks as well as mechanical forces and their coupling through mechano-chemical feedback loops^1,2,3,4. In recent years, the advent of spatial omics techniques⁵ has enabled the profiling of gene expression^6,7, protein composition⁸ and chromatin accessibility⁹ at single-cell resolution in whole embryos and tissue sections, opening a window on the correlation between cell state and spatial cues.

Despite their promise, spatial omics methods and associated computational analysis pipelines currently struggle to integrate molecular profiling measures with interpretable cell morphology metrics and local mechanical forces. While high-throughput sequencing technologies such as Slide-seq¹⁰ enable coverage of the entire transcriptome, they are limited to supracellular spatial resolution and, as such, cannot recover such information. In contrast, in situ hybridization (ISH)-based methods such as seqFISH^11,12 and MERFISH^13,14, offer a more limited transcriptomic coverage, yet provide single-cell or even subcellular spatial resolution in addition to access to cell morphology. Indeed, immunostaining of transmembrane proteins allows segmentation of cell contours and extraction of whole-cell morphometric measures. Such cellular morphologies have been used either alone, for cell-type classification and pseudotime inference¹⁵, or in combination with gene expression data, for cell-type clustering refinement^16,17 and cross-modality prediction¹⁸.

However, computational frameworks for linking genomics to tissue-level mechanical signatures such as tension at cell–cell junctions, strain and stress are currently lacking. Indeed, when considering the joint modeling of gene expression and morphology, existing approaches target only ‘local’ morphological properties (for example, cell roundness or volume), treating cells as independent from each other and from their spatial environment. Since mechanical morphometrics are global properties of cellular aggregates, new methods are needed to estimate these quantities from images and to test for associations between them and gene expression signatures in the presence of spatial confounders.

Here, to meet this challenge, we introduce a joint spatial mechano-transcriptomics framework to investigate simultaneously the transcriptional, morphological and mechanical state of cells in a tissue context at single-cell resolution. To develop this method, we make use of image-based mechanical force inference, an approach rooted in the physics of cellular materials¹⁹. To illustrate the potential of this approach, we use it to quantify tensions at cell–cell junctions and intracellular pressure in the context of multicellular tissues^20,21,22,23. In particular, we use selected regions of an embryonic day (E)8.5 mouse embryo spatially profiled using seqFISH²⁴. We show that, by integrating transcriptomic profiling with local mechanical measures, we can gain insight into the mechanisms that promote boundary formation during development, as well as the role of mechano-responsive regulatory pathways in driving cell segregation and spatial patterning. We investigate the relationship between transcriptional profiles and mechanical forces at the single-cell level, demonstrating the existence of gene modules whose expression patterns are significantly associated with the mechanical state of the cell, while accounting for spatial confounders. Finally, exploring higher-order interactions between gene expression and mechanics, we show that mechano-associated genes display a variety of nonlinear responses to mechanical signals. Overall, this study provides a computational framework to investigate mechano-biology in an unbiased manner, offering the potential to uncover the directional relationships between mechanical forces and gene expression in a spatial context, identify candidate mechano-sensors or mechano-effectors, and delineate mechanical and mechano-chemical feedback loops involved in cell fate decisions, pattern formation and tissue morphogenesis.

Results

An integrated mechano-transcriptomics analysis of mouse organogenesis

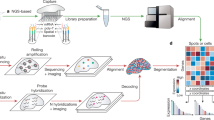
Can the gene expression signature of cells provide information on the local mechanical forces that act upon them? How does the interaction between genomics and mechanics inform the acquisition of cell identity and establishment of tissue compartments in developmental contexts? To begin to answer these questions, we developed a multistep computational framework based on spatial transcriptomics for the integrated statistical analysis of mechanical forces and gene expression at cellular resolution (Fig. 1a). First, we compile input data of multiple types, including immunostained cell membranes, seqFISH images and single-cell transcriptomic references (step 1). Next, we process and segment these images to delineate cell boundaries (step 2) and streamline image-based mechanical force inference (step 3). We then perform a joint statistical analysis of mechanical forces and gene expression at cellular resolution (step 4). Finally, we generate spatial maps of tension, pressure and significant gene expression profiles associated with mechanical phenotypes (step 5).

Fig. 1: A spatial mechano-transcriptomics framework applied to a E8.5 mouse embryo seqFISH dataset.

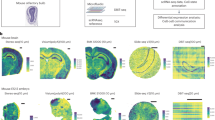
a, An overview of the spatial mechano-transcriptomics pipeline, showing immunostained membrane images and single-cell RNA-sequencing references as inputs, followed by deep learning segmentation, tension and pressure inference, gene expression imputation and final integrated mechanical-transcriptomic output maps. b, A schematic (top left) and images of the two different embryo sagittal sections considered in this study with close-ups of the three different brain regions studied in more details thereafter. Dataset 1: FMH and NC regions of embryo 1 brain; dataset 2: CM and FHM regions of embryo 2 brain; and dataset 3: MHB region of embryo 2 brain. Panels adapted from: a (bottom left), ref. 24 under a Creative Commons license CC BY 4.0; b (top left and middle), ref. 24 under a Creative Commons license CC BY 4.0.

In detail, we take as input, images of tissue or embryo sections where cell membranes have been labeled with fluorescent markers (see, for example, the spatial transcriptomics seqFISH dataset in Fig. 1b). The fluorescent markers enable image-based segmentation of cell contours as well as the quantification and spatial localization of selected transcripts at cellular resolution; Fig. 2a). On the basis of this analysis, we then generate segmentation masks with annotated coordinates of cell–cell junctions and vertices (Methods). We take advantage of a mechanical force inference approach and to quantify the mechanical forces that act upon cells²³ (Fig. 2b,c). To apply this method effectively, it is necessary to recover information on precise cellular shapes and physical cell–cell contacts, calling for high-quality image segmentation. Moreover, to fulfill the constraints of our inference method, fourfold vertices—junctions that are shared between four neighboring cells—must be reconciled and removed while cell edges must be convex at vertices (Methods). The resulting spatial mask serves as input into an image-based mechanical force inference pipeline (Fig. 1a and Supplementary Fig. 1a).

Different algorithms exist for image-based force inference²³. Here, we chose to implement the variational method of stress inference (VMSI) approach proposed by Noll et al.²². This algorithm uses a nonplanar triangulation of junctional tensions to form a dual representation of the cell array geometry. A simultaneous fit of junctions with circular arcs then allows the inference of both tensions and cellular pressures up to a multiplicative and additive constant, respectively (Methods). In doing so, it exhibits both increased accuracy and robustness compared with other force inference methods²³, particularly when the pressure differential between adjacent cells is large. We benchmark and calibrate this variational method for mechanical force inference against a variety of optimizers, choices of hyperparameters in real data and simulations (Supplementary Fig. 1b–g), ensuring it is robust to perturbations and noise sources encountered in experimental data, and make it available as a Python package. Here, we have expanded the utility of the original mechanical stress inference method by providing improved quality control tools for the resolution of ‘invalid’ vertices and options for image tiling for large images (Methods). The mechanical stress inference pipeline provides as output inferred intracellular pressures, tensions at cell–cell junctions and mechanical stress tensors for each segmented cell in the image. Both scalar and tensor quantities are determined. Scalar quantities are directly output as features, while tensorial quantities, such as the mechanical stress tensor, are converted to features that summarize the eigenvectors, orientation and anisotropy of the tensor. This ensures that all resulting features are independently interpretable (Methods).

Alongside the measured transcriptomic readouts, the mechanical estimates—tensions, pressures and stress tensor—comprise a mosaic representation of spatial cellular identity. We use these interpretable features to quantify statistical associations between genomic and mechanical measures. Using this approach, we can then build structural equation models which take into account spatial confounders²⁵, and identify known mechano-sensors as well as genes and ligand–receptor (LR) pairs associated with cell–cell junctional tension variability along tissue compartment boundaries.

Boundaries between tissue compartments are characterized by both gene expression and elevated interfacial tension

To illustrate the application and potential of this approach, we first apply our pipeline to the study of boundary formation in the gastrulating mouse embryo. The mechanisms that drive the formation of precise boundaries between tissue compartments in the developing embryo have been the subject of long-standing interest and debate^26,27. Does cell fate specification precede a phase of cell rearrangement and boundary formation or does the positioning of cells induce cell fate acquisition? In the context of cell sorting, emphasis has been placed on the ability of cells to discriminate contacts between cells of the same cell type—homotypic contacts—and between cells of a different cell type—heterotypic contacts^28,29. Evidence for this phenomenon was first shown in pioneering work by Townes and Holtfreter, who demonstrated that mixed dissociated cells from different embryonic regions could progressively sort into segregated cell clusters³⁰.

Various hypotheses have been proposed to explain the basis of this phenomenon, either through differential cell adhesion (also known as the differential adhesion hypothesis (DAH))³¹, preferential cell adhesion (also known as the selective adhesion hypothesis)³², differential cell contractility (also known as the differential interfacial tension hypothesis (DITH))³³ or juxtacrine signaling generating cell–cell repulsion at heterotypic cell contacts (also known as higher interfacial tensions (HIT))^34,35. On the basis of modeling-based approaches and experimental studies^36,37,38, it was established that both cell–cell adhesion and cell contractility contribute to the tuning of a single physical quantity, the cell–cell junctional tension (also known as interfacial tension or contact tension), which is the quantity that is directly inferred with our image-based force inference algorithm. Thus, it is possible to formulate the four hypotheses above in terms of cell–cell junctional tension. To understand how, consider two different cell types, A and B, displaying homotypic junctional tensions between cells of the same type, T_AA and T_BB, respectively, and an heterotypic junctional tension, T_AB, between cells of different types. For the boundary to be maintained between segregated populations of A and B type cells, or for A and B cells to segregate if initially mixed, DAH and DITH require that T_AA > T_AB > T_BB, whereas the selective adhesion hypothesis and HIT require that T_AB > max(T_AA,T_BB). Therefore, using a combination of cell-type annotation based on the transcriptomics data and the results of the mechanical force inference analysis, it should be possible to distinguish between these two scenarios.

To test our framework, we applied the force inference pipeline to three published spatial transcriptomics datasets of the embryonic day E8.5 mouse embryo obtained using seqFISH²⁴ (Fig. 2a–c and Supplementary Fig. 2). We generated instance segmentation masks of cell contours (Fig. 2a), derived spatial tension (Fig. 2b) and pressure (Fig. 2c) maps using the VMSI algorithm, and classified cell types via gene expression analysis (Fig. 2d). We focused on three examples of boundary formation (Figs. 2 and 3a), where we could distinguish between distinct cell types based on their transcriptional signature: dataset 1 shows a boundary between cells with a neural crest (NC) signature and the forebrain/midbrain/hindbrain (FMH), two tissues of ectodermal origin; dataset 2 shows a boundary between cranial mesoderm (CM) and the FMH; and dataset 3 shows a boundary separating the midbrain and hindbrain (Figs. 2d and 3a). The formation of this last boundary is particularly well studied³⁹ as it plays a crucial role in the development of the brain, the boundary functioning both as a signaling center, also known as the isthmus organizer, and as a physical barrier for the developing brain ventricles⁴⁰.

Fig. 2: Spatial mechano-transcriptomic profiling of different E8.5 mouse embryo brain regions.

a, Instance segmentation masks of cell contours (Methods) for datasets 1 (left), 2 (middle) and 3 (right). b, Spatial tension (T) maps obtained with the VMSI algorithm from the cell segmentation masks of datasets 1 (left), 2 (middle) and 3 (right). c, Spatial pressure (P) maps obtained with the VMSI algorithm from the cell segmentation masks of datasets 1 (left), 2 (middle) and 3 (right). d, Spatial maps and Uniform Manifold Approximation and Projection (UMAP) clustering plots of the cell types present in the datasets 1 (left), 2 (middle) and 3 (right). Clusters and cell types were obtained by gene expression analysis on the basis of the seqFISH and inputed gene expression profiles for all cells contained in each dataset.

Fig. 3: Tissue compartment boundaries defined by gene expression are characterized by a high interfacial tension pattern, which is sufficient to explain their maintenance.

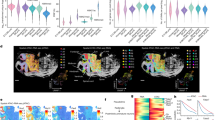
a, Spatial maps of the dominant cell types as defined by gene expression analysis for datasets 1 (left), 2 (middle) and 3 (right). b, Spatial maps of the boundary likelihood highlighting cells at the boundary between spatially distinct tissue compartments for datasets 1 (left), 2 (middle) and 3 (right). c, Violin plots for inferred heterotypic tension (cell–cell tensions for junctions at the boundary between spatially distinct tissue compartments) and homotypic tension (cell–cell tensions for junctions within each tissue compartment) for datasets 1 (left), 2 (middle) and 3 (right). Error bars indicate s.e.m. ^*P < 0.05 and ^**P < 0.01 by one-sided pairwise Mann–Whitney U test. Exact P values and test statistics can be found in Supplementary Table 1. d, Boundary maintenance simulations based on experimentally measured heterotypic and homotypic tensions for datasets 1 (left), 2 (middle) and 3 (right). Renderings of typical boundary maintenance simulations (top) and of typical control simulations where the homotypic tensions are equal to the heterotypic tensions (bottom).

To determine the locus of the physical boundary between tissue compartments, we used the results of our joint image-based force inference (Fig. 2a–c) and spatial transcriptomics pipeline (Fig. 2d and Supplementary Fig. 3b,c) to obtain an assessment for the transcriptomics-based boundaries likelihood (Methods). From this approach, it was possible to determine the compartment boundaries for each of the datasets, as shown in Fig. 3a,b. Using the data associated with the tension maps shown in Fig. 2b, we then computed, for each dataset, the homotypic junctional tension for each tissue compartment and the heterotypic junctional tension existing at each boundary. As evidenced by the violin plots in Fig. 3c, homotypic tensions in tissue compartments are ~12−35% lower than heterotypic tensions at the compartment boundaries depending on the dataset considered, with dataset 1 displaying the smallest difference and dataset 3 the largest.

Examining the robustness of the mechanical differences between heterotypic and homotypic junctions involves investigating whether elevated junctional tensions at heterotypic junctions are also present in neighboring, parallel sagittal sections of the same embryos. To accomplish this, we analyzed an additional slice located at a 12 μm separation in the z direction from the previously examined midbrain–hindbrain region (Supplementary Fig. 4a,b). With this level of z separation, the parallel slices contain different cells within the same tissue region, thereby offering biological validation for the inferred boundary mechanical properties. It is important to note that the midbrain–hindbrain region is the sole one present in the dataset containing boundaries preserved across multiple z slices. Our analysis reveals that our mechano-transcriptomic pipeline recapitulates the previously observed elevated heterotypic junctional tension (Supplementary Fig. 4c,d), underscoring the robustness of our method. Further, we confirm that the gene expression-derived midbrain–hindbrain boundary (MHB) occupies the same spatial location in both dataset 3 (z-slice 1) and the parallel z slice (z-slice 2) (Supplementary Fig. 5a). To account for cellular composition differences, we computed a Gaussian-smoothed spatial field of cell pressure and stress tensor magnitude quantities (Supplementary Fig. 5b,d) for each z slice at a common set of sampled points (Methods). We found that there was no significant global correlation in mechanical properties across the entire region; this was consistent with our observation of spatial variance in cellular mechanical properties within each sagittal (x–y) plane. However, we hypothesized that there may be local spatial correlation in mechanical properties at regions where cell mechanics are particularly biologically relevant. We therefore used scHOT⁴¹ to calculate local spatial correlation in cell pressure and stress tensor magnitude across the region. Indeed, we found that distinct regions exhibited different degrees of spatial correlation in mechanical properties, with some regions showing high correlation while others demonstrated high anticorrelation (Supplementary Fig. 5c,e). In particular, we observed that regions close to the MHB were more mechanically correlated than regions far away from the boundary (Supplementary Fig. 5f,g). These results reinforce the robustness of our observation that heterotypic junctional tension is elevated at tissue compartment boundaries. Similarly, the local coherence in cell mechanical properties at the boundary suggests the existence of molecular mechanisms that are responsible for maintaining this coherence. Taken together, our results seem to rule out a scenario based on DAH or DITH in favor of a mechanism of boundary maintenance based on HIT for all three distinct boundaries.

To challenge this scenario, we ran in silico experiments using a simple and well-characterized biophysical model of multicellular tissues^42,43. Specifically, for each dataset, we simulated the maintenance of the boundary between the two tissue compartments using experimental values for homotypic and heterotypic tensions with all other model parameters taken as the same. We also ran control in silico experiments where the homotypic and heterotypic were taken as equal (Methods). As shown in the upper panel of Fig. 3d, in silico experiments confirm that, for all three datasets, a higher interfacial tension at the boundary between tissue compartment is sufficient for boundary maintenance. This phenomenon is characterized by an invariance of the heterotypic boundary length (Methods) over the length of the simulations (Supplementary Fig. 6d). Here, we also note that the ‘roughness’ of the boundary is inversely proportional to the ratio of the homotypic and heterotypic tensions. Moreover, control simulations confirm that, in the absence of a higher heterotypic tension, cells of both cell types start to mix, leading to a progressive dissolving of the boundary between the tissue compartments, as shown in Fig. 3d, bottom, and evidenced by the increasing values taken by the heterotypic boundary length in these simulations (Supplementary Fig. 6d). Moreover, further in silico simulations using similar numerical parameters, but with different initial conditions where cells are mixed at random, demonstrated that a higher interfacial tension is also sufficient to explain the formation of segregated tissue compartments via a cell sorting mechanism, as shown in Supplementary Fig. 6b,c.

Overall, HIT appears to be a particularly robust mechanism for tissue compartment boundary maintenance, as even a difference as small as ~10% between homotypic and heterotypic tensions appear to be enough to maintain a boundary. Moreover, spatial tension profiles might provide a highly accurate way to determine, with subcellular resolution, the location of the boundary between tissue compartments. For example, the one-dimensional (1D) tension profile at the boundary between the midbrain and hindbrain is shown in Supplementary Fig. 7a, plotted against the 1D gene expression profiles of Otx2 and Gbx2, two well-characterized markers of the mesencephalon/prosencephalon and of the rhombencephalon, respectively (Supplementary Fig. 7b). In this case, the position of the boundary can be very accurately pinpointed as the maximum of the 1D tension profile and corresponds to the intersection of the midpoints of the Otx2 and Gbx2 gradients. A similar phenomenon is observed at the boundary between the cranial mesoderm and the FMH tissue compartments, as shown in Fig. 4a, where the maximum of the 1D tension profile coincides with the intersection of the midpoints of the Wnt5b and Bmp4 gradients, two well-characterized markers of the FMH and CM, respectively (Fig. 4b).

Fig. 4: Spatial transcriptomics-based LR analysis demonstrates ephrin signaling is a molecular determinant of elevated interfacial tension at tissue compartment boundaries.

a, The 1D tension profile along the tissue compartment boundary for dataset 2 (top) and 1D normalized gene expression (Norm. GeX) profile for CM and FMH markers Bmp4 and Wnt5b for dataset 2 (bottom) (mean ± 95% confidence interval). b, Spatial gene expression maps for CM and FMH markers Bmp4 and Wnt5b. c, Absolute interaction likelihood of LR pairs for pair of cells at the boundary between CM and FMH in dataset 2, with ligands expressed in CM cells and receptors in FMH cells. The insert displays the top 20 LR pairs with the highest absolute interaction likelihood. d, GO enrichment term analysis for the top 100 LR pairs for pair of cells at the boundary between CM and FMH in dataset 2, with ligands expressed in CM cells and receptors in FMH cells. GO term are ranked according to P value by hypergeometric test and gene count. e, The same as c but for ligands expressed in FMH cells and receptors in CM cells. f, The same as d but for ligands expressed in FMH cells and receptors in CM cells. g, Violin plots of junction interaction potentials for some top-ranked LR pairs (Wnt5a–Fzd5, Efna1–Epha5 and Efnb1–Ephb1). h, Spatial gene expression maps for the same selected LR pairs (top) and 1D gene expression profiles along the tissue compartments boundary for the same LR pairs (bottom) (mean ± 95% confidence interval).

LR analysis identifies putative molecular determinants of elevated interfacial tension at tissue compartment boundaries

Next, we quantified the interaction between transcriptional profiling data and force inference readouts. As higher interfacial tension is a likely physical determinant of tissue compartment boundaries maintenance, we questioned whether the spatial transcriptomics data can provide insight into the molecular mechanisms underpinning this phenotype. As a first step, we used unbiased LR analysis using the spatial gene expression data, making use of the CellChatDB LR annotation database (Methods). We analyzed a dataset involving the boundary between the cranial mesoderm and the FMH tissue compartments and a dataset involving the boundary between midbrain and hindbrain tissue compartments.

Focusing on cells sharing heterotypic contacts (that is, on the boundary), it was possible to screen for the expression levels of known LR pairs and then to compute from their interaction potential (Fig. 4g and Supplementary Fig. 7g) an absolute interaction likelihood (Fig. 4c,e and Supplementary Fig. 7c,e), distinguishing the directionality of interactions. Considering only LR pairs displaying a positive interaction likelihood and filtering out the top 50 pairs, we ran a Gene Ontology (GO) overrepresentation analysis, the results of which are reported in Fig. 4d,f, and Supplementary Fig. 7d,f. The results emphasize the role of LR signaling in controlling mechano-biological processes such as ‘response to mechanical stimulus’, ‘regulation of cell adhesion’, ‘anatomical structure morphogenesis’ and ‘ephrin receptor signaling pathway’ at the tissue compartment boundaries in both datasets.

Notably, considering LR pairs displaying the highest positive interaction likelihoods, it is apparent that some of these pairs involve canonical transmembrane receptors and diffusible ligands such as Wnt5a–Fzd5, which are known to play a crucial role in anterior–posterior axis formation and patterning during mammalian development⁴⁴, Fgf18–Fgfr1, known to play a key role in the establishment of the boundary between midbrain and hindbrain in mouse⁴⁵ and Edn1–Ednra, shown to be a key determinant of cranio-facial morphogenesis in mouse and human⁴⁶. Interestingly, 2D maps and 1D spatial gene expression profiles in Fig. 4h and Supplementary Fig. 7h show that these LR pairs are involved in directional signaling. For example, in dataset 2, the CM acts as an almost spatially homogeneous source of Wnt5a, whereas its expression sharply decreases into the FMH region beyond the compartment boundary. This expression profile is mirrored by the spatial expression pattern of the receptor, Fzd5, which is not expressed in CM, but displays a spatially graded profile in the FMH, with the highest point of the gradient found in cells proximate to the boundary on the FMH side.

Furthermore, a substantial fraction of the top LR pairs are ephrin ligand (Efn) receptor (Eph) pairs, such as Efna1–Epha5, Efnb1–Ephb1 or Efnb3–Ephb2, as shown in Fig. 4c,e and Supplementary Fig. 7c,e. Ephrin ligands are membrane-bound proteins, which can only interact with ephrin receptors expressed in neighboring cells, with cells expressing a ligand usually downregulating the expression of its associated ephrin receptor(s) and vice versa^34,47. This leads to a characteristic spatial expression pattern, which can be observed in the 2D maps and 1D spatial gene expression profiles in Fig. 4h where the ephrin ligand (Efna1 or Efnb1) is strongly expressed in one of the two tissue compartments (here the CM), while the receptor (Epha5 or Ephb1) is expressed almost exclusively in cells proximate to the boundary in the other tissue compartment (here the FMH). The same characteristic spatial pattern is also observed in dataset 3, where one can observe in Supplementary Fig. 7h the mutually exclusive spatial pattern of Efnb3 and Ephb2 at the MHB.

Ephrin–LR signaling is well known to generate ‘repulsion’ at heterotypic cell–cell contacts and tissue compartment boundaries via downstream signaling pathways that increase interfacial tension for cell–cell junctions located on the boundary^28,29,47. Consequently, the presence of multiple ephrin–LR pairs with high interaction likelihood on the boundary between CM and FMH provides a potential mechanistic explanation for the observed higher heterotypic interfacial tension at the boundary, and could be generalized to explain the higher interfacial tension also observed for other tissue compartment boundaries in dataset 3 or dataset 1.

While these findings emerge naturally from the combined transcriptomic and force inference analysis of the E8.5 mouse embryo, this mechanism constitutes a ubiquitous feature of boundary formation in vertebrates, and has been observed in a variety of developmental contexts such as the boundary between mesoderm and ectoderm in the Xenopus laevis embryo³⁵, the boundary between the different segments of the hindbrain (rhombomeres) in zebrafish and chick embryos⁴⁸, the boundaries between somites^26,49, and compartments of the neural tube^50,51 in zebrafish embryos. In all these systems, the mechanism driving the increase in interfacial tension at the boundary appears to be caused both by an increase in actomyosin contractility due to myosin II phosphorylation directly downstream ephrin–LR signaling via Ephexin-mediated RhoA activation and a localized decrease in cell–cell adhesion due to selective expression of cell–cell adhesion molecules such as cadherins or protocadherins^29,47,51,52.

While our approach, based on spatial transcriptomics, does not allow us to directly quantify actomyosin activity, we could nonetheless investigate the spatial patterns of cell–cell adhesion molecules at the boundary between CM and FMH in dataset 2, as shown in Supplementary Fig. 11a. Interestingly, CM and FMH display reciprocal patterns of cadherin expression so that when one particular cadherin is upregulated in one tissue compartment, such as Cdh2 in the FMH or Cdh11 in the CM, it is downregulated in the other compartment. As homophilic cadherin adhesion is energetically favorable over (or equivalent to for type I cadherins) heterophilic cadherin adhesion⁵¹, this creates a situation where cell–cell adhesion is markedly decreased at the boundary between tissue compartments and increased within the respective tissue compartment, correlating once again with the pattern of higher heterotypic tension at the boundary and lower homotypic tension within tissue compartments. Previous work suggests that, during zebrafish neural tube compartmentalization, this mechanism is also regulated via a signaling gradient of the morphogen Shh to Cdh2 and Cdh11 via protocadherin Pcdh19 (ref. ⁵⁰), an observation we are able to corroborate in our system as shown in Supplementary Fig. 11a.

Interestingly, another study on mouse neural tube patterning has shown that a dorso-ventral (DV) gradient of mechanical forces exists in the embryo and leads to a graded activation of YAP signaling along the DV axis, causing a spatially compartmentalized expression of the transcription factor Foxa2 and its downstream transcriptional target Shh⁵³. Since such a gradient of mechanical tension exists in the vicinity of the boundary between the CM and FMH in dataset 2 (Fig. 4a), it is tempting to speculate that it could also lead to the formation of a gradient of YAP signaling activity in this system, and thus be the origin of the observed Shh gradient at the compartment boundary. This hypothesis is supported by the observation of a graded expression of Cyr61, a well-characterized transcriptional target of Yap, and of Foxa2 and its transcriptional targets, such as Ptch1, at the border between CM and FMH, as shown in Supplementary Fig. 11b. In addition, as shown in Supplementary Fig. 11c, markers of neural tube DV patterning, Nkx2.2, Nkx6.1, Pax7 and Pax3, are also expressed at the boundary between the CM and FHM tissue compartments in a spatial sequence that follows the spatial gradient of mechanical forces and is reminiscent of that observed in the mouse neural tube⁵³.

Overall, these results provide a rational molecular mechanism to explain the higher heterotypic interfacial tension observed at the boundary between tissue compartments in our different datasets and support the conclusion that this mechanism may play an important role in maintaining a sharp boundary at the interface of two tissue compartments. The LR analysis was performed with spatial transcriptomics data alone, without taking the inferred mechanical properties of the boundary into account. Nevertheless, these independent analyses yielded complimentary results; the LR gene pairs with highest interaction potential are enriched in adhesion and mechano-transduction, providing putative molecular mechanisms for the mechanical properties of the boundary. This illustrates how the combination of force inference analysis with spatial molecular profiling can provide insight into the mechanism of boundary formation in the context of embryonic development.

GSEMs detect gene expression modules associated with cellular mechanics while controlling for spatial confounders

Our previous analysis identified putative mechanisms for cooperativity between gene expression and cellular mechanics in establishing and maintaining boundaries during development. To identify additional developmental processes in which cellular mechanical and transcriptional states are coordinated, we next sought to perform unsupervised tests for associations between gene expression and mechanical measurements.

We first tested the association between gene expression and mechanical state for datasets 1 and 2 by using a linear model to regress single-cell gene expression levels on two mechanical quantities: cellular pressure and the magnitude of the cellular stress tensor (Methods). Statistical analysis identified a number of ‘mechano-associated’ genes, that is, genes whose expression is significantly up- or downregulated with cellular pressure or stress tensor magnitude. To identify genes that are confidently associated with mechanics, we searched for genes that were significantly associated with mechanical quantities in both datasets. Supplementary Fig. 10a shows that there were 150 pressure-associated and 1,049 stress tensor-associated genes shared by datasets 1 and 2, respectively. Among these, a total of 131 mechano-associated genes showed significant association with both pressure and stress tensor magnitude for both datasets. GO overrepresentation analysis (Methods) showed that this gene set is enriched in genes associated with ‘cell migration’, ‘tissue morphogenesis’ and ‘ECM organization’ (Supplementary Fig. 10b), processes that are highly dependent on cellular mechanical state.

To further identify specific signaling pathways and mechanisms, we examined the specific genes involved. Volcano plots in Supplementary Fig. 10c show these mechano-associated genes for dataset 2, highlighting in red some of the 131 top associated genes discussed above. Some genes, such as Hpln1 or Col4a1, are associated with extracellular matrix (ECM) structure and mechanical properties, while others, such as Ccnl2, are involved in cell cycle regulation or cell metabolism, including Igf2. Some genes such as Arhgef15 (involved in ephrin–LR signaling), Actb, Dchz1 and Rhod are involved in cytoskeleton organization and contractility. Consistently, others are known transcriptional targets of well-characterized mechano-transducers such as Cav1 and Cyr61, which are downstream of Yap. Interestingly, all of the aforementioned genes have gene expression patterns that negatively correlate with the magnitude of the pressure and stress tensor, that is, they tend to be upregulated in cells under tensile stress and downregulated in cells under more compressive stress.

However, a limitation of linear regression testing is that it does not account for spatial confounding effects. Spatial confounding could interfere with the estimated effects because both morpho-mechanical measurements and transcriptomic states are themselves spatially dependent; in particular, tissue regions comprising common cell types or subtypes may show similarities in both bulk mechanical properties and transcriptomic states. Therefore, we performed a second analysis, utilizing a geoadditive structural equation model (gSEM), which accounts for spatial confounding effects in both predictor and response variables by modeling and subtracting the spatial confounding effects from both variables, resulting in spatially regressed variables with no spatial confounding. This methodology provides a means for rigorously accounting for spatial confounding effects in our data.

We tested the association between gene expression and mechanical state for all three datasets using a linear model to regress spatially regressed single-cell gene expression levels on the two spatially regressed mechanical quantities (Methods). We identified a number of mechano-associated genes, as expected, accounting for spatial confounding resulted in fewer statistically significant genes being identified. Most of these genes appear to be cell type and tissue specific, suggesting that the effects of cellular mechanics on gene expression are context dependent; this highlights the utility of our approach to infer mechanical properties and gene expression in the same cells. Despite differences in specific mechano-sensitive genes, GO overrepresentation analysis (Methods) showed that GO terms relevant to both developmental processes and cellular mechanics were enriched across multiple datasets (Fig. 5b,d and Supplementary Fig. 8b,d). For example, we identified terms such as ‘negative regulation of substrate adhesion-dependent cell spreading’ and ‘negative regulation of cell morphogenesis involved in differentiation’ enriched in dataset 2, while dataset 3 was enriched in the terms ‘regulation of actin cytoskeleton organization’ and ‘leukocyte migration’.

Fig. 5: Structural equation regression identifies significant correlations between gene expression and cellular mechanics accounting of spatial confounding effects.

a, A volcano plot for dataset 2 showing, for each gene, the adjusted (adj.) P value by two-sided t-test followed by BH adjustment (y axis) plotted against the regression coefficient, β_spatial, obtained by regressing the spatially regressed residual of gene expression on the spatially regressed residual of cellular pressure (x axis). Side plots represent such linear regressions for two example genes whose spatially regressed gene expression residuals are respectively negatively (left) and positively (right) associated with the spatially regressed residual of cellular pressure. b, GO overrepresentation analysis for up- and downregulated genes with cellular pressure. GO terms are ranked according to P value by hypergeometric test and gene count. c, A volcano plot for dataset 2 showing, for each gene, the adjusted P value by two-sided t-test followed by BH adjustment (y axis) plotted against the regression coefficient, β_spatial, obtained by regressing the spatially regressed residual of gene expression on the spatially regressed residual of the magnitude of the cellular stress tensor. Side plots represent such linear regressions for two example genes whose spatially regressed gene expression residuals are respectively negatively (left) and positively (right) associated with the spatially regressed residual of the cellular stress tensor. d, GO overrepresentation analysis for up- and downregulated genes with cellular stress tensor. GO terms are ranked according to P value by hypergeometric test and gene count. e, Spatial gene expression maps for selected genes (labeled in purple in a) displaying significant correlations between gene expression and cellular pressure in both the linear and the structural equation regression analyses.

Volcano plots in Fig. 5a,c and Supplementary Fig. 8a,b show the mechano-associated genes identified for datasets 2 and 3. We found that, although there was generally a low degree of overlap between genes identified as significantly associated in the linear regression analysis above and the gSEM analysis, the inferred effect sizes showed good correlation across both analyses (Supplementary Fig. 8c,e). Furthermore, several genes were highlighted in both analyses. Many of these genes have known roles in regulating cellular mechanical properties, for example, Slc9a3r2 (NHERF2), Lima1 and Crabp2 (Fig. 5e). Slc9a3r2 interacts with and regulates the ERM complex, which couples the actomyosin cortex with the cell membrane and enables forces generated through cytoskeletal dynamics to influence the overall mechanical properties of the cell and, more particularly, the cell–cell junctional tensions⁵⁴. Lima1 is also relevant in actin cytoskeletal dynamics through regulating actin fiber crosslinking and depolymerization⁵⁵, while Crabp2, a component of the retinoic acid signaling pathway, has previously been shown to modulate mechano-sensing in the context of pancreatic cancer⁵⁶. Our analysis also revealed a number of novel links between mechanics and gene expression. One such example is Apba2, which interacts with and stabilizes the amyloid precursor protein (APP). Interestingly, previous work has shown that aggregation of the amyloid-β peptide generated by APP affects the mechanical properties of single cells in a pathological context⁵⁷. This novel association suggests a potential role for Apba2, and thus APP, in responding to changes in mechanical state during development.

Analysis of nonlinear associations between gene expression and mechanical properties identifies distinct patterns of association with cellular mechanics

We next turned to investigate nonlinear associations between cellular mechanics and gene expression at the single-cell level. To that aim, we ranked cells in each dataset by either cellular pressure or stress tensor magnitude, and computed smoothed expression value estimates using a local weighted-median metric. Subsequently, we used scHOT⁴¹ to identify statistically significant patterns of association between the weighted median gene expression and cellular mechanical property. Significant gene–mechanics associations were then clustered using hierarchical clustering to identify clusters of genes with consistent association patterns. We performed this analysis for both dataset 2 (Fig. 6) and dataset 3 (Supplementary Fig. 9). For dataset 2, we obtained seven clusters of genes associated with pressure and four clusters of genes associated with stress tensor magnitude. For dataset 3, we obtained seven clusters of genes associated with pressure and five clusters of genes associated with stress tensor magnitude.

Fig. 6: Statistical analysis of higher-order interactions establishes the existence of significant nonlinear associations between gene expression and cellular mechanics.

a, Analysis of nonlinear associations between gene expression and cellular pressure in dataset 2. The summary statistic used is the weighted median gene expression. For each gene, the association between this statistic and the cellular pressure ranking is tested. Significant (P_adj < 0.1 by permutation test followed by BH adjustment) association profiles are z normalized and clustered. Line plots of the weighted-median expression z score against cellular pressure ranking are shown for selected clusters, along with bar plots showing GO overrepresentation analysis of genes in each cluster. Bottom: spatial gene expression maps for example genes with representative behaviors. GO terms are ranked according to P value by hypergeometric test and gene count. b, Analysis of nonlinear associations between gene expression and cellular stress tensor magnitude in dataset 2. The analysis was performed as for a. Line plots of the weighted-median expression z score against cellular pressure ranking are shown for selected clusters, along with bar plots showing GO overrepresentation analysis of genes in each cluster. Bottom: spatial gene expression maps for example genes with representative behaviors. GO terms are ranked according to P value by hypergeometric test and gene count.

The clusters identified in dataset 2 revealed that different clusters showed distinct patterns of association with cellular mechanics, and different spatially localized patterns of expression, suggesting that mechanical differences between tissue regions may influence region-specific gene expression. Interestingly, we also identified functional differences between genes in different clusters. In dataset 2, amongst genes nonlinearly associated with pressure, cluster 1 displayed a sigmoid expression profile where gene expression is upregulated at low intracellular pressure and downregulated after a certain pressure threshold (Fig. 6a). GO overrepresentation analysis (Methods) revealed that these genes were involved in developmental processes such as ‘cell fate commitment’, ‘neuron differentiation’ and ‘glial cell migration’. Genes in cluster 4 display the opposite behavior, being expressed at a low levels before becoming upregulated at higher intracellular pressure when values exceeded a certain threshold (Fig. 6a). These genes were found to be associated with a variety of cellular and developmental processes such as ‘pattern specification process’, ‘epithelial tube formation’ and ‘forebrain neuron development’. Reflecting the GO overrepresentation analysis, we also observed known master regulators of neural development (for example, Wnt7b, Lhx2, Pax3 and En1), as well as genes involved in cell adhesion and contractility (for example, Epha7 and Shroom3) within the same clusters, suggesting cooperativity between cellular mechanics and regulation of developmental processes.

As for genes nonlinearly associated with stress tensor magnitude, clusters 1 and 4 also displayed the two kinds of sigmoid response previously encountered (Fig. 6b). Genes in cluster 1 were associated with ‘forebrain development’ and ‘telencephalon development’, and were upregulated at low stress tensor magnitude before sharply decreasing their expression beyond a certain threshold. Mirroring this behavior were genes of cluster 2, which were associated with ‘central nervous system development’ and ‘proximal/distal pattern formation’, and were downregulated at low and high stress tensor magnitude, with expression within only a narrow range of stress tensor magnitude values. Notably, the expression profiles displayed by gene clusters 1 and 2 showed a remarkable sensitivity, suggesting that the expression of these genes is regulated by either a mechano-sensitive band-pass (cluster 2) or band-stop (cluster 1) filter. Corroborating this, we observed similar band-pass behavior in gene clusters identified in dataset 3 (Supplementary Fig. 6); again, we also observed co-localization of factors important in development and regulators of cellular mechanics within the same clusters. This suggests that these band-pass and band-stop behaviors may be general mechanisms for coupling mechanics and gene expression during development. While such nonlinear gene expression dependencies have been engineered in synthetic bacterial and mammalian systems in response to external biochemical signals⁵⁸, their observation in the setting of a native tissue is, to our knowledge, unprecedented.

Discussion

In this study, we presented a computational framework for combined spatial transcriptomics and image-based mechanical force inference at single-cell resolution. Using synthetically generated images of multicellular tissues, we showed that our approach is accurate and robust to noise associated with confocal fluorescence imaging of immunostained tissue sections and cell instance segmentation. We demonstrated that our framework can be applied to ISH-based spatial transcriptomics datasets by performing an integrated analysis of a seqFISH dataset of the E8.5 mouse embryo. Using three different brain regions from two different embryos as benchmark datasets, we were able to perform an integrated analysis of mechanical forces and gene expression at single-cell resolution.

Our analyses revealed that boundaries defined by differential gene expression are consistently associated with elevated cell–cell junctional tension, which remains conserved across parallel z planes and underscores the role of mechanical forces in boundary formation and maintenance. Biophysical simulations demonstrated that heightened heterotypic tension alone can sustain these boundaries and may initiate them when cell types are initially intermixed. LR analysis further indicated that ephrin signaling contributes to this elevated tension through locally enhanced actomyosin contractility and differential cell adhesion. Finally, a gSEM uncovered numerous genes whose expression correlates nonlinearly with tension and pressure. These genes span key biological processes, including cell migration, cell metabolism, mechano-transduction, responses to morphogens and hormones, and tissue morphogenesis. Notably, the expression of some genes was found to be up- or downregulated over a narrow range of mechanical forces, suggesting the existence of mechano-sensitive band-pass and band-stop filters.

The nonlinear associations with mechanical forces identified in our analyses provide a compelling case for further experimental work aimed at elucidating the precise molecular mechanisms underpinning these behaviors. There are a number of promising experimental approaches that would enable the quantitative characterization of putative band-pass and band-stop mechano-sensing genes. For example, combining optogenetic control of actomyosin contractility with in vivo live mRNA imaging through the MS2 reporter system^59,60,61,62 would enable the measurement of changes in gene expression in response to local perturbations of cellular interfacial tension. Indeed, our computational methods complement this approach well. Experimental approaches to live mRNA imaging, such as the MS2 reporter system, cannot be multiplexed to image many genes or transcripts simultaneously; our pipeline for inferring tissue mechanical properties and identifying nonlinear associations between mechanics and gene expression can therefore be used to select candidate genes of interest for experimental investigation.

However, our analysis also highlights the limitations of the seqFISH technology. First, the fidelity of this approach is highly dependent on the quality of staining and 2D sectioning. The quality of membrane immunostaining can hinder the segmentation of individual cell contours, leading to inaccurate recovery of cell junction curvatures, imprecise inference of mechanical forces and difficulties in processing large datasets. Alternative membrane staining strategies, such as the use of antibodies against other membrane proteins or against other components of the cell membrane such as glycolipids⁶³, can improve membrane staining and allow large-scale automated cell segmentation and accurate mechanical force inference. Furthermore, all current ISH-based spatial transcriptomics methods require successive rounds of probe hybridization and imaging, and therefore must undergo tissue fixation before antibody staining for membrane segmentation. Different fixation strategies, including the paraformaldehyde fixation used for the seqFISH data used in this study, have been shown to induce morphological distortions such as cytoplasmic shrinkage in cultured cells⁶⁴. Since force inference requires accurate cell morphologies that are reflective of the true mechanical state of the tissue, the potential effects of fixation on the accuracy of inferred mechanics must be considered. Second, our current approach focuses on 2D slices. While it has been shown that 2D force inference is a good proxy for 3D inference for simple isotropic cellular ensembles, such as those found in components of early mouse or nematode embryos⁶⁵, this is not generally true for nonplanar and anisotropic systems. For example, the seqFISH dataset used in this analysis includes whole-embryo sagittal sections, where some regions may intersect the plane of the section rather than being parallel to it. This means that the inferred 2D stress tensor captures only a subset of the information present in the full 3D stress state of a cell. In addition, E8.5 mouse embryos contain a variety of regions that are not populated by cells, but by ECM and fluid-filled cavities whose mechanical properties influence the mechanical behavior of adjacent tissue layers in ways that cannot be captured by the present 2D method. Generalizing the current framework through 3D gene expression profiling⁶⁶, cell segmentation and force inference^67,68 will be a critical step toward a more integrative and precise understanding of the reciprocal role of mechanical forces and gene expression, cell fate decisions and tissue morphogenesis during development. Taking advantage of improved staining and 3D imaging, future studies will aim to extend the scope of our analysis by incorporating additional morphometric measures to capture cell shape, such as point cloud-based methods¹⁶ or Fourier shape descriptors¹⁵. In addition, the measurement of additional genomic modalities, such as metabolomics, proteomics and chromatin accessibility, as well as metrics that capture the nature of the local cell environment, such as the size and composition of the cell neighborhood or the coarse-grained stress tensor, could help us to better understand how cellular mechanical and transcriptional phenotypes are regulated and integrated at the tissue and organismal level. Finally, advances in computational methods for analyzing spatial omics will enable a more robust and comprehensive characterization of the relationship between tissue mechanical properties and its transcriptomic, epigenetic and proteomic state. For instance, our analysis of LR communication across boundaries did not consider potential communication between nonadjacent cells via diffusible ligands. This is due, in part, to the highly pathway- and context-dependent nature of paracrine signaling with which existing methods for inferring spatial intercellular communication struggle. As improved computational methods are developed for analyzing spatial data, the utility of our approach will undoubtedly increase.

Overall, our computational framework can be applied directly to ISH-based spatial transcriptomics datasets with minimal additional processing required. Although some previous studies have performed combined analysis of single-cell morphometrics and gene expression⁶⁹ and others have investigated the relationship between mechanical forces or mechanical properties and expression of individual genes^70,71, integration of mechanical force inference and spatial transcriptomics at single-cell resolution has not been previously reported. The work presented here contributes to our understanding of the interplay between mechanical forces and gene expression at the cell and tissue level and provides an innovative and powerful tool that can be applied to other spatial transcriptomics datasets to further investigate this interplay in a variety of physiological and pathological contexts.

Methods

Transcriptomics quantification

A previously published multi-embryo seqFISH dataset was used to examine the utility of the spatial mechano-transcriptomics workflow²⁴. In this approach, the abundance and positions of individual transcripts were obtained at subcellular resolution for 387 genes across sections of three mouse embryos at developmental stage E8.5. This dataset was used to impute a broader pattern of gene expression taking advantage of the mouse gastrulation atlas dataset, a previous single-cell atlas obtained from single-cell RNA-sequencing analysis using a 10X Genomics pipeline⁷². We targeted the correlation between cell mechanics and gene expression in the context of boundary formation in three different brain regions (Fig. 1b), spanning the intersection between the FMH and NC (dataset 1), the boundary between the CM and FHM (dataset 2) and an upper brain region involving the MHB (dataset 3).

Image segmentation

High-quality segmentation masks are essential for accurate image-based mechanical force inference. As the existing segmentation masks for the E8.5 mouse seqFISH dataset exhibited high variability across biological regions and replicates with frequent instances of over- or undersegmentation, we reprocessed the imaging datasets as follows. We first preprocessed the membrane segmentation immunofluorescence images by local contrast enhancement in Fiji⁷³ using the Contrast Limited Adaptive Histogram Equalization algorithm⁷⁴ with parameters (blocksize = 99, histogram bins = 128, slope = 5), followed by denoising via outlier removal. Next, we performed automated segmentation of 4,6-diamidino-2-phenylindole (DAPI)-labeled cell nuclei using a custom deep learning pipeline. The ground-truth dataset used for training was composed of 12 image and mask pairs tilled into 16 random 256 × 256 pixel image patches and split into three batches comprising training, validation and test datasets in a 70:15:15 ratio. The convolutional neural network trained for binary segmentation involved a custom ‘light weight’ U-Net with a reduced depth of one level as compared with the original implementation⁷⁵ resulting in a network with ~0.5 million nodes and using ELU instead of ReLu as activation functions. Training was carried out using Tensorflow 2.0 and Keras 2.8 libraries⁷⁶, using a custom loss function combining weighted binary cross-entropy and dice index loss, and using the Adam optimizer, a batch size of 16 and a learning rate of 0.0001. Then, the resulting nuclei centroids were used as seeds to a initialize a watershed algorithm⁷⁷ to generate cell instance segmentation masks on the basis of the averaged E-cadherin, N-cadherin, pan-cadherin and β-catenin immunostaining fluorescence signals. The cell contour segmentation masks were further preprocessed and curved edges between cell–cell contacts were identified via circular arc fitting. Poor-quality edges were manually corrected using Fiji⁷³.

Circular arc polygon tiling

Following image segmentation, circular arcs approximating the locus of cell boundaries and their contact points are required for downstream stress inferences²². This results in a circular arc polygon (CAP) tiling. More precisely, the CAP tiling fits a circular arc parameterized by the center of curvature ρ_αβ and radius of curvature R_αβ to each cell–cell junction between two cells α and β. In cases where the cell–cell junction is not curved or exhibits inconsistent curvature (for example, ‘wiggly’ boundaries where the sign of curvature changes along the boundary), a straight line was fit to the junction instead. The curve-fitting procedure, as well as the criteria for identifying straight junctions, were adapted from ref. ²².

Spatial transcriptomics processing

Cells identified in the corrected segmentation were correlated with cells in the original segmentation using a pairwise Jaccard index. Real overlaps were defined as cells with greater than 0.1 Jaccard similarity, and all overlaps were filtered out. Weights for each cell in the original segmentation mask for each cell in the corrected segmentation mask were calculated using the fraction of overlap in the segmentation masks. Cells in the corrected segmentation with ≤0.4 total overlap were filtered out. The resulting weights were used to compute corrected expression matrices, using a weighted mean of both the imputed expression values and raw counts for genes profiled by seqFISH. Corrected raw counts were further normalized by the total mRNAs identified in each cell and log transformed.

Tissue boundaries defined by transcriptomic profiles

Boundaries within the three datasets were defined using a boundary likelihood metric. For a given cell i with neighbors N and two sets of cell types A and B, the boundary likelihood between A and B at cell i was defined as

$$L=\frac{1}{N}\sum _{i\in N}[i\in A]\times \frac{1}{N}\sum _{i\in N}[i\in B].$$

(1)

A threshold of L > 0.15 was applied to identify cells at a boundary. The boundary within the ‘embryo 2 midbrain–hindbrain’ region was defined manually, similarly to the method applied in the original study²⁴.

To investigate properties of cell–cell junctions at boundaries, each cell was assigned a distance to boundary d, defined as the number of neighbors between that cell and the closest cell belonging to the boundary. A cell–cell junction between the cell pair {α, β} was defined as ‘near-boundary’ if min(d_α, d_β) ≤5 and ‘at-boundary’ if min(d_α, d_β) =0. At-boundary junctions were then classified as homotypic if both cells belonged to the same cell-type set, or heterotypic otherwise.

LR signaling analysis across tissue compartment boundaries

Log-transformed, normalized imputed gene expression values were derived after correction using the method described above and used for analysis of LR signaling potential across tissue boundaries.

LR annotations from the CellChat database⁷⁸ were obtained with Omnipath⁷⁹ and filtered for LR pairs for which both ligand and receptor showed non-zero expression in our transcriptomic data. An ‘interaction potential’ P_L→R,α,β = L_α × R_β was defined for each LR pair {L, R} across the cell pair {α, β} to quantify the potential degree of signaling through the receptor. This definition takes into account the directionality of signaling interactions and allows for the signaling through the receptor to be investigated independently for both tissues at a boundary.

LR signaling interactions were compared for two spatially adjacent cell types {A, B} using the interaction likelihood metric l, defined as

$${l}_{L\to R}=\min ({W}_{A},{W}_{B}),$$

(2)

where W_A represents the Wilcoxon rank-sum test statistic between the interaction potential distribution P_L→R,α,β for α ∈ A, β ∈ B and the interaction potential distribution for {α, β} ∈ A. Signaling interactions were ranked by interaction likelihood, with negative interaction likelihoods (that is, where the {A, A} interaction likelihood or {B, B} interaction potential is higher than the {A, B} interaction likelihood) filtered out, and genes in the top 50 interactions were tested for overrepresentation of GO terms compared to the total set of ligand and receptor genes (see the 'GO analysis' section).

Mechanics quantification

Inferring tension from images

There are a variety of methods for inferring intercellular stress in tissues at mechanical equilibrium, that is, where the tensions at each vertex of the cell array sum to zero²³. These methods vary in sophistication, which mechanical features are inferred and dependence on the image segmentation quality. At the most basic level, segmentation-free methods exploit the correlation between cell shape anisotropy and stress anisotropy to derive coarse-grained estimates of tissue stress in tissues where accurate cell segmentation cannot be performed⁸⁰. If segmentation is possible, but there is high noise that prevents a precise determination of the geometry of cell–cell junctions and vertices, methods such as chord inference can be used that model cell–cell junctions as straight lines and therefore discount the contribution of cell pressure to the geometry of the cell array²⁰. Tangent inference methods improve on chord inference by using the angle between cell–cell junctions at vertices. This allows for less noisy output but requires more precise image segmentation. However, cell pressures are again not taken into account in this approach⁸¹. Recent methods are able to infer both cell junction tension and cell pressure by measuring the curvature at cell–cell junctions as well as vertex angles. However, these methods generally require increased segmentation precision and are not robust to noise. The VMSI method²² circumvents these issues by inferring both pressures and tensions simultaneously from fitted CAP tilings instead of the segmented image, as the CAP tiling provides additional noise reduction over the segmentation itself. Hence, we build on and extend the VMSI method to probe the mechanical properties of seqFISH generated data.

Mechanical phenotypes

Following²², three mechanical phenotypes were computed for each cell α and each adjacent cell pair (α, β): the cellular pressure p_α, the cell–cell junctional tension T_α,β and the stress tensor σ_α.

Given a CAP tiling, let ρ_αβ be the center of the curvature of the circular arc at the (α, β) cell–cell junction, and let R_αβ be the radius of curvature of the same arc. Force balance equations result in geometrical constraint variables {q, θ_α}, which parameterize the curvature center and radius

$${{{\mathbf{\rho} }}}_{\alpha \beta }=\frac{{p}_{\beta }{{{\bf{q}}}}_{\beta }-{p}_{\alpha }{{{\bf{q}}}}_{\alpha }}{{p}_{\beta }-{p}_{\alpha }},$$

(3)

$${R}_{\alpha \beta }=\sqrt{\frac{{p}_{\alpha }{p}_{\beta }| {{{\bf{q}}}}_{\alpha }-{{{\bf{q}}}}_{\beta }{| }^{2}}{{({p}_{\alpha }-{p}_{\beta })}^{2}}-\frac{{\theta }_{\alpha }-{\theta }_{\beta }}{{p}_{\alpha }-{p}_{\beta }}}.$$

(4)

Cellular pressure

Cellular pressures were computed in two steps²². First, initial values for cell pressures p_α and geometric constraint parameters q enforced the condition that ρ_αβ the center of curvature to the edge vertices r_i, r_j, must be perpendicular to the edge tangents τ_i, τ_j, minimizing the functional

$${E}_{p,\bf{q}}=\frac{1}{{n}_{e}}{\Sigma }_{(\alpha ,\beta )}{[{{\hat{\bf{t}}}}_{i}\times {{{\hat{\bf{\tau} }}}}_{j}]}^{2}+{[{{\hat{\bf{t}}}}_{j}\times {{{\hat{\mathbf{\tau} }}}}_{j}]}^{2},$$

(5)

where ${\hat{{\boldsymbol{t}}}}_{i}$ is the unit vector along r_i − ρ_αβ and ${{{\hat{\tau }}}}_{i}$ is the edge tangent at vertex i. Similarly, initial values θ optimized the functional

$${E}_{\theta }={\Sigma }_{(\alpha ,\beta )}{R}_{\alpha \beta }^{2}-{\left(\frac{1}{2}| {{{\bf{r}}}}_{{{i}}}-{{{\mathbf{\rho} }}}_{\alpha \beta }| +\frac{1}{2}| {{{\bf{r}}}}_{{{j}}}-{{{\mathbf{\rho}}}}_{\alpha \beta }| \right)}^{2},$$

(6)

where ρ_αβ were calculated using the {p, q} values determined previously. Second, the initial values (p_α, q_α, θ_α) were used to instantiate the gradient descent optimization of the objective

$${E}_{p,q,\theta }=\frac{1}{2{n}_{e}}\sum _{(\alpha ,\beta )}\mathop{\sum }\limits_{n}^{{N}_{\alpha ,\beta }}{(| {{{\bf{r}}}}_{\alpha \beta }(n)-{{\mathbf{\rho}}}_{\alpha \beta }| -{R}_{\alpha \beta })}^{2},$$

(7)

finding the mechanical equilibrium parameters resulting in a CAP tiling which best approximated the one obtained through image segmentation. Here, r_αβ(n) denotes the nth pixel along the circular arc approximation of the edge between cells (α, β) in the segmented CAP tiling, and n_e denotes the total number of edges.

Cell–cell junctional tension

Cell–cell junctional tensions were computed as functions of the corresponding cellular pressures and the corresponding radius of curvature using the Young–Laplace law: T_αβ = (p_α − p_β)R_αβ.

Stress tensor

The 2D cellular stress tensors σ_α were defined from the inferred cellular pressures and cell–cell junctional tensions using Batchelor’s formula⁸²

$${\sigma }_{\alpha }=-{p}_{\alpha }{{\delta }}+\sum _{\{\beta \}\alpha }\frac{{T}_{\alpha \beta }}{2{A}_{\alpha }}\int_{{r}_{\alpha \beta}}{\mathrm{d}}r\, {\hat{{\bf{r}}}}_{\alpha \beta }\otimes {\hat{{\bf{r}}}}_{\alpha \beta },$$

(8)

where p_α and A_α denote the pressure and area of cell α, respectively, T_αβ denotes the junctional tension between adjacent cells (α, β), and ${\hat{{\bf{r}}}}_{\alpha \beta }$ is the unit vector along the junction. The resulting 2 × 2 stress tensor encodes all of the stress information of a cell⁶⁵. Using the elements of the cellular stress tensor, five interpretable descriptors of the mechanical state of a cell can be computed: the two eigenvalues of the stress tensor, the stress tensor magnitude, the stress tensor anisotropy and the stress tensor orientation. The stress tensor magnitude was defined as the sum of its eigenvalues, its anisotropy was defined as the eccentricity of ellipse formed by the two eigenvectors and its orientation was defined as the angle between the major axis of the ellipse formed by the two eigenvectors and the x axis of the image.

Practical considerations

Calibration via mask processing

For force inference results to be valid, variational methods such as VMSI²² assume that all vertices between cells are threefold, as a large proportion of vertices with more than three cells would violate the assumption of mechanical equilibrium²³. The dual triangulation used by VMSI explicitly forbids fourfold (or greater) vertices. In our implementation (Fig. 1a), these vertices are filtered before inference by recursively splitting each invalid vertex into two vertices in the direction of greatest variance of neighbor vertices until all vertices are threefold. Further, VMSI assumes that all angles between cell junctions at a vertex are convex. Concave vertices under the VMSI formulation imply negative tension at one of the junctions²³, a situation that is hard to motivate biologically and beyond the scope of the method. Therefore, concave vertices are assumed to be a precision error in the cell segmentation, and are dealt with by moving the vertex until all angles between junctions are concave, as shown in Fig. 1a.

Robustness checks via simulations

Synthetic images of 2D multicellular tissues (Supplementary Fig. 1a) for which the ground-truth values of cell pressures and cell–cell junction tensions are known were generated to test the accuracy and robustness of force inference. The estimated force inference values were highly correlated with their corresponding ground-truth values (Spearman’s ρ > 0.96; Supplementary Fig. 1b) across a range of average pressure differentials (Supplementary Fig. 1f,g) and image sizes (Supplementary Fig. 1e). Furthermore, our approach showed robustness against noise in the measured vertex position as well as occasional incorrect merging of adjacent cells (undersegmentation) during image segmentation (Supplementary Fig. 1c,d). This is notable as these are common sources of error in instance cell segmentation and demonstrates the practical applicability of our image-based force inference algorithm to real microscopy images.

Optimization details

We developed a Python implementation of the VMSI algorithm. All optimization steps were performed using the augmented Lagrangian method with a subsidiary L-BFGS algorithm using the NLopt optimization library⁸³. Analytic Jacobians were supplied for the objective and constraint functions for increased speed and accuracy.

Tissue boundary maintenance and cell sorting simulations

To simulate tissue compartments boundary maintenance and cell sorting, we used a custom C++ implementation⁴³ of the Cellular Potts Model⁴². In this framework, multicellular tissues are represented as 2D lattices of pixels, k, partitioned into N cells. Each cell, i, is composed of all the lattice sites with a pixel value equal to i, with i ∈ {1…N}. Each cell is assigned a cell-type, τ_k, which is defined at the pixel level, and is thus a function of its position on the lattice. The dynamics of this system is driven by two components: a membrane surface energy term and an elastic deformation term. The membrane surface energy is determined by cell–cell junctional tensions—the outputs of the mechanical force inference algorithm—and controlled by a cell-type dependent parameter ${J}_{{\tau }_{k},{\tau }_{{k}^{{\prime} }}}$. The elastic deformation term enforces the condition that cell volumes V_i do not markedly deviate from a target value V₀ and are parameterized by a bulk modulus κ. The cell–cell interactions and the volume constraints can be combined into a global energy function, E in which

$$E=\sum _{i}\frac{1}{2}\kappa {\left({V}_{i}-{V}_{0}\right)}^{2}+\sum _{(k,{k}^{{\prime} })}{J}_{{\tau }_{k},{\tau }_{{k}^{{\prime} }}}\left(1-{\delta }_{i(k)i({k}^{{\prime} })}\right),$$

(9)

where i represents the cell index and $(k,{k}^{{\prime} })$ represent pairs of neighboring pixels, ${\delta }_{i(k)i({k}^{{\prime} })}$ takes the value of unity when both pixels belong to the same cell and 0 otherwise, to solely account for interactions at cell–cell junctions. Moreover, ${J}_{{\tau }_{k},{\tau }_{{k}^{{\prime} }}}={J}_{hom}$ if k and ${k}^{{\prime} }$ belong to two cells of the same cell type, and ${J}_{{\tau }_{k},{\tau }_{{k}^{{\prime} }}}={J}_{het}$ if k and ${k}^{{\prime} }$ belong to two cells of a different cell type. The system dynamics results from the iterative minimization of this energy function through the Metropolis Monte Carlo algorithm⁸⁴, where the level of noise in the system is accounted for by a temperature parameter T. Time is here expressed in Monte Carlo steps (MCS), where 1 MCS corresponds to an average of one iteration per pixel over the whole lattice. For the simulations described in Fig. 3 and Supplementary Fig. 6, parameters are set to V₀ = 40, κ = 1.0 and T = 10.0. The numerical values used in simulations for parameters J_hom and J_het differ for each dataset and are those inferred for the homotypic and heterotypic junctional tensions reported in Fig. 3c. For simulating tissue compartment boundary maintenance, a cell aggregate was initially split in two by a straight boundary separating two distinct cell types. For cell sorting simulations, initial conditions were set to a cell aggregate where the two cell types were allocated at random. For all simulations the total number of cells was set to N = 540 cells, which were equally assigned to both cell types considered. All simulations were run for 50,000 MCS and at least in 6 replicates. To quantify the boundary maintenance and sorting dynamics, we computed the heterotypic boundary length, l_HB, defined as the total length of the interface between cells of a different cell type

$${l}_{\mathrm{HB}}=\sum _{(k,{k}^{{\prime} })}\left(1-{\delta }_{{\tau }_{k},{\tau }_{{k}^{{\prime} }}}\right),$$

(10)

where ${\delta }_{{\tau }_{k},{\tau }_{{k}^{{\prime} }}}$ takes the value of unity when k and ${k}^{{\prime} }$ belong to cells of the same cell type and 0 otherwise. As shown in Supplementary Fig. 6c, l_HB decreases over time in cell sorting simulations, as cells of a different cell type sort out in spatially distinct clusters. However, as shown in Supplementary Fig. 6d, during boundary maintenance simulations, l_HB remains constant, as long as the boundary between the two tissue compartments is maintained.

Integrative analysis of tissue mechanics in serial sagittal planes

Inferred cellular mechanical properties were compared across serial sagittal planes of the mouse MHB as follows. The two z slices available from this tissue section were separated by 12 μm in the z direction, but with the same x and y positions as dataset 3. Owing to the 12 μm z separation, these parallel z slices do not contain the same cells. Therefore, to enable an unbiased comparison of inferred mechanical properties, we devised a method to smooth the cell pressure and stress tensor magnitude, and sample these smoothed values across a grid of points common to both planes to be used for further analysis.

We first initialized a 40 × 40 square grid of sampling points to cover the entire field of view of the tissue image. To filter out points that are outside of the tissue region for which mechanical properties are inferred in at least one z slice, we approximated each cell for which we have inferred mechanical properties as a rectangle defined by the cell centroid and bounding box dimensions; any sampled points which do not lie within a cell in both z slices was filtered out. Next, we calculated a Gaussian-smoothed mechanical quantity at each sampled point using the following smoothing function

$${q}_{i}=\mathop{\sum }\limits_{j}^{N}{q}_{j}\times {w}_{ij},$$

(11)

$${w}_{ij}=\frac{\exp \left(-\frac{1}{2}{\left(\frac{d(i,\,j)}{\sigma }\right)}^{2}\right)}{\mathop{\sum }\nolimits_{k}^{N}\exp \left(-\frac{1}{2}{\left(\frac{d(i,k)}{\sigma }\right)}^{2}\right)},$$

(12)

for each mechanical quantity q_i at a sampled point i, smoothing across N cell centroids indexed by j. We use the Euclidian pixel distance as our distance function d(i, j), and take σ = 100.

We next computed local spatial correlations for the smoothed cell pressure and stress tensor magnitude across z slices using scHOT⁴¹. In detail, we defined a conical weight matrix with span 0.05, and computed the local weighted Spearman correlation for each sampled point. For a weighting scheme w that assigns a weight to each point, and two vectors of mechanical properties x and y, we determined the weighted Spearman correlation by first calculating the weighted rank for each vector of mechanical properties

$${\,\text{r}\,}_{i}^{x}=\mathop{\sum }\limits_{j}^{N}{w}_{j}{{1}}({\bf{x}}_{i} < {\bf{x}}_{j}),$$

(13)

$${\,\text{r}\,}_{i}^{y}=\mathop{\sum }\limits_{j}^{N}{w}_{j}{{1}}({\bf{y}}_{i} < {\bf{y}}_{j}),$$

(14)

where 1 is the indicator function, and i, j ∈ N are sampled points. The weighted Spearman correlation is then the weighted Pearson correlation of the weighted ranks

$${r}_{{\rm{weightedSpearman}}}=\frac{\mathop{\sum }\nolimits_{i}^{N}{w}_{i}\left({r}_{i}^{\,x}-\bar{{r}^{x}}\right)\left({r}_{i}^{\,y}-\bar{{r}^{y}}\right)}{\sqrt{\mathop{\sum }\nolimits_{i}^{N}{w}_{i}{\left({r}_{i}^{\,x}-\bar{{r}^{x}}\right)}^{2}\mathop{\sum }\nolimits_{i}^{N}{w}_{i}{\left({r}_{i}^{\,y}-\bar{{r}^{y}}\right)}^{2}}}.$$

(15)

Finally, to determine how the local correlation in cell pressure and stress tensor magnitude varies as a function of the distance to the MHB, we computed for each sampled point an average distance to the boundary, defined as the mean of the distance to the closest boundary cell in each z slice, and binned these average boundary distances into 10 bins, each containing an equal number of sampled points.

Statistical mechano-transcriptomics analysis

Linear regression

Associations between gene expression and mechanical properties were first tested using linear regression. Two mechanical properties: cell pressure and stress tensor magnitude, were tested. Mechanical properties were first log normalized and regression was performed using the linear model:

$${g}_{i}={\beta }_{{\rm{linreg}}}{q}_{i}+{\epsilon }_{i},$$

(16)

for a gene g and log-transformed mechanical property q with a standard normal error term ϵ. Significance was determined by the false discovery rate-adjusted P value of the t-test statistic for the regression coefficient β_linreg, using a threshold of P_adj ≤ 0.05 after correction using the Benjamini–Hochberg (BH) procedure.

Structural equation regression

The linear regression model described above does not take into account potential spatial confounding effects, which are probably present in our data. Spatial location can influence both gene expression and cell mechanics. On a local scale, cells in close spatial proximity influence each others’ expression profiles and mechanical properties through cell–cell interactions. On a global scale, cell types, which are highly spatially structured, play important roles in dictating gene expression and mechanical properties. To account for this potential spatial confounding in both the predictor and response variables, we therefore used a gSEM²⁵.

The gSEM accounts for spatial confounding by fitting a thin plate regression spline to determine the effect of spatial location on both the predictor and response variables,

$${x}_{i}={f}^{\,x}({{{c}}}_{i})+{\epsilon }_{i}^{\,x},$$

(17)

where x is the predictor or response variable, c_i is the spatial coordinate associated with x_i, and ϵ is a standard normal error term. The fitted values are then subtracted from the predictor and response variables to give the spatially regressed residual r. The gSEM is the linear model

$${r}_{i}^{\,g}={\beta }_{{\rm{spatial}}}{r}_{i}^{q}+{\epsilon }_{i},$$

(18)

where r^g = g − f^g(c) is the spatially regressed residual for the normalized gene expression g and r^q = q − f^q(c) the residual for the log-transformed mechanical property q. Significance testing was performed as for the linear regression model described above.

Nonlinear associations between gene expression and mechanical forces

The regression methods described above uncover linear relationships between gene expression and mechanical forces. However, nonlinear relationships may also exist. Specifically, gene expression may be associated with mechanical stress in a nonlinear monotonic manner, which could indicate the presence of feedback loops or auto-regulation in mechano-sensitive signaling pathways. Alternatively, nonlinear nonmonotonic associations may suggest the presence of band-pass filter-like mechanisms wherein gene programs are only active within certain ranges of cellular mechanical stress or pressure.

To test this, we ranked cells by pressure or stress tensor magnitude, and computed a smoothed estimate of gene expression along the ranked cells using the weighted median. The stress tensor magnitude was computed as either λ₁ + λ₂, the sum of the stress tensor eigenvalues for each cell (dataset 2), or $\max ({\lambda }_{1},{\lambda }_{2})$, the max eigenvalue for each cell (dataset 3). Given a weighting scheme w that assigns a weight to each cell, and a vector of gene expression values g, the weighted median is the solution of the optimization problem

$${a}^{* }={\arg }_{a}\min \mathop{\Sigma }\nolimits_{i}^{{n}}{w}_{i}| {\bf{g}}_{i}-a|.$$

(19)

We used a triangular weight matrix with span 0.1, which assigns non-zero weights to cells which have a pressure/stress tensor ranking within 10 percentiles of a given cell. This corresponds to ~150 cells in our datasets.

Significance testing was performed using scHOT⁴¹, which implements a permutation test-based method. scHOT randomly permutes the cell ranking and recomputes the weighted median along the permuted ranking. The variance of the weighted median values was then used as a test statistic. We used 200 permutations per gene to ensure robust significance estimates. Permutation test P values were then corrected for multiple hypothesis testing using the BH procedure.

To ensure computational tractability, the top 3,000 highly variable genes were identified using Scanpy, and scHOT testing was used to identify genes for which the weighted median expression changes significantly along the pressure or stress tensor magnitude ranking. A threshold of P_adj ≤ 0.1 was used to determine significantly associated genes. Weighted median profiles were then clustered using hierarchical clustering and the number of clusters was estimated automatically using dynamicTreeCut. Overrepresentation of GO terms within clusters compared to the total set of scHOT-tested genes was then performed as described in the GO analysis section.

GO analysis

GO overrepresentation analysis was performed using the enrichGO() function from the clusterProfiler R package⁸⁵. Each gene set was tested for overrepresentation of GO terms against a background set composed of all 29,452 genes for which expression values have been measured or imputed. As GO terms are organized hierarchically, the simplify function was used to remove redundant terms.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.