Introduction

With the growth of the social economy, users’ consumption levels and frequency of online shopping have significantly increased, leading to a remarkable expansion of the logistics and transportation industry. Logistics and transportation play a pivotal role in promoting economic development. However, this growth has also brought about a series of problems, such as increased energy consumption and environmental pollution in the logistics and transportation processes, which are currently constraining the development of the logistics industry. Given the context of environmental and energy concerns, the progress in new technology has catalyzed the development of the new energy vehicle industry. As a result, new energy logistics vehicles have emerged as the primary focus for the development of logistics and distribution systems. According to statistics, the growth and application of Electric Vehicles (EVs) have been steadily increasing year by year. In comparison to traditional fuel vehicles, EVs offer significant advantages, including no pollution, energy efficiency, and lower energy costs. Consequently, the large-scale integration of EVs into logistics transportation is an inevitable trend. The Edison Institute1 counted a 79%, 78%, and 34% increase in electric vehicle sales in the United States, China, and Europe, respectively, in 2018. Projections indicate that there will be 250 million electric vehicles on the road by 20302.

In 2020, the General Office of the State Council issued the New Energy Vehicle Industry Development Plan (2021–2035), which aims to accelerate the in-depth integration and efficient synergy between new energy vehicles and energy systems, transportation networks, and communication platforms. The plan seeks to optimize energy consumption structures, transportation systems, and enhance city intelligence levels. EVs possess energy storage characteristics and can function as mobile distributed power sources, allowing them to connect to the grid. Leveraging Vehicle-to-Grid (V2G) technology enables the rational planning of EV charging and discharging times. Consequently, this approach can effectively reduce the difference between peak and off-peak periods and ensure a smooth power supply, enhancing the safety and reliability of the grid.

EVs are subject to various factors that influence their performance during logistics transportation, including battery capacity and energy consumption. Such factors can lead to mileage anxiety among drivers. In cases where the battery power runs low during transportation, drivers must select appropriate charging stations for power exchange or fast charging. Consequently, effective EV logistics distribution path planning and electric energy replenishment management are of utmost importance. The electric vehicle path problems (EVRP) have emerged as a prominent research topic in the field of modern logistics, attracting significant attention from academia and industry alike. The primary focus of research in this domain revolves around charging methods and energy consumption models, tailored to the application scenarios and characteristics of EVs. Bruglieri3 investigates the economic and safety benefits associated with the full charging of EVs during transportation. Based on this, Erdelić4 compares two strategies: partial charging and full charging. It has been determined that partial charging reduces waiting time and costs. However, it also leads to an increase in the psychological stress experienced by drivers, and results in both an expanded distribution of vehicles and an increase in driving distance. Erdelić5 has examined the EVRP with both single and multiple charging strategies. Yang6 proposed an EVRP with mixed return and charging strategies. Different charging strategies affect the path selection. The calculation of electrical energy consumption directly affects the accuracy of the overall path optimization model. He7 investigates the impact of traffic congestion on EV energy consumption. In the literature8, electrical energy consumption is represented using a fuzzy number based on reliability theory. Kancharla2 presents a nonlinear model for charging and vehicle load-related electrical consumption. Basso9 has also examined an enhanced electric power consumption model, taking into account factors such as terrain and speed. In recent years, logistics companies and operators have been striving to maximize their economic benefits from electric vehicle distribution and aim to apply vehicle network connectivity in a more flexible manner.

V2G technology can mitigate the electrical load on the power grid by addressing peak demand and low demand periods. As a result, optimizing the EV charging and discharging strategy becomes crucial. Nevertheless, the effectiveness and profitability of V2G technology, along with the potential impact of frequent charging and discharging on battery performance degradation, remain to be considered. The issue of EV dispatch in the smart grid is closely tied to electricity pricing. Rasheed10 proposes a distributed pricing mechanism, while11 suggests a coordinated dynamic pricing mechanism. Xu12 proposes an electricity pricing strategy based on regional and time partitioning. These novel pricing mechanisms dynamically adjust price incentives to encourage EV charging during off-peak periods. Implementing V2G effectively necessitates data from both vehicles and the grid. Grée13 proposes a cloud-based big data platform to harness this data. Triviño-Cabrera14 applies V2G technology to EVRP. Das15 proposes a charge/discharge model for EVRP aiming to minimize both the cost of power input and battery degradation. Yao16 presents a two-tier optimization model that considers temporal variations in toll prices. Barco17 estimated electric vehicle energy consumption by employing a model with longitudinal kinetic equations of motion for electric vehicle charging, discharging, and scheduling. In a related study, it was shown14 that fine-tuning driving habits can benefit electric vehicle users and improve the overall effectiveness of network operation. The proper design of tariffs plays a crucial role in promoting V2G participation. Currently, none of the existing literature addresses the charging and discharging management, as well as the resulting cost of battery depletion, within the context of EV logistics. Therefore, further research is required in the domains of path optimization and charge/discharge management for EV logistics distribution.

Upon meticulous review of the existing literature, it becomes clear that urban logistics distribution and air pollution have garnered significant attention in recent times. EV distribution stands as a promising avenue to tackle these concerns. Nevertheless, prior investigations have primarily concentrated on individual user behaviors towards EV charging and discharging, overlooking a comprehensive assessment of battery degradation dynamics within the logistics distribution cycle. Additionally, there is a notable absence of research delving into the management of EV charging and discharging upon their return to distribution centers. These limitations highlight gaps in the EVRP literature, particularly concerning the interplay of slow charge/discharge management and battery degradation within the intricate logistics and distribution processes, encompassing both charge swap and fast charging scenarios. Recognizing these gaps, the present study contributes by proposing two complementary models: an EV logistics distribution path optimization model and a charge/discharge management model, both rooted in V2G technology. These models aim to comprehensively address the aforementioned issues, offering practical insights and solutions for the logistics sector to navigate the challenges of sustainable EV distribution.

Electric vehicle charging and discharging path optimization

Problem description

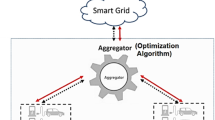
The problem of optimizing EV logistics distribution path and charging/discharging management in a smart grid can be described as follows: there is a single distribution center with charging piles for slow charging and discharging. Before distribution, we have information about customer demand, time windows, and geographical locations. The charging station is available for charging and swapping, and its location is known. Additionally, we have data on charging and swapping tariffs and grid tariffs. All EVs are subject to uniform specifications, and their load capacity and distance traveled must remain within the maximum design specifications of the vehicle. The distribution process must adhere to both time window and power constraints. If the electric vehicle does not have enough power to support the distribution needs, it needs to go to the nearest charging station for charging. The act of charging is only considered when the vehicle has run out of power and needs to reach a full state of charge. The mathematical model aims to minimize fixed costs, driving costs, electric energy consumption costs, and charging and discharging costs to optimize EV logistics path selection and charging/discharging management. Figure 1 shows a schematic diagram of the charge/discharge management process using V2G technology.

Fig. 1
figure 1

Electric vehicle charging and discharging management.

Full size image

The tariff program is dynamically adjusted according to the time of use, with rates varying throughout the day. Higher tariffs are applied at times when energy demand exceeds supply, i.e., during peak hours, while tariffs are comparatively lower during off-peak hours. This time-of-day tariff scenario is derived from the distribution network load data in Literature18, and the time-of-day tariff diagram is shown in Fig. 2.

Fig. 2
figure 2

Schematic diagram of time-sharing tariff.

Full size image

Battery degradation analysis

Electric vehicles rely on power exchange and fast or slow charging to replenish their electric energy. In logistics city distribution, time efficiency is crucial. Hence, we separately consider the charging and switching costs for fast charging and power exchange modes. Electric vehicles handle distribution tasks, returning to the distribution center for slow charging and discharging management. While generating profits, the battery incurs wear and tear costs accordingly.

The actual lifetime of a battery is influenced by a combination of factors, including the rate of charge, state of charge, ambient temperature, and degree of discharge18. It is particularly important to consider the ambient temperature and the degree of discharge during the energy conversion process using vehicle-to-grid (V2G) technology. In the case of lithium-ion batteries, the performance degradation is rooted in the chemical reactions that occur internally, which contribute to the formation of an oxide layer on the surface of the electrodes. This change in turn causes an increase in the internal resistance of the battery. Moreover, the ambient temperature directly impacts the rate of these chemical reactions occurring inside the battery, which typically follows the Arrhenius formula19.

$$\mu = Ae^{{ - \frac{E}{kT}}}$$
(1)

where \(\mu\) is the reaction rate; \(A\) is the Arrhenius constant in the same units as \(\mu\); \(E\) is the activation energy, a temperature-independent constant; \(k\) is the Boltzmann constant; \(T\) represents the absolute temperature,\(K\).

Assuming the same time for each charge and discharge cycle, denoted by \(\Delta t\), Then the increase in the internal resistance of the battery after a single cycle is obtained according to the Arrhenius formula.

$$\Delta r = r_{0} Ae^{{ - \frac{E}{kT}\Delta t}}$$
(2)

where \(r_{0}\) is the increment of resistance value per unit time, The unit is \(\Omega\).

According to the test standard of lithium-ion battery cycle life, combining with Eq. (2), the increase in internal resistance of a lithium-ion battery over its full life cycle can be obtained as follows.

$$r_{N} = L_{N} r_{0} Ae^{{ - \frac{E}{{kT_{N} }}\Delta t}}$$
(3)

The subscript \(N\) is the quasi-side value under standard conditions. It is known that at any temperature, \(T\). The actual cycle life of the lithium-ion battery is

$$L = \frac{{r_{N} }}{\mu } = e^{{\frac{E}{k}\left( {\frac{1}{T} - \frac{1}{{T_{N} }}} \right)}} L_{N}$$
(4)

where \(e^{{\frac{E}{k}\left( {\frac{1}{T} - \frac{1}{{T_{N} }}} \right)}}\) represents the temperature adjustment coefficient that influences the cycle life of a lithium-ion battery at temperature \(T\), denoted as \(\omega\).

The lifetime of Li-ion batteries is also dependent on the depth of discharge (DOD) during each charge and discharge cycle. The cycle life is shorter with a deeper depth of discharge20,21. The battery life test value is measured at a 100% depth of discharge, implying that the actual battery life exceeds the nominal value under the same ambient temperature conditions. Additionally, an exponential relationship exists between the actual cycle life and the depth of discharge22.

$$L = L_{N} D^{ - 0.795}$$
(5)

where: \(D\) represents the depth of discharge, expressed as a percentage; \(L_{N}\) denotes the lifespan of the lithium-ion battery when operating under normal conditions (\(D\) = 1).

Thus, the value − 0.795 can be identified as the correction factor for depth of discharge, impacting the cycle life of lithium-ion batteries at varying depths of discharge (\(D\)), and is referred to as \(\varphi\).

Models

\(M = \{ 1,2, \cdots ,m\}\) is a collection of the number of EVs used. \(N = \{ 0,1,2, \cdots ,n\}\) is a collection of the distribution center and customer credits. \(W = \{ n,n + 1, \cdots ,n + m\}\) represents the collection of \(m\) charging stations. \(q_{i}\) denotes the demand of customer \(i\). \(P_{1}\) stands for the fixed cost per EV unit, \(P_{2}\) represents the transportation cost per unit of time for the EV, \(P_{3}\) corresponds to the price per unit of electricity consumed, \(P_{4}\) is the price per unit of time of fast charging electricity, and \(P_{5}\) is the cost of single exchange of electricity. \(Q\) and \(D\) represent the maximum load and maximum distance the electric vehicle can cover, respectively. \(a_{ik}\) and \([B_{i} ,E_{i} ]\) indicate the arrival time of vehicle \(k\) at node \(i\) and the time window for node \(i\). \(E_{0}\) is the anticipated minimum charge needed while driving the electric vehicle. \(x_{ij}^{k}\) is a 0–1 variable for whether the EV is transporting on that roadway, \(y_{i}^{k}\) is a 0–1 variable for whether the EV is delivering to that customer point, and \(z_{i}^{k}\) is a 0–1 variable for whether the EV is charging or switching at that charging station.

A mathematical model of EV path optimization with a minimum total cost is constructed by considering charging and discharging cases. The model’s cost structure includes fixed costs, transportation fees, energy use, expenses for charging efficiency, extra costs from slow charging and discharging, and wear and tear costs from prolonged battery usage.

(1) Fixed costs and transportation costs

$$C_{1} = K \times P_{1} + P_{2} \sum\limits_{k = 1}^{m} {\sum\limits_{i = 0}^{n} {\sum\limits_{j = 0}^{n} {t_{ijk} x_{ij}^{k} } } }$$
(6)

In Eq. (6), \(K\) represents the number of transport vehicles, m is the total number of vehicles at the distribution center (\(k = 1,2, \cdots ,m\)), and \(t_{ijk}\) denotes the travel time of the EVs in the selected area.

(2) Energy costs.

The energy consumption of an electric vehicle is affected by a variety of factors, mainly including the amount of load, driving speed, and duration, especially in a dynamically changing road network. When the vehicle passes through road sections \([i,j]\), its energy consumption can be calculated as

$$E_{ijk} = \sum\limits_{t}^{n} {P\left( {Q_{ik} ,v_{ijk}^{t} } \right)} * t_{ijk}$$
(7)
$$P\left( {Q_{k} ,v} \right) = \frac{{\left( {Q_{0} + Q_{k} } \right) \cdot g \cdot f \cdot v + \frac{{C_{d} \cdot A \cdot v^{3} }}{21.15}}}{3600\eta }$$
(8)

Thus the total energy cost of the distribution process is

$$C_{2} = P_{3} \sum\limits_{k = 1}^{m} {\sum\limits_{i = 0}^{n} {\sum\limits_{j = 1}^{n} {x_{ij}^{k} } } } t_{ijk} E_{ijk}$$
(9)

In Eqs. (7), (8), \(P\left( {Q_{k} ,v} \right)\) represents the power level during operation, \(g\) corresponds to the physical quantity of gravitational acceleration, \(A\) is set as the area of wind blowing on the electric vehicle, while \(C_{d}\) and \(f\) portray the coefficients of air resistance and friction resistance, respectively, encountered by the vehicle during traveling. In addition, \(\eta\) reflects the efficiency of the mechanical transmission of the whole system. As for \(Q_{0}\) and \(Q_{k}\), they point to the performance parameters of the EV under no-load condition and the specific performance when carrying current load, respectively.

(3) Fast charging or power exchange cost.

When the remaining power of an electric vehicle is not sufficient for it to reach the next service point to complete its task, it has to travel to the nearest charging station for emergency fast charging. The cost to be paid for charging is related to the length of charging, where the length of charging is \(t_{ik}^{c} = \frac{{E_{\max } - E_{ik} }}{{r_{c} }}z_{i}^{k}\). The corresponding cost is calculated by the formula

$$C_{31} = P_{4} \sum\limits_{k = 1}^{m} {\sum\limits_{i = 0}^{w} {t_{ik}^{c} } } \cdot z_{i}^{k}$$
(10)

where \(E_{\max }\) represents the electric vehicle’s maximum battery capacity,\(E_{ik}\) is the remaining power when the vehicle reaches charging station \(i\), and \(r_{c}\) indicates the charging station’s efficiency.

The cost of a battery change will vary depending on the charging method used. For electric logistics vehicles, the cost will be directly affected by the number of battery changes. The formula for calculating the switching cost is

$$C_{32} = P_{5} \sum\limits_{k = 1}^{m} {\sum\limits_{i = 0}^{w} {z_{i}^{k} } }$$
(11)

(4) V2G slow charge and discharge costs and battery wear costs.

At the end of the distribution mission, the electric vehicle will return to the distribution center and perform a slow charging and discharging operation using a time-sharing tariff system to obtain some economic return. In this process, the costs involved in charging and discharging are

$$C_{4} = \left( {a\sum\limits_{{T_{0} }}^{{T_{1} }} {P_{c} W_{c} } - b\sum\limits_{{T_{0} }}^{{T_{1} }} {P_{d} W_{d} } } \right)\left( {T_{1} - T_{0} } \right)$$
(12)

In Eq. (19), \(P_{c}\) and \(P_{b}\) are set as specific identifiers of the charging cost rate and the discharging cost rate, while \(W_{c}\) and \(W_{b}\) correspond to the power involved in the charging process and the power required in the discharging process, respectively. Further, \(a\) and \(b\) are introduced as parameters that assume the roles of characterizing the charging and discharging states, respectively: when the system is engaged in charging operations, \(a\) is transformed to 0, while \(b\) is changed to 1, which clearly reflects the conduct of discharging activities and the cessation of charging activities. In addition, two time points, \(T_{0}\) and \(T_{1}\) are precisely defined to delineate the start and end moments of the charging and discharging operations.

$$C_{6} = \frac{{P_{b} }}{{\omega \varphi L_{N} E_{\max } }}$$
(13)

In summary, the overall cost component model for distribution, charging and discharging of EVs in the switching mode can be expressed as follows

$$\begin{gathered} C = K \times P_{1} + P_{2} \sum\limits_{k = 1}^{m} {\sum\limits_{i = 0}^{n} {\sum\limits_{j = 0}^{n} {t_{ijk} x_{ij}^{k} } } } + P_{3} \sum\limits_{k = 1}^{m} {\sum\limits_{i = 0}^{n} {\sum\limits_{j = 1}^{n} {x_{ij}^{k} } } } t_{ijk} E_{ijk} \hfill \\ \, + P_{4} \sum\limits_{k = 1}^{m} {\sum\limits_{i = 0}^{w} {t_{ik}^{c} } } \cdot z_{i}^{k} + \left( {a\sum\limits_{{T_{0} }}^{{T_{1} }} {P_{c} W_{c} } - b\sum\limits_{{T_{0} }}^{{T_{1} }} {P_{d} W_{d} } } \right)\left( {T_{1} - T_{0} } \right) + \frac{{P_{b} }}{{\omega \varphi L_{N} E_{\max } }} \hfill \\ \end{gathered}$$
(14)

The following constraints apply

$$\sum\limits_{k = 1}^{m} {\sum\limits_{i = 1}^{n} {x_{ij}^{k} } } \le m, \, i = 0$$
(15)
$$\sum\limits_{k = 1}^{m} {\sum\limits_{j = 1}^{n} {x_{ij}^{k} } } = \sum\limits_{k = 1}^{m} {\sum\limits_{j = 1}^{n} {x_{ji}^{k} } } , \, i = 0, \, k = 1,2, \cdots ,m$$
(16)
$$\sum\limits_{k = 1}^{m} {y_{i}^{k} } = 1, \, i = 1,2, \cdots ,n$$
(17)
$$\sum\limits_{i = 1}^{n} {q_{i} } y_{i}^{k} \le Q,{\text{ i}} \ne j, \, k = 1,2, \cdots ,m$$
(18)
$$\sum\limits_{i = 0}^{n} {\sum\limits_{j = 0}^{n} {d_{ij} x_{ij}^{k} } } \le D,{\text{ i}} \ne j, \, k = 1,2, \cdots ,m$$
(19)
$$a_{ik} + t_{ik} \ge B_{i}$$
(20)
$$a_{ik} + t_{ik} \le E_{i}$$
(21)
$$\sum\limits_{k = 1}^{m} {\sum\limits_{i = 0}^{w} {E_{ik}^{a} } } \left( {1 - z_{i}^{k} } \right) + E_{\max } = \sum\limits_{k = 1}^{m} {\sum\limits_{i = 0}^{w} {E_{ik}^{l} } }$$
(22)
$$E_{0} \le E_{ik}^{a} \le E_{\max }$$
(23)

(15) states that the number of EVs allocated should at least match the number of distribution routes or more. (16) Requires that the distribution vehicles depart from the distribution center and complete the established distribution tasks. (17) Provide that each demand location can be visited only once by an EV and only once at that location. (18) Ensure that the total demand at all customer locations on each distribution route does not exceed the maximum load capacity of the electric vehicle. (19) Provide that the total distance of each distribution route must be within the maximum range of the electric vehicle. (20) and (21) relate to time window constraints. (22) stipulates that EVs must complete charging at a charging station prior to departure. (23) addresses the limitation regarding the energy supply of each electric vehicle at each customer site.

The overall expenses associated with distribution and the charging/discharging processes in the rapid charging mode of electric vehicles are represented as.

$$\begin{gathered} C^{\prime } = K \times P_{1} + P_{2} \sum\limits_{k = 1}^{m} {\sum\limits_{i = 0}^{n} {\sum\limits_{j = 0}^{n} {t_{ijk} x_{ij}^{k} } } } + P_{3} \sum\limits_{k = 1}^{m} {\sum\limits_{i = 0}^{n} {\sum\limits_{j = 1}^{n} {x_{ij}^{k} } } } t_{ijk} E_{ijk} \hfill \\ \, + P_{5} \sum\limits_{k = 1}^{m} {\sum\limits_{i = 0}^{w} {z_{i}^{k} } } + \left( {a\sum\limits_{{T_{0} }}^{{T_{1} }} {P_{c} W_{c} } - b\sum\limits_{{T_{0} }}^{{T_{1} }} {P_{d} W_{d} } } \right)\left( {T_{1} - T_{0} } \right) \hfill \\ \end{gathered}$$
(24)

The constraints are as above.

Algorithm research

An enhanced genetic algorithm is developed for addressing the electric vehicle path optimization and charging/discharging management issues using V2G. Genetic algorithms are efficient parallel search algorithms for solving global optimization problems. Unlike traditional exact algorithms, they can handle various types of complex optimization problems. By virtue of their adaptive ability, genetic algorithms show great applicability when dealing with objective functions and constraints that contain nonlinear and discrete properties. Because of this, they show strong robustness and high efficiency in dealing with complex nonlinear and discrete problem challenges. Figure 3 illustrates the basic flow framework of the enhanced genetic algorithm used in this study.

Fig. 3
figure 3

Basic flowchart of the algorithm.

Full size image

In order to improve the accuracy of model solving and accelerate the process of local convergence, genetic algorithms incorporate a reverse evolution strategy, which in turn enhances the search efficiency. The specific steps of the genetic algorithm in solving the electric vehicle path planning problem are described in detail next.

Step 1: Encoding and decoding. This step represents the order in which each client is accessed. The clients are encoded with natural numbers. The length of the chromosome is \(n + m + k - 1\), where \(n\) represents the number of client sites, labeled as client numbers 1, 2,\(...\),\(n\). \(m\) represents the number of charging stations, denoted as \(n + 1,n + 2,...,n + m.\) \(k\) denotes the number of electric vehicles utilized and the total number of distribution paths. The position of the distribution center on the chromosome is indicated by \(k - 1\), which is marked as 0. For instance, the number series (6, 2, 5, 4, 3, 1, 7, 10, 9, 8) indicates the visitation sequence to various customer locations. After accounting for load limits, timing restrictions, and incorporating distribution hubs, the initial sequence transforms to (0, 6, 2, 5, 0, 4, 3, 1, 7, 0, 10, 9, 8, 0), with ‘0’ denoting a distribution hub or the journey’s start/end points. Moreover, should the electric vehicle require recharging en route, the plan includes detours through charging stations, revising the sequence to (0, 6, 2, 11, 5, 0, 4, 12, 3, 1, 7, 0, 10, 9, 8, 0), where ‘11’ and ‘12’ are specific charging station locations. The decoding phase reverses the encoding process, translating the coded sequence back into actual delivery routes. In detail, this deciphers into three routes: Route 1 from 0 (beginning), passing through 6, 2, to 11 (charging stop), then 5, ending at 0; Route 2 starting anew at 0, proceeding through 4, 12 (a different charging spot), 3, 1, 7, concluding at 0; and Route 3 kicking off again at 0, through 10, 9, 8, to finish at 0. This setup effectively depicts task allocation among three EVs, including necessary charging station visits within the delivery network to recharge.

Step 2: The process of initializing the population involves calculating the total energy consumption of the electric vehicle path planning model from the starting node. Whenever the vehicle reaches a node, the system checks whether the remaining power is sufficient to travel to the next customer node or the nearest charging station. If the power is not enough to continue the journey, the nearest charging station marker will be inserted after the current node. This process will continue until all nodes have been visited. The specific way in which each chromosome is coded can be illustrated by the example in step 1, where the customers are arranged in a randomized order. We integrate the distribution centers and charging stations into the chromosome structure, taking into account the load and power constraints. This process is repeated until a predetermined population size is reached.

Step 3: Setting criteria for adaptation assessment. Adaptation functions are often tailored to the specific problem at hand. In the EVRP model and the charging/discharging strategy in the charge-switching mode, the core objective is to reduce the overall cost. Chromosomes that possess a higher fitness value are more competitive when passed on to the next generation. Accordingly, the fitness function is set as the reciprocal of the objective function value.

Step 4: Selection. In the selection phase, an elite retention strategy was first used, i.e., chromosomes were sorted according to their fitness values. In the subsequent population composition, the top 5% of the optimal chromosomes are directly retained as elites, while the remaining 95% are screened by a roulette wheel selection mechanism. In this process, chromosomes with higher fitness values are more likely to be selected for crossover and mutation operations, thus generating a new generation of populations.

Step 5: Crossover. During the chromosome encoding process of the EVRP problem, the numbering information of the charging stations is included. However, this practice may cause problems as the original layout of the charging stations may be corrupted, which in turn leads to a large number of non-optimal solutions in the offspring. To cope with this challenge, the extra added genes need to be removed before performing crossover and mutation operations. In the crossover session, we select unique gene segments from the paternal chromosomes and arrange them in order in the offspring. For example, if there are two paternal chromosomes P1 (1,2,3,4,5,6,7) and P2 (6,4,2,3,7,1), crossover may produce offspring chromosomes O1 (1,6,2,4,3,5,7) (and O2 (6,1,4,2,3,7,5), where the example of O1 suffers from the problem of duplicate elements, which is required to ensure that crossover results in practical applications are Validity.

Step 6: Mutation. Genetic variation plays a key role in the whole process of genetic manipulation. Mutation on chromosomes is an important means of preventing premature convergence due to rapid descent into a local optimum, as well as maintaining chromosomal population diversity. During the mutation phase, a number of gene loci are randomly selected from the parental chromosomes for rearrangement, while the remaining loci are maintained as they are.

Step 7: The quality of the solution can be optimized, and the acceleration of local convergence can be facilitated by using the evolutionary inversion technique, a process that focuses on chromosomes that have been subjected to selection, crossover, and mutation. In the inversion operation, two random integers are first generated to identify a specific interval on the chromosome. Subsequently, the genes within that interval are reversed in order to generate a new chromosome. In the case of the parent P1 (1,2,3,4,5,6,7), for example, if the random integers are 3 and 6, the offspring O1 will become (1,2,6,5,4,3,7). It is worth noting that the change is accepted only if the inversion operation enhances the fitness value.

The algorithm’s iteration limit is established at 500. The process automatically concludes once the iteration reaches this threshold.

Example analysis

Example data and parameter settings

The experimental dataset used in this study was obtained from the figshare database (https://doi.org/https://doi.org/10.6084/m9.figshare.10288326), ensuring accessibility and replicability for researchers. Specifically, we selected the R-2-C-30 simulation example from which to conduct the experimental analysis, as it comprehensively reflects a real-world scenario involving 30 customer nodes and two charging stations. This choice was not arbitrary but rather driven by the need to balance complexity and comprehensibility to facilitate a deeper understanding of potential optimization challenges. Each customer node in the dataset is identified by a unique number ranging from 1 to 30, representing a discrete demand point in the network. In addition, the distribution center, which serves as the starting point for all service routes, is designated as node 0. The two charging stations, which are important components of the logistics system, are explicitly labeled as nodes 31 and 32. To substantiate the veracity and applicability of our findings, detailed information is provided for each customer node, which includes the demand, the service time, and the time window, among others. This careful attention to data granularity allows us to accurately model real-world constraints and evaluate the performance of our proposed strategies under different operating conditions.

Electric vehicles return to the distribution centers after completing their distribution tasks and are connected to the grid through batteries. Here, they are able to both charge and discharge from the grid in order to utilize the time-of-use tariff mechanism to generate revenue by selling excess electricity through the market. This decision is based on time-of-use tariff data provided in the relevant literature12 and aims to optimize charging and discharging behavior. The day is divided into peak and off-peak hours, and the specific time-of-day tariffs are shown in Table 1. When electric vehicles finish their distribution tasks and reconnect to the distribution center’s grid, they maximize their potential profit by deciding whether to receive or deliver power based on time-of-day tariff fluctuations.

Table 1 Time-sharing tariff.
Full size table

The genetic algorithm was implemented on a computer equipped with a 2.20 GHz processor and 4 GB of random access memory, and the data were analyzed using MATLAB software (version R2018b). See Table 2 for specific parameter configurations.

Table 2 Model parameter values.
Full size table

Algorithm comparison analysis

In order to verify the effectiveness of the improved genetic algorithm in this study, it is solved with the particle swarm algorithm, simulated annealing algorithm, and genetic algorithm, respectively, for the optimization model of electric vehicle logistics and distribution path under the above power exchange mode for comparative analysis. The experimental data use R-2-C-30 instances, and the iterative comparison graph of the solution results of the four algorithms is shown in Fig. 4, where NV denotes the number of iterations.

Fig. 4
figure 4

Comparison of iteration results under different algorithms.

Full size image

As can be seen from Fig. 4, the improved algorithm (IGA) of this paper solves the minimum total cost optimum of the electric vehicle path optimization model under the power switching model with better convergence speed. In contrast, the particle swarm algorithm (PSO) has a faster convergence speed, but it is easy to fall into the local optimal solution, is sensitive to the parameters, and needs to be carefully adjusted to ensure the stability of the algorithm and the convergence of the algorithm. The simulated annealing algorithm (SA) has a relatively slow search speed and is prone to fall into local optimal solutions. When dealing with complex problems similar to the model of this study, it may be difficult to find the global optimal solution due to the large search space. Genetic Algorithm (GA) has strong global search ability and is not easy to fall into local optimal solutions. However, the local search ability is poor, often can only get the suboptimal solution, slow convergence speed, and strong dependence on parameters. The above comparative analysis verifies the applicability and effectiveness of the improved algorithm of this paper in solving the electric vehicle path optimization problem.

Analysis of distribution path planning and charging and discharging management results

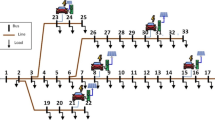
In order to verify the effectiveness of the designed path planning and charge/discharge management models, four different scenarios are designed for comparative analysis. Scenarios 1 and 2 mainly focus on cost reduction by optimizing the distribution paths, where Scenario 1 employs a power switching strategy, while Scenario 2 chooses a fast charging method that specifically considers the impact of fast charging on battery life and the cost it incurs. Scenarios 3 and 4 are based on the logistical framework of Scenarios 1 and 2 and further incorporate the management of slow charging and discharging when EVs return to the distribution center. A modified genetic algorithm is applied to solve the four scenarios, with examples of R-2-C-30 and R-2-60 sizes. The optimal path assignments for the EVs are shown in Figs. 5, 6, 7, 8, while Table 3 lists the charging times under Scenario 2 and Scenario 4 in the R-2-30 example.

Fig. 5
figure 5

Distribution path diagrams for two scales in scenario 1.

Full size image
Fig. 6
figure 6

Distribution path diagrams for two scales in scenario 2.

Full size image
Fig. 7
figure 7

Distribution path diagrams for two scales in scenario 3.

Full size image
Fig. 8
figure 8

Distribution path diagrams for two scales in scenario 4.

Full size image
Table 3 Charging time in two charging scenarios.
Full size table

As depicted in Figs. 5, 6, 7, 8, the number of intersections among electric vehicle distribution paths in cases 1 and 3 is noticeably lower compared to cases 2 and 4. A higher number of crossings indicates longer total logistics distribution paths, leading to increased logistics and distribution costs as well as longer charging times. Specifically, the two models employing the fast charging method during transportation have longer charging times than the model using the power exchange method. Due to the complexity of distribution costs, fast charging takes more time than power exchange. Consequently, a higher number of path crossings will result in increased charges and swaps, ultimately leading to higher total distribution costs.

In the experimental results, we obtained data on the number and duration of charging and discharging in the four scenarios. Scenarios 1 and 3 share the same charging time and frequency. As shown in Table 3, the scenario 4 has more charging cycles but a shorter total charging time compared to scenario 2. Scenario 2’s charging time (h) is 1.21-0.49-1.14-1.05-0.32, while scenario 4’s charging time (h) is 1.31-0.72-1.28-0.71-1.04-1.15. This difference is mainly attributed to the charging and discharging costs, along with battery wear and tear, when scenario 4 utilizes V2G technology to connect to the grid. To maximize the benefits of charging and discharging, it’s essential to consider not only the time-sharing tariff differences but also the power load of the electric vehicle upon returning from the distribution task. By doing so, the vehicle can charge more effectively. However, it’s important to note that charging and discharging activities can impact battery health, leading to a reduction in charging time.

Table 4 summarizes the experimental results for each type of cost. Specifically, GC represents the fixed cost, YC is the transportation cost, NC represents the energy consumption cost, CC is the charging cost, HC is the variable power cost, VC represents the slow charging and discharging cost, DC is the battery depletion cost, and TC is the total cost, all of which are measured in yuan.

Table 4 Distribution cost comparison.
Full size table

From Table 4, it is evident that:

  • (1) The optimal solution for all four scenarios is the use of four electric vehicles for distribution. Among these scenarios, Scenario 1 exhibits a lower total delivery cost compared to Scenario 2. This difference is primarily attributed to the longer time spent on fast charging during transit and the need for multiple charging instances due to varying degrees of battery aging. In the model, transportation costs are primarily influenced by transportation time, resulting in higher overall transportation expenses. Additionally, more energy costs are incurred due to the necessity of making multiple trips to the charging station for recharging. Although the cost of a single charge change is higher than the average cost of a single charge, the difference in charge and exchange costs for completing the final distribution task is not significant, owing to variations in the number of charges and exchange times. Therefore, it is considered more economical to opt for distribution in case 1, i.e., logistics distribution in the power exchange mode.

  • (2) Scenarios 3 and 4 involve utilizing V2G technology at the distribution center for charging and discharging management. Compared to scenarios 1 and 2, the cost is lower. The primary reason is the negative cost associated with slow charging and discharging in both cases, indicating that the benefits from discharging outweigh the charging cost. This reduction in overall logistics and distribution costs is significant. When examining Scenarios 3 and 4, it is clear that the cost of slow charging and discharging in Case 4 is reduced by 43.2 yuan vs. 84.55 yuan for the two case sizes, respectively. The main reason for this difference is that scenario 3 replenishes power during distribution, eliminating the need to consider battery loss resulting from charging and discharging. In contrast, scenario 4 necessitates accounting for battery loss costs, which are primarily influenced by the depth of discharge. Consequently, the advantages of employing slow charging and discharging at the distribution center, under the power exchange mode, become more apparent without concerns about battery depletion.

  • (3) For all four scenarios, calculation R-2–60 costs more than twice as much as R-2–30, and although the customer locations are exactly twice as large, the number of charging stations remains unchanged, so the travel to the charging stations becomes more complicated. Compared to Scenario 1 and Scenario 3 in the switching mode, Scenario 2 and Scenario 4 in the fast charging mode have a larger percentage increase in total cost for the larger R-2–60 example. This is due to the fact that there are more customer points and the number of charging trips and charging time increases, leading to more transportation and energy costs. Therefore, the switching mode is more suitable for urban logistics and distribution of EVs with multiple scale customer points than the charging mode.

Battery loss sensitivity analysis and V2G impact on the grid

The efficiency of electric vehicle batteries in supplying power to the grid is mainly affected by the ambient temperature and the degree of discharge. Tables 5 and 6 demonstrate the relevant experimental results, while Figs. 9 and 10 depict the specific effects of ambient temperature and degree of discharge on battery losses, respectively.

Table 5 Ambient temperature sensitivity analysis.
Full size table
Table 6 Discharge depth sensitivity analysis.
Full size table
Fig. 9
figure 9

Trend of temperature on battery loss.

Full size image
Fig. 10
figure 10

Trend of depth of discharge on battery loss.

Full size image

From the graph above, it is evident that the depth of discharge remains constant. With the rise in ambient temperature, the battery loss cost also increases. The trend of the curve indicates that higher temperatures lead to a smaller magnitude of increased cost loss. This is mainly due to the fact that the higher the temperature, the lower the temperature correction factor \(\omega = e^{{k\left( {T\,T_{N} } \right)}}\) and the smaller the magnitude of the curve. Similarly, at a constant ambient temperature of 20 ℃. The deeper the discharge depth is, the lower the correction factor \(\sigma = D^{ - 0.795}\) is, and the magnitude of the reduction is not significant. Consequently, the greater the depth of discharge, the higher the cost of battery deterioration.

While slow charging and discharging may have an impact on battery life, it is possible to select appropriate charging and discharging strategies during different tariff periods to achieve specific revenue goals. This approach can help in reducing the base load during peak hours of electricity consumption and shifting the peak load, thereby significantly smoothing the grid load fluctuations. The simulation data presented in this paper focuses on a single logistics small-scale distribution study. However, the charge/discharge management model proposed here can be extended to large-scale logistics distribution services to optimize power efficiency and effectively reduce the peak-to-valley load difference.

Conclusions

The optimization model of electric vehicle logistics paths under power exchange and fast charging modes is centered on minimizing the total distribution cost. We also explore the slow charging and discharging management strategy when EVs return to the distribution site. The total cost of logistics and distribution in the switching mode covers fixed costs, transportation overhead, energy costs, switching cost, and slow charging and discharging costs. In contrast, in the fast charging mode, the logistics and distribution costs reflect more of the conversion of electricity costs to fast charging costs. In addition, slow charging and discharging entails additional battery depletion costs, the calculation of which has been optimized for ambient temperature and discharge depth. We have solved each model using an enhanced genetic algorithm. The main conclusions drawn from the experiments include: (1) compared with the fast charging mode, the power switching mode reduces the complexity of path intertwining in route planning, which cuts down the total distribution cost. (2) Effective management of slow charging and discharging when returning to the distribution site can generate certain discharge benefits, which in turn reduces the overall logistics and distribution cost. (3) In the power switching mode, the slow charging and discharging management is more advantageous than fast charging, as it not only reduces the total logistics and distribution costs, but also provides more benefits than fast charging, as it can reduce the total distribution cost. Advantageous because it not only reduces the total cost but also enhances the load balancing capability within the distribution system. (4) The cost of battery depletion in EVs increases with decreasing ambient temperatures, while deepening the depth of discharge leads to a steady increase.