Introduction

The widespread adoption of electric vehicles (EVs) represents a pivotal solution for reducing dependence on fossil fuels and alleviating associated environmental challenges1. However, the widespread adoption of EVs significantly increases the load on utility grids due to the high energy demands of charging. This surge in demand can overwhelm existing grid infrastructure, necessitating costly expansions, such as upgrading transmission lines and substations. Without intervention, utilities may face unplanned load increases, leading to operational challenges and potential reliability issues. To accommodate the growing number of EVs without incurring these substantial capital costs, a coordinated charging scheme is essential. By managing when and how EVs charge, the distribution of demand can be smoothed, preventing spikes that would otherwise strain the grid2. Coordinated charging not only reduces the need for immediate infrastructure upgrades but also aligns charging with periods of lower demand or higher renewable energy generation, creating a more efficient and cost-effective system. This strategic approach helps to mitigate the financial and operational challenges posed by mass EV adoption while supporting sustainable energy goals. Moreover, an integrated infrastructure with renewable energy sources (RESs) and energy storage systems (ESSs) facilitates reducing the utility grid’s burden while attaining long-term net-zero goals3. Collaborative and coordinated efforts can lead to economic advantages for all participants, more equitable distribution of energy and costs, and reduced dependence on retailers or aggregators4. A synergy among RESs, ESSs, loads, and prosumers is crucial for sustainable electromobility infrastructure, thus avoiding increased capital costs while reducing the overall burden on the utility grid5, 6.

Literature survey

The International Energy Agency (IEA) estimated a continuous increase in global EV sales until 2023, reaching 14 million units by year-end, representing a 35% year-on-year growth7. A well-developed EV charging infrastructure plays a key role in facilitating the widespread adoption of EVs8, 9. Approximately 26% of EV charging stations worldwide are situated within parking lots10. Hence, a community parking lot (CPL) with EV charging facilities and neighbourhood buildings would be a future-ready solution to benefit multiple stakeholders.

Most EV owners prefer overnight charging at CPLs with Level 1 or Level 2 charging equipment11. CPLs with RESs and ESSs need smart energy management systems (EMS) to provide reduced electricity bills for parking lot operators (PLOs)12. It has become important to consider optimal coordination between EV charging facilities and neighbourhood buildings due to limited parking spaces and increased hosting in the electrical network13, 14. Researchers have proposed various EMSs15 with objectives to minimize the cost incurred in EV charging16, 17, maximize the profit for PLOs18, minimize load variance19, minimize power losses20, and maximize renewable energy consumption21.

Historical datasets, including the real-time information from CPLs, help obtain global optimal operations. Previously proposed works have reported optimal coordinated charging of EVs using day-ahead scheduling (DAS) methods22. However, the real-time uncertainties in power generation and the demand for scheduling are not considered23, leading to a non-economic plan to charge EVs. An economical operation with a DAS framework is designed in Ref.24 using the salp swarm algorithm to provide collective benefit to PLOs, EV owners, and the grid operators without considering the preferences and uncertainties in the travelling behaviour of EV owners. Similarly, in Ref.25, a game theory approach has been formulated for the optimal scheduling of EVs in a parking lot to optimize a set of coupled control problems without analysing uncertainty in EV charging demand and power grid fluctuations. The flexibility in the travelling behaviour of EV owners is considered in Ref.26, with a two-stage optimization to determine the optimal scheduling of EVs at an office building parking lot. However, its primary goal is to reduce the peak load of the office rather than considering the state of charge (SOC) of the parked EVs. A two-stage EMS based on DAS and real-time energy markets is proposed in Ref.27 to minimize the operating cost of microgrids with a delayed market model.

Fast-charging infrastructure plays a crucial role in enabling widespread EV adoption, yet existing solutions often face challenges such as grid dependency and inefficiency28. While hybrid energy storage systems and machine learning-based control have shown promise in managing power for light EVs29, they remain largely confined to individual vehicle scenarios, leaving significant gaps in addressing multi-vehicle setups. Efficient and reliable EV charging strategies enhance power quality and stability30, but many fail to incorporate real-time energy adjustments or prioritize user preferences, both of which are critical for scalable applications in CPLs. The placement of charging stations using hybrid algorithms to improve network resilience has also been explored31, yet these efforts predominantly focus on infrastructure design rather than the operational challenges faced by CPLs, such as balancing renewable energy integration and fluctuating charging demand. Business models for EV ecosystems emphasize stakeholder engagement32, and unified power quality conditioners for solar EV charging stations reduce grid reliance33; however, these approaches often lack the coordination needed to address the complexities of multi-user environments like CPLs. Load management techniques help mitigate grid impacts of EV charging stations34, while dynamic economic dispatch models underscore the importance of coordination in renewable energy systems35. Nonetheless, existing frameworks often fail to integrate real-time scheduling with fairness in charging and adaptive power management36, 37. Peer-to-peer energy trading systems demonstrate the potential for decentralized energy exchanges among prosumers38, yet these strategies frequently neglect EV-specific requirements such as SOC prioritization and time-dependent charging constraints, which are critical in CPL scenarios. Prediction models for EV charging demand improve reliability39, but their utility is limited without mechanisms to adapt to the uncertainties of RES generation and real-time power availability. Fuzzy-based microgrid controls for PV-powered EV stations40 and optimization techniques for parking lot configurations41, 42 provide insights into improving operational efficiency; however, they fail to address the interconnected challenges of fairness, sustainability, and economic viability. Advances in power quality improvement and energy management for microgrids have highlighted the importance of robust control strategies43, 44, yet their application to CPLs remains underexplored, especially in integrating distributed energy sources and managing user-specific needs. Similarly, energy management frameworks for residential microgrids leverage RESs and ESSs effectively45, 46, but they often fall short of addressing real-time adaptability required for EV charging in shared spaces.

Few researchers have studied the interconnected system of multiple PLs intending to maximize their profits using Mixed-Integer Non-linear Programming (MINLP) to schedule their operation and facilitate energy trading among themselves as well as with the grid operator47. MINLP is widely used for solving complex optimization problems in interconnected energy systems due to its ability to handle discrete and continuous variables, enabling the scheduling of PL operations while considering non-linear constraints. However, MINLP is inherently complex and intensively computational which can be mitigated by using real time rule-based algorithm. Cost benefits to PLOs can also be obtained through intelligent management of CPLs, which allows the participation of different distributed energy sources to decrease operational costs and flatten the load profile during on-peak demand48, 49. Generally, priority-based charging is used to flatten the load profile with the penetration of a large fleet of EVs19 while considering the perspectives of the grid operators only. The assessment of priority-based charging of EVs can be quantified by introducing fairness indices with the primary goal of improving fairness in EV charging in different types of charging contracts16. It is observed that stochastic behaviour and decisions of EV owners have a significant role in the framework of EMSs for providing priority-based charging50 and optimal scheduling51, both in the short-term as well as long-term.

In the above-mentioned literature, the authors have proposed either single or multi-stage EMSs to provide benefits to PLOs by one or more means of maximizing revenue, minimising operational costs, reducing electricity costs, and increasing the use of RESs. The research challenges from the above studies are found as follows:

  1. (1)

    Few researchers have proposed DAS methods without considering EV owners’ and grid operators’ preferences. However, real-time optimization with priority-based charging of EVs considering the uncertainties in DAS and the interests of multiple stakeholders is still missing in the existing literature. Also, the indices representing techno-economic-environmental factors are not discussed in detail.

  2. (2)

    Most of the work is done on home-based charging, and community-based charging schemes with RES are rarely discussed; thus, CPL-based EV charging covers much scope for research.

  3. (3)

    Generally, the binary charging technique is employed for EVs at charging stations, where each EV will be charged at the maximum rate. It is necessary to manage the EV charging requirements while maximizing the profit of PLO. This technique has a negligible impact on the EV battery health, as it utilizes the complete charging cycle of the EV battery. However, for a large-scale optimal decision using the binary charging technique, the problem needs to be formulated as a binary optimization task, which requires exhaustive search and testing. It becomes highly challenging for large-scale real-time implementation due to its computational requirements.

  4. (4)

    Few studies have developed a convex relaxation approach for the above-mentioned problem, as coordinated charging of EVs acts as a non-convex problem due to large solution space and uncertain parameters. Moreover, convex optimization for coordinated charging of EVs can lead to suboptimal solutions, computational complexities, memory requirements, scalability issues, and sensitivity to uncertainties. These issues may hinder the real-time and large-scale application of the previously discussed EV charging techniques.

The proposed method in this article aims to address key research challenges identified throughout the literature survey. To better understand the above literature survey, Table 1 summarises and compares the existing works on various parameters, such as objective, scheduling method, stages and uncertainty consideration, power management, priority charging, and performance.

Contributions

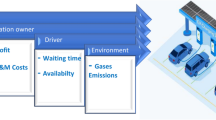
This article establishes a new ground for investigating techno-economic-environmental performance indices for PLOs in a CPL. The primary objective of using a three-stage EMS is to benefit both community PLO and EV owners. The proposed EMS is divided into three stages: day-ahead scheduling (DAS), real-time power management (RTPM), and priority-based electric vehicle (EV) charging (PEVC). In the first stage, the DAS utilizes linear programming to determine the optimal charging rates for each EV parked at a community parking lot (CPL) to maximize the profit for the PLO. The DAS commits day-ahead power purchases from the power utility while considering uncertainties in generation, consumption, and tariff. In the second stage, the RTPM utilizes a rule-based algorithm to compensate for the imbalances in the day-ahead power purchases and the real-time power purchases by utilizing renewable power generation, and battery backup units located at each building. During the excess power scenario, the RTPM takes care of the residential loads in each building by utilizing the surplus solar generation and charging the building backup units (BBUs). On the other hand, during a deficit power scenario, the RTPM takes care of the EVs parked at CPL by discharging the BBUs installed at each building. The RTPM is generalized for ‘m’ buildings with separate residential loads and BBUs, and the charge/discharge of BBUs depends up on their state of charge (SOC) values. In the third stage, the PEVC utilizes a rule-based algorithm to prioritize the charging of each EV parked at CPL using a weight parameter, respecting the techno-economic constraints. The total power available to support PLO is obtained from the RTPM, where the EVs must be charged in real-time at increased prices. The power purchase at real-time tariff is costlier than day-ahead power purchase commitments, which underscores the significance of the PEVC stage to optimally utilize the real-time power available from various sources for reduced costs for PLO and increased EV owners’ satisfaction.

Later, the effectiveness of the proposed three-stage EMS is backed by various techno-economic-environmental performance indices such as, fairness coefficient (FC), net carbon emission (NCE), self-sufficiency ratio (SSR), and self-consumption ratio (SCR).

The key contributions of this article are as follows.

  1. 1.

    A novel coordinated three-stage EMS is proposed for a community consisting of a CPL for EV charging, two buildings as prosumers, their building backup units (BBUs), and RESs.

  2. 2.

    EMS utilizes DAS to procure power from the utility to maximize the profit of the PLO, followed by compensation for imbalances in renewable power generation and load demand.

  3. 3.

    A priority decision-making system is incorporated to charge parked EVs while considering the interests of the PLO and EV owners.

  4. 4.

    The economic and environmental benefits to the PLO are obtained for various scenarios with six different indices.

This article is organized as follows. “Problem formulation” section describes the system, modelling, and assumptions. “Proposed energy management system” section discusses the proposed methodology and performance indices in detail. Simulation results and discussion are presented in “Results and discussion” section, followed by the Conclusion in “Conclusion and future research directions” section.

Table 1 Comparison of different models in the literature with the proposed model.
Full size table

Problem formulation

System description

In this paper, a CPL having multiple ports is considered, which can charge several numbers of EVs at a time. The parking lot is integrated with two buildings, each having a rooftop solar PV, loads, and BBUs. Each building has energy storage backup, which is used during the unavailability of grid power. It is anticipated that the building’s advanced charging meters will be installed, enabling the community EMS to obtain real-time SOC of EVs. Based on the initial SOC, parking time, cost of charging, and arrival and departure time, the PLO will decide whether to charge or discharge specific EVs. Hence, the proposed EMS utilises real-time renewable power generation, load demand, and EV requirements to manage the charging of EVs optimally. Figure 1 shows the complete architecture of the modelled system. Also, the specific parameter values considered in this research work are taken from Ref.57 and mentioned in Table 2.

Fig. 1
figure 1

The community parking lot integrated with renewable energy and loads.

Full size image
Table 2 Specifications of the proposed system.
Full size table

Solar PV and wind

This study considers Sydney, a city in the southeastern part of New South Wales state of Australia57. A time-series wind and PV generation dataset was collected for an entire year, generating 8760 samples, followed by monthly and hourly divisions. The average of these datasets is obtained from the prior per-hour location-specific solar irradiance and wind speed, combined with uncertainties. The samples are predicted using the autoregressive integrated moving average (ARIMA) technique, and errors are predicted while estimating the solar and wind within a specific timeframe. Due to the unpredictable nature of weather conditions, solar and wind generation can be represented mathematically as a stochastic or random function that varies over time56. Figure 2a, b show the uncertainty in solar irradiance, wind speed, and building loads using (1) and (2).

$${P_{pv}}(i) = {P_{PV}}(i)\left\{ {1+{\eta _s}(i)} \right\}$$
(1)
$${P_w}(i) = {P_W}(i)\left\{ {1+{\eta _w}(i)} \right\}$$
(2)
Fig. 2
figure 2

Monthly predicted and actual average value of (a) solar irradiance, (b) wind speed, (c) B1 load, and (d) B2 load.

Full size image

where Ppv and Pw are the total solar and wind power, \({P_{PV}}(i)\) and \({P_W}(i)\) are the forecasted values of PV and wind, \({\eta }_{s }\left(i\right)\) and \({\eta }_{w}\left(i\right)\) are the errors due to prediction exhibited using Gaussian random variables with variance \({\sigma }_{pv}\) and \({\sigma }_{w}\) of PV and wind.

EV fleet

This study considers a separate charging port for each EV in the parking lot. The daily EV fleet was determined based on assumptions about their travel behaviour, including arrival and departure times and the SOC of their batteries. Each charging port has a maximum charging/discharging power of 7 kW. The SOC for each EV is assumed to be between 0.3 and 0.7, with a storage capacity of 40 kWh21 but in the proposed work, the SOC of each arriving EV is generated randomly between 10 and 90% using a normal probability distribution. Such an assumption is taken to consider a wider range of SOC values in each arriving EV in the CPL. CPL is assumed to charge EVs at five distinct charging rates. The charging rate of an nth EV can take any value from a set \({\rho }_{c}\)at the instant of time i, denoted by \({\rho }_{cn}\)(i) given by (3).

$$\rho c \in \left\{ {0,c1,c2,c3,c4} \right\}$$
(3)

where 0 < c1 < c2 < c3 < c4 are distinct charging rates, c4 indicates the maximum allowable charging rate, and \(\rho\)cn(t)  =  0 means that the EV is not charging at that time. The system cannot satisfy EV charging demand, even charging EVs at the maximum rate due to randomness in arrival time and charge demand.

Building load

In this study, two buildings with separate BBUs were considered along with rooftop solar PV arrays. Buildings B1 and B2 have an average load demand of 40 kW and 60 kW, respectively. The peak load demand for both buildings occur at 20:00. Figure 2c and d show the uncertainty in building loads by using (4).

$${P_L}(m) = {P_L}(m)\{ 1+{\eta _d}(i)\}$$
(4)

where \({P}_{L}\) is the total household demand for both buildings, \({{P}_{L}}_{\left(m\right)}\left(i\right)\) is predicted building demand, and \({\eta }_{d}\left(i\right)\) is the error demonstrated using Gaussian random variables with variance \({\sigma }_{d}\) .

Battery backup unit

Integrating batteries can smooth out the demand curve by shaving peaks and filling valleys, shift both renewable and off-grid energy for cost savings, and offer rapid response to meet demand58. Both buildings have a battery as a backup unit to provide power without PV, wind, and grid power. Each BBU has a capacity of 50 kWh. This storage system stores energy when the charging cost is low and supplies power to a household load when the cost is high. However, when there is deficient power in charging stations, EV owners get power from these BBUs depending on their SOC values. The charging and discharging power and SOC of BBUs are given by (5) and (6)59.

$$SO{C_C}(i) = (1 - \delta )soc(i - 1)+\frac{{{P_C}\Delta T{\eta _C}}}{{{E_C}}}$$
(5)
$$SO{C_d}(i) = (1 - \delta )soc(i - 1) - \frac{{{P_d}\Delta T}}{{{E_C}{\eta _d}}}$$
(6)

where Pc denotes the instantaneous charging power, Pd denotes the instantaneous discharging power, δ denotes the self-discharging rate, \(\varDelta T\) denotes the calculation time, \({E}_{c}\) denotes the BBU’s capacity, and \({\eta }_{c} \text{a}\text{n}\text{d} {\eta }_{d}\) are charging and discharging efficiency, respectively.

Assumptions

This section summarises the assumptions made in this study. These assumptions govern the charging rate of each EV in the parking lot, their driving behaviour, utility tariff, building backup rental service, and uncertainties in power generation and loads. The assumptions that align with the study’s objectives are presented below.

  1. 1.

    The day-ahead information on renewable generation, consumer loads, utility tariffs, and arrival or departure of EVs in the parking lot are considered to remain constant for each hour.

  2. 2.

    Each EV in the parking lot is connected to a separate charging port capable of charging the connected EV battery at multiple distinct charging rates at different hours.

  3. 3.

    Vehicle-to-building or vehicle-to-grid concepts are not considered as they may reduce EV battery lifetime or increase maintenance costs.

  4. 4.

    A variable tariff from the utility and a fixed rate contract with building owners to use their installed backup supply are expected.

Proposed energy management system

The overview of the proposed three-stage EMS is shown in Fig. 3. The methodology starts with historical data collection followed by prediction of solar PV and wind generation, building load demand, EV requirements, and electricity tariff. The first stage, as shown in Fig. 4, involves a DAS approach based on linear programming to meet consumer demands by minimizing electricity costs for the PLO while considering load demands, generation, and tariffs. The second stage, as shown in Fig. 5, involves a rule-based strategy to maintain the power coordination between renewable sources, loads, BBUs, and the utility in case of deviations from the predicted values. The third stage, as shown in Fig. 6, priorities parked EVs at the CPL based on their SOC levels, expected departure time, and exclusivity of EV owners. The proposed EMS provides coordination among communities with high renewable shares to meet energy demands from buildings and EVs while ensuring fairness in the charging of EVs.

Fig. 3
figure 3

Block diagram of the proposed EMS.

Full size image
Fig. 4
figure 4

Stage 1 flowchart of the day ahead of planning of CPL.

Full size image
Fig. 5
figure 5

Stage 2: flowchart of real-time power management.

Full size image
Fig. 6
figure 6

Stage 3: flowchart of priority-based charging.

Full size image

Stage 1: day-ahead planning

Distribution system operators provide the predicted data of EV charging requirements, renewable generation, day-ahead electricity price, and grid tariff as inputs to formulate and solve the deterministic optimization problem and to achieve the day-ahead power exchange with the utility. The formulated optimization problem provides an optimal charge scheduling of EVs to maximize profits for PLOs using the objective function as given by (7).

Revenue is the PLO’s earnings from charging EVs, and expenses are the electricity bills paid by the PLO to the utility. EV owners with high \({CD}_{n}\) and low \({i}_{an}\), pay an extra per kW-hour of energy than customers with low \({CD}_{n}\) and high \({i}_{an}\). The total revenue for the PLO is calculated by using (8). The total cost paid by the customer is the summation of base cost and variable cost, as shown in (9). The base cost is the fixed cost, and it is generally considered a low charging cost, whereas the variable cost is the added cost paid by a consumer during a high charging rate. The entire expenses of EV charging at the time i for interval \(\varDelta t\) may be expressed by using (10). ř(i) is real-time power consumption calculated by using (11). \({C}_{Tn}\) and \({CD}_{n}\) are the constants for EV charging. Thus, revenue is a fixed quantity; expenses must be minimized to maximize the profits of the PLO.

Therefore, we denote the second term of (13) by ‘b’ as shown in (15). Expenses are the linear function of electricity tariff and real-time power consumption; thus, they can be optimized using linear programming. The objective function can be written as shown in (1).

$$Max({{\varvec{\upzeta}}}) = {\text{ }}\sum\limits_{{i = 1}}^{{24}} {Revenue(i)} - Expense(i)$$
(7)
$$Revenue(i) = \sum\limits_{{n = 1}}^{k} {{C_T}_{n}} {\rho _c}_{n}(i)\Delta t$$
(8)
$${C_{Tn}} = {C_b}+{C_{vn}}$$
(9)
$$Expenses(i) = [\xi (i)\gamma (i)]\Delta i - \left[ {(\xi (i) - {{\check{r}(i)}}\alpha (i)} \right]\Delta i+[({{\check{r}(i)}} - \xi (i))\beta (i)]\Delta i$$
(10)
$${{\check{r}(i)}} = \sum\limits_{{n = 0}}^{k} {{\rho _{cn}}(i) - {\rho _{re}}(i)}$$
(11)

Equation (7) can be written using (8) and (10) as:

$${{\varvec{\upzeta} = }}\sum\limits_{{i = 1}}^{T} {\left[ {\sum\limits_{{n = 1}}^{N} {{C_{Tn}}{\rho _{Cn}}} (i)\Delta i} \right]} - [\xi (i)\gamma (i)]\Delta i[(\xi (i) - {{\check{r}(i)}})\alpha (i)]\Delta i+[({{\check{r}(i)}} - \xi (i))\beta (i)]]\Delta i$$
(12)
$${{\varvec{\upzeta} = }}\sum\limits_{{i = 1}}^{T} {\left[ {\sum\limits_{{n = 1}}^{N} {{C_{Tn}}{\rho _{Cn}}} (i)\Delta i} \right]} - [\xi (i)\left( {\gamma (i)] - \alpha (i)} \right)]\Delta i - \left( {\alpha (i)({{\check{r}(i)}}\Delta i} \right) - \left( {\beta (i) - \alpha (i)} \right)[{{\check{r}(i)}} - \xi (i)]\Delta i$$
(13)

where the first term of (13) can be denoted by ‘\(a\)’ and second term denoted by ‘b’

$$a = \sum\limits_{{i = 1}}^{T} {\left[ {\sum\limits_{{n = 1}}^{N} {{C_T}_{n}{\rho _{cn}}(i)\Delta i} } \right]} = \sum\limits_{{n = 1}}^{N} {{C_T}_{n}} \left[ {\sum\limits_{{i = 1}}^{T} {{\rho _{cn}}(i)\Delta i} } \right] = \sum\limits_{{n = 1}}^{N} {{C_{Tn}}} C{D_n}$$
(14)
$$b = \sum\limits_{{i = 1}}^{T} {\left[ {\xi (i)\left( {\gamma (i) - \alpha (i)} \right)} \right]} \Delta i - \left( {\alpha (i){{\check{r}}}(i)\Delta i} \right) - \left( {\beta (i) - \alpha (i)} \right)\left[ {{{\check{r}(i)-}}\xi {\text{(i)}}} \right]\Delta i$$
(15)
$$\hbox{min} \sum\limits_{{i = 1}}^{T} b$$
(16)

subject to

$$\sum\limits_{{i = 1}}^{T} {{\rho _{cn}}} (i)\Delta t - CDn(i) = 0\forall n$$
(17)
$$0 \leqslant {\rho _{cn}}(i) \leqslant c4\forall i<{i_{an}}$$
(18)
$$\sum\limits_{{n = 0}}^{N} {{\rho _{cn}}} (i) - {\rho _{re}}(i) \leqslant {\rho _{\hbox{max} }}\forall n$$
(19)

According to the equality constraints in (17), the system must fulfill the energy requirements of each EV as per their SOC values. Equations (18) and (19) are inequality constraints that include lower and upper limits of charging rate and power drawn from the grid. In this stage, a linear programming solver is utilized for the DAS of the parked EVs. The system parameters, such as renewable generation, TOU tariff structure, and number of EVs arriving at CPL, are updated after each hour, followed by optimization in the next iteration for 24 h. DAS maximizes the profit to the PLO by determining the optimal set of charging rates for each EV connected to the CPL. The profit maximization depends on the day-ahead profiles of electricity tariffs, EV charging demand, and power generation profiles for solar plants and wind turbines. Various equality and inequality constraints are generated and solved using LP-based optimization, where the obtained solutions are checked for violation of the constraints. Finally, a day-ahead optimal set of charging rates for EVs is obtained which may deviate under real-time conditions. In this work, the aggregated real-time load at the PLO is denoted by Pcpl, which is different from the total power available to support the PLO. The next stage involves real-time power management where the surplus solar energy in buildings is used for charging of BBUs and deficient solar energy in buildings requires discharging of BBUs. In this way, both stages contribute to optimal energy management for PLO as well as building prosumers. Moreover, after allocating the total power available to support the PLO, it becomes important to charge the parked EVs in a prioritized manner to enhance the experience of EV owners.

Stage 2: real-time power management

If the DAS approach does not fulfil the instantaneous power demand of parked EVs, then a second stage is invoked to satisfy the load demand of the parked EVs. It should be noted that the BBUs are not allowed to charge above 90% or discharge below 30% to reduce battery degradation and improve lifecycle60. This rule-based power management scheme is shown in Fig. 5, generalized for ‘m’ buildings with separate loads and BBUs, which can be categorized into excess and deficit renewable power generation scenarios.

Excess power scenario

When the combination of real-time renewable power generation at the CPL and day-ahead scheduled electricity from the utility exceeds the real-time load demand at the CPL and buildings, the rule-based technique balances the excess power. This extra power generation can be used to power the building’s loads before being used to charge the BBUs. If the rooftop PV generation at Bm is less than the load requirements, the incoming power from the CPL and utility can be used by the load at Bm, with the remaining power used to charge Bm’s BBU. Similarly, if Bm’s rooftop solar PV generation exceeds its load requirements, the excess power after load utilization can be used to charge BBU Bm. The charging rate is determined by the BBU’s SOC level, which is estimated to be no more than 90% while meeting building load standards.

Deficit power scenario

The rule-based approach gets invoked when the combination of real-time renewable power generation at the CPL and day-ahead scheduled power from the utility is less than the real-time load demand at CPL and buildings. The deficit in power generation can be fulfilled by the rooftop solar PV generation at Bm followed by the discharging of the depleted BBUs61. If the rooftop solar PV generation at Bm is lower than the load requirements at Bm, then the BBU at Bm can be discharged to satisfy load requirements at the PLO. The discharge depends on the SOC level of the BBU, which is assumed to be a minimum of 30% while satisfying CPL load requirements.

Stage 3: priority-based EV charging

In stage 2, if both buildings cannot supply power to CPL, then charging all EVs becomes difficult. Therefore, priority-based charging of EVs is needed. A variable \(\kappa\) is used to determine the charging status of connected EVs, i.e., when \(\kappa\) = 1, EVs charging at a time interval of ‘\({\Delta }\)i’ and \(\kappa\) = 0 employs that EVs are not charging at that time interval. \(\phi\) is an index used to check the connection status of EVs. If \(\phi\) = 1, then \(\kappa\) can be 1 or 0 depending on whether EVs are charging or not, but when \(\phi\) = 0, then indeed \(\kappa\) = 0. At \({\Delta }i\) time interval, the needed charging time intervals are calculated as given in (20).

$${U_n} = \lambda - \Delta i$$
(20)

An inconstant rank function \(\psi \in \left[\text{0,1}\right]\) is defined for each EV that is parked at CPL for charging. A lower rank is given to customers who are unwilling to pay high charges and a higher rank is given to privileged customers. The weighted charging priority of each EV linked to the N charging port during the time interval \({\Delta }i\) is calculated as given in (21)

$$\omega = \left\{ {\begin{array}{*{20}{l}} {\frac{{{\psi _n}{\phi _n}({\chi _{\hbox{max} }} - {\chi _n})}}{{{\rho _{c\hbox{max} }}{U_n}}},}&{if\;\varphi = 1} \\ {0,}&{if\;\varphi = 0} \end{array}} \right.$$
(21)

where \({\varphi }_{n}\left({\chi }_{max}-{\chi }_{n}\right)\) denotes the EV battery capacity that needed to be fulfilled when it parked at CPL for charging at maximum SOC (\({\chi }_{max})\) level. The denominator term signifies that maximum charging is given to the EVs; however, the required charging time is low. The EVs must charge on priority before the potential departure time when Un is low. After the charging procedure is complete, if an EV leaves the CPL, the N charging port is set to be accessible by setting \(\phi\) = 0 and the weighted charging priority factor \(\omega\) = 0. If a new EV arrives and is connected to the Nth charging port, the charging port will be enabled once again by setting \(\phi\) = 1, and its associated weighted charging priority factor \(\omega\) will be calculated once more using (21).

Performance assessment criteria

Load equality

The self-sufficiency ratio (SSR) reflects the percentage of the overall electric demand met by renewable production and stored energy. In contrast, the self-consumption ratio (SCR) is the ratio of the renewable generation used in the building cluster to the total output. Equations (22) and (23) show the formula calculated for SCR and SSR, respectively21.

$$SCR = 1 - \frac{{\int\nolimits_{{i = 1}}^{\begin{subarray}{l} T \\ \end{subarray} } {{\rho _{\exp }}dt} }}{{\int\nolimits_{{i = 1}}^{\begin{subarray}{l} T \\ \end{subarray} } {{\rho _{re}}dt} }}$$
(22)
$$SSR = 1 - \frac{{\int_{{i = 1}}^{T} {{\rho _{imp}}(t)dt} }}{{\int_{{i = 1}}^{T} {{\rho _l}dt} }}$$
(23)

where \({\rho }_{re}\) are total generated renewable power and \({\rho }_{l}\) are total load demand in the community.

Environmental performance

The net carbon emission (NCE) is computed by using (24)

$$NCE = q \cdot \left( {\int\limits_{{i = 1}}^{T} {{\rho _{\exp }}(t)dt} - \int\limits_{{i = 1}}^{T} {{\rho _{imp}}(t)dt} } \right)$$
(24)

where q is the carbon emission factor of grid electricity, which is 0.71 kg CO2,e/kWh. \({\rho _{\exp }}\) is the exported power to the grid and \({\rho _{imp}}\) is the imported power from the grid at time t21.

Fairness index

When there are limitations on the amount of power available, it is difficult to charge all EVs to the same level; thus, the major goal of this index is to gauge the equity between the charging processes of the parked EVs at the CPL. Fairness is considered important in EV charging stations where power availability limits a few of the EVs to not get charged to their maximum SOC values16. The fairness index is measured by calculating the average of the SOC values of EVs at their departure time. If the SOC of each EV is charged with 100%, then \({F}_{ind } = 1\). \({F}_{ind }\) is calculated by using (25)16,

$${F_{ind}} = \frac{{\sum\nolimits_{{n = 1}}^{{0.5Nev}} {SOC(n\lambda )} }}{{Nev}}$$
(25)

where Nev represents the number of EVs, n represents each EV, and λ represents the departure time of EVs. To consider charging EVs with lower SOC values (below 50%), the Find is assumed.

Results and discussion

The proposed three-stage EMS is assessed for a single day in a realistic environment of a community in Australia. The proposed methodology analyzes power-sharing among the connected assets and electricity bills incurred by the PLO for charging demand fulfillment of parked EVs. The simulation study is carried out for various scenarios with a time step of one hour, implying that each variable is assumed to be constant throughout the given time step. The simulation is conducted on a computer with Intel® Core™ i5-13500 H processor, 4.70 GHz clock, and 16 GB RAM.

Simulation setup

The values of the parameters considered in the simulation study are based on the existing literature and logical analysis. In this paper, a total of 50 EVs are assumed to be owned by community members whose charging demand profiles may differ. The charging demand of each EV is dictated by the total distance travelled before entering the CPL for the recharging event. It is assumed that the distance travelled in a trip by an EV is modelled through the logarithmic probability density function, which has a mean of 150 km and a standard deviation of 50 km. The SOC of arriving EVs at CPL depends on their travel distance, which typically varies between 60 and 270 km. The logarithmic probability density function for the distance travelled by EVs is shown in Fig. 7(a), and the distance travelled by individual EVs is shown in Fig. 7(b). Thus, by combining the known data, the number of EVs parked at CPL in each hour can be obtained, as shown in Fig. 8(a). The SOC of each arriving EV is generated randomly between 10 − 90% using a normal probability distribution, as shown in Fig. 8(b). The time-of-use (TOU) tariff scheme, i.e., day-ahead, and real-time tariff under the TOU scheme is shown in Fig. 9. It can be observed that the real-time purchase tariff is set to be 15% more than the day-ahead tariff57. Similarly, the real-time selling tariff is set to be 15% less than the day-ahead tariff. In this paper, 1 AUD is divided into 100 ¢ for analysis.

Fig. 7
figure 7

(a) Logarithmic of distance travelled by each EV and (b) distance travelled by each EV.

Full size image
Fig. 8
figure 8

(a) number of EVs parked per hour and (b) SOC of each arriving EV at CPL.

Full size image
Fig. 9
figure 9

TOU tariffs throughout the day in Australia.

Full size image

Performance analysis of energy management scenarios

In this section, the energy required and the cost incurred by the PLO are analysed through various scenarios, as given in Table 3. In the reference scenario, the CPL acts as a load to supply EV charging through the utility with a real-time tariff. Thus, this paper considers the reference scenario as the baseline to assess and validate the proposed EMS. Each scenario is simulated for 24 h at a one-hour time interval. The number of parked EVs is maximum during midnight (00:00–03:00), which gets reduced in subsequent hours (04:00–10:00). A few EVs will return to the CPL for charging during midday (11:00–15:00), and other few EVs will depart from CPL during evening hours (16:00–19:00). In an uncoordinated charging scenario, EVs arrive at the CPL throughout the day at different hours, is independent of the day-ahead tariff. Figure 10(a) shows the power consumption pattern of the parked EVs at CPL, which is lowest during the morning hours (04:00–10:00) and highest during the late-night hours (20:00–00:00). It can be observed that power demand falls from 110 kW to 60 kW during morning hours and rises from 100 kW to a peak demand of 170 kW during late night hours. The hourly electricity bill is a product of real-time purchase tariff and hourly power demand, the pattern of which is shown in Fig. 10(b). It can be observed that the hourly electricity bill reaches a maximum value of 4000¢ and touches a minimum value of 1000¢. In the uncoordinated charging scenario, the PLO pays a daily electricity bill of 525 AUD which can be reduced by scheduling the power purchase from the utility on the appropriate day-ahead.

Fig. 10
figure 10

Reference scenario: (a) power demand of CPL and (b) electricity bill.

Full size image
Table 3 Scenarios of energy management.
Full size table

In Scenario 1, the CPL is assumed to be integrated with rooftop solar PV arrays and wind generation systems. A centralized linear program is utilized for day-ahead planning of power purchases from the utility based on historical data or patterns of generation and loads throughout a typical day. Figure 11(a) shows the hourly power shared by renewable energy sources and the utility to feed charging power demand at the CPL. It can be observed that a large amount of power, as high as 120 kW, gets scheduled for the PLO during the midnight hours (00:00–03:00) due to a low tariff. During the daytime hours (08:00–17:00), the share of power from the utility gets reduced to as low as 25 kW, which is compensated by renewable energy generation. The power procurement from the utility is reflected in the hourly electricity bill with a maximum value of 3500 ¢ during evening hours and a minimum value of 500 ¢ during large generation of renewable energy, as shown in Fig. 11(b). The PLO utilizes day-ahead planning for energy management and pays a daily electricity bill of 462 AUD which has dropped from 525 AUD to indicate daily savings of 12%, as shown in Fig. 12(b). The daily electricity bill of PLO can be further reduced by integrating buildings as prosumers.

Fig. 11
figure 11

Scenario 1: (a) power share of assets in the community and (b) electricity bill.

Full size image
Fig. 12
figure 12

(a) Performance comparison and (b) electricity bill and bill saving of different energy management scenarios.

Full size image

Scenario 2 is an extension of the previously discussed Scenario 1, where the CPL is assumed to be integrated with buildings and has its own rooftop solar PV array and distinct load profiles, which may act as prosumers to support charging power demand at the CPL. It is assumed that the building owners are not interested in revenue stacking through selling excess renewable energy generation. Figure 13(a) shows the hourly power shared by renewable energy sources and the utility to feed charging power demand at the CPL. The power procured from the utility is reduced to a maximum of 150 kW during daytime hours (09:00–16:00), which gets increased during the early morning (00:00–07:00) and night hours (17:00–00:00). The hourly electricity cost incurred by the PLO is reflected in the hourly electricity bill with a maximum value of 3900 ¢ during evening hours, and a minimum value of 200 ¢ during morning hours, as shown in Fig. 13(b). In Scenario 2, the PLO utilizes day-ahead planning for energy management and pays a daily electricity bill of 385 AUD, which has dropped from 462 AUD to indicate daily savings of 17%, as shown in Fig. 12(b). The daily electricity bill of PLO can be further reduced by integrating BBUs and priority-based charging of EVs.

Fig. 13
figure 13

Scenario 2: (a) power share of assets in the community and (b) electricity bill.

Full size image

In Scenario 3, the CPL is assumed to be integrated with two BBUs to support EVs and building loads. It is also assumed that the PLO is required to pay a higher compensation amount for utilizing BBU 1 than BBU 2. During the early morning hours (00:00–03:00), a large amount of power gets scheduled from the utility to charge the BBUs at a low tariff, and during peak tariff hours (07:00–09:00 and 17:00–20:00), the stored energy in BBUs get utilized to feed building loads, and EVs at the CPL, as shown in Fig. 14(a). The combined charging/discharging of BBUs has reduced the electricity bill for the CPL, as shown in Fig. 14(b). The initial SOC for both BBUs is 70% which is reduced to nearly 30% at the end of the day. It can be observed that the charging/ discharging rate of BBU 2 is more than that of BBU 1, as shown in Fig. 15(a). Thus, the SOC of each BBU varies according to its charging/ discharging rate, as shown in Fig. 15(b). The SOC of BBUs reach above 90% during 04:00–06:00 and 14:00–17:00. This is because, during 04:00–06:00, the power purchased from the grid is higher than the CPL load requirements, and the renewable power generation is very low, which forces the BBUs to utilize the excess power imported from the grid. Similarly, during 14:00–17:00, the power purchased from the grid satisfies both the CPL and building load requirements, but renewable power generation is very high, which forces the BBUs to utilize the excess renewable power generation. It can be observed that the hourly electricity cost incurred by the PLO is reflected in the hourly electricity bill with a maximum value of 2500 ¢ during evening hours and a minimum value of 100 ¢ during peak tariff hours. In Scenario 3, the PLO pays a daily electricity bill of 288 AUD which has dropped from 385 AUD, indicating daily savings of 26%, as shown in Fig. 12(b). However, the total daily savings in the electricity bill for the PLO has dropped to 45% of the daily electricity bill in the case of Scenario 3 as compared to uncoordinated charging of EVs without building prosumers. The indices for different scenarios of energy management are presented in Fig. 12a on technical and environmental grounds. Table 4 lists the daily electricity bill, savings, SSR, SCR, NCE, and FC values for different energy management scenarios. It can be concluded that the proposed EMS in Scenario 3 performs very well as compared to other scenarios based on various indices.

Fig. 14
figure 14

Scenario 3: (a) power share of assets in the community and (b) electricity bill.

Full size image
Fig. 15
figure 15

Building backup units (a) power share and (b) state of charge.

Full size image
Table 4 Performance comparison of different energy management scenarios.
Full size table

Conclusion and future research directions

Charging infrastructure plays a crucial role in the adoption, aggregation, and management of EVs for a sustainable future. Coordination frameworks for charging stations must be adopted to reduce the burden of EV charging requirements on the utility grid. In this research, a novel three-stage coordinated EMS is proposed for day-ahead scheduling, real-time power management, and prioritized charging of EVs. The simulation model considers a single PLO integrated with renewables, neighborhood building prosumers, and the utility grid. Each neighborhood building prosumer consists of residential loads, local solar power plants and BBUs. Also, it is assumed that each EV is connected to a separate charging port at the PLO. The PLO is equipped with the proposed three-stage EMS, where the first stage uses linear programming to maximize the profit to the PLO by determining the optimal charging rates for EVs with day-ahead power purchase from the utility grid, the second stage uses real-time power management to obtain the total available power support for EV charging by optimally charging/ discharging BBUs, and the third stage effectively utilizes the total available power support through prioritized charging of EVs, based on the nature of the contracts with EV owners and the initial SOC values of the EVs. The effectiveness of the proposed EMS is validated on the MATLAB® platform under four different scenarios. Afterwards, distinct techno-economic-environmental indices were investigated, including fairness index, net carbon emissions, self-consumption ratio, self-sufficiency ratio, and cost savings, under each scenario. Comparative analysis of each scenario is presented in terms of the techno-economic-environmental indices. The key conclusions of this study are summarized below.

  1. (1)

    When compared with Reference (uncoordinated charging), the proposed EMS exhibits improvements in fairness index, net carbon emissions, and cost savings by 18%, 40%, and 45%, respectively.

  2. (2)

    When compared with Scenario 1 (day-ahead planned charging), the proposed EMS exhibits improvements in fairness index, net carbon emissions, self-consumption ratio, self-sufficiency ratio, and cost savings by 10.8%, 25%, 63.4%, 66.7%, and 37.6%, respectively.

  3. (3)

    When compared with Scenario 2 (building prosumer-based charging), the proposed EMS exhibits improvements in fairness index, net carbon emissions, self-consumption ratio, self-sufficiency ratio, and cost savings by 4.6%, 16.7%, 23.2%, 27.1%, and 25%, respectively.

From the above-mentioned points, it is observed that coordination among the PLO, neighborhood building prosumers, and the utility grid contributes towards broader sustainability goals. Future research could explore the effect of sparse charging points on the coordination among EVs, neighborhood building prosumers and the utility grid, along with vehicle-to-grid and vehicle-to-building interactions. Future work could extend the EMS to a broader network of parking lots or test its scalability across different geographic locations and grid infrastructures, ensuring that the system remains flexible and adaptable to diverse environments.