Introduction

Gradual depletion of fossil fuel sources and constantly increasing demand have strongly contributed to promoting the penetration of distributed generation resources, especially renewable energies, in meeting electricity demand as well as improving the efficiency and flexibility of the networks1,2. According to published data by the U.S. Energy Information Administration in 2017, 17% of the electricity supply for the total energy demand of the United States is from renewable energy sources, and this proportion is estimated to increase sharply in the future3. Some other large countries, such as India and China, have also reported significant penetration. The Indian government has stated that 175 GW will be generated by renewable energy resources in 2022, including 100 GW for solar energy and 60 GW for wind energy, and a penetration of 227 GW by 2027 will be considered an energy target4. In addition, China also generated up to 94 GW from solar energy in 2017, aiming for non-fossil energy to be 20% of total energy demand by 20303. Due to the enormous economic and technical benefits gained, the penetration of distributed generation units (DGUs) is increasing rapidly. However, unplanned connections can seriously affect the power grid, such as increased branch power loss, changed bus voltage, voltage transients, and reduced reliability5. Therefore, integration of DGUs requires careful consideration to maximize welfare and avoid negative impacts.

Previous studies have proposed different approaches to determine the suitable connection of distributed generation units in the distributed system. As6,7,8, studies have applied particle swarm optimization (PSO) as an optimum technique to solve the problem of DGU installation for minimizing losses on distribution branches and improving the voltage at the buses. PSO is one of the most popular meta-heuristic algorithms used to optimization problems in the real world. PSO stands out for its simple structure and few control parameters. Its most significant disadvantage is early convergence in the local regions, which leads to poor performance. Similarly, another popular method is the artificial bee colony (ABC) algorithm, which is inspired by the behavior of bees from nature. While the authors in9 applied ABC to reduce both total power loss and improve the voltage sag index in the system through connecting distributed generators, the authors10 used ABC for minimizing voltage deviation index, line loading and branch power losses in the distribution systems by using BESS. The authors significantly enhanced the distribution system’s performance by identifying a suitable installation that could improve the voltage profile, mitigate line loading, and reduce total loss. ABC is a relatively good method, but its algorithm structure is complicated. Moreover, there are three phases of onlooker bee, employed bee and scout bee, which are implemented in the model, so it takes a lot of time to process data. Besides, other studies such as11,12 also introduced ant lion optimization algorithm (ALOA) to minimize total power loss and maximize the net savings thanks to installing renewable energy units in several distribution systems. Like the stochastic algorithms, ALOA handles optimization problems by iteratively trying to improve the quality of solutions. Although ALOA is considered a friendly method, its biggest drawback is instability. It is more likely to fall into local optima, so it is limited to solving problems with the large search space. With the same objective function for the above optimization problem, the authors in13,14 suggested applying an adaptive biogeography-based optimization (BBO) method. BBO is known to be a helpful method for solving various complex problems. However, the processing speed of BBO is quite slow, and its performance is mainly affected by the control parameters. Additionally, for reducing energy losses, some authors15 have also successfully found a suitable installation of BESS in the balanced system considering the duck curve phenomenon by using whale optimization algorithm (WOA), firefly algorithm (FA), and PSO. The results obtained show that WOA performs better than the compared methods. Similarly, research16 suggested a coyote optimization algorithm (COA) to compare with WOA, FA, and PSO in determining the optimal allocation and sizing of the lithium-ion BESS in cases without and with photovoltaic units. Energy loss reduction has increased significantly by integrating BESS and photovoltaic generation units simultaneously. In that study, COA also proved outstanding in solving optimization problems compared to others. In addition to the mentioned methods, many other approaches are applied to optimize the installation of DGUs in distribution power network, such as the modified moth flame optimization (MMFO) algorithm17, garra rufa optimization (GRO)18, improved decomposition based evolutionary algorithm (I-DBEA)1, harmony search (HS) algorithm19, genetic algorithm (GA)20, harris hawks optimizer (HHO)21, Kalman filter algorithm (KFA)22 and intelligent water drop (IWD) algorithm23. Most of these studies have only focused on reducing total power loss on the branches as well as enhancing voltage profile as the primary target. However, to fully evaluate the effectiveness of an integrated system, it is most important to consider the total costs of operating the system for a long time, and only a few studies in the past have taken this into account24,25. Those studies have calculated the associated costs, including investment costs, operation, and maintenance of grid-connected units. However, the authors applied optimization algorithms that are less efficient in terms of performance and stability, such as ABC24 and water cycle algorithm (WCA)25. On the other hand, total costs are only considered at the peak load level. Therefore, the found global solutions are uneconomical at different loads. Several researchers have recently considered the time-varying generation and consumption to enhance the quality of the optimal solution. Specifically, study26 looks at a 24-h variation of photovoltaic, wind turbines, and load demand to cut the long-term costs of operating the distribution system using a mixed-integer program (MIP). Similarly, research27 sought the optimal strategy for integrating BESS with high penetration from wind turbines and photovoltaic units considering 24-time segments. By applying an efficient algorithm, which has been published in recent years, called the salp swarm algorithm (SSA), this research has succeeded in minimizing costs incurred in the operating system, preventing reverse power flow and peak shaving in the balanced distribution system. Generally, most studies in the past were only implemented in the balanced three-phase distribution systems with objectives related to total costs that have not been fully considered. However, unbalanced three-phase distribution systems are more complicated than balanced three-phase distribution systems, and it has received very little attention from researchers28. In addition, integrating renewable energy resources into distribution systems will significantly increase the harmonic distortions due to applied inverters. However, harmonic generation from inverter-based renewable energy sources has yet to be considered much in the published papers. A summary of previous relevant studies and existing gaps is also presented as Table 1.

Table 1 Summary of shortcomings of previous studies.
Full size table

Previous studies have successfully determined the optimal solution for connecting DGUs to the distribution grid to minimize losses and enhance the voltage profile. However, to implement a project for integrating generation sources into the existing grid, it is necessary to comprehensively consider the economic-technical-environmental aspects in the long term of the entire project life cycle. As referenced from the past studies in the introduction section, previous studies have many limitations such as (1) poorly established constraints, (2) simple objective functions (mostly only concerned with technical factors), (3) applied algorithms are inefficient, (4) test systems are small and often consider balanced distribution systems (rarely consider unbalanced systems), (5) little consideration is given to harmonics from nonlinear loads and power converters, and (6) little attention is paid to considering load and generation changes over time. Therefore, this study is conducted to overcome the shortcomings of past studies. This paper considers the integration of wind farms (WFs), photovoltaic farms (PVFs), and battery energy storage systems (BESS) simultaneously into IEEE 123-bus UDS with devices such as capacitors, switches, and voltage regulators29 and 55-bus BDS in Nha Be District, Ho Chi Minh City, Vietnam30. The paper’s main objective is to (1) minimize the total costs of investment and O&M of WFs, PVFs, and BESS, (2) cut the electricity purchasing cost for load demand and branch losses from the primary grid through the substation, and (3) reduce the emissions cost from electricity production of the traditional power plants. Furthermore, this study proposes a co-simulation from OpenDSS and MATLAB to solve power flow problems in frequency domains. This is considered a powerful tool for flexibly and quickly calculating complex distribution systems. On the other hand, this paper also introduces an effective algorithm that was recently published for solving the optimization problem, named modified coyote optimization algorithm (MCOA)31. MCOA is considered an enhanced version modified in COA’s new solution generation equations, leading to more efficiency in MCOA. The achieved results by applying MCOA are compared with the original method and another robust method for the same objective function and technical constraints. In summary, the primary contribution of this research is briefly presented below:

  1. 1.

    This study proposed the optimal solution for simultaneous installation of WFs, PVFs, and BESSs to two gird types of unbalanced and balanced distribution networks to minimize total costs, including (1) investment as well as O&M costs for connected units, (2) the cost of purchasing electricity from the primary grid through the substation and (3) the emissions cost from the traditional power plants.

  2. 2.

    This paper has contributed to considering harmonic distortions from nonlinear loads and power conversion devices of distributed sources to keep the harmonic indices to IEEE Std. 519.

  3. 3.

    The study analyzed the impact of the simultaneous penetration of WFs, PVFs, and BESSs on the distribution system. Notably, the BESS’s strategy of suitable charging and discharging energy over time has significantly contributed to reducing operating costs and improving system efficiency. These findings have practical implications for the design and operation of power networks, highlighting the relevance of this research.

  4. 4.

    The research has successfully developed a co-simulation from OpenDSS and MATLAB software. This co-simulation created a robust platform for tackling quick and convenient optimization problems in various distribution systems. This supports the enhancement of the research capabilities.

  5. 5.

    The study also introduced a novel method with high performance and stability compared to other meta-heuristic algorithms to address optimization problems in IEEE 123-bus UDS and 55-bus BDS in Ho Chi Minh City, Vietnam. The results from the suggested method (MCOA) are shown to be more effective than other methods (SSA and COA).

The rest of the paper consists of the following sects: “Problem formulation” section gives the objective function and constraints; “Modified coyote optimization algorithm” section introduces modified coyote optimization algorithms; “Introduced method in solving the considering problem” section describes the suggested method’s application for handling the optimization problem; “Simulation results” section shows the simulation results and the analysis; And “Conclusions” section summarizes the paper.

Problem formulation

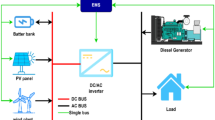
In this work, the optimal integration for distributed generation units, including photovoltaic farms, wind turbine farms, and battery energy storage systems in IEEE 123-bus unbalanced and 55-bus balanced distribution systems, is determined to minimize total costs while still satisfying the technical criteria. This integrated distribution system is briefly illustrated in Fig. 1. In this model, WFs and PVFs are connected to the primary power grid to supply energy for the loads and losses through power conversion devices. If the amount of generated power is insufficient, electricity from the primary grid will be imported. Besides, to improve the system efficiency, BESS is also integrated into the grid to charge and discharge power at each time by the electricity price to save on operating the system.

Fig. 1
figure 1

The integrated system of distributed generation units.

Full size image

The objective function of the study

This paper considers cutting total cots by integrating WFs, PVFs, and BESS as the objective function for the balanced and unbalanced distribution networks. These costs should be minimized and expressed in the mathematical equation like follows:

$${\text{Minimize}}\;TC^{OF} = TC_{WF - PVF - BESS}^{Inv\& OM} + TC_{Purch\_Elec}^{Sub} + TC_{Emission}^{Sub}$$
(1)

where \({TC}^{OF}\) is the total costs of the considered system; \(T{C}_{WF-PVF-BESS}^{Inv\&OM}\) is the costs of the investment, O&M of WFs, PVFs and BESS; \({TC}_{Purch\_Elec}^{Sub }\) is the cost of importing electricity for consumption; \({TC}_{Emission}^{Sub}\) is defined as the cost of generating emissions (CO2, SO2 and NOX) from traditional power plants.

Costs for the investment, O&M of PVFs, WFs and BESS

\(TC_{PVF - WF - BESS}^{Inv\& OM}\) is an important economic factor that needs to be identified for building a suitable strategy for connecting distributed generation units. It includes investment cost and O&M cost for WFs, PVFs and BESS.

$$TC_{WF - PVF - BESS}^{Inv\& OM} = TC_{WF} + TC_{PVF} + TC_{BESS}$$
(2)

In the Eq. (2),\({TC}_{WF}\), \({TC}_{PVF}\) and \({TC}_{BESS}\) are the costs of WFs, PVFs and BESS, and they can be calculated by applying below equations, respectively32.

$$TC_{WF} = \mathop \sum \limits_{i = 1}^{WF} \left( {C_{WF}^{Cap} .P_{WF,i}^{Rated} } \right) + 365 \times \mathop \sum \limits_{y = 1}^{20} \mathop \sum \limits_{h = 1}^{24} \mathop \sum \limits_{i = 1}^{{N_{WF} }} \left( {\tau_{y} .C_{WF}^{O\& M} .P_{WF,i,h,y}^{Gen} } \right)$$
(3)
$$TC_{PVF} = \mathop \sum \limits_{j = 1}^{{N_{PVF} }} \left( {C_{PVF}^{Cap} .P_{PVF,j}^{Rated} } \right) + 365 \times \mathop \sum \limits_{y = 1}^{20} \mathop \sum \limits_{h = 1}^{24} \mathop \sum \limits_{j = 1}^{{N_{PVF} }} \left( {\tau_{y} .C_{PVF}^{O\& M} .P_{PVF,j,h,y}^{Gen} } \right)$$
(4)
$$TC_{BESS} = \mathop \sum \limits_{k = 1}^{{N_{BESS} }} \left( {C_{BESS}^{Cap} .En_{BESS,k}^{Rated} } \right) + \mathop \sum \limits_{y = 1}^{20} \mathop \sum \limits_{k = 1}^{{N_{BESS} }} \left( {\tau_{y} .C_{BESS}^{O\& M} .En_{BESS,k,y}^{Rated} } \right)$$
(5)

This study assumes the project’s lifetime is 20 years. A year has 365 days, and a day is represented by 24 h to show the change in consumption and generation during the year. As a result, the system’s O&M cost will vary from year to year, so \({\tau }_{y}\) is added and defined as the present value factor, which can be determined by26. The cost is presented in the following sections.

Electricity purchasing cost

The electricity purchasing cost for supplying the loads and branch losses from the primary grid will be paid to the electric power company if the energy generation from distributed units is insufficient. This cost must be computed as follows:

$$TC_{Purch\_Elec}^{Sub} = 365 \times \mathop \sum \limits_{y = 1}^{20} \mathop \sum \limits_{h = 1}^{24} \left( {\tau_{y} .EP_{h,y}^{Sub} .P_{h,y}^{Sub} } \right){ }$$
(6)

where \({EP}_{h,y}^{Grid}\) ($/MWh) and \({P}_{h,y}^{Grid}\) (MW) are, respectively, the electricity price announced by the electric power company and the active power that is supplied by the primary grid from the hth hour and the yth year.

Emissions cost for traditional power plants

The operation of traditional power plants that use fossil fuel sources emits large amounts of CO2, SO2 and NOX. Therefore, the consumption that uses power from the above plants needs to pay a bill of emissions cost, and it is determined as33:

$$TC_{Emission}^{Sub} = 365 \times \mathop \sum \limits_{y = 1}^{20} \mathop \sum \limits_{h = 1}^{24} \left[ {\left( {\tau_{y} .P_{h,y}^{Sub} } \right) \times \left( {EP_{h,y}^{CO} .EF_{h,y}^{CO} + EP_{h,y}^{SO} .EF_{h,y}^{SO} + EP_{h,y}^{NO} .EF_{h,y}^{NO} } \right)} \right]$$
(7)

where \({EP}_{h,y}^{CO} \& {EF}_{h,y}^{CO}, {EP}_{h,y}^{SO} \& {EF}_{h,y}^{SO}, \text{and} {EP}_{h,y}^{NO} \& {EF}_{h,y}^{NO}\) are the emission prices ($/t) & emission factors (gkWh−1) of CO2, SO2 and NOX from the hth hour and the yth year, respectively.

Constraints of the study

Power balance constraints

BESS which is connected to the system, can operate in charging or discharging mode. Hence, the balance equation for active power should be included two stages of above modes as Eqs. (8) and (9), respectively34:

$$P_{h,y}^{Sub} + \mathop \sum \limits_{i = 1}^{{N_{WF} }} P_{WF,i,h,y}^{Gen} + \mathop \sum \limits_{j = 1}^{{N_{PVF} }} P_{PVF,j,h,y}^{Gen} = \mathop \sum \limits_{b = 1}^{{N_{bh} }} P_{b,h,y}^{ls} + \mathop \sum \limits_{l = 1}^{{N_{ld} }} P_{l,h,y}^{ld} + \mathop \sum \limits_{k = 1}^{{N_{BESS} }} P_{BESS,k,h,y}^{Ch}$$
(8)
$$P_{h,y}^{Sub} + \mathop \sum \limits_{i = 1}^{{N_{WF} }} P_{WF,i,h,y}^{Gen} + \mathop \sum \limits_{j = 1}^{{N_{PVF} }} P_{PVF,j,h,y}^{Gen} + \mathop \sum \limits_{k = 1}^{{N_{BESS} }} P_{BESS,k,h,y}^{DisCh} = \mathop \sum \limits_{b = 1}^{{N_{bh} }} P_{b,h,y}^{ls} + \mathop \sum \limits_{l = 1}^{{N_{ld} }} P_{l,h,y}^{ld}$$
(9)

The reactive power balance equation can be expressed by Eqs. (10) and (11):

$$Q_{h,y}^{Sub} + \mathop \sum \limits_{i = 1}^{{N_{WF} }} Q_{WF,i,h,y}^{Gen} + \mathop \sum \limits_{j = 1}^{{N_{PVF} }} Q_{PVF,j,h,y}^{Gen} = \mathop \sum \limits_{b = 1}^{{N_{bh} }} Q_{b,h,y}^{ls} + \mathop \sum \limits_{l = 1}^{{N_{ld} }} Q_{l,h,y}^{ld} + \mathop \sum \limits_{k = 1}^{{N_{BESS} }} Q_{BESS,k,h,y}^{Ch}$$
(10)
$$Q_{h,y}^{Sub} + \mathop \sum \limits_{i = 1}^{{N_{WF} }} Q_{WF,i,h,y}^{Gen} + \mathop \sum \limits_{j = 1}^{{N_{PVF} }} Q_{PVF,j,h,y}^{Gen} + \mathop \sum \limits_{k = 1}^{{N_{BESS} }} Q_{BESS,k,h,y}^{DisCh} = \mathop \sum \limits_{b = 1}^{{N_{bh} }} Q_{b,h,y}^{ls} + \mathop \sum \limits_{l = 1}^{{N_{ld} }} Q_{l,h,y}^{ld}$$
(11)

Constraint of the feeder

The loading at each phase of branches should not exceed the distribution system’s acceptable limit17.

$$S_{\rho ,b,h,y} \le S_{\rho ,b}^{Max} ; \rho \forall N_{\rho } \;\;{\text{and}}\;\; b \forall N_{bh}$$
(12)

Constraints of the phase voltage

Phase voltage values from all buses should be kept between upper and lower bounds as follows:

$$V^{Max} \ge V_{\rho ,s,h,y} \ge V^{Min} ; \rho \forall N_{\rho } {\text{and}} s \forall N_{bs}$$
(13)

The limits are set to 1.05 pu and 0.95 pu for this work, respectively31.

Constraints of charging power and discharging power

The charging and discharging power limits by BESS are constrained as35:

$$0 \le P_{BESS,k,h}^{Ch} \le \varepsilon^{Ch} .P_{BESS}^{Rated} ;\;\;h \forall N_{H} \;\;{\text{and}}\;\;k\;\;\forall \;N_{BESS}$$
(14)
$$0 \ge P_{BESS,k,h}^{DisCh} \ge - P_{BESS}^{Rated} .\varepsilon^{DisCh} ;\;\;h \forall N_{H} \; {\text{and}}\;\;k\;\forall \;N_{BESS}$$
(15)

In the Eqs. (14, 15), \({\varepsilon }^{DisCh}\) and \({\varepsilon }^{Ch}\) are the efficiencies of discharging and charging stages; \({P}_{BESS,k,h}^{DisCh}\) and \({P}_{BESS,k,h}^{Ch}\) are discharging power and charging power at the kth BESS during the hth hour, respectively.

Constraints of the harmonic voltage distortions

In this paper, the maximum values of total harmonic voltage distortion (\({THD}^{Max}\)) and individual harmonic voltage distortion (\({THD}^{Max}\)) are assigned as 5.0% and 3.0%, according to the IEEE Std. 519, respectively36.

$$THD^{Max} \ge THD_{\rho ,s,h,y} ;\;\;\rho \forall N_{\rho } , s \forall N_{bs} , h \forall N_{H} \;\; {\text{and}}\;\;y \forall N_{Y}$$
(16)
$$IHD^{Max} \ge IHD_{\rho ,s,h,y}^{Hr} ;\;\;\rho \forall N_{\rho } , s\; \forall N_{bs} , h \forall N_{H} , y \forall N_{Y} \;\;{\text{and}}\;\; Hr \forall N_{Hr}$$
(17)

In Eqs. (16, 17), \(THD_{\rho ,s,h,y}\) and \(IHD_{\rho ,s,h,y}^{Hr}\) in percentage are computed by using Eqs. (18, 19)36

$$IHD_{\rho ,s,h,y}^{Hr} (\% ) = \left[ {\frac{{V_{\rho ,s,h,y}^{r} }}{{V_{\rho ,s,h,y} }}} \right] \times 100;\;{\text{r}} > 1\;\;{\text{and}}\;\;r \forall Hr$$
(18)
$${\text{THD}}_{\rho ,s,h,y} (\% ) = \left[ {\frac{{\sqrt {\mathop \sum \nolimits_{r = 2}^{Hr} \left( {V_{\rho ,s,h,y}^{r} } \right)^{2} } }}{{V_{\rho ,s,h,y} }}} \right] \times 100$$
(19)

Constraints of the penetration of WFs, PVFs and BESS:

The rated capacity for each WF and each PVF, and the rated power and rated capacity for BESS should be set to the predetermined limits as follows37:

$$P_{WF}^{Max} \ge P_{WF,i}^{Rated} \ge P_{WF}^{Min} \& P_{PVF}^{Max} \ge P_{PVF,j}^{Rated} \ge P_{PVF}^{Min} ; i \forall N_{WF} ; j \forall N_{PVF}$$
(20)
$$P_{BESS}^{Max} \ge P_{BESS,k}^{Rated} \ge P_{BESS}^{Min} \& E_{BESS}^{Max} \ge E_{BESS,k}^{Rated} \ge E_{BESS}^{Min} ; k \forall N_{BESS}$$
(21)

The BESS’s energy at each hour must be within the limits of 20% and 90% of the rated capacity as follows35:

$$0.2 \times E_{BESS,k}^{Rated} \le E_{BESS,k,h} \le 0.9 \times E_{BESS,k}^{Rated} ;\;\;k \forall N_{BESS} \;\;{\text{and}}\;\; h \forall N_{H}$$
(22)

Co-simulation from OpenDSS & MATLAB software

This research proposes a co-simulation by OpenDSS and MATLAB as an effective tool for solving power flow problem in frequency domains38. OpenDSS has many advantages of accuracy and fast processing speed in solving power flows in large and complex systems. However, it is limited in changing the control variables flexibly28. Therefore, this co-simulation is an excellent solution for using MATLAB to control the change of the variables from the proposed solutions in OpenDSS through the COM interface.

This basic co-simulation can be briefly shown in Fig. 2. In this model, the power grid data is described in OpenDSS, and MATLAB contains the code of the optimization algorithm. The possible solutions for the optimization problem, which are implemented in MATLAB thanks to the optimization algorithm, are transmitted to OpenDSS via the COM interface to solve power flows. Then, obtained results from OpenDSS, including bus voltage, branch current, and branch power loss will be sent back to MATLAB for calculating and evaluating the fitness of each solution. This implementation is repeated until the stopping criterion of the algorithm is satisfied and the globally optimal solution is determined.

Fig. 2
figure 2

The working principle of co-simulation.

Full size image

Modified coyote optimization algorithm

The intelligent behavior of the natural phenomena from animals and plants are the most popular inspiration sources for researchers in the world to develop the optimization algorithms against which they use to solve many problems in engineering, computing, and science fields. In recent years, a positive optimization algorithm, which was developed by researchers in 2018 and named coyote optimization algorithm (COA), has attracted much attention39. COA is inspired from the smart behavior of coyote species (scientific name: Canis latrans) based on its social structure and exchange experiences. With the special characteristics of this species, the algorithm is designed with considering the coyote’s social organization and adaptation to the living environment for addressing various real-world optimization problems effectively. In nature, the coyote population comprises many packs (\({N}_{a}\)), and many individuals (\({N}_{o}\)) exist in each pack. Hence, the coyote population is defined as (\({N}_{a}\times {N}_{o}\)). In this algorithm, the quality of living conditions and living conditions are considered to be the two significant factors that are used to represent individuals. Here, the living condition’s quality indicates the fitness of the positive solution, and the living condition presents the position of the positive solution, which is proposed for the optimization problem39. Although many previous studies have proven COA to be an excellent method for handling problems related to optimization40,41, it still has many shortcomings that need to be improved. Thus, in the last year, researchers in31 successfully modified two new solution generation processes in the original algorithm and released a modified coyote optimization algorithm (MCOA) with many outstanding features. Basically, MCOA is built on the foundation of COA, so MCOA not only inherits outstanding characteristics from original algorithm but also has positive improvements that can enhance the performance as well as the stability of the algorithm.

The first new solution generation of MCOA

Due to the stochastic characteristics of this meta-heuristic algorithm, initial solutions are created by using random generation in the predetermined range of \([{\mathcal{X}}^{Min};\) \({\mathcal{X}}^{Max}]\) for the control variables. The initial solutions’ equation can be described as Eq. (23)39:

$${\mathcal{X}}_{a,o} = {\mathcal{X}}^{Min} + r.\left( {{\mathcal{X}}^{Max} - {\mathcal{X}}^{Min} } \right); a \forall N_{a} \;\;{\text{and}}\;\; o \forall N_{o}$$
(23)

In the first stage of MCOA, the new solution generation is described as the below mathematical equation31:

$${\mathcal{X}}_{a,o}^{New} = {\mathcal{X}}_{a,o} + r_{1} .\left( {{\mathcal{X}}_{best\_pk,a} - {\mathcal{X}}_{r1,a} } \right) + r_{2} .\left( {{\mathcal{X}}_{best\_pn} - {\mathcal{X}}_{r2,a} } \right); \;\;a \forall N_{a} \;\;{\text{and}}\;\;o \forall N_{o}$$
(24)

Obviously, the new solutions are generated by two increased intervals: \([{r}_{1}.\left({\mathcal{X}}_{best\_pk,a}-{\mathcal{X}}_{r1,a}\right)]\) and [\({r}_{2}.\left({\mathcal{X}}_{best\_pn}-{\mathcal{X}}_{r2,a}\right)\)]. The comer is responsible for finding new quality solutions close the best current solution of each pack, and the latter supports to the search orientation of the new solutions around the best solution of the found current population. This brings many advantages in exploiting potential solutions around high-quality solutions, such as \({\mathcal{X}}_{best\_pk,a}\) and \({\mathcal{X}}_{best\_pn},\) and found optimal solutions are positive for various optimization problems. As a result, the solution’s quality in the next generation is significantly improved.

The second new solution generation of MCOA

In this step, only one solution is generated in each pack by using Eq. (25) or Eq. (26) through considering the condition of selecting the equation accordingly31.

$${\mathcal{X}}_{a}^{New} = {\mathcal{X}}_{best\_pn} + r_{3} .\left( {{\mathcal{X}}_{best\_pn} - {\mathcal{X}}_{best\_pk,r1} } \right) + r_{4} .\left( {{\mathcal{X}}_{best\_pn} - {\mathcal{X}}_{best\_pk,r2} } \right)$$
(25)
$${\mathcal{X}}_{a}^{New} = {\mathcal{X}}_{best\_pn} + r_{3} .\left( {{\mathcal{X}}_{best\_pn} - {\mathcal{X}}_{best\_pk,r1} } \right) + r_{4} .\left( {{\mathcal{X}}_{best\_pn} - {\mathcal{X}}_{best\_pk,r2} } \right) + r_{5} .\left( {{\mathcal{X}}_{best\_pn} - {\mathcal{X}}_{best\_pk,r3} } \right)$$
(26)

Clearly, the equations above differ in the number of increased intervals. Two increased intervals in Eq. (25) contribute a high enough change to find new solutions far from the best quality solutions in the current population for avoiding local traps. Besides, to limit missing good solutions, Eq. (26) is suggested by adding one more increased interval, which is determined by using the same way with two previously increased intervals in Eq. (25). Equation (26) significantly contributes to the expansion of the search space for exploiting new solutions to enhance the efficiency of the discovered solution. However, it is essential for determining the possibility to apply the effective equation at this generation. Therefore, Eq. (27) is calculated to compare with a predefined threshold (\(\gamma\)) through the survey for selecting a suitable equation of the second new solution generation.

$$\mathcal{g}=\frac{\phi }{{\phi }^{Max}}$$
(27)

In Eq. (27), \(\mathcal{g}\) is considered as the ratio of the numbers of close couple solution (\(\phi\)) to the maximum couple solution (\({\phi }^{Max}\)). If \(\mathcal{g}\) in Eq. (27) is less than the threshold \(\gamma\), Eq. (25) is applied to produce the new solution at this stage, and vice versa.

Introduced method in solving the considering problem

Initializing for the population

Control variables of newly created solutions should be kept within predefined limits between \({\chi }^{Min} \text{and} {\chi }^{Max}\). The values between them are search space of the control variables, and they are determined as follows:

$$[\chi^{Min} ;\chi^{Max} \left] = \right[L_{WF,i}^{Min} ,P_{WF,i}^{Min} ,L_{PVF,j}^{Min} ,P_{PVF,j}^{Min} ,L_{BESS,k}^{Min} ,P_{BESS,k,h}^{Min} ; L_{WF,i}^{Max} ,P_{WF,i}^{Max} ,L_{PVF,j}^{Max} ,P_{PVF,j}^{Max} ,L_{BESS,k}^{Max} ,P_{BESS,k,h}^{Max} ]$$
(28)

Evaluating the fitness for each solution

Each generated solution is evaluated via the calculation of the fitness function, which is determined as follows:

$$Fit_{a,o} = TC_{a,o}^{OF} + \alpha_{I} .\mathop \sum \limits_{b = 1}^{{N_{bh} }} \Delta I_{b,a,o}^{2} + \alpha_{V} .\mathop \sum \limits_{s = 1}^{{N_{bs} }} \Delta V_{s,a,o}^{2} + \alpha_{IHD} .\mathop \sum \limits_{s = 1}^{{N_{bs} }} \Delta IHD_{s,a,o}^{2} + \alpha_{THD} .\mathop \sum \limits_{s = 1}^{{N_{bs} }} \Delta THD_{s,a,o}^{2}$$
(29)

where \({TC}_{a,o}^{OF}\) is the value from objective function at the oth solution in the ath pack, which is shown in Eq. (1). Other terms on the right-hand side of Eq. (29) can be obtained by referring to31.

Adjusting and updating new solutions

Control variables of each newly produced solution should be checked for correcting their permissible limits if they violate their predetermined limits shown in Eq. (28). The correction process is simple: Set control variables that are lower than the lower limits to the lower limits and higher than the upper limits to the upper limits. Then, the new solutions are evaluated by finding the value of the fitness function. The excellent quality solutions, as well as their fitness, are retained through comparison by applying Eqs. (30) and (31).

$$\chi_{a,o} = \left\{ {\begin{array}{*{20}l} {\chi_{a,o}^{New} \;\;if\;\;Fit_{a,o}^{New} < Fit_{a,o} } \hfill \\ {\chi_{a,o} \;\;else} \hfill \\ \end{array} } \right.;\;\;a \forall N_{a} \;\;{\text{and}}\;\;o \forall N_{o}$$
(30)
$$Fit_{a,o} = \left\{ {\begin{array}{*{20}l} {Fit_{a,o}^{New} \;\; if\;\;Fit_{a,o}^{New} < Fit_{a,o} } \hfill \\ {Fit_{a,o} \;\;else } \hfill \\ \end{array} } \right.;\;\;a \forall N_{a} \;\;{\text{and}}\;\;o \forall N_{o}$$
(31)

The flowchart for considering problem

This study considers the simultaneous integration of WFs, PVFs, and BESS in IEEE 123-bus unbalanced and 55-bus balanced distribution networks. The optimal solution is determined using MCOA as an optimization algorithm, and co-simulation (MATLAB & OpenDSS) is used as an effective computing platform for determining power flows in the frequency domains. The flowchart for determining the optimal solution is presented in Fig. 3.

Fig. 3
figure 3

The flowchart for determining the global optimal solution.

Full size image

Simulation results

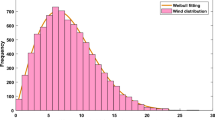
This study solved the optimization problem from installing WFs, PVFs, and BESS using the suggested method (MCOA) and other robust methods, such as SSA and COA, to minimize total costs in IEEE 123-bus unbalanced and 55-bus balanced distribution systems. As mentioned, this study considers the generation from renewable energy sources, including wind energy and solar energy. The output of these renewable sources is highly dependent on natural conditions, so it is important to consider the uncertainty of these sources. Several studies have applied different methods, such as Weibull and Beta distribution probability density functions, to consider uncertainty by predicting wind speed and solar radiation based on historical data in the real area42,43. From there, the corresponding output power for wind turbines and photovoltaic modules is calculated42. As assumed, this study applies the results obtained in44 to determine the power output of wind and solar energy sources. Therefore, the power generation from each renewable will depend on the coefficients of each output curve, as shown in Fig. 4. Besides, the load changing model is also plotted in this figure44. For the simulation of implemented methods, the maximum number of iterations (IteMax) for each independent trial is 150 for IEEE 123-bus UDS and 120 for 55-bus BDS to ensure complete convergence, and the trial running number (NTrial) is selected as 40. To model both MCOA and COA, the individual number for each pack (No) equals the number of packs in the community (Na), and it is 4. Besides, the threshold (γ) is chosen to be 0.2 through the survey. For applying SSA, the population (Npop) is chosen as 20, and their remaining parameters are also referenced from the studies in45,46. The implemented methods are simulated on MATLAB ver-2017 from a desktop PC with 16.0 GB RAM and a 3.70 GHz Processor. As mentioned, this study considers harmonic sources emitted from nonlinear loads and inverters of WFs, PVFs, and BESS. In the IEEE 123-bus system, Type-1 nonlinear loads are located at buses 55, 68, and 84, and Type-2 nonlinear loads are considered at buses 10, 32, and 111 as supposed. For the 55-bus system, the loads connected at buses 3, 20, 25, 44, and 55 are assumed to be Type-1 nonlinear loads, and buses 19, 22, 35, 43, and 54 are Type-2 nonlinear loads. The detailed information of harmonic sources is also presented in Table 247,48.

Fig. 4
figure 4

The output curves of load demand, WFs and PVFs.

Full size image
Table 2 Harmonic spectrum.
Full size table

This work has assumed that two wind farms, two photovoltaic farms and one battery energy storage system are integrated into the distribution systems by applying inverters with a fixed 0.9 lagging power factor31. Minimum and maximum numbers of the WFs and PVFs are 2 and 15 wind turbines, and 2,000 and 10,000 photovoltaic modules, respectively. The rated power is assumed as 100 kW for each wind turbine and 75 W for each PV module30. Moreover, a BESS is considered for connection to IEEE 123-bus and Nha Be 55-bus distribution systems with maximum rated capacity and maximum rated power assumed to be 4.0 MWh and 1.0 MW, respectively. In this case, the initial stored energy from this BESS is also supposed as 1.0 MWh. The efficiency of energy charge (\({\varepsilon }^{Ch}\)) and discharge (\({\varepsilon }^{DisCh}\)) of BESS is chosen to be 90% for lead-acid batteries. In addition, the parameters for computing total costs of connecting WFs, PVFs, and BESS are also listed in Table 3.

Table 3 Used parameters in calculating total costs.
Full size table

Realistically, if distributed generation units (WFs, PVFs, and BESS) do not have enough power to supply the loads due to high demand and low generation, purchasing electrical energy from the traditional power plants through the substation at the slack node is necessary. However, the electricity price is different, and it is divided into three stages including peak, standard and off-peak hours. Therefore, this study assumed the hourly electricity price (\({EP}_{h}^{Sub}\)), which the utility company declares according to Fig. 535.

Fig. 5
figure 5

Electricity prices at different hours in a day.

Full size image

Case 1: IEEE 123-bus UDS

IEEE 123-bus unbalanced distribution system, which operates at a voltage level of 4.16 kV with grid-connected devices such as switches, capacitors, and voltage regulators, is used as a test system in this case. At peak load, this network has total power consumption of 3.448 MW and 1.358 MVar and a total power loss of 96.7 kW and 193.8 kVAr. The system data are clearly described in29, and the single-line diagram is also shown in Fig. 6.

Fig. 6
figure 6

The IEEE 123-bus UDS.

Full size image

With the stochastic characteristics of applied methods, 40 trials are implemented to determine the most suitable location and capacity of WFs, PVFs, and BESS, and the best results from the implemented methods are presented in Table 4, and their convergence characteristics are presented as shown in Fig. 7. Obviously, at the 46th iteration, the convergence is almost achieved for MCOA, while it is the 63rd iteration for COA and the 70th iteration for SSA. Besides, each fitness point on the convergence curve of MCOA is always lower than that of SSA and COA. In other words, MCOA has better local trap avoidance than others. Not only that, the average processing time for the MCOA’s simulation takes 5275.8 min, and it is slightly faster than that of SSA and COA, which are 1.054 times and 1.014 times, respectively. This shows that the suggested method not only has better convergence characteristics but also faster data processing speed than others.

Table 4 The best solution in 40 trial runs from three implemented methods.
Full size table
Fig. 7
figure 7

The convergence curves of applied methods.

Full size image

From the optimal solutions of methods, the associated costs are calculated and shown in detail in Table 5. As indicated in this table, total costs of MCOA are the lowest, with $15.4660 million, while SSA and COA are $15.6739 million and $15.5410 million, respectively. Although the costs from investment and O&M of MCOA ($7.3186 million) are slightly higher than COA ($7.3185 million), they are much lower than those of SSA ($7.9153 million). Besides, considering the cost of importing energy from the primary grid if WFs, PVFs, and BESS do not have enough capacity to supply energy for demand, the cost of MCOA is only $7.1663 million, it is lower than that of COA with $7.2367 million. However, it is higher than the remaining method of $6.8195 million. Lastly, the cost of emissions from power plants that use fossil energy is the highest for COA ($0.9858 million), followed by MCOA ($0.9811 million) and SSA ($0.9390 million). In summary, the optimal solution from MCOA is more economical than others, so the suggested method is the best of the three implemented methods. In other words, the modifications in the equations for generating new solutions for MCOA are more effective than the original method (COA) and powerful method (SSA).

Table 5 Comparision for involved costs of implemented methods.
Full size table

On the other hand, determining the optimal solution for installing WFs, PVFs, and BESS into the distribution system also provides a huge benefit over the original system without integration. Specifically, applying the suggested method’s solution can save up to $4.9176 million, equivalent to 24.13% compared to the base system. The saving cost in the percentage of MCOA is also higher than others, such as SSA and COA, with 23.11% and 23.76%, respectively, as presented in Table 5. The results indicate that suitable integration of WFs, PVFs, and BESS can provide excellent economic benefits compared to the non-integrated system.

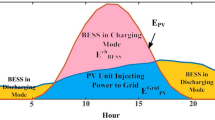
Multiple benefits have been achieved thanks to the appropriate penetration of renewables and BESS. Specifically, as shown in Fig. 8, the total power generation in a day to the grid from renewables is 38.7978 MW, including 69.26% coming from wind energy and 30.74% coming from solar energy. Moreover, BESS has flexible charging and discharging stages according to the hourly electricity price to save operating costs by reducing the cost of importing electricity from the main grid. For a typical day, the total discharging power from the BESS is 1.4332 MW, and the total charging power is 1.7694 MW. Therefore, the total power generation to the grid from these units is 38.4616 MW, while the demand of the loads is 69.1300 MW, so the main grid will provide the energy deficit. As plotted in Fig. 9, during hours with favorable natural conditions (strong wind and high solar radiation), the distributed sources supply high power to the grid and almost enough to supply the entire demand of the system. On the contrary, during times when natural conditions are not favorable for the operation of these sources, the main power supply for load demand is still electricity from the main grid. Therefore, building a suitable power generation strategy for renewable sources and a charging/discharging strategy for BESS is important in optimizing grid operation to minimize costs while still ensuring the satisfaction of technical constraints. As mentioned, BESS is integrated to deploy a reasonable charging/discharging strategy to increase the system operating cost saving, as shown in Figs. 10 and 11. Figure 10 indicates the energy storage capacity, and Fig. 11 plots the charging and discharging stages after connecting BESS to the system. Generally, BESS tends to save energy during the light load periods and the off-peak hours due to the cheapest electricity price. BESS releases energy into the grid during the heavy load periods and the peak hours due to the highest electricity price at these hours. For the remaining hours, BESS has a reasonable strategy of charging and discharging energy to save money from purchasing energy of the primary grid. Optimally charging and discharging energy has contributed significantly to saving costs for operating the distribution network. Besides, the operating process of BESS completely also satisfies the constraints of discharging and charging limits for BESS with 20% and 90% of the rated capacity, respectively. For an example, with a rated capacity of BESS of 0.486 MW/1.342 MWh as the obtained solution from the suggested method, BESS can store up to 1.208 MWh as fully charged and vice versa, BESS down to 0.268 MWh; it will stop generating energy.

Fig. 8
figure 8

The consumed and generated power of each distributed unit in power grid.

Full size image
Fig. 9
figure 9

The total consumption (loads and losses) and generation of all units.

Full size image
Fig. 10
figure 10

The energy storage capacity from BESS.

Full size image
Fig. 11
figure 11

The charging and discharging stages from BESS.

Full size image

As mentioned, one of the great benefits of integrating WFs, PVFs, and BESS is power loss reduction in distribution branches. Precisely, as indicated in Fig. 12, total power loss of the distribution system is enormously cut from 1.6578 to 1.2976 MW in one day after connecting the grid-connected units, corresponding to a 21.73% loss reduction. Besides, thanks to the distributed connection of generation sources on the grid, the voltage drop at the buses, especially the weak buses, which are located far from the main power source, has also been significantly enhanced. The appropriate placement and generation of distribution sources brought great voltage profile improvement. Specifically, before connecting the WFs, PVFs, and BESS, the voltage values of phases in the system are within the range of [0.9265, 1.0031] (pu) throughout all times. However, after integration of WFs, PVFs, and BESSs into the system, the phase voltage improved drastically with fluctuating values within the range of [0.9516, 1.0229] (pu) like plotted in Fig. 13, and this satisfies the voltage constraints of [0.950, 1.050] (pu). This shows the great benefit of properly connecting WFs, PVFs, and BESS in reducing power loss and enhancing voltage profile of the distribution system.

Fig. 12
figure 12

The power loss of the system before and after integrating PVFs, WFs and BESS.

Full size image
Fig. 13
figure 13

The lowest and highest voltages before and after connecting PVFs, WFs and BESS.

Full size image

Moreover, this study also considers harmonic distortions caused by nonlinear loads and inverters of WFs, PVFs, and BESS. Nonlinear loads generated harmonics in the original system with the highest THD values at every hour are shown in Fig. 14, in which the highest value is 1.453% at the peak load hours. However, after connecting distributed units, their inverters significantly increased the harmonics of the system to 2.853% for the maximum value of THD. This indicates that the use of power conversion devices contributes mainly to increasing the harmonic distortions in the power grid, and it is necessary to keep the harmonic indices not exceeding the allowable limits. Like the obtained results from this study, all values of THD after integration of units are lower than the limit of 3%, so IHD values do not exceed 3%, and thus, harmonic indices in this scenario completely satisfy the IEEE Std. 519.

Fig. 14
figure 14

THD’s maximum value from each hour with and without connecting PVFs, WFs and BESS.

Full size image

Case 2: Nha Be 55-bus BDS

This study selects a real case with a 55-bus BDS in Nha Be District, Ho Chi Minh City, Vietnam, operating at 22 kV as a test system. At peak load, total consumption is 7.630 MW and 2.342 MVar with total power loss of 51.2 kW and 72.1 kVAr. Line and load data are also shown in Table S1 and Table S2 in Supplementary Material, and the system’s single-line diagram is plotted in Fig. 15.

Fig. 15
figure 15

The 55-bus BDS.

Full size image

Similarly, in this case, 40 independent trials are implemented for each method to find the best results. The best solutions for the executed algorithms are indicated in Table 6, and convergence curves are also shown in Fig. 16. At the 36th iteration, MCOA achieved convergence, while SSA and COA obtained convergence at the 42nd and 60th iteration, respectively. The fitness points on the curve of MCOA through 120 iterations are always better than those of SSA and COA. On the other hand, the average processing time for the MCOA’s simulation is 2485.2 min, and it is also a little faster than SSA (1.025 times) and COA (1.011 times). This indicates that the suggested method has better convergence properties and convergence speed than other methods.

Table 6 The best solution in 40 trial runs from three implemented methods.
Full size table
Fig. 16
figure 16

The convergence curves of applied methods.

Full size image

On the other hand, the relevant costs from the optimal solutions are also calculated and shown in Table 7. Obviously, the found \({TC}^{OF}\) value of MCOA is the lowest at $32.3283 million compared to $32.7566 million of SSA and $32.6309 million of COA. Although \({TC}_{WF-PVF-BESS}^{Inv\&OM}\) of MCOA is $13.9730 million and higher than that of SSA and COA ($13.8673 million and $12.2049 million), \({TC}_{Purch\_Elec}^{Sub}\) of MCOA is more economical than the two compared methods with the difference of $0.4848 million and $1.3746 million for SSA and COA, respectively. Not only that, the \({TC}_{Emission}^{Sub}\) value of MCOA is $2.2240 million, and also smaller than that of SSA and COA ($2.2733 million and $2.4354 million). The above results have shown that the optimal solution from MCOA is economically better than the compared methods, including SSA and COA.

Table 7 Comparision for involved costs of implemented methods.
Full size table

Furthermore, the optimal solutions from integrating distributed generation units such as WFs, PVFs, and BESS also bring great benefits compared to the non-integrated system. In the base system, total costs are very high and equal to $44.5685 million. On the contrary, the total costs are significantly smaller in the modified system. MCOA, COA, and SSA found solutions with total costs of $32.3283 million, $32.6309 million, and $32.7566 million. Those costs are smaller than the base systems by 27.46%, 26.78%, and 26.50%. The values conclude that installing WFs, PVFs, and BESS in the distribution networks is essential, and selecting the location and size to work for these devices by using robust algorithms is also extremely important.

By applying the optimal solution from the suggested method, total power generation from WFs, PVFs, and BESS in 24 h is also presented. As plotted in Fig. 17, the total daily generation capacity from renewables is 82.4821 MW, including 53.84% from solar power and 46.16% from wind power. Additionally, with the appropriate charging/discharging strategy of BESS, the total daily discharging power from BESS is 2.5933 MW, and the total daily charging power is 3.2016 MW. Therefore, the total daily grid injected power of these sources is 81.8738 MW, while the total demand is 151.3970 MW. Therefore, the deficit will also be compensated by the main grid. As shown in Fig. 18, the compensation amount from the main grid will depend on the generation capacity of the grid-connected distributed units. At each time of the day, the generation capacity of the renewables will vary depending on the weather conditions. During periods of good weather for renewables operation, the amount of electricity taken from the main grid will be low and vice versa. Besides, BESS, with a reasonable energy charging/discharging strategy according to each electricity price period, also greatly saves operating costs. It can also be affirmed that determining the appropriate operating strategy for units is necessary to maximize the received benefits. In addition, to further elucidate the operation of BESS, Fig. 19 also shows the energy storage process of BESS throughout 24 h of a day. As a typical example, in this system, BESS’s rated energy is 1.9871 MWh with a rated charging and discharging power of 0.8049 MW. In other words, BESS can store up to 1.7884 MWh, which is considered full energy, and the remaining energy of 0.3974 MWh is considered exhausted energy. This completely satisfies the constraints of 90% and 20% for BESS’s charging and discharging limits to avoid physical damage to the battery banks. Besides, Fig. 20 also plots the appropriate charging and discharging power of BESS at each time. Clearly, BESS tends to charge power at low electricity price periods and generate power at high electricity price periods to reduce total cost of importing electricity.

Fig. 17
figure 17

The consumed and generated power of each distributed unit in power grid.

Full size image
Fig. 18
figure 18

The total consumption (loads and losses) and generation of all units.

Full size image
Fig. 19
figure 19

The energy storage capacity from BESS.

Full size image
Fig. 20
figure 20

The charging and discharging stages from BESS.

Full size image

One of the positive points of determining the optimal connection of distributed generation sources in the distribution network is power loss minimization. Thanks to the proper integration of WFs, PVFs, and BESS, total power loss on the branches has been cut noticeably from 878.6491 to 364.3910 kW, corresponding to a 58.53% loss reduction as shown in Fig. 21. This reduction of 514.2581 kW has contributed significantly to cutting costs in operating the integrated system. Furthermore, thanks to the decentralized connection of the power sources, the bus voltage is supported significantly, especially for buses located far from the main power source. There is no integration of distributed generation units; the system phase voltage is within the range of [0.989, 1.000] (pu). However, this voltage range is sharply raised to [0.991, 1.001] (pu) after the integration of WFs, PVFs, and BESS, as shown in Fig. 22. Lastly, as mentioned, this study considers harmonic sources emitted by nonlinear loads and inverters of WFs, PVFs, and BESS. In this case, the maximum THD value in the system with nonlinear loads is 1.01%. However, this value has increased to 1.70% with the penetration of distributed units. This indicates that the connection of inverter-based wind turbines, photovoltaic modules, and BESS can strongly inject harmonics into the grid. Therefore, it is recommended that the harmonic indices satisfy the IEEE Std. 519. Like Fig. 23, the maximum THD value at each time of the day is less than 3%, so all IHD values are also less than 3%, completely satisfying the given constraints.

Fig. 21
figure 21

The power loss before and after integrating PVFs, WFs and BESS.

Full size image
Fig. 22
figure 22

The lowest and highest phase voltages without and with connecting PVFs, WFs and BESS.

Full size image
Fig. 23
figure 23

Maximum THD value from each hour without and with connecting PVFs, WFs and BESS.

Full size image

Conclusions

This work introduced a novel high-performance meta-heuristic algorithm named the modified coyote optimization algorithm to determine the suitable location and sizing of WFs, PVFs, and BESS in both IEEE 123-bus unbalanced and Nha Be 55-bus balanced distribution systems. The study considered harmonics that are caused by nonlinear loads, and inverters of WFs, PVFs, and BESS to keep measurement values of the harmonics in compliance with IEEE Std. 519. Additionally, the research also successfully developed co-simulation of OpenDSS and MALAB through COM. This co-simulation has brought significant advantages in solving power flow problems in frequency domains flexibly and quickly. The primary objective of this work is to minimize the total costs considering environmental, technical, and economic aspects. The results obtained show that the optimal solution for integrating WFs, PVFs, and BESS could save up to 24.33% and 27.46% compared to the initial system for the 20-year project period. Besides, total power loss is also decreased by 21.73% and 58.53% in loss reduction, and the voltage profile is also enhanced from [0.9265, 1.0031] to [0.9516, 1.0229] and from [0.989, 1.000] to [0.991, 1.001] under the satisfaction of IEEE Std. 519 on harmonics for IEEE 123-bus and 55-bus distribution systems, respectively. Finally, MCOA has also proven its superior performance for addressing various optimization problems compared to strong methods of SSA and COA with the same objective function and technical constraints.

Although this study has successfully considered harmonics from nonlinear loads and renewable energy sources, the presence of supraharmonics has not been evaluated. Hence, this will be implemented in future work. Moreover, to increase the welfare, the smart inverters that are capable of setting Volt/VAR and Volt/Watt functions to increase the penetration of renewables without violating the constraint will be integrated. In addition, charging stations for electric vehicles, as well as harmonics from their power converters, will also be considered in the future.