Introduction

Inverse problems arise in many scientific and engineering applications, where the goal is to infer unknown parameters or functions from indirect and often incomplete observations. These problems are inherently ill-posed, as small errors in data can lead to large deviations in the solution, making them challenging to solve using traditional methods. In this paper, we focus on simultaneously reconstructing the full spatio-temporal solution of a system governed by partial differential equations (PDEs) and estimating unknown parameters, using only limited boundary or internal measurements.

In recent years, machine learning approaches, especially neural networks, have gained significant attention for solving inverse problems. They offer a flexible and data-driven framework to capture complex dependencies in high-dimensional spaces, where classical methods struggle. In particular, Physics-informed neural networks (PINNs) have garnered significant attention for solving PDEs and inverse problems in the rapidly expanding field of scientific machine learning1,2,3,4. By embedding the governing mathematical model directly into the loss function, PINNs enforce constraints on the network’s output, ensuring that the predicted solutions adhere to the underlying PDEs. This approach allows for the solution of both forward and inverse problems by leveraging limited observational data while exploiting the structure of the physical laws. The emergence of automatic differentiation5,6, along with advances in computational power, made the implementation of these concepts more accessible and scalable.

Data-driven approaches for discovering PDEs have gained significant traction due to advances in deep learning techniques7. Presents PDE-Net, a deep learning model that learns both differential operators and nonlinear responses from data to predict system dynamics and uncover the underlying partial differential equations (PDEs). By constraining convolutional filters based on wavelet theory, PDE-Net identifies the governing PDEs while maintaining strong predictive capabilities, even in noisy environments8. Proposes a new framework combining neural networks, genetic algorithms, and adaptive methods to address challenges in discovering PDEs from sparse, noisy data. A physics-encoded discrete learning framework for uncovering spatio-temporal PDEs from limited and noisy data, utilizing a deep convolutional-recurrent network to embed prior physics knowledge and reconstruct high-quality data, followed by sparse regression to identify the governing PDEs9. These approaches represent a major step forward in data-driven PDE discovery, offering robust and flexible tools for tackling real-world problems in complex environments.

The success of a neural network can hinge on its architecture. Various applications often necessitate distinct architectures. For instance, the Convolutional Neural Networks10 are effective in handling image recognition while the Recurrent Neural Networks (RNNs)11 is crucial for modeling sequential data. According to the universal approximation theorem12, any continuous function can be arbitrarily closely approximated by a sufficiently large perception13. However, determining the proper parameters of networks to solve some complicated PDEs is difficult14. The selection of suitable architectures is essential for improving the performance. Ying et al.15 approximate the iteration scheme by using the fully connected neural network. In this work, we mainly implement the RNNs in estimating time-dependent PDEs. The RNNs have the gradient vanishing problem hindering the model’s ability to capture long-range dependencies16. To address this problem, two advanced variants, Long Short-Term Memory (LSTM)17 and Gated Recurrent Unit (GRU)18, are designed. Their update and reset gating mechanisms, along with improved memory cell structures, make GRUs well-suited for various sequential data tasks.

In this study, we employ the Gated Recurrent Units (GRU) network to solve time-dependent PDEs and identify the unknown parameters using sparse data. The neural network serves as an approximation for time iteration schemes, and we introduce the Adams–Moulton implicit method to guide convergence to solutions during network training. Integration of sparse data as a regulatory component enhances the model’s accuracy significantly. The efficacy of this algorithm is demonstrated through numerous numerical experiments, encompassing scenarios such as Burgers, Allen–Cahn, and non-linear Schrödinger equations, validating its feasibility and performance across diverse applications.

Outline of paper: In “Methodology” section, the architecture of our model is described, and the algorithm is presented. “Numerical experiments” section presents the results of numerical experiments. The conclusion is mentioned in “Conclusion” section.

Methodology

“Methodology” section primarily presents the algorithm for solving time-dependent PDEs.

Problem setup

Consider the time-dependent PDE of the form:

$$\begin{aligned} u_{t}({\textbf{x}},t) = f \left( t,{\textbf{x}},u,\frac{\partial u}{\partial x},\frac{\partial ^{2}u}{\partial x^{2}}, \varvec{\tau }\right) , \hspace{1.5mm} u \in [{\textbf{x}}_{1},{\textbf{x}}_{2}], \hspace{1.5mm} t \in [t_{0},T], \end{aligned}$$
(1)

subject to initial and boundary conditions,

$$\begin{aligned} u(t_{0},{\textbf{x}})&= u_{0}, \\ u(t,{\textbf{x}}_{1})&= h_{1}, \\ u(t,{\textbf{x}}_{2})&= h_{2}, \end{aligned}$$

where \(u = u(t, {\textbf{x}})\) is the latent solution of Eq. (1), and f is a function of u, t, u and its partial derivatives of u with respect to \({\textbf{x}}\). Here, \({\textbf{x}}_{1}\) and \({\textbf{x}}_{2}\) denote the lower and upper bounds of \({\textbf{x}}\) respectively. \(\varvec{\tau }\) represents unknown parameters in Eq. (1). We aim to propose a neural network to approximate the \(u({\textbf{x}},t)\) and estimate the unknown parameters \(\varvec{\tau }\) using only a few interior observations with initial conditions.

Algorithm

In this section, we mainly describe our algorithm. The architecture is comprised of one layer of GRUs and several fully connected layers. We utilize the finite difference to approximate the partial derivatives of Eq. (1) so we can discretize the domain into a \(M\times N\) mesh grid, defined by \(x_{i}, i = 0,1,2,\dots , M-1\) and \(t_{j}, j = 0,1,2,\dots , N-1\), with step size \(\Delta x\) and \(\Delta t\).

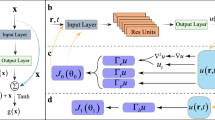
The flow chart of our approach is presented in Fig. 2. From the left side of this figure, we use a neural network, denoted by \({\bar{u}}(t,u;\varvec{\theta })\), to approximate u(t, u), and \(\varvec{\theta }\) represents the parameters of neural network. The number of neurons for each layer is set to N, with each neuron providing an estimation of the solution at \(t_{j}\). The different neurons of the output layer generate the approximations \({\bar{u}}(t_{j},u;\varvec{\theta })\) at \(t_{j}, j = 0,1,2,\dots , N-1\).

As for spatial discretization of the governing partial differential equation, we considered several finite difference schemes, including forward, backward, and upwind approximations. Ultimately, the central difference scheme was selected due to its second-order accuracy, which offers a more precise approximation of spatial derivatives compared to the first-order accuracy of the forward and backward schemes19. While upwind differences are commonly employed in advection-dominated problems to enhance numerical stability and suppress spurious oscillations20, we are not focusing on strongly convection-driven problems. As a result, the central difference scheme provided a favorable balance between accuracy and computational efficiency. A stability analysis was also conducted using von Neumann analysis, confirming that the central difference scheme, in combination with the chosen time-stepping method, yields a stable and convergent numerical solution within the tested parameter regime21.

Figure 1 presents a geometric interpretation of finite difference approximations for the first derivative of a smooth function u(x). The function is evaluated at three points: \(x-\Delta x, x, x + \Delta x\), corresponding to the locations of points A, P, and B, respectively. The secant line between A and P approximates the backward difference, while the secant between P and B represents the forward difference. The line connecting A and B captures the central difference approximation:

$$\begin{aligned} {\bar{u}}_{x}(t_{j},x_{i};\varvec{\theta }) = \frac{1}{2\Delta x}({\bar{u}}(t_{j},x_{i+1};\varvec{\theta }) - {\bar{u}}(t_{j}, x_{i-1};\varvec{\theta })), \end{aligned}$$
(2)

with an error of order \(\Delta x^{2}\). This figure illustrates how central differencing provides a more symmetric and accurate estimate of the derivative at x by leveraging function values on both sides of the point.

Fig. 1
figure 1

Central difference approximation22.

Full size image

Then, we apply the central difference scheme to approximate the second-order spatial derivatives23,

$$\begin{aligned} {\bar{u}}_{xx}(t_{j}, x_{i};\varvec{\theta }) = \frac{1}{\Delta x^{2}}({\bar{u}}(t_{j}, x_{i+1};\varvec{\theta }) - 2{\bar{u}}(t_{j},x_{i};\varvec{\theta }) + {\bar{u}}(t_{j}, x_{i-1};\varvec{\theta })), \end{aligned}$$
(3)

Multistep methods are particularly well-suited to recurrent frameworks because both approaches leverage information from multiple previous states to compute the next state. In recurrent neural networks, the hidden state at each time step depends on past hidden states. Similarly, in multistep numerical methods, the next solution value is computed as a function of several previous time steps24. This shared structure allows multistep methods to naturally align with the sequential and memory-based nature of recurrent systems.

Also, when dealing with sequential data on recurrent neural networks, multi-step methods are highly effective due to their superior stability, accuracy, and reliability as compared to the one-step multi-stage method. Let \(h = f(x,{\bar{u}},{\bar{u}}_{x},{\bar{u}}_{xx})\), then h is employed to approximate the new time iteration scheme \({\tilde{u}}(x,t)\) by applying the Adams–Moulton Implicit methods25. For instance, the one-step implicit method or trapezoidal rule:

$$\begin{aligned} {\tilde{u}}(t_{j+1},u) = {\bar{u}}(t_{j},{\textbf{x}};\varvec{\theta }) + \frac{\Delta t}{2}(f({\bar{u}}(t_{j+1},{\textbf{x}};\varvec{\theta })) + f({\bar{u}}(t_{j},{\textbf{x}};\varvec{\theta }))). \end{aligned}$$
(4)

Then, one component of the loss function can be constructed as the mean square error between the \({\bar{u}}\) and \({\tilde{u}}\).

$$\begin{aligned} Loss_{1} = \frac{1}{N-1}\Sigma _{j=1}^{N-1}||{\bar{u}}(t_{j},{\textbf{x}};\varvec{\theta }) - {\tilde{u}}(t_{j},{\textbf{x}};\varvec{\theta })||^{2}_{2} \end{aligned}$$
(5)
Fig. 2
figure 2

Flowchart of the algorithm for identifying parameters of PDEs using sparse data.

Full size image

As for the right side of Fig. 2, we randomly select some sparse observations represented by \(u_{data}\) at first. Correspondingly, the \(x_{data}\) is denoted as values at these selected spatial points. The \({\bar{u}}_{data}(t_{0},x_{data}), \dots , {\bar{u}}_{data}(t_{N-1},x_{data})\) are the output of the neural network. Then, inspired by26, we apply \(\lambda\) as a weighting factor on the data term in the loss function to emphasize data fidelity, ensuring the neural network closely fits the data points. This hyperparameter balances the trade-off between fitting the data and other loss components.

$$\begin{aligned} Loss_{data} = \lambda \frac{1}{N}\Sigma _{i=0}^{N-1}||{\bar{u}}_{data}(t_{j},x_{data}) - u_{data}||^{2}_{2} \end{aligned}$$
(6)

We also incorporate the initial condition into the loss function.

$$\begin{aligned} Loss_{0} = ||{\bar{u}}_{0} - u_{0}||^{2}_{2} \end{aligned}$$
(7)

The total loss function is comprised of these three terms.

$$\begin{aligned} Loss = Loss_{0} + Loss_{1} + Loss_{data}. \end{aligned}$$
(8)

In Fig. 2, the neural networks on both sides use identical parameters, meaning they share the same weights and biases across all layers. This ensures that both networks produce consistent outputs for the same inputs. By incorporating randomly selected known data points into the loss function, we enforce the network to align its predictions with the given data, guaranteeing consistency and agreement at these selected points. Algorithm 1 describes the procedures mentioned above.

Algorithm 1
figure a

Approximate the unknown parameters from sparse data using GRU neural network

Full size image

Numerical experiments

In this section, we present the results of Burgers’ equation, Allen–Cahn equation, and non-linear Schrödinger to validate the effectiveness of our method. We utilize the numerical method or analytical solution to generate the synthetic data and randomly pick sparse data at each time step. Our model infers the complete spatio-temporal solutions of these equations while also approximating the unknown parameters. The architecture comprises one layer of GRUs and some dense layers, and each cell or neuron of the output layer will give the prediction at \(t_{j}\). Thus, each layer’s number of cells or neurons depends on the \(\Delta t\). We train the network by applying the Adam optimizer27, and then followed by L-BFGS28 to minimize the loss function. The idea behind this is that the Adam optimizer avoids the local minimum, and then the solutions can be refined by the L-BFGS optimizer29. We adopt the Tanh function as the activation function for neural networks. We utilize the Learning Rate decay30, which started with a relatively large learning rate and reduced it after a certain number of iterations. The Algorithm 1 is implemented by utilizing the computing package PyTorch31. To further evaluate the performance of our algorithm, we introduce Gaussian noise into the data and rerun the program. This allows us to assess the robustness of the model and its ability to estimate parameters accurately under realistic conditions with data imperfections.

Burgers’ equation

The viscous Burgers’ equation is the fundamental nonlinear PDEs in fluid dynamics and shock waves. The Burgers’ equation with periodic boundary condition is given by

$$\begin{aligned} \begin{aligned}&u_{t} + uu_{x} - (\tau /\pi )u_{xx} = 0, x\in [-1,1], t\in [0,1], \\&u(0,x) = -\sin (\pi x),\\&u(t,-1) = u(t,1), \end{aligned} \end{aligned}$$
(9)

where \(\tau /\pi\) is the viscosity coefficient, and \(\tau\) will be estimated by using the Algorithm 1. We set the time-step \(\Delta t = 0.01\) and obtain 10000 uniformly spaced x values from \(-\)1 to 1. The observations are obtained by solving the Eq.(3) numerically, given that \(\tau = 0.01\). We randomly select 20 data points for each time step, and after several experiments, the corresponding \(\lambda\) is set to 25. The network consists of a single GRU layer followed by two dense layers, each with 100 neurons. Initially, \(\tau\) is set to 1. Then, we implement the Algorithm 1 to estimate the \(\tau\) and the complete solution across the entire domain. The model is trained in 6000 epochs with the Adam optimizer at a learning rate of 0.005, followed by an additional 6000 epochs with a learning rate of 0.001, and subsequently refined using L-BFGS to achieve convergence. The approximated parameter \({\bar{\tau }}\) and solution \({\bar{u}}\) are utilized to construct the loss function. Firstly, we calculate

$$\begin{aligned} f_{{\bar{u}}} = -{\bar{u}}{\bar{u}}_{x} + ({\bar{\tau }}/\pi ){\bar{u}}_{xx}. \end{aligned}$$
(10)

Then, we apply the Adams–Moulton Three-Step implicit method to obtain:

$$\begin{aligned} {\tilde{u}}^{n} \approx {\bar{u}}^{n-1} + \frac{\Delta t}{12}(5f^{n}_{{\bar{u}}} + 8f^{n-1}_{{\bar{u}}} - f^{n-2}_{{\bar{u}}}). \end{aligned}$$
(11)

The loss function can be expressed as follows:

$$\begin{aligned} loss = ||{\bar{u}}_{0} - u_{0}||^{2} + ||{\bar{u}}_{i} - {\tilde{u}}_{i}||^{2} + \lambda ||{\bar{u}}_{data} -u_{data}||^{2}. \end{aligned}$$
(12)

Figure 3 illustrates the results at several selected time values, providing a comparison between the predicted solution and the exact solution. In the figure, the blue data points represent randomly selected points that are used for regularization in the loss function. From the comparison, it is evident that the predictions made by our neural network align closely with the exact solution, demonstrating the model’s ability to accurately capture the underlying dynamics of the problem. This strong agreement between the predicted and exact solutions highlights the effectiveness of our network in solving the given task.

The vanilla PINN is applied to solve this inverse problem under the same conditions for comparison with our method. The network consists of five hidden layers, each with 200 neurons, and uses the Tanh activation function. The model undergoes training in the same manner as our approach. Let \({\hat{u}}\) be the output of the network, representing the network’s output, with partial derivatives computed via automatic differentiation. The loss function is formulated as follows:

$$\begin{aligned} loss = ||{\hat{u}}_{0} - u_{0}||^{2} + ||{\hat{u}}_{t} + {\hat{u}}{\hat{u}}_{x} - ({\hat{\tau }}/\pi ){\hat{u}}_{xx}||^{2} + \lambda ||{\bar{u}}_{data} -u_{data}||^{2}, \end{aligned}$$
(13)

where \({\hat{\tau }}\) is the approximation of parameter \(\tau\) by PINN, and \(\lambda\) is set to 40. Table 1 presents the results of PINN and Algorithm 1. The first row presents the relative \(L_{2}\) errors between the solutions obtained using a numerical PDE solver and those predicted by the neural network, calculated using Eq. (14). The second row displays the parameters estimated by the two methods. As shown in the Table 1, Algorithm 1 achieves lower relative \(L_{2}\) errors and more accurate parameter identification compared to PINN. The Table 2, shows good performance of Algorithm 1 under low noise levels, where the estimated parameters are close to the exact values. As noise increases, errors grow, and the parameter estimates deviate further, but the results remain acceptable for moderate noise levels.

$$\begin{aligned} L_{2} = \sqrt{\frac{\Sigma _{i,j}^{N}({\bar{u}}_{i,j}-u_{i,j})^{2}}{\Sigma _{i,j}^{N}u_{i,j}^{2}}} \end{aligned}$$
(14)
Fig. 3
figure 3

Burgers’ equation: snapshots of the predicted solutions and exact solutions at \(t = \{0.0,0.3,0.5,0.7,0.9,1.0\}\).

Full size image
Table 1 Comparison between the PINN and Algorithm 1 for Burgers’ equation.
Full size table
Table 2 Results of Algorithm 1 with gaussian noise added to sparse data for Burgers’ equation.
Full size table

Allen–Cahn equation

To further validate the effectiveness of our method, we implement the Algorithm 1 to solve the Allen–Cahn PDE, which is a reaction-diffusion equation. It describes the phase separation process in multi-component alloy systems, including order-disorder transitions. The Allen–Cahn PDE is given as follows:

$$\begin{aligned} \begin{aligned}&u_{t} - Du_{xx} + R(u^{3} -u) = 0, x\in [-1,1], t\in [0,1],\\&u(x,0) = x^{2}\cos (\pi x), \\&u(t,-1) = u(t,1). \end{aligned} \end{aligned}$$
(15)

where D is the diffusion rate, and R is the reaction term coefficient. We set the time-step \(\Delta t = 0.005\) in this experiment and use the same x values. Let \(D = 0.00001\) and \(R = 5\), the synthetic data is obtained using the numerical PDE solver. We randomly pick 15 data points from each time step. Considering the smaller \(\Delta t\) in this case so that there are more collocation data points, we increase the \(\lambda\) to 40. The network is constructed by one GRUs layer and three dense layers with 201 neurons per layer, it is trained for 5000 epochs using the Adam optimizer with a learning rate of 0.005, followed by another 5000 epochs with a learning rate of 0.001, and then further optimized using L-BFGS to reach convergence. Both D and R are initially set to one. After we obtaining \({\bar{u}}\), and approximated \({\bar{D}}\) and \({\bar{R}}\), we calculate

$$\begin{aligned} f({\bar{u}},{\bar{u}}_{x},{\bar{u}}_{xx}) = {\bar{D}}{\bar{u}}_{xx} - {\bar{R}}({\bar{u}}^{3} - {\bar{u}}), \end{aligned}$$
(16)

where \(u_{x}\) and \(u_{xx}\) are calculated by finite difference. The Adams–Moulton Four-Step implicit method is adopted to calculate \({\tilde{u}}\). Then, the loss function is constructed as follows:

$$\begin{aligned} loss = ||{\bar{u}}_{0} - u_{0}|| + ||{\bar{u}}_{i} - {\tilde{u}}_{i}||^{2} + \lambda ||{\bar{u}}_{data} -u_{data}||^{2}. \end{aligned}$$
(17)

Figure 4 shows the comparison between the predicted and exact solutions of a system at different time steps. The solid lines are the predicted solutions, the dashed lines represent the numerical solutions, and the scatter points are randomly selected data points. The lines for both time steps show a close alignment between the predicted and exact solutions, indicating that the network model provides an accurate approximation for both time steps.

A similar PINN is utilized to solve the inverse problem of the Allen–Cahn equation. The loss function is

$$\begin{aligned} loss = ||{\hat{u}}_{0}-u_{0}||^{2} + ||{\hat{u}}_{t} - {\hat{D}}{\hat{u}}_{xx} + {\hat{R}}({\hat{u}}^{3} - {\hat{u}})||^{2} + \lambda ||{\hat{u}}_{data} - u_{data}||^{2}, \end{aligned}$$
(18)

where \({\hat{D}}\) and \({\hat{R}}\) are PINN’s approximated diffusion rate and reaction term coefficient, respectively, and \(\lambda = 40\). From Table 3, the first row displays the relative \(L_{2}\) errors between the numerical solution and the predictions from the two networks. The second row presents the estimated diffusion rate, while the third row shows the reaction coefficients obtained by the two methods. The error in the diffusion rate appears relatively large because the true diffusion value is very small, which amplifies the relative error. Additionally, Algorithm 1 demonstrates better performance in this experiment. Similarly, Table 4 shows that for smaller noise levels, the Algorithm 1 provides accurate approximations and parameter estimates close to the true values.

Fig. 4
figure 4

Allen–Cahn equation: snapshots of the predicted solutions and exact solutions at different time steps.

Full size image
Table 3 Comparison between the PINN and Algorithm 1 for Allen–Cahn equation.
Full size table
Table 4 Results of Algorithm 1 with gaussian noise added to sparse data for Allen–Cahn equation.
Full size table

Non-linear schrodinger equation

The non-linear Schrödinger equation, describing the behavior of complex-valued wavefunctions, is chosen as another example to validate the effectiveness of our methodology further. The equation with the periodic boundary conditions is given as follows:

$$\begin{aligned} \begin{aligned} ih_{t} + Dh_{xx} + |h|^{2}h&= 0, \hspace{1.5mm} x \in [-5,5], \hspace{1.5mm} t\in [0,\pi /2], \\ h(0,x)&= 2{{\,\textrm{sech}\,}}(x), \\ h(t,-5)&= h(t,5), \\ h_{x}(t,-5)&= h_{x}(t,5), \end{aligned} \end{aligned}$$
(19)

where h is complex, and D is the diffusion rate. Then, Eq. (19) can be redefined as \(h(x,t) = u(x,t) + iv(x,t)\), where u(x, t) represents the real part and v(x, t) represents the complex part. The split equations are as follows:

$$\begin{aligned} \begin{aligned} u_{t}&= -Dv_{xx} - (u^{2} + v^{2})v, \\ v_{t}&= Du_{xx} + (u^{2} + v^{2})u, \\ u(0,x)&= 2{{\,\textrm{sech}\,}}(x), v(0,x) = 0,\\ u(t,-5)&= u(t,5), v(t,-5) = v(t,5),\\ u_{x}(t,5)&= u_{x}(t,5), v_{x}(t,-5) = v_{x}(t,5). \\ \end{aligned} \end{aligned}$$
(20)

Let the time-step size be \(\Delta t = \pi /400\) with \(D = 0.5\), and 10,000 x-collocation points between \(-\)5 and 5. The PDE solver is used to solve Eq. (20) and generate the synthetic data. For each time step, 20 data points are randomly selected. Two networks are employed to approximate u and v respectively. Each network is constructed by one layer of GRUs and three dense layers with 200 neurons per layer. The activation function of hidden layers is Tanh, and the ReLU is applied to the output layer to keep the values non-negative. Then, the output \({\bar{u}}\) and \({\bar{v}}\) are used to get

$$\begin{aligned} \begin{aligned} f_{u}&= - {\bar{D}}{\bar{v}}_{xx} - ({\bar{u}}^{2} + {\bar{v}}^{2}){\bar{v}}, \\ f_{v}&= {\bar{D}}{\bar{u}}_{xx} + ({\bar{u}}^{2} + {\bar{v}}^{2}){\bar{u}}. \end{aligned} \end{aligned}$$
(21)

Then, combined with the Adams–Moulton implicit methods, \(f_{u}\) and \(f_{v}\) are utilized to calculate the \({\tilde{u}}\) and \({\tilde{v}}\). The parameters of these two networks are learned by adopting 6000 iterations of Adam with a learning rate 0.005 and 6000 iterations of \(L-BFGs\) with a learning rate 0.5 to minimize the loss functions \(loss = loss_{{\bar{u}}} + loss_{{\bar{v}}}\).

$$\begin{aligned} \begin{aligned} loss_{{\bar{u}}}&= ||u_{0} - {\bar{u}}_{0}||^{2} + ||{\bar{u}}_{i} - {\tilde{u}}_{i}||^{2} + \lambda ||{\bar{u}}_{data} -u_{data}||^{2}, \\ loss_{{\bar{v}}}&= ||v_{0} - {\bar{v}}_{0}|| + ||{\bar{v}}_{i} - {\tilde{v}}_{i}||^{2} + \lambda ||{\bar{v}}_{data} -v_{data}||^{2} \end{aligned} \end{aligned}$$
(22)

Figure 5 presents the comparison between the prediction \(|h| = \sqrt{{\bar{u}}^{2} + {\bar{v}}^{2}}\) and numerical solution. It demonstrates that the network’s predictions closely align with the numerical solution. The regular PINN is applied to solve the Schrödinger equation for comparison. The neural network architecture includes 6 dense layers, each with 200 neurons. The input and output layers both contain two neurons, where the output layer produces \({\hat{u}}\) and \({\hat{v}}\). The loss function is defined as:

$$\begin{aligned} \begin{aligned} loss_{{\hat{u}}} = ||u_{0} - {\hat{u}}_{0}||^{2} + ||{\hat{u}}_{t} + {\hat{D}}{\hat{v}}_{xx} + ({\hat{u}}^{2}+{\hat{v}}^{2}){\hat{v}}||^{2} + \lambda ||{\hat{u}}_{data} - u_{data}||^{2}, \\ loss_{{\hat{v}}} = ||v_{0} - {\hat{v}}_{0}||^{2} + ||{\hat{v}}_{t} - {\hat{D}}{\hat{u}}_{xx} - ({\hat{u}}^{2}+{\hat{v}}^{2}){\hat{u}}||^{2} + \lambda ||{\hat{v}}_{data} - v_{data}||^{2}, \end{aligned} \end{aligned}$$
(23)

\(\lambda\) is set to 50. The total loss, defined as \(loss_{{\hat{u}}} + loss_{{\hat{v}}}\), is minimized using 2000 iterations of the Adam optimizer with a learning rate of 0.005, followed by 8000 iterations with a learning rate of 0.001. The solution is then further refined using the L-BFGS algorithm. Table 5 provides a more accurate parameter approximation and smaller relative \(L_{2}\) errors compared to the PINN. From Table 6, the Algorithm 1 performs well with small noise, with parameter estimates aligning closely with the exact values.

Fig. 5
figure 5

Schrodinger equation: snapshots of the predicted solutions and exact solutions at \(t = \{0,\frac{\pi }{12},\frac{2\pi }{12},\frac{3\pi }{12},\frac{4\pi }{12},\frac{\pi }{2}\}\).

Full size image
Table 5 Comparison between the PINN and Algorithm 1 for Schrödinger equation.
Full size table
Table 6 Results of Algorithm 1 with gaussian noise added to sparse data for Schrödinger equation.
Full size table

Two-dimentional heat equation

We then applied Algorithm 1 to the 2D Heat Equation with Neumann boundary conditions. The equation is given by

$$\begin{aligned} \begin{aligned}&\frac{\partial u}{\partial t} = \alpha (\frac{\partial ^{2} u}{\partial x^{2}} + \frac{\partial ^{2} u}{\partial y^{2}}), \Omega \in [0,1]\times [0,1], t \in [0,1], \\&u(0,x,y) = cos(n\pi x)cos(n\pi y), \\&\frac{\partial u}{\partial x} = 0 \text { on } x = 0 \text { and } x = 1,\\&\frac{\partial u}{\partial y} = 0 \text { on } y = 0 \text { and } y = 1, \end{aligned} \end{aligned}$$
(24)

where \(\alpha\) is thermal diffusivity. Under the given initial and boundary conditions, the analytical solution is

$$\begin{aligned} u(x,y,t) = cos(\pi x)cos(\pi y)cos(\sqrt{2}\pi t). \end{aligned}$$
(25)

We set \(\alpha = 4\), the step-sizes \(\Delta t = 0.005\), \(\Delta x = 0.002\), and \(\Delta y = 0.002\). The analytical solution described in Eq. 25 generates the data, from which 20 data points are randomly selected at each time step. The neural network architecture consists of a single layer of GRUs, followed by five fully connected dense layers, each containing 200 neurons. The Tanh activation function is applied to each dense layer, except for the final output layer, where the activation function is not applied. To construct the loss function, we first calculate

$$\begin{aligned} f_{u} = {\bar{\alpha }}({\bar{u}}_{xx} + {\bar{u}}_{yy}), \end{aligned}$$
(26)

where the \({\bar{\alpha }}\) is the estimated thermal diffusivity by neural network. As presented in the Algorithm 1, \({\tilde{u}}\) is calculated using the four-step Adams-Moultto implicit method. The loss function is constructed as

$$\begin{aligned} loss = ||{\bar{u}}_{0}-u_{0}||^{2} + ||{\bar{u}} - {\tilde{u}}||^{2} + \lambda ||{\bar{u}}_{data}-u_{data}||. \end{aligned}$$
(27)

The \({\bar{\alpha }}\) represents the approximated thermal diffusivity by minimizing the loss function Eq. (27), and we set \(\lambda = 20\). Figure 6 presents heatmaps comparing the predicted and exact solutions for a 2D time-dependent PDE at \(t=\{0.0, 0.05, 0.1\}\). The heatmaps of the predicted solutions (left column) and exact solutions (right column) visually demonstrate the accuracy of the predictions. The optimization process begins with 2000 iterations of the Adam optimizer at a learning rate of 0.005, followed by 8000 iterations at a reduced learning rate of 0.001. Subsequently, the solution is further refined using the L-BFGS algorithm. As shown in Table 7, this approach yields more accurate parameter approximations and smaller relative \(L_{2}\) errors compared to the PINN. For the 2D heat equation in Table 8, the Algorithm 1 provides accurate parameter estimates under small noise, closely matching the exact values. However, errors and deviations increase with higher noise levels, highlighting limitations under excessive noise.

Fig. 6
figure 6

2D heat equation: snapshots of the predicted solutions and exact solutions at \(t = \{0,0.05, 0.1\}\).

Full size image
Table 7 Comparison between the PINN and Algorithm 1 for 2D heat equation.
Full size table
Table 8 Results of Algorithm 1 with gaussian noise added to sparse data for 2D heat equation.
Full size table

Conclusion

The Gated Recurrent Units neural network is designed to handle time-series data, while the implicit numerical method estimates values at the next time step. Additionally, physical laws are embedded directly into the loss function. This seamless integration of time-series modeling, implicit numerical techniques, and physics-informed learning creates a robust framework for parameter identification and deriving the full solution across the domain using sparse data. Initially, neural networks are employed to approximate the iterative scheme for solving partial differential equations. The finite difference method is then applied to compute derivatives, followed by the formulation of new iteration schemes through the implicit approach. By minimizing the discrepancy between the original and newly derived schemes, the network effectively converges to the solution of the partial differential equation and identifies unknown parameters. Sparse interior observation data acts as a regularizer, improving the network’s convergence. The non-Linear Schrödinger equation is transformed into a system of equations, demonstrating the effectiveness of our proposed method for solving such systems. Across all examples, the results indicate that Algorithm 1 consistently generates accurate approximations from sparse data even with moderate Gaussian noise. However, if the noise becomes excessively large, the Algorithm 1 struggles to produce reliable approximations. Additionally, the current predictions of parameters are static. Future work will focus on extending the methodology to handle parameters of partial differential equations that vary dynamically in both space and time. Another important consideration for future exploration is the scenario where the entire solution or the parameters to be predicted exhibit discontinuities, which presents additional numerical and modeling challenges.