Introduction

The success of smart farming and precision agriculture in improving crop yields depends on the accuracy of sensor data. Real-time sensor node denoising is a significant challenge, as valuable data and noise are captured simultaneously1. Sensor noise refers to measurement errors, irregularities, or imperfections significantly affecting part or all of a system2,3. With the rapid adoption of low-cost Internet of Things (IoT) devices in heterogeneous agricultural environments, real-time sensor denoising requires immediate attention4. Furthermore, sensor noise is a significant issue, causing many IoT solutions to fail in real-world applications due to their inability to handle diverse noise characteristics (Fig. 1) from the deployed environment4,5.

Fig. 1
figure 1

Noise types in sensor data. Adapted from5.

Full size image

Successful implementation of real-time agricultural sensor denoising can enhance crop production and promote the sustainability of agricultural land use6. It reduces the time, costs, and environmentally destructive practices associated with traditional methods. Currently, obtaining accurate data requires routine recalibration or industrial-grade sensors, which are often unaffordable for small-scale farmers3.

Sensor denoising models have been derived from polynomial regression equations generated from the observed and simulated data,7,8 to mitigate the need for frequent recalibration and expensive sensors. However, polynomial models require large datasets and show limited adaptability to unseen conditions9,10.

Despite the success of sensor denoising techniques like band filters11, particle filters12, moving horizon estimation13, and artificial neural networks14 in image processing, they have failed to perform optimally in IoT scenarios due to resource constraints.

The linear Kalman filter (KF) is widely recognized as the best real-time sensor denoising technique for linear systems15. However, agricultural systems are complex and highly nonlinear, necessitating higher-order extensions of the KF to handle this nonlinearity16. These high-order KF variants are particularly suited for heterogeneous agricultural environments17,18.

The superiority of the Unscented Kalman filter (UKF) over its extensions (UKFs) and the Cubature Kalman filter (CKF) remains an open question despite their effectiveness in handling first and third-order nonlinear systems, respectively, without requiring Jacobian derivation19,20. A summary of considered studies is presented in Table 1

Table 1 Summary of considered studies.
Full size table

From Table 1, it is evident that few studies have addressed the deployment of high-order UKF and their extensions on IoT devices for real-time agricultural soil data denoising. This study addresses this gap by pioneering the enhancement of real-time sensor denoising through the integration of UKF with Artificial Neural Networks or Fuzzy Logic, as well as CKF models, on a Raspberry Pi 5.

This paper seeks to answer the research question: Can extensions of the Unscented Kalman Filter (UKF) or the Cubature Kalman Filter (CKF) improve real-time sensor denoising for agricultural soil parameters on resource-constrained devices? The key contributions of this paper include: (1) introducing innovative hybrid methods that integrate the Unscented Kalman Filter (UKF) with Artificial Neural Networks (UKF_ANN) and Fuzzy Logic (UKF_FL) to tackle challenges specific to resource-constrained IoT devices. These methods have low computational demands of 75% while achieving up to 99% accuracy in real-time open-field agricultural soil analysis monitoring. (2) By optimizing these denoising models for low-power devices like the Raspberry Pi 5, this study significantly contributes to deploying IoT systems in smallholder farming contexts, such as those in Rwanda, and (3) UKF_ANN and CKF have the potential to enhance crop production and sustainability through better data accuracy.

For inferences, the paper evaluates the performance of IoT-based UKF extensions for enhancing real-time soil sensor denoising based on i) root mean square errors (RMSE) to measure the model’s prediction error, ii) mean absolute error (MAE) to measure the average prediction error, iii) square root (R2) to explain the variance contained in data, iv) computation Memory (CM) to measure the memory used to compute each model, and v) Computation Time (CT) to quantify to the time used to execute each model. It aims to provide practical solutions for improving the reliability of IoT-based soil monitoring systems. The remainder of this paper is organized as follows.

Materials and methods

Description of the study area

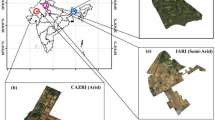
The sensor node was deployed in the Kinazi sector of Ruhango district, Rwanda (Fig. 2), at a longitude of 30.03333 E and a latitude of 2.016667 S, with altitudes ranging from 1500 to 2000 m. The region has a tropical savanna wet (Aw) climate, clay-silt soil, an average annual temperature of 31.29 ± 2.14 °C, and an average yearly precipitation of 1000 mm rain. During the experiment, rainfall varied from 110 mm in April to 190 mm in October, temperatures ranged from 23.2 °C in February to 34.57 °C in September, and humidity fluctuated from 51.29% in November to 65.22% in March. This district has the most potential in cassava farming due to its edaphoclimatic conditions.

Fig. 2
figure 2

Area of Study. Source: QGIS 3.38, available at: https://qgis.org/download/

Full size image

Soil sensor node design

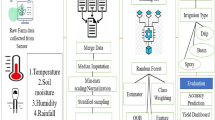
The soil sensor node consisted of hardware, middleware, and software (Fig. 3). The hardware comprised the sensor node’s physical components (Fig. 3b). Meanwhile, the middleware layer utilized ThingSpeak, which communicated via MQTT protocols. The software layer was built under Python 3.12 through the Plotly library.

Fig. 3
figure 3

Soil sensor node design. (a) Sensor node architecture, (b) Sensor node deployment, (c) integrated soil sensor .

Full size image

The hardware layer comprised a Raspberry Pi 5 (Arm Cortex A76), a JXBS-3001-NPK-RS, integrated soil sensors (temperature, humidity, electrical conductivity, pH, nitrogen, phosphorus, and potassium) from https://www.jxctiot.com/product1/product195.html, and a waterproof air temperature and relative humidity sensor (STH30). Table 2 presents a detailed description of the hardware components.

Table 2 Description of the hardware layer components.
Full size table

After the physical system development, four real-time sensor denoiser models were implemented (Fig. 4), on Raspberry Pi 5, then the system was deployed, Fig. 3b-c

Fig. 4
figure 4

Topology of the models’ implementation. UT – Unscented transformation, UKF—Unscented Kalman Filter, CKF – Cubature Kalman Filter, ANN – Unscented Kalman Filter Artificial Neural Network, FL—Unscented Kalman Filter Fuzzy Logic.

Full size image

Data collection

The data was collected in a 10-hectare model cassava farm, planted with NAROCASS cassava variety, 8-month cycle.

We implemented real-time Unscented Kalman Filter (UKF), Unscented Kalman Filter with Fuzzy Logic (FL), Unscented Kalman Filter with Artificial Neural Network (ANN), and Cubature Kalman Filter (CKF) sensor noise filters on Raspberry Pi 5. After that, we collected soil temperature, humidity, electrical conductivity, pH, nitrogen, phosphorus, and potassium every 30 min from September 2023 to April 2024 (the 2023–2024 season). We developed a web-based dashboard using the Plotly library for real-time data visualization.

Models’ implementation

The implementation of each model (UKF, UKF_ANN, UKF_FL, and CKF) comprised two states (state prediction and state estimation), as described in Fig. 4. The state prediction steps consisted of predicting the next soil parameter state, based on the previous state and system dynamic, relying only on the internal model system. The state prediction corrected the prediction from the state prediction by adjusting the predicted state and covariance to improve the system’s current state, incorporating sensor data.

The UKF and CKF were executed individually. Meanwhile, the UKF_ANN and UKF_ANN are extensions of the UKF, adopting specific rules to select the generated sigma points used to compute the Kalman gain. Thus, integrating the ANN and FL extensions to the UKF aimed to overcome the intrinsic instability reported in the UKF32. The steps of each model are presented with the phases (Fig. 4).

Unscented Kalman filter

The two states of the UKF were executed in six steps, as in Eqs. 1 to 6. The state prediction steps consisted of i) generating sigma points and propagating them through the state function, ii) computing the predicted state, iii) computing the predicted mean state, and calculating the predicted covariance. Meanwhile, the state update steps consisted of (i) predicting the measurement mean, (ii) calculating innovation covariance and cross-covariance, (iii) calculating the Kalman gain, and (iv) updating state and covariance. Detailed information is described in32,33. The state and observation models are described in Eq. (1).

$$\left\{\begin{array}{c}{x}_{k}=f\left({x}_{k-1}\right)+ {Q}_{k} \\ {Z}_{k}=g\left({x}_{k}\right)+ {R}_{k}\end{array} \right.$$
(1)

where: \({x}_{k}\)—state model, \({Z}_{k}\)—observation model,—\({u}_{k-1}\)input vector from sensors, \(k\)—time stage, \(k-1\), prior time stage,—\({Q}_{k}\)state covariance matrix–vector—\({Q}_{t}\cong \text{\rm N} \left(0,{\Sigma }_{{w}_{k}}\right)\),—\({R}_{k}\)observation covariance matrix vector \(R_{k} \cong {\text{\rm N}} \left( {0,{\Sigma }_{{V_{t} }} } \right)\) \(f and g\) – are nonlinear process and measurement functions.

Then, the computation of the sigma points \({x}_{i, k-1}\) of n-dimensional vectors \({{x}_{i, k-1}}_{i=0}^{i=2n}\) is represented in Eq. (2).

$$\left\{ {\begin{array}{*{20}c} {x_{i,k - 1} = \overline{x}_{k - 1} \,fori = 0} \\ {x_{i,k - 1} = \overline{x}_{k - 1} + \left( {\sqrt {\left( {n + \lambda } \right)P_{k - 1} } } \right)_{i} fori = 1, \ldots n + 1, \ldots n} \\ {x_{i,k - 1} = \overline{x}_{k - 1} - \left( {\sqrt {\left( {n + {\mkern 1mu} \lambda } \right)P_{k - 1} } } \right)_{i - n} ,fori = 1,n + 1, \ldots 2n} \\ \end{array} } \right.$$
(2)

The scalar \(\lambda\) is a semi-positive parameter determining the sigma points spread around the estimated state vector \({\widehat{x}}_{k-1}\). The term \(i\) refers to the ith column of the square root matrix \(P\), represented by \(\left(\sqrt{P}\right)i\) obtained through Cholesky factorization. After the computation of new points, the transition function \(f,\) was computed the mean \({\overline{x} }_{k}\), covariance error \({P}_{k}\), sigma points weights \({w}_{i}\), and updated the sampling points \({X}_{i,k}\), respectively, as in Eq. (3).

$$\left\{\begin{array}{c}u=f\left({X}_{i,k-1}\right) \\ {\widehat{x}}_{k}= {\sum }_{i=0}^{2n}{W}_{0}^{\left(c\right)}{X}_{i,k } \\ {P}_{k}={\sum }_{i=0}^{2n}{W}_{0}^{\left(c\right)}\left({X}_{i,k}-{\widehat{x}}_{k}\right){\left({X}_{i,k}- {\widehat{x}}_{k}\right)}^{T}+{Q}_{k}\end{array}\right.$$
(3)

The sigma points weights were computed from Eq. (4).

$$\left\{ {\begin{array}{*{20}c} {y = \sum\limits_{j = 1}^{m} {\left( {\left( {1 - \pi_{j} } \right)s_{j} \overline{\varphi }_{j} + \pi_{j} \overline{s}_{j} \overline{\phi }} \right)} \therefore \sum\limits_{j = 1}^{m} {y_{j} } } \\ {\delta_{ij} = \left( {Q_{k} \,\gamma \,R_{k} } \right)} \\ \end{array} } \right.$$
(4)

The sigma points measurements, predicted weights, and measurement updates we computed throughout the observation matrix \(H,\) Eq. (5).

$$\left\{\begin{array}{c}{P}_{k}={\sum }_{i=0}^{2n}{W}_{i}^{\left(c\right)}\left({X}_{i,k}-{\widehat{x}}_{t}\right){\left({X}_{i,k}- {\widehat{x}}_{k}\right)}^{T}+{Q}_{k} \\ {Z}_{k}=H\left({X}_{i,k}-{\widehat{x}}_{k}\right) \\ {\widehat{Z}}_{k}= {\sum }_{i=0}^{2n}{W}_{i}^{\left(c\right)}{X}_{i,k } \end{array}\right.$$
(5)

Finally, the Kalman gain, state model, and observation update were as in Eq. (6).

$$\left\{\begin{array}{c}{K}_{k}={P}_{{\widehat{x}}_{k},{\widehat{Z}}_{t}}{{P}_{{\widehat{x}}_{k},{\widehat{Z}}_{k}}}^{-1} \\ {\widehat{x}}_{k}= {K}_{k}\left({Z}_{k}-{\overline{Z} }_{k}\right) \\ {\widehat{P}}_{k}= {P}_{k}-{{K}_{k}{P}_{{\widehat{x}}_{k},{\widehat{Z}}_{k}}{K}_{k}}^{T}\end{array}\right.$$
(6)

In summary, the UKF mitigates Gaussian noise by propagating sigma points through the nonlinear system and iteratively updating the Kalman gain. Uniform noise is reduced by averaging variations in sigma points, while salt-and-pepper noise is addressed during measurement updates that reject outliers. This process ensures accurate state estimation while preserving the underlying trends in soil parameters. Appendix A presents the pseudo-code for the UKF implementation.

Unscented Kalman filter with fuzzy logic

The UKF_FL incorporates fuzzy logic into the Kalman filtering process to adaptively adjust the Kalman gain based on noise characteristics. Gaussian noise is filtered through minor, incremental gain adjustments, ensuring smooth state updates. Uniform noise is mitigated by scaling corrections to prevent overcompensation for significant measurement variations. In the case of salt-and-pepper noise, fuzzy rules prioritize the rejection of extreme deviations during the measurement update phase, ensuring that substantial outliers do not affect the state estimation. This adaptive mechanism guarantees effective noise removal while preserving the critical trends and integrity of the soil parameter data.

This method’s innovation involves incorporating Eqs. 7 and 8 into the UKF for specific sigma points through Fuzzy Logic rules. It also addresses the intrinsic limitations of the UKF by normalizing the non-differentiable and differentiable matrix (\({\overline{\varphi } }_{j}\), \({\overline{\phi }}_{j})\) elements of the intuitionistic fuzzy set, and calculating the hesitation margin index \({\pi }_{j} ,\) as in Eq. (7).

$$\left\{\begin{array}{c}{\overline{\varphi } }_{j}=\frac{{\overline{\mu }}_{j}}{{\sum }_{j}^{m}{\overline{\mu }}_{j}} \\ {\overline{\phi }}_{j}= \frac{\overline{\gamma }}{{\sum }_{j}^{m}{\gamma }_{j}} \\ {\pi }_{j}=1- {\overline{\varphi } }_{j}-{\overline{\phi }}_{j}\end{array}\right.$$
(7)

To compute the Fuzzy Logic rules \(y\) was done as in Eq. (8).

$$\left\{ {\begin{array}{*{20}c} {y = \mathop \sum \limits_{j = 1}^{m} \left( {\left( {1 - \pi_{j} } \right)s_{j} \overline{\varphi }_{j} + \pi_{j} \overline{s}_{j} \overline{\phi }} \right)\therefore \mathop \sum \limits_{j = 1}^{m} y_{j} } \\ {\delta_{ij} = \left( {Q_{k} \,\gamma \,R_{k} } \right)} \\ \end{array} } \right.$$
(8)

The polynomial parameters \(s, {s}_{i}\) were determined using least square regression techniques. We compared the possibility matrix to the Gaussian probability of \(\left( {Q_{k} \,\gamma \,R_{k} } \right)\), with \(\delta_{ij} = \left( {Q\,\gamma \,R} \right)\). The detailed implementation is described in19,20. Equations 7 and 8 were integrated to replace Eqs. 3, 4, and 5 from the UKF, and the Kalman gain, state model, and observation executing Eq. 6 were updated. The pseudocode for the UKF_FL is presented in Appendix B.

Unscented Kalman filter with artificial neural network

The ANN initially learns the nonlinear relationships present in the sensor data, producing a preliminary denoised signal. This denoised output is then fed into the UKF for further refinement, reducing residual Gaussian noise and minor deviations. The ANN’s mappings effectively suppress uniform noise while ignoring impulsive salt-and-pepper noise during training, ensuring smooth and consistent outputs and Kalman gain convergence. This hybrid approach preserves the underlying trends in the data while providing robust noise reduction across various noise types that can affect soil sensors.

The state prediction was computed by introducing a look-back function to create sequences (batches) of the 10 previous sensor readings used for training (80%) and testing (20%) to compute the Kalman gain. Thus, LTSM was defined by configuring the forget gate (\({f}_{k}\)), input gate (\({i}_{k}\)), Cell state update (\({C}_{k}\)), and output gate (\({O}_{k}\)) to interactively update the cell state, as in Eq. (9–12).

$${Forgate gate\therefore f}_{k}=\sigma ({W}_{f}\left[{h}_{k-1,}{x}_{k}\right]+{b}_{f})$$
(9)
$$Input gate \therefore \left\{\begin{array}{c}{i}_{k}=\sigma \left({W}_{i}\left[{h}_{k-1,}{x}_{k}\right]+{b}_{i}\right)\\ {\widehat{C}}_{k}=\text{tan}({W}_{c}\left[{h}_{k-1,}{x}_{k}\right]+{b}_{c})\end{array}\right.$$
(10)
$${Cell State Upadte \therefore C}_{k}={f}_{k}{C}_{k-1}+{i}_{k}{\widehat{C}}_{k}$$
(11)
$$Ouput~gate~\therefore \left\{ {\begin{array}{*{20}c} {O_{k} = ~\sigma \left( {W_{o} \left[ {h_{{k - 1,}} x_{k} } \right] + b_{o} } \right)} \\ {h_{k} = o_{k} \tan C_{k} ~~~~~~~~~~~~~~~~~~~~~~~} \\ \end{array} } \right.$$
(12)

The designed LSTM model consisted of two layers, each with 64 units. The first layer was configured to return sequences to the second layer, followed by a 20% dropout to prevent overfitting. The output and hidden layers were aligned with the number of predicted features to generate the final prediction.

To complement the LSTM, we run a parallel ANN model to approximate the Kalman gain, using \({Q}_{k},{R}_{k}\), as the input layer, 32 a unit-dense layer using a Rectified Linear Unit, \(ReLU\) activation, and a single-unit output layer that predicted the Kalman gain. The input layer of the ANN comprised two nodes \(\widehat{P}\) \(R\), while the hidden layer’s ReLU activation function was as in Eq. (13)

$$ReLU\left(x\right)=\text{max}(0,x)$$
(13)

The output layer from ANN (Kalman gain) was computed from the linear regression of the predicted stage, weights \(w\), and bias \(b\), as in Eq. (14)

$${K}_{ANN}={w}_{2}*ReLU*\left({w}_{1}*\left[{P}_{pred},R\right]+{b}_{1}\right)+{b}_{2}$$
(14)

In the update state, we recursively updated the Kalman gain (\({K}_{k}\)), by first computing the predicted step (\({\widehat{P}}_{k}\)) from the initial \({P}_{0}\), adding the measurement covariance \({Q}_{k}\), as in Eq. (15)

$$\left\{\begin{array}{c}{\widehat{P}}_{k}={P}_{0}+Q \\ {K}_{kC}={K}_{ANN}({\widehat{P}}_{k}, R)\end{array}\right.$$
(15)

This approach dynamically adjusted the \({K}_{k}\) iteratively, refining the predictions in real-time. This method’s novelty was the introduction of a mechanism to monitor the Kalman gain convergence \({K}_{kC}\) over multiple data points, thereby identifying the stabilization point, which signifies the algorithm’s effective calibration and reliability (Fig. 5).

Fig. 5
figure 5

Optimization of Kalman gain using ANN.

Full size image

After the \({K}_{kC}\) we updated the state model and covariance, as in Eq. (15).

$$\left\{\begin{array}{c}{\widehat{x}}_{k}={\widehat{x}}_{k}+ {K}_{kC}\left({z}_{k}-{\widehat{z}}_{k}\right)\\ {\widehat{P}}_{k}=\left(1-{K}_{kC}\right){\widehat{P}}_{k}\end{array}\right.$$
(16)

Equations 10–14 were integrated to replace Eqs. 1—5 from the UKF and state model, and observation executing Eq. 6 was updated, similarly to Eq. 15. Appendix C describes the pseudocode for the UKF_ANN implementation.

Cubature Kalman filter implementation

The CKF employs symmetric cubature points to manage nonlinear dynamics and decrease Gaussian noise. Uniform noise is minimized through covariance updates, and extreme outliers from salt-and-pepper noise are partially filtered out. The algorithm preserves soil data trends while balancing state estimation and noise suppression. We replaced Eqs. 3 to 5 from UKF to generate sigma points with the spherical-radial cubature rules for the Cubature Kalman Filter implementation \({x}_{k}\), Eq. (16).

$${x}_{k}=\sqrt{\frac{m}{2}} \left\{\left[\begin{array}{c}\begin{array}{c}1\\ 0\\ \vdots \end{array}\\ 0\end{array}\right],\dots ,\left[\begin{array}{c}\begin{array}{c}0\\ 0\\ \vdots \end{array}\\ 1\end{array}\right],\left[\begin{array}{c}\begin{array}{c}-1\\ 0\\ \vdots \end{array}\\ 0\end{array}\right],\dots ,\left[\begin{array}{c}\begin{array}{c}0\\ 0\\ \vdots \end{array}\\ -1\end{array}\right]\right\}$$
(17)

\(m\) = number of cubature points computed by \({\omega }_{i}=\frac{1}{m};i=1, 2, . . . , m;m=2n\);

\({\omega }_{i}\) = positive weights; \(n\) = dimension of vector state. Detailed information about the CKF is described in16,18. The pseudocode of the CKF is shown in Appendix D. We implemented parameters auto-tuning to minimize the covariance error, preventing overfitting. Thus, the initial condition was set as in Table 3.

Table 3 Parameters tuning of the variables.
Full size table

Data analysis

The primary assumption for the collected parameters is that they have piecewise nonstationary characteristics, with no abrupt changes and only smooth variations between the a priori and posterior (Fig. 1) sampling times3,7. To this end, four UKF, UKF_FL, UKF_ANN, and CKF algorithms were tested for their performance in sensor noise removal for IoT applications. Inferences were based on root mean square errors (RMSE), mean absolute error (MAE), square root (R2), computation Memory (CM), and Computation Time (CT). In addition (Fig. 6), we plotted a graph (Fig. 7) of the model’s behavior to evaluate the effectiveness of the filters in eliminating different types of sensor noises (uniform, Gaussian, and salt-and-pepper) for each soil parameter.

Fig. 6
figure 6

Boxplot of soil parameters data. Real—censored data, UKF—Unscented Kalman filter, CKF—Cubature Kalman filter, ANN—Unscented Kalman filter with Artificial Neural Network, FL—Unscented Kalman filter with Fuzzy Logic.

Full size image
Fig. 7
figure 7figure 7

Real-time state prediction of the soil parameters. (a)—temperature, (b)—moisture, (c) – conductivity, (d)—pH, (e)—nitrogen, (f)—phosphorous, (g)—potassium.

Full size image

Furthermore, we plotted the Pearson correlation matrix of the normalized sensor data after performing outlier detection using Bayesian decision theory and hypothesis testing with theoretical guarantees, as proposed by34. Concurrently, we calculated the Pearson correlation matrix of CKF, identified as the best-performing algorithm, to compare the inferences drawn before and after removing data noise. The analysis was performed in Python 3.12 using a feed-forward model on a Raspberry Pi 5, 64-bit quad-core Cortex-A72 processor running at 1.5 GHz and 4 GB of RAM.

Results

Boxplots

The boxplots (Fig. 6) of soil temperature, electrical conductivity, and phosphorus showed that CKF matched the sensor data patterns, followed by FL and ANN. Additionally, ANN demonstrated potential for removing outliers despite slight variations in data pattern structure (mean values) and amplitude. In contrast, the UKF failed to copy the real data structure, affecting the mean value and distribution within the quartiles. Despite the failure of the UKF to effectively preserve the variability, it reduced the interquartile range (IQR) comparable to the sensor data, indicating salt-and-pepper noise suppression (Fig. 6a) for the soil moisture and soil phosphorus.

The ANN removed the abrupt data variation (associated with Gaussian and pepper-and-salt noise) suspected to be present in soil EC and pH sensor data. The soil potassium and nitrogen parameters (Fig. 6e–g) were prone to several data abrupt associated with Uniform and Gaussian noise types, that only FL effectively handled.

CKF was generally ideal for IoT-based soil monitoring sensor data denoising, with ANN and UKF_FL as alternative solutions for specific cases based on noise types.

Models’ performance

To strengthen our inferences, we developed a dashboard to visualize the real-time data of each parameter, allowing for a comparison of model performance (Fig. 7). The CKF (\({R}^{2}\cong 0.96\)) and ANN (\({R}^{2}\cong 0.96\)) effectively filtered the Gaussian, Uniform, and Salt-and-Pepper noise across all variables. However, the FL filter failed (\({R}^{2}\cong 0.88\)) to remove the Gaussian noise for soil moisture, temperature, and electrical conductivity.

Additionally, the CKF quickly converged (12 input entries) to the sensor data, followed by the UKF_FL (Appendix E). The delayed convergence of the ANN is due to the time required to compute the 9 batches of 10 inputs Fig. 5 for the Kalman gain to converge across each variable. The Kalman gain convergence is noticeable in model’s initial phase, where the ANN produces inconsistent results until data splitting, training, and testing are completed, and the Kalman gain convergence, enabling accurate state estimation (see the red line fluctuation at the start of the process), Fig. 7.

Additionally, CKF and ANN effectively sharpened the data and reducing abrupt changes observed in the censored data (Fig. 7b).

The Cubature Kalman Filter (CKF) demonstrated potential for managing soil temperature sensor Gaussian noise (RMSE ± 0.35), highlighting significant differences in convergence and stability. Meanwhile, the UKF integrated with an artificial neural network (UKF_ANN) effectively suppressed the evaluated sensor noise types, but tended to be over-smooth, which could compromise data accuracy (RMSE ± 0.18). In contrast, the UKF integrated with fuzzy logic (UKF_FL) exhibited exceptional adaptability, efficiently suppressing various types of noise while preserving data integrity, making it particularly well-suited for practical applications in noisy environments.

The CKF and UKF_FL provided stable and accurate results; however, the UKF_FL showed superior adaptability, Uniform, Gaussian, and Salt-and-pepper sensor noise types. While the UKF struggled with Gaussian noise, it stabilized over time. A zoom-in (Appendix E) of the UKF_ANN demonstrated its potential in showing a gradual state change, reflecting the true field scenario rather than replicating the abrupt state variations caused by sensor noise. This makes the filter a promising approach for expert systems in real-time sensing and actuation in precision agriculture.

Reducing sensor noise in precision agriculture enhances resource efficiency. Uniform sensor noise can obstruct the delineation of management zones, which is particularly critical when farmers use variable-rate fertilizer applications. This process requires accurate real-time mapping of soil parameter variability for the correct functioning of the fertilizer application system. If noise accumulates, whether Gaussian or salt-and-pepper, it can cause the entire system to overlook minor variations, leading to increased costs. While uniform and Gaussian noise can significantly affect management zones (MZs), Salt-and-pepper noise within the MZs (e.g., due to lakes, rocks, channels, and drift) necessitates targeted optimization management.

The CKF, ANN, and FL real-time models demonstrated stable and responsive performance regarding soil nitrogen (N), phosphorus (P), and potassium (K), showcasing their effectiveness in managing MZs while minimizing soil acidification associated with biased application rates of N, P, and K due to noisy data. However, FL underestimated the sensor data and failed to effectively smooth the local state transitions caused by Gaussian and uniform sensor noise (Fig. 7e–g), which risks applying higher rates and potentially contaminating water and the environment. The CKF and UKF_ANN variants were the most accurate (R2 = 0.96) and reliable models for precision agriculture applications.

All applied filters removed the abrupt state changes related to sensor node path loss, delays, and network noises. These issues are associated with salt-and-paper noise and lead to anomalous data.

Evaluation metrics

The CKF numerical evaluation of the model’s performance (Table 4) demonstrated a 32% reduction in RMSE compared to the UKF, with the ANN and FL models showing a 2%. Additionally, the CKF and ANN exhibited comparable performance regarding R2 and MAE, though ANN outperformed CKF in predicting soil phosphorus.

Table 4 Evaluation metrics.
Full size table

Moreover, the CKF reduced the UKF’s computation memory and time by 75%, while the ANN increased them by 50% and 450%, respectively. Despite this, the ANN and FL performed similarly regarding RMSE, R2, and MAE. The ANN outperformed the CKF in predicting soil phosphorous, even with uniform noise (Fig. 7f-g). These findings suggest combining graphical visualization with numerical evaluation can enhance model selection.

Pearson correlation

The Pearson correlation analysis (Fig. 8) showed a significant (p < 0.05) association between the variables, supporting the alternative hypothesis. A strong linear association (Fig. 8a) was observed between soil moisture and soil pH, soil moisture and soil electrical conductivity, soil temperature and soil electrical conductivity, and soil pH and soil temperature.

Fig. 8
figure 8

Scatter plot showing the Pearson correlation coefficients (r < 0.05) of bivariate. The red dot in the scatter shows significance with p < 0.01. (a) sensor data, (b) cubature Kalman filter.

Full size image

Additionally, the relationships between soil moisture and soil pH and soil pH and soil temperature showed negative correlations, with strengths ranging from moderate to vigorous, based on the35,36 scale. In contrast, the combinations of soil moisture, soil electrical conductivity, and soil temperature and electrical conductivity demonstrated positive correlations, with strengths varying from firm to very strong.

Additionally, undetected outliers in the scatter plots for the nitrogen-phosphorus, nitrogen-soil temperature, and nitrogen-potassium pairs (Fig. 8a), impacted the performance of the Pearson correlation. The CK (Fig. 8b) effectively removed these outliers, revealing more precise data patterns among the variables. Furthermore, the CKF enhanced the associations between variables, which were previously obscured by noise in the censored data.

Moreover, the CKF improved the data structure of the association between potassium and conductivity, as well as phosphorous and potassium (Fig. 8b). Additionally, the CKF provided better data smoothing, accurately capturing the state transitions of the soil parameters. Using CKF-processed data to evaluate the relationships between variables enhanced the inferences about soil agricultural parameters, underscoring the importance of denoising soil sensor data for more informed decision-making.

Discussions

The correlation analysis demonstrated that soil moisture enhances the accuracy of the data on soil pH (r = 0.96) and electrical conductivity (r = 0.89) measurements29. while clear linear associations were not evident, strong evidence suggests causal relationships between nitrogen and phosphorus and between nitrogen and temperature.

Soil pH directly influences the biological processes regulating nitrogen availability and alters the chemical forms of phosphorus, affecting its availability to plants37. Additionally, a nonlinear relationship between soil phosphorus and temperature was observed. Despite a negligible Pearson correlation (r =—0.10), the data pattern suggests a sigmoidal trend, Fig. 8.

Moreover, the strong correlation observed between soil temperature, moisture, and electrical conductivity (Fig. 8) aligns with previous findings38 that reported a casual association between electrical conductivity and soil moisture linked to temporal patterns of these parameters. Analyzing the interrelationships among these parameters using Pearson correlation provides clear insights into how managing one can affect another. Moreover, inferences drawn from one variable can be applied to others based on their relationships. For instance, reduced soil moisture can lead to inaccurate results from NPK and EC, which may cause improper fertilizer application and poor irrigation management, ultimately affecting crop yield.

The increased convergence time in the ANN model, which has a delay of 11 s, is unlikely to affect inferences for soil parameters with less abrupt variations (pH, N, P, K, EC) despite the additional computational resources required for training and testing39.

The soil pH and moisture showed predictability, even with low-order nonlinearity models (n < 3). The lower variability of the soil pH can be related to its dependence on soil nutrients, soil origin, and soil management40. Related studies (Table 4) conducted by Chana et al.,41 applying the random forest algorithm to integrated soil sensor 7-in-1 data for predicting crop yield demonstrated limited generalization and extensive data requirement for better generalization, leading to increased computation time.

Singha et al.,29 Support Vector Machines and Partial Least Squares Regression were used to predict soil parameters through VIs–NIR reflectance spectroscopy for proximal sensing. This method depended on cross-validation of censored data and laboratory analysis for inferences, as real-time online data denoising was not utilized. While VIs–NIR reflectance spectroscopy can accurately predict soil parameters, the overlapping spectrum frequencies of various soil parameters necessitate careful desegregation of frequencies. Additionally, post-processing VIs–NIR spectroscopy data restricts its feasibility for on-field, real-time applications. These limitations underscore the need for implementing real-time nonlinear sensor denoising filters to improve sensor data before any inference processing.

Despite the quick convergence shown by the FL model (Appendix E), it underestimated the states of soil nitrogen, phosphorus, potassium, and pH while effectively maintaining the global data trends and removing Gaussian, uniform, and salt-and-pepper noise (Fig. 7b). The underestimation issues in FL can be attributed to the inability of the fuzzy logic rules to represent the entire data set, suggesting truncation during the computation of the possibility matrix \({\delta }_{ij}\). Additionally, the failure of FL to compute \({\delta }_{ij}\) accurately may result in a wide truth zone that can be incapable of detecting uniform noise (Fig. 7a – c) within that zone.

Optimizing the Kalman gain using ANN by splitting the data into batches of 10 inputs for training and testing (Fig. 5) enabled copying of the local and global variations, overcoming the limitations observed in FL (Fig. 7a–c). This highlights the hypotheses of implementing truncation to enhance the capture of local variation.

The gradual state transition of the CKF and ANN, which eliminates uniform, Gaussian, and pepper-and-salt noise from sensor data related to soil parameters (Appendix E), can be linked to the radial approaches for selecting sigma and the complexity of specific parameters with delayed convergence (soil temperature, moisture, and electrical conductivity). These may require highly robust filters to replicate the behavior of complex time series parameters, as observed by20,42,43,44, when dealing with high (\(n\ge 3\)) nonlinearity problems.

The multifactorial characteristics of soil temperature, humidity, and electrical conductivity that lead to delayed convergence and rapid data fluctuations can be traced back to the heterogeneous environment (sensor deployed in an open field without mulching), resulting in swift variations in these parameters, as observed by40. Therefore, these results suggest implementing CKF as an integrated real-time operating system (ROS) to minimize sensor noise in heterogeneous environments. The numerical results of the related studies are presented in Table 5.

Table 5 summary of comparative studies
Full size table

Compared to the one obtained29,41, the strength of our results lies in the real-time removal of sensor noise using only the current and past states to estimate future states, reducing complexity. This contrasts with post-processing approaches that require large datasets for improved results and are prone to issues like gradient vanishing. Similarly,27 a hybrid Kalman filter enhanced soil sensor data in a controlled environment. However, the transferability of their results to uncontrolled environments was limited due to several uncontrolled parameters in natural conditions, which led to model failures or required higher-order models. Additionally,27 models implemented on resource-constrained devices did not report resource utilization, limiting the ability for numerical comparison. In contrast, our study comprehensively evaluates advanced Kalman filters to improve real-time sensor denoising for agricultural soil parameters on IoT resource-constrained devices, highlighting the CKF and UKF_ANN as practical approaches for real-time sensor management in heterogeneous, open-field environments.

Conclusion

This paper aimed to evaluate the performance of IoT-based Unscented Kalman Filter (UKF) extensions on resource-constrained devices for enhancing real-time sensor denoising of agricultural soil parameters to provide practical solutions for improving the reliability of IoT-based soil monitoring systems.

The cubature Kalman filter and unscented Kalman, combined with the artificial neural network, keep the censored data structure intact, removing sensor Gaussian, uniform, and salt-and-pepper noise.

The cubature Kalman filter quickly converged with only ten input data, with 75% reduced computation memory and time.

CKF (R2 = 0.99), ANN (R2 = 0.99), and UKF (R2 = 0.89) accurately predicted the soil pH, even with the increased computation time (11 s) observed in the ANN. A delay of this time for soil parameters cannot interfere with the inference, considering the advantage of converging the Kalman gain, which can better handle high-order (\(n>3\)) nonlinearity.

In future work, we will extend our study by predicting soil nutrient mobility to provide real-time optimal fertilization dates and amounts.