Introduction

Tunnel construction has emerged as a viable solution to address the challenges of densely populated surface spaces and growing traffic congestion costs1. Among various tunnel construction methods, there has been a substantial increase in demand for tunnel boring machines (TBMs) due to their eco-friendliness, stability, and constructability. However, the inherent risk arising from various uncertainties associated with TBM excavation cannot be disregarded. Therefore, during the design phase, effective risk management is required for optimal decision-making, which mitigates delays and potential casualties resulting from accidents.

Risk is generally defined as the expected losses of a specific factor, which is expressed through two risk components: impact and probability2. Due to the site-specificity of these components and challenges in collecting and analyzing quantitative data, risk management during the design phase has relied on expert elicitation. As a widely adopted scientific consensus methodology, expert elicitation aggregates expert judgments on a particular subject, especially in situations with limited information3. Previous studies on tunnel risk management have integrated expert elicitation with various techniques2,4,5,6,7,8. For instance, Eskesen et al.2 provided guidelines for expert elicitation in tunnel risk management with systematic risk management techniques. Hong et al.4 analyzed the probability of risk in underwater TBM tunneling by applying event tree analysis (ETA). Hyun et al.5 developed a risk matrix method that incorporated fault tree analysis (FTA) and analytic hierarchy process (AHP). Chung et al.6 assessed the degree of risk of potential accidents for each geological source based on Bayesian networks and detailed cost analysis of mitigation measures. Chung et al.7 improved the risk matrix method by employing causal networks. Sharafat et al.8 integrated FTA and ETA, presenting a risk management method featuring a generic bow-tie structure. In these approaches, each expert first selects a class or value for impact and probability. The aggregated expert judgments are then employed in various methods (e.g., ETA, FTA, and AHP) to evaluate the overall impact, probability, and associated risk level. However, expert judgments in TBM excavation are subject to significant uncertainty due to limited available information9. Accordingly, relying on a single selection to assess impact and probability may be insufficient to fully capture the inherent uncertainties. Moreover, these studies tend to focus exclusively on major responses, overlooking the uncertainties reflected in less frequent ones, which may lead to limited or less robust decision-making. For example, Hyun et al.5 and Chung et al.7 determined risk levels solely based on the most frequently selected impact and probability classes (e.g., Low), without accounting for the contributions of responses falling into other possible classes (e.g., Medium or High).

Fuzzy set theory (FST) addresses uncertainties by distributing an expert’s evaluation confidence across multiple classes using the concept of membership degree, which indicates the degree to which an element belongs to a set. Accordingly, FST has been widely applied to risk management in various domains, including tunnel construction10,11,12,13,14,15, rock or coal bursts16,17, and other related fields18,19,20,21,22. Nonetheless, these FST-based studies face challenges in interpretability, particularly in illustrating how uncertainties arising from expert elicitation are distributed across multiple classes and whether any specific class exhibits dominance. Moreover, risk management involving concurrent sources has not been fully explored, although their complex interactions can significantly increase the risk of certain types of accidents23. In other words, most of previous studies struggle to adequately capture the synergistic risk arising from the simultaneous occurrence of multiple sources. For instance, Nezarat et al.10 assessed the risk of each geological source independently and prioritized them accordingly, without considering potential interactions among concurrent sources. Although Koohathongsumrit and Chankham12 considered multiple concurrent sources using FTA, the inherent logic of the OR gate in FTA may lead to an overestimation of accident probability, even when the individual probabilities of all contributing sources are relatively low.

This study proposes an interpretable risk management method to support optimal decision-making by addressing uncertainties and multiple risk sources. By integrating an expert elicitation framework with FST, this method accommodates expert responses that reflect uncertainties. Representing impact, probability, and risk as distributions enables a comprehensive interpretation of expert judgment trends, thereby capturing underlying uncertainties. A comparative analysis further assesses the influences of concurrent sources on risk compared to individual sources. The validity of the proposed method is demonstrated through its application to a slurry shield TBM tunneling project.

Theory

Fuzzy set theory (FST)

Fuzzy set theory (FST), initially proposed by Zadeh24, has been utilized for addressing qualitative and subjective problems with uncertainties induced by a lack of data or natural sources25. In classical set theory, an element must be either a member of the set or not, indicating that the membership degree is zero (non-member) or one (member) due to the crisp set boundary. However, FST allows elements to have arbitrary membership degrees between zero and one with the aid of an ambiguous set boundary. This feature makes FST a suitable tool for modeling uncertainty in various fields, such as risk management, decision-making, and pattern recognition.

Assuming that the fuzzy set is \(A\) and the elements are \(x\), the membership function is expressed as \({\mu }_{A}(x)\). Although various forms of membership functions exist, such as Gaussian and parabolic types, triangular and trapezoidal functions are commonly employed due to their ease of definition, representation, and computation26. These two function types effectively capture uncertainty while maintaining clear relationships between elements and their membership degrees, which is an essential feature in risk management based on expert elicitation. Moreover, their widespread use and demonstrated applicability in previous studies18,19,20,21,22,26,27,28 support their adoption. Accordingly, this study employs these two simpler forms, as detailed in Section “Risk analysis”.

The triangular membership function, denoted as (a, b, c), is mathematically formulated using Eq. (1), where b gives the maximum value, and a and c denote the lower and upper bounds of the available area, respectively27.

$$\mu _{A} (x) = \left\{ {\begin{array}{*{20}l} {\frac{{x - a}}{{b - a}}} \hfill & {(a \le x < b)} \hfill \\ {\frac{{c - x}}{{c - b}}} \hfill & {(b \le x \le c)} \hfill \\ 0 \hfill & {(Otherwise)} \hfill \\ \end{array} } \right.$$
(1)

The trapezoidal membership function is denoted as (a, b, c, d) and mathematically formulated as Eq. (2), where the interval [b, c] gives the maximum value, and a and d connote the lower and upper bounds of the available area, respectively27.

$$\mu _{A} (x) = \left\{ {\begin{array}{*{20}l} {\frac{{x - a}}{{b - a}}} \hfill & {(a \le x < b)} \hfill \\ {1} \hfill & {(b \le x < c)} \hfill \\ {\frac{{d - x}}{{d - c}}} \hfill & {(c \le x \le d)} \hfill \\ 0 \hfill & {(Otherwise)} \hfill \\ \end{array} } \right.$$
(2)

Risk matrix

A risk matrix has been widely applied to determine a risk level as it is an intuitive and effective approach2,5,7. Specifically, the risk level determination involves combining the impact and probability classes evaluated for the corresponding adverse factor. For example, according to Fig. 1, the risk level is classified as Tolerable when the impact and probability classes are evaluated as Low and Medium, respectively. Here, the risk level serves as a criterion for determining the required level of mitigation measures for the associated adverse factors, facilitating implementation of appropriate mitigation measures.

Fig. 1
figure 1

Risk matrix example.

Full size image

Analytic hierarchy process (AHP)

The analytic hierarchy process (AHP) has been widely adopted as a technique for determining the weight of each decision-making factor in tunnel risk management5,10,11. It involves conducting a pairwise comparison between elements based on a specific criterion to determine their relative importance29. A pairwise comparison matrix (Eq. 3) is constructed based on expert surveys, and the eigenvalue method is employed to derive the relative importance of each element, which is represented as weight. In Eq. (3), \({a}_{ij}\) represents the importance ratio of the ith to jth element. In this study, comparative expert judgments are conducted using a 1–5 scale. A rating of 1 represents equal importance between the two elements, while a rating of 5 indicates that one element is considered to have a significantly stronger influence than the other, as detailed in Table 1. The eigenvalue method identifies the principal eigenvector of a pairwise comparison matrix and derives the component of the vector as the weight of each element30. In this study, it is used to construct the weighted risk matrix (WRM), as discussed later in Section “Risk evaluation”.

$$\begin{aligned} A & = \left| {a_{ij} } \right| where \, i, j = 1,2, \ldots , n \\ & = \left( {\begin{array}{*{20}c} 1 & {a_{12} } & \cdots & {a_{1n} } \\ {\frac{1}{{a_{12} }}} & 1 & \cdots & {a_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {\frac{1}{{a_{1n} }}} & {\frac{1}{{a_{2n} }}} & \cdots & 1 \\ \end{array} } \right) \\ \end{aligned}$$
(3)
Table 1 Scale for pairwise comparison in the AHP29.
Full size table

Method

Risk identification

Adverse factors requiring risk management are identified in risk identification. In this study, the factor under consideration is a causal combination, representing a one-to-one causal relationship between a potential accident and its source specific to a target tunneling site. This approach accounts for the varying probability of accidents depending on the accident-inducing source. Accordingly, identifying accidents, sources, and causal combinations associated with the target tunneling site is essential for this study.

Moreover, the proposed method addresses the coexistence of multiple sources that could independently contribute to a specific accident. In this context, a concurrent causal combination is defined as a causal relationship between an accident and each concurrent source affecting the accident. This study focuses on potential geological sources because these are inherent to the site and contribute significantly to a large proportion of reported accidents31,32. In addition, estimating the probabilities associated with operational sources must account for potential improper TBM operations, a challenging task during the design phase33. To enhance the reliability of risk identification results, this study employs both literature reviews and expert interviews concurrently34.

Risk analysis

In this study, the objective of risk analysis is to derive impact and probability distributions through expert elicitation integrated with FST. These distributions are expressed with the membership degree allocated to each class, as later illustrated in Figs. 5, 6, and 7. This study adopts four classes (i.e., None [N], Low [L], Medium [M], and High [H]) represented with two membership function forms (i.e., triangular and trapezoidal). Furthermore, 12 scores (i.e., integers between 1 and 12) are used to quantify the membership degree of each impact and probability class. Establishing membership functions for the adopted classes involves three key considerations:

  1. 1.

    The total membership degree of two classes is set to one when a given score is associated with them.

  2. 2.

    The classes at the extremes (i.e., N and H classes) possess a wider range with a membership degree of one because they may have higher judgmental clarity compared to the intermediate classes.

  3. 3.

    An appropriate number of scoring options should be available to enable differentiated distributions of membership degrees between two adjacent classes (e.g., 1/3 for N class and 2/3 for L class), while also avoiding an excessive number of choices.

The membership functions corresponding to each impact/probability class and score are shown in Fig. 2 and summarized in Table 2, respectively.

Fig. 2
figure 2

Membership functions employed in this study.

Full size image
Table 2 Membership degree corresponding to each class and score.
Full size table

Subsequently, each expert is required to select one of the 12 available scores when assessing impact and probability. Unlike the probability of an accident, this study assumes that the impact of the accident remains relatively constant, even if the accident-inducing source changes. Thus, the impact scores relate to the accident, while the probability scores pertain to the causal combination. In this method, the impact of a causal combination is assumed to be equal to that of an accident within the same causal combination.

Meanwhile, due to the inherent subjectivity of expert judgment, some experts may provide outlier responses that significantly deviate from others, potentially influencing the outcomes of risk management. To mitigate the impact of such outliers during the aggregation of expert opinions, this study employs an outlier exclusion approach based on the interquartile range (IQR). In general, the IQR is the difference between the first quartile (Q1) and third quartile (Q3) of the data, as expressed in Eq. (4). The data falling outside the lower bound (Eq. 5) and upper bound (Eq. 6), as defined by the IQR, are excluded.

$$IQR={Q}_{3}-{Q}_{1}$$
(4)
$$Lower \, bound={Q}_{1}-1.5*IQR$$
(5)
$$Upper \, bound={Q}_{3}+1.5*IQR$$
(6)

Although this general IQR-based outlier exclusion method is effective, the difference between the bounds may decrease when the IQR approaches zero, resulting in the exclusion of data slightly differing from the majority. To address this limitation, cases where the IQR is less than two are adjusted to set the IQR to two. Following outlier exclusion using the modified IQR, the membership degrees for all impact and probability classes are calculated using Eqs. (7) and (8). Here, \({MD}_{I}\) and \({MD}_{P}\) represent the membership degrees for impact and probability, respectively, while \(i\), \(j\), and \(n\) denote the class, score, and number of non-excluded experts. Consequently, the impact and probability distributions are represented based on the calculated membership degrees. Importantly, a comprehensive interpretation of these distributions can clarify how uncertainties are distributed across all classes and indicate whether any specific class demonstrates dominance.

$${MD}_{I, i}=\frac{{\sum }_{j=1}^{12}{MD}_{I,i,j}}{n}$$
(7)
$${MD}_{P, i}=\frac{{\sum }_{j=1}^{12}{MD}_{P,i,j}}{n}$$
(8)

Furthermore, this method derives the probability and risk distributions corresponding to concurrent causal combinations. In this study, a probability set is defined as a combination of the four probability classes of single causal combinations, such as None–Low (involving two sources) and High–Medium–Medium (involving three sources). Each single causal combination represents the relationship between one source and a specific accident within a specific concurrent causal combination. The representative probability class for each probability set is the most dangerous class among the combined probability classes; for instance, None–Low corresponds to Low, and High–Medium–Medium corresponds to High.

The process for determining the probability distributions of concurrent causal combinations consists of two steps. First, the membership degree of each probability set is calculated by multiplying the membership degrees of the probability classes within that probability set. Second, the membership degree of each individual probability class (i.e., None, Low, Medium, and High) is determined by summing the membership degrees of all probability sets where that class is representative, which can also be expressed as Eq. (8). This approach supports risk management for any combination of existing sources by incorporating the individual causal combinations associated with each source. Furthermore, it enables dynamic updates to risk management through real-time assessment of unforeseen causal combinations among known sources.

Risk evaluation

The risk evaluation aims to determine risk distributions and risk levels based on the impact and probability distributions with a risk matrix. It is crucial to define specific criteria when constructing the risk matrix for application to a particular project. For example, a symmetric risk matrix may be limited as it yields the same risk level regardless of whether the analyzed impact and probability classes are reversed. Depending on project’s specific objectives and financial margins, one risk component may need to be considered more influential than the other. This prioritization necessitates the use of an asymmetric risk matrix that reflects the differing importance of each component. In this study, weights are assigned to the impact and probability components to quantify their relative significance, and an asymmetric risk matrix, referred to as the weighted risk matrix (WRM), is constructed accordingly. AHP (refer to Section “Analytic hierarchy process (AHP)”) is employed to determine the weight of each risk component and construct the WRM. Experts with professional experience and knowledge compare two risk components for weight distribution and evaluate the relative importance of one risk component over the other based on Table 1. Applying AHP to the aggregated expert judgments, the impact weight (\({\omega }_{I}\)) and probability weight (\({\omega }_{P}\)) are determined.

The proposed method involves the development of questionnaires that require experts to assign scores for both impact and probability assessments, as well as to evaluate the relative importance of impact compared to probability. For instance, experts are asked to: (1) assess the probability score of Faults-Collapse on a scale from 1 to 12; (2) assess the impact score of Collapse on a scale from 1 to 12; and (3) evaluate the relative importance of Impact compared to Probability using the scale [5, 3, 1, 1/3, 1/5].

This study adopts four risk levels (i.e., Negligible [N], Tolerable [T], Significant [S], and Intolerable [I]). Notably, the risk level is classified based on a combination of impact and probability classes to construct the WRM. The class representative score (CRS) of the impact and probability is defined as N = 2, L = 5, M = 8, and H = 11, with reference to Fig. 2. Subsequently, the risk level score (RLS) of each component set (i.e., the combination of the impact and probability classes) is calculated using the assigned weights and CRS, as expressed in Eq. (9). The risk level of each component set is determined based on the magnitude of the calculated RLS (i.e., \(N:2<RLS\le 4.25\), \(T:4.25<RLS\le 6.5\), \(S:6.5<RLS\le 8.75\), \(I:8.75<RLS\le 11\)). It is important to note that the WRM should be reconstructed for each project considering its objective and financial margin. An example of the constructed WRM is provided in Fig. 8, as presented later in Section “Results of risk evaluation”. Table 3 summarizes whether to take mitigation measures according to each risk level.

Table 3 Need for mitigation measures according to risk level.
Full size table
$$RLS={CRS}_{I}\times {\omega }_{I}+{CRS}_{P}\times {\omega }_{P}$$
(9)

This study first determines the risk distributions based on the impact and probability distributions as well as the WRM. Then, it provides the risk levels that facilitate an intuitive understanding of the results of risk management. This study recommends optimal decision-making for mitigation measures based on the comprehensive interpretation of risk management results, including impact, probability, risk distributions, and risk levels, during the design phase. The risk evaluation process is summarized as follows.

  1. 1.

    The membership degree of each component set (e.g., None-Low) is calculated by multiplying that of the corresponding impact class (e.g., MDI,N) and probability class (e.g., MDP,L) that constitute the component set.

  2. 2.

    The membership degree of each risk level is then determined by summing the membership degrees of all component sets that contribute to that risk level, based on the WRM, thereby obtaining a complete risk distribution. For example, considering Table 8 in Section “Results of risk evaluation”, the membership degree of the Negligible risk level is calculated by summing the membership degrees of four component sets (i.e., None-None, None-Low, None-Medium, and Low-None).

  3. 3.

    The final risk level is identified as the one with the highest membership degree. If multiple risk levels share the highest degree, the more severe level is selected to ensure a conservative approach to risk management.

Both single and concurrent causal combinations are applied identically in this risk evaluation process. The risk evaluation results for both individual and concurrent causal combinations support the development of mitigation measures tailored to each source and their interactions. Notably, decisions regarding the implementation and extent of mitigation measures should consider not only the final risk level but also the membership degrees of the various risk levels. For instance, if the membership degree of Intolerable is substantial when the final risk level is classified as Significant, mitigation measures should still be applied. In this way, the interpretable results provided by the proposed method can support more informed and comprehensive risk management decisions. Figure 3 presents a flowchart illustrating the process of the interpretable risk management method, covering risk identification, analysis, and evaluation.

Fig. 3
figure 3

Flowchart of the proposed method.

Full size image

Results

Project overview

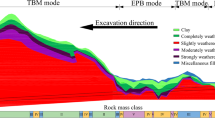
The proposed method was applied to a 2.86 km under-river tunnel project to verify its practical applicability. This tunnel has been under construction since 2022, with its alignment passing through several hazardous sections associated with shallow cover depth, mixed ground conditions, and high water pressure exceeding 300 kPa. A slurry shield TBM with a 14.01 m diameter was utilized, which is advantageous for face pressure control. Details of the slurry shield TBM are summarized in Table 4. The ground along the tunnel alignment primarily comprises weathered, soft, fair, and hard rocks. The longitudinal geological profile along the tunnel alignment is depicted in Fig. 4.

Table 4 Utilized slurry shield TBM specifications.
Full size table
Fig. 4
figure 4

Geological profile of the site investigated in this study.

Full size image

Results of risk identification

Through literature reviews and expert interviews, five potential accidents likely to occur during the under-river tunneling project were identified at this site. Table 5 presents these accidents and the sources of high association with each accident present at this site. Table 6 summarizes the causal combinations based on the identified sources and accidents. The concurrent causal combinations are identified by linking one accident with multiple related sources, such as [Faults and Shallow cover depth–Collapse].

Table 5 Identified accidents and sources of the target project.
Full size table
Table 6 Identified causal combinations of the target project.
Full size table

Table 6 is organized based on findings from a review of relevant previous studies. Faults can induce shear failure along discontinuities and deform the surrounding ground, resulting in collapse, surface settlement, and mud/water inflow. The slurry can infiltrate the tunnel face and be ejected onto the ground surface (i.e., blow-out) due to the high hydraulic conductivity of the faults. Additionally, clay minerals within fault gouges can adhere to cutter head and disc cutters depending on soil properties such as cohesion and water content, inducing cutter head clogging35. Shallow cover depth can expand the displacement of the surrounding ground to the ground surface, and if displacement continues, the ground can collapse. Moreover, heaving or blow-out can occur when the face pressure exceeds the overburden pressure arising from the shallow cover depth. Mixed ground conditions can cause uneven face pressure on the TBM, leading to face instability and over-excavation of weaker parts of the mixed ground, resulting in collapse and surface settlement36.

Stress concentration can occur during cross-passage excavation owing to the different constraints and behaviors at the connection37, and deform the surrounding ground and segment lining, thereby enabling collapse, surface settlement, and mud/water inflow. High water pressure is a primary consideration for face pressure management. Unless the management is appropriate, ground loss due to the mud/water inflow increases, leading to collapse or severe surface settlement. Finally, weathering can lead to the inability to maintain face pressure, inducing collapse or excessive settlement38. Discontinuities in weathered rock can also increase the possibility of mud/water inflow into the TBM39.

Results of risk analysis

Expert elicitation engaged 30 experts possessing relevant expertise and experience to determine impact and probability distributions. Specifically, five of these experts have over 15 years of experience in TBM tunnel design and construction, while the remaining experts have over 10 years of experience. This process was conducted through written evaluations using questionnaires, which required the experts to assign scores for impact and probability, as well as to determine the relative importance of impact compared to probability. Figure 5 presents the impact distributions for the five identified accidents, with each distribution labeled using the corresponding symbol defined in Table 5.

Fig. 5
figure 5

Impact distributions.

Full size image

According to Fig. 5, none of the identified accidents showed a single dominant class with a membership degree above 0.5. However, the sum of the membership degrees corresponding to the M and H classes, except for cutter head blockage (A5), exceeded 0.5, suggesting that the occurrence of these accidents causes severe damage during TBM tunneling. Meanwhile, the impact distribution was more left-skewed in the order of A1, A2, A3, A4, and A5, implying that the impact of these accidents was relatively low in the same order. This observation is in line with the findings of Sousa and Einstein40, which identified collapse as the most critical accident in tunnel excavation.

The probability distributions of all identified causal combinations are shown in Fig. 6, with each distribution labeled according to the corresponding symbol defined in Table 6. Similar to the impact distributions, except for S4-A1, all causal combinations showed balanced probability distributions with no noticeably high membership degree in any of the classes. Particularly, in the case of S5-A1, the membership degrees of three classes were evidently comparable (N: 0.32, L: 0.31, and M: 0.29).

Fig. 6
figure 6

Probability distributions of single causal combinations.

Full size image

Figures 5 and 6 indicate that the impact and probability distributions should be considered comprehensively rather than focusing solely on the class with the highest membership degree. Relying on a single class in risk management may result in limited decision-making. In contrast, a comprehensive interpretation of impact and probability distributions clarifies how uncertainties are distributed across all classes and reveals whether any specific class exhibits dominance.

Meanwhile, the probability distributions of causal combinations associated with the collapse (S1-A1, S2-A1, S3-A1, S4-A1, and S5-A1) were more left-skewed compared to those of the remaining combinations (i.e., the N and L classes exhibit relatively higher membership degrees than the others). This implies that adequate preventive measures are being designed or implemented to mitigate the most critical accident (A1). In addition, the causal combinations with the highest membership degree of the M class pertained to surface settlement and heaving/blow-out sourced from shallow cover depth (S2-A2 and S2-A3). Moreover, the H class’s membership degree of S2-A1 was higher than that of the remaining combinations. Therefore, shallow cover depth can be identified as the most accident-inducing source during TBM tunneling at this site.

Furthermore, this study specifically examined the probability distributions of concurrent causal combinations involving two sources that induce collapse, although the proposed method is applicable to other combinations as well. The ten concurrent causal combinations under consideration and their probability distributions are summarized in Table 7 and Fig. 7, respectively.

Table 7 Concurrent causal combinations consisting of two sources inducing collapse.
Full size table
Fig. 7
figure 7

Probability distributions of concurrent causal combinations consisting of two sources inducing collapse.

Full size image

As shown in Fig. 6, the five single causal combinations associated with collapse (i.e., S1-A1, S2-A1, S3-A1, S4-A1, and S5-A1) exhibited the highest membership degree in the N and L classes. In contrast, their concurrent causal combinations had the highest membership degree in the L and M classes, as illustrated in Fig. 7. These differences indicate that the proposed method effectively captures the increased probability arising from concurrent multiple sources compared to a single source.

Results of risk evaluation

Through expert elicitation from the 30 experts participating in risk analysis, the impact weight (\({\omega }_{I}\)) and probability weight (\({\omega }_{P}\)) were determined to be 0.74 and 0.26, respectively. Figure 8 and Table 8 present the WRM and the corresponding risk levels for each component set, determined based on the assigned weights, CRS, and RLS described in Section “Risk evaluation”. Figure 9 illustrates the risk distributions of single causal combinations determined by integrating the impact and probability distributions with the WRM.

Fig. 8
figure 8

WRM determined at this site.

Full size image
Table 8 Determined risk level corresponding to each component set.
Full size table
Fig. 9
figure 9

Risk distributions of single causal combinations.

Full size image

As shown in Fig. 9, none of the risk distributions exhibit a single dominant risk level with a membership degree greater than 0.5. Additionally, 12 out of the 19 causal combinations were classified as the S risk level, where mitigation measures are recommended, though their implementation depends on the specific situation (refer to Table 3). Therefore, it is essential to consider the various risk levels (i.e., N, T, and I risk levels) to optimize decision-making regarding the implementation of mitigation measures. This analysis is facilitated by the comprehensive interpretation of risk distributions offered by the proposed method, which allows for an examination of how uncertainties are distributed across all risk levels and the identification of any dominant risk level.

Meanwhile, despite having the same component set consisting of the impact and probability classes with the highest membership degree, several causal combinations resulted in different risk levels. For instance, compared with S2-A1 and S3-A1, the final risk level was observed to be the I risk level for the former and the S risk level for the latter, although they equally had the highest membership degree at the H impact class and L probability class. This discrepancy stems from that S2-A1 and S3-A1 exhibited relatively high membership degrees of the H and N classes regarding probability, respectively. These findings also highlight the necessity of a comprehensive interpretation of the probability distribution for the elaborate determination of the risk level, which is not possible when considering only a single probability class with the highest membership degree.

Similar to the probability analysis, the importance of the proposed method’s interpretability for uncertainty consideration was confirmed through balanced risk distributions across most causal combinations. Specifically, ten causal combinations demonstrate minor differences (< 0.05) in the first and second-highest membership degrees of risk levels, as shown in Fig. 9. For all causal combinations associated with mud/water inflow (S1-A4, S4-A4, S5-A4, and S6-A4) and cutter head blockage (S1-A5 and S3-A5), the difference in membership degree between the T and S risk levels was less than 0.05. It arose from the similar membership degree between the L and M classes of those accidents’ impact. Notably, S5-A1 demonstrates the same highest membership degree in two risk levels (i.e., S and I risk levels), which may result from the high standard deviation value described in the probability analysis. Such absence of a single dominant risk level demonstrates the danger of the limited consideration of only the risk level with the highest membership degree. The proposed method can overcome this limitation by exploring the presented risk distribution comprehensively.

Meanwhile, S1-A1, S2-A1, and S5-A1 were categorized under the I risk level, necessitating mitigation measure implementation. In collaboration with professional site managers, mitigation measures are identified for managing the causal combinations at the I risk level, despite minor differences (less than 0.05) in membership degrees between the S and I risk levels for S3-A1 and S4-A1. Overall, real-time monitoring and control of face pressure and muck discharge volume are planned to ensure face stability and reduce the risk of over-excavation during TBM excavation. Injecting high-density slurry proves advantageous in quickly forming filter cakes, especially under high water pressure conditions where groundwater inflow may otherwise dilute the slurry or hinder proper filter cake formation.

Subsequently, Fig. 10 presents the risk distributions of concurrent causal combinations listed in Table 7. As observed in Fig. 9, three out of the five causal combinations associated with collapse were classified as the I risk level, while the remaining exhibited the S risk level. In contrast, all concurrent causal combinations were categorized as the I risk level, as depicted in Fig. 10. The risk distributions for these concurrent causal combinations emphasize that the proposed method effectively addresses higher-risk scenarios arising from concurrent sources, unlike the previous studies.

Fig. 10
figure 10

Risk distributions of concurrent causal combinations consisting of two sources inducing collapse.

Full size image

Comparative analysis

A comparative analysis was conducted for two cases to examine the influence of comprehensive interpretation. Case 1 is the proposed method, incorporating all impact and probability classes in determining risk levels, whereas Case 2 focuses only on the single class with the highest membership degree. The results of the comparative analysis are summarized in Table 9.

Table 9 Comparative analysis results.
Full size table

Although the risk levels of the two cases are consistent overall, five causal combinations obtained different risk levels. For four out of these causal combinations (S3-A1, S4-A1, S4-A4, and S6-A4), the risk level considering all classes was less dangerous than when considering a single class. These differences were investigated by comparing the risk analysis and evaluation results of these causal combinations with those of other causal combinations associated with the same accidents (i.e., A1 and A4). Specifically, S3-A1 and S4-A1 were compared with S1-A1 and S2-A1; in addition, S4-A4 and S6-A4 were compared with S1-A4 and S5-A4. The observed differences in the four causal combinations occurred, as only Case 1 reflected meaningful membership degrees for the N probability class (more than 0.25). In contrast, in the case of S5-A1, the risk level considering all classes was derived as more dangerous because it considered its close membership degrees of three probability classes (N: 0.32, L: 0.31, and M: 0.29).

These observations suggest a risk of limited decision-making when meaningful membership degrees are disregarded, thereby highlighting the importance of a comprehensive interpretation. Although the risk level in the proposed method was elaborately derived by addressing uncertainties, its consideration along with the risk distribution in parallel can enable a more comprehensive interpretation of the risk management results.

Discussion

The proposed interpretable risk management method offers three key contributions. First, the FST-based expert elicitation framework addresses uncertainties by allowing experts to distribute their evaluation confidence. Second, the proposed method facilitates a comprehensive interpretation of overall expert judgment trends by representing impact, probability, and risk as distributions. This approach makes it possible to examine how uncertainties are distributed and to identify any dominant class or risk level, ensuring that meaningful but less prominent responses are also considered. Third, this method effectively captures the increased probability and risk associated with concurrent sources that may induce a specific accident.

However, the proposed method focuses on geological sources, excluding operational sources. As previously mentioned, estimating the probability of accidents induced by TBM operational sources is challenging during the design phase because it necessitates assumptions about improper TBM operations during construction. Moreover, a limitation of the proposed method lies in the absence of analyses incorporating diverse types of membership functions. Future studies could incorporate incremental weighting for operational sources into the results based on geological sources, particularly when accidents or unexpected geological sources are predicted by real-time models using electrical resistivity surveys or machine learning techniques41,42,43,44,45,46. Furthermore, exploring a broader range of membership function types, such as Gaussian and parabolic functions, could further enrich and diversify risk management approaches.

Conclusions

This study presented an interpretable risk management method for optimizing decision-making in TBM risk management. It incorporates an FST-based expert elicitation designed to manage uncertainties. In addition, a comparative analysis evaluated the influence of multiple concurrent sources. This method was applied to a slurry shield TBM tunnel project, emphasizing its relevance. The main conclusions of this study are summarized as follows:

  1. 1.

    Most of the impact, probability, and risk distributions exhibited no single dominant class or risk level due to significant uncertainties. This highlights the importance of comprehensive interpretation for optimizing decision-making, as it can analyze how uncertainties are distributed and identifies any dominant class or risk level.

  2. 2.

    While only three out of five single causal combinations associated with collapse were classified as the I risk level, all concurrent causal combinations were categorized as the I risk level. These differences demonstrate the method’s effectiveness in capturing the increased risk associated with concurrent sources.

  3. 3.

    The comparative analysis showed variations in risk levels based on the consideration of meaningful yet minor responses in risk management, indicating the importance of comprehensive interpretation. These observations demonstrate the potential for limited decision-making when meaningful responses are disregarded simply because they are not dominant.