Hyperbolic geometry enhanced feature filtering network for industrial anomaly detection

Abstract

In recent years, Cutting-edge machine learning algorithms and systems in Industry 4.0 enhance quality control and increase production efficiency. The visual perception algorithms have become extensively utilized in surface defect detection, progressively replacing manual inspection methods. As a crucial component of the Industrial Internet of Things (IIoT), this technology is pivotal for ensuring industrial production quality and has garnered significant attention from the military and aerospace sectors. Nonetheless, most existing methods rely on Euclidean space, which constrains their effectiveness in handling non-Euclidean space data. Additionally, challenges such as addressing pre-trained feature redundancy and bias in the pre-training process persist. This paper presents HADNet, a hyperbolic space-based anomaly detection method. Specifically, we begin by mapping the extracted features to hyperbolic space, a non-Euclidean geometric space. This mapping leverages the unique geometric properties of hyperbolic space, particularly the hyperbolic distance metric, to represent the distances between features more effectively. Next, the most relevant features for anomaly detection are selected through the anomaly-aware feature subset selection module, enhancing anomaly detection performance. Finally, we introduce adaptive residuals discrimination, an adaptive analysis technique that discards residuals lacking anomaly information, thereby isolating the most effective regions for anomaly detection. Extensive experiments on four benchmark datasets NEU-Seg, MT-Defect, FSSD-12, and UCF-EL demonstrate the efficacy of HADNet, achieving mIoU scores of 87%, 81.46%, 77.04%, and 59.41% respectively, significantly surpassing the current state-of-the-art methods.

Introduction

Image anomaly detection plays a crucial role in intelligent industrial production and is extensively utilized in quality control and safety monitoring. In recent years, State-of-the-art machine learning algorithms and systems in Industry 4.0 contribute to the advancement of quality control and boost production efficiency¹.The vision-based metal defect detection has become increasingly prevalent across industries such as construction, aerospace, military, and energy. Surface and internal defects, including cracks and pores, can pose significant safety risks². Traditional methods of detecting these defects, such as visual inspection, are often inefficient and prone to inaccuracies due to variability in the operator’s skill. As industrial automation and intelligent manufacturing advance, the demand for more precise and faster defect detection technologies has increased³. Consequently, there is a pressing need to develop advanced detection technologies to meet the modern industry’s standards for high-quality and safe metal products (Fig. 1).

Fig. 1

Comparisons between conventional Euclidean space (a) and hyperbolic space (b). Mean intersection over union of anomaly detection methods on NEU-Seg, MT-Defect and FSSD-12 datasets (c).

The detection process is complicated by the diverse types and characteristics of metal surface defects⁴. Traditional methods often struggle with these defects, particularly when identifying small or deep flaws, and typically lack the required accuracy. Additionally, environmental factors such as changes in lighting, temperature fluctuations, and noise can disrupt the detection process, leading to inaccurate results. Complex surfaces and internal structures of metallic materials often exhibit similar surface characteristics and potential defects. Leveraging this similarity, analyzing metal surface scratch data can enhance our understanding of defect detection methods and aid in the development of more accurate algorithms. The complex geometries of these components pose challenges in capturing hierarchical relationships within the data. As shown in Fig. 2a, metal surface defect images exhibit a natural hierarchical structure, transitioning from global semantic nodes to local feature nodes, and finally to base nodes that encompass more refined attributes, resembling the hierarchical structure of a tree.Traditional methods, often based on the assumption of flat Euclidean space, may fail to model the intricate relationships in data with complex structures effectively, thereby compromising defect detection accuracy. Therefore, we advocate representing data in hyperbolic space. The unique geometric properties of hyperbolic space enable it to more effectively characterize the subtle differences in metal defects. Specifically, hyperbolic space resembles the branching structure of tree roots, with its volume expanding exponentially in the radial direction. This characteristic can naturally represent the hierarchical structures commonly found in metal defects, while also geometrically amplifying minor deformation differences, as shown in Fig. 2b. Metal defect data typically exhibit non-uniform distribution and self-similar fractal features, which are highly compatible with the exponential expansion properties of hyperbolic space. By representing data in hyperbolic space, we can more accurately model complex component structures and defect modes, thereby improving the accuracy of data analysis.

Fig. 2

Illustrates the hierarchical relationships of metal surface defect images. (a) The entire image serves as the root node, with local regions acting as branch nodes and detailed areas representing deeper branch nodes. (b) The positions of these nodes in hyperbolic space are depicted accordingly.

A variety of detection methods have been developed to identify different types of defects. For instance, ultrasonic testing employs high-frequency sound waves to detect internal micro inclusions within materials⁵. Eddy current testing, a non-destructive method based on electromagnetic induction, can detect surface or near-surface defects⁶. Faster-R-CNN utilizes a Region Proposal Network (RPN) to generate candidate regions, enabling accurate detection of anomalies in engine components, such as cracks, pores, or wear⁷. Additionally, You Only Look Once(YOLO) is a real-time object detection technology that efficiently detects defects by dividing images into grids and predicting object bounding boxes and categories within each grid⁸. Despite significant advancements in manufacturing, maintenance, and repair processes, several challenges persist. These include difficulties in detecting complex geometric shapes, the impact of material non-uniformity on detection accuracy, and the challenge of identifying deep defects.

In this paper, we propose an anomaly detection method based on hyperbolic space to address the aforementioned challenges. We convert the feature map from Euclidean space to hyperbolic space to better capture subtle features and hierarchical relationships of defects. As shown in Fig. 1, Euclidean space is characterized by a flat structure, where parallel lines never intersect, and area and volume grow according to polynomial laws. In contrast, hyperbolic space, a non-Euclidean geometry with negative curvature, exhibits a curved structure. Additionally, in hyperbolic space, the exponential increase in area and volume with the radius offers superior capacity to encapsulate the hierarchical structures inherent in complex datasets, thereby conferring a natural advantage for the embedding of such hierarchically structured data. In the anomaly perception feature selection module, we effectively reduce redundant information by refining the feature representation within the layer, which mitigates bias introduced by the pre-trained model. Additionally, the feature reconstruction module, ARD, is used to obtain the anomaly score for detecting abnormal areas. We validated our approach on three datasets, and the results demonstrate that our model outperforms the previously best-performing method.

Our contributions are summarized as follows:

• We propose a curvature-sensing network, HADNet, which uses AnomalySelect adaptive screening for highly discriminative features to efficiently integrate multi-scale pre-trained features for anomaly detection.

• We introduce hyperbolic Space Transformation, a method that utilizes hyperbolic geometry to exploit latent hierarchical information, achieving results that are not attainable in Euclidean space.

• We conduct extensive experiments on three real datasets, demonstrating the effectiveness and superiority of HADNet for anomaly detection in metal surface.

Related work

Industrial anomaly detection

Anomaly detection involves identifying a small number of outliers in the data that deviate from the majority. These outliers may indicate potential problems or abnormal events. This technique is widely applied across various fields, including manufacturing and aerospace, to enhance system security and reliability^9,10. Anomaly detection methods can be categorized into supervised and unsupervised^11,12,13. Supervised methods depend on labeled data for model training, unsupervised methods utilize the intrinsic structure of the data to identify anomalies.

Recent advancements in anomaly detection methods have been substantial, with traditional statistical methods being among the simplest. These methods define the distribution of normal data based on statistical characteristics such as mean and standard deviation, and identify data points that deviate from these distributions as anomalies¹⁴. For instance, the Z-score method relies on Gaussian distribution . However, statistical methods may struggle to capture the complex structure and nonlinear characteristics of high-dimensional data. To address this, non-parametric statistical methods, such as those based on kernel density estimation, have been introduced to reduce reliance on data distribution assumptions . Despite this, non-parametric methods can become unstable and computationally expensive in high-dimensional spaces.

To address these challenges, machine learning and deep learning methods have recently been integrated into the field of anomaly detection. Zhang et al. improved the capability of pulsed infrared thermography (PIT) for detecting subsurface defects as small as 101 $\upmu$m in high-strength stainless steel 316 by employing an advanced unsupervised learning-based algorithm, which enhances both defect visibility and segmentation¹⁵. Thorsten Joachims et al. employed a small amount of labeled data along with a large volume of unlabeled data for training, developing a semi-supervised method well-suited for scenarios in the aerospace field where data annotation is challenging¹⁶ . zhou et al. incorporated multi-scale feature fusion and efficient convolution operations to achieve precise detection and segmentation of targets across various scales¹⁷. Su et al. proposed a deep learning method based on complementary attention networks adaptively suppresses background noise features and highlights defect features to ensure accurate detection of small and complex defects¹⁸.

The aforementioned methods can autonomously learn and extract key features from data, thereby reducing the need for manual feature engineering. However, challenges persist when handling large-scale or high-dimensional datasets, such as resource consumption, model complexity, and the ability to effectively extract and process features in high-dimensional spaces. Tang et al .proposed a detection network that integrates Transformer and convolutional neural network (CNN) architectures¹⁹. By optimizing the network structure, this approach achieves efficient extraction and fusion of multi-scale features. Wu et al. implemented a lightweight module design to strike a balance between speed and accuracy²⁰. munkhdalai et al. introduce a new attention mechanism, Infini-attention, with transformer capable of handling infinitely long inputs with fixed memory²¹. these methods excel in Euclidean space, they face limitations when applied to image data in non-Euclidean spaces. To address this issue, we explore extending anomaly detection methods to hyperbolic space to better leverage the intrinsic geometric features of the data.

Hyperbolic embeddings

In hyperbolic space, the volume grows exponentially with increasing distance from the origin, whereas in Euclidean space, the volume increases polynomially. Consequently, as the distance from the origin increases in hyperbolic space, the volume available for accommodation expands rapidly. This characteristic allows hyperbolic space to represent larger data structures within a more compact space, making it particularly effective for processing data with inherent hierarchical structures, such as tree structures or hierarchical relationships²². For instance, in hyperbolic space, shallower tree nodes are positioned closer to the origin, while deeper nodes are situated further away, reflecting the natural hierarchical organization of the tree structure. Additionally, the geodesic distance between points in hyperbolic space mirrors the path length between nodes in a tree, enhancing the ability to model hierarchical data. Hyperbolic space embedding methods include Poincaré Embeddings and Hyperbolic Neural Networks. Poincaré Embeddings leverage the geometric properties of hyperbolic space to minimize the

distance between data points by optimizing their positions in the embedding space, thereby better capturing hierarchical structures²³. Hyperbolic neural networks integrate hyperbolic geometry with neural networks, allowing the networks to more effectively process data with hierarchical structures through training in hyperbolic space.

Previous research has demonstrated that mapping embeddings generated by deep neural networks into hyperbolic space can significantly enhance classifier performance. For instance, Kyriakis et al. proposed a method to learn hyperbolic representations of persistence diagrams, which leverages the Poincaré ball to preserve the relative importance of topological features, especially those with infinite persistence, by mapping them infinitesimally close to the boundary of the ball²⁴. Liu et al. introduced a hyperbolic visual embedding learning network designed for zero-shot recognition²⁵. This network, by learning image embeddings in hyperbolic space, not only preserves the hierarchical structure of semantic categories in a low-dimensional space but also leverages the exponential growth properties of hyperbolic space, thus improving its ability to capture subtle image differences. Similarly, Ermolov et al. integrated hyperbolic space with the visual transformer (ViT) architecture to develop an advanced target detection model²⁶. Incorporating hyperbolic embeddings into the ViT model allows it to better handle subtle differences and complex backgrounds in images, thereby enhancing detection accuracy and effectively managing hierarchical structure information, such as objects and backgrounds at various scales. Teng et al. proposed embedding the hierarchical relationships between videos and categories into a hyperbolic shared space to address the challenges of video retrieval with hierarchical structures²⁷. This approach maintains the relationships between videos and categories within hyperbolic space, ensuring that during retrieval, similar videos are prioritized, followed by those with hierarchical similarities.kim et al. introduced a self-supervised regularization technique is proposed for supervised metric learning, aimed at enhancing the supervisory signal. By leveraging hierarchical agents in hyperbolic space to capture the underlying hierarchical structure of data, the method constructs loss functions using triplets and hierarchical agents. This approach encourages the sample embeddings to form a tree-like structure, where agents represent class levels, thereby improving the performance of metric learning methods based on hyperspheres or hyperbolic space²⁸.

Methods

Overall architecture

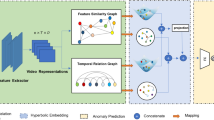
In this section, we provide a detailed introduction to our proposed anomaly detection method, HADNet. HADNet is a sophisticated detection technology that operates in hyperbolic space and is specifically designed for identifying anomalies in data. By mapping data from traditional Euclidean space to hyperbolic space, HADNet enhances the ability to capture hierarchical relationships and geometric structures within the data.

HADNet comprises three key components: hyperbolic space transformation, anomaly-aware feature subset selection, and adaptive residuals discrimination. The hyperbolic space transformation component converts the original data into hyperbolic space, enhancing the expressiveness of data features by leveraging the unique properties of hyperbolic geometry. This conversion makes features that may have been less prominent in Euclidean space more distinct in hyperbolic space. The anomaly-aware feature subset selection module identifies the most relevant features for anomaly detection from the transformed data, ensuring that the model focuses on the most discriminative features, thereby improving detection accuracy and reducing redundancy. Adaptive residuals discrimination captures subtle deviations in anomalous data and effectively filters out noise in normal data by adaptively analyzing the distribution characteristics of residuals. It also generates anomaly scores by selecting the reconstructed residuals containing the most significant abnormal information, thus enhancing the detection of anomalous regions. The overall process of HADNet is illustrated in Fig. 3.

Fig. 3

The overall architecture of HADNet. The architecture consists of three main modules: Hyperbolic Space Transformation (HST), Anomaly-aware Feature Subset Selection (AFSS), and Adaptive Residuals Discrimination (ARD). The input features are first mapped from Euclidean space to hyperbolic space using HST to enhance the representation of hierarchical relationships. The AFSS module then selects the most relevant features for anomaly detection, reducing redundancy and improving detection accuracy. Finally, the ARD module analyzes the residuals to isolate the most effective regions for anomaly detection and generates anomaly scores.

Hyperbolic space transformation

As the size and complexity of data continue to grow, traditional Euclidean space exhibits limitations in handling highly nonlinear and complex datasets, particularly when dealing with hierarchical structures and nonlinear boundaries. To address these challenges, we introduce hyperbolic Space, a geometric structure better suited for processing high-dimensional, complex data. Unlike Euclidean space, hyperbolic Space is a Riemannian manifold characterized by constant negative curvature, making it more efficient in representing hierarchical relationships. Due to its significantly greater capacity than Euclidean space, hyperbolic Space allows for more concise parameterization while maintaining equivalent expressive power.There are multiple isometric models for representing hyperbolic space. To more intuitively observe the properties of hyperbolic space, we use the Poincaré model for modeling and processing. The n-dimensional Poincaré ball, characterized by constant negative curvature k, is defined as $(H_{_k}^{_n},g_{_x}^{_k})$, with manifold $\text{H}_k^n = \{ x \in {R^n}:k\left\| x \right\| < 1\}$ and Riemannian metric is defined as (1):

$$\begin{aligned} g_{_x}^{_k} = {(\lambda _{_x}^{_k})^2}{I_{_n}} = \frac{2}{{1 - k{{\left\| x \right\| }^2}}}{I_{_n}} \end{aligned}$$

(1)

where $\lambda _{_x}^{_k}$ denotes the conformal factor. The conformal factor defines the inner product as $\langle u,v\rangle _{_x}^{_k} = {(\lambda _{_x}^{_k})^2}\langle u,v\rangle$ and the norm as $\left\| v \right\| _{_x}^{_k} = \lambda _{_x}^{_k}\left\| v \right\|$ for all $u,v \in {T_{_x}}H_{_x}^{_k}$, ${T_{_x}}$ refers to the tangent space of the manifold at the point. Several isometric models exist for hyperbolic space. Gyrovector space is an algebraic structure designed for performing vector operations in hyperbolic geometry. Specifically, gyrovector space offers a method for vector operations within this context. In the Poincaré sphere model, point addition and distance calculations can be executed using operations in gyrovector space, a process known as Möbius addition. Vector addition of two points in the Poincaré ball model can be defined as Equation (2), where denotes the inner product.

$$\begin{aligned} u{ \oplus _k}v = \frac{{(1 + 2k\langle u,v\rangle + k{{\left\| v \right\| }^2})u + (1 - k{{\left\| u \right\| }^2})v}}{{1 + 2k\langle u,v\rangle + {k^2}{{\left\| u \right\| }^2}{{\left\| v \right\| }^2}}} \end{aligned}$$

(2)

To achieve the transformation from Euclidean space to Poincaré space, we define an exponential map. This map provides a method for mapping vectors from the tangent space to the manifold. Typically, v is set to the origin. The mapping can be expressed as (3):

$$\begin{aligned} {\exp _{_x^k}}(v) = x{ \oplus _k}(\tanh (\sqrt{k} \frac{{\lambda _x^k\left\| v \right\| }}{2})\frac{v}{{\sqrt{k} \left\| v \right\| }}) \end{aligned}$$

(3)

where $\lambda _x^k = \frac{2}{{1 - k{{\left\| x \right\| }^2}}}$,x can be set to 0. Correspondingly, the inverse of this mapping is the logarithmic map, which transforms points from Poincaré space back to Euclidean space. This map can be expressed as (4):

$$\begin{aligned} {\log _{_x^k}}(u) = \frac{2}{{\sqrt{k} \lambda _x^k}}{\tanh ^{ - 1}}(\sqrt{k} \left\| { - x{ \oplus _{_k}}u} \right\| )\frac{{ - x{ \oplus _{_k}}u}}{{\left\| { - x{ \oplus _{_k}}u} \right\| }} \end{aligned}$$

(4)

As we approach the boundary of the Poincaré ball, the hyperbolic distance increases at a much faster rate than the Euclidean distance. This phenomenon can be further elucidated by a specific mathematical formula.the distance between $a,b \in H_{_n}^{_k}$ is defined as (5):

$$\begin{aligned} {d_H}(a,b) = \frac{1}{{\sqrt{k} }}{\cosh ^{ - 1}}(1 + 2\frac{{\sqrt{k} {{\left\| {a - b} \right\| }^{^2}}}}{{(1 - {{\left\| a \right\| }^{^2}})(1 - {{\left\| b \right\| }^{^2}})}}) \end{aligned}$$

(5)

When the hyperbolic distance approaches the boundary of the sphere, the denominator in the formula decreases rapidly, causing the inverse hyperbolic cosine function to increase sharply. This leads to the hyperbolic distance growing significantly faster than the Euclidean distance. In image segmentation tasks, hyperplanes are frequently used as decision boundaries. The Poincaré hyperplane represents a low-dimensional plane structure within hyperbolic geometry. In the Poincaré model, it partitions hyperbolic space according to the metric rules of hyperbolic geometry.For $p \in H_{_n}^{_k},w \in {T_{_x}}H_{_n}^{_k}\backslash \{ 0\}$, the the Poincaré hyperplane is defined as (6):

$$\begin{aligned} {E^{^c}} = \{ z \in H_{_n}^{_k}, < - p{ \oplus _{_k}}z,w > = 0\} \end{aligned}$$

(6)

Where w is normal vector Fig. 4 shows the hyperbolic distance of z to the hyperplane is given as (7):

$$\begin{aligned} {d_{_k}}(z,{H^{^c}}) = \frac{1}{k}{\sinh ^{^{ - 1}}}(\frac{{2\sqrt{k} \langle - p{ \oplus _{_k}}z,w\rangle }}{{(1 - k{{\left\| { - p{ \oplus _{_k}}z} \right\| }^{^2}})\left\| w \right\| }}) \end{aligned}$$

(7)

Fig. 4

Hyperbolic Space Transformation process. The features embedding of Euclidean space is converted to hyperbolic space by exponential mapping $EXP_{_n}^{_k}$. For Poincare’s ball, given a point z, the distance to the hyperplane ${H^{_c}}$ is expressed as ${d_{_k}}(z,{H^{_c}})$.

AnomalySelect

In this section, we provide a detailed description of the AnomalySelect module, which comprises Anomaly-aware Feature Subset Selection (AFSS) and Adaptive Residuals Discrimination (ARD). In practical applications, data often includes numerous irrelevant or redundant features. AFSS addresses this issue by selecting the most representative and discriminative features from pre-trained data, thereby reducing noise interference, dimensionality, and computational cost while enhancing detection performance. ARD focuses on identifying residual features that contain the most significant anomaly information, leading to more precise detection of anomalous regions. The integration of AFSS and ARD ensures that the model remains both efficient and sensitive while managing computational resources effectively.

In Anomaly-aware Feature Subset Selection, efficient feature selection is achieved through a detailed analysis of the extracted feature maps from each layer, with a particular focus on the differences between normal and abnormal images. Specifically, consider the j-th feature map from the i-th layer, denoted as $\phi (i,j),i,j = 1,2 \ldots n$ . By comparing the activation values of the normal image ${I_{_n}}$ and the abnormal image ${G_{_n}}$ on this feature map, the difference $\varepsilon (i,j)$ between the two can be quantified. This quantification of difference aids in identifying the most significant features in the feature space, thereby guiding subsequent feature selection and model optimization. The specific calculation process is shown in (8):

$$\begin{aligned} \varepsilon (i,j) = \phi {(i,j)_{_{{I_n}}}} - \phi {(i,j)_{_{{G_{_n}}}}} \end{aligned}$$

(8)

Next, we calculate the square of the difference, denoted as ${\varepsilon ^2}(i,j)$. This value is then normalized and aligned with the spatial resolutions of the hyperbolic distance ${d_{_k}}(z,{H^{_c}})$ to ensure comparison and analysis on a unified scale. The resulting value is the normalized difference after alignment with ${d_{_k}}(z,{H^{_c}})$,as shown in (9):

$$\begin{aligned} M = R(N({\varepsilon ^{^2}}(i,j))) \end{aligned}$$

(9)

Here,N denotes the normalization operation, and R represents the spatial resolution alignment operation. Ideally, M and ${d_{_k}}(z,{H^{_c}})$ should be very similar, meaning they should exhibit high consistency in both value and distribution. Additionally, we introduce an Anomaly-aware Feature Subset Selection loss function, denoted as ${L_{_{AFSS}}}$, to evaluate the effectiveness of each layer of the feature map. This loss function adaptively adjusts the feature selection strategy and optimizes each layer of the feature map,the process is shown in (10):

$$\begin{aligned} {L_{_{AFSS}}} = \frac{1}{N}\sum \limits _{n = 1}^N {\left\| {M - {d_{_H}}} \right\| } _2^2 \end{aligned}$$

(10)

Finally, we select r feature maps for reconstruction based on the minimum Anomaly-aware Feature Subset Selection (AFSS) loss ${L_{_{AFSS}}}$ obtained at each layer. For instance, for the t-th layer, ${r_{_t}}$ feature maps with the minimum AFSS loss ${L_{_{AFSS}}}$ are chosen for reconstruction, denoted as $\{ \phi {(t,1)_{_{{G_{_n}}}}},\phi {(t,2)_{_{{G_n}}}}, \ldots ,\phi {(t,r)_{_{{G_n}}}}\}$. Additionally, by performing feature selection at various levels, we obtain multi-scale features, denoted as$\{ \phi (1),\phi (2), \ldots ,\phi (n)\}$. We use these n multi-scale features for feature reconstruction. The subsequent calculation yields the reconstruction residual$\gamma (k)$, representing the difference between the original and reconstructed features. This process can be summarized as $\gamma (k) = \phi (k) - \Phi (k)$, where $\Phi (k)$ denotes the feature generated after reconstruction at the k-th layer. The reconstruction residual $\gamma (k)$ is then used as input for the subsequent Anomaly-aware Residual Discrimination process.

Anomaly-aware Feature Subset Selection identifies the most discriminative subset of features within each layer, whereas Adaptive Residuals Discrimination focuses on selecting the optimal layer. Features at various levels are suited for detecting anomalies of different scales and semantic meanings. For instance, low-level features are effective for detecting small-scale texture anomalies but may overlook or fail to detect large-scale functional anomalies. Conversely, high-level features are less effective for detecting fine-grained texture anomalies. ARD addresses the issue of missed anomaly detection by retaining only the partial reconstruction errors that contain the most significant abnormal information, thereby improving the accuracy of the final anomaly map.

Adaptive Residuals Discrimination enhances the recall rate of anomaly detection by selecting a subset of reconstructed residuals that contain the most significant anomaly information. Initially, we construct a global reconstruction residual to generate a comprehensive feature map. Specifically, we upsample the low-resolution reconstruction residuals to a uniform resolution and then concatenate them to form the global reconstruction residual $\Gamma$. Subsequently, Global Max Pooling (GMP) and Global Average Pooling (GAP) operations are applied to $\Gamma$, resulting in two feature maps, ${\Gamma _{_M}}$ and ${\Gamma _{_A}}$, which capture the global maximum and average values, respectively, after pooling. The specific process is shown in (11) and (12):

$$\begin{aligned} {\Gamma _{_M}}= & \max (\Gamma ) \end{aligned}$$

(11)

$$\begin{aligned} {\Gamma _{_A}}= & \frac{1}{{H \times W}}\sum \nolimits _{_{i - 1}}^{_H} {\sum \nolimits _{_{j = 1}}^{_W} \Gamma } \end{aligned}$$

(12)

Here, H and W denote the height and width of the reconstructed residual, respectively. To identify the most significant elements in the global statistical features, we select the largest s elements from ${\Gamma _{_M}}$ and ${\Gamma _{_A}}$ and determine their corresponding positions in $\Gamma$, denoted as ${\Gamma _{_{MM}(s)}}$ and ${\Gamma _{_{AM}(s)}}$, respectively. Since Global Max Pooling (GMP) is effective at capturing local anomalies, while Global Average Pooling (GAP) is better at identifying global anomalies, we combine the outputs of GMP and GAP to enhance the anomaly detection capability of Adaptive Residuals Discrimination (ARD). The process is shown in (13):

$$\begin{aligned} \Lambda = {\Gamma _{_{MM}}}\left( \frac{s}{2}\right) \oplus {\Gamma _{_{AM}}}\left( \frac{s}{2}\right) \end{aligned}$$

(13)

In this process, $\oplus$ represents the connection operation, while $\Lambda$ denotes the enhanced reconstruction residual. To ensure data consistency, we set $\frac{s}{2}$ as the value for ${\Gamma _{_{MM}(s)}}$ and ${\Gamma _{_{AM}(s)}}$. Finally, $\Lambda$ is input into the discriminator to obtain the final anomaly score.

Experiments

Datasets

The NEU-Seg dataset is a standardized, high-quality database commonly utilized for defect detection and segmentation²⁹. It includes three types of textures: inclusion, patch, and scratch. Each category contains 300 defect texture images, each with a resolution of 200 × 200 pixels. To support pixel-level surface defect detection tasks, the dataset provides pixel-level labels annotated using the open-source annotation tool LabelMe. The texture defects in the test images are complex, featuring significant intra-class variation and low contrast between defect regions and the background, making NEU-Seg a particularly challenging dataset.

The MT-Defect dataset is primarily used for research and development in defect detection technology³⁰. It encompasses five types of defects under varying lighting conditions: blowhole, crack, fray, break, and unevenness. The dataset contains 392 defect images and 952 defect-free images, with resolutions ranging from 105 × 283 to 388 × 516 pixels. The diversity of defect shapes, the complexity of textures, and the similarity of features between classes present significant challenges for detection.

The FSSD-12 dataset is a newly released, publicly available dataset for small sample segmentation of pure strip steel surface defects³¹. It includes 600 defect images across 12 categories, with 50 images per category. The Defect categories encompass abrasion mask, iron-sheet ash, liquid, oxide scale, oil-spot, water-spot, patch, punching, red-iron sheet, roll-printing, scratch, and inclusion. Each image has a resolution of 200 × 200 pixels and contains pixel-level annotations for the entire defective area.

The UCF-EL dataset is primarily used for research on defect detection in solar photovoltaic (PV) modules and encompasses nine types of faults³². It contains 17,064 electroluminescence images, of which 16,808 were captured from 368 crystalline silicon (c-Si) PV modules, with each image having a resolution of 300 × 300 pixels.

Implementation details

This study utilizes an 11th Gen Intel Core i9-11900F processor in conjunction with a single NVIDIA GeForce RTX 4090 GPU for computing. The software environment is configured with Python 3.9 and CUDA 11.2. Data preprocessing is vital for preparing datasets for training and evaluation. Images are resized to a consistent 256 × 256 pixels and normalized with RGB mean values of [0.491, 0.449, 0.410] and standard deviations of [0.231, 0.219, 0.220]. To enhance robustness, data augmentation techniques are applied, including random adjustments to brightness, contrast, and saturation using ColorJitter with a probability of 0.25. This helps simulate variations in lighting and color conditions.

Training HADNet requires careful configuration. The dataset is split into training, validation, and testing sets in an 8:1:1 ratio to facilitate hyperparameter tuning and prevent overfitting. The training process uses a batch size of 8 and an initial learning rate of 0.001, with a step decay schedule to adjust the learning rate during training. The model is trained for 150 epochs to ensure sufficient learning while maintaining generalizability. The Anomaly-aware Feature Subset Selection (AFSS) module enhances the model’s ability to focus on relevant information by guiding the selection of the most discriminative features for anomaly detection.Additionally, an Autoencoder is used to extract global reconstruction features, and teacher-student distillation is employed to enhance generalization performance.

Evaluation criterion

Evaluation criteria are crucial for a fair comparison of model performances. In this paper, we utilize Intersection over Union (IoU) for detection and segmentation, a widely used metric in anomaly detection, as defined in (14):

$$\begin{aligned} {IoU} = \frac{{A \cap B}}{{A \cup B}} \end{aligned}$$

(14)

A represents the predicted area, while B represents the true area.

In multi-category anomaly detection, average Intersection-over-Union (IoU) is preferred as the evaluation criterion due to its objectivity and comprehensiveness, as defined by the formula shown in (15):

$$\begin{aligned} {MIoU} = \frac{1}{N}\sum \limits _{n = 1}^N {Io{U_n}} \end{aligned}$$

(15)

Where ${IoU}_n$ represents the detection IoU of category n.

Compare with state-of-the-arts

Table 1 Performance comparison of our method with the state-of-the-art methods on the NEU-Seg dataset.

Table 2 Segmentation performance comparison of our method with the state-of-the-art methods on the MT-Defect dataset.

Table 3 Performance comparison on the FSSD-12 dataset.

Table 4 Performance comparison on the UCF-EL dataset.

Table 1 presents the experimental results of IoU performance for state-of-the-art methods on the NEU-Seg dataset. Our method demonstrates significant performance on the NEU-Seg dataset, achieving an average IoU of 87%. Compared to DDSNet, our method improves mIoU by 2.21%, with notable gains of 3.34% and 3.55% in IoU for the “Inclusion” and “Scratch” categories, respectively. Additionally, the hyperbolic space-embedded HADNet exhibits optimal anomaly detection and localization capa-bilities compared to Euclidean space-based counterparts. This architecture addresses fundamental representational limitations of conventional Euclidean geometry through its hierarchical feature learning mechanism, demonstrating superior performance in feature representation for industrial anomaly detection. These results also indicate that our method overcomes the limitations of Euclidean space in representing image data. Furthermore, we visualize the original images, ground truth, and predicted masks using various methods. Qualitative results of our anomaly localization method are shown in Fig. 5. Compared to other methods, our approach significantly enhances pixel-level anomaly identification and localization for inclusions, patches, and scratches.In addition, Our approach attains a more streamlined model with only 11.352 M parameters and a computational complexity of merely 1.113 G. When juxtaposed with the PoolFormer method, HADNet not only delivers superior performance but also significantly trims down the parameter count by 4.290 M and slashes the computational load by a substantial 3.761 G.

Fig. 5

Comparative detection results of HADNet on the NEU-Seg dataset.

Table 2 presents the segmentation performance of our method compared to existing approaches on the MT-Defect dataset. Utilizing WideResNet50 as the backbone, our method outperforms other state-of-the-art techniques, achieving an average IoU of 81.46%, which is 6.47% higher than the previous best method, DDSNet. Additionally, our method delivers improvements of 5.81%, 6%, and 14.53% in the detection of blowholes, breaks, and cracks, respectively, compared to other surface defect detection methods. Qualitative results of our method on the MT-Defect dataset are shown in Fig. 6, further demonstrating the advantages of the proposed approach.

Fig. 6

Comparative detection results of HADNet on the MT-Defect dataset.

For the FSSD-12 dataset, we use other methods to evaluate our method, and the comparison results are shown in Table 3. It is worth noting that our method achieves 77.04% mIoU on the FSSD-12 dataset. Compared with DDSNet, our method outperforms by 4.35% mIoU. Some qualitative detection results are shown in Fig. 7. Compared with other methods, our method has better recognition ability for inclusion, patch and scratch, and its segmentation results are closer to the ground truth.

Fig. 7

Comparative detection results of HADNet on the FSSD-12 dataset.

For the UCF-EL dataset, we evaluated our approach using UNet, Deeplab v3+, PAN, PSPNet, FPN, and SegFormer. In addition to the original metrics, we incorporated F1 score, weighted F1 score, and pixel accuracy for a more comprehensive assessment. The comparative results are presented in Table 4. It is worth noting that our method achieved an mIoU of 59.41% on the UCF-EL dataset, outperforming SegFormer by 2.88% in terms of mIoU.

Ablation studies

To assess the performance impact of AFSS and ARD on our method, we conducted a comprehensive ablation study on the NEU-Seg dataset. Instead of dimensionality reduction method AFSS, we employed Random Dimensionality Reduction (RDR) and Random Linear Projection Reduction (RLPR). RDR selects features randomly from high-dimensional data, while RLPR applies untrained linear transformation layers for projection. The HADNet results using RDR and RLPR are presented in Experiment 1 and Experiment 3 of Table 5, respectively. To generate anomaly scores, we input the global reconstruction residuals into the discriminator. The relevant results are provided in Experiment 1 and Experiment 2 of Table 5. As shown in Experiment 3 of Table 5, component ARD significantly influences model performance. When all reconstructed residuals are used to generate anomaly scores, residuals lacking anomaly information can lead to the omission of abnormal regions, thereby considerably reducing anomaly detection performance. In contrast, AFSS outperforms RDR and RLPR in anomaly detection.

Table 5 Impact of AFSS and ARD on HADNet on the NEU-Seg dataset.

Table 6 Anomaly detection performance of different curvature values $\rho$ under different datasets.

Hyperbolic space can indicate the presence of geometric features in an image but is limited in determining the exact location of defects. In this subsection, we examine the impact of the curvature value $\rho$ of hyperbolic space on anomaly detection performance. When selecting the curvature for hyperbolic embeddings, the characteristics of the data type, such as hierarchical structure, complexity, and dimensionality, are important considerations. Lower curvatures are generally preferred for capturing features with rich hierarchical relationships while maintaining embedding stability. Therefore, for metal surface defect images with complex backgrounds and multi-level features, we set a range of candidate curvature values $\rho$ (0.001, 0.005, 0.01, 0.05, 0.1, 0.3, and 0.5). As shown in Table 6, we present the mIoU scores obtained with our method across different curvature values $\rho$ for various hyperbolic spaces on the NEU-Seg, MT-Defect, FSSD-12, and UCF-EL datasets. Table 6 reveals that as the curvature $\rho$ increases, it initially improves detection performance up to a certain point, beyond which further increases in $\rho$ lead to degradation. When $\rho$ approaches zero, the curvature radius of hyperbolic space approaches infinity, making the space locally similar to Euclidean flatness. Conversely, higher values of $\rho$ increase the curvature of hyperbolic space, resulting in a steeper spatial structure. This indicates that the flatness of Euclidean space might be insufficient to capture the data’s complexity, thereby constraining its representational capacity. Empirical results demonstrate that our method performs optimally when $\rho$ = 0.01; hence, we set $\rho$ to 0.01 for the experiments.

Discussion

This work seeks to enhance the representation of anomalous features by addressing the limitations of Euclidean space in capturing complex structural information. As interest in hyperbolic space with negative curvature within non-Euclidean frameworks grows, HADNet introduces a metric representation based on hyperbolic embeddings combined with anomaly-aware selection. Compared to the state-of-the-art DDSNet, HADNet demonstrates superior performance on the MT-Defect dataset, achieving an IoU improvement exceeding 6.92% for Blowhole, Break, and Crack defects. The hyperbolic embedding-based metric representation, which involves distance measures transitioning from Euclidean to hyperbolic space, warrants further attention from researchers. By leveraging the distance metrics in hyperbolic space, we can effectively construct a hierarchical structure of defect categories and cluster unlabeled defects into hierarchical classes. This approach provides potential applications for unsupervised classification and analysis of defects.

Despite the promising results of HADNet, certain limitations remain. Specifically, the method struggles with scenarios where defects significantly overlap with the background or are obscured by noise and artifacts, leading to inaccuracies in defect boundary detection. Addressing these challenges necessitates exploring models that can handle hierarchical or scale-free data distributions. Furthermore, the current architecture of HADNet primarily focuses on enhancing anomaly detection performance. Although explicit hierarchical classification has not yet been implemented, the inherent hierarchical embedding properties of hyperbolic space have already laid the groundwork for more refined classification in the existing design, offering the potential for further expansion into hierarchical classification. Future work could build on this foundation by introducing a hierarchical feature analysis module, leveraging the advantages of hyperbolic space in representing tree-like structures, or exploring graph clustering-based methods to identify subcategories within specific defect categories, thereby achieving more precise defect classification and analysis. Additionally, a more accurate estimation of hyperbolic parameters is crucial for adapting to complex scenarios, as these parameters can be sensitive to initial conditions and data noise. Future research should focus on developing robust parameter estimation techniques and integrating adaptive methods tailored to diverse data characteristics.

Conclusions

This paper introduces HADNet, a novel anomaly detection method for metal surface inspection based on hyperbolic space. By overcoming the limitations inherent in Euclidean space, HADNet effectively captures complex anomaly patterns. The primary advantage of HADNet lies in its use of the non-Euclidean geometric properties of hyperbolic space, which enhances anomaly detection accuracy. Additionally, HADNet integrates the Anomaly-aware Feature Subset Selection module with the Adaptive Residuals Discrimination module to further refine detection performance. The AFSS module selects the most relevant features from a large set, optimizing the detection process, while the ARD module adaptively analyzes residuals to improve detection accuracy. Extensive experiments conducted on surface defect datasets, including NEU-Seg, MT-Defect, FSSD-12, and UCF-EL demonstrate that HADNet significantly outperforms existing state-of-the-art methods.