An intelligent algorithm for optimizing player positioning using circular intuitionistic fuzzy COCOSO with Einstein aggregation

Abstract

In the highly competitive world of modern football, each millisecond and centimeter can influence match outcomes. A team’s overall performance often hinges on the positioning and movement of even a single player. Thus, the positioning of each player according to his skill set is crucial to enhance overall performance. This study develops a mathematical model that optimizes player positioning for a football team, considering key attributes such as technical awareness and decision-making, stamina and endurance, ball control and passing (technical ability), coordination, and communication. The combined composite solution (COCOSO) and circular intuitionistic fuzzy set (CrIFS) consider the factors affecting the player’s performance. Furthermore, a data aggregation model based on the weighted averaging mean and weighted geometric mean is developed using the Einstein t-norm (ETN) and the Einstein t-conorm (ETCN). The developed model aggregates the data collected, integrating the COCOSO method. The resulting aggregation operators (AOs) are examined for their fundamental properties and then used in conjunction with COCOSO to identify the most suitable player positions, balancing individual strengths and weaknesses. A comparative analysis confirms that the proposed AOs offer noticeable advantages over existing aggregation techniques, underscoring the practical significance of the model.

Introduction

The highly competitive world of professional sports leads to changes in results, even in milliseconds and centimeters. A victory can be turned into defeat even at the last moment of the game due to the slightest negligence of a single player. Consequently, the overall team may face the consequences. Thus, the positioning of the players in every game is a significant matter. Each player has a different skill set and approach to face the challenges. Therefore, a single player may not be suitable for a position where they play. This problem leads to a keen observation based on several factors. However, observing the factors that affect a player’s performance is very difficult and uncertain.

Zadeh¹ introduced the concept of a fuzzy set (FS) to cope with such uncertainties and ambiguities. The idea of the FS was based on the membership function, which assigned a membership grade (MG) to an object, indicating its belongingness to a particular scenario. Several terms became meaningful in their descriptions using the idea of the FS, e.g., beauty, intelligence, etc. However, using the concept of the FS, one can only assign MG to an object to show a single aspect. Atanassov² proposed the idea of intuitionistic fuzzy sets (IFS), one of the most widely used extensions in fuzzy set theory.

In contrast to traditional FS theory, non-membership and uncertainty degrees are explained in addition to membership degrees. IFS can benefit from the capabilities of several technologies to indicate uncertainty and confusion by integrating them to aid in solving issues and decision-making processes. To expand the scope of the IFS, Atanassov³ presented CrIFS in 2020. In short, a CrIFS represents a circle that centers the IFS MG and non-MG (NMG) and has a radius $\hat{r}$. Several researchers have applied the FS theory and its extensions in various fields. For example, Sun et al.⁴ investigated the control of time in Markov jump systems using the idea of FS. Xia et al.⁵ investigated the application of FS in stabilizing chaotic nonlinear systems. Zhang et al.⁶ utilized FS to observe the control of stochastic switching systems. Gao et al.⁷ used FS to study the time delay in the jump system. Ge and Zhang⁸ studied adaptive inventory control in neural networks. Sarwar and Li⁹ employed FS to define a fuzzy metric space.

Practical and methodological aims

The purpose of this research is to assist football coaches in selecting the best player to fill a defensive-modifier position, even when the assessment is unclear or confusing. As a result, mathematically consistent evaluations based on expert opinions are created and can be verified. The study introduces the combination of CrIFEWA, CrIFWG, and the COCOSO algorithm. As a result, both uncertainty (using Einstein operators) and criterion interaction (using COCOSO) can be managed simultaneously in multi-attribute decision making (MADM), which is particularly suitable for cases where things are not well-defined and decision-makers must compromise on different aspects. The procedure developed for describing player-position selection can also be used to rank items in any subject that uses CrIFS.

Motivation and research gap of the study

Positioning players wisely is key in sports because even minor changes in a player’s actions can affect the whole team’s performance. Computerized systems for players’ tracking and movement have been widely studied using devices such as GPS and local positioning systems^{10,11,12,13,14,15,16,17,18,19,20,21,22,23}. Still, not many studies have considered how to improve team strategy using the results of such analyses. Additionally, research frequently does not consider the uncertain and unclear factors in player performance, especially when using several criteria to rate players and build up teams. The usual techniques are missing the strong mathematical support needed to address unclear and complicated data that appear in sports.

To overcome these problems, this study recommends a new decision-making approach using CrIF operators, which can address the uncertainty and recurring nature of player stats. It improves the stability and accuracy of how players are ranked, which also helps teams make better choices and use better tactics during games. Because the suggested method unites analysis of player motion with MCDM under uncertainty, it significantly advances sports analytics and gives teams a thorough and well-organized method.

Contributions of the study

According to earlier research, numerous AOs utilize the FS framework, which mathematicians developed. However, many fuzzy structures are unable to aggregate complete information. For this reason, this study introduced new AOs from scratch for the first time based on CrIFS as follows:

• 1. Several factors can help assess the most suitable player for a particular position in the football team. When analyzing specific players. The aggregation of the information received is crucial. Thus, the AOs are developed based on CrIFS using ETN and ETCN operations.

• 2. The circular intuitionistic fuzzy Einstein weighted averaging (CrIFEWA) and circular intuitionistic fuzzy Einstein weighted geometric (CrIFEWG) operators are constructed using ETN and ETCN, which provide enhanced flexibility in modeling uncertainty. The inclusion of parameters within ETN and ETCN enables these operators to adapt dynamically to varying degrees of uncertainty, allowing the decision-maker to analyze how changes in parameter values affect the aggregation outcomes under different scenarios.

• 3. Develop the MADM algorithm for proposed AOs and the COCOSO method using CrIFS-based information.

• 4. To investigate the applicability of the proposed AOs, compare the proposed theory with other AOs. For a more precise understanding, a graphical representation is also provided.

Organization of the paper

The structure of this article is as follows. Section “Literature review” discusses the literature review related to this study. Section “Fundamentals of study” provides an overview of the research background and score function. Section “New operational laws” describes the circular intuitionistic fuzzy Einstein and a few Einstein operations of CrIFS. The new AOs are developed using ETN and ETCN, as outlined in Sect. “New aggregation model”. In Sect. “Information aggregation in MADM”, the method of information aggregation is applied in MADM problems using developed AOs. Section “Analysis of player positioning using new aggregation operator” discusses the analysis of player positioning using new AOs. In Sect. “Comparative analysis”, the results are compared with the existing aggregation models. Section “Information aggregation in the COCOSO method” deals with the aggregation of fuzzy information using the COCOSO method. Section “Conclusion” concludes the study.

Literature review

This section reviews earlier studies on AOs within decision-making sciences, Einstein aggregation, and COCOSO-based MADM models, ultimately pinpointing the unresolved gap that this study aims to address.

Role of player position in MCDM

In modern sports, every millisecond and centimetre count changes as a result. Sometimes, the overall performance of the whole team is affected by the movement of only a single player. Therefore, positioning players according to their strengths and weaknesses is crucial and the most significant issue in optimizing the team’s overall performance. Gonçalves et al.¹⁰ investigated the impact of player movement in football. Leser et al.¹¹ discussed a local positioning system for tracking movements and their effects on players’ game performances. Blauberger et al.¹² investigated the effects of movement on ball tracking using a local positioning system. Wehbe et al.¹³ utilized GPS technology to analyze the movement of players in the Australian National Soccer League. Edgecomb and Norton¹⁴ compared worldwide positioning and computer-based tracking systems to measure the movement of the players and their distance in an Australian football team. Carvalho et al.¹⁵ investigated the effects of the relative positioning of players in a football team. Dick and Brefeld¹⁶ investigated the significance of player positioning in soccer. Kannekens et al.¹⁷ investigated the importance of critical factors in decision-making based on the positions of soccer players. MacLeod et al.¹⁸ studied the validity of the global positioning system for the movement of soccer players. Morgans et al.¹⁹ investigated the impact of players’ positions on their performances. Sarlis and Tjortjis²⁰ investigated the effects of positioning, age, and injuries on players’ game performances. Zapardiel et al.²¹ analyzed the profiles based on the players’ positioning in the women’s basketball team. Hodder et al.²² investigate the factors influencing the positioning of players in netball and their impact on performance. Ribeiro et al.²³ investigated the effect of player rotation in basketball on enhancing player performance.

Multi-attribute decision making

The concept of MADM is valuable in decision-making sciences, where a decision-maker seeks to identify the most optimal option among several alternatives, considering multiple attributes. The idea of CrIFS finds numerous applications in MADM techniques, Çakır et al.^24,25,26 researched medical waste landfill site selection, healthcare tourism, supplier selection²⁷, new vehicle purchasing²⁸, and the assessment of companies as a form of industrial cooperation. They also suggested a novel CrIFS MADM approach. The literature has recently begun combining CrIFS with pre-existing MADM models. Irem and Kahraman²⁹ combined CrIFS with the AHP and VIKOR approaches to solve the vendor selection issue. Thus, using the CrIFS can help cope with uncertain situations by considering several factors in analyzing player positioning for improved performance.

Role of AOs in decision-making sciences

The information obtained from different fuzzy frameworks has various shapes. It typically involves human perceptions of objects in the universe. Hence, the aggregation of such type of information is very crucial. Familiar operators cannot deal with such information. Consequently, several AOs have been developed to address information with various characteristics and applications. Some novel AOs are based on the CrIFS for data aggregation, as presented by Chen³⁰, and the parametric CrIFS-based AOs for complex decision-making problems proposed by Bozyiğit and Ünver³¹. The compromised CrIFS-based AOs for fuzzy decision support system discussed by Wang and Chen³², and some new AOs using CrIFS information biomass resources challenges discussed by Alinejad et al.³³. Einstein operational-based AOs using Fermatean IFS information discussed by Aruchsamy et al.³⁴ and the CrIFS-based AOs to evaluate industrial problems using MADM techniques.

Abbas et al.³⁵ developed the AOs by prioritizing the objects according to their weights. Ahmed et al.³⁶ developed AOs for the framework of the complex IFS and used them for group decision-making (GDM). Ahn et al.³⁷ developed AOs to aggregate information in medical diagnosis for the interval-valued IFS. Al-Kenani et al.³⁸ developed AOs for aggregating the information obtained from real-life scenarios in the form of the IFS by considering the weights of the attributes on a priority basis. Alcantud³⁹ developed AOs for the ranking of the objects based on various attributes and experts. Alcantud et al.⁴⁰ developed the AOs for the aggregation of a finite chain of the IFS and discussed the application in decision-making problems. Ali⁴¹ developed AOs for the GDM for the framework of IFS. Albaity et al.⁴² studied the impact of machine learning in artificial intelligence by developing AOs for aggregating information obtained from complex systems. Ali et al.⁴³ introduced the AOs based on the concept of data power aggregation. Akram et al.⁴⁴ developed a new decision-making technique to solve complex problems using Hamacher operational laws. Abdullah and Awang⁴⁵ developed an algorithm to determine the weights of unknown attributes for complex decision-making problems. Ahmad et al.⁴⁶ involved Aczel-Alsina operational laws to introduce robust decision-making techniques for GDM. Abdullah et al.⁴⁷ integrated Choquet integral to develop AOs for the aggregation of information in a more nuanced way. Some AOs for various applications can be found in^48,49,50. Hussain and Pamucar⁴⁹ studied the use of the MADM model in risk management. Hussain et al.⁵¹ studied the MADM model using the Maclaurin symmetric mean operator.

Significance of Einstein operations

In fuzzy set theory, Einstein’s t-norm and t-conorm are essential because they offer different operators for representing conjunction (AND) and disjunction (OR) in fuzzy logic systems. When combining fuzzy sets, the Einstein procedures maintain essential characteristics, including associativity, commutativity, and monotonicity, in a mathematically logical manner. Whereas the t-conorm treats disjunction in a complementary manner, the Einstein t-norm is especially helpful in situations that require a softer, nonlinear aggregation of fuzzy memberships. Due to their adaptability, they are helpful in various applications, including control systems and decision-making processes.

The dual operation laws named ETN and ETCN were introduced by Xu⁵² to deal with the information in the form of the ${\left[0, 1\right]}^{2}$. There are several applications of the ETN and ETCN due to their desirable behavior in information fusion. Abosuliman et al.⁵³ introduced the AOs to solve GDM problems using ETN and ETCN for IFS. Ajay et al.⁵⁴ introduced the exponential AOs using ETN and ETCN for various applications. Akram et al.⁵⁵ developed a hybrid technique to solve MADM problems using ETN and ETCN. Ali et al.⁵⁶ developed AOs based on geometric mean, integrating the ETN and ETCN. Ali Khan et al.⁵⁷ utilized ETN and ETCN to introduce a new class of AOs, aiming to enhance accuracy in GDM problem-solving. Arora⁵⁸ developed the AOs by integrating the ideas of soft sets and IFS using the ETN and ETCN. Attaullah et al.⁵⁹ developed an algorithm utilizing ETN and ETCN for wind power management applications. Biswas et al.⁶⁰ investigated the application of ETN and ETCN to develop a novel approach for solving the MADM problem.

COCOSO method

Alternatives are ranked according to many criteria using the creative MADM method known as the COCOSO method. The COCOSO method combines components of weighted sum models and compromise programming to provide a more thorough assessment of options based on several criteria. By assigning criterion weights, the COCOSO approach evaluates how well each option performs in relation to these weights. The method calculates three aggregated compromise solutions: the combined compromise solution, the weighted normalized value product, and the weighted normalized value sum. These calculations are combined by COCOSO to represent the trade-offs between many criteria, resulting in a robust and equitable ranking of solutions. Using a compromised solution called COCOSO, Yazdani et al.⁶¹ presented an intriguing model for the MADM. Due to its later popularity among researchers, the COCOSO technique has undergone several adaptations and applications. The COCOSO model was proposed by Deveci et al.⁶² and used in MADM for QROFS. Haseli et al.⁴⁴ developed COCOSO for Z-numbers, which was subsequently applied in MADM. Narang et al.⁴⁵ employed the COCOSO approach for stock portfolio selection. Using the COCOSO model, Peng and Luo⁶³ assessed the Chinese stock market. Tešić et al.⁴⁷ employ the COCOSO approach to select the optimal boats. The COCOSO approach for TSFS was enhanced and used in MADM by Wang et al.⁶⁴. COCOSO was utilized by Wang and colleagues⁶⁵ to choose trash recycling pathways. The stock markets in Tehran were ranked by RouhaniRad et al.⁶⁶ using the COCOSO algorithm. Yu et al.⁶⁷ assessed the hazards associated with compressed natural gas storage using the COCOSO technique. Wen and Pan⁵¹ employed the COCOSO model to determine the quality of instruction in institutions. The COCOSO model was utilized by Oliveira et al.⁶⁸ to select the aircraft, and the DEA-FUCOM-COCOSO model was used for selecting efficient suppliers⁶⁹. Additional COCOSO uses are shown in^70,71.

Fundamentals of study

This section discusses the fundamental concepts related to this study.

Definition 1.¹

Let $K$ be a universal set. To define a FS $H$ on $K$ as:

$$H=\left\{\left(\mathcal{x},{\uppi }_{H}\left(\mathcal{x}\right)\right) | \mathcal{x}\in K\right\}$$

(1)

where ${\uppi }_{H}\left(\mathcal{x}\right)$ be the MG of $\mathcal{x}$ on $K$ for each $\mathcal{x}\in K$, and ${\uppi }_{H}\left(\mathcal{x}\right)\in \left[0, 1\right]$.

Definition 2.²

Let $K$ be a universal set. To define an IFS $\theta$ on $K$ as:

$$\theta =\left\{\left(\mathcal{x},{\uppi }_{\theta }\left(\mathcal{x}\right), {n}_{\theta }\left(\mathcal{x}\right)\right)| \mathcal{x}\in K\right\}$$

where ${\uppi }_{H}\left(\mathcal{x}\right)$ be the MG and ${n}_{\theta }\left(\mathcal{x}\right)$ be the NMG of $\mathcal{x}$ on $K$ for each $\mathcal{x}\in K$, and ${\uppi }_{\theta }\left(\mathcal{x}\right)\in \left[0, 1\right]$, ${n}_{\theta }\left(\mathcal{x}\right)\in \left[0, 1\right]$ and $0\le {\uppi }_{\theta }\left(\mathcal{x}\right)+ {n}_{\theta }\left(\mathcal{x}\right)\le 1$. The hesitancy degree is listed as below:

$${\upgamma }_{\theta }\left(\mathcal{x}\right)=1-\left({\uppi }_{\theta }\left(\mathcal{x}\right)+{n}_{\theta }\left(\mathcal{x}\right)\right)$$

(2)

For each $\mathcal{x}$ in $K$, it is clear that $0\le\upgamma \left(\mathcal{x}\right)<1$.

Definition 3.³

Let $K$ be a universal set. To define a CrIFS $P$ on $K$ as:

$$P=\left\{\left(\mathcal{x},{\uppi }_{\theta }\left(\mathcal{x}\right), {n}_{\theta }\left(\mathcal{x}\right), r\left(\mathcal{x}\right)\right)| \mathcal{x}\in K\right\}$$

(3)

where $0\le {\uppi }_{\theta }\left(\mathcal{x}\right)+{n}_{\theta }\left(\mathcal{x}\right)\le 1$ and ${\uppi }_{\theta }\left(\mathcal{x}\right)\in \left[0, 1\right]$ be the MG, ${n}_{\theta }\left(\mathcal{x}\right)\in \left[0, 1\right]$ be the NMG and $r\left(\mathcal{x}\right)$ be the radius of the circle and $r\left(\mathcal{x}\right)\in \left[0, \sqrt{2}\right]$. The hesitancy degree is listed as below:

$${\upgamma }_{P}\left(\mathcal{x}\right)=1-\left({\uppi }_{\theta }\left(\mathcal{x}\right)+{n}_{\theta }\left(\mathcal{x}\right)\right)$$

(4)

For convenience, the triplet $\left({\uppi }_{\theta },{n}_{\theta },{r}_{\theta }\right)$ is called circular intuitionistic fuzzy values (CrIFVs).

Definition 4.⁵²

Assume ${P}_{\text{i}}=\left({\uppi }_{\text{i}}, {n}_{\text{i}},{r}_{\text{i}}\right),\text{ i}=1, 2, 3, \dots ,\text{ m}$ be the group of CrIFVs. So, score function $\left({}_{P}\right)$ and accuracy function $\left({\upphi }_{P}\right)$ are listed below:

$$\left({S}_{P}\right)=\frac{\left({\uppi }_{\text{i}}-{n}_{\text{i}}+\sqrt{2}{r}_{\text{i}}\left(2\partial -1\right)\right)}{3}:\left({S}_{P}\right)\in \left[-1, 1\right], \partial \in \left[0, 1\right]$$

(5)

$$\left({\upphi }_{P}\right)=\frac{\left({\uppi }_{\text{i}}+{n}_{\text{i}}+\sqrt{2}{r}_{\text{i}}\left(2\partial -1\right)\right)}{3} :\left({\upphi }_{P}\right)\in \left[0, 1\right],\partial \in \left[0, 1\right]$$

(6)

Here the $\partial$ value is $\partial =0.6$.

New operational laws

The CrIFS is better able to gather information from random situations due to its looped structure. When discussing the effects of player movements in specific styles, the data used is usually not very accurate. The CrIFS is required to collect real-time information about factors affecting a player’s location on the playing field. The ETN and ETCN are used to combine these assessments, as they offer solutions that avoid the frequent excessive or unfair treatment caused by the use of algebraic products. This section introduces some new operational rules for the CrIFS based on ETN and ETCN.

Consider ${P}_{1}$ and ${P}_{2}$ be two circular intuitionistic fuzzy values (CrIFVs), the fusion of two CrIFVs with different TNs and TCNs is given below.

$${P}_{1}\vee {P}_{2}=\left\{W\left({\uppi }_{1}, {\uppi }_{2}\right), X\left({n}_{1}, {n}_{2}\right), W\left({r}_{1}, {r}_{2}\right)\right\}$$

$${P}_{1}\wedge {P}_{2}=\left\{X\left({\uppi }_{1}, {\uppi }_{2}\right), W\left({n}_{1}, {n}_{2}\right), X\left({r}_{1}, {r}_{2}\right)\right\}$$

Additionally, it could state:

$${P}_{1}\vee {P}_{2}=\left\{max\left({\uppi }_{1}, {\uppi }_{2}\right), min\left({n}_{1}, {n}_{2}\right), max\left({r}_{1}, {r}_{2}\right)\right\}$$

$${P}_{1}\wedge {P}_{2}=\left\{min\left({\uppi }_{1}, {\uppi }_{2}\right), max\left({n}_{1}, {n}_{2}\right), min\left({r}_{1}, {r}_{2}\right)\right\}$$

The TN and TCN are represented by $W$ and $X$ in the above equations. As is well known, the terms TN and TCN are broad terms that encompass all operator types and satisfy the requirements for conjunction and disjunction operators, accordingly. In Table 1, list a few varieties of TNs and TCNs.

Table 1 Types of TNs and TCNs.

Still, the algebraic norm is used to generate algebraic sum and product. Algebraic operators can perform union and intersection operations in addition to being norm operators. Numerous families of norm operators are available that can be utilized for comparable intersection and union operations. The ETN and ETCN are members of the practical norm operator class. The algebraic sum and the product can be replaced with the Einstein product and the sum to provide the exact perfect approach. For a circular intuitionistic fuzzy structure, ETN and ETCN are listed below:

$$E\left(\eta , V\right)=\frac{\eta .V}{1+\left(1-\eta \right)\left(1-V\right)}$$

$$\quad \Gamma\kern-8pt\reflectbox{\rm c} \left(\eta , V\right)=\frac{\eta +V}{1-\eta .V}$$

where $E\left(\eta , V\right)$ be the ETN and $\quad \Gamma\kern-8pt\reflectbox{\rm c} \left(\eta , V\right)$ be the ETCN. ETN fulfills the following conditions:

The mapping $U :M\times M \to M$ for the unity interval $M=\left[0, 1\right]$ is referred to as TCN if:

• (a) $U\left(\eta , 0\right)=\eta$

• (b) $U$ is monotonic, associative, and commutative.

The mapping $U :M\times M \to M$ for the unity interval $M=\left[0, 1\right]$ is referred to as TN iff:

• (c) $U\left(\eta , 1\right)=\eta$

• (d) $U$ is monotonic, associative, and commutative.

Definition 5.

Suppose ${P}_{i}=\left({\pi }_{i}, {n}_{i},{r}_{i}\right)$, ${P}_{1}=\left({\pi }_{1}, {n}_{1},{r}_{1}\right)$ and ${P}_{2}=\left({\pi }_{2}, {n}_{2},{r}_{2}\right)$ be the set of CrIFS. So, some Einstein operation rules for CrIFS are listed below:

• 1. ${P}_{1}\oplus {P}_{2}=\left(\frac{{\uppi }_{1}+{\uppi }_{2}}{1-{\uppi }_{1}{\uppi }_{2}}, \frac{{n}_{1}.{n}_{2} }{1+\left(1-{n}_{1}\right)\left(1-{n}_{2}\right)}, \frac{{r}_{1}+{r}_{2}}{1-{r}_{1}{r}_{2}}\right)$

• 2. ${P}_{1}\otimes {P}_{2}=\left(\frac{{\uppi }_{1}.{\uppi }_{2} }{1+\left(1-{\uppi }_{1}\right)\left(1-{\uppi }_{2}\right)}, \frac{{n}_{1}+{n}_{2} }{1-{n}_{1}.{n}_{2} }, \frac{{r}_{1}.{r}_{2} }{1+\left(1-{r}_{1}\right)\left(1-{r}_{2}\right)}\right)$

• 3. $p.{P}_{i}=\left(\frac{{\left(1+{\uppi }_{i}\right)}^{p}-{\left(1-{\uppi }_{i}\right)}^{p}}{{\left(1+{\uppi }_{i}\right)}^{p}+{\left(1-{\uppi }_{i}\right)}^{p}}, \frac{2.{n}_{i}^{p}}{{\left(2-{n}_{i}\right)}^{p}+{n}_{i}^{p}}, \frac{{\left(1+{r}_{i}\right)}^{p}-{\left(1-{r}_{i}\right)}^{p}}{{\left(1+{r}_{i}\right)}^{p}+{\left(1-{r}_{i}\right)}^{p}}\right)$, $p>0$;

• 4. ${P}_{i}^{p}=\left(\frac{2.{\uppi }_{i}^{p}}{{\left(2-{\uppi }_{i}\right)}^{p}+{}_{i}^{p}}, \frac{{\left(1+{n}_{i}\right)}^{p}-{\left(1-{n}_{i}\right)}^{p}}{{\left(1+{n}_{i}\right)}^{p}+{\left(1-{n}_{i}\right)}^{p}}, \frac{2.{r}_{i}^{p}}{{\left(2-{r}_{i}\right)}^{p}+{r}_{i}^{p}}\right)$, $p>0$

Theorem 1.

Assume ${P}_{i}=\left({\uppi }_{I}, {n}_{I},{r}_{I}\right)$, ${P}_{1}=\left({\uppi }_{1}, {n}_{1},{r}_{1}\right)$ and ${P}_{2}=\left({\uppi }_{2}, {n}_{2},{r}_{2}\right)$ be the set of CrIFS and $p, {p}_{1}, {p}_{2}>0$. It gets;

• 1. ${P}_{1}\oplus {P}_{2}={P}_{2}\oplus {P}_{1}$

• 2. $p\left({P}_{1}\oplus {P}_{2}\right)={pP}_{2}\oplus {pP}_{1}$

• 3. ${p}_{1}{P}_{i}\oplus {p}_{2}{P}_{i}=\left({p}_{1}+{p}_{2}\right){P}_{i}$

• 4. $\left({p}_{1}.{p}_{2}\right){P}_{i}={p}_{1}\left({p}_{2}{P}_{i}\right)$

New aggregation model

Suppose ${P}_{\text{i}}=\left({\uppi }_{\text{i}}, {n}_{\text{i}},{r}_{\text{i}}\right)$ be the set of CrIFS. So, the Circular intuitionistic fuzzy Einstein averaging aggregation operator is indicated by (CrIFEWA) and described below;

$$\text{CrIFEWA}\left({P}_{1}, {P}_{2},\dots ,{P}_{\text{i}}\right)=\sum_{i=1}^{z}{m}_{i}{P}_{\text{i}}$$

(7)

where ${m}_{i}$ be the weight vector (WV), and ${0<m}_{i}<1$, $\sum_{i=1}^{z}{m}_{i}=1$.

Theorem 2.

Suppose ${P}_{i}=\left({\uppi }_{i}, {n}_{i},{r}_{i}\right)$ be the set of CrIFS and weight vector of ${P}_{i}$ be ${m}_{i}={\left({m}_{1}, {m}_{2},\dots ,{m}_{i}\right)}^{t}$ with ${0<m}_{i}<1$, $\sum_{i=1}^{z}{m}_{i}=1$. The operation of CrIFEWA is listed below:

$$CrIFEWA\left({P}_{1}, {P}_{2},\dots ,{P}_{i}\right)=\sum_{i=1}^{z}{m}_{i}{P}_{i}$$

(8)

$$CrIFEWA\left({P}_{1}, {P}_{2},\dots ,{P}_{i}\right)=\left(\begin{array}{c}\frac{\prod_{i=1}^{z}{\left(1+{\uppi }_{i}\right)}^{m}-\prod_{i=1}^{z}{\left(1-{\uppi }_{i}\right)}^{m}}{\prod_{i=1}^{z}{\left(1+{\uppi }_{i}\right)}^{m}+\prod_{i=1}^{z}{\left(1-{\uppi }_{i}\right)}^{m}},\\ \frac{2.\prod_{i=1}^{z}{n}_{i}^{m}}{\prod_{i=1}^{z}{\left(2-{n}_{i}\right)}^{m}+\prod_{i=1}^{z}{n}_{i}^{m}},\\ \frac{\prod_{i=1}^{z}{\left(1+{r}_{i}\right)}^{m}-\prod_{i=1}^{z}{\left(1-{r}_{i}\right)}^{m}}{\prod_{i=1}^{z}{\left(1+{r}_{i}\right)}^{m}+\prod_{i=1}^{z}{\left(1-{r}_{i}\right)}^{m}}\end{array}\right)$$

Proof:

This theorem is proved in Appendix A.

With definitions, the following characteristics of the CrIFEWA operator can be proved.

Theorem 3.

• (1) Idempotency: Consider ${P}_{i}=\left({\uppi }_{i}, {n}_{i},{r}_{i}\right)$ $\left(i=1, 2,\dots ,z\right)$ be the set of CrIFS. If ${P}_{1}={P}_{2}=\dots ={P}_{i}=P$. So,

  $$CrIFEWA\left({P}_{1}, {P}_{2},\dots ,{P}_{i}\right)=P$$

  (9)

• (2) Boundedness: Consider ${P}_{i}=\left({\uppi }_{i}, {n}_{i},{r}_{i}\right)$ $\left(i=1, 2,\dots ,z\right)$ be the set of CrIFS. So, ${\left({P}_{i}\right)}^{+}=\left(\mathit{max}{\uppi }_{i},\mathit{min}{n}_{i},\mathit{max}{r}_{i}\right)$ and ${\left({P}_{i}\right)}^{-}=\left(\mathit{min}{\uppi }_{i},\mathit{max}{n}_{i},\mathit{min}{r}_{i}\right)$.

  $${\left({P}_{i}\right)}^{-}\le CrIFEWA\left({P}_{1}, {P}_{2},\dots ,{P}_{i}\right)\le {\left({P}_{i}\right)}^{+}$$

  (10)

• (3) Monotonicity: Consider ${P}_{i}=\left({\uppi }_{i}, {n}_{i},{r}_{i}\right)$ and ${P}_{i}^{a}=\left({\uppi }_{i}^{a}, {n}_{i}^{a},{r}_{i}^{a}\right)$ be the group of CrIFS for all $i$. So,

  $$CrIFEWA\left({P}_{1}, {P}_{2},\dots ,{P}_{i}\right)\le CrIFEWA\left({P}_{1}^{a}, {P}_{2}^{a},\dots ,{P}_{i}^{a}\right)$$

  (11)

Circular intuitionistic fuzzy Einstein geometric aggregation operator

Suppose ${P}_{\text{i}}=\left({\uppi }_{\text{i}}, {n}_{\text{i}},{r}_{\text{i}}\right)$ be the set of CrIFS. So, the Circular intuitionistic fuzzy Einstein geometric aggregation operator is indicated by CrIFEWG and described below;

$$\text{CrIFEWG}\left({P}_{1}, {P}_{2},\dots ,{P}_{\text{i}}\right)=\prod_{i=1}^{z}{P}_{\text{i}}^{{m}_{i}}$$

(12)

where ${m}_{i}$ be the weight vector (WV), and ${0<m}_{i}<1$, $\sum_{i=1}^{z}{m}_{i}=1$.

Theorem 4.

Suppose ${P}_{i}=\left({\uppi }_{i}, {n}_{i},{r}_{i}\right)$ be the set of CrIFS and weight vector of ${P}_{i}$ be ${m}_{i}={\left({m}_{1}, {m}_{2},\dots ,{m}_{i}\right)}^{t}$ with ${0<m}_{i}<1$, $\sum_{i=1}^{z}{m}_{i}=1$. The operation of CrIFEWG is listed below:

$$CrIFEWG\left({P}_{1}, {P}_{2},\dots ,{P}_{i}\right)=\prod_{i=1}^{z}{P}_{i}^{{m}_{i}}$$

(13)

$$CrIFEWG\left({P}_{1}, {P}_{2},\dots ,{P}_{i}\right)=\left(\begin{array}{c}\frac{2.\prod_{i=1}^{z}{\uppi }_{i}^{m}}{\prod_{i=1}^{z}{\left(2-{\uppi }_{i}\right)}^{m}+\prod_{i=1}^{z}{\uppi }_{i}^{m}},\\ \frac{\prod_{i=1}^{z}{\left(1+{n}_{i}\right)}^{m}-\prod_{i=1}^{z}{\left(1-{n}_{i}\right)}^{m}}{\prod_{i=1}^{z}{\left(1+{n}_{i}\right)}^{m}+\prod_{i=1}^{z}{\left(1-{n}_{i}\right)}^{m}},\\ \frac{2.\prod_{i=1}^{z}{r}_{i}^{m}}{\prod_{i=1}^{z}{\left(2-{r}_{i}\right)}^{m}+\prod_{i=1}^{z}{r}_{i}^{m}}\end{array}\right)$$

Proof:

To prove this theorem using all steps of Theorem 2.

The CrIFEWG operators also fulfill the basic conditions of AOs, such as idempotency, monotonicity, and boundedness.

Information aggregation in MADM

This study presents a new MADM problem of player selection, based on the analysis and description provided above. Assume that the set of players is ${q}_{i}=\left({q}_{1}, {q}_{2},\dots ,{q}_{n}\right)$, where ${q}_{i}$ Represents the alternative that needs to be evaluated. Let ${Q}_{i}=\left({Q}_{1}, {Q}_{2},\dots ,{Q}_{n}\right)$ be a collection of attributes. Let us assume that the weight vector set for the attributes is ${m}_{i}=\left({m}_{1}, {m}_{2},\dots ,{m}_{i}\right)$, where ${m}_{i}$ represents the corresponding weight or importance degree concerning attributes ${Q}_{i}$. Let $l=\left\{1, 2, \cdots , k\right\}$ represent the set of $l$ experts in sports during the selection process. The player’s selection process is based on decision-making processes based on CrIFEWA and CrIFEWG. The steps involved in choosing an alternative are described below.

Step 1. Take data from the experts and construct a circular intuitionistic fuzzy decision matrix ${M}_{i\times j}$.

Step 2. In this step, all the data is changed into one cost type or benefit type.

Step 3. Use the CrIFEWA and CrIFEWG operators to aggregate the CrIFS for every alternative ${q}_{i}$ in the decision matrix ${M}_{i\times j}$.

$$\text{CrIFEWA}\left({P}_{1}, {P}_{2},\dots ,{P}_{\text{i}}\right)=\left(\begin{array}{c}\frac{\prod_{i=1}^{z}{\left(1+{\uppi }_{\text{i}}\right)}^{m}-\prod_{i=1}^{z}{\left(1-{\uppi }_{\text{i}}\right)}^{m}}{\prod_{i=1}^{z}{\left(1+{\uppi }_{\text{i}}\right)}^{m}+\prod_{i=1}^{z}{\left(1-{\uppi }_{\text{i}}\right)}^{m}},\\ \frac{2.\prod_{i=1}^{z}{n}_{\text{i}}^{m}}{\prod_{i=1}^{z}{\left(2-{n}_{\text{i}}\right)}^{m}+\prod_{i=1}^{z}{n}_{\text{i}}^{m}},\\ \frac{\prod_{i=1}^{z}{\left(1+{r}_{\text{i}}\right)}^{m}-\prod_{i=1}^{z}{\left(1-{r}_{\text{i}}\right)}^{m}}{\prod_{i=1}^{z}{\left(1+{r}_{\text{i}}\right)}^{m}+\prod_{i=1}^{z}{\left(1-{r}_{\text{i}}\right)}^{m}}\end{array}\right)$$

$$\text{CrIFEWG}\left({P}_{1}, {P}_{2},\dots ,{P}_{\text{i}}\right)=\left(\begin{array}{c}\frac{2.\prod_{i=1}^{z}{\uppi }_{\text{i}}^{m}}{\prod_{i=1}^{z}{\left(2-{\uppi }_{\text{i}}\right)}^{m}+\prod_{i=1}^{z}{\uppi }_{\text{i}}^{m}},\\ \frac{\prod_{i=1}^{z}{\left(1+{n}_{\text{i}}\right)}^{m}-\prod_{i=1}^{z}{\left(1-{n}_{\text{i}}\right)}^{m}}{\prod_{i=1}^{z}{\left(1+{n}_{\text{i}}\right)}^{m}+\prod_{i=1}^{z}{\left(1-{n}_{\text{i}}\right)}^{m}},\\ \frac{2.\prod_{i=1}^{z}{r}_{\text{i}}^{m}}{\prod_{i=1}^{z}{\left(2-{r}_{\text{i}}\right)}^{m}+\prod_{i=1}^{z}{r}_{\text{i}}^{m}}\end{array}\right)$$

Step 4. Using Definition 5, calculate the score value of the total outcomes. Where $\partial =0.6$

Step 5. Arrange all the aggregated data in ascending order to select the best player for the defensive-modifier position.

Step 6: End.

Analysis of player positioning using new aggregation operator

Developing strategies to enhance the team’s overall performance is crucial, yet uncertain, in football. The observation of a player’s strengths and weaknesses depends on multiple factors. Significantly, the players’ positions in football play a crucial role in overall performance. Proper player positioning enhances the team’s attacking and defensive strategies. However, assigning players to their appropriate positions according to their skills and past experiences can be pretty hectic. The defenders are near the goalkeeper. The task of the defender is to protect the goal from opposition attackers. The back line of the defenders provides support to the central defender, who faces the opponents’ attackers directly. The coordination of the backline and frontline defenders is essential. Additionally, the decision-making power of the frontline defender also affects the performance of the defender positions. Another critical position is known as a modifier. A modifier is positioned in the center of the field. He bridges the players between defensive and offensive positions. He plays a crucial role in distributing the ball. He is also responsible for creating the scoring opportunities with possession control. Some modifiers play in defensive mode, while others play in attacking mode. Again, the selection of the appropriate player for the modifier position is hazardous and full of uncertainty. The modifier should be selected based on his skills and previous performances to avoid any uncertain situation.

Similarly, the players play at the wingers’ positions on the left and right sides. They widen the attack and deliver crosses to the penalty area. Overall, tram performance requires the players to be well-positioned according to their skills and roles. The following figure describes the players’ essential positions (Fig. 1).

Fig. 1

Positions of the players in the football team (https://www.progressivesoccertraining.com).

According to modern football, the positions of the defensive and holding modifiers are crucial. The players in that position are responsible for protecting the backline, intercepting attacks, breaking up play, and distributing the ball to initiate an attack. Thus, the overall performance of the football team cannot be improved without a good defensive modifier. This study selects an appropriate defensive modifier based on the essential characteristics. The following are the common properties of an excellent defensive modifier.

• 1. Technical awareness and decision-making ${Q}_{1}$: An excellent defensive modifier can understand the game flow and anticipate what will happen next. He makes strategies and decisions according to his awareness. Thus, the selected defensive modifier needs a sharp understanding. He must know the proper timings of pressing, sitting back, and reading the opponent’s strategies.

• 2. Stamina and endurance ${Q}_{2}$: In football, physical stamina is essential. However, the role of physical stamina becomes more significant in the case of the defensive modifier position. This position requires moving up and down the field, tracking back to defend, and moving forward to support the attackers. The difference of even one centimeter or millisecond may cause a change in the result. Thus, the player’s selection for this position must be analyzed based on his physical stamina. Additionally, the player in this position should also possess significant endurance. His endurance enables him to remain influential throughout the game, thanks to his high stamina. Hence, a player who can play a 90-min game with total energy should be selected to improve the team’s overall performance.

• 3. Ball control and passing (Technical ability) ${Q}_{3}$: The technical skills of any player are essential for their performance. However, the position of the defensive modifier requires a player with high technical skills. The defensive modifier should have excellent ball control. He also needs excellent ball-passing skills with high accuracy. This attribute must be analyzed carefully when selecting a player for the defensive modifier position.

• 4. Coordination and communication ${Q}_{4}$: Good coordination between all players enhances the overall performance in football. However, the position of the defensive modifier requires a player with extraordinary coordination skills. The player in this position acts as the team’s voice, directing the movement of the other players. He is responsible for coordinating the teammates throughout the game. Thus, an expert player has extraordinary coordination skills.

The most appropriate player for the position of the defensive modifier has the above skills. As all the players may not be good at a time in all the attributes mentioned above. In the following example, a thorough analysis of these characteristics is made to select the most suitable player for the defensive modifier position.

Example 1:

Consider there are five players $\left\{{{\varvec{q}}}_{1},{{\varvec{q}}}_{2},{{\varvec{q}}}_{3},{{\varvec{q}}}_{4},{{\varvec{q}}}_{5}\right\}$ That looks suitable for the position of the defensive modifier. However, the coach wants to select the most appropriate player for this position. He needs a player who is good in all the attributes mentioned above. He can utilize the developed approach in the following manners.

Step 1: Take opinions about the players from an expert and construct a circular intuitionistic fuzzy decision matrix ${M}_{i\times j}$. The decision matrix is displayed in Table 2.

Table 2 Circular intuitionistic fuzzy decision matrix.

Step 2: Here, normalization is not needed because all the attributes are of benefit type. Regarding the cost type attributes, it will normalize the decision matrix.

Step 3: Apply the developed aggregation model to aggregate the information in Table 2. The aggregation of the data is shown in Table 3. Table 3 displays the total values obtained using the CrIFEWA and CrIFEWG operators.

Table 3 Displays aggregation results.

Step 4: Here need the score value for each player to rank them according to their skills. Using Definition 5, calculate the score value of the total outcomes. All the score values are displayed in Table 4. Where $\partial =0.6$.

Table 4 Presentations of the score value of calculated data.

The blue line in Fig. 2 represents the aggregated values of the CrIFEWA operator, and the grey line represents the aggregated outcomes of the CrIFEWG operators.

Fig. 2

Graph the scores obtained in the case of the CrIFEWA and CrIFEWG operators.

Step 5: Table 5 presents the ranking ordering of the aggregated findings using the suggested AOs.

Table 5 Arrangement of score function.

Table 5 shows the data noticed. Out of all the possibilities, using the CrIFEWA and CrIFEWG operator ${q}_{4}$ is the best player.

Comparative analysis

This part presents a comparative analysis between the proposed work and the previously published MADM techniques, which are illustrated in Table 6, and circular intuitionistic fuzzy (CrIF) weighted averaging (WA) (CrIFWA) and CrIF weighted geometric (WG) (CrIFWA) operators introduced by Cakir and Tas²⁵ and intuitionistic fuzzy Yager WA (IFYWA) and intuitionistic fuzzy Yager WG (IFYWG) operators proposed by Alcantud³⁹. Table 6 shows that the AOs submitted by Seikh and Mandal⁷² proposed intuitionistic fuzzy Dombi WA (IFDWA) and intuitionistic fuzzy Dombi WG (IFDWG), Huang⁷³ diagnosed intuitionistic fuzzy Hamacher WA (IFHWA) and intuitionistic fuzzy Hamacher WG (IFHWG), and Verma and Rajkumar⁷⁴ presented intuitionistic fuzzy prioritized Einstein WA (IFPEWA) and intuitionistic fuzzy prioritized Einstein WG (IFPEWG) operators did not meet the decision-makers requirements based on the data provided in Table 2. The circular radius data provided in IFVs is the reason these operators failed.

Table 6 Comparing the suggested work to a few earlier AOS.

Moreover, one can see how using Einstein AOs in the context of IFVs leads to different outcomes from the comparison analysis above. Because Einstein AOs based on ETN and ETCN produce accurate results, the results can be trusted to be reliable. Also, it is clear from Seikh and Mandal⁷², Huang⁷³, and Verma and Rajkumar⁷⁴ that the AOs of IFSs are limited in their scope because they cannot be applied to data with a more excellent range.

The above Table 6 compares some other existing approaches. It found that when using CrIFWA, CrIFWG, IFYWA, IFYWG then ${{\varvec{q}}}_{4}$ be the best alternative among all other considered alternatives. It also noticed that many fuzzy set-based environments could not aggregate CrIFVs-based information. Some existing aggregation operators, such as IFYWA, IFYWG, IFHWA, IFHWG, IFEPWA, IFEPWG, IFDWA and IFDWG, cannot generate a proper ranking and are assigned a fail in Table 6. This happens because these operators come from classical IFS and cannot manage the unique phase-based and circular structures found in CrIFS. CrIFS introduces directional or angular details to the framework, which is more than what can be addressed by simply following IFS. As a result, these operators output missing, unclear or repeated scores, making it challenging to identify an accurate ranking. In contrast, the proposed CrIF operators successfully include the circular aspects, resulting in separating calculations that make the ranked list clear and steady, showing that the proposed strategy works well for circular fuzzy data.

The efficiency and comprehension of the suggested Einstein AOs of CrIFS can be derived from these facts. The benefits of the proposed work are shown in a geometrical Fig. 3.

Fig. 3

Graph of the score values obtained from comparison of different aggregation models with new AOs.

The above figure shows that comparison with the proposed AOs and other present CrIFWA, CrIFWG developed by Alcantud³⁹ and IFYWA, IFYWG presented by Wang and Feng⁷⁵.

Rank-correlation validation

To verify consistency with other approaches, Spearman’s rank-correlation coefficient⁷⁶ has computed between the proposed ranking ($q_{4} > q_{2} > q_{3} > q_{1} > q_{5}$) and the orders produced by two representative operators:

$${\varvec{p}}=1-\frac{6\sum {{\varvec{d}}}_{{\varvec{i}}}^{2}}{{\varvec{n}}\left({{\varvec{n}}}^{2}-1\right)},\boldsymbol{ }{\varvec{n}}=5$$

$$p_{{CrIFWG}} = 0.90,~~p_{{IFWG}} = 0.60$$

The high ${\varvec{p}}$ value for CrIFWG operator confirms that the proposed CrIF COCOSO ranking aligns closely with modern circular-fuzzy techniques, while the lower ${\varvec{p}}$ with IFWG highlights its improved discriminative ability over earlier non-circular operators.

Information aggregation in the COCOSO method

To enhance the preciseness over the traditional approaches for MADM problems, this portion discusses the COCOSO method with the combination of CrIFVs. The description of the proposed methodology is given as follows:

Step 1: First, investigate the attributes and the alternatives. The lists of other options and criteria are denoted by $A=\left\{{q}_{1},{q}_{2},{q}_{3},\cdots ,{q}_{m}\right\}$ and $C=\left\{{Q}_{1},{Q}_{2},{Q}_{3},\cdots ,{Q}_{n}\right\}$, respectively, and considering $\left\{{\omega }_{1},{\omega }_{2},{\omega }_{3},\cdots ,{\omega }_{n}\right\}$ as the weights of the attributes, their sum of the weights must be $1$.

Step 2: Construct the decision matrix using CrIFVs-based information.

Step 3: Normalize the decision matrix: there are typically two categories of qualities. To get consistent outcomes, must change their nature.

Step 4: To find the WNDM, first see the cumulative opinions about the alternatives concerning each factor using the score function formula discussed in Definition 5.

Step 5: To calculate the weighted normalized decision matrix (WNDM)${\left[{B}_{ij}\right]}_{m\times n}$, using the normalized decision information obtained in step 2. Here, use the following equation to get the weighted normalized decision matrix.

$${C}_{ij}={w}_{j}.{scrx}_{ij}^{n}$$

where ${w}_{j}$ shows the weight of ${j}^{th}$ attribute such that $\sum_{j=1}^{n}{w}_{j}=1$.

Step 6: To find the sum of the weighted normalized values of the attributes for each alternative using the following equation.

$${S}_{i}=\sum_{j=1}^{n}{C}_{ij}$$

(14)

Step 7: Evaluate the product of the weighted normalized values of the attributes for each option using the following equation.

$${p}_{i}=\prod_{j=1}^{n}{C}_{ij}$$

(15)

Step 8: To calculate the average sum and the product of the weighted normalized values obtained in steps 6 and 7 using the following equation.

$${A}_{i}=\frac{{p}_{i}+{S}_{i}}{2}$$

(16)

Step 9: Here find the relative importance score of each alternative using the following equation.

$${C}_{i}={A}_{i}.\left(1+\frac{{S}_{i}-min{S}_{i}}{{maxS}_{i}-min{S}_{i}}+\frac{{p}_{i}-min{p}_{i}}{{maxp}_{i}-min{p}_{i}}\right)$$

(17)

Step 10: Finally, rank the alternatives based on the obtained score values.

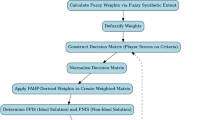
For convince, the proposed algorithm of the COCOSO method for Cr-IFVs is described in Fig. 4.

Fig. 4

The steps of the COCOSO method use fuzzy information to analyze the player’s positioning.

Solve Example 2 using the COCOSO method to select the most suitable player for the defensive modifier position. The detailed steps are as follows. Further, find the score values of all alternatives using Definition 5 (see Table 7). Now, evaluate the sum and product of each attribute for each alternative using the following Eqs. 14 and 15. The sum and the product of factors give the combined solutions for other options. The sum and product for each alternative are calculated in Table 8 below. Further, need the average solution of the sum and the product of the other options. Using Eq. 16, find each alternative’s average sum and product, presented in Table 8. Furthermore, refer to the relative scores for each alternative using Eq. 17. The relative scores are also provided in Table 5.

Table 7 Defuzzification of the information in Table 2.

Table 8 Sum, product, average, and the relative scores of alternatives.

Table 7 shows the score values for the players.

Here $\left(0.52, 0.34, 0.51\right)$, apply Eq. 5 to find score values.

$${S}_{11}=\frac{\left(0.52-0.34+\sqrt{2}*0.51*\left(2*0.6-1\right)\right)}{3}=0.10808$$

Now using Step 5 of the COCOSO method, evaluate the WNDM with the help of that given in Table 9.

Table 9 Weighted normalized decision matrix.

$${C}_{11}=0.28*0.10808=0.03026$$

Applying steps 6-9.

$${S}_{1}=0.03026+0.02295+\left(-0.00763\right)+0.01409=0.05967$$

$${p}_{1}=0.03026*0.02295*\left(-0.00763\right)*0.01409=-7.46196\text{E}-08$$

$${A}_{1}=\frac{0.05967+-7.46196\text{E}-08}{2}=0.02983$$

$${C}_{1}=0.02983*\left(1+\frac{0.05967-0.04761}{{0.07758}_{i}-0.04761}+\frac{-7.46196\text{E}-08--2.53581\text{E}-07}{5.82874\text{E}-08--2.53581\text{E}-07}\right)$$

The ranking order of alternatives is provided in Table 10.

Table 10 The relative scores of alternatives.

For a better understanding, the ranking results are also presented in a graphical format, allowing us to identify players’ rankings quickly. The ranking sequence is illustrated in Fig. 5.

Fig. 5

Graph of the ranking of the players using the COCOSO method.

Sensitivity analysis

A sensitivity analysis shows how players ($q_{1}$ to $q_{5}$) are ranked when the parameter $\partial$ changes from $0$ to $1$. The parameter $\partial$ is essential for adjusting the relative importance of the aggregated and compromise scores. If $\partial$ it is very close to $1$, the model favors overall agreement; if it is close to $0$, it values being close to what is expected. As seen in Fig. 6, regardless of changes in $\partial$, the ranking order in the model is not significantly altered, which means this parameter does not overly influence it. It is worth noting that player $q_{4}$ does well in every value $\partial$ and continues to place first under all conditions. Such consistency implies that the CrIF-COCOSO model stays effective and trustworthy, regardless of decision-making preferences. That is why the sensitivity analysis supports the stability of the rankings and demonstrates that the chosen parameter works well in real applications.

Fig. 6

Sensitivity analysis.

Comparison analysis with existing methods

Table 11 compares the key strengths of the proposed CrIF-COCOSO approach with those of other CrIF-based MCDM approaches, judged by six features: stability of ranking, level of accuracy, flexibility, how easily the parameters can be selected, ease of implementation and overall practicality. Since the ranking always stayed the same despite variations in all the model settings in the sensitivity analysis, the high stability of the method has been confirmed. This is not the same as with MOORA⁷⁷, TOPSIS³¹, and VIKOR⁷⁸, which changed rankings and deserved a medium stability rating. The proposed system is more reliable, leading to score values that are more helpful in distinguishing between similar options. Such a difference indicates that other methods like MOORA or EDAS⁷⁹ are less precise in finding ideal solutions, often leading to identical or very close results and explaining their scores. Being able to handle many types of fuzzy data and several aggregation approaches makes the method highly flexible and earns a high score. MOORA and EDAS have fewer options for forming models, so they are marked low to medium in flexibility. How easy it is to set the parameters in a model is examined. Only $\partial$ the change is in CrIF-COCOSO, and its effect on results is clear and steady. Unlike other methods, PROMETHEE⁸⁰ needs users to define several detailed preference functions, which can be time-consuming. Because of this, the method receives a high grade for how simple it is to tune its parameters. Likewise, the simplicity of using the proposed method is high because there are no complex normalization or distance routines needed. PROMETHEE is considered lower because it uses pairwise comparisons and sets of preference functions, which add to its straightforwardness. The method’s efficiency is rated as high, since it has a balanced score across all the assessment measures. It is designed to be user-friendly and adapts to different situations, which helps us use it for player position analysis. These ratings are objective and rely on studying theories, previous experiments’ results and how various methods are implemented.

Table 11 Comparison analysis with existing methods.

Practical implications

The proposed framework can be applied outside of football, as it requires a list of alternatives, a set of evaluation criteria, and expert opinions provided similarly, using familiar everyday terms. Any domain where decisions are needed in uncertain situations can benefit from them. In supply-chain management, teams may combine their assessments of price, quality, reliability, and sustainability to determine which supplier is best. Project-portfolio committees can distinguish between poor and good proposals by aggregating experts’ opinions on each project’s return, risk, importance to the strategy, and social impact. Clinicians may choose among different treatments by considering the therapy’s benefits, potential side effects, the patient’s preferences, and the cost of each treatment, especially when data from studies is uncertain. Assessing potential sites for smart cities in terms of their economic, environmental, and social aspects is often uncertain, so urban planners utilize fuzzy indicators. At the same time, human resource managers can find suitable candidates for positions by combining distinct evaluations of relevant abilities and experience. Since users can enter any number of criteria into the Einstein-based aggregators and the COCOSO stage creates a balanced ranking, the model acts as a helpful choice for many real-life problems.

Limitations of the proposed approach

Although the approach is flexible and reliable, it also has limitations that make it worthwhile. Using experts ensures that their expertise is reflected in the choices, thereby increasing the relevance of the decisions. As more data is available, computational complexity rises; however, this means the method is capable of handling fine details and accurately representing complex data. Besides, if the criteria are shown to be independent, the analysis becomes simpler and the framework is more understandable, leading to a practical and straightforward application of the model.

Some advantages and disadvantages of the proposed theory

The proposed theory is based on CrIFS-based information; here discuss some pros and cons of the suggested framework.

Advantages

The CrIFS is a more generalized and supreme format of IFS, due to its involvement of circular degrees. An ordinary IFS is only based on the MG and NMG within the range of a closed interval $\left[0, 1\right]$ while the radius of the circle is within the range of $\left[0, \sqrt{2}\right]$ covered by CrIFS and constructed the CrIFEWA and CrIFEWG operators. These discussed AOs are also suitable for simple IFS-based AOs by taking the value of the circular degree as zero.

On the other hand, the COCOSO method was defined using CrIFVs for ranking alternatives. The defined COCOSO method is also suitable for IFV-based information, with the circular degree set to zero.

Disadvantages

The CrIFS is superior to IFS, but in many complex situations, the CrIFS framework is not applicable for handling more extensive data. In this regard, it aims to extend the proposed theory to Pythagorean FS and q-rung orthopair FS environments.

Conclusion

MADM is a crucial tool for selecting the best option among several alternatives. This study proposes a new algorithm for choosing the most suitable player to play at the defensive modifier position using the MADM methodology. This study selected the most appropriate player among the five, considering the players’ crucial characteristics for the defensive modifier’s position. Using the CrIFS concept, this study developed two new AOs, namely, CrIFEWA and CrIFEWG operators. The developed algorithm is based on integrating with the ETN and ETCN. The role of the ETN and ETCN in obtaining flexible results is crucial, especially in uncertain situations. This study also developed the COCOSO method using CrIFS information for the MADM problem, including a detailed algorithm. The overall performance of the football team cannot be improved without a good defensive modifier. This study selects an appropriate defensive modifier based on the essential characteristics, which is a more accurate approach. The developed approach considers the weights of the attributes. To verify the authenticity of the proposed methodologies, compare them with existing methods. A graphical representation of aggregated outcomes using CrIFEWA, CrIFEWG operators, and the COCOSO method is also provided for convenience.

Future directions

The role of the developed approach in aggregating information is significant due to its involvement with the ETN and ETCN. However, the developed method has some limitations as well. The developed model cannot handle the information obtained from the format defined in^81,82,83. In the future, aim to develop aggregation models that can effectively deal with these frameworks. Further, the developed approach can be utilized for the uncertain frequency control of suspension system⁸⁴, uncertain feedback control of active suspension⁸⁵, static output feedback control⁸⁶, lateral dynamic control⁸⁷ and domain-constrained output feedback control⁸⁸. Similarly, the developed model can be utilized in event-triggered filtering⁸⁹, fault-tolerant control^90,91, active-passive damping⁹², human-machine sharing steering control⁹³ and observed-based gain scheduling⁹⁴.

Table 12 shows the abbreviations used in the proposed theory.

Table 12 Abbreviation used in the proposed theory.