Abstract
The study of similarity and distance measures plays a key role in understanding the relationships between fuzzy sets and their extensions, especially when applied to decision-making problems. While there has been notable progress in developing similarity measures for various types of generalized fuzzy sets, including fractional fuzzy sets, there is still a lack of well-developed measures suited to the structure of \(\:p,q,r-\)fractional fuzzy sets. This limitation reduces the effectiveness of fuzzy models in complex decision-making tasks where uncertainty needs to be handled more carefully and flexibly. To overcome this issue, we introduce new similarity measures that use three independent fractional exponents \(\:p\), \(\:q\), and \(\:r\) corresponding to the membership, neutral, and non-membership degrees. This approach offers greater flexibility and a more detailed way of capturing the relationships between fuzzy values. We also apply these similarity measures within a decision-making model designed to assess alternatives in uncertain environments. The proposed method is tested through a multi-criteria decision-making case study. The results highlight that regulatory and policy barriers (\(\:{{\uprho\:}}_{6}\)) are the most influential factor, with a final score of \(\:0.8641\), showing the method’s usefulness in real-world settings. Compared to other approaches, our framework adapts better to changes in uncertainty, responds more accurately to variations in input values, and offers clearer, more interpretable results.
Similar content being viewed by others
Introduction
Decision-making is a fundamental process aimed at selecting the most appropriate alternative from a set of possible options. In recent years, a wide range of studies and applications have explored the use of fuzzy set (FS) theory to support decision-making under uncertainty. The concept of fuzzy sets was first introduced by Zadeh1, marking a pivotal shift from the strict binary logic of classical set theory—where an element either belongs or does not belong to a set toward a framework that allows for partial membership. This foundational idea laid the groundwork for the development of fuzzy logic and its many extensions. One such extension is the intuitionistic fuzzy set (IFS), introduced to represent both the degree of membership (MD) and non-membership (NMD), along with a degree of hesitation, thus enabling a more nuanced representation of uncertainty2. However, IFSs are limited in scenarios where the sum of MD and NMD exceeds 1, which restricts their use in certain decision-making contexts. To address this, Yager3 proposed the Pythagorean fuzzy set (PFS), which replaces the linear summation condition of IFSs with a squared sum constraint, thereby allowing a broader and more flexible modeling of complex decision problems. Further extending this idea, Yager4 introduced the \(\:q-\)rung orthopair fuzzy set (\(\:q-\)ROFS), which generalizes PFS by allowing the sum of the \(\:qth\) powers of MD and NMD to remain within the unit interval. This provides an even greater degree of flexibility in balancing membership-related information. Seikh and Mandal5 proposed the \(\:p,q-\)quasirung orthopair fuzzy set (\(\:p,q-\)QOFS), which introduces adjustable power parameters for MD and NMD. These studies have been utilized by scholars across a wide range of fields, with their applications prominently highlighted in areas such as decision-making, pattern recognition, medical diagnosis, data mining, and engineering6,7,8,9. The versatility of these models demonstrates their practical relevance and effectiveness in addressing complex, real-world problems10,11.
The aforementioned fuzzy extensions account only for MDs and NMDs, while overlooking the neutral membership degree (NEMD), which plays a critical role in the comprehensive evaluation of alternatives. To overcome these limitations, picture fuzzy sets were introduced12, incorporating MD, NMD, and NEMD, with the constraint that their sum does not exceed one. Various extensions of picture fuzzy sets have been proposed in the literature. For instance, Gündoğdu and Kahraman13 introduced the spherical fuzzy set (SFS), which employs a squared summation constraint over the three membership components MD, NMD, and NEMD thereby enhancing the model’s ability to represent uncertainty more effectively. However, SFSs exhibit limitations when dealing with extreme or boundary values. To overcome this issue, the T-spherical fuzzy set (T-SFS) was proposed14, preserving the squared sum condition while offering improved flexibility in accommodating such extreme cases. This development represents a notable advancement in the modeling of complex and uncertain real-world decision-making problems. Rrecently, Ali et al.15 proposed the \(\:p,q,r-\)spherical fuzzy set (\(\:p,q,r-\)SFS), which removes many of the restrictive conditions of previous models by introducing three independent parameters corresponding to MD, NMD, and NEMD. Gulistan et al.16 proposed \(\:p,q,r-\)fractional fuzzy sets which is the most recent extension of fuzzy set theory. These extensions have been employed by scholars to address various real-world decision-making problems, as evidenced in studies such as15,17,18,19.
Decision-making (DM) is the process of selecting the most suitable course of action from a set of alternatives through systematic evaluation of relevant data and assessment variables. In the context of Green Supply Chain Management (GSCM), effective decision-making plays a pivotal role in enhancing both environmental and operational performance. It enables the identification of strategies that promote sustainability without compromising efficiency. Well-structured decision-making helps organizations mitigate risks related to regulatory compliance, resource availability, and environmental impact. Moreover, it contributes to improved economic outcomes by promoting cost-effective and eco-friendly practices throughout the supply chain. Such an approach supports the integration of green initiatives into broader business strategies, fostering long-term sustainability by balancing profitability with environmental responsibility. A variety of decision-making frameworks have been extensively explored in this context. For instance, Akram et al.20 proposed a multi-criteria decision-making (MCDM) model using interval-valued spherical fuzzy Bonferroni mean operators to evaluate solar cell performance under uncertain conditions. Waqar et al.21 employed Dombi operations within an interval-valued intuitionistic fuzzy set (IVIFS) environment for sustainable energy selection in Pakistan. In another study, Akram et al.22 utilized \(\:q-\) ROFS with Aczel–Alsina-based operators to develop a decision-making method for selecting optimal energy sources. Similarly, Rahim et al.23 introduced an MCDM method based on \(\:p,q,r-\)spherical fuzzy sets for the selection of solar panels. Wang et al.24 contributed to the field by developing Sugeno–Weber power-weighted operators for solving complex decision-making problems. Recent advancements have also incorporated sophisticated fuzzy logic techniques into decision-making and network analysis frameworks25,26,27. Additionally, novel aggregation operators (AOs) have been developed to improve MCDM under uncertainty. For example, Sen et al.28 proposed a hybrid model based on Einstein weighted averaging to extend the lifetime of wireless sensor networks. In real-time applications, the integration of Einstein operators with adaptive neuro-fuzzy inference systems has led to improvements in road crack detection and segmentation29. Riaz and Frid30 introduced linear Diophantine fuzzy soft-max aggregation operators to enhance the efficiency of green supply chains. Moreover, Maclaurin symmetric mean operators have been applied to optimize market risk assessment using interval-valued intuitionistic fuzzy sets31. Emerging developments in complex fuzzy set theory have focused on improving decision-making precision through confidence-level-based aggregation techniques. Rahman and Muhammad32 introduced induced-level complex polytopic fuzzy operators for more refined aggregation processes. In another contribution, Rahman33 applied a complex polytopic fuzzy model to optimize the placement of nuclear power plants in Pakistan. Furthermore, Ahmed et al.34 explored complex intuitionistic hesitant fuzzy aggregation to address ambiguity in multi-criteria decision-making. To facilitate better understanding, a list of abbreviations is provided in Table 1.
Literature review
Similarity measures (SMs) are powerful mathematical tools widely used in numerous real-world applications, particularly in fields where comparing datasets and evaluating alternatives is essential. These measures quantify the closeness or degree of resemblance between two objects or datasets based on their attributes or features. The continued development, refinement, and practical application of SMs underscore their central role in the advancement of fuzzy logic and decision sciences, especially within complex and uncertain environments. In fuzzy set theory and its extensions, SMs also referred to as closeness functions serve as the basis for making informed decisions, enabling effective comparisons between fuzzy data. Their versatility has led to applications in a wide range of areas, including but not limited to clustering35,36, data mining and exploration37, pattern recognition38, information retrieval39, medical diagnosis40, and MCDM41,42,43. Early foundational work on SMs in the context of classical FSs was presented by researchers such as Hong and Hwang44 and Xuecheng45. These efforts laid the groundwork for more advanced models, such as IFSs, hesitant fuzzy sets, PFSs, PIFSs, and SFSs. Xu and Chen46 established a formal structure of SMs for IFSs, while Xu47 also developed correlation coefficients for IFSs. Xu et al.48 extended the concept further by introducing similarity metrics for hesitant fuzzy environments.
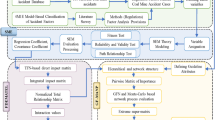
In the domain of PFSs, Zhang49 proposed a similarity-based algorithm for decision-making, and Wei50 introduced cosine-based SMs. Singh51 examined correlation coefficients tailored for PiFSs, with further contributions from Wei et al.52 focusing on practical applications of PIFS models. A number of studies have thoroughly reviewed various similarity and distance metrics, as well as correlation coefficients designed specifically for PIFSs and SFSs53,54,55,56. Further innovations have emerged in the form of novel SM structures. For instance, Nguyen57 introduced exponential similarity measures, and Hussain and Yang58 proposed measures based on the Hausdorff distance. Verma and Merigó59 presented a hybrid trigonometric SM incorporating cosine functions to improve flexibility and accuracy. In the context of \(\:q-\)ROFSs, Wang et al.60 developed cosine-based similarity measures, while Farhadinia et al.61 proposed an integrated framework combining similarity and distance metrics. Additional works62,63,64 have contributed to the growing body of research on SMs for \(\:q-\)ROFSs. Recent studies have expanded these methodologies further, applying SMs and MCDM techniques to newer fuzzy models such as circular IFSs and separable N-soft sets. These approaches have demonstrated effectiveness across a variety of practical domains, highlighting the continuous evolution and relevance of SM research65,66,67,68. The structural layout of the proposed study and its methodological framework is illustrated in Fig. 1.
Problem statement of the study
Although fuzzy set theory has witnessed significant advancements, current similarity measures remain insufficient for effectively capturing the nuanced distinctions inherent in \(\:\varvec{p},\varvec{q},\varvec{r}-\)fractional fuzzy similarity models (\(\:\varvec{p},\varvec{q},\varvec{r}-\)FFSMs). This limitation hampers their utility in complex multi-criteria decision-making (MCDM) contexts where a high degree of precision and flexibility is required. Specifically, these shortcomings undermine the quality, robustness, and interpretability of decisions in environments characterized by uncertainty and imprecision—such as the evaluation of barriers in green supply chain management (GSCM). Therefore, there is a pressing need to develop more expressive and adaptable similarity measures tailored to the structural complexity of \(\:\varvec{p},\varvec{q},\varvec{r}-\)FFSMs to support accurate and meaningful decision-making.
Research gap and motivation of the study
SMs serve as vital mathematical tools in FS theory, allowing the quantification of how closely two fuzzy sets resemble each other. This is particularly important in addressing imprecision, uncertainty, and partial truth core challenges in real-world DM scenarios. However, traditional similarity measures often fall short when applied to complex systems where multiple membership components, such as MD, NEMD, and NMD, must be evaluated independently or asymmetrically. Most existing SMs adopt uniform exponentiation or apply identical structural constraints across all components, thereby limiting their capacity to model situations where different attributes inherently carry varying degrees of uncertainty or significance. In sensitive and high-stakes applications such as medical diagnosis, fault detection, or recommendation systems this uniform treatment fails to capture the complexity of the underlying data. Rigid term levels lead to a loss of interpretability and reduced decision-making effectiveness. To address these limitations, this study introduces a new class of similarity measures under the framework of \(\:p,q,r-\)FFSMs. This approach provides a more refined structure for similarity assessment by assigning independent exponent parameters: \(\:p\) for the MD, \(\:q\) for the neutral NMD, and \(\:r\) for the NEMD. The model adheres to the constraint: \(\:0\le\:\frac{1}{p}{\mu}_{\mathcal{F}}\left(\mathcal{a}\right)+\frac{1}{r}{\eta}_{\mathcal{F}}\left(\mathcal{a}\right)+\frac{1}{q}{\vartheta}_{\mathcal{F}}\left(\mathcal{a}\right)\le\:1\). where \(\:p,q\ge\:1\), and \(\:r=LCM(p,q)\) is selected to ensure computational consistency and normalization. The principal motivation for proposing the \(\:p,q,r-\)FFSM lies in overcoming the structural rigidity of earlier models by enabling component-level adaptability. By introducing separate fractional scaling parameters for each membership component, the model gains the flexibility required to more accurately reflect varying levels of influence or uncertainty. This makes the proposed framework particularly suitable for applications in clustering, classification, and pattern recognition, where nuanced differences in fuzzy information can significantly affect the quality of decisions. Ultimately, the \(\:p,q,r-\)FFSM offers a more expressive and customizable approach to similarity measurement, better aligning with the needs of modern, data-intensive decision environments.
Objectives and novelty of the study
The primary objectives of this study are as follows:
-
(1)
To develop cosine-based, grey relational, and set-theoretic similarity measures within the framework of \(\:\varvec{p},\varvec{q},\varvec{r}-\)FFSMs.
-
(2)
To design a flexible DM model that allows independent weighting of membership-related components through the use of adjustable fractional exponents.
-
(3)
To validate the applicability and robustness of the proposed model through a real-world case study on Green Supply Chain Management (GSCM), demonstrating improvements in performance compared to existing methods.
The novelty of this research lies in the development of similarity measures—specifically cosine-based, grey, and set-theoretic that incorporate fractional parameters for membership, neutral membership, and non-membership degrees. This level of flexibility and granularity in similarity computation has not been explored in the existing literature. Additionally, the integration of these advanced similarity measures into a MCDM framework, supported by empirical validation through a real-world application, highlights both the theoretical significance and practical relevance of the proposed approach. The proposed structure enhances interpretability, increases model adaptability to varying uncertainty levels, and improves decision accuracy, thereby contributing a meaningful advancement to the field of fuzzy decision-making.
Contribution of the study
This study offers several important contributions to the advancement of the fractional fuzzy (FF) framework and DM under uncertainty:
-
(1)
Development of Novel Similarity Measures: Three new similarity measures cosine-based, grey relational, and set-theoretic are introduced within the \(\:p,q,r-\)FF framework. These measures incorporate independent fractional exponents \(\:p\), \(\:q\), and \(\:r\) corresponding to the MD, NEMD, and NMD, respectively. This structure allows for a more precise and flexible quantification of similarity, representing a significant methodological innovation over existing models.
-
(2)
Flexible and Adaptive Decision-Making Framework: The proposed model introduces structural adaptability through the use of tunable fractional parameters, enabling decision-makers to control the influence of each membership component based on the context. This flexibility is further supported through a sensitivity analysis, which confirms the consistency and robustness of ranking outcomes across various parameter configurations.
-
(3)
Application to Real-World Decision Contexts: The practical effectiveness of the proposed similarity measures is demonstrated through both numerical examples and a real-world case study on GSCM. In the case study, the model effectively identifies regulatory and policy barriers as the most critical challenges, validating the relevance and applicability of the approach.
-
(4)
Comparative Evaluation with Existing Methods: A comparison with traditional similarity measures reveals that the proposed model achieves superior ranking stability, discriminative power, and alignment with expert evaluations. These improvements contribute to enhanced interpretability and greater decision accuracy in uncertain and multi-criteria environments.
Overall, this study introduces a comprehensive and innovative similarity-based decision-making framework that significantly enhances the capability of fuzzy models to handle complex and uncertain decision scenarios.
Materials and methods
This section provides a concise overview of the fundamental definitions of FSs, IFSs, PIFSs, SFSs, FFSs, and existing similarity measures (SMs).
Definition 1
1 A FSs over a non-empty set \(\:\mathcal{A}\) is of the following form:
In Eq. (1), \(\:{\phi\:}_{F}\left(\mathcal{a}\right)\in\:\left[\text{0,1}\right]\) show the MMG of an element \(\:\mathcal{a}\in\:\mathcal{A}\).
Definition 2
2 An IFSs over a non-empty set \(\:\mathcal{A}\) is of the following form:
In Eq. (2), \(\:{\phi\:}_{F}\left(\mathcal{a}\right),{\psi\:}_{F}\left(\mathcal{a}\right)\in\:\left[\text{0,1}\right]\) denote the MD and NMD of an element \(\:\mathcal{a}\in\:\mathcal{A}\), such that \(\:{\mathcal{M}}_{IF}\left(\mathcal{a}\right)+{\mathcal{V}}_{IF}\left(\mathcal{a}\right)\le\:1.\)
Definition 3
12 An PIFSs over a non-empty set \(\:\mathcal{A}\) is of the following form:
In Eq. (3), \(\:{\mathcal{M}}_{F}\left(\mathcal{a}\right),{\mathcal{V}}_{F}\left(\mathcal{a}\right),{\mathcal{N}}_{IF}\left(\mathcal{a}\right)\in\:\left[\text{0,1}\right]\) show the MD, NMD and NEMD of an element \(\:\mathcal{a}\in\:\mathcal{A}\), such that \(\:{\mathcal{M}}_{PI}\left(\mathcal{a}\right)+{\mathcal{V}}_{PI}\left(\mathcal{a}\right)+{\mathcal{N}}_{PI}\left(\mathcal{a}\right)\le\:1.\)
Definition 4
13 An SFSs \(\:{S}_{p}\) over a non-empty set \(\:\mathcal{A}\) is of the following form:
In Eq. (4), \(\:{\mathcal{M}}_{{S}_{p}}\left(\mathcal{a}\right),{\mathcal{V}}_{{S}_{p}}\left(\mathcal{a}\right),{\mathcal{N}}_{{S}_{p}}\left(\mathcal{a}\right)\in\:\left[\text{0,1}\right]\) are the MD, NMD and NIMD of an element \(\:\mathcal{a}\in\:\mathcal{A}\), such that \(\:{\left({\mathcal{M}}_{{S}_{p}}\left(\mathcal{a}\right)\right)}^{2}+{\left({\mathcal{V}}_{{S}_{p}}\left(\mathcal{a}\right)\right)}^{2}+{\left({\mathcal{N}}_{{S}_{p}}\left(\mathcal{a}\right)\right)}^{2}\le\:1.\)
Definition 6
69 Let \(\:{\mathcal{F}}_{1}=\left({\mathcal{M}}_{{\mathcal{F}}_{1}},{\mathcal{N}}_{{\mathcal{F}}_{1}}\right)\) and \(\:{\mathcal{F}}_{2}=\left({\mathcal{M}}_{{\mathcal{F}}_{2}},{\mathcal{N}}_{{\mathcal{F}}_{2}}\right)\) be any two IFNs in \(\:\mathcal{A}\). A cosine similarity measure (CSM) based on cosine function between these two IFNs are defined as:
Definition 7
69 Let \(\:{\mathcal{F}}_{1}=\left({\mathcal{M}}_{{\mathcal{F}}_{1}},{\mathcal{N}}_{{\mathcal{F}}_{1}}\right)\) and \(\:{\mathcal{F}}_{2}=\left({\mathcal{M}}_{{\mathcal{F}}_{2}},{\mathcal{N}}_{{\mathcal{F}}_{2}}\right)\) be any two IFNs in \(\:\mathcal{A}\). A set-theoretic similarity measure (STSM) based on set-theoretic function between these two IFNs are defined as:
Definition 8
69 Let \(\:{\mathcal{F}}_{1}=\left({\mathcal{M}}_{{\mathcal{F}}_{1}},{\mathcal{N}}_{{\mathcal{F}}_{1}}\right)\) and \(\:{\mathcal{F}}_{2}=\left({\mathcal{M}}_{{\mathcal{F}}_{2}},{\mathcal{N}}_{{\mathcal{F}}_{2}}\right)\) be any two IFNs in \(\:\mathcal{A}\). A grey similarity measure (GSM) between these two IFNs is defined as:
where,
Definition 9
16 For any non-empty set \(\:\mathcal{A}\), A \(\:p,q,r-\)Fractional fuzzy set (\(\:p,q,r-\)FFS) over an element \(\:\mathcal{a}\in\:\mathcal{A}\) is defined as follows:
where \(\:{\mathcal{M}}_{\mathcal{F}}\left(\mathcal{a}\right)\in\:\left[\text{0,1}\right]\), \(\:{\mathcal{V}}_{\mathcal{F}}\left(\mathcal{a}\right)\in\:\left[\text{0,1}\right]\) and \(\:{\mathcal{N}}_{\mathcal{F}}\left(\mathcal{a}\right)\in\:\left[\text{0,1}\right]\) represents the MD, NEMD, and NMD of an element \(\:\mathcal{a}\in\:\mathcal{A}\) under the following conditions: \(\:0\le\:\frac{1}{p}{\mu}_{\mathcal{F}}\left(\mathcal{a}\right)+\frac{1}{r}{\eta}_{\mathcal{F}}\left(\mathcal{a}\right)+\frac{1}{q}{\vartheta}_{\mathcal{F}}\left(\mathcal{a}\right)\le\:1\), where \(\:p\) and \(\:q\) are positive integers such that \(\:p,q\ge\:1\) and \(\:r=LCM(p,q)\).
\(\:\varvec{p},\varvec{q},\varvec{r}-\)fractional fuzzy similarity measures
In this section, we proposed some SMs between \(\:p,q,r-\)FFNs, and their fundamental properties are discussed.
Definition 10
Let \(\:{\mathcal{F}}_{1}=\left\{{\mathcal{a}}_{i},\langle {\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\rangle |{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) and \(\:{\mathcal{F}}_{2}=\left\{{\mathcal{a}}_{i},\langle {\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right) \rangle |{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) be any two \(\:p,q,r-\)FFSs in \(\:\mathcal{A}\). A CSM based on cosine function between these two \(\:p,q,r-\)FFNs are defined as:
Theorem 1
Let \(\:{\mathcal{F}}_{1}=\left\{{\mathcal{a}}_{i},\langle\:{\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\rangle\:|{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) and \(\:{\mathcal{F}}_{2}=\left\{{\mathcal{a}}_{i},\langle\:{\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\rangle\:|{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) be any two \(\:p,q,r-\)FFSs; then CSM \(\:{\mathcal{C}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)\) between the two \(\:p,q,r-\)FFNs, satisfy the following properties:
-
iii.
\(\:{\mathcal{C}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)=1\) if \(\:{\mathcal{F}}_{1}={\mathcal{F}}_{2}\), that is \(\:{\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right).\)
Proof
(i). As MM of both fractional fuzzy numbers (FFN) belong to [0,1], so it is obvious that\(\:{\mathcal{C}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)\in\:\left[\text{0,1}\right].\)
(ii). Holds trivially.
If \(\:{\mathcal{F}}_{1}={\mathcal{F}}_{2}\), that is, \(\:{\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),\) which implies that
then \(\:{\mathcal{C}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)=1\) is obtained.
Example 1
Let \(\:{\mathcal{F}}_{1}=\left(\text{0.5,0.6,0.7}\right)\) and \(\:{\mathcal{F}}_{2}=\left(\text{0.6,0.7,0.8}\right)\) be two \(\:p,q,r-\)FFNs, then the CSM for \(\:p=q=r=3\), is calculated as
Theorem 2
Let \(\:{\mathcal{F}}_{1}=\left\{{\mathcal{a}}_{i},\langle\:{\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\rangle\:|{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) and \(\:{\mathcal{F}}_{2}=\left\{{\mathcal{a}}_{i},\langle\:{\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\rangle\:|{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) be any two \(\:p,q,r-\)FFNs. I\(\:{\mathcal{F}}_{1}\subseteq\:{\mathcal{F}}_{2}\subseteq\:{\mathcal{F}}_{3}\), then
Proof
Easy to prove.
Definition 11
Let \(\:{\mathcal{F}}_{1}=\left\{{\mathcal{a}}_{i},\langle {\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right) \rangle |{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) and \(\:{\mathcal{F}}_{2}=\left\{{\mathcal{a}}_{i},\langle {\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right) \rangle |{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) be any two \(\:p,q,r-\)FFSs in \(\:\mathcal{A}\). A weighted CSM based on cosine function between these two \(\:p,q,r-\)FFNs are defined as:
where \(\:\mathcal{W}={\left({\mathcal{w}}_{1},{\mathcal{w}}_{2},\dots\:,{\mathcal{w}}_{n}\right)}^{T}\) represent the weight vector such that \(\:{\mathcal{w}}_{i}\in\:\left[\text{0,1}\right]\) and \(\:\sum\:_{i=1}^{n}{\mathcal{w}}_{i}=1\).
Theorem 3
Let \(\:{\mathcal{F}}_{1}=\left\{{\mathcal{a}}_{i},\langle {\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\rangle |{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) and \(\:{\mathcal{F}}_{2}=\left\{{\mathcal{a}}_{i},\langle {\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\rangle |{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) ant two \(\:p,q,r-\)FFNs; then weighted CSM \(\:{\mathcal{W}\mathcal{C}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)\) between the two \(\:p,q,r-\)FFNs, satisfy the following properties:
-
iii.
\(\:{\mathcal{W}\mathcal{C}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)=1\) if \(\:{\mathcal{F}}_{1}={\mathcal{F}}_{2}\), that Is.
Let \(\:\mathcal{W}={\left({\mathcal{w}}_{1},{\mathcal{w}}_{2},\dots\:,{\mathcal{w}}_{n}\right)}^{T}\) denote the weight vector, where each \(\:{\mathcal{w}}_{i}\in\:\left[\text{0,1}\right]\) and \(\:\sum\:_{i=1}^{n}{\mathcal{w}}_{i}=1\).
Proof
The approach follows a similar structure to that used in Theorem 1.
Theorem 4
Let \(\:{\mathcal{F}}_{1}=\left\{{\mathcal{a}}_{i},\langle\:{\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\rangle\:|{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) and \(\:{\mathcal{F}}_{2}=\left\{{\mathcal{a}}_{i},\langle\:{\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\rangle\:|{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) are any two \(\:p,q,r-\)FFNs. If \(\:{\mathcal{F}}_{1}\subseteq\:{\mathcal{F}}_{2}\subseteq\:{\mathcal{F}}_{3}\), then
Proof
Easy to prove.
Set-theoretic similarity measures for \(\:\varvec{p},\varvec{q},\varvec{r}\)-FFNs
In this section we introduce set-theoretic and weighted STSMs for two \(\:\varvec{p},\varvec{q},\varvec{r}\)-FFNs, in the view of39,40, following Eq. (7).
Definition 12
Let \(\:{\mathcal{F}}_{1}=\left\{{\mathcal{a}}_{i},\langle {\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\rangle |{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) and \(\:{\mathcal{F}}_{2}=\left\{{\mathcal{a}}_{i},\langle {\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\rangle |{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) are any two \(\:p,q,r-\)FFSs in \(\:\mathcal{A}\). A STSM \(\:{{\mathcal{C}\mathcal{{\prime\:}}}^{{\prime\:}}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)\) is defined as follows:
Theorem 5
Let \(\:{\mathcal{F}}_{1}=\left\{{\mathcal{a}}_{i},\langle\:{\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\rangle\:|{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) and \(\:{\mathcal{F}}_{2}=\left\{{\mathcal{a}}_{i},\langle\:{\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\rangle\:|{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) be any two \(\:p,q,r-\)FFSs; then STSM \(\:{{\mathcal{C}}^{{\prime\:}{\prime\:}}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)\) between the two \(\:p,q,r-\)FFNs, fulfill the conditions outlined below:
-
(iii)
\(\:{{\mathcal{C}}^{{\prime\:}{\prime\:}}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)=1\) if \(\:{\mathcal{F}}_{1}={\mathcal{F}}_{2}\), that is \(\:{\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right).\)
Proof
(i) Since the membership of both \(\:p,q,r-\)FFNs belongs to [0,1], it follows that \(\:{{\mathcal{C}}^{{\prime\:}{\prime\:}}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)\in\:\left[\text{0,1}\right],\) which shows the first property.
(ii) The symmetry property holds trivially. (iii) If \(\:{\mathcal{F}}_{1}={\mathcal{F}}_{2}\), for all \(\:{\mathcal{a}}_{i}\in\:\mathcal{A},\) \(\:{\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),\:\:{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),\:\:{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),\) then the SM simplifies as:
Since the numerator and denominator are same for each \(\:{\mathcal{a}}_{i},\) further this simplifies as follows: \(\:{{\mathcal{C}}^{{\prime\:}{\prime\:}}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)\)
\(\:=\frac{\frac{1}{p}{\mathcal{M}}_{{\mathcal{F}}_{1}}^{2}\left({\mathcal{a}}_{i}\right)+\frac{1}{r}{\mathcal{N}}_{{\mathcal{F}}_{1}}^{2}\left({\mathcal{a}}_{i}\right)+\frac{1}{q}{\mathcal{V}}_{{\mathcal{F}}_{1}}^{2}\left({\mathcal{a}}_{i}\right)}{\frac{1}{p}{\mathcal{M}}_{{\mathcal{F}}_{1}}^{2}\left({\mathcal{a}}_{i}\right)+\frac{1}{r}{\mathcal{N}}_{{\mathcal{F}}_{1}}^{2}\left({\mathcal{a}}_{i}\right)+\frac{1}{q}{\mathcal{V}}_{{\mathcal{F}}_{1}}^{2}\left({\mathcal{a}}_{i}\right)}=\frac{1}{n}\sum\:_{i=1}^{n}1=\frac{n}{n}=\)1.
Example 2
Let \(\:{\mathcal{F}}_{1}=\left(\text{0.5,0.6,0.7}\right)\) and \(\:{\mathcal{F}}_{2}=\left(\text{0.6,0.7,0.8}\right)\) be two \(\:p,q,r-\)FFNs, then the STSM for \(\:p=q=r=3\), is calculated as
Theorem 6
Let \(\:{\mathcal{F}}_{1}=\left\{{\mathcal{a}}_{i},\langle\:{\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\rangle\:|{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) and \(\:{\mathcal{F}}_{2}=\left\{{\mathcal{a}}_{i},\langle\:{\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\rangle\:|{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) be any two \(\:p,q,r-\)FFNs. I\(\:{\mathcal{F}}_{1}\subseteq\:{\mathcal{F}}_{2}\subseteq\:{\mathcal{F}}_{3}\), then
Proof
Straightforward.
Definition 13
Let \(\:{\mathcal{F}}_{1}=\left\{{\mathcal{a}}_{i},\langle {\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\rangle |{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) and \(\:{\mathcal{F}}_{2}=\left\{{\mathcal{a}}_{i},\langle {\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\rangle |{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\).
be any two \(\:p,q,r-\)FFSs in \(\:\mathcal{A}\). A weighted STSM (\(\:{\mathcal{W}{\mathcal{C}}^{{\prime\:}{\prime\:}}}_{p,q,r-\text{F}\text{F}})\) between these two \(\:p,q,r-\)FFNs is defined as follows:
Let \(\:\mathcal{W}={\left({\mathcal{w}}_{1},{\mathcal{w}}_{2},\dots\:,{\mathcal{w}}_{n}\right)}^{T}\) denote the weight vector, where each \(\:{\mathcal{w}}_{i}\in\:\left[\text{0,1}\right]\) and \(\:\sum\:_{i=1}^{n}{\mathcal{w}}_{i}=1\).
Theorem 7
Let \(\:{\mathcal{F}}_{1}=\left\{{\mathcal{a}}_{i},\langle {\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\rangle |{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) and \(\:{\mathcal{F}}_{2}=\left\{{\mathcal{a}}_{i},\langle {\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\rangle |{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) be any two \(\:p,q,r-\)FFNs; then weighted CSM \(\:{\mathcal{W}{\mathcal{C}}^{{\prime\:}{\prime\:}}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)\) between the two \(\:p,q,r-\)FFNs, satisfy the following properties:
-
(iii)
\(\:{\mathcal{W}{\mathcal{C}}^{{\prime\:}{\prime\:}}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)=1\) if \(\:{\mathcal{F}}_{1}={\mathcal{F}}_{2}\), that is\(\:{\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\) \(={\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right).\)
Where \(\:\mathcal{W}={\left({\mathcal{w}}_{1},{\mathcal{w}}_{2},\dots\:,{\mathcal{w}}_{n}\right)}^{T}\) represent the weight vector such that \(\:{\mathcal{w}}_{i}\in\:\left[\text{0,1}\right]\) and \(\:\sum\:_{i=1}^{n}{\mathcal{w}}_{i}=1\).
Proof
The approach follows a similar structure to that used in Theorem 1.
Theorem 8
Let \(\:{\mathcal{F}}_{1}=\left\{{\mathcal{a}}_{i},\langle\:{\mathcal{M}}_{{\mathcal{F}}_{i}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{i}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{i}}\left({\mathcal{a}}_{i}\right)\rangle\:|{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) \(\:(i=\text{1,2},3)\) be any three \(\:p,q,r-\)FFNs. If \(\:{\mathcal{F}}_{1}\subseteq\:{\mathcal{F}}_{2}\subseteq\:{\mathcal{F}}_{3}\), then
Proof
(i) Since \(\:{\mathcal{F}}_{1}\subseteq\:{\mathcal{F}}_{2}\subseteq\:{\mathcal{F}}_{3}\), this implies that \(\:{\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right){\le\:\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right){\le\:\mathcal{M}}_{{\mathcal{F}}_{3}}\left({\mathcal{a}}_{i}\right)\), \(\:{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\ge\:{\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\ge\:{\mathcal{N}}_{{\mathcal{F}}_{3}}\left({\mathcal{a}}_{i}\right)\) and \(\:{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\ge\:{\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\ge\:{\mathcal{V}}_{{\mathcal{F}}_{3}}\left({\mathcal{a}}_{i}\right)\) and \(\:\frac{1}{p}{\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\frac{1}{p}{\mathcal{M}}_{{\mathcal{F}}_{3}}\left({\mathcal{a}}_{i}\right)\le\:\frac{1}{p}{\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\frac{1}{p}{\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\), \(\:{\frac{1}{r}\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right){\frac{1}{r}\mathcal{N}}_{{\mathcal{F}}_{3}}\left({\mathcal{a}}_{i}\right)\ge\:{\frac{1}{r}\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right){\frac{1}{r}\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\), \(\:\frac{1}{q}{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\frac{1}{q}{\mathcal{V}}_{{\mathcal{F}}_{3}}\left({\mathcal{a}}_{i}\right)\ge\:\frac{1}{q}{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\frac{1}{q}{\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\). Therefore, for all \(\:i=\text{1,2},\dots\:,n\) we have
, and hence
Thus, \(\:{\mathcal{W}{\mathcal{C}}^{{\prime\:}{\prime\:}}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{3}\right)\le\:{\mathcal{W}{\mathcal{C}}^{{\prime\:}{\prime\:}}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)\). The second part of Theorem 8 can be proved in a similar manner.
Grey similarity measures for \(\:\varvec{p},\varvec{q},\varvec{r}\)-FFNs
Definition 14
Let \(\:{\mathcal{F}}_{1}=\left\{{\mathcal{a}}_{i},\langle {\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)\rangle |{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) and \(\:{\mathcal{F}}_{2}=\left\{{\mathcal{a}}_{i},\langle {\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\rangle |{\mathcal{a}}_{i}\in\:\mathcal{A}\right\}\) be any two \(\:p,q,r-\)FFSs in \(\:\mathcal{A}\). A GSM \(\:{{\mathcal{C}}^{{\prime\:}{\prime\:}{\prime\:}}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)\) is defined as follows:
Where \(\:{\Xi\:}{\mathcal{M}}_{\text{m}\text{i}\text{n}}=\underset{i}{\text{min}}\left\{\left|{\frac{1}{p}\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)-{\frac{1}{p}\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\right|\right\}=\underset{i}{\text{min}}\left\{\frac{1}{p}\left|{\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)-{\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\right|\right\}\),
Theorem 9
Let \(\:{\mathcal{F}}_{1}=\left({\mathcal{M}}_{{\mathcal{F}}_{1}},{\mathcal{N}}_{{\mathcal{F}}_{1}},{\mathcal{V}}_{{\mathcal{F}}_{1}}\right)\) and \(\:{\mathcal{F}}_{2}=\left({\mathcal{M}}_{{\mathcal{F}}_{2}},{\mathcal{N}}_{{\mathcal{F}}_{2}},{\mathcal{V}}_{{\mathcal{F}}_{2}}\right)\) be any two \(\:p,q,r-\)FFNs; then GSM \(\:{{\mathcal{C}}^{{\prime\:}{\prime\:}{\prime\:}}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)\) between the two \(\:p,q,r-\)FFNs, hold the following characteristics:
-
(iii)
\(\:{{\mathcal{C}}^{{\prime\:}{\prime\:}{\prime\:}}}_{p,q,r-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)=1\) if \(\:{\mathcal{F}}_{1}={\mathcal{F}}_{2}\), that is \(\:{\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{N}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{N}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right),{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)={\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right).\).
Proof
The approach follows a similar structure to that used in Theorem 1.
Theorem 10
Let \(\:{\mathcal{F}}_{1}=\left({\mathcal{M}}_{{\mathcal{F}}_{1}},{\mathcal{N}}_{{\mathcal{F}}_{1}},{\mathcal{V}}_{{\mathcal{F}}_{1}}\right)\), \(\:{\mathcal{F}}_{2}=\left({\mathcal{M}}_{{\mathcal{F}}_{2}},{\mathcal{N}}_{{\mathcal{F}}_{2}},{\mathcal{V}}_{{\mathcal{F}}_{2}}\right)\) and \(\:{\mathcal{F}}_{2}=\left({\mathcal{M}}_{{\mathcal{F}}_{3}},{\mathcal{N}}_{{\mathcal{F}}_{3}},{\mathcal{V}}_{{\mathcal{F}}_{3}}\right)\) be any three \(\:p,q,r-\)FFNs. I\(\:{\mathcal{F}}_{1}\subseteq\:{\mathcal{F}}_{2}\subseteq\:{\mathcal{F}}_{3}\), then
Proof
Easy to prove.
Definition 15
Let \(\:{\mathcal{F}}_{1}=\left({\mathcal{M}}_{{\mathcal{F}}_{1}},{\mathcal{N}}_{{\mathcal{F}}_{1}},{\mathcal{V}}_{{\mathcal{F}}_{1}}\right)\) and \(\:{\mathcal{F}}_{2}=\left({\mathcal{M}}_{{\mathcal{F}}_{2}},{\mathcal{N}}_{{\mathcal{F}}_{2}},{\mathcal{V}}_{{\mathcal{F}}_{2}}\right)\) be any two \(\:p,q,r-\)FFSs in \(\:\mathcal{A}\). A weighted GSM (\(\:{\mathcal{W}{\mathcal{C}}^{{\prime\:}{\prime\:}{\prime\:}}}_{p,q,r-\text{F}\text{F}}\)) between these two \(\:p,q,r-\)FFNs is defined as follows:
Where \(\:{\Xi\:}{\mathcal{M}}_{\text{m}\text{i}\text{n}}=\underset{i}{\text{min}}\left\{\left|{\frac{1}{p}\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)-{\frac{1}{p}\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\right|\right\}=\underset{i}{\text{min}}\left\{\frac{1}{p}\left|{\mathcal{M}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)-{\mathcal{M}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\right|\right\}\),
\(\:{\Xi\:}{\mathcal{V}}_{i}=\left|{\frac{1}{p}\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)-{\frac{1}{p}\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\right|=\frac{1}{p}\left|{\mathcal{V}}_{{\mathcal{F}}_{1}}\left({\mathcal{a}}_{i}\right)-{\mathcal{V}}_{{\mathcal{F}}_{2}}\left({\mathcal{a}}_{i}\right)\right|\) and \(\:\mathcal{W}={\left({\mathcal{w}}_{1},{\mathcal{w}}_{2},\dots\:,{\mathcal{w}}_{n}\right)}^{T}\) represent the weight vector such that \(\:{\mathcal{w}}_{i}\in\:\left[\text{0,1}\right]\) and \(\:\sum\:_{i=1}^{n}{\mathcal{w}}_{i}=1.\).
Theorem 11
Let \(\:{\mathcal{F}}_{1}=\left({\mathcal{M}}_{{\mathcal{F}}_{1}},{\mathcal{N}}_{{\mathcal{F}}_{1}},{\mathcal{V}}_{{\mathcal{F}}_{1}}\right)\) and \(\:{\mathcal{F}}_{2}=\left({\mathcal{M}}_{{\mathcal{F}}_{2}},{\mathcal{N}}_{{\mathcal{F}}_{2}},{\mathcal{V}}_{{\mathcal{F}}_{2}}\right)\) are any two \(\:p,q,r-\)FFNs; the weighted GSM \(\:{(\mathcal{W}{\mathcal{C}}^{{\prime\:}{\prime\:}{\prime\:}}}_{p,q,r-\text{F}\text{F}})\) between these two \(\:p,q,r-\)FFNs, satisfies the following properties:
Where \(\:\mathcal{W}={\left({\mathcal{w}}_{1},{\mathcal{w}}_{2},\dots\:,{\mathcal{w}}_{n}\right)}^{T}\) denote the weight vector, where each \(\:{\mathcal{w}}_{i}\in\:\left[\text{0,1}\right]\) and \(\:\sum\:_{i=1}^{n}{\mathcal{w}}_{i}=1\).
Proof
The approach follows a similar structure to that used in Theorem 1.
Theorem 12
Let \(\:{\mathcal{F}}_{1}=\left({\mathcal{M}}_{{\mathcal{F}}_{1}},{\mathcal{N}}_{{\mathcal{F}}_{1}},{\mathcal{V}}_{{\mathcal{F}}_{1}}\right)\), \(\:{\mathcal{F}}_{2}=\left({\mathcal{M}}_{{\mathcal{F}}_{2}},{\mathcal{N}}_{{\mathcal{F}}_{2}},{\mathcal{V}}_{{\mathcal{F}}_{2}}\right)\) and \(\:{\mathcal{F}}_{3}=\left({\mathcal{M}}_{{\mathcal{F}}_{3}},{\mathcal{N}}_{{\mathcal{F}}_{3}},{\mathcal{V}}_{{\mathcal{F}}_{3}}\right)\) be three arbitrary \(\:\text{p},\text{q},\text{r}-\)FFNs. If \(\:{\mathcal{F}}_{1}\subseteq\:{\mathcal{F}}_{2}\subseteq\:{\mathcal{F}}_{3}\), then\(\:{\mathcal{W}{\mathcal{C}}^{{\prime\:}{\prime\:}{\prime\:}}}_{\text{p},\text{q},\text{r}-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{3}\right)\le\:{\mathcal{W}{\mathcal{C}}^{{\prime\:}{\prime\:}{\prime\:}}}_{\text{p},\text{q},\text{r}-\text{F}\text{F}}\left({\mathcal{F}}_{1},{\mathcal{F}}_{2}\right)\).
Proof
Easy to prove.
Application of similarity measures in decision-making
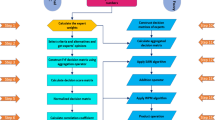
Similarity measures are fundamental tool across various scientific and engineering disciplines. Their applications are particularly relevant in fuzzy environments, impacting fields like pattern recognition, medical diagnosis, and clustering39. Additionally, several approaches in MADM, such as Vlsekriterijumska Optimizacija I KOmpromisno Resenj, elimination and choice translating reality, and Technique for Order Preference by Similarity to Ideal Solution also utilize these measures for ranking and selecting optimal alternatives40,44. Figure 2 illustrates the structure of the proposed methodology.
In this section, we propose TOPSIS-based MCDM method utilizing using \(\:p,q,r\:-\)FFSs. Decision makers assess a set of alternatives \(\:{\Psi\:}=\left\{{{\Psi\:}}_{1},{{\Psi\:}}_{2},\dots\:,{{\Psi\:}}_{m}\right\}\), based on a set of criteria \(\:\mathbb{C}=\left\{{\mathbb{C}}_{1},{\mathbb{C}}_{2},\dots\:,{\mathbb{C}}_{m}\right\}\). Each assessment is expressed as \(\:p,q,r-\text{F}\text{F}\text{N}\text{s}:\)
The weight vector associated with each criterion is given by:
\(\:\mathcal{w}=\left({\mathcal{w}}_{1},{\mathcal{w}}_{2},\dots\:,{\mathcal{w}}_{n}\right)\), where \(\:\sum\:_{i=1}^{n}{\mathcal{w}}_{i}=1\) and \(\:{0\le\:\mathcal{w}}_{j}\le\:1\) for all \(\:j=1\) to n.
The \(\:p,q,r-\)FF decision matrix \(\:Q\) is defined as:
Step 1
The positive ideal solution and negative ideal solution are defined as.
For each criterion j:
Positive ideal solution
Negative ideal solution
Step 2. To determine the weight vector \(\:w\), the importance of each criterion is represented by \(\:p,q,r-\text{F}\text{F}\text{N}\text{s}\):
Normalization of \(\:p,q,r-\text{f}\text{r}\text{a}\text{c}\text{t}\text{i}\text{o}\text{n}\text{a}\text{l}\:\text{f}\text{u}\text{z}\text{z}\text{y}\:\text{n}\text{u}\text{m}\text{b}\text{e}\text{r}:\)
The weight of each criterion:
Normalization of weights:
Step 3. Calculate the similarity between alternative \(\:{{\Psi\:}\:}_{i}\) and the ideal solutions using the following expression:
Step 4. The closeness coefficient \(\:{{\uprho\:}}_{i}\) for each alternative is calculated as:
Step 5. Finally the alternatives are ranked according to their relative similarity degrees \(\:{{\uprho\:}}_{i}\). The alternatives with the highest similarity value is considered the most preferred option.
Illustrative example
We are dealing with a case where several experts give their opinion on barriers and strategic enhancements for GSCM based on several attributes. To obtain a complete assessment, we apply the suggested mathematical method to merge the experts’ points of view while taking into account their relative expertise. The layout of the proposed case study is presented in Fig. 3.
Case study
In this section, we present a case study on barriers and strategic enhancements for GSCM using SMs in a \(\:p,q,r-\) FF approach. The environment is critical view of human life, different forms of pollution i.e. air pollution, soil pollution, noise pollution, and water pollution. These environmental pollutants contribute to severe health issues, including respiratory diseases, global warming, and heart ailments. The primary contributors among these all pollutants, air pollution contribute a significant challenge with industries. To moderate industrial pollution, GSCM has developed as a key approach, end of life product management, integrating sustainability into production, and logistic. The aim of GSCM is to reduce waste, enhance sustainability, and promote recycling. However, several barriers hinder the effective implementation of GSCM, necessitating strategic interventions. In this study, we employ a group decision makers using \(\:p,q,r-\) FFSMs to evaluate six alternative enhancement strategies for reducing GSCM barriers. Based on expert insights, six different types of barriers for GSCM are:
-
a.
\(\:{{\uprho\:}}_{1}\): Outsourcing Barriers.
-
b.
\(\:{{\uprho\:}}_{2}:\) Market Barriers.
-
c.
\(\:{{\uprho\:}}_{3}:\) Financial Barriers.
-
d.
\(\:{{\uprho\:}}_{4}:\) Managerial Barriers.
-
e.
\(\:{{\uprho\:}}_{5}\): Technological Barriers.
-
f.
\(\:{{\uprho\:}}_{6}\): Regulatory and Policy Barriers.
Further analysis of different types of sub-barriers and based on these sub-barriers we select one of the barriers has a significant impact on GSCM.
-
a.
\(\:{\mathbb{C}}_{1}:\) Environmental risk contribution.
-
b.
\(\:{\mathbb{C}}_{2}:\:\)Hindrance to sustainability goals.
-
c.
\(\:{\mathbb{C}}_{3}:\) Implementation cost/feasibility.
-
d.
\(\:{\mathbb{C}}_{4}:\) Technological adaptability.
-
e.
\(\:{\mathbb{C}}_{5}:\) Policy and stakeholder alignment.
The evaluation values for strategies according to attributes in the form of linguistic terms is given in Table 1. The experts’ qualitative judgments were mapped to corresponding p, q,r-FFNs using a consensus-driven calibration scale, aligning linguistic terms with fractional values to ensure a consistent and interpretable evaluation model.
Table 2 shows how the \(\:p,q,r-\text{F}\text{F}\text{N}\text{s}\) correspond to each criterion, indicating whether they represent the degree of membership, neutral or non-membership for this criterion.
Table 2 outlines each criterion with levels of \(\:p,q,r\) -fractional fuzzy numbers categorized as membership, neutral and non-membership, reflecting the relative advantages, acceptable conditions, and disadvantages of each location based on the given criteria to the investment decisions for a new manufacturing plant. Their assessments of the alternatives \(\:{\varvec{A}}_{\varvec{i}}(\varvec{i}=\text{1,2},3\dots\:,6)\) using linguistic terms relative to the criteria \(\:{\mathbb{C}}_{j}(j=\text{1,2},\dots\:,5)\) are outlined in Table 3.
Table 4 shows the p, q,r-FFNs of alternatives.
Step 1. The positive ideal solution \(\:{{\Psi\:}}^{+}\) and negative ideal solution \(\:{{\Psi\:}}^{-}\) of the data provided in Table 4 can be calculated by using Eqs. (25) and (26).
Step 2. Calculate the weight vector for criteria by using (27) to (29), resulting in \(\:w=\left(\text{0.12,0.31,0.23,0.13,0.21}\right)\).
Step 3. Cpmpute the similarity grade between \(\:{{\Psi\:}}_{i}\) and the ideal solutions as determined in Step 2.
Step 4. Calculate the relative similarity grades \(\:{{\uprho\:}}_{i}\) using Eq. (32) as follows:
Step 5. Based on the relative similarity grades, the alternatives are ranked in the following order; \(\:{{\uprho\:}}_{6}>{{\uprho\:}}_{5}>{{\uprho\:}}_{1}>{{\uprho\:}}_{2}>{{\uprho\:}}_{3}>{{\uprho\:}}_{4}\), as depicted in Fig. 4.
As shown in Fig. 4, regulatory and policy barriers (\(\:{{\uprho\:}}_{6}\)) are identified as the most significant barrier. In countries where environmental laws are strict, companies are more likely to adopt GSCM practices rapidly. In contrast, in regions with weak enforcement or outdated regulations, GSCM adoption tend to be slow or superficial, even whwn other resources are available. Therefore, regulatory and policy barriers have emerged as the most critical factor in GSCM, as selected by the experts after a thorough evaluation process. The values presented in Table 4 were generated synthetically for demonstration purpose. While framed using commonly accepted linguitic terms in expeet evaluations, the corresponding p, q,r-FFNs were assumed based on logical consistency with the model’s structural constraintsand satisfy the normalization condition required by p, q,r-FF framework. This assumption-based dataset serves to illustrate the applicability and behavior of the proposed DM framewrok in a context that reflects realistic challenges in GSCM.
Sensitivity analysis
In the previous subsection, we examined the process of selectig the term levels \(\:p,q\), and \(\:r\). In practical applicayions, decision-makers may require the flexibility to adjust these levels to influence the decision-making process. Howvevr, many existing SMs do not provide this flexibility. This section investigates the impact of varying p, q, and r on the final results. The closeness ratios and ranking order of the alternatives for different sets of (\(\:p\), \(\:q\), \(\:r\)) are presented in Table 1.
Table 1 presents the ranking orders for different values of \(\:p,q,\) and \(\:r\). Remarkably, option \(\:{{\uprho\:}}_{6}\) consistently ranks as the best alternative, irrespective of these parameters’ values. This consistency highlights the flexibility and the robustness of the proposed method. Within a single framework, the decision-makers have strong control over the DM process. This influence derived from the power to modify the parameters \(\:p\), \(\:q\), and \(\:r\) to meet particular requirements and situations to make flexible comparisons among different alternatives. The effect of these parameters are shown in Fig. 5.
The findings indicate that higher values of \(\:p\),\(\:q\), and \(\:r\) give rise to higher closeness ratios, providing a more positive direction to decision-makers. Optimistic decision-makers can select larger parameter values, while pessimistic decision-makers may select lower values, resulting in lower total scores. Notably, the ranking of the best alternative is not changing, suggesting that the approach yields objective and stable results irrespective of the decision-make’s preference. Figure 5. Illustrates ranking of alternative for various (\(\:p\), \(\:q\), \(\:r\)) combinations. The research validates that the best-ranked choice is consistent under a variety of triplet variations, reflecting the resistance of the approach suggested in realistic DM problems. This flexibility permits decision-makers to set parameters levels whenever necessary without loss of result reliability. The relative rank remains constant with \(\:{{\uprho\:}}_{6}\) always providing the highest closeness ratio and \(\:{{\uprho\:}}_{4}\) the smallest, supporting objectivity and reliability of the process.
The ranking of existing locations for different sets of triples (\(\:p\),\(\:q\),\(\:r\)). From the above discussion, it is clear that the optimal location never changes its rank for different sets of \(\:p,q\), and \(\:r\). This is one of the key features of the proposed method, which is of serious concern in practical DM applications. For example, it allows decision-makers to refine the term level values depending on the existing condition during the entire DM process. This adaptability increases the flexibility and efficiency of the method in real-world applications. As a result, the relative ranking of alternatives remains consistent, with \(\:{{\uprho\:}}_{6}\) often having the highest closeness ratio \(\:{{\uprho\:}}_{4}\) the lowest. This consistency suggests that the results are objective and reliable, as the best alternative remains unchanged regardless of parameter variations, making the ranking robust for DM purposes.
Comparative study
The SMs proposed in this study represent a generalization and advancement over those developed in earlier works48,49,50, and51. Specifically, the SMs defined in Equations (10) through (15) encompass and extend the models presented in references48,49,53,56. By incorporating \(\:p,q,r-\)fractional fuzzy numbers (p, q,r-FFNs), the proposed measures offer a more nuanced and flexible approach to similarity assessment. The use of fractional parameters enhances both precision and adaptability, enabling these models to address complex scenarios that traditional SMs may not adequately capture. The integration of fractional-order parameters allows the fractional fuzzy similarity measures (FFSMs) to generalize classical models, significantly increasing their versatility. This advantage is particularly notable when compared to the cosine-based SMs for intuitionistic fuzzy sets (IFSs) introduced by Xu and Chen46, and the comprehensive family of SMs for IFSs developed by Xu et al.48. Similarly, the newly proposed SMs for PIFSs53 and SFSs70 are further enhanced through the incorporation of p, q,r-fractional parameters, resulting in more refined and context-sensitive similarity evaluations. The fractional nature of the proposed models enables them to represent levels of uncertainty and partial truth that are not adequately addressed by existing similarity frameworks. This makes them especially suitable for applications involving complex fuzzy relationships, such as pattern recognition, classification, and MCDM. The extended SMs not only build upon foundational research particularly that of Xu et al.48 but also integrate structural improvements introduced in later studies, thereby enhancing their modeling capacity and interpretability. Moreover, the p, q,r-FFSM framework facilitates more flexible modeling through its additional fractional-order parameters, which allow for asymmetric weighting of membership components. This structural adaptability results in improved performance across various decision-making contexts, as demonstrated by recent advancements reported in the works of Wei50,52. A summary of the comparative performance evaluation and ranking outcomes is presented in Table 5, highlighting the advantages of the proposed approach over traditional SMs.
Table 5 shows that alternative associated with \(\:{{\uprho\:}}_{6}\) consistently rank as the most preferred option across all methods, aligning with the results derived from the proposed model. This consistency reinforces the robustness and effectivemess of the suggested method. Table 6 provides a comparative overview of the key characteristics of the proposed techniques alongside those of existing methods. A visual comparision of relative similarity grades from various existing approaches is illustrated in Fig. 6.
Limitations
Although the proposed p, q,r-FFSMs present a versatile and adaptive approach to handling fuzzy data, some inherent limitations remain. First, the selection of feactional parameters (p, q,r) introduces a level of subjectivity that can influence decision outcomes. Since there is no universlly accepted guideline for choosing these values, different choices may lead to different results. Furthermore, the mathematical structure, while theoretically robust, may be difficult to interpret or implement for practitioners without a strong background in fuzzy logic or decision theory. Another consideration is domain specificity; although the approach is validated within GSCM, its generalizability to other fields requires further testing and refinement. Lastly, the framework presumes accurate and consistent transformation of qualitative assessments into p, q,r-FFNs, which in practice may vary dependi ng on expert interpretation or data quality, potentially affecting the reliability of results.
Conclusion
This study introduced a novel DM framework based on \(\:p,q,r-\)FFSMs to address the limitations of traditional fuzzy set models in handling imprecision, hesitancy, and asymmetric membership structures. By incorporating adjustable fractional parameters for the MD, NEMD, and NMD, the proposed model significantly enhances the flexibility, granularity, and interpretability of multi-criteria decision-making (MCDM) under uncertainty. To operationalize the framework, we developed three new types of similarity measures—cosine-based, set-theoretic, and grey relational measures specifically tailored to the structure of \(\:p,q,r-\)FFNs. These measures allow for precise similarity computation and facilitate more reliable ranking of alternatives. The framework was validated through a real-world case study on GSCM. The results clearly identified regulatory and policy barriers as the most critical obstacle to effective GSCM implementation, with a final ranking score of 0.8641. This outcome not only demonstrates the practical applicability and discriminative capability of the proposed method but also emphasizes the importance for organizations and policymakers to prioritize regulatory alignment in sustainability initiatives. Furthermore, sensitivity and comparative analyses revealed that the proposed model consistently delivers robust and stable rankings across varying parameter settings. When compared to traditional similarity measures based on intuitionistic, Pythagorean, and spherical fuzzy sets, the \(\:p,q,r-\)FFSM approach outperformed existing models in terms of ranking precision, adaptability, and alignment with expert evaluations. From a theoretical perspective, this research contributes to the advancement of fuzzy decision-making by extending similarity measure design into the fractional fuzzy domain, allowing for more refined uncertainty modeling and greater structural flexibility in representing complex decision environments. Looking forward, future research could explore the integration of the proposed similarity measures with other MCDM techniques such as VIKOR, TOPSIS, or COPRAS, and investigate their applicability in domains such as artificial intelligence, machine learning, and predictive analytics, where decision-making under uncertainty plays a critical role.
Data availability
The datasets generated during and analysed during the current study are available in the paper.
References
Zadeh, L. A. Fuzzy sets. Inf. Control. 8 (3), 338–353 (1965).
Atanassov, K. T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 20 (1), 87–96 (1986). 1986/08/01/.
Yager, R. R. Pythagorean fuzzy subsets, in 2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS), pp. 57–61: IEEE. (2013).
Yager, R. R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 25 (5), 1222–1230 (2016).
Seikh, M. R. & Mandal, U. Multiple attribute group decision making based on quasirung orthopair fuzzy sets: application to electric vehicle charging station site selection problem. Eng. Appl. Artif. Intell. 115, 105299 (2022).
Zhao, Z. et al. Quasirung orthopair fuzzy linguistic sets and their application to multi criteria decision making. Sci. Rep. 14 (1), 25513 (2024).
Chu, Y. M. et al. Some p, q-cubic quasi-rung orthopair fuzzy operators for multi-attribute decision-making. Complex. Intell. Syst. 10 (1), 87–110 (2024).
Rahim, M., Bajri, S. A., Alqahtani, H., Alhabeeb, S. A. & Khalifa, H. A. E. W. Multi-criteria group Decision-Making using complex p, q-quasirung orthopair fuzzy sets: application in the selection of renewable energy projects for investments. Cogn. Comput. 17 (2), 86 (2025).
Redhu, A. & Kumar, K. Multi-attribute group decision making based on p, q-quasirung orthopair fuzzy Yager prioritized weighted geometric aggregation operator of p, q-quasirung orthopair fuzzy numbers. Granul. Comput. 9 (4), 75 (2024).
Rahim, M., Amin, F., Ali, A. & Shah, K. An extension of bonferroni mean under cubic pythagorean fuzzy environment and its applications in Selection-Based problems. Math. Probl. Eng. 2022 (1), 9735100 (2022).
Rahim, M. Multi-criteria group decision-making based on Frank aggregation operators under pythagorean cubic fuzzy sets. Granul. Comput. 8 (6), 1429–1449 (2023).
Cường, B. C. Picture fuzzy sets. J. Comput. Sci. Cybernetics. 30 (4), 409–409 (2014).
Kutlu Gündoğdu, F. & Kahraman, C. Spherical fuzzy sets and spherical fuzzy TOPSIS method. J. Intell. Fuzzy Syst. 36 (1), 337–352 (2019).
Ullah, K., Mahmood, T. & Jan, N. Similarity measures for T-spherical fuzzy sets with applications in pattern recognition, Symmetry, vol. 10, no. 6, p. 193, (2018).
Ali, J. & Naeem, M. r, s, t-spherical fuzzy VIKOR method and its application in multiple criteria group decision making. IEEE Access. 11, 46454–46475 (2023).
Gulistan, M. et al. $$ p, q, r-$$ fractional fuzzy sets and their aggregation operators and applications. Artif. Intell. Rev. 57 (12), 1–29 (2024).
Rahim, M., Khan, S. Z., Widyan, A. M., Almutairi, A. & Khalifa, H. A. E. W. A novel complex (p, q, r)-spherical fuzzy TOPSIS framework for sustainable urban development assessment. Expert Syst. Appl. 278, 127288 (2025).
Khan, S. Z. et al. Development of AHP-Based divergence distance measure between p, q, r–Spherical fuzzy sets with applications in Multi-Criteria decision making. Computer Model. Eng. & Sci. (CMES), 143, 2185–2211 (2025).
Rahim, M., Bajri, S. A., Khan, S., Alqahtani, H. & Khalifa, H. A. E. W. Innovative Multi-Criteria group decision making with Interval-Valued p, q, r-Spherical fuzzy sets: A case study on optimal solar energy investment location. International J. Fuzzy Systems, pp. 1–28, (2025).
Akram, M., Ullah, K. & Pamucar, D. Performance evaluation of solar energy cells using the interval-valued T-spherical fuzzy Bonferroni mean operators, Energies, vol. 15, no. 1, p. 292, (2022).
Waqar, M., Ullah, K., Pamucar, D., Jovanov, G. & Vranješ, Ð. An approach for the analysis of energy resource selection based on attributes by using Dombi T-norm based aggregation operators, Energies, vol. 15, no. 11, p. 3939, (2022).
Akram, M., Ullah, K., Ćirović, G. & Pamucar, D. Algorithm for energy resource selection using priority degree-based aggregation operators with generalized orthopair fuzzy information and Aczel–Alsina aggregation operators, Energies, vol. 16, no. 6, p. 2816, (2023).
Rahim, M., Ahmad, S., Bajri, S. A., Alharbi, R. & Khalifa, H. A. E. W. Confidence levels-based p, q, r–spherical fuzzy aggregation operators and their application in selection of solar panels. IEEE Access12, (2024).
Wang, Y., Hussain, A., Yin, S., Ullah, K. & Božanić, D. Decision-making for solar panel selection using Sugeno-Weber triangular norm-based on q-rung orthopair fuzzy information. Front. Energy Res. 11, 1293623 (2024).
Habib, A., Akram, M. & Kahraman, C. Minimum spanning tree hierarchical clustering algorithm: a new pythagorean fuzzy similarity measure for the analysis of functional brain networks. Expert Syst. Appl. 201, 117016 (2022).
Khan, M. J., Ding, W., Jiang, S. & Akram, M. Group decision making using circular intuitionistic fuzzy preference relations. Expert Syst. Appl. 270, 126502 (2025).
Akram, M., Fatima, U. & Alcantud, J. C. R. Group decision-making method based on pythagorean fuzzy rough numbers. J. Appl. Math. Comput. 71 (2), 2179–2210 (2025).
Sen, S., Sahoo, L. & Ghosh, S. Lifetime extension of wireless sensor networks by perceptive selection of cluster head using K-means and Einstein weighted averaging aggregation operator under uncertainty. J. Ind. Intell. 2 (1), 54–62 (2024).
Hussain, I. & Alam, L. Adaptive road crack detection and segmentation using Einstein operators and ANFIS for real-time applications. J. Intell. Syst. Control. 3 (4), 213–226 (2024).
Riaz, M. & Farid, H. Enhancing green supply chain efficiency through linear Diophantine fuzzy soft-max aggregation operators. J. Industrial Intell. 1 (1), 8–29 (2023).
Sarfraz, M. & Božanić, D. Optimization of market risk via Maclaurin symmetric mean aggregation operators: an application of interval-valued intuitionistic fuzzy sets in multi-attribute group decision-making. J. Eng. Manag Syst. Eng. 3 (2), 100–115 (2024).
Rahman, K. & Muhammad, J. Enhanced decision-making through induced confidence-level complex polytopic fuzzy aggregation operators. Int. J. Knowl. Innov. Stud. 2 (1), 11–18 (2024).
Rahman, K. Strategic placement of nuclear power plants in pakistan: A complex polytopic fuzzy model approach with confidence level assessment. J. Oper. Strat Anal. 2, 107–118 (2024).
Ahmed, M., Ashraf, S. & Mashat, D. Complex intuitionistic hesitant fuzzy aggregation information and their application in decision making problems. Acadlore Trans. Appl. Math. Stat. 2 (1), 1–21 (2024).
Yang, M. S. & Lin, D. C. On similarity and inclusion measures between type-2 fuzzy sets with an application to clustering. Comput. Math Appl. 57 (6), 896–907 (2009).
De Oliveira, J. V. & Pedrycz, W. Advances in Fuzzy Clustering and its Applications (Wiley, 2007).
Nasraoui, O., Frigui, H., Joshi, A. & Krishnapuram, R. Mining web access logs using relational competitive fuzzy clustering, in Proceedings of the Eight International Fuzzy Systems Association World Congress, vol. 1, pp. 195–204: Citeseer. (1999).
Dengfeng, L. & Chuntian, C. New similarity measures of intuitionistic fuzzy sets and application to pattern recognitions. Pattern Recognit. Lett. 23, 1–3 (2002).
Saqlain, M. & Saeed, M. From ambiguity to clarity: unraveling the power of similarity measures in multi-polar interval-valued intuitionistic fuzzy soft sets. Decis. Mak. Adv. 2 (1), 48–59 (2024).
Panagoulias, D. P., Virvou, M. & Tsihrintzis, G. A. Augmenting large language models with rules for enhanced domain-specific interactions: The case of medical diagnosis, Electronics, vol. 13, no. 2, p. 320, (2024).
Kumar, S. A new exponential knowledge and similarity measure with application in multi-criteria decision-making. Decis. Analytics J. 10, 100407 (2024).
Rahim, M., Abosuliman, S. S., Alroobaea, R., Shah, K. & Abdeljawad, T. Cosine similarity and distance measures for p, q – quasirung orthopair fuzzy sets: Applications in investment decision-making, Heliyon, vol. 10, no. 11, (2024).
Rahim, M., Amin, F., Alhabeeb, S. A., Alshehri, M. H. & Khalifa, H. A. E. W. Cosine similarity and information measures of p, q, r-spherical fuzzy sets: application in selecting migration destination. Expert Syst. Appl. 265, 125932 (2025).
Hong, D. H. & Hwang, S. Y. A note on the value similarity of fuzzy systems variables. Fuzzy Sets Syst. 66 (3), 383–386 (1994).
Xuecheng, L. Entropy, distance measure and similarity measure of fuzzy sets and their relations. Fuzzy Sets Syst. 52 (3), 305–318 (1992).
Xu, Z. & Chen, J. An overview of distance and similarity measures of intuitionistic fuzzy sets. Int. J. Uncertain. Fuzziness Knowledge-Based Syst. 16 (04), 529–555 (2008).
Xu, Z. On correlation measures of intuitionistic fuzzy sets, in International conference on intelligent data engineering and automated learning, pp. 16–24: Springer. (2006).
Xu, Z., Cai, X., Xu, Z. & Cai, X. Correlation, distance and similarity measures of intuitionistic fuzzy sets. Intuitionistic Fuzzy Inform. Aggregation: Theory Applications, pp. 151–188, (2012). https://link.springer.com/chapter/10.1007/978-3-642-29584-3_3
Zhang, X. A novel approach based on similarity measure for pythagorean fuzzy multiple criteria group decision making. Int. J. Intell. Syst. 31 (6), 593–611 (2016).
Wei, G. & Wei, Y. Similarity measures of pythagorean fuzzy sets based on the cosine function and their applications. Int. J. Intell. Syst. 33 (3), 634–652 (2018).
Singh, P. Correlation coefficients for picture fuzzy sets. J. Intell. Fuzzy Syst. 28 (2), 591–604 (2015).
Wei, G., Lin, R. & Wang, H. Distance and similarity measures for hesitant interval-valued fuzzy sets. J. Intell. Fuzzy Syst. 27 (1), 19–36 (2014).
Rani, P., Chen, S. M. & Mishra, A. R. Multi-attribute decision-making based on similarity measure between picture fuzzy sets and the MARCOS method. Inf. Sci. 658, 119990 (2024).
Alolaiyan, H. et al. Improving similarity measures for modeling real-world issues with interval-valued intuitionistic fuzzy sets. IEEE Access. 12, 10482–10496 (2024).
Gupta, R. & Kumar, S. Novel similarity measure between hesitant fuzzy set and their applications in pattern recognition and clustering analysis. J. Eng. Appl. Sci. 71 (1), 5 (2024).
Ma, Q., Zhu, X., Bai, K., Pu, Q. & Zhang, R. A novel uncertain information modeling method based on cosine similarity and cross entropy under spherical uncertain linguistic fuzzy set. J. Intell. Fuzzy Syst. 46 (2), 3339–3361 (2024).
Nguyen, X. T., Nguyen, V. D., Nguyen, V. H. & Garg, H. Exponential similarity measures for pythagorean fuzzy sets and their applications to pattern recognition and decision-making process. Complex. Intell. Syst. 5, 217–228 (2019).
Hussian, Z. & Yang, M. S. Distance and similarity measures of pythagorean fuzzy sets based on the hausdorff metric with application to fuzzy TOPSIS. Int. J. Intell. Syst. 34 (10), 2633–2654 (2019).
Verma, R. & Merigó, J. M. On generalized similarity measures for pythagorean fuzzy sets and their applications to multiple attribute decision-making. Int. J. Intell. Syst. 34 (10), 2556–2583 (2019).
Wang, P., Wang, J., Wei, G. & Wei, C. Similarity measures of q-rung orthopair fuzzy sets based on cosine function and their applications, Mathematics, vol. 7, no. 4, p. 340, (2019).
Farhadinia, B., Effati, S. & Chiclana, F. A family of similarity measures for q-rung orthopair fuzzy sets and their applications to multiple criteria decision making. Int. J. Intell. Syst. 36 (4), 1535–1559 (2021).
Khan, M. J., Kumam, P., Alreshidi, N. A. & Kumam, W. Improved cosine and cotangent function-based similarity measures for q-rung orthopair fuzzy sets and TOPSIS method. Complex. Intell. Syst. 7, 2679–2696 (2021).
Peng, X. & Dai, J. Research on the assessment of classroom teaching quality with q-rung orthopair fuzzy information based on multiparametric similarity measure and combinative distance‐based assessment. Int. J. Intell. Syst. 34 (7), 1588–1630 (2019).
Ali, J. Norm-based distance measure of q-rung orthopair fuzzy sets and its application in decision-making. Comput. Appl. Math. 42 (4), 184 (2023).
Gurmani, S. H., Khan, M. J., Ding, W. & Zulqarnain, R. M. Aczel–Alsina operations-based linguistic q-rung orthopair fuzzy aggregation operators and their application to site selection of electric vehicle charging station. Eng. Appl. Artif. Intell. 154, 110989 (2025).
Khan, M. J., Alcantud, J. C. R., Akram, M. & Ding, W. Separable N-soft sets: A tool for multinary descriptions with large-scale parameter sets. Appl. Intell. 55 (6), 561 (2025).
Khan, M. J., Jiang, S., Ding, W., Huang, J. & Wang, H. An infrared and visible image fusion using knowledge measures for intuitionistic fuzzy sets and Swin transformer. Inf. Sci. 684, 121291 (2024).
Alreshidi, N. A., Shah, Z. & Khan, M. J. Similarity and entropy measures for circular intuitionistic fuzzy sets. Eng. Appl. Artif. Intell. 131, 107786 (2024).
Ye, J. Cosine similarity measures for intuitionistic fuzzy sets and their applications. Math. Comput. Model. 53, 1–2 (2011).
Sharaf, I. M. A cognitive-based similarity measure for decision-making with spherical fuzzy information. J. Comput. Cogn. Eng. 2 (4), 331–342 (2023).
Shishavan, S. A. S., Gündoğdu, F. K., Farrokhizadeh, E., Donyatalab, Y. & Kahraman, C. Novel similarity measures in spherical fuzzy environment and their applications. Eng. Appl. Artif. Intell. 94, 103837 (2020).
Gupta, R. & Kumar, S. A new similarity measure between picture fuzzy sets with applications to pattern recognition and clustering problems, Granular computing, vol. 7, no. 3, pp. 561–576, (2022).
Acknowledgements
The authors would like to express their gratitude to the United Arab Emirates University, Al-Ain, UAE, for providing financial support with Grant No. G00004702.
Author information
Authors and Affiliations
Contributions
S. K and H. A. A: Conceptualization; Writing - original draft; Data curation; Formal analysis; Investigation; Methodology. M. I. S and M. R: Project administration; Resources; Software. H. A. W. K and A. A: Supervision; Validation; Visualization.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Khan, S., Syam, M.I., Abujabal, H.A. et al. A strategic decision-making framework for evaluating barriers to green supply chain management using fractional fuzzy similarity measures. Sci Rep 15, 29089 (2025). https://doi.org/10.1038/s41598-025-13963-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-13963-8