A novel extension of the power lindley distribution with statistical properties and application to COVID-19 data

Abstract

In the recent years, there has been a notable shift in the landscape of statistical and data science research, with increasing attention directed toward the development of advanced probability distributions aimed at addressing the challenges posed by medical and health-related data. In response to this need, the present study introduces a novel probability distribution model termed as the Exponentiated Odd Lomax Power Lindley distribution constructed by embedding the Power Lindley distribution within the Lomax family framework through the T-X transformation technique. This article delves into the application of probability distributions in medical data analysis, with a special focus on their role in understanding and managing the COVID-19 data. A comprehensive theoretical investigation is conducted, deriving key statistical properties including the probability and cumulative distribution functions, reliability functions, moments, moment generating function, order statistics, and entropy measures. To ensure accurate parameter estimation, several estimation methods are employed and rigorously compared through simulation studies. The real-world applicability of the developed distribution is illustrated through the modelling of COVID-19 datasets, where its performance is evaluated against a range of well-established probability distribution models. Empirical findings demonstrate the superior adaptability and modelling accuracy of the distribution while analysing real-world datasets.

Introduction

In the field of medical science, there has been an ongoing challenge and need in transforming vague and complex data into useful insights that can improve healthcare outcomes. Given the sophisticated nature of human health influenced by environmental, biological and behavioural factors, the data is rarely comprehensible. It is generally high-dimensional, noisy and subject to varied degrees of uncertainty, making it complicated to draw specific conclusions. To overcome these challenges, the application of probability distribution models has become increasingly indispensable. Such models provide systematic approach to quantify and understand the inherent randomness in medical science data, enabling researchers to draw meaningful insights that are otherwise unpredictable. In particular, the COVID-19 pandemic has emphasized the significance of probabilistic models in studying and analysing global health problems. The stochastic nature of the pandemic, where outcomes are affected by different variables, need novel statistical approaches to model and forecast.

In response to this global challenge, numerous researchers have analysed COVID-19 data using a variety of probabilistic models to better understand its spread and impact. These efforts primarily focused on proposing models that offer improved fit and predictive accuracy for pandemic-related data. Such developments are useful for supporting evidence-based decision making and improving diagnostic accuracy. For example, Exponentiated transformation of Gumbel type-II distribution is studied by Sindhu et al.¹ to model COVID-19 death case data. In this study, the authors have examined various mathematical properties of the model and have given their in-depth analysis. Hassan et al.² provided a new generalization of the inverted Topp-Leone model by combining with the Kumaraswamy-G family. The application of the developed distribution to model COVID-19 data, demonstrated that this new distribution provides better fit than the other existing distributions. Azm et al.³ developed transmuted generalised Lomax distribution to analyse COVID-19 datasets. Odd Weibull Inverted Topp-Leone distribution explored by Almetwally⁴ as a generalisation of inverted Topp-Leone distribution with the Weibull-G family. Similarly, Almongy et al.⁵ studied extended Odd Weibull Rayleigh distribution, specifically designed to model COVID-19 mortality rates. The authors^6,7,8,9 and¹⁰ have explored the novel probability distribution models and have demonstrated their superiority to model real-world scenarios through their application to COVID-19 pandemic. By compounding the Half-Logistic and Odd Frechet-G class, Bhat et al.¹¹ introduced the Odd Frechet Half-Logistic distribution. Generalising the Lindley distribution by DUS transformation, the authors¹² highlighted the effectiveness of the developed model while analysing real-life data sets. More recently, Qayoom et al.¹³ proposed a novel extension of the Rayleigh distribution. This new model was validated using COVID-19 data and compared with several established distributions. In a related contribution, Rather and Subramanian¹⁴ introduced the exponentiated Mukherjee-Islam distribution and demonstrated its practical utility through empirical applications. Extending this research field, Rather and Ozel¹⁵ developed the Weighted Power Lindley distribution, and in a subsequent study¹⁶, introduced a length-biased variant of the same. Both models were analysed in terms of their structural properties and real-world relevance. Moreover, the authors^17,18, and¹⁹ have made notable contributions to the field by developing innovative extensions of probability distribution models and validating their effectiveness through real-world applications.

All these advancements reflect a broader trend in recent years to development flexible probability models that can better capture the complex characteristics of real-world data. One effective strategy to achieve such flexibility is through the use of generator functions that can transform existing baseline distributions into new classes of probability models. In this article, we used the transformed-transformer (T-X) family by Alzaatreh et al.²⁰ to introduce new generalized probability distribution model, with cumulative distribution function (CDF) as:

$$\Phi_{Z} (z) = \int\limits_{{m_{1} }}^{H\left( z \right)} {f(v) dv}$$

,

Where $f(v)$ is the probability density function of a random variable $V$ taking values in the range $\left[ {m_{1} , m_{2} } \right]$ such that $- \infty \le m_{1} < m_{2} \le + \infty$; $Z$ is another random variable with CDF $G_{Z} (z)$, and $H(z)$ is a function of $G_{Z} (z)$. This function takes different forms as mentioned by Alzaatreh et al.²⁰. In this study, we consider the exponentiated odds function form,

$$H(z) = \left( {\frac{{G_{Z} (z)}}{{1 - G_{Z} (z)}}} \right)^{\lambda }$$

Therefore, the resulting cumulative distribution function of the new generalised probability distribution is

$$\Phi_{Z} (z) = \int\limits_{{m_{1} }}^{{\left( {\frac{{G_{Z} (z)}}{{1 - G_{Z} (z)}}} \right)^{\lambda } }} {f(v) dv} = F_{V} \left( {\left( {\frac{{G_{Z} (z)}}{{1 - G_{Z} (z)}}} \right)^{\lambda } } \right)$$

(1)

where, $F_{V} (v)$ is the cumulative distribution function of random variable $V$.

Recently, many researchers have focused on extending the flexibility of probability distributions by applying the T-X transformation approach. For instance, Hassan and Mohamed²¹ introduced the Weibull Inverse Lomax distribution, a four-parameter lifetime model. The authors²² developed the new generalization of the Power Lomax distribution with Topp-Leone type-II family. Using the Gompertz-G family, Gompertz Frechet distribution is introduced by Oguntunde et al.²³. Odd Frechet inverse Lomax distribution studied by ZeinEldin et al.²⁴ as an extension of inverse Lomax distribution using Frechet-G family. Marshall-Olkin Alpha Power Weibull distribution introduced by Almetwally et al.²⁵ as an extended generalization of the Weibull distribution. The new Exponential-X Frechet distribution developed by Alzeley et al.²⁶ through T-X method to increase the flexibility of Frechet distribution. The Odd Lomax inverted Nadarajah-Haghighi distribution has been studied by Almongy et al.²⁷ by incorporating inverted Nadarajah-Haghighi distribution with the Lomax-G family. Similarly, the authors^{28,29,30,31,32,33,34,35} and³⁶ have explored many probability distribution models using T-X transformation approach and have demonstrated their practical utility while analysing real-life datasets. Building upon this foundation, our study introduces a novel extension of the Power Lindley distribution, aiming to achieve superior performance compared to existing models. By capturing the complex dynamics of the data more effectively, this new distribution has the potential to offer valuable insights and contribute meaningfully to public health planning and decision-making.

The structure of the manuscript is organised to present a comprehensive understanding of the proposed model. Section “Exponentiated Odd Lomax Power Lindley distribution” outlines the derivation of the probability density function, cumulative distribution, survival function and failure rate, together with their graphical representation. Section “Linear Representation” is dedicated to a linear representation of the various theoretical properties of the developed model mentioned in Section “Exponentiated Odd Lomax Power Lindley distribution”. Section “Statistical Properties” explores the statistical moments, and reliability analysis measures of the underlying probability distribution model. Section “Ordered statistics” and Section “Entropy measures” address ordered statistics and entropy measures respectively. Parameter estimation techniques are discussed in detail under Sect. “Parameter Estimation”. Section “Simulation” presents an extensive simulation study to assess the performance of the different estimation techniques. In Sect. “Application”, the applicability of the model is demonstrated through analysis of real-life data sets. Finally, Sect. “Conclusion” concludes the manuscript with a summary of key findings and discussions.

Exponentiated odd lomax power lindley distribution

In this study, we introduce a novel and flexible probability distribution, termed the Exponentiated Odd Lomax Power Lindley (EOLxPL) distribution, by integrating the Power Lindley (PL) distribution as the baseline model within the Lomax-G family framework, as proposed by Dhungana and Kumar³⁰. This construction utilizes the versatile T-X transformation method, previously outlined in Sect. “Introduction”, which facilitates the development of complex distributional forms through systematic approach.

The Lomax-G family is a well-known heavy-tailed model extensively employed in diverse domains such as reliability engineering and survival analysis, medical sciences, actuarial science, economics, and environmental studies. Its capacity to accommodate extreme values and long right tails makes it a suitable generator for constructing new, flexible families of distributions such as Lomax-normal, Lomax–Weibull, Lomax-loglogistic, Lomax–Pareto distributions and many more. These models have shown greater flexibility in analysing real-life data.

The probability density function (PDF) and cumulative distribution function (CDF) of the Lomax distribution³⁷ are respectively defined as:

$$f(v; \alpha ,\beta ) = \left\{ {\begin{array}{*{20}c} {\frac{\alpha }{\beta }\left( {1 + \frac{v}{\beta }} \right)^{ - (\alpha + 1)} ,v> 0;\alpha ,\beta> 0} \\ {0,\,\quad \quad \quad \quad otherwise} \\ \end{array} } \right.$$

(2)

and

$$F_{V} (v) = 1 - \left( {1 + \frac{v}{\beta }} \right)^{( - \alpha )}$$

An essential tool used in enhancing distributional shapes is the Exponentiated Odd transformation, which modifies the baseline CDF by introducing parameters that offer control over skewness, kurtosis, and tail behaviour. This transformation, as introduced by Alzaatreh et al.²⁰, is particularly effective when modelling datasets with heavy tails, asymmetry, or multimodal patterns. The general form of the Exponentiated Odd transformation applied to a baseline CDF is given by:

$$H(z) = \left( {\frac{{G_{Z} (z)}}{{1 - G_{Z} (z)}}} \right)^{\lambda }$$

In the formulation of the EOLxPL distribution, we extend the Lomax generator with the exponentiated odd transformation applied to the Power Lindley distribution using the T-X methodology. This results in a five-parameter model that summarises the combined advantages of the three foundational techniques: The Power Lindley distribution for baseline flexibility, the Lomax distribution for tail robustness, and the exponentiated odd transformation for shape control.

The PL distribution, a two-parameter model introduced and extensively analysed by Ghitany et al.³⁸, offers greater flexibility compared to the standard Lindley distribution. It allows for more varied shapes in the density and hazard rate functions, as well as adjustments in skewness and kurtosis. Assuming that $Z$ be a random variable following PL distribution with parameters $(\gamma ; \delta )$. The PDF and the corresponding CDF are given by:

$$g(z;\gamma ,\delta ) = \left\{ \begin{gathered} \frac{{\gamma \delta^{2} (1 + z^{\gamma } )z^{\gamma - 1} e^{{ - \delta z^{\gamma } }} }}{(\delta + 1)},z> 0;\gamma ,\delta> 0 \hfill \\ 0,\quad \quad \quad \quad otherwise \hfill \\ \end{gathered} \right.$$

(3)

and

$$G_{Z} (z) = 1 - \left\{ {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right\}e^{{ - \delta z^{\gamma } }}$$

(4)

Now using Eq. (2) in the transformation explained in Eq. (1) we have

$$\Phi_{Z} (z) = \int\limits_{0}^{{\left( {\frac{{G_{Z} (z)}}{{1 - G_{Z} (z)}}} \right)^{\lambda } }} {\frac{\alpha }{\beta }\left( {1 + \frac{v}{\beta }} \right)^{ - (\alpha + 1)} dv}$$

$$\Phi_{Z} (z) = 1 - \left\{ {1 + \frac{1}{\beta }\left( {\frac{{G_{Z} (z)}}{{1 - G_{Z} (z)}}} \right)^{\lambda } } \right\}^{( - \alpha )}$$

(5)

where $G_{Z} (z)$ is the CDF of PL distribution defined in Eq. (4). Substituting the Eq. (4) in Eq. (5), we get

$$\Phi_{Z} (z) = 1 - \left\{ {1 + \frac{1}{\beta }\left( {\frac{{1 - \left\{ {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right\}e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right)^{\lambda } } \right\}^{( - \alpha )}$$

(6)

The expression represented by Eq. (6) is the required CDF of the newly explored probability distribution model named as EOLxPL distribution. The graphical pattern of the CDF of EOLxPL distribution is shown in Fig. 1, Fig. 2 as below:

Fig. 1

CDF plot of EOLxPL distribution under different parameter combinations.

Fig. 2

CDF plot of EOLxPL distribution under different parameter combinations.

To derive the PDF of EOLxPL distribution, we take the derivative of Eq. (5) with respect to z, which gives:

$$\varphi (z; \alpha , \beta , \gamma , \delta ,\lambda ) = \alpha \beta^{\alpha } \lambda \frac{g(z; \gamma ,\delta )}{{\left( {1 - G_{Z} (z)} \right)^{2} }}\left\{ {\beta + \left( {\frac{{G_{Z} (z)}}{{1 - G_{Z} (z)}}} \right)^{\lambda } } \right\}^{ - (\alpha + 1)} \left( {\frac{{G_{Z} (z)}}{{1 - G_{Z} (z)}}} \right)^{\lambda - 1}$$

(7)

where $g(z; \gamma ,\delta )$ and $G_{Z} (z)$ are the PDF and CDF of PL distribution defined in Eq. (3) and (4) respectively. Substituting Eq. (3) and (4) in Eq. (7) we obtain

$$\begin{gathered} \varphi (z; \alpha , \beta , \gamma , \delta ,\lambda ) = \alpha \beta^{\alpha } \lambda \frac{{\frac{{\gamma \delta^{2} (1 + z^{\gamma } ) z^{\gamma - 1} e^{{ - \delta z^{\gamma } }} }}{(\delta + 1)}}}{{\left[ {1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}} \right]^{2} }}\left[ {\beta + \left\{ {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right\}^{\lambda } } \right]^{ - (\alpha + 1)} \hfill \\ \quad \quad \quad \quad \quad \quad \times \left[ {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)}}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right]^{\lambda - 1} \hfill \\ \end{gathered}$$

(8)

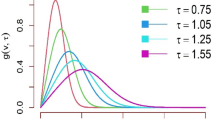
Equation (8) is the required PDF of EOLxPL distribution. The behaviour of the PDF of EOLxPL distribution is graphical explained in Fig. 3, Fig. 4 for different combination of parameters.

Fig. 3

PDF plot of EOLxPL distribution under different parameter combinations.

Fig. 4

PDF plot of EOLxPL distribution under different parameter combinations.

The PDF plot as shown in Fig. 3, demonstrate how variations in the shape parameters $\gamma$ and $\delta$, with fixed values of other parameters $\alpha = 1.3$, $\beta = 1.1$, and $\lambda = 4$ systematically influence the distributions form. A consistent pattern emerges as $\gamma$ and $\delta$ increase: the PDF becomes more peaked, less skewed, and increasingly concentrated around lower values of the random variable $Z$. Additionally, the tail behaviour changes significantly—distributions with smaller shape parameters exhibit heavier right tails, indicating a greater likelihood of extreme outcomes, while those with larger parameters display shorter, and lighter tails. The overall trend indicates a transition from broad, skewed, and heavy-tailed distributions to sharply peaked forms. Similarly, we can interpret Fig. 4.

Thus, the behaviour of PDF is strongly influenced by its underlying parameters, namely $\alpha$,$\beta$, $\gamma$, $\delta$, and $\lambda$, which respectively represent shape and scale. The parameters $\alpha$, $\gamma$, $\delta$, and $\lambda$ serve as shape parameters, governing the overall form of the distribution, including features like skewness, tail behaviour, and peak sharpness. The scale parameter $\beta$ controls the spread or dispersion of the distribution. Collectively, these parameters allow for high flexibility, enabling the PDF to adapt to a wide range of data characteristics by adjusting its symmetry, concentration, and central tendency. Such parameter-driven adaptability makes the distribution particularly effective for modelling diverse real-world datasets across various applications.

The survival function, which describe the behaviour of the EOLxPL distribution over time, are mathematically expressed as follows:

$$S_{Z} (z) = \left\{ {1 + \frac{1}{\beta }\left( {\frac{{1 - \left\{ {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right\}e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right)^{\lambda } } \right\}^{( - \alpha )}$$

The graphical behaviour of the survival function over different values of parameters is presented in Fig. 5 and Fig. 6.

Fig. 5

Survival function plot of EOLxPL distribution under different parameter combinations.

Fig. 6

Survival function plot of EOLxPL distribution under different parameter combinations.

Figure 5 and Fig. 6 illustrate the impact of varying different parameter values on the survival function’s behaviour. In Fig. 5, when parameters $\gamma$, $\delta$, and $\lambda$, are varied while keeping the remaining parameters $\alpha$ and $\beta$ constant, the survival curve shifts towards the origin. This indicates a higher likelihood of early failures, leading to a reduced expected lifespan and diminished system reliability. Conversely, in Fig. 6, parameters $\alpha$,$\beta$, and $\lambda$ while holding $\gamma$, and $\beta$ constant, results in the survival function shifting to the right. This shift signifies prolonged survival times, suggesting a lower failure rate, increased system longevity, and enhanced overall reliability.

The failure rate is a time-dependent function that quantifies the instantaneous likelihood of failure, given that the system or component has survived up to that specific time. For the EOLxPL distribution, the failure rate denoted by $F_{R} (z)$, is given by:

$$\begin{gathered} F_{R} (z) = \alpha \lambda \frac{{\frac{{\gamma \delta^{2} (1 + z^{\gamma } ) z^{\gamma - 1} e^{{ - \delta z^{\gamma } }} }}{(\delta + 1)}}}{{\left[ {1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}} \right]^{2} }}\left[ {\beta + \left\{ {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right\}^{\lambda } } \right]^{ - 1} \hfill \\ \quad \quad \quad \times \left[ {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right]^{\lambda - 1} \hfill \\ \end{gathered}$$

Figure 7 depicts the variation in the failure rate of the EOLxPL distribution corresponding to different parameter values.

Fig. 7

Failure rate plot of EOLxPL distribution under different parameter combinations.

The failure rate plot shown in Fig. 7, demonstrates the flexibility and richness of the model in capturing various failure rate behaviours through parameter variation. The curves exhibit a wide range of shapes, including monotonically increasing and decreasing, unimodal (hump-shaped), and bathtub-shaped hazard rates. This diversity reflects the model’s ability to represent systems with different reliability characteristics—such as early-life failures, aging effects, and systems with constant or varying risk over time. Such adaptability makes the model highly suitable for real-world reliability and survival analysis data where failure patterns are often complex and non-linear.

Linear representation

In this section, we will provide linear representation of the various theoretical properties of the EOLxPL distribution mentioned in Section “Exponentiated Odd Lomax Power Lindley distribution” such as PDF, CDF, survival function and failure rate. With the help of these linear representations, various statistical properties of the developed model can be easily evaluated. Such approach aims to enhance our ability to examine and interpret the behaviour of the EOLxPL distribution and draw valuable insights for its application and further development.

Consider the power series expansion for $(1 + \Delta )^{ - s}$ and $(1 - \Delta )^{ - s}$ provided $|\Delta | < 1$, which are respectively expressed mathematically as

$$(1 + \Delta )^{ - s} = \sum\limits_{i = 0}^{\infty } {\left( {^{ - s} C_{i} } \right)\Delta^{i} ;} \quad provided|\Delta | < 1$$

(9)

and

$$(1 - \Delta )^{ - s} = \sum\limits_{i = 0}^{\infty } {\left( {{}^{ - s}C_{i} } \right)( - 1)^{i} \Delta^{i} ; \quad \quad \quad provided|\Delta | < 1}$$

(10)

From Eq. (5), we have

$$\Phi_{Z} (z) = 1 - \left\{ {1 + \frac{1}{\beta }\left( {\frac{{G_{Z} (z)}}{{1 - G_{Z} (z)}}} \right)^{\lambda } } \right\}^{( - \alpha )}$$

To ensure the validity of the series expansion used in the expression

$$\left\{ {1 + \frac{1}{\beta }\left( {\frac{{G_{Z} (z)}}{{1 - G_{Z} (z)}}} \right)^{\lambda } } \right\}^{( - \alpha )}$$

it is necessary to establish the convergence of the associated power series. Specifically, we express this term as a generalized binomial expansion of the form $(1 + \Delta )^{ - s} = \sum\limits_{i = 0}^{\infty } {\left( {{}^{ - s}C_{i} } \right) \Delta^{i} }$, which converges absolutely for $|\Delta | < 1$. In our case, the expansion variable is

$$\Delta = \frac{1}{\beta }\left( {\frac{{G_{Z} (z)}}{{1 - G_{Z} (z)}}} \right)^{\lambda }$$

where $G_{Z} (z)$ is the CDF, satisfying $0 \le G_{Z} (z) \le 1$, so for the convergence of the expansion across the domain of interest, the following condition of convergence must be satisfied

$$\left| {\frac{1}{\beta }\left( {\frac{{G_{Z} (z)}}{{1 - G_{Z} (z)}}} \right)^{\lambda } < 1} \right|$$

$$\Rightarrow \left( {\frac{{G_{Z} (z)}}{{1 - G_{Z} (z)}}} \right)^{\lambda } < \beta$$

Under this condition the expansion.

$\left\{ {1 + \frac{1}{\beta }\left( {\frac{{G_{Z} (z)}}{{1 - G_{Z} (z)}}} \right)^{\lambda } } \right\}^{( - \alpha )} = \sum\limits_{i = 0}^{\infty } {\left( {{}^{ - \alpha }C_{i} } \right) \frac{1}{{\beta^{i} }}\left( {\left( {\frac{{G_{Z} (z)}}{{1 - G_{Z} (z)}}} \right)^{\lambda } } \right)^{i} }$ converges absolutely.

Now, Using the power series expansion mentioned in Eq. (9) and Eq. (10), we obtain

$$\Phi_{Z} (z) = 1 - \sum\limits_{i = 0}^{\infty } {\left( {{}^{ - \alpha }C_{i} } \right) \frac{1}{{\beta^{i} }}\left( {\left( {\frac{{G_{Z} (z)}}{{1 - G_{Z} (z)}}} \right)^{\lambda } } \right)^{i} }$$

$$\Phi_{Z} (z) = 1 - \sum\limits_{i = 0}^{\infty } {\left( {{}^{ - \alpha }C_{i} } \right) \frac{1}{{\beta^{i} }}\left( {G_{Z} (z)} \right)^{\lambda i} \left( {1 - G_{Z} (z)} \right)^{ - \lambda i} }$$

$$\Phi_{Z} (z) = 1 - \sum\limits_{i = 0}^{\infty } {\left( {{}^{ - \alpha }C_{i} } \right) \frac{1}{{\beta^{i} }}\left( {G_{Z} (z)} \right)^{\lambda i} \sum\limits_{j = 0}^{\infty } {( - 1)^{j} \left( {{}^{ - \lambda i}C_{j} } \right) } \left( {G_{Z} (z)} \right)^{j} }$$

$$\Phi_{Z} (z) = 1 - \sum\limits_{i = 0}^{\infty } {\sum\limits_{j = 0}^{\infty } {( - 1)^{j} \left( {{}^{ - \alpha }C_{i} } \right)\left( {{}^{ - \lambda i}C_{j} } \right) } \frac{1}{{\beta^{i} }}\left( {G_{Z} (z)} \right)^{\lambda i + j} }$$

$$\Phi_{Z} (z) = 1 - \sum\limits_{i = 0}^{\infty } {\sum\limits_{j = 0}^{\infty } {\frac{{( - 1)^{j} \left( {{}^{ - \alpha }C_{i} } \right)\left( {{}^{ - \lambda i}C_{j} } \right)}}{{\beta^{i} }} } \left[ {1 - \left\{ {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right\}e^{{ - \delta z^{\gamma } }} } \right]^{\lambda i + j} }$$

(11)

Again using the power series expansion for $\left[ {1 - \left\{ {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right\}e^{{ - \delta z^{\gamma } }} } \right]^{\lambda i + j}$, and it will be expanded as

$$\left[ {1 - \left\{ {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right\}e^{{ - \delta z^{\gamma } }} } \right]^{\lambda i + j} = \sum\limits_{k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {( - 1)^{k} \left( {{}^{\lambda i + j}C_{k} } \right) \left( {{}^{k}C_{l} } \right)\left( {\frac{\delta }{\delta + 1}} \right)^{l} z^{l \gamma } } e^{{ - \delta k z^{\gamma } }} }$$

On substituting the value of above expression in Eq. (11), the required representation of the CDF of EOLxPL distribution is

$$\Phi_{Z} (z) = 1 - \sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\left( {( - 1)^{j + k} \left( {{}^{ - \alpha }C_{i} } \right) \left( {{}^{ - \lambda i}C_{j} } \right) \left( {{}^{\lambda i + j}C_{k} } \right) \left( {{}^{k}C_{l} } \right)} \right) \left( {\frac{1}{{\beta^{i} }}} \right)\left( {\frac{\delta }{\delta + 1}} \right)^{l} z^{l \gamma } e^{{ - \delta k z^{\gamma } }} } }$$

$$\Phi_{Z} (z) = 1 - \sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Theta (i,j,k,l,\alpha ,\lambda ) \left( {\frac{1}{{\beta^{i} }}} \right)\left( {\frac{\delta }{\delta + 1}} \right)^{l} z^{l \gamma } e^{{ - \delta k z^{\gamma } }} } }$$

(12)

where,

$$\Theta (i,j,k,l,\alpha ,\lambda ) = \left( {( - 1)^{j + k} \left( {{}^{ - \alpha }C_{i} } \right) \left( {{}^{ - \lambda i}C_{j} } \right) \left( {{}^{\lambda i + j}C_{k} } \right) \left( {{}^{k}C_{l} } \right)} \right)$$

Similarly, the PDF, survival function and failure rate of EOLxPL distribution using power series expansions can be expressed as

$$\begin{gathered} \varphi (z; \alpha , \beta , \gamma , \delta ,\lambda ) = \sum\limits_{i = 0}^{\infty } {\sum\limits_{j = 0}^{\infty } {\sum\limits_{k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {( - 1)^{j + k} \left( {{}^{ - (\alpha + 1)}C_{i} } \right) \left( {{}^{ - (\lambda (i + 1) + 1)}C_{j} } \right) \left( {{}^{\lambda ( i + 1) + j - 1}C_{k} } \right) \left( {{}^{k}C_{l} } \right) } } } } \hfill \\ \quad \quad \quad \times \frac{{\alpha \lambda \gamma \delta^{l + 2} (1 + z^{\gamma } ) (z)^{\gamma (l + 1) - 1} e^{{ - \delta (k + 1) z^{\gamma } }} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }} \hfill \\ \end{gathered}$$

$$\varphi (z; \alpha , \beta , \gamma , \delta ,\lambda ) = \sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \gamma \delta^{l + 2} (1 + z^{\gamma } ) (z)^{\gamma (l + 1) - 1} e^{{ - \delta (k + 1) z^{\gamma } }} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }}$$

(13)

where,

$$\Omega (i,j,k,l,\alpha ,\lambda ) = ( - 1)^{j + k} \left( {{}^{ - (\alpha + 1)}C_{i} } \right) \left( {{}^{ - (\lambda (i + 1) + 1)}C_{j} } \right) \left( {{}^{\lambda ( i + 1) + j - 1}C_{k} } \right) \left( {{}^{k}C_{l} } \right)$$

$$S_{Z} (z) = \sum\limits_{i = 0}^{\infty } {\sum\limits_{j = 0}^{\infty } {\sum\limits_{k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\frac{{( - 1)^{j + k} \left( {{}^{ - \alpha }C_{i} } \right) \left( {{}^{ - \lambda i}C_{j} } \right) \left( {{}^{\lambda i + j}C_{k} } \right) \left( {{}^{k}C_{l} } \right)}}{{\beta^{i} }} } } } \left( {\frac{\delta }{\delta + 1}} \right)^{l} z^{l \gamma } e^{{ - \delta k z^{\gamma } }} }$$

$$S_{Z} (z) = \sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Theta (i,j,k,l,\alpha ,\lambda ) \left( {\frac{1}{{\beta^{i} }}} \right)\left( {\frac{\delta }{\delta + 1}} \right)^{l} z^{l \gamma } e^{{ - \delta k z^{\gamma } }} } }$$

and

$$F_{R} (z) = \left[ {\frac{{\sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \gamma \delta^{l + 2} (1 + z^{\gamma } ) (z)^{\gamma (l + 1) - 1} e^{{ - \delta (k + 1) z^{\gamma } }} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }}}}{{\sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Theta (i,j,k,l,\alpha ,\lambda ) \left( {\frac{1}{{\beta^{i} }}} \right)\left( {\frac{\delta }{\delta + 1}} \right)^{l} z^{l \gamma } e^{{ - \delta k z^{\gamma } }} } } }}} \right]$$

Statistical properties

Moments

The $q^{th}$ moment about origin for the EOLxPL distribution usually denoted by $\mu^{\prime}_{q}$ is given by

$$\mu^{\prime}_{q} = E(Z^{q} ) = \int\limits_{0}^{\infty } {z^{q} \varphi (z; \alpha , \beta , \gamma , \delta ,\lambda )} dz$$

(14)

For computing the moments of the EOLxPL distribution, we will use linear representation of the PDF explained in the Eq. (13). Therefore, from Eq. (14) we have

$$\mu^{\prime}_{q} = \int\limits_{0}^{\infty } {\left[ {z^{q} \sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \gamma \delta^{l + 2} (1 + z^{\gamma } ) (z)^{\gamma (l + 1) - 1} e^{{ - \delta (k + 1) z^{\gamma } }} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }}} \right]} dz$$

$$\mu^{\prime}_{q} = \sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \gamma \delta^{l + 2} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }}\left[ {\int\limits_{0}^{\infty } {e^{{ - \delta (k + 1) z^{\gamma } }} (z)^{\gamma (l + 1) + q - 1} dz + \int\limits_{0}^{\infty } {e^{{ - \delta (k + 1) z^{\gamma } }} (z)^{\gamma (l + 2) + q - 1} dz} } } \right]$$

Now make transformation $z^{\gamma } = y$, so $dz = \frac{{y^{{\frac{1 - \gamma }{\gamma }}} }}{\gamma }dy$. Also ${\text{when}} z \to 0,{\text{then}} y \to 0$ and ${\text{when}} z \to \infty , {\text{then}} y \to \infty$.

$$\begin{gathered} \mu^{\prime}_{q} = \sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \gamma \delta^{l + 2} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }} \hfill \\ \quad \quad \quad \times \left[ {\frac{1}{\gamma }\int\limits_{0}^{\infty } {e^{ - \delta (k + 1) y} (y)^{{\frac{(\gamma (l + 1) + q - \gamma )}{\gamma }}} dy + \frac{1}{\gamma }\int\limits_{0}^{\infty } {e^{ - \delta (k + 1) y} (y)^{{\frac{(\gamma (l + 2) + q - \gamma )}{\gamma }}} dy} } } \right] \hfill \\ \end{gathered}$$

$$\mu^{\prime}_{q} = \sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \delta^{l + 2} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }}\left[ {\frac{{\Gamma \left( {\frac{(\gamma (l + 1) + q)}{\gamma }} \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 1) + q)}{\gamma }} \right)}} }} + \frac{{\Gamma \left( {\frac{(\gamma (l + 2) + q)}{\gamma }} \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 2) + q)}{\gamma }} \right)}} }}} \right]$$

(15)

Putting $q = 1, 2, 3, 4$ in Eq. (15), we obtain first four moments about origin for the EOLxPL distribution and are expressed as

$$\mu^{\prime}_{1} = \sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \delta^{l + 2} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }}\left[ {\frac{{\Gamma \left( {\frac{(\gamma (l + 1) + 1)}{\gamma }} \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 1) + 1)}{\gamma }} \right)}} }} + \frac{{\Gamma \left( {\frac{(\gamma (l + 2) + 1)}{\gamma }} \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 2) + 1)}{\gamma }} \right)}} }}} \right]$$

$$\mu^{\prime}_{2} = \sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \delta^{l + 2} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }}\left[ {\frac{{\Gamma \left( {\frac{(\gamma (l + 1) + 2)}{\gamma }} \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 1) + 2)}{\gamma }} \right)}} }} + \frac{{\Gamma \left( {\frac{(\gamma (l + 2) + 2)}{\gamma }} \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 2) + 2)}{\gamma }} \right)}} }}} \right]$$

$$\mu^{\prime}_{3} = \sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \delta^{l + 2} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }}\left[ {\frac{{\Gamma \left( {\frac{(\gamma (l + 1) + 3)}{\gamma }} \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 1) + 3)}{\gamma }} \right)}} }} + \frac{{\Gamma \left( {\frac{(\gamma (l + 2) + 3)}{\gamma }} \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 2) + 3)}{\gamma }} \right)}} }}} \right]$$

$$\mu^{\prime}_{4} = \sum\limits_{i,\,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \delta^{l + 2} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }}\left[ {\frac{{\Gamma \left( {\frac{(\gamma (l + 1) + 4)}{\gamma }} \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 1) + 4)}{\gamma }} \right)}} }} + \frac{{\Gamma \left( {\frac{(\gamma (l + 2) + 4)}{\gamma }} \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 2) + 4)}{\gamma }} \right)}} }}} \right]$$

So, the variance of the EOLxPL distribution usually denotes as $\mu_{2}$ is calculated from the above expressions using the relation

$$\mu_{2} = \mu^{\prime}_{2} - (\mu^{\prime}_{1} )^{2}$$

A detailed overview is presented in Table 1, highlighting how the central tendency, dispersion, and shape characteristics of the EOLxPL distribution vary with changes in its parameters.

Table 1 Summary of mean central tendency, dispersion, and shape characteristics of the EOLxPL distribution.

Incomplete moments

The $q^{th}$ incomplete moment about origin based on the EOLxPL distribution is defined as

$$IC_{q} = \int\limits_{0}^{s} {z^{q} \varphi (z; \alpha , \beta , \gamma , \delta ,\lambda )} dz$$

$$IC_{q} = \int\limits_{0}^{s} {\left[ {z^{q} \sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \gamma \delta^{l + 2} (1 + z^{\gamma } ) (z)^{\gamma (l + 1) - 1} e^{{ - \delta (k + 1) z^{\gamma } }} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }}} \right]} dz$$

Using the above transformation and after simplification we get,

$$IC_{q} = \sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \delta^{l + 2} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }}\left[ {\frac{{\gamma \left( {\frac{(\gamma (l + 1) + q)}{\gamma }; \delta (k + 1)(z)^{r} } \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 1) + q)}{\gamma }} \right)}} }} + \frac{{\gamma \left( {\frac{(\gamma (l + 2) + q)}{\gamma }; \delta (k + 1)(z)^{r} } \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 2) + q)}{\gamma }} \right)}} }}} \right]$$

Moment generating function

The moment generating function associated with EOLxPL distribution is given by

$$\begin{gathered} M_{Z} (t) = \int\limits_{0}^{\infty } {e^{t z} \varphi (z; \alpha , \beta , \gamma , \delta ,\lambda )} dz \hfill \\ M_{Z} (t) = \sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\sum\limits_{v = 0}^{\infty } {\Omega (i,j,k,l,\alpha ,\lambda )} } } \frac{{(t)^{v} }}{v !}\frac{{\alpha \lambda \gamma \delta^{l + 2} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }}\left[ {\int\limits_{0}^{\infty } {e^{{ - \delta (k + 1) z^{\gamma } }} (z)^{\gamma (l + 1) + q + v - 1} dz + \int\limits_{0}^{\infty } {e^{{ - \delta (k + 1) z^{\gamma } }} (z)^{\gamma (l + 2) + q + v - 1} dz} } } \right] \hfill \\ M_{Z} (t) = \sum\limits_{i,j,k,v = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \gamma \delta^{l + 2} (t)^{v} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} (v !)}}\left[ {\int\limits_{0}^{\infty } {e^{{ - \delta (k + 1) z^{\gamma } }} (z)^{\gamma (l + 1) + q + v - 1} dz + \int\limits_{0}^{\infty } {e^{{ - \delta (k + 1) z^{\gamma } }} (z)^{\gamma (l + 2) + q + v - 1} dz} } } \right] \hfill \\ M_{Z} (t) = \sum\limits_{i,j,k,v = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \gamma \delta^{l + 2} (t)^{v} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} (v !)}}\left[ {\frac{{\Gamma \left( {\frac{(\gamma (l + 1) + q + v)}{\gamma }} \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 1) + q + v)}{\gamma }} \right)}} }} + \frac{{\Gamma \left( {\frac{(\gamma (l + 2) + q + v)}{\gamma }} \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 2) + q + v)}{\gamma }} \right)}} }}} \right] \hfill \\ \end{gathered}$$

Similarly, the characteristics function $Cz(t)$ and the cumulant generating function $Kz(t)$ are mathematically expressed as

$$\begin{gathered} C_{Z} (t) = \sum\limits_{i,j,k,v = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \gamma \delta^{l + 2} (\iota t)^{v} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} (v !)}}\left[ {\frac{{\Gamma \left( {\frac{(\gamma (l + 1) + q + v)}{\gamma }} \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 1) + q + v)}{\gamma }} \right)}} }} + \frac{{\Gamma \left( {\frac{(\gamma (l + 2) + q + v)}{\gamma }} \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 2) + q + v)}{\gamma }} \right)}} }}} \right] \hfill \\ and \hfill \\ K_{Z} (t) = \log \left[ {\sum\limits_{i,j,k,v = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \gamma \delta^{l + 2} (t)^{v} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} (v !)}}\left\{ {\frac{{\Gamma \left( {\frac{(\gamma (l + 1) + q + v)}{\gamma }} \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 1) + q + v)}{\gamma }} \right)}} }} + \frac{{\Gamma \left( {\frac{(\gamma (l + 2) + q + v)}{\gamma }} \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 2) + q + v)}{\gamma }} \right)}} }}} \right\}} \right] \hfill \\ \end{gathered}$$

Mean residual life and mean past life

In the field of reliability theory and survival analysis, the concept of mean residual life (MRL) and mean past life (MPL) are essential for studying the behaviour of lifetimes of systems or components. These functions provide useful insights about the remaining and elapsed lifetime of a component, which are essential in modelling, diagnostics, and decision-making in engineering, biomedical studies, and actuarial science.

The MRL determines the average time a component is expected to continue working after time $T$, provided it is still working at time $T$. This measure is important in maintenance and warranty analysis, helping to assess when a component may likely fail after operating for a certain period. Under the assumption that the lifetime $T$ of the component follows EOLxPL distribution, the MRL is defined as:

$$\begin{gathered} MRL(T; \alpha , \beta , \gamma , \delta ,\lambda ) = E(T - t|T> t) = \frac{1}{{1 - \Phi_{T} (t)}}\int\limits_{t}^{\infty } t \varphi (t; \alpha , \beta , \gamma , \delta ,\lambda )dt - t \hfill \\ MRL(T; \alpha , \beta , \gamma , \delta ,\lambda ) = \frac{1}{{1 - \Phi_{T} (t)}}\int\limits_{t}^{\infty } {\left[ {t\sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \gamma \delta^{l + 2} (1 + t^{\gamma } ) (t)^{\gamma (l + 1) - 1} e^{{ - \delta (k + 1) t^{\gamma } }} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }}} \right]} dt - t \hfill \\ MRL(T; \alpha , \beta , \gamma , \delta ,\lambda ) = \frac{1}{{1 - \Phi_{T} (t)}}\sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )\frac{{\alpha \lambda \gamma \delta^{l + 2} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }}} } \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \times \int\limits_{z}^{\infty } {\left[ { (t)^{\gamma (l + 1) + 1 - 1} e^{{ - \delta (k + 1) t^{\gamma } }} + (t)^{\gamma (l + 1) + \gamma + 1 - 1} e^{{ - \delta (k + 1) t^{\gamma } }} } \right]} dt - t \hfill \\ MRL(T; \alpha , \beta , \gamma , \delta ,\lambda ) = \frac{1}{{1 - \Phi_{T} (t)}}\sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \delta^{l + 2} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \times \left[ {\frac{{\Gamma \left( {\frac{(\gamma (l + 1) + 1)}{\gamma }; \delta (k + 1)(t)^{r} } \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 1) + 1)}{\gamma }} \right)}} }} + \frac{{\Gamma \left( {\frac{(\gamma (l + 2) + 1)}{\gamma }; \delta (k + 1)(t)^{r} } \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 2) + 1)}{\gamma }} \right)}} }}} \right] - t \hfill \\ \end{gathered}$$

where, $\Phi_{T} (t)$ is the CDF of EOLxPL distribution with expression given in Eq. (12).

Similarly, The MPL measures the average lifetime of the components that have failed before or at time T. It presents the past behaviour of failures and helps in studying post-failure analysis of the component. The MPL is important in the fields like warranty return analysis, used product market analysis, forensics, and many more areas. For the lifetime $T$ of the component following EOLxPL distribution, the MPL is defined as:

$$MPL(T; \alpha , \beta , \gamma , \delta ,\lambda ) = E(t - T|T \le t) = t - \frac{1}{{\Phi_{T} (t)}}\int\limits_{0}^{t} t \varphi (t; \alpha , \beta , \gamma , \delta ,\lambda )dt$$

$$MPL(T; \alpha , \beta , \gamma , \delta ,\lambda ) = t - \frac{1}{{\Phi_{T} (t)}}\int\limits_{0}^{t} {\left[ {t\sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \gamma \delta^{l + 2} (1 + t^{\gamma } ) (t)^{\gamma (l + 1) - 1} e^{{ - \delta (k + 1) t^{\gamma } }} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }}} \right]} dt$$

$$\begin{gathered} MPL(T; \alpha , \beta , \gamma , \delta ,\lambda ) = t - \frac{1}{{\Phi_{T} (t)}}\sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )\frac{{\alpha \lambda \gamma \delta^{l + 2} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }}} } \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \times \int\limits_{0}^{t} {\left[ { (t)^{\gamma (l + 1) + 1 - 1} e^{{ - \delta (k + 1) t^{\gamma } }} + (t)^{\gamma (l + 1) + \gamma + 1 - 1} e^{{ - \delta (k + 1) t^{\gamma } }} } \right]} dt \hfill \\ \end{gathered}$$

$$\begin{gathered} MPL(T; \alpha , \beta , \gamma , \delta ,\lambda ) = t - \frac{1}{{\Phi_{T} (t)}}\sum\limits_{i,j,k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\Omega (i,j,k,l,\alpha ,\lambda )} } \frac{{\alpha \lambda \delta^{l + 2} }}{{\beta^{i + 1} (\delta + 1)^{l + 1} }} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \times \left[ {\frac{{\gamma \left( {\frac{(\gamma (l + 1) + 1)}{\gamma }; \delta (k + 1)(t)^{r} } \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 1) + 1)}{\gamma }} \right)}} }} + \frac{{\gamma \left( {\frac{(\gamma (l + 2) + 1)}{\gamma }; \delta (k + 1)(t)^{r} } \right)}}{{\left\{ {\delta (k + 1)} \right\}^{{\left( {\frac{(\gamma (l + 2) + 1)}{\gamma }} \right)}} }}} \right] \hfill \\ \end{gathered}$$

Ordered statistics

Ordered statistics is a fundamental concept in statistical theory and data analysis, focusing on the properties and behaviour of data points when arranged in a specific order. Specifically, it involves studying the values that correspond to certain positions in a sorted sequence of observations. Ordered statistics plays an important role in both descriptive and inferential statistics, helping to characterize data, identify trends, and perform hypothesis testing.

Ordered statistics refer to the statistics that are derived from the values of sample observations once they have been arranged in ascending or descending order. Consider a random sample $z_{1} , z_{2} , z_{3} ,..., z_{n}$ of size $n$ following EOLxPL distribution. Then the ordered statistics corresponding to the given random sample is $\left( {Z_{(1)} , Z_{(2)} , Z_{(3)} ,..., Z_{(n)} } \right)$ such that.

$Z_{(1)} = \min (z_{1} , z_{2} , z_{3} ,..., z_{n} )$ and $Z_{(n)} = \max (z_{1} , z_{2} , z_{3} ,..., z_{n} )$.

In this section, we will obtain the PDF for the minimum and maximum ordered statistics. The PDF of the $i^{th}$ ordered statistics based on EOLxPL distribution is

$$\varphi_{{Z_{(i)} }} (z; \alpha , \beta , \gamma , \delta ,\lambda ) = \frac{n !}{{(n - i) ! (i - 1) !}}\varphi (z; \alpha , \beta , \gamma , \delta ,\lambda )\left[ {\Phi_{Z} (z)} \right]^{i - 1} \left[ {1 - \Phi_{Z} (z)} \right]^{n - i}$$

On substituting Eq. (6) and Eq. (8) in the above expression, the required PDF of the $i^{th}$ ordered statistics is given by

$$\begin{aligned} \begin{gathered} \varphi_{{Z_{(i)} }} (z; \alpha , \beta , \gamma , \delta ,\lambda ) = \frac{n !}{{(n - i) ! (i - 1) !}}\alpha \beta^{\alpha (n - i + 1)} \lambda \frac{{\frac{{\gamma \delta^{2} (1 + z^{\gamma } ) z^{\gamma - 1} e^{{ - \delta z^{\gamma } }} }}{(\delta + 1)}}}{{\left[ {1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}} \right]^{2} }} \\\left\{ {\beta + \left( {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right)^{\lambda } } \right\}^{ - (\alpha + 1) - \alpha (n - i)} \hfill \\ \quad \quad \quad \quad \times \left[ {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right]^{\lambda - 1} \times \left[ {1 - \left\{ {1 + \frac{1}{\beta }\left( {\frac{{1 - \left\{ {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right\}e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right)^{\lambda } } \right\}^{( - \alpha )} } \right]^{i - 1} \hfill \\ \end{gathered}\end{aligned}$$

(16)

Put $i = 1 {\text{and}} n$ in Eq. (16), we get the PDF of minimum and maximum ordered statistics for EOLxPL distribution respectively. That.

$$\begin{gathered} \varphi_{{Z_{(1)} }} (z; \alpha , \beta , \gamma , \delta ,\lambda ) = n\alpha \beta^{\alpha n} \lambda \frac{{\frac{{\gamma \delta^{2} (1 + z^{\gamma } ) z^{\gamma - 1} e^{{ - \delta z^{\gamma } }} }}{(\delta + 1)}}}{{\left[ {1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}} \right]^{2} }}\left\{ {\beta + \left( {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right)^{\lambda } } \right\}^{ - (\alpha n + 1)} \hfill \\ \quad {\kern 1pt} \quad \quad \quad \quad \quad \quad \times \left[ {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right]^{\lambda - 1} \hfill \\ {\text{and}} \hfill \\ \varphi_{{Z_{(n)} }} (z; \alpha , \beta , \gamma , \delta ,\lambda ) = n\alpha \beta^{\alpha } \lambda \frac{{\frac{{\gamma \delta^{2} (1 + z^{\gamma } ) z^{\gamma - 1} e^{{ - \delta z^{\gamma } }} }}{(\delta + 1)}}}{{\left[ {1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}} \right]^{2} }}\left\{ {\beta + \left( {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right)^{\lambda } } \right\}^{ - (\alpha + 1)} \hfill \\ \times \left[ {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right]^{\lambda - 1} \times \left[ {1 - \left\{ {1 + \frac{1}{\beta }\left( {\frac{{1 - \left\{ {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right\}e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right)^{\lambda } } \right\}^{( - \alpha )} } \right]^{n - 1} \hfill \\ \end{gathered}$$

Entropy measures

Entropy is a foundational concept in several scientific disciplines, including information theory, physics (thermodynamics), statistics, and even machine learning. While its specific interpretation varies by field, the core idea revolves around uncertainty, randomness, or information content.

Entropy was formally introduced by Claude Shannon³⁹ as a measure of the uncertainty or unpredictability associated with a random variable or information source. If the outcome of a random process is highly predictable, entropy is low (close to zero). If the outcome is very uncertain or random, entropy is high. In this section we consider two entropy measures namely Renyi’s entropy⁴⁰ and Tsalli’s entropy⁴¹ for the EOLxPL distribution. The Renyi’s entropy associated with EOLxPL distribution is defined as:

$$E_{R} (\varsigma ) = \frac{1}{1 - \varsigma }\log \left\{ {\int\limits_{0}^{\infty } {\left[ {\varphi (z; \alpha , \beta , \gamma , \delta ,\lambda )} \right]^{\varsigma } dz} } \right\}$$

$$E_{R} (\varsigma ) = \frac{1}{1 - \varsigma }\log \left\{ {\int\limits_{0}^{\infty } {\left[ \begin{gathered} \alpha \beta^{\alpha } \lambda \frac{{\frac{{\gamma \delta^{2} (1 + z^{\gamma } ) z^{\gamma - 1} e^{{ - \delta z^{\gamma } }} }}{(\delta + 1)}}}{{\left[ {1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}} \right]^{2} }}\left[ {\beta + \left\{ {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right\}^{\lambda } } \right]^{ - (\alpha + 1)} \hfill \\ \quad \quad \times \left[ {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right]^{\lambda - 1} \hfill \\ \end{gathered} \right]^{\varsigma } dz} } \right\}$$

$$E_{R} (\varsigma ) = \frac{1}{1 - \varsigma }\log \left\{ {\int\limits_{0}^{\infty } {\left[ \begin{gathered} (\alpha \lambda )^{\varsigma } (\beta )^{ - \varsigma } \frac{{\frac{{(\gamma \delta^{2} )^{\varsigma } (1 + z^{\gamma } )^{\varsigma } z^{(\gamma - 1) \varsigma } e^{{ - \delta \varsigma z^{\gamma } }} }}{{(\delta + 1)^{\varsigma } }}}}{{\left[ {1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}} \right]^{2 \varsigma } }}\left[ {1 + \frac{1}{\beta }\left\{ {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right\}^{\lambda } } \right]^{ - \varsigma (\alpha + 1)} \hfill \\ \quad \quad \quad \quad \times \left[ {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right]^{\varsigma (\lambda - 1)} \hfill \\ \end{gathered} \right]dz} } \right\}$$

Using the power series expression for $\left[ {1 + \frac{1}{\beta }\left\{ {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right\}^{\lambda } } \right]^{ - \varsigma (\alpha + 1)}$we get,

$$E_{R} (\varsigma ) = \frac{1}{1 - \varsigma }\log \left\{ {\int\limits_{0}^{\infty } {\left[ \begin{gathered} (\alpha \lambda )^{\varsigma } (\beta )^{ - \varsigma } \frac{{\frac{{(\gamma \delta^{2} )^{\varsigma } (1 + z^{\gamma } )^{\varsigma } z^{(\gamma - 1) \varsigma } e^{{ - \delta \varsigma z^{\gamma } }} }}{{(\delta + 1)^{\varsigma } }}}}{{\left[ {1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}} \right]^{2 \varsigma } }} \times \left[ {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right]^{\varsigma (\lambda - 1)} \hfill \\ \times \sum\limits_{i = 0}^{\infty } {\left( {{}^{ - \varsigma (\alpha + 1)}C_{i} } \right) \left( {\frac{1}{\beta }} \right)^{i} \left\{ {\frac{{1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} }}{{1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}}}} \right\}^{\lambda i} } \hfill \\ \end{gathered} \right]dz} } \right\}$$

$$E_{R} (\varsigma ) = \frac{1}{1 - \varsigma }\log \left\{ {\int\limits_{0}^{\infty } {\left[ \begin{gathered} (\alpha \lambda )^{\varsigma } (\beta )^{ - \varsigma } \frac{{(\gamma \delta^{2} )^{\varsigma } (1 + z^{\gamma } )^{\varsigma } z^{(\gamma - 1) \varsigma } e^{{ - \delta \varsigma z^{\gamma } }} }}{{(\delta + 1)^{\varsigma } }}\sum\limits_{i = 0}^{\infty } {\left( {{}^{ - \varsigma (\alpha + 1)}C_{i} } \right)\left( {\frac{1}{\beta }} \right)^{i} \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}^{\lambda (i + \varsigma ) - \varsigma } } \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \times \left[ {1 - \left\{ {1 - \left( {1 + \left( {\frac{\delta }{\delta + 1}} \right)z^{\gamma } } \right)e^{{ - \delta z^{\gamma } }} } \right\}} \right]^{ - (\lambda (\iota + \varsigma ) + \varsigma )} \hfill \\ \end{gathered} \right]dz} } \right\}$$

$$E_{R} (\varsigma ) = \frac{1}{1 - \varsigma }\log \left\{ {\int\limits_{0}^{\infty } {\left[ {(\alpha \lambda )^{\varsigma } (\beta )^{ - \varsigma } \frac{{(\gamma \delta^{2} )^{\varsigma } (1 + z^{\gamma } )^{\varsigma } z^{(\gamma - 1) \varsigma } e^{{ - \delta \varsigma z^{\gamma } }} }}{{(\delta + 1)^{\varsigma } }}\sum\limits_{i = 0}^{\infty } {} } \right]dz} } \right\}$$

Again, using power series expression and after some simplification, we obtain

$$E_{R} (\varsigma ) = \frac{1}{1 - \varsigma }\log \left\{ \begin{gathered} \sum\limits_{i = 0}^{\infty } {\sum\limits_{j = 0}^{\infty } {\sum\limits_{k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\sum\limits_{m = 0}^{\infty } {\left( {{}^{ - \varsigma (\alpha + 1)}C_{i} } \right) \left( {{}^{ - (\lambda (i + \varsigma ) + \varsigma )}C_{j} } \right) \left( {{}^{\lambda (i + \varsigma ) + j - \varsigma )}C_{k} } \right) \left( {{}^{k}C_{l} } \right) \left( {{}^{\varsigma }C_{m} } \right)} } } } ( - 1)^{j} } \hfill \\ (\alpha \lambda )^{\varsigma } (\beta )^{ - (\varsigma - i)} \frac{{(\gamma )^{\varsigma } (\delta^{2} )^{\varsigma + l} }}{{(\delta + 1)^{\varsigma + l} }}\int\limits_{0}^{\infty } {z^{\gamma ( \varsigma + m + l) - \varsigma } e^{{ - \delta ( \varsigma + k)z^{\gamma } }} dz} \hfill \\ \end{gathered} \right\}$$

Now make a substitution $w = z^{\gamma }$. So,

$$z = (w)^{{\frac{1}{\gamma }}}$$

$$dz = \frac{1}{\gamma }(w)^{{\frac{1}{\gamma } - 1}} dw$$

Also, when $z \to 0, {\text{then}} w \to 0$ and when $z \to \infty , {\text{then}} w \to \infty$. Therefore,

$$E_{R} (\varsigma ) = \frac{1}{1 - \varsigma }\log \left\{ \begin{gathered} \sum\limits_{i = 0}^{\infty } {\sum\limits_{j = 0}^{\infty } {\sum\limits_{k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\sum\limits_{m = 0}^{\infty } {\left( {{}^{ - \varsigma (\alpha + 1)}C_{i} } \right) \left( {{}^{ - (\lambda (i + \varsigma ) + \varsigma )}C_{j} } \right) \left( {{}^{\lambda (i + \varsigma ) + j - \varsigma )}C_{k} } \right) \left( {{}^{k}C_{l} } \right) \left( {{}^{\varsigma }C_{m} } \right)} } } } ( - 1)^{j} } \hfill \\ (\alpha \lambda )^{\varsigma } (\beta )^{ - (\varsigma - i)} \frac{{(\gamma )^{\varsigma } (\delta^{2} )^{\varsigma + l} }}{{(\delta + 1)^{\varsigma + l} }}\int\limits_{0}^{\infty } {e^{ - \delta ( \varsigma + k)w} (w)^{{\frac{\gamma (\varsigma + m + l) - \varsigma }{\gamma }}} \frac{1}{\gamma }(w)^{{\frac{1}{\gamma } - 1}} dw} \hfill \\ \end{gathered} \right\}$$

$$E_{R} (\varsigma ) = \frac{1}{1 - \varsigma }\log \left\{ \begin{gathered} \sum\limits_{i = 0}^{\infty } {\sum\limits_{j = 0}^{\infty } {\sum\limits_{k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\sum\limits_{m = 0}^{\infty } {\left( {{}^{ - \varsigma (\alpha + 1)}C_{i} } \right) \left( {{}^{ - (\lambda (i + \varsigma ) + \varsigma )}C_{j} } \right) \left( {{}^{\lambda (i + \varsigma ) + j - \varsigma )}C_{k} } \right) \left( {{}^{k}C_{l} } \right) \left( {{}^{\varsigma }C_{m} } \right)} } } } ( - 1)^{j} } \hfill \\ \times (\alpha \lambda )^{\varsigma } (\beta )^{ - (\varsigma - i)} \frac{{(\gamma )^{\varsigma - 1} (\delta^{2} )^{\varsigma + l} }}{{(\delta + 1)^{\varsigma + l} }}\frac{{\Gamma \left( {\frac{\gamma (\varsigma + m + l) - \varsigma + 1}{\gamma }} \right)}}{{\left( {\delta ( \varsigma + k )} \right)^{{\frac{\gamma (\varsigma + m + l) - \varsigma + 1}{\gamma }}} }} \hfill \\ \end{gathered} \right\}$$

This is the required expression for the Renyi’s entropy for the EOLxPL distribution. Similarly, the Tsalli’s entropy based of EOLxPL distribution is given by

$$E_{T} (\zeta ) = \frac{1}{\zeta - 1}\left\{ {1 - \int\limits_{0}^{\infty } {\left[ {\varphi (z; \alpha , \beta , \gamma , \delta , \lambda )} \right]^{\zeta } dz} } \right\}$$

$$E_{T} (\zeta ) = \frac{1}{\zeta - 1}\left[ {1 - \left\{ \begin{gathered} \sum\limits_{i = 0}^{\infty } {\sum\limits_{j = 0}^{\infty } {\sum\limits_{k = 0}^{\infty } {\sum\limits_{l = 0}^{k} {\sum\limits_{m = 0}^{\infty } {\left( {{}^{ - \zeta (\alpha + 1)}C_{i} } \right) \left( {{}^{ - (\lambda (i + \zeta ) + \zeta )}C_{j} } \right) \left( {{}^{\lambda (i + \zeta ) + j - \zeta )}C_{k} } \right) \left( {{}^{k}C_{l} } \right) \left( {{}^{\zeta }C_{m} } \right)} } } } ( - 1)^{j} } \hfill \\ \times (\alpha \lambda )^{\zeta } (\beta )^{ - (\zeta - i)} \frac{{(\gamma )^{\zeta - 1} (\delta^{2} )^{\zeta + l} }}{{(\delta + 1)^{\zeta + l} }}\frac{{\Gamma \left( {\frac{\gamma (\zeta + m + l) - \zeta + 1}{\gamma }} \right)}}{{\left( {\delta ( \zeta + k )} \right)^{{\frac{\gamma (\zeta + m + l) - \zeta + 1}{\gamma }}} }} \hfill \\ \end{gathered} \right\}} \right]$$

Parameter estimation

In statistical modelling, estimating the parameter(s) of a probability distribution is fundamental for fitting the model to observed data. This section discusses a range of estimation techniques employed to determine the unknown parameter(s) of a distribution. Each method operates by optimizing a particular objective function, which is formulated based on the observed sample and depends on the parameter(s) of interest. The following are the principal methods considered:

Maximum likelihood estimation is a widely used method for estimating the parameters of the probability distribution models. It involves constructing the likelihood function, which represents the joint probability density function of the observed sample given the parameters. The estimate of the parameters is obtained by maximizing this function with respect to each of the parameter. For computational convenience, the log-likelihood function is often used, and the parameter are estimated by solving the resulting likelihood equation. For EOLxPL distribution, the objective function for estimating distribution parameters is mathematically given by:

$$L(z; \alpha , \beta , \gamma , \delta , \lambda ) = \prod\limits_{i = 1}^{n} {\varphi (z_{i} ; \alpha , \beta , \gamma , \delta , \lambda )}$$

where, $\varphi (z; \alpha , \beta , \gamma , \delta , \lambda )$ is the PDF of EOLxPL distribution, and $z_{1} , z_{2} , z_{3} ,..., z_{n}$ is the random sample of size $n$ drawn from EOLxPL distribution.

The Anderson–Darling estimation method (ADEM) is another approach for estimating parameters. This method focuses on minimizing the Anderson–Darling statistics, which quantifies the distance between the empirical cumulative distribution function and the theoretical cumulative distribution function of the model. It gives more weight to the tails of the distribution, making it suitable for application where tail behaviour is of particular interest. The objective function for Anderson–Darling method in order to obtain parameters of EOLxPL distribution is expressed as

$$AD_{E} (z; \alpha , \beta , \gamma , \delta , \lambda ) = - n - \sum\limits_{i = 1}^{n} {\frac{(2 i - 1)}{n}} \left[ {\log \left\{ {\Phi_{Z} (z_{i} )} \right\} + \log \left\{ {S_{Z} (z_{i} )} \right\}} \right]$$

where, $\Phi_{Z} (z)$, and $S_{Z} (z)$ denotes the CDF and survival function respectively of EOLxPL distribution.

Right-tailed Anderson–Darling estimation method is a variant of ADEM that emphasizes the right tail of the distribution. The objective function of this method is a modified version of the standard Anderson–Darling statistics and is mathematically expressed as:

$$AD_{RTE} (z; \alpha , \beta , \gamma , \delta , \lambda ) = \frac{n}{2} - 2\sum\limits_{i = 1}^{n} {\left[ {\Phi_{Z} (z_{i} )} \right]} - \sum\limits_{i = 1}^{n} {\frac{(2i - 1)}{n}} \left[ {\log \left\{ {S_{Z} (z_{n + 1 - i} )} \right\}} \right]$$

Similarly, the left-tailed version of the ADEM focuses on the lower tail of the distribution. The estimate of the parameters of the EOLxPL distribution under this method is obtained by minimizing the objective function given by:

$$AD_{LTE} (z; \alpha , \beta , \gamma , \delta , \lambda ) = - \frac{3 n}{2} + 2\sum\limits_{i = 1}^{n} {\left[ {\Phi_{Z} (z_{i} )} \right]} - \sum\limits_{i = 1}^{n} {\frac{(2i - 1)}{n}\left[ {\log \left\{ {\Phi_{Z} (z_{i} )} \right\}} \right]}$$

The Cramer-Von Mises method estimates parameter(s) by minimizing a Cramer-Von Mises statistic that evaluates the squared difference between the empirical cumulative distribution function and the theoretical cumulative distribution function of the model across all data points. Unlike the ADEM, it assigns equal weight to all parts of the distribution, offering a more uniform fit over the entire range. For Cramer-Von Mises estimation method, the objective function to estimate parameters of EOLxPL distribution is equal to:

$$CVM_{E} (z; \alpha , \beta , \gamma , \delta , \lambda ) = \frac{1}{12n} + \sum\limits_{i = 1}^{n} {\left[ {\left\{ {\Phi_{Z} (z_{i} )} \right\} - \frac{(2i - 1)}{{2i}}} \right]}^{2}$$

Least squares estimation method aims to minimize the sum of squared differences between the empirical cumulative distribution function and the theoretical cumulative distribution function values. In this method the objective function that is to be minimized is generally presented as:

$$LS_{E} (z; \alpha , \beta , \gamma , \delta , \lambda ) = \sum\limits_{i = 1}^{n} {\left[ {\left\{ {\Phi_{Z} (z_{i} )} \right\} - \frac{i}{n + 1}} \right]}^{2}$$

As an extension of least squares estimation, the weighted least square estimation method introduces a weight function into the objective function. This allows the method to assign different levels of importance to different regions of the distribution, thereby improving flexibility and robustness. The estimation involves minimizing the weighted sum of squared differences between the empirical and theoretical cumulative distribution functions, and is enumerated as:

$$WLS_{E} (z; \alpha , \beta , \gamma , \delta , \lambda ) = \sum\limits_{i = 1}^{n} {\frac{{(n + 1)^{2} (n + 2)}}{i (n - i + 1)}\left[ {\left\{ {\Phi_{Z} (z_{i} )} \right\} - \frac{i}{n + 1}} \right]}^{2}$$

The maximum product of spacing method of estimation is based on maximizing the product of spacing between successive theoretical cumulative distribution function values at ordered sample points. The objective function that needs to maximized to estimate unknown parameters represents the geometric mean of these spacing, which reflects how well the model fits the data and is mathematically expressed as:

$$MPS_{E} (z; \alpha , \beta , \gamma , \delta , \lambda ) = \frac{1}{n + 1}\sum\limits_{i = 1}^{n} {\left[ {\log \left\{ {\Omega_{i} } \right\}} \right]}$$

where, $\Omega_{i} = \Phi_{{Z_{(i)} }} (z) - \Phi_{{Z_{(i - 1)} }} (z)$, and $\Phi_{{Z_{(i)} }} (z)$ is the CDF of $i^{th}$ ordered statistics of EOLxPL distribution.

In this approach, the estimation is performed by minimizing the sum of absolute differences between adjacent spacing of the theoretical CDF evaluated at ordered sample values. So, the objective function in order to estimate unknown parameters of the given distribution is given by:

$$MSAD_{E} (z; \alpha , \beta , \gamma , \delta , \lambda ) = \sum\limits_{i = 1}^{n + 1} {\left| {\Omega_{i} - \frac{1}{n + 1}} \right|}$$

The minimum spacing absolute log-distance estimation method is based on taking the logarithm of the absolute spacing differences before summing them. The log transformation helps to stabilize variance and enhance estimation performance in distributions where spacing varies significantly across the support. To obtain estimates of the unknown parameters of the EOLxPL distribution under minimum spacing absolute log-distance estimation method, the following objective function is to be minimized:

$$MSALD_{E} (z; \alpha , \beta , \gamma , \delta , \lambda ) = \sum\limits_{i = 1}^{n + 1} {\left| {\log (\Omega_{i} ) - \log \left( {\frac{1}{n + 1}} \right)} \right|}$$

Simulation

To evaluate the performance of the various parameter estimation techniques proposed in Sect. “Parameter Estimation” for the EOLxPL distribution, a comprehensive Monte Carlo simulation study is carried out using the R-software⁴². The primary aim of this study is to systematically compare the efficiency, precision, and reliability of each estimation method under different sampling conditions. The following terminology is used to denote these estimation methods:

$$\begin{gathered} {\upkappa }_{{1}} {\text{ = Maximum Likelihood Estimation Method}} \hfill \\ {\upkappa }_{{2}} {\text{ = Anderson - Darling Estimation Method}} \hfill \\ {\upkappa }_{{3}} {\text{ = Cramer Von Mises Estimation Method}} \hfill \\ {\upkappa }_{{4}} {\text{ = Maximum Product of Spacing Estimation Method}} \hfill \\ {\upkappa }_{{5}} {\text{ = Least Squares Estimation Method}} \hfill \\ {\upkappa }_{{6}} {\text{ = Weighted Least Squares Estimation Method}} \hfill \\ {\upkappa }_{{7}} {\text{ = Right tailed Anderson Darling Estimation Method}} \hfill \\ {\upkappa }_{{8}} {\text{ = Left tailed Anderson Darling Estimation Method}} \hfill \\ {\upkappa }_{{9}} {\text{ = Minimum Spacing Absolute Distance Estimation Method}} \hfill \\ {\upkappa }_{{{10}}} {\text{ = Minimum Spacing Absolute Log Distance Estimation Method}} \hfill \\ \end{gathered}$$

This simulation framework is designed to assess the estimators using three widely accepted performance measures: Bias, Mean Squared Error (MSE), and Mean Relative Error (MRE). These metrics respectively quantify the average deviation of the estimator from the true parameter, the variability of the estimation error, and the relative magnitude of the error in relation to the true parameter value. Together, they offer a holistic view of the quality of each estimation method. Under this simulation study, the random samples are generated from the EOLxPL distribution using the inverse cumulative distribution function method. The four distinct sets of initial parameter values used in this simulation study are:

Set 1-$(\alpha = 0.25, \beta = 0.05, \gamma = 0.50, \delta = 0.15, \lambda = 0.90)$.

Set 2-$(\alpha = 0.40, \beta = 0.10, \gamma = 0.35, \delta = 0.25, \lambda = 0.70)$.

Set 3-$(\alpha = 0.15, \beta = 1.05, \gamma = 1.30, \delta = 0.35, \lambda = 1.15)$.

and Set 4-$(\alpha = 0.20, \beta = 0.95, \gamma = 1.15, \delta = 0.25, \lambda = 1.05)$.

These values are selected to cover a wide range of possible conditions for the given parameters defined on $(0,\infty )$. These values represent both small and moderately large cases, allowing us to see how different estimation methods behave across different parts of the parameter space. This range helps test whether each method is stable and reliable when the parameters change in size. Some estimation techniques may work well when parameters are small but may lose accuracy as values increase. By using a varied set of values, we can better understand if a method performs consistently or only under certain conditions. To ensure the robustness of the results, each simulation is replicated 1000 times for a series of predefined sample sizes: 20, 50, 100, 150, 250, 400, and 600. These sample sizes are chosen to reflect small to moderately large data scenarios that may arise in practical applications. For each replicate, parameter estimates are obtained using the different estimation techniques under consideration. The performance metrics (Bias, MSE, and MRE) are then computed across all replications for each method and sample size. The corresponding mathematical expressions are given by:

$Bias(\hat{\Theta }) = \frac{1}{r}\sum\limits_{m = 1}^{r} {|\hat{\Theta }_{m} - \Theta |}$,$MSE = \frac{1}{r}\sum\limits_{m = 1}^{r} {\left( {\hat{\Theta }_{m} - \Theta } \right)}^{2}$, and $MRE = \frac{1}{r}\sum\limits_{m = 1}^{r} {\left| {\frac{{\hat{\Theta } - \Theta }}{\Theta }} \right|}$.

Where, $\hat{\Theta }_{m}$ denotes the estimate of the parameter in the $m^{th}$ replication, $\Theta$ is the true parameter value, and $r$ is the total number of replications or iterations.

The computed values for each metric across all the methods and sample sizes are presented in Table 2, Table 3, Table 4 and Table 5. These results provide a detailed comparative analysis that highlights the relative strengths and limitations of each estimation technique. Specifically, they allow us to identify which methods perform more consistently as sample size increases and which technique may be more sensitive to sample variability.

Table 2 Comparison of Bias, MSE, MRE for parameter estimates when $\alpha = 0.25$; $\beta = 0.05$; $\gamma = 0.50$;$\delta = 0.15$; and $\lambda = 0.9$.

Table 3 Comparison of Bias, MSE, MRE for parameter estimateswhen $\alpha = 0.40$; $\beta = 0.10$; $\gamma = 0.35$;$\delta = 0.25$; and $\lambda = 0.70$.

Table 4 Comparison of Bias, MSE, MRE for parameter estimateswhen $\alpha = 0.15$; $\beta = 1.05$; $\gamma = 1.30$;$\delta = 0.35$; and $\lambda = 1.15$.

Table 5 Comparison of Bias, MSE, MRE for parameter estimateswhen $\alpha = 0.20$; $\beta = 0.95$; $\gamma = 1.15$;$\delta = 0.25$; and $\lambda = 1.05$.

To evaluate and compare the performance of various estimation methods, ranks were assigned to the Bias, MSE, and MRE values based on their magnitudes based on their magnitudes in ascending for each parameter corresponding to the same sample size. Table 6 presents the partial and overall ranks for each estimation method, derived by summing the individual ranks of Bias, MSE, and MRE. As seen in Table 2 to Table 5, all estimation methods exhibit reduced Bias, MSE, and MRE with increasing sample size, indicating improved accuracy and consistency of the estimators. Table 6 shows that the minimum spacing absolute log-distance estimation method consistently achieved the lowest overall rank followed by minimum spacing absolute distance and maximum likelihood estimation methods, demonstrating their superiority in estimating parameters of the EOLxPL distribution.

Table 6 Partial and overall ranks ofBias, MSE, MRE for parameter estimatesunder different estimation methods.

Overall, this simulation study offers valuable insights into practical performance of the proposed estimators, supporting theoretical findings and guiding the selection of appropriate estimation methods for empirical application involving the EOLxPL distribution.

Application

This section illustrates the practical utility and effectiveness of the newly proposed EOLxPL distribution in modelling real-world data. To validate its performance, we analyse two real life datasets pertaining to COVID-19 cases from China and Italy. The objective is to demonstrate the superiority of the EOLxPL distribution compared to several existing models, namely Exponentiated Odd Lomax Log Logistic (EOLxLogL), Exponentiated Odd Lomax Frechet (EOLxFrt), Exponentiated Odd Lomax Lomax (EOLxLx), Frechet (Frt), Lomax (Lx) and Power Lindley (PL) distributions. All data analysis and computations are carried out using the R-software⁴².

Dataset 1: This data set is about number of daily deaths due to COVID-19 in China from 23^rd January to 28^th March. The data set has been taken from (https://www.worldometers.info/coronavirus/country/china/) and had been studied by Sindhu et al⁴³.:

8, 16, 15, 24, 26, 26, 38, 43, 46, 45,57,64,65,73,73,86,89,97,108, 97, 146, 121, 143, 142, 105, 98, 136, 114, 118, 109, 97, 150, 71, 52, 29, 44, 47, 35, 42, 31, 38, 31, 30, 28, 27, 22, 17, 22, 11, 7, 13, 10, 14, 13, 11, 8, 3, 7, 6, 9, 7, 4, 6, 5, 3, 5

Dataset 2:The second dataset presents COVID-19 mortality rates in Italy over a period of 59 days recorded from February 27 to April 27, 2020. This dataset is also studied by Almongy et al⁵.:

4.571, 7.201, 3.606, 8.479, 11.410, 8.961, 10.919, 10.908, 6.503, 18.474, 11.010, 17.337, 16.561, 13.226, 15.137, 8.697, 15.787, 13.333, 11.822, 14.242, 11.273, 14.330, 16.046, 11.950, 10.282, 11.775, 10.138, 9.037, 12.396, 10.644, 8.646, 8.905, 8.906, 7.407, 7.445, 7.214, 6.194, 4.640, 5.452, 5.073, 4.416, 4.859, 4.408, 4.639, 3.148, 4.040, 4.253, 4.011, 3.564, 3.827, 3.134, 2.780, 2.881, 3.341, 2.686, 2.814, 2.508, 2.450, 1.518.

The summary statistics for the given real life datasets are presented in Table 7 to get idea about the behaviour of such dataset.

Table 7 Summary statistics of the real life data.

The maximum likelihood estimator (MLE) and the corresponding standard error of the parameters involved in the EOLxPL distribution and the other well-known distribution used for comparative study has enumerated in Table 8 as below:

Table 8 MLE estimation and corresponding standard error of the probability distribution parameters.

To evaluate and compare the goodness-of-fit and modelling capabilities of the EOLxPL distribution against the aforementioned distributions, we employ three different methodologies: Information criteria measures, goodness-of-fit tests, and graphical diagnostics.

Information criteria measures

To assess model adequacy, we utilize several information-based criteria, including Log-likelihood (−2logL), Akaike Information Criterion (AIC), Corrected Akaike Information Criterion (CAIC), Hannan-Quinn Information Criterion (HQIC), and Bayesian Information Criterion (BIC). These metrics are widely used to identify the most appropriate model, with lower values indicating a better fit. The corresponding values for each distribution are provided in Table 9 and Table 10. Based on these results, the EOLxPL distribution consistently exhibits the lowest values across all criteria, indicating its superior performance in fitting the real-world datasets compared to the competing models.

Table 9 Information criterions for different probability distribution models based on dataset-1.

Table 10 Information criterions for different probability distribution models based on dataset-2.

Goodness of fit test

To further validate the fit of the proposed model, we apply goodness-of-fit tests: The Kolmogorov–Smirnov (K-S), Cramer-von Mises (CVM), and Anderson–Darling (A-D) statistics. These tests compare the empirical distribution of the data with the theoretical distributions under consideration. The computed test statistics and corresponding p-values for each distribution are also summarized in Table 9 and Table 10. The EOLxPL distribution yields the smallest test statistics and the highest p-values, indicating the best agreement with the empirical data and confirming its superiority over other distributions.

Graphical measures

Visual tools provide an intuitive understanding of how well a distribution models real-world data. To this end, several graphical analyses are presented, including: Histograms over laid with estimated probability density functions, plots comparing empirical and theoretical cumulative distribution functions, estimated (or empirical) and theoretical survival function plot, probability–probability (P–P) plot and quantile–quantile (Q–Q) plot. These visualizations are shown below in Fig. 8, Fig. 9, Fig. 10, Fig. 11, Fig. 12, Fig. 13, Fig. 14, Fig. 15, Fig. 16 and Fig. 17. The EOLxPL distribution is observed to align more closely with the empirical data across all graphical measures, outperforming the other considered distributions for both datasets.

Fig. 8

Histogram and fitted density curves corresponding to dataset-1.

Fig. 9

Plot of theoretical CDF and empirical CDF of EOLxPL distribution based on dataset 1.

Fig. 10

Plot of theoretical survival function and empirical survival function of EOLxPL distribution based on dataset 2.

Fig. 11

P-P Plot of EOLxPL distribution based on dataset 2.

Fig. 12

Q-Q Plot of EOLxPL distribution based on dataset 2.

Fig. 13

Histogram and fitted density curves corresponding to dataset-2.

Fig. 14

Plot of theoretical CDF and empirical CDF of EOLxPL distribution based on dataset 2.

Fig. 15

Plot of theoretical survival function and empirical survival function of EOLxPL distribution based on dataset 2.

Fig. 16

P-P Plot of EOLxPL distribution based on dataset 2.

Fig. 17

Q-Q Plot of EOLxPL distribution based on dataset 2.

Daily mortality rates due to COVID-19.

Conclusion

This study presents a significant advancement in statistical modelling through the introduction of the EOLxPL distribution model, developed by embedding the Power Lindley distribution within the Lomax family via the T-X transformation method. The proposed model demonstrates a high degree of flexibility and adaptability, addressing limitations of existing distributions in capturing real-world data complexities. A thorough theoretical examination was undertaken, encompassing the derivation of fundamental statistical characteristics, including the probability density function, cumulative distribution function, survival and hazard rate functions, moments, moment generating function. ordered statistics and entropy measures. These derivations provide a robust foundation for both theoretical exploration and practical applications. To ensure the accuracy and reliability of parameter estimation for the EOLxPL distribution, several estimation techniques were analysed. Among them, the minimum spacing absolute log-distance estimation method emerged as the most efficient, offering superior performance in terms of bias, MSE, and MRE, as confirmed by comprehensive Monte Carlo simulation studies. These findings offer valuable guidance for selecting optimal estimation methods in empirical applications. The practical utility of the EOLxPL distribution was further validated through its application to real-world datasets from the COVID-19 pandemic. Comparative goodness-of-fit analyses demonstrated its superior performance over several established models, including the EOLxLogL, EOLxFrt, EOLxLx, Frt, Lx, and PL distributions. These results affirm the model’s capacity to effectively capture diverse data structures, making it a versatile and valuable tool for a wide range of applied statistical tasks.