Multiscale energetics and submesoscale instabilities of eddy shedding at the Kuroshio loop current in the South China Sea

Abstract

The multiscale energetics and submesoscale instabilities after the eddy shedding of Kuroshio Loop Current (KLC) intrusion into the South China Sea (SCS) remain ambiguous. Here, a typical KLC eddy shedding process is well simulated using a downscaled submesoscale-permitting model. Then, energy and dynamics diagnostics are employed to investigate the cross-scale interactions between mesoscales and submesoscales during and after this process. In energetics, although the forward and inverse energy cascades coexist, the forward cascade of available potential energy (APE) is crucial in energizing submesoscales, while the strength of forward kinetic energy (KE) is relatively weak. The submesoscale KE is primarily charged by strong buoyancy conversion and secondarily by horizontal advection from upstream, which is mainly balanced by turbulence dissipation and vertical pressure work. In dynamics, except for the release of submesoscale APE by baroclinic instability, symmetric instability (SI) can extract KE from geostrophic flows and drive forward KE cascades. Specifically, strain-induced advective frontogenesis can rapidly sharpen submesoscales by enhancing lateral buoyancy gradients, the increased baroclinicity together with atmospheric-forced buoyancy loss causes negative total Ertel potential vorticity and creates favorable conditions for SI. These results highlight the significance of submesoscales in multiscale energetics and dynamical instabilities of the KLC eddy shedding.

Introduction

Oceanic submesoscale processes (submesoscales hereafter) with spatiotemporal scales of O (1–50) km and O (1–10) days preferentially generated in upper ocean manifesting elongated fronts, filaments and coherent vortices through various dynamical mechanisms such as mixed layer baroclinic instabilities, strain-induced frontogenesis and flow-topography interactions^{1,2,3,4,5,6,7,8}. Dynamically, submesoscales are characterized by order one Rossby (Ro) and Richardson (Ri) number, indicating that they are marginally constrained by the Earth’s rotation and oceanic stratification⁹. The increased vertical velocities driven by ageostrophic component can significantly enhance the exchanges between the ocean surface and subsurface^{6,10,11,12,13,14}. Energetically, as the intermediate between quasi-geostrophic mesoscales and three-dimensional turbulences, submesoscales play crucial roles in closing ocean energy cascades^4,5,15,16,17. Recent studies have confirmed the bidirectional nature of energy cascades in submesoscales and their critical contributions to global ocean energy balances^16,18,19.

As the largest marginal sea in the Western Pacific, the South China Sea (SCS) connects to the Pacific Ocean through the Luzon Strait and is characterized by abundant multiscale dynamical processes^{20,21,22,23,24,25}. In winter, the Kuroshio always intrudes into the SCS in a looping current form and sheds anticyclonic eddies under certain conditions^26,27. Then, the anticyclonic eddies propagate into the northeastern SCS along the continental shelf at the speed of the first baroclinic Rossby wave and motivate cyclonic mesoscale eddies in the wake²⁵. Furthermore, the strong effects of the East Asia monsoon, together with meandering islands and undulating topography, can stimulate active submesoscales at the periphery of the eddy when it propagates downstream^28,29,30. These abundant submesoscales have been validated to be generated by the combination of mixed-layer baroclinic instability and strain‐induced frontogenesis from both mooring observations³⁰ and high-resolution ocean model simulations³¹. Furthermore, the energy cascades and thermohaline transports driven by the submesoscales within the eddy shedding region have also been thoroughly investigated³².

However, the picture of multiscale energetics and submesoscale instabilities during and after the KLC eddy shedding remains unclear. Given the significance of submesoscales in energy cascades and biogeochemical transports in the northeastern SCS²⁵we attempt to address the above scientific issue by analyzing a 1/70° high-resolution ocean model results downscaled from a 1/20° resolution simulation. The remainder is organized as follows. Section 2 describes the downscaled ocean model configurations and diagnostic methods. Section 3 focuses on the multiscale interactions and submesoscale instabilities during and after the KLC eddy shedding. Finally, conclusions and summaries are given in Sect. 4.

Methods

A high-resolution regional ocean model for downscaling simulation

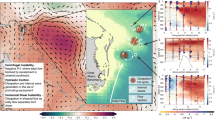
The Regional Oceanic Modeling System (ROMS) is employed in this study^33,34. The model configuration is illustrated in Fig. 1, of which the parent domain covers the Northwest Pacific Subtropical region and the whole SCS of 105–158°E to 4–31°N with a relatively low horizontal resolution of mesoscale-resolving 1/20°. Then, the offline nesting approach is adopted for the child domain covering the Luzon Strait and northeastern SCS with a refined horizontal resolution to submesoscale-permitting 1/70°. This child domain covers the crucial area of KLC eddy shedding area, consisting of 1040 × 818 orthogonal grid points along zonal and meridional directions from 112° to 127°E and 15° to 27°N. The high-resolution bathymetry of GEBCO 2023 with 15 arc seconds is linearly interpolated for both grids and slightly smoothed to avoid exceeding computational restrictions of topography steepness and roughness³⁵.

Fig. 1

Domain illustration of downscaling experiment design for KLC eddy shedding in the northeastern SCS. The red box denotes the downscaled region with a horizontal resolution of 1/70° inside a 1/20° resolution large domain, and the high-resolution region within the red box is the focus of this study. The black contours depict the 200, 2000, and 3500 m isobaths, respectively. The solid red curve represents a typical intrusion path of the Kuroshio Looping Current into the northeastern SCS while the red circle and dotted arrow illustrate the mesoscale eddy and its moving direction after the eddy sheds from the KLC.

Due to the importance of local wind in KLC eddy shedding²⁶the surface atmospheric forcings, including heat fluxes and wind stress, are all derived from hourly CFSv2 reanalysis data with a spatial resolution of 1/4°. The oceanic initial field and lateral boundary driving parent grid are interpolated from daily 1/12° HYCOM reanalysis data and the K-profile parameterization is employed for vertical turbulence closure scheme³⁶. The tidal model is not included in the simulation. Vertically, both parent and child domains consist of 50 layers with stretching parameters of 8.5 and 1 and the transition depth of 20 m, configuring concentrated vertical levels from 0.2 to 15 m within the upper 200 m. The parent domain simulation is spun up from its initial state on January 1, 2012 and runs for 9 years to January 1, 2021 under the realistic atmospheric and oceanic forcings. It takes approximately 2 years for the model to achieve numerical equilibrium within the upper 200 m and subsequently provides the daily-averaged data and snapshots at 12:00 UTC in the remaining simulation. The model outputs, including seasonal sea level anomalies, large-scale Kuroshio current and western boundary circulation of the South China Sea, sea surface temperature/salinity, mixed layer depth (MLD), and thermohaline structure, are all verified with the satellite observations and reanalysis datasets before downscaling (Supplementary Figure S1-S9). Then, the high-resolution downscaling simulation is carried out under the same atmospheric forcing and low-resolution oceanic boundary from November 01, 2016 to April 30, 2017 when a prominent KLC is observed in reality³². Particularly, a KLC eddy shedding process is well simulated, ensuring the accuracy and reliability of the model in characterizing the realistic oceanic dynamical processes in the northeastern SCS. Moreover, since the activity of symmetric instability (SI) depends on larger submesoscales, such as mixed layer instability (MLI), are resolved in the model^37,38. Dong³⁹ estimates the MLI sinusoidal wavelength globally and indicates that it is the smallest in summer with the KPP vertical turbulence closure scheme⁴⁰the corresponding bounds of the MLI sinusoidal wavelength is approximately 12 km within the child domain. According, the resolution of 1/70° (about 1.5 km) used in this study can resolve the MLI, which indirectly improve the ability to estimate the SI activity.

Multiscale energetics analysis

The multiscale energy and vorticity analysis (MS-EVA)⁴¹ method has always been utilized to evaluate diverse multiscale dynamical processes in the atmosphere and ocean^{42,43,44,45,46,47,48}. Based on the theory of multiscale window transform (MWT), Liang and Robinson⁴⁹ decomposed a function space into several orthogonal subspaces termed scale windows, with each one occupying an exclusive time scale range. The advantage of this scale decomposition is that it not only ensures the conservation of total energy but also retains its locality^43,47.

Here, the high-resolution 1/70° outputs of 3-hour mean with a temporal length of 1024 from November 30, 2016 to April 6, 2017 (128 days) are split into low-frequency mesoscale window (> 16 days, $\bar{\omega } = 0$) and high-frequency submesoscale window (≤ 16 days, $\bar{\omega } = 1$). The choice of 16 days as the separation threshold is based on submesoscale mooring array observations in the northeastern SCS, which indicate that 15 days is the optimal temporal scale for distinguishing mesoscales and submesoscales³⁰. Therefore, a 16-day (the nearest to 15-day) window that could be evenly divided by 2 required by this method is selected in this study. Additionally, Zhao⁵⁰ points out that the lifespans of mesoscales in the SCS typically range from 30 to 240 days according to statistical results and spectral analysis. Consequently, a two-window decomposition is employed in this paper. Although the results of largescale and mesoscales would be mixed up to some extent, it doesn’t affect our focus of submesoscales.

Liang⁴¹ obtained KE and APE budget equations on window$~\bar{\omega }$ (denoted as $KE^{{\bar{\omega }}}$ and $APE^{{\bar{\omega }}}$) by applying MWT to the oceanic primitive equations:

$$\begin{aligned} \frac{{\partial KE^{{\bar{\omega }}} }}{{\partial t}} = & \underbrace {{\frac{1}{2}~\left[ {~\left( {\widehat{{VV_{h} }}} \right)^{{\sim \bar{\omega }}} :{\triangledown }\widehat{{V_{h} }}^{{\sim \bar{\omega }}} - {\triangledown } \cdot \left( {\widehat{{VV_{h} }}} \right)^{{\sim \bar{\omega }}} \cdot \widehat{{V_{h} }}^{{\sim \bar{\omega }}} } \right]}}_{{\Gamma _{K}^{{\bar{\omega }}} }} + \underbrace {{\left\{ { - \frac{1}{2}{\triangledown }_{h} \cdot \left[ {\left( {\widehat{{V_{h} V_{h} }}} \right)^{{\sim \bar{\omega }}} \cdot \widehat{{V_{h} }}^{{\sim \bar{\omega }}} } \right]} \right\}}}_{{\Delta _{h} Q_{K}^{{\bar{\omega }}} }} + \underbrace {{\left\{ { - \frac{1}{2}\frac{\partial }{{\partial z}}\left[ {\left( {\widehat{{wV_{h} }}} \right)^{{\sim \bar{\omega }}} \cdot \widehat{{V_{h} }}^{{\sim \bar{\omega }}} } \right]} \right\}}}_{{\Delta _{z} Q_{K}^{{\bar{\omega }}} }} \\ & + \underbrace {{\left[ { - {\triangledown }_{h} \cdot \left( {\frac{1}{{\rho _{0} }}\widehat{{V_{h} }}^{{\sim \bar{\omega }}} \hat{P}^{{\sim \bar{\omega }}} } \right)} \right]}}_{{\Delta _{h} Q_{P}^{{\bar{\omega }}} }} + \underbrace {{\left[ { - \frac{\partial }{{\partial z}}\left( {\frac{1}{{\rho _{0} }}\hat{w}^{{\sim \bar{\omega }}} \hat{P}^{{\sim \bar{\omega }}} } \right)} \right]}}_{{\Delta _{z} Q_{P}^{{\bar{\omega }}} }} + \underbrace {{\left[ { - \frac{g}{{\rho _{0} }} \cdot \left( {\hat{\rho }^{{\sim \bar{\omega }}} \hat{w}^{{\sim \bar{\omega }}} } \right)} \right]}}_{{b^{{\bar{\omega }}} }} + F_{K}^{{\bar{\omega }}} \\ \end{aligned}$$

(1)

$$\begin{aligned} \frac{{\partial APE^{{\bar{\omega }}} }}{{\partial t}} = & \underbrace {{\frac{c}{2}~\left[ {~\left( {\widehat{{V\rho }}} \right)^{{\sim \bar{\omega }}} \cdot {\triangledown }\hat{\rho }^{{\sim \bar{\omega }}} - \hat{\rho }^{{\sim \bar{\omega }}} {\triangledown } \cdot \left( {\widehat{{V\rho }}} \right)^{{\sim \bar{\omega }}} } \right]}}_{{\Gamma _{A}^{{\bar{\omega }}} }} + \underbrace {{\left\{ { - \frac{1}{2}{\triangledown }_{h} \cdot \left[ {c\hat{\rho }^{{\sim \bar{\omega }}} \left( {\widehat{{V_{h} \rho }}} \right)^{{\sim \bar{\omega }}} } \right]} \right\}}}_{{\Delta _{h} Q_{A}^{{\bar{\omega }}} }} \\ & + \underbrace {{\left\{ { - \frac{1}{2}\frac{\partial }{{\partial z}}\left[ {c\hat{\rho }^{{\sim \bar{\omega }}} \left( {\widehat{{w\rho }}} \right)^{{\sim \bar{\omega }}} } \right]} \right\}}}_{{\Delta _{z} Q_{A}^{{\bar{\omega }}} }} + \underbrace {{\left( {\frac{g}{{\rho _{0} }}\hat{\rho }^{{\sim \bar{\omega }}} \hat{w}^{{\sim \bar{\omega }}} } \right)}}_{{ - b^{{\bar{\omega }}} }} + \underbrace {{\frac{1}{2}\hat{\rho }^{{\sim \bar{\omega }}} \left( {\widehat{{w\rho }}} \right)^{{\sim \bar{\omega }}} \frac{{\partial c}}{{\partial z}}}}_{{S_{A}^{{\bar{\omega }}} }} + F_{A}^{{\bar{\omega }}} \\ \end{aligned}$$

(2)

Here, 

$KE^{{\bar{\omega }}}$ and $APE^{{\bar{\omega }}}$ are expressed as $\frac{1}{2}\hat{V}_{h}^{{\sim \bar{\omega }}} \cdot\hat{V}_{h}^{{\sim \bar{\omega }}}$ and $\frac{1}{2}c\left( {\hat{\rho }^{{\sim \bar{\omega }}} } \right)^{2}$, of which $c = \frac{{g^{2} }}{{\rho _{0} ^{2} N^{2} }}$.$~\Gamma _{K}^{{\bar{\omega }}}$($\Gamma _{A}^{{\bar{\omega }}}$) is the KE (APE) barotropic (baroclinic) canonical transfer between different scale windows. $\Delta Q_{K}^{{\bar{\omega }}}$($\Delta Q_{A}^{{\bar{\omega }}}$) and $\Delta Q_{P}^{{\bar{\omega }}}$ are KE (APE) transports by advection and pressure work, which can be further divided into horizontal and vertical component denoted by the subscripts h and z respectively. $b^{{\bar{\omega }}}$ is the buoyancy conversion connecting the APE and KE; $S_{A}^{{\bar{\omega }}}$ serves as the source/sink of stratification term. The implicit $\:F\:$term indicates the residuals, including contributions from other external forcing, friction and other unresolved subgrid processes⁴¹. The oceanic energy cycle within a two-scale window is schematically illustrated in Fig. 2, in which the canonical transfer of KE (APE) from mesoscales $\left( {\bar{\omega } = 0} \right)$ to submesoscales $\left( {\bar{\omega } = 1} \right)$ is denoted as $\Gamma _{K}^{{0~ \to ~1}} \left( {\Gamma _{A}^{{0~ \to ~1}} } \right)$. A positive value of $\Gamma _{K}^{{0~ \to ~1}} \left( {\Gamma _{A}^{{0~ \to ~1}} } \right)$ indicates the forward cascades of KE (APE), which corresponds to the barotropic (baroclinic) instability in the classical geophysical fluid dynamics, respectively^44,49.

Fig. 2

Schematic energy pathways within a two-scale window framework. Arrows with different colors illustrate different dynamical processes. The blue (green), red, and purple arrows denote the canonical transfers of KE (APE) between different scale windows, buoyancy conversions of APE and KE, and other processes (such as advection, pressure work et al.), respectively. The KE source/sink includes wind stress and internal dissipation etc. and APE source/sink includes buoyancy flux and diffusion etc.

Dynamical diagnostics of submesoscale instability

After shedding from the Kuroshio looping current, the mesoscale eddy moves downstream and generates active submesoscales by strain-induced frontogenesis in the surroundings. The horizontal strain rate ($St$) is defined as^51,52:

$$St = \sqrt {\left( {\frac{{\partial u}}{{\partial x}} - \frac{{\partial v}}{{\partial y}}} \right)^{2} + \left( {\frac{{\partial u}}{{\partial y}} - \frac{{\partial v}}{{\partial x}}} \right)^{2} }$$

(3)

The lateral density gradients can be increased by frontogenesis at a rate of advective frontogenetic tendency $\:F$⁵³:

$$F = Q\cdot{\triangledown }_{h} b$$

(4)

Where $Q = \left( { - \partial u/\partial x\cdot{\triangledown }_{h} b, - \partial u/\partial y\cdot{\triangledown }_{h} b} \right)$ is the Q vector. $b = - g\rho /\rho _{0}$ is the buoyancy, $\rho$ and $\rho _{0}$ is the potential density and reference density ($1025kg/m^{3}$), respectively.

The Ertel potential vorticity (EPV) has always been employed to diagnose submesoscale instabilities⁵⁴. Various instabilities can develop when the EPV $q$ takes a sign opposite to the Coriolis parameter$~f$⁵³. It can be further decomposed into the vertical $q_{v}$ and horizontal $q_{h}$ components,

$$q = ~\omega _{a} \cdot{\triangledown }b = \underbrace {{\left( {f + \zeta } \right)N^{2} }}_{{q_{v} }} + \underbrace {{\omega _{h} \cdot{\triangledown }_{h} b}}_{{q_{h} }}$$

(5)

Here, $\omega _{a} = f\hat{k} + {\triangledown } \times u$ is the absolute vorticity with a vertical component ($A = f + \zeta$) and horizontal component $\omega _{h}$. $\zeta$ refers to the vertical component of relative vorticity. $N^{2} = \partial b/\partial z$ is the squared vertical buoyancy frequency. By applying the thermal wind relation to $\:{q}_{h}$ in Eq. (6)⁵⁵, we have

$$q_{h} = - \frac{{M^{4} }}{f}$$

(6)

where $M^{4} = \left| {{\triangledown }_{h} b} \right|^{2} = \left| {\left( {\partial b/\partial x,\partial b/\partial y} \right)} \right|^{2}$ measures the amplitude of the lateral buoyancy gradient. According to Eq. (6), $q_{h}$ depends on the frontal sharpness ($M^{4}$) and is consistently negative in the Northern Hemisphere. This means that the baroclinicity of submesoscales always reduces the total EPV and is conducive to SI when $\:q$ decreases below 0 under the atmospheric forced surface buoyancy loss^16,54. SI is a category of forced submesoscale shear instability, which can extract KE from geostrophic flow at a rate given by the geostrophic shear production (GSP)^54,55,56,

$$GSP = - V_{h}^{1} w^{1} \cdot\frac{{\partial V^{0} }}{{\partial z}}$$

(7)

where $V_{h}^{1}$ and $w^{1}$ means horizontal and vertical velocity in submesoscale window, $V^0$ refers to the horizontal velocity in mesoscale window. Meanwhile, APE stored in submesoscales can be released by geostrophic adjustment and baroclinic instability at a rate set of vertical buoyancy flux (BFLUX), which is also the term $b^{{\bar{\omega }}}$ in submesoscale window of Eq. (2) ^54–55,

$$BFLUX = - \frac{g}{{\rho _{0} }}\left( {\rho ^{1} w^{1} } \right)$$

(8)

in which $\rho ^{1}$ is the density anomaly in submesoscale window. Previous studies have highlighted the significance of GSP and BFLUX in energizing submesoscale turbulence and their roles in forward energy cascade from mesoscale to submesoscale^15,54,57.

The submesoscales can be quantified by the Rossby number ($Ro = \zeta /f$), which is defined as the ratio of the vertical component of relative vorticity to the local Coriolis parameter. The quasi-geostrophic mesoscales are characterized by order O (0.1) of Ro while submesoscales display a larger magnitude of O (1). Additionally, submesoscales can generate large vertical velocities and induce strong convergence or divergence in the upper ocean, which can be estimated using the divergence normalized by the local Coriolis parameter ($\delta = \left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}} \right)/f$). Here, $\delta < 0(> 0)$ represents the convergence (divergence). The variable of $A - St$ and geostrophic Richardson number ($Ri_{g} = f^{2} N^{2} /M^{4}$) are also employed to assess the dominance of rotation or straining and the type of submesoscale instabilities⁵⁴. The negative $A - St$ in submesoscale zones indicates a loss of geostrophic balance and is primarily dominated by unbalanced submesoscale mode⁵⁸. SI will be generated if $0 < Ri_{g} < 1$ for anticyclonic and $0 < Ri_{g} < f/A$ for cyclonic vorticity when the total EPV $q < 0$⁵⁴.

The atmospheric forced surface buoyancy loss considered in this study includes the air-sea flux and wind-driven Ekman buoyancy flux (including down-front wind forcing and surface cooling). They can be quantitatively expressed by the Ekman buoyancy flux $EBF = M_{e} \cdot{\triangledown }_{h} b|_{{z = 0}}$ and surface buoyancy flux $B_{0} = B_{S} + B_{T}$, respectively. Here, $M_{e} = \left( {\tau _{y} , - \tau _{x} } \right)/f\rho _{0}$ is the Ekman transport, $\tau _{x} ~$and $\tau _{y} ~$ are the wind stress along zonal and meridional velocity. $B_{0}$ includes two types of buoyancy losses caused by freshwater $B_{S} = g\beta \left( {E - P} \right)S$ and net heat flux $\left( {B_{T} = g\alpha Q_{{heat}} /\rho _{0} C_{P} } \right)$, of which $\beta$ and $\alpha$ indicates the saline contraction and thermal expansion coefficient, respectively. $C_{P}$ is the specific heat capacity of seawater (all the parameters can be calculated using the Matlab seawater toolboxes). $E - P$ and $S$ are the net freshwater exchange and sea surface salinity, respectively. $Q_{{heat}}$ is the sea surface net heat flux. The three atmospheric variables are also included in the model outputs.

Results

Simulation of the KLC eddy shedding and downstream moving

We first compare the evolution of sea level anomaly (SLA) and surface velocity in the 1/70° high-resolution simulation with AVISO satellite observations in Fig. 3. It should be noted that due to the complexity of the eddy shedding, we don’t expect that the downscaling simulation can match the real observed eddy shedding process exactly without data assimilation⁵⁹so the timing of comparisons isn’t precisely synchronized. However, the results show a good performance in describing the general lifecycle of eddy, magnitudes of SLA and surface velocity despite a slight overestimation of size and strength. This suggest that the high-resolution simulation can effectively capture the crucial dynamical characteristics of the KLC eddy shedding process. Moreover, since no data assimilation interrupts the forward running, the results are dynamically consistent and suitable for energy budget analyses⁵⁹. Specifically, in late November 2016 (Figs. 3a1 & a2), the northward-flowing Kuroshio begins to intrude into the northeastern SCS in form of looping with a large entrance angle and brings into strong seawater convergences in the southwest of Taiwan. Then, an anticyclonic eddy gradually matures, and subsequently moves southwestward along the continental shelf after about a month to late December (Figs. 3b1 & b2), ultimately leading to the eddy shedding from KLC by cutting the neck in early January of 2017 (Figs. 3c1 & c2). Such a ‘‘necking-down’’ phenomenon of looping current is also observed in previous studies for the Gulf of Mexico⁵⁹. As moving downstream, the anticyclonic eddy further motivates a cyclonic mesoscale eddy in the tailing (Figs. 3d1 & d2)^24,25,60but it occurs earlier in the downscaled simulation than the satellite observation. The cyclonic eddy is relatively weak and has a short lifecycle, which dissipates quickly at the late (in AVISO) but early (in ROMS) February 2017 (Figs. 3e1 & e2). Then, the anticyclonic eddy continues to move downstream and eventually flows out of the domain. Next, we will focus on the analysis of high-resolution simulation results for four key moments of eddy shedding and moving, starting from 19 December, 2016.

Fig. 3

Snapshots of sea level anomaly (SLA) (in m, shaded) and surface velocity (in m/s, vector) between the 1/70° high-resolution ROMS simulations (left, a1-e1) and AVISO satellite observations (right, a2-e2) during a typical KLC eddy shedding process in 2016 winter (note that the timings of comparisons are not exactly synchronized). The red curves denote the main axis of KLC and edges of the mesoscale eddy, which is defined as the SLA contour of 0.1 m.

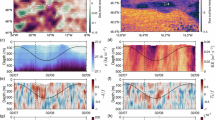
Figure 4 displays instantaneous distributions of simulated Rossby number, $Ro$, at different depths for four typical moments: KLC west extending (December 19, 2016), eddy forming and beginning to shed (January 11, 2017), eddy shedding (January 24, 2017) and eddy moving westward (February 6, 2017). When the Kuroshio intrudes into the Luzon Strait, abundant submesoscales manifesting elongated filaments and fronts appear (Fig. 4a1) due to the obstruction of complex topography and island^32,61. Then the KLC becomes a clockwise curve in the southwest of Taiwan and tends to generate anticyclonic eddy. When the eddy develops and becomes mature with a radius of approximately 150 km, it detaches from the KLC and moves downstream, exhibiting large negative $Ro$ values within its core (Fig. 4a2)³². Meanwhile, active submesoscale filaments and fronts with alternative large positive and negative $Ro$ values appear at the periphery of the mesoscale eddy. In late January 2017, the tailing cyclonic eddy exhibited a large positive $Ro$ within its core (Fig. 4a3), but it was stretched and quickly dissipated in early February 2017 (Fig. 4a4)²⁵. Along the vertical direction, the large $Ro$ values are mainly concentrated on the upper 200 m (Figs. 4a-c), indicating a rapid decrease of submesoscales in depth. So, the next analyses will focus on the upper 200 m.

Fig. 4

Snapshots of the simulated Rossby number $\:Ro\:$ at various depths (rows, denoted by letters a-d) for different moments (columns, denoted by numbers 1–4). The four moments correspond to the snapshots of (b1) to (e1) in Fig. 3, i.e., KLC west extending (20161219), eddy forming and beginning to shed (20170111), eddy shedding (20170124) and eddy moving westward (20170206).

Figure 5 illustrates the horizontal distributions of upper 200 m vertically integrated mesoscale and submesoscale KE and APE at four defined moments. Since most of the eddy shedding and moving process takes place within the black solid box, we will concentrate our analysis on this region and refer to the mesoscale eddy shedding and moving (MESM, 114.2-120.6°E, 18.8–22.5°N) region. In the initial stage of Kuroshio’s intrusion into the northeastern SCS, mesoscale $\:{KE}^{0}$ is relatively weak (Fig. 5a1) since the eddy has not fully developed yet. However, mesoscale $\:{APE}^{0}$ is strong (Fig. 5b1), which can be attributed to the significant differences in water mass properties between the SCS and subtropical Pacific Ocean. As the looping strength increases, the intensifying mesoscale $\:{KE}^{0}$ gradually meanders to a closed ring structure in the western Luzon Strait³² while $\:{APE}^{0}$ remains relatively large values within the eddy (Figs. 5a2 & b2). After the anticyclonic eddy sheds from the KLC, it moves downstream with weakening mesoscale $\:{APE}^{0}$. However, there is a notable $\:{APE}^{0}$ increase at the core of the tailing cyclonic eddy in late January 2017 but it dissipates quickly (Figs. 5b3 & b4). For mesoscale $\:{KE}^{0}$, it strengthens first and reaches its maximum in late January 2016 before progressively decreasing (Figs. 5a3 & a4). The $\:{KE}^{0}$ of the tailing cyclonic eddy is negligible (Fig. 5a3). For submesoscale $\:{KE}^{1}$ and $\:{APE}^{1}$, the high values in Figs. 5c & d) closely correspond to the elongated submesoscale filament and front characterized by large $\:Ro$ number as shown in Fig. 4, suggesting the existence of abundant submesoscales at the periphery of the mesoscale eddy. These submesoscale activities will move downstream with the eddy and display no significant spatial or temporal variation throughout the simulation period.

Fig. 5

Horizontal maps of vertically integrated mesoscale $\:{KE}^{0}$(a1-a4), $\:{APE}^{0}$(b1-b4) and submesoscale $\:{KE}^{1}$(c1-c4), $\:{APE}^{1}$(d1-d4) (color shading; $\:{m}^{3}/{s}^{2}$) within the upper 200 m at four key moments. The black box in each panel denotes the mesoscale eddy shedding and moving (MESM, 114.2-120.6°E, 18.8–22.5°N) region, the focus of this study.

Energetic analysis and multiscale interactions of mesoscales and submesoscales after the KLC eddy shedding

Figure 6 shows the horizontal distributions of vertically integrated mesoscale APE budgets within the upper 200 m at four defined moments. As illustrated, the $\:{APE}^{0}$ budget is dominated by three terms of buoyancy conversion $\:{-b}_{0}$, horizontal advection $\:{\varDelta\:}_{h}{Q}_{A}^{0}$ and the residual term $\:{F}_{A}^{0}$. The buoyancy conversion $\:{-b}_{0}$ displays complex spatial patterns with positive and negative values within the eddy. This indicates complicated energy conversions between APE and KE associated with baroclinic instability^41,47which can be attributed to strong interactions between physically-different water masses of the northeastern SCS and the Subtropical Pacific Ocean water wrapped by the mesoscale eddy.

Despite interspersed with sporadic opposite zones, the horizontal advection term $\:{\varDelta\:}_{h}{Q}_{A}^{0}$ is predominantly positive while the residual term $\:{F}_{A}^{0}$ is primarily negative. The two terms display a negative spatial correlation with comparable magnitude, suggesting that the horizontal advection of $\:{APE}^{0}$ from upstream is largely balanced by the residual term associated with buoyancy flux or diffusion⁵⁹.

The baroclinic canonical transfer $\:{\varGamma\:}_{A}^{1\to\:0}$ is relatively weak and has minor effect on $\:{APE}^{0}$, the large values are observed in the wake of the island and at the periphery of the mesoscale eddy. Additionally, while the vertical transport of $\:{\varDelta\:}_{z}{Q}_{A}^{0}$ is initially negligible, it gradually strengthens as the eddy moves downstream. The large values are mainly concentrated within the eddy, suggesting that a small portion of $\:{APE}^{0}$ can be vertically transported and redistributed. This phenomenon may be associated with the convergence induced by anticyclonic eddy. The last term, the stratification source/sink $\:{S}_{A}^{0}$ is so weak that it can be ignored.

Fig. 6

Horizontal maps of vertically integrated mesoscale APE budgets (color shading; 10⁻⁴ $\:{m}^{3}/{s}^{3}$) within the upper 200 m at four key moments, showing baroclinic canonical transfer from submesoscale to mesoscale window $\:{\varGamma\:}_{A}^{1\to\:0}$ (a1-a4), buoyancy conversion $\:{-b}_{0}$ (b1-b4), horizontal advection of $\:{\varDelta\:}_{h}{Q}_{A}^{0}$ (c1-c4), vertical transport of $\:{\varDelta\:}_{z}{Q}_{A}^{0}$ (d1-d4), stratification source/sink $\:{S}_{A}^{0}$ (e1-e4), and the residual term $\:{F}_{A}^{0}$ (f1-f4).

Correspondingly, Fig. 7 displays the horizontal maps of vertically integrated mesoscale KE budgets within the upper 200 m. As illustrated, the $\:{KE}^{0}$ budget is dominated by three terms: horizontal advection $\:{\varDelta\:}_{h}{Q}_{K}^{0}$, horizontal pressure work $\:{\varDelta\:}_{h}{Q}_{P}^{0}$ and the residual term $\:{F}_{K}^{0}$. Among these, $\:{\varDelta\:}_{h}{Q}_{K}^{0}$ and $\:{\varDelta\:}_{h}{Q}_{P}^{0}$ show relatively large magnitudes and a negative spatial correlation distribution. Here, a positive (negative) $\:{\varDelta\:}_{h}{Q}_{K}^{0}$ or $\:{\varDelta\:}_{h}{Q}_{P}^{0}$ indicates the convergence (divergence) of mesoscale KE. The dominant roles of horizontal advection and horizontal pressure work within mesoscales are also clearly evident during the shedding of looping currents in the Gulf of Mexico⁵⁹. However, in this study, the opposite spatial patterns of these two terms indicate that the horizontal advection of mesoscale KE is primarily balanced by horizontal pressure work during and after KLC eddy shedding. Interestingly, both of them exhibit a similar quadrupole structure. Combined with the $\:{KE}^{0}$ distribution shown in Figs. 5a1-a4, we attribute this phenomenon to the spatial redistribution of mesoscale KE driven by horizontal advection, but a clear proof requires more depth analyses, which is beyond the scope of this study and could be performed in follow-up studies.

The primary role of $\:{F}_{K}^{0}$ suggests that external forcing significantly impacts mesoscale KE after KLC eddy shedding, which sharply contrasts with the scenario observed in other regions such as the Gulf of Mexico⁵⁹where $\:{F}_{K}^{0}$ typically serves as a minor sink of $\:{KE}^{0}$ by friction or dissipation. Here, $\:{F}_{K}^{0}$ displays a negative-dominated spatial pattern in the northwest of the mesoscale eddy while a positive-dominated pattern in the southeast. Given the strong winter northeast Asia monsoon in the northeastern SCS (Fig. 14g) and the southwestward movement of the anticyclonic eddy, the work done by surface wind stress along (against) the eddy may contribute to the increase (decrease) of KE^25,27.

The strength of other energy terms is relatively weak. The slightly positive barotropic canonical transfer $\:{\varGamma\:}_{K}^{1\to\:0}$ indicates a weak inverse energy cascade from submesoscales to mesoscales, which has been observed from both ocean model and mooring observations in the northeastern SCS^19,32. However, weak and scattered negative values of $\:{\varGamma\:}_{K}^{1\to\:0}$, indicating a forward energy cascade, are also observed (Fig. 7a4) and recognized as a dissipation mechanism for mesoscale eddy in the SCS by previous study²⁴. Though as a main energy term in $\:{APE}^{0}$ balance (Figs. 6b1-4), the buoyancy conversion $\:{b}_{0}$ in $\:{KE}^{0}$ is relatively insignificant.

Although the strength of vertical pressure work $\:{\varDelta\:}_{z}{Q}_{P}^{0}$ is relatively weak, previous studies have shown the main dynamical mechanism of oceanic upper layer vertical pressure work in modulating intraseasonal fluctuations of the abyssal South China Sea^43,44and its significance in the vertical redistribution of KE should not be overlooked. Here, the magnitude is constrained within the mesoscale eddy and gradually reinforced as the eddy moves downstream. The vertical transport $\:{\varDelta\:}_{z}{Q}_{K}^{0}$ is considerably weaker than the vertical pressure work $\:{\varDelta\:}_{z}{Q}_{P}^{0}$ and only displays sporadic enhancements within the eddy in the late phase. This can be attributed to that the mesoscale eddy is nearly in quasi-geostrophic balance and the resulting vertical velocity is negligible.

Fig. 7

Same as Fig. 6, but for mesoscale KE budgets (color shading; 10⁻³ $\:{m}^{3}/{s}^{3}$), showing barotropic canonical transfer from submesoscale to mesoscale window $\:{\varGamma\:}_{K}^{1\to\:0}$ (a1-a4), buoyancy conversion $\:{b}_{0}$ (b1-b4), horizontal advection $\:{\varDelta\:}_{h}{Q}_{K}^{0}$ (c1-c4), vertical transport $\:{\varDelta\:}_{z}{Q}_{K}^{0}$ (d1-d4), horizontal pressure work $\:{\varDelta\:}_{h}{Q}_{P}^{0}$ (e1-e4), vertical pressure work $\:{\varDelta\:}_{z}{Q}_{P}^{0}$ (f1-f4), and the residual term $\:{F}_{K}^{0}$ (g1-g4).

The horizontal distributions of vertically integrated submesoscale APE budget are presented in Fig. 8. Different from $\:{APE}^{0}$ budget in Fig. 6, the $\:{APE}^{1}$ budget exhibits complex spatial scales and are primarily dominated by three terms of baroclinic canonical transfer $\:{\varGamma\:}_{A}^{0\to\:1}$, buoyancy conversion $\:{-b}_{1}$ and horizontal advection $\:{\varDelta\:}_{h}{Q}_{A}^{1}$. The baroclinic canonical transfer $\:{\varGamma\:}_{A}^{0\to\:1}$ displays positive-dominated horizontal distributions around the mesoscale eddy, indicating an effective forward cascade of APE from mesoscales to submesoscales. Additionally, the spatial pattern of $\:{\varGamma\:}_{A}^{0\to\:1}$ correlates well with that of submesoscale $\:{APE}^{1}$ in Fig. 5d, highlighting the significance of APE forward cascade in energizing submesoscales at the periphery of the mesoscale eddy^32,55. The zones with negative $\:{\varGamma\:}_{A}^{0\to\:1}$ suggest an inverse energy cascade of APE from submesoscales to mesoscales but its strength and coverage are limited. Furthermore, the buoyancy conversion $\:{-b}_{1}$ is predominantly negative in the surrounding of the mesoscale eddy and demonstrates a weak negative spatial correlation with $\:{\varGamma\:}_{A}^{0\to\:1}$. This implies that a portion of submesoscale APE cascading from mesoscales can be convert to submesoscale KE through buoyancy conversion^25,29,47.

The horizontal advection $\:{\varDelta\:}_{h}{Q}_{A}^{1}$ is the most dominant term in $\:{APE}^{1}$ budget and shows complex spatial patterns with concentrated positive and negative values at the periphery of the mesoscale eddy. However, its strength is fairly diminished in the interior, this underscores the main dynamical mechanism of horizontal advection at the periphery of the mesoscale eddy in $\:{APE}^{1}$ budget after KLC shedding.

Although submesoscales can generate significant vertical velocity within the mixed layer⁵⁵the contribution of vertical transport $\:{\varDelta\:}_{z}{Q}_{A}^{1}$ is relatively minor, rendering it almost negligible in submesoscale APE balance. The stratification source/sink $\:{S}_{A}^{0}$ is also very weak and has little influence on submesoscale APE. Similar to $\:{\varDelta\:}_{h}{Q}_{A}^{1}$, the residual term $\:{F}_{A}^{1}$ also exhibits elevated values in the surrounding of the eddy, indicating a complex spatial distribution associated with external forcing such surface wind stress and dissipation^25,47.

Fig. 8

Same as Fig. 6, but for submesoscale APE budget (color shading; 10⁻⁴$\:\:{m}^{3}/{s}^{3}$).

We show the vertically integrated submesoscale KE budget in Fig. 9. Different from the $\:{APE}^{1}$ budget shown in Fig. 8, the magnitude of $\:{KE}^{1}$ is approximately an order smaller than that of mesoscales (Fig. 7). It includes mainly four major terms: barotropic canonical transfer $\:{\varGamma\:}_{K}^{0\to\:1}$, horizontal advection $\:{\varDelta\:}_{h}{Q}_{K}^{1}$, horizontal pressure work $\:{\varDelta\:}_{h}{Q}_{P}^{1}$ and the residual term $\:{F}_{K}^{1}$. Due to the small spatiotemporal scales of submesoscales, all terms exhibit more heterogeneous and complex spatial patterns than these in Fig. 7. The horizontal advection $\:{\varDelta\:}_{h}{Q}_{K}^{1}$ and horizontal pressure work $\:{\varDelta\:}_{h}{Q}_{P}^{1}$ remain the two dominant terms and display a slightly opposite spatial pattern, implying that the balance of horizontal advection and pressure observed in mesoscales (Figs. 7c & e) can further extend to the range of submesoscales. The positive-dominated barotropic canonical transfer $\:{\varGamma\:}_{K}^{0\to\:1}$ suggests a primary forward cascade of KE from mesoscales to submesoscales, which corresponds to the barotropic instability in the ocean⁴⁷ and has been verified by observations²⁹. Concurrently, the presence of fragmented negative zones in $\:{\varGamma\:}_{K}^{0\to\:1}$ indicates a weak inverse energy cascade from submesoscales to mesoscales and is also validated by mooring observations³⁰. The residual term $\:{F}_{K}^{1}$ exhibits a remarkable negative pattern at the periphery of the mesoscale eddy, which corresponds to the enhanced vertical mixing dissipation associated with turbulence in the northeastern SCS^24,25. Meanwhile, there are some positive zones in the northwest SCS, this may be associated with the external surface wind stress that performs positive work on the ocean²⁴.

Although the strength of buoyance conversion $\:{b}_{1}$ is relatively weak, it displays overwhelming positive at the periphery of the mesoscale eddy, suggesting strong buoyancy conversion from submesoscale APE to KE associated with baroclinic instability^42,43,44. Furthermore, the large values of $\:{b}_{1}$ in Fig. 9b correspond well to the submesoscale $\:{KE}^{1}$ in Fig. 5c, indicating that $\:{b}_{1}$ serves as a main energy source for submesoscale KE during and after KLC eddy shedding. The vertical pressure work $\:{\varDelta\:}_{z}{Q}_{P}^{1}$ is relatively weak but its contribution to KE vertical redistribution is non-negligible. Different from $\:{\varDelta\:}_{z}{Q}_{P}^{0}$ in mesoscales (Fig. 7f), vertical pressure work in submesoscales is no longer constrained within the eddy and can extend to the entire northeastern SCS. Although submesoscales can generate strong vertical velocity in the upper ocean, the vertical transport $\:{\varDelta\:}_{h}{Q}_{K}^{1}$ remains relatively weak and its contribution to submesoscale KE is negligible.

Fig. 9

Same as Fig. 7, but for submesoscale KE budgets (color shading; 10⁻⁴ $\:{m}^{3}/{s}^{3}$).

We show the depth-time diagrams of mesoscale and submesoscale APE budget averaged within the MESM region (marked by the black box in Fig. 5) from November 30, 2016 to February 20, 2017 in Fig. 10. In general, all budget terms display significant differences bounded by the mixed layer depth (MLD), in which the upper layer (above MLD) exhibits strong energy level while the lower layer (below MLD) shows weak energy.

For mesoscale APE budget, two dominant terms of horizontal advection $\:{\varDelta\:}_{h}{Q}_{A}^{0}$ and the residual $\:{F}_{A}^{0}$ (as shown in Fig. 6) are primarily concentrated within the upper 50 m and display a significant negative correlation pattern, further validating that the convergence of $\:{APE}^{1}$ by horizontal advection is largely balanced by external forcing within the ocean upper layer after the KLC eddy shedding. However, their strength decreases rapidly below the MLD. The other three terms $\:{\varGamma\:}_{A}^{1\to\:0}$, $\:{-b}_{0}$ and $\:{\varDelta\:}_{z}{Q}_{A}^{0}$ also display weak negative value within the mixed layer, which emphasizes their roles in balancing the upstream-advected $\:{\varDelta\:}_{h}{Q}_{A}^{0}$ by forward energy cascade, buoyancy conversion from APE to KE, and divergence of vertical transport, separately. In later stages, the residual term $\:{F}_{A}^{0}$ gradually transitions to positive at the surface, indicating that the external forcing performs positive work on the eddy. The other primary term, buoyancy conversion $\:{-b}_{0}$ illustrated in Fig. 6b, decreases significantly after performing horizontal regional average, suggesting that energy conversion between APE and KE mainly occurs locally within the MESM region. Besides, $\:{-b}_{0}$ exhibits opposite spatial patterns bounded by the MLD, which signifies an opposite energy conversion direction above and below it. The stratification source/sink $\:{S}_{A}^{0}$ is mainly concentrated at the surface and shows a strong vertical pattern of surface intensification.

The vertical distribution of submesoscale APE budgets exhibits higher frequency temporal variations than the mesoscales. The most prominent characteristic is that the positive baroclinic canonical transfer $\:{\varGamma\:}_{A}^{0\to\:1}\:$shows a significant opposite correlation with the negative buoyancy conversion $\:-{b}_{1}$ within the mixed layer (Fig. 10b). This means that amounts of submesoscale APE downscaled from the mesoscales will transfer to submesoscale KE by buoyancy conversion^30,47. The vertical transport of $\:{\varDelta\:}_{Z}{Q}_{A}^{1}$ is also relatively strong and displays pronounced stratification within the mixed layer, verifying the significance of vertical transport in the redistribution of submesoscale APE. Although illustrated as one of the main energy terms in Fig. 8c, the strength of horizontal advection $\:{\varDelta\:}_{h}{Q}_{A}^{1}$ is relatively weak vertically. It displays overwhelming positive within the whole water column, suggesting strong APE convergence occurs within the MESM region by horizontal advection. The term $\:{S}_{A}^{1}$ shows typical characteristics of surface intensification due to the nonlinearity of the reference stratification within the mixed layer and is usually ignored. The residual term $\:{F}_{A}^{1}$ is characterized by rapid vertical variations with staggered positive and negative values within the upper ocean.

Fig. 10

Depth-time diagrams of the spatially averaged mesoscale (left, a1-f1) and submesoscale (right, a2-f2) APE budgets (color shading; 10⁻⁷ $\:{m}^{2}/{s}^{3}$) within the MESM region (marked by the black box in Fig. 5) from November 30, 2016 to February 20, 2017. The thick-black line in each panel denotes the spatially averaged mixed layer depth (MLD), which is defined as the depth at which potential density is different from the sea surface density anomaly by 0.03⁵⁵.

The corresponding depth-time diagrams of mesoscale and submesoscale KE budget are shown in Fig. 11. For mesoscale KE, the residual term $\:{F}_{K}^{0}$ serves as the primary energy source and is mainly balanced by horizontal and vertical pressure work $\:{\varDelta\:}_{h}{Q}_{P}^{0}$ and $\:{\varDelta\:}_{z}{Q}_{P}^{0}$ within the mixed layer. While below the mixed layer, the intensity of the three terms rapidly decreases and mostly reverses to the opposing sign. Combining with the horizontal distributions shown in Fig. 7e and f, this phenomenon suggests that the pressure work is significant in both the horizontal and vertical redistributions of mesoscale KE after KLC eddy shedding. It facilitates transporting KE from the upper to deep ocean and generating significant influence on abyssal oceanic dynamical processes⁴⁴. However, the dominant term $\:{\varDelta\:}_{h}{Q}_{K}^{0}$ shown in Fig. 7c significantly weakens after performing region average, suggesting that the horizontal advection of mesoscale KE primarily occurs within the MESM region, with little exchange with the external. The remaining terms $\:{\varGamma\:}_{K}^{1\to\:0}$, $\:{b}_{0}$ and $\:{\varDelta\:}_{z}{Q}_{K}^{0}$ are comparatively weak and have insignificant impacts on mesoscale KE budget.

In contrast to mesoscale KE budget, the submesoscale KE budget displays approximately-even magnitudes among energy terms. Moreover, its vertical distribution patterns can penetrate the MLD, further evidencing that mixed-layer baroclinic instability is not the primary generation mechanism of submesoscale KE after KLC eddy shedding. Previous studies have concluded that submesoscales within the KLC are mainly generated by strain-induced frontogenesis while the role of mixed‐layer baroclinic instability is secondary³². The barotropic canonical transfer, $\:{\varGamma\:}_{K}^{0\to\:1}$, displays positive-dominated vertical patterns interspersed with scattered negative zones, suggesting complicated KE transfer between mesoscales and submesoscales primarily driven by forward cascade, which is consistent with previous observations of forward KE cascade in the northwest SCS²⁹. Buoyancy conversion $\:{b}_{1}$ shows the largest and overwhelming positive value within the mixed layer, suggesting strong energy conversion of submesoscales from APE to KE within the upper ocean. However, its strength decreases rapidly beneath the mixed layer. The horizontal advection $\:{\varDelta\:}_{h}{Q}_{K}^{1}$ also displays predominately positive vertically, implying the convergence of submesoscale KE within the MESM region. That might be associated with the abundant submesoscale KE generated by strong topography-induced currents in the Luzon Strait, then propagating downstream accompanied by the mesoscale eddy. The vertical transport, $\:{\varDelta\:}_{Z}{Q}_{K}^{1},$ is relatively weak compared to other terms, with relatively large values concentrated in the mixed layer, which may be associated with the large transport caused by submesoscale ageostrophic vertical velocity although having little effect on the submesoscale KE balance. The vertical average of primary energy term (horizontal pressure work $\:{\varDelta\:}_{h}{Q}_{P}^{1}$ shown in Fig. 9) is also relatively weak, suggesting that pressure work mainly occurs in local with little exchange with the external region. The vertical pressure term $\:{\varDelta\:}_{z}{Q}_{P}^{1}$ appears overwhelming negative within the mixed layer but predominately positive below, indicating that the vertical transportation of KE from oceanic upper to interior is mainly done by pressure work instead of $\:{\varDelta\:}_{Z}{Q}_{K}^{1}$. The residual $\:{F}_{K}^{1}$ exhibits significant negative values throughout the vertical domain, and combined with its horizontal distribution shown in Fig. 9f, we may conclude strong submesoscale KE dissipation associated with turbulences.

Fig. 11

Same as Fig. 10, but for mesoscale (left, a1-g1) and submesoscale (right, a2-g2) KE budgets (color shading; 10⁻⁷ $\:{m}^{3}/{s}^{3}$).

We show the time series of volume-averaged mesoscales and submesoscales APE and KE budgets within the upper 200 m over the MESM region from November 30, 2016 to February 20, 2017 in Fig. 12. Similar to Figs. 10 and 11, the submesoscale energy budget terms demonstrate higher frequency temporal variability than that of mesoscales. The mesoscale $\:{APE}^{0}$ continues to decrease except for a temporary increase in late January 2017. Combined with $\:{APE}^{0}$ horizontal distributions shown in Fig. 5b, we attribute this slight increase to the appearance of the cyclonic eddy in the wake of the shedding anticyclonic eddy, but it can’t be sustained due to quick dissipations. In the initial stage (before January 2017), the mesoscale energy budget is mainly balanced by the positive horizontal advection $\:{\varDelta\:}_{h}{Q}_{A}^{0}$ and the negative residual term $\:{F}_{A}^{0}$. However, the strength of $\:{F}_{A}^{0}$ (absolute value) decreases dramatically in the late phase. The other terms are relatively weak throughout the whole period. For mesoscale $\:{KE}^{0}$, it increases initially and reaches to the maximum in late January 2017 before decreases, in which the positive residual term $\:{F}_{K}^{0}$ is primarily balanced by pressure works $\:{\varDelta\:}_{h}{Q}_{P}^{0}$ and $\:{\varDelta\:}_{z}{Q}_{P}^{0}$, and the other terms are relatively weak and have negligible effect on mesoscale KE balance.

For the submesoscale $\:{APE}^{1}$ budget (Fig. 12c), the vertical transport and stratification terms are so weak that they are ignored. Instead, the positive baroclinic canonical transfer $\:{\varGamma\:}_{A}^{0\to\:1}$ and horizontal advection $\:{\varDelta\:}_{h}{Q}_{A}^{1}$ are mainly balanced by the negative buoyancy conversion $\:{-b}_{1}$. This suggests that the strong forward cascade of APE together with advective process during and after the KLC eddy shedding is mainly balanced by buoyancy conversion. While the residual term $\:{F}_{A}^{1}$ and submesoscale $\:{APE}^{1}\:$show periodic fluctuations without distinct characteristics. Similarly, for the submesoscale $\:{KE}^{1}$ budget, the vertical transport is also disregarded because of its locality and small magnitudes. In general, the positively-dominated barotropic canonical transfer $\:{\varGamma\:}_{K}^{0\to\:1}$, together with buoyancy conversion $\:{b}_{1}$ and horizontal advection $\:{\varDelta\:}_{h}{Q}_{K}^{1}$ is commonly balanced by the negative vertical pressure $\:{\varDelta\:}_{z}{Q}_{P}^{1}$ and residual terms $\:{F}_{K}^{1}$. The submesoscale $\:{KE}^{1}$ also displays no significant variations throughout the entire period.

Fig. 12

Time series of volume-averaged mesoscale (a)$\:{APE}^{0}$, (b)$\:{KE}^{0}\:$and submesoscale (c) $\:{APE}^{1}$, (d)$\:{\:KE}^{1}\:$(right label, in $\:{m}^{2}/{s}^{3}$) and their budgets (left label, in $\:{m}^{2}/{s}^{2}$) within the upper 200 m over the MESM region from November 30, 2016 to February 20, 2017. The four typical moments shown in Figs. 4, 5, 6, 7, 8 and 9 are marked by vertical dotted lines in each panel. Note only part of energy budget terms are illustrated in submesoscale panels (c) and (d), and the red axis marks on the left are for energy budget terms while the black axis marks on the right are for energy (black lines), and the slope of an energy line represents its time tendency.

Figure 13 summarizes the time-space averaging mesoscale and submesoscale APE and KE budgets within the upper 200 m of the MESM region from November 30, 2016 to February 20, 2017. Although some energy terms, such as horizontal advection $\:{\varDelta\:}_{h}{Q}_{K}^{0}$, horizontal pressure work $\:{\varDelta\:}_{h}{Q}_{P}^{0}$ and $\:{\varDelta\:}_{h}{Q}_{P}^{1}$, are strong locally, the results of time-space averaging appear significant differences. The primary energy source in mesoscale $\:{APE}^{0}$ is horizontal advection $\:{\varDelta\:}_{h}{Q}_{A}^{0}$, while the secondary is buoyancy conversion $\:-{b}_{0}$ (but much weaker). Three main energy sinks are the residual term $\:{F}_{A}^{0}$, vertical transport $\:{\varDelta\:}_{z}{Q}_{A}^{0}$ and baroclinic canonical transfer $\:{\varGamma\:}_{A}^{1\to\:0}$. For mesoscale $\:{KE}^{0}$, the only energy source is the residual term $\:{F}_{K}^{0}$, which is associated with the strong surface wind stress in winter from the East Asian monsoon system²⁴. The $\:{F}_{K}^{0}$ is mainly balanced by vertical pressure work $\:{\varDelta\:}_{z}{Q}_{P}^{0}$, horizontal pressure work $\:{\varDelta\:}_{h}{Q}_{P}^{0}$ and horizontal advection $\:{\varDelta\:}_{h}{Q}_{P}^{0}$, while the strength of buoyancy conversion $\:{b}_{0}$ and barotropic canonical transfer $\:{\varGamma\:}_{K}^{1\to\:0}$ is weak. Correspondingly, for submesoscale $\:{APE}^{1}$, consistent the study for the Gulf of Mexico⁴⁷positive baroclinic canonical transfer $\:{\varGamma\:}_{A}^{0\to\:1}$ and horizontal advection $\:{\varDelta\:}_{h}{Q}_{A}^{1}$ are mainly balanced by buoyancy conversion $\:-{b}_{1}$, while other terms are negligible. This suggests that although baroclinic canonical transfer only accounts for a small fraction of mesoscale $\:{APE}^{0}$ energy budget, it serves as the primary source for submesoscale $\:{APE}^{1}$ and exert significant influences on submesoscale dynamics. For submesoscale $\:{KE}^{1}$, three main energy sources of buoyancy conversion $\:{b}_{1}$, horizontal advection $\:{\varDelta\:}_{h}{Q}_{K}^{1}$ and barotropic canonical transfer $\:{\varGamma\:}_{K}^{0\to\:1}$ are primarily balanced by the residual term $\:{F}_{K}^{1}$ and vertical pressure work $\:{\varDelta\:}_{z}{Q}_{P}^{1}$. The terms of vertical transport $\:{\varDelta\:}_{h}{Q}_{K}^{1}$ and horizontal pressure work $\:{\varDelta\:}_{h}{Q}_{P}^{1}$ are so weak that they are negligible. This means that the submesoscale KE is dominated by buoyancy conversion of submesoscale APE while the influence of barotropic instability is comparatively limited.

Fig. 13

Mesoscale (a) $\:{APE}^{0}$, (b) $\:{KE}^{0}$ and submesoscale (c) $\:{APE}^{1}$, (d) $\:{KE}^{1}$ budgets ($\:{m}^{3}/{s}^{3}$) as the results of time-volume average in the upper 200 m and within the MESM region from November 30, 2016 to February 20, 2017.

Dynamics diagnosis of submesoscale instability after the KLC eddy shedding

We examine various submesoscale instability parameters and show their evolution in Fig. 14. The instability parameters include strain rate $\:St$, advective frontogenetic tendency $\:F$ and frontal sharpness $\:{M}^{4}$ etc. As described in Sect. 2.3, after shedding from the KLC, the mesoscale eddy moves downstream and generate strong straining shear in the surroundings (Figs. 14a1-a4). As one of the crucial dynamical mechanism in generating submesoscales, straining deformation of quasi-geostrophic flow can rapidly sharpen submesoscale filaments and fronts along the edges at the rate of advective frontogenetic tendency $\:F$ (Figs. 14b1-b4)^3,5,51. The positive-dominated advective frontogenetic tendency $\:F$ represents the developing and intensifying of submesoscales⁵⁵. Correspondingly, the frontal sharpness $\:{M}^{4}$ displays conspicuous increases at the periphery of the mesoscale eddy, suggesting the enhancement of baroclinicity within the ocean upper layer (Figs. 14c1-c4)⁶². The strain rate $\:St$ closely coincides with the increased advective frontogenetic tendency $\:F$ and frontal sharpness $\:{M}^{4}$, further verifying the main generating mechanism of mesoscale straining instead of mixed layer baroclinic instability in activating abundant submesoscale activities after KLC eddy shedding³². Then, the enhanced lateral buoyancy gradients contribute to total EPV $\:q$ as negative values (Figs. 14d1-d4), and create favorable conditions for various submesoscale instabilities such as symmetric, gravitational and centrifugal instabilities^53,57,63. However, in zones of positive total EPV, only geostrophic baroclinic mixed layer instabilities are present⁶⁴. Here, we focus on symmetric instability, which is a type of forced submesoscale instability that occurs when negative total EPV and the Richardson number criterion are both satisfied under the influence of strong surface atmospheric forcing^54,55. The pink points in Figs. 14d1-d4 depict the zones that meet the criteria of SI, they predominantly concentrate at the periphery of the mesoscale eddy and within the Taiwan Strait. Then, SI can induce large vertical velocities and drive strong convergence or divergence (Figs. 14e1-e4) under the condition of intense atmospheric forced buoyancy loss (shown in Figs. 14g1-g4)⁵⁵. Additionally, the negative values of $\:A-St$ in these zones mean that they tend to deviate from geostrophic balance and are primarily dominated by unbalanced submesoscale mode (Figs. 14f1-f4)⁵⁸.

Fig. 14

Snapshots of surface submesoscale instability parameters for strain rate $\:St$ (a1-a4; color shading; $\:{s}^{-1}$), advective frontogenetic tendency $\:F$ (a1-a4; color shading; $\:{s}^{-5}$), frontal sharpness $\:{M}^{4}$ (c1-c4; color shading; $\:{s}^{-4}$), total EPV $\:q$ (d1-d4; color shading; $\:{s}^{-3}$), normalized vertical divergence $\:\delta\:/f$ (e1-e4), the difference between absolute vertical vorticity and strain rate $\:A-St$ (f1-f4; color shading; $\:{s}^{-1}$) and atmospheric forced surface buoyancy loss (g1-g4; color shading; $\:{m}^{2}/{s}^{3}$). The dotted and solid black contours in each panel denote negative and positive SLA, respectively. The pink dots in panels d1-d4 refer to the zones that meet the SI criteria based on $\:q$ and $\:{Ri}_{g}$. The vector in panels g1-g4 denotes the surface wind stress. The solid blue line in panels a1-f4 denotes the zonal profiles to be analyzed in Fig. 15.

We show the zonal-vertical cross-section of corresponding submesoscale instability parameters along the mesoscale eddy center (marked by blue segments in Fig. 14) in Fig. 15. We see that the isopycnal surfaces are steep in the upper layer after the eddy sheds from the KLC, especially in active submesoscale zones. This indicates a weak stratification within the mixed layer and an increase of baroclinicity in submesoscales zones. The large strain rate $\:St$ (Fig. 15a) corresponds well to positive advective frontogenetic tendency $\:F$ (Fig. 15b) and enhanced frontal sharpness $\:{M}^{4}$ (Fig. 15c), especially in submesoscale zones. This further proves that the strong straining shear of the mesoscale eddy can rapidly generate submesoscale fronts and filaments and increase baroclinicity within the upper layer⁵⁵. Then, the increased baroclinicity contributes to a negative total EPV $\:q$ (Fig. 15d) and forms favorable conditions for triggering submesoscale instabilities⁵⁴. As the mesoscale eddy moves downstream, these submesoscales drive large vertical velocities within the mixed layer. Thus, the strength of convergence and divergence is significantly enhanced in submesoscale zones (Fig. 15e), greatly promoting the exchanges between the interior and upper oceans. Meanwhile, the negative $\:A-St$ indicates that the unbalanced submesoscale modes are prevalent in the upper ocean and can extend below the mixed layer (Fig. 15f). Afterward, these submesoscale instabilities tend to restratify the water column and induce isopycnal surface slumping^38,55,65. Late on, the isopycnal surfaces become more flatten while the MLD deepens because of the convergence of anticyclonic eddy, while submesoscales remain active at the periphery of the mesoscale eddy.

Fig. 15

Same as Fig. 14, but for the zonal-vertical cross-section of corresponding submesoscale instability parameters (a-f) within the upper 200 m marked by the blue solid line in Fig. 14. The red line in each panel indicates the MLD. The blue and grey contours above and below the MLD denote isopycnal surfaces with a spacing of 0.1 and 0.3$\:kg/{m}^{3}$, separately.

Figure 16 displays the horizontal distributions of vertical velocity $\:w$, BFLUX and GSP at 10 m depth as well as their vertical structures. We can see that the spatial pattern of BFLUX and GSP (Figs. 16b-c, e-f) correlate well with diagnostic submesoscale instability parameters shown in Figs. 14 and 15, of which BFLUX appears overwhelming positive values in the upper ocean, indicating the strong buoyancy conversion from submesoscale APE to KE^54,55. Meanwhile, $\:\text{G}\text{S}\text{P}$ also displays large positive values in submesoscale zones, suggesting that submesoscales are energized by geostrophic KE through symmetric instability^47,55. The vertical structures shown in Figs. 16d-f further validate above conclusions. The enlarge vertical velocity in Fig. 16(a) can reach approximately 100 m/day, and coincide well with large values of GSP and BFLUX. All the diagnosed results imply that submesoscale KE can be fueled by geostrophic KE and submesoscales APE by submesoscale baroclinic and symmetric instability separately during and after KLC eddy shedding²⁴.

Fig. 16

Snapshots of vertical velocity w (a, d) (color shading; $\:m/\text{s}$), BFLUX (b, e) and GSP (c, e) (color shading; $\:{m}^{3}/{s}^{3}$) at 10 m depth within the MESM domain (panels a-c) and the upper 200 m zonal-vertical cross-section marked by black segments in panels a-c (panels d-f).

Conclusion

The multiscale energetics and submesoscale instabilities during and after a typical KLC eddy shedding process have been investigated using a realistic downscaled submesoscale-permitting 1/70° high-resolution ocean simulation. While the numerical simulation in general matches well with satellite observations in the eddy’s lifecycle, including genesis, shedding and moving, as well as the magnitudes of SLA and surface velocity, multiscale energetics and submesoscale instabilities are thoroughly analyzed. Based on MS-EVA method, two scale windows termed the low-frequency mesoscale window and the high-frequency submesoscale window are employed to investigate the mesoscale and submesoscale energetic budgets. Subsequently, dynamical diagnostics are utilized to explore the submesoscale baroclinic and symmetric instability, as well as their roles in energy cascades. The gained results are summarized in Fig. 17.

Fig. 17

The schematic diagram of the multiscale interactions and submesoscale instabilities during and after eddy shedding from the Kuroshio Loop Current (KLC) in the northeast South China Sea (NESCS). (a) The general configuration of mesoscale eddy shedding from KLC at the NESCS domain. The black-dashed curve and red-dashed circle with arrows represent the looping path of KLC and the shed anticyclonic mesoscale eddy. The mesoscale eddy can energize submesoscales at the periphery by forward energy cascade (yellow solid-curved arrow). These abundant submesoscales can generate various submesoscale instabilities (pink spirals) within the upper ocean. Such submesoscales can also feedback to the mesoscale eddy) (purple dotted-curved arrow). (b) Illustration of major processes of mesoscale eddy energizing submesoscale activities as buoyancy conversion (submesoscale baroclinic instability, light grey), horizontal advection (black arrow), vertical pressure work (brown angle-down) and turbulence dissipation (light-brown). SI is illustrated in pink spirals at the periphery of the mesoscale eddy.

Energetically, the results reveal that both the forward and inverse energy cascades coexist during and after KLC eddy shedding. Overall, the forward cascade of mesoscales APE plays a crucial role in energizing submesoscales, while the contribution of mesoscale KE forward cascade associated with barotropic instability is relatively weak. Then, buoyancy conversion facilitates the growth of submesoscale KE by the release of submesoscale APE. Specifically, the submesoscale KE is primarily charged by strong buoyancy conversion (light grey curve in Fig. 17b) and secondarily from horizontal advective upstream (black arrow in Fig. 17b), which is predominantly balanced by vertical pressure work (brown angle-down fracture line in Fig. 17b) and turbulence dissipation (light-brown curve in Fig. 17b).

Dynamically, except for the release of submesoscale APE by baroclinic instability, symmetric instability (SI) can extract KE from geostrophic flows and drive forward KE cascades. Specifically, strain-induced advective frontogenesis by geostrophic flows after KLC eddy shedding can rapidly sharpen submesoscales at the periphery of the mesoscales by enhancing lateral buoyancy gradient. The increased baroclinicity can further induce a negative total EPV and create favorable conditions for submesoscale symmetric instability (SI) coupled with atmosphere-forced surface buoyancy loss. Then, SI can generate large vertical velocities and induce strong divergence and convergence in submesoscale zones, facilitating the release of geostrophic KE. The vertical velocity can reach 100 m/d, significantly enhancing vertical exchanges between the surface and subsurface ocean in the northeastern SCS.

The results gained from this study highlight the significance of multiscale energetics and submesoscale instabilities during and after the KLC eddy shedding in the SCS. However, the horizontal resolution in this study is relatively coarse to full resolving SI activities, leading to an underestimation of its strength. Higher-resolution models are required to conduct a detailed study on this topic in the future. The findings presented in this paper provide us the confidence to pursue further in-depth research. Additionally, this study only serves as the first step on multiscale interactions in the mesoscale-submesoscale regimes, which focuses on forward cascading from mesoscale to submesoscale. More studies are required to further clarify the mechanisms of submesoscale processes in inverse cascading from submesoscale to mesoscale (denoted by purple dotted-curved arrow of Fig. 17). For example, a two-way nesting downscaling numerical experiment can be designed to address the inverse cascading process. Especially, in such a two-way nesting framework, by controlling the strength of the feedback of resolved submesoscale signals in the child domain to the mesoscales simulated in the parent domain, the role and mechanism of specific submesoscale processes can be detected through examination of sensitivities. Then, thorough energetics and dynamics analyses can provide a complete picture of multiscale interactions in SCS eddy and front activities.