An innovative Squid Game Optimizer for enhanced channel estimation and massive MIMO detection using dilated adaptive RNNs

Abstract

The Multiple-Input Multiple-Output (MIMO) system can provide improved spectral efficiency and energy performance. However, the computational demand faced by conventional signal recognition techniques has significantly increased due to the growing number of antennas and higher-order modulations. To overcome these challenges, deep learning approaches are adopted as they offer versatility, nonlinear modelling capabilities, and parallel computation efficiency for large-scale MIMO detection. Therefore, a deep network for channel estimation and massive MIMO detection is developed to reduce computational complexity issues. Initially, a channel estimation scheme is developed to enhance the channel capacity of the MIMO system. It correlates the transmitted and received signals using a confusion matrix. The proposed Modified Squid Game Optimizer (MSGO) is employed for channel state estimation. Based on the obtained channel state information, MIMO detection is performed within the communication system. Here, Multiuser Interference Cancellation (MIC)-based iterative sequential detection is initially conducted. Then, massive MIMO detection is performed using the Dilated Adaptive Recurrent Neural Network with Attention Mechanism (DARNN-AM) through learnable parameters. Moreover, to further optimize the detection performance by fine-tuning the attributes of DARNN-AM, the MSGO is utilized. The proposed network performs multi-segment mapping across multiple constellation points with different modulation schemes. The effectiveness of the proposed deep learning-based MIMO detection system is evaluated by comparing it with existing techniques and algorithms to validate its superior performance.

Introduction

One of the foremost intriguing developments in Fifth Generation (5G) mobile communications is Machine-to-Machine (M2M) communication and other networks using MIMO, which substantially improve spectral efficiency and energy conservation¹. This system employs a large number of antennas at the Base Stations (BS), enabling high-speed connectivity and low-latency transmission². However, these large-scale deployments also pose significant challenges for MIMO detection³. To separate the originally transmitted signal from the signal received at the BS antennas, the MIMO detection process is employed⁴. Yet, designing a MIMO detector that provides high accuracy with low complexity remains difficult, especially in massive MIMO configurations⁵. Various wireless communication systems incorporate MIMO technology, which can significantly enhance spectral efficiency and network reliability. Effective channel estimation and signal detection mechanisms must strike a balance between computational speed and complexity, playing a critical role in receiver design and prompting extensive research to fully realize the advantages of MIMO⁶.

Since the introduction of Third-Generation (3G) wireless networks, MIMO has played a critical role in enhancing the performance of wireless transceivers⁷. For improved spectral efficiency and link reliability, multiple antennas are utilized at both the receiver and the transmitter ends⁸. However, the MIMO receiver requires a detection mechanism to distinguish signals corrupted by noise and interference. Over its five-decade evolution, MIMO detection has attracted significant research attention⁹. Massive MIMO systems are a natural extension of conventional small-scale MIMO technology, incorporating a large number of antennas at the base station or gateway¹⁰. The number of antennas at the BS is significantly higher than the number of antennas present in user devices within the same cell or service area¹¹. This is a key characteristic of the traditional massive MIMO architecture, which typically operates at frequencies up to 6 GHz. As a result, pilot contamination poses challenges to accurate channel estimation, and multiuser interference increases the additive noise throughout the network¹².

The Deep Neural Network (DNN) is one of the most powerful and promising deep learning architectures, currently applied in various domains such as channel encoding and decoding, channel estimation, signal detection, CSI feedback, and interference management¹³. Nevertheless, these networks are often trained as “black boxes,” making their internal functioning difficult to interpret¹⁴. Traditional detection methods also exhibit several limitations¹⁵. For instance, conventional detection algorithms typically treat signal instances independently, lacking any connection between adjacent signal observations, as they rely on “snapshot” detection¹⁶. This significantly impairs detection performance. Additionally, KBest is considered the most effective technique among classical detection methods, achieving a balance between accuracy and complexity. KBest utilizes a flexible data structure and identifies segments of the sample space for processing¹⁷. However, tree-based search approaches require substantial computational resources, as they rely solely on optimizing an objective function. To overcome this, incorporating detection memory and designing efficient compressed storage structures can enable low complexity and robust detection mechanisms. Despite advancements, many existing systems still face major challenges. Some deep networks are highly complex and demand extensive vector processing. Others, such as DetNet¹⁸ and MMNet¹⁹, underperform in downlink MIMO scenarios but show strong performance in uplink MIMO. Hence, this work developed a deep learning architecture for channel estimation and MIMO detection to address these limitations.

The significant offerings of the deep structure-based channel estimation with the MIMO detection model are organized as follows.

• To establish a deep structure-based channel assessment with an MIMO signal detection model to identify the channel characteristics and hence the distortion, as well as the noise effects occurring in the signal, is highly prevented.

• To develop MSGO for optimizing the channel matrix to minimize the Bit Error Rate (BER), Normalized Mean Square Error (NMSE), Symbol Error Rate (SER), and Pairwise Error Probability (PEP) in the received signal during channel estimation. This helps in achieving higher throughput or data rate by maintaining good BER.

• To detect the channel matrix for efficient communication, a DARNN-AM is suggested in which the data is collected from MSGO-based channel estimation, where the channel state information is given to train the DARNN-AM to get a channel estimate. The proposed MSGO is also used to optimize the parameters in the DARNN-AM to improve the channel estimation performance.

• The results attained by the MSGO-DARNN-AM-based channel estimation with the MIMO detection model are compared with the usual approaches to determine the usefulness of the explored MSGO-DARNN-AM-based channel estimation with the MIMO detection model.

The persisting portions of the recommended MSGO-DARNN-AM-based channel assessment with the MIMO detection model are enumerated as follows. The pros and cons of the conventional channel judgment and the massive MIMO detection model are elucidated in fragment II. In fragment III, the MIMO system model with the need for channel estimation and massive MIMO identification in wireless communiqué systems and the proposed channel estimation with the MIMO detection model is offered in a brief way. Fragment IV explores the details of the channel judgment in MIMO for attaining channel coefficients from the received signal for detecting MIMO. In fragment V, deep learning-based massive MIMO detection using a dilated adaptive deep learning network with optimal tuning of parameters is detailed in detail. The outcome generated by developed channel estimation with the MIMO detection model and the discussion part is briefly given in fragment VI. At last, fragment VII concludes the developed channel estimation with the MIMO detection model.

Literature survey

Related works

In 2023, Yu et al.²⁰ presented an effective data-driven detection network called the Accelerated Multiuser Interference Cancellation Network (AMIC-Net). To enhance convergence performance, an extrapolation factor was integrated into the Multiuser Interference Cancellation (MIC) algorithm for the Iterative Sequential Detection (ISD) detector. Then, using a weakly connected approach instead of a fully connected one, the accelerated iterative method was employed to design a relatively simple Deep Neural Network (DNN) structure, which improved the detection rate when combined with the data-driven deep learning approach. An innovative activation function was developed by combining multiple soft sign activation functions with different modulations. The proposed deep learning network outperformed existing detectors with similar or lower computational complexity.

In 2021, Mahmoud et al.²¹ proposed a deep learning approach for non-coherent multiple-symbol detection in Differential Phase-Shift Keying (DPSK) multi-user massive MIMO systems. The proposed model reduced the high computational complexity required by traditional DPSK detection algorithms. For the same system characteristics, Decision-Feedback Differential Detection (DFDD) and conventional Multiple-Symbol Differential Detection (MSDD) were compared with two deep-learning-based multiple-symbol detection receiver designs. Traditional MSDD was implemented using Multiple-Symbol Differential Sphere Detection (MSDSD). The final results demonstrated the effectiveness of the proposed channel estimation process.

In 2020, Wei et al.²² developed an iterative Conjugate Gradient Descent (CGD) detector to construct a Learned Conjugate Gradient Descent Network (LcgNet). The network learned generalizable features. A novel quantized version of LcgNet was also proposed to reduce memory costs, where the learned parameters were quantized using a low-resolution, non-uniform quantizer. The quantizer function was specifically designed to reshape the soft staircase function. Moreover, the proposed networks were easy to train due to the limited number of learnable parameters. According to numerical results, the network achieved promising performance with significantly reduced complexity.

In 2023, Nigatu and Zhang²³ introduced two DNN-based detectors that effectively addressed limitations of conventional methods. The DNN architecture was designed to model adaptive penalty parameters efficiently, resulting in improved performance. Additionally, a sub-DNN architecture was utilized with the Alternating Direction Method of Multipliers (ADMM) for computation. The researchers proposed a detection framework with comparable effectiveness and lower computational complexity. Numerical results indicated that the proposed method outperformed modern detectors with similar or lower complexity.

In 2021, Xu and Du²⁴ proposed a Machine Learning Network (MLNet) for sample space classification. For time-varying channels, MLNet significantly outperformed Deterministic Networks (DetNet) and Multi-Modal Networks (MMNet). MLNet required less computation than existing neural network algorithms. A novel training approach was also introduced to enhance DetNet’s detection performance, contributing further to MLNet’s advantages.

In 2020, Tan et al.²⁵ presented a DNN architecture to enhance massive MIMO systems by embedding Message-Passing Detectors (MPDs). Recurrent MPDs were used to build a DNN-based MIMO detection model. Modified MPDs such as damped Belief Propagation (BP), Max-Sum (MS), and simplified Channel Hardening-Exploiting Message Passing (CHEMP) were deployed to construct the DNN. To improve performance, the DNN correction factors were optimized. Simulation results showed that the proposed DNN detectors achieved lower bit error rates and better reliability under various antenna and channel conditions while maintaining complexity similar to conventional detectors. The DNN could be reused for multiple detection tasks with high efficiency, proving the flexibility and effectiveness of the proposed framework.

In 2020, Liao et al.²⁶ proposed an efficient DNN-based massive MIMO detector. Deep learning was used for the detection process, integrating an iterative detection strategy into the DNN structure. Additionally, Multiuser Interference (MUI) cancellation was incorporated at each layer of the proposed model. The learning process was designed to optimize the auxiliary parameters. Compared to existing detectors for massive MIMO systems, the proposed model demonstrated superior detection performance.

In 2023, Nguyen et al.²⁷ developed a DNN model for massive MIMO detection. The latest advances in DNN-based MIMO detection were combined with well-established MIMO detection techniques. Neural networks (NN), machine learning (ML), and deep learning (DL) techniques have emerged as powerful approaches for improving various aspects of wireless communication networks^{28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55}, including signal processing, channel estimation, resource allocation, and network optimization. The proposed model’s key numerical performance indicators were compared against existing methods to validate its effectiveness.

Problem statement

Deep learning networks used for MIMO detection are often too complex. Additionally, a large number of matrix inversions are required for accurate detection. Some algorithms suffer from increased complexity, which leads to degraded detection performance. The uses and limitations of existing deep learning-based massive MIMO detection techniques are summarized in Table 1. AMIC-Net²⁰ uses backpropagation to learn input sequences more effectively and significantly reduces gradient vanishing. However, it struggles to handle the complexities of massive MIMO scenarios. MSDSD²¹ significantly reduces the computational complexity required for detection and lowers the energy consumption during channel estimation. Nonetheless, it is ineffective at detecting non-coherent signals and lacks accuracy due to the absence of encoding techniques. LcgNet²² greatly reduces memory costs and eliminates signal detection complexity. Yet, it requires a large volume of training data and incurs high operational costs. DNN²³ efficiently manages penalty parameters to enhance network performance and does not require extensive computations for variable updates. However, its computational complexity remains high. MLNet²⁴ substantially reduces the computational effort for detection and offers lower complexity. However, it suffers from high latency and packet loss. CHEMP²⁵ provides high robustness and requires less training time. Yet, it is costly and unsuitable for software-based implementations. DNN²⁶ efficiently manages layer-wise connectivity. However, it struggles to process data with complex or large dimensions. DNN²⁷ offers high efficiency and can be reused for multiple detection tasks. Nevertheless, it requires a large dataset and fails to consider essential information during training. Therefore, to address these challenges, a deep network for massive MIMO detection is proposed.

Table 1 Features and challenges of existing deep learning-based massive MIMO detection.

MIMO system model with need of channel estimation and massive MIMO detection in wireless communication system

System model of MIMO

Throughout the communication process, the phantom efficiency rate is enhanced with the assistance of the MIMO network. This is primarily due to the roles of the transmitter and receiver in the MIMO system. The spreaders and receivers in the MIMO network are represented as $t_{mimo} ,\,\,and\,r_{mimo}$ accordingly. The signal transmitted through the MIMO network contains a high level of noise, which is reduced by the subcarrier, denoted as $T_{d}$. The signal $W^{n} (r)$ is transmitted from the MIMO network antenna $n$. This transmitted signal is then mapped into a vector space of dimension $B \times 1$. A cyclic prefix is added to the MIMO network by passing the vector value to the Fast Fourier Transform (FFT) block. The length of the cyclic prefix is selected within the range of $m \ge O - 1$, and the dimension of the MIMO channel is denoted as $O$. A receiver antenna $u$ is added to the MIMO network. This process is mathematically represented in Eq. (1).

$$d^{u} (r) = \sum\limits_{n = 1}^{{t_{mimo} }} {X_{mr}^{u,n} } \aleph^{X} E^{u} (r) + \nu^{u} (r)$$

(1)

Here, the process of removal of the cyclic prefix from the MIMO network is indicated as $d^{u} (r)$, the vector of the spherical part is represented as $X_{mr}^{u,n}$, the desire retort of the channel is indicated as $X_{{}}^{u,n}$ and here, the breadth of the vector space is taken as $B \times 1$. The primary column of the spherical shape vector is indicated as $\left[ {X_{{}}^{{u,n^{ \cup } }} ,0_{r \times (B - O)} } \right]^{ \cup }$, the unitary matrix of size $B \times B$ is attained by the term $\aleph$. The spherical vector has some specific Eigenvalue, and its decomposition process is illustrated in Eq. (2).

$$X_{mr}^{u,n} = \aleph^{X} di\left\{ {\sqrt {B\aleph } \left[ {X^{{u,n^{ \cup } }} ,0_{{1_{r \times (B - O)} }} } \right]^{ \cup } } \right\}\aleph$$

(2)

The result attained from the FFT is indicated as $d^{u} (r)$, and it is evaluated by Eq. (3).

$$d^{u} (r) = \sum\limits_{n = 1}^{{t_{mimo} }} {di\left\{ {\sqrt {B\aleph } \left[ {X^{{u,n^{ \cup } }} ,0_{{1_{r \times (B - O)} }} } \right]^{ \cup } } \right\} \times D^{u} (r) + \wp^{u} (r)}$$

(3)

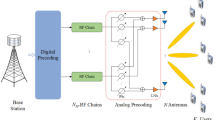
In the above Eq. (3), the term $\wp^{u} (r)$ is substituted instead of $\nu^{u} (r)$. The system model of the MIMO is shown in Fig. 1.

Fig. 1

Explored view of the MIMO system model.

Problem formulation and analysis

The hybridized precoding is indicated by $T_{F}$, which is generated in the mmWave system for estimating the vector channel. The uplink channel present in it assists in attaining the downlink channel through the estimation of vector channels in the channel dataset. Here, the developed model is employed to acquire downlink precoding. In terms of the uplink channel, the BS requires more power, and the sequenced orthogonal pilots $Z = D^{S \times S}$ have been shifted via different signals along with the users $H$. There are totally $H$ analogue precoding vectors $T_{F}^{q} \in D^{{R_{c} \times U_{T} }}$ and digitalized precoding vectors $T_{C}^{q} \in D^{{U_{T} \times U_{T} }}$ are present in the uplink channel, wherein the term $q$ lies in $1,2,..Q$ . The BS received the sequenced pilots in $Q^{th}$ sender, as per Eq. (4).

$$A_{q}^{up} = \left( {T_{F}^{q} T_{C}^{q} } \right)^{V} R^{V} Z + \left( {T_{F}^{q} T_{C}^{q} } \right)^{V} R_{q}$$

(4)

In Eq. (4), the additive white Gaussian noise matrix is indicated by $R_{q}$ for the transmission $Q$. Here, every vector in all the entries $Q$ has the criteria $QH = \left( {q,\alpha^{2} } \right)$. This is the criterion of the associated user, which is equally orthogonal to that of the sequenced pilot, which is indicated by $FF^{Q} = P_{S}$, with it, the terms such are $A_{q}^{up}$ and $F^{R}$ are multiplied. Then, the results will be obtained using Eq. (5) to Eq. (7).

$$G_{q} = A_{q}^{up} F^{R} = \left( {T^{q} } \right)^{V} R^{T} + \overline{{R_{q} }}$$

(5)

$$T^{q} = T_{F}^{q} T_{C}^{q} \in D^{{U_{T} \times U_{T} }}$$

(6)

$$\overline{{R_{q} }} = \left( {T_{F}^{q} T_{C}^{q} } \right)^{V} R_{q} F^{r} \in D^{{U_{T} \times S}}$$

(7)

Here, the term $G_{q}$ is stacked whenever the sequences are shared via every user at a time $Q$ for every transmission $q = 1,2,..Q$, which is indicated in Eq. (8).

$$H = \left[ {G_{F}^{q} ,...G_{F}^{q} } \right] = T^{V} R^{V} + \overline{R}$$

(8)

$$T = \left[ {T^{1} ,...T^{Q} } \right] \in D^{{R_{C} \times U_{T} Q}}$$

(9)

$$\overline{R} = \left[ {\overline{R}_{1}^{V} ,...\overline{R}_{q}^{V} } \right] \in D^{{U_{C} \times S}}$$

(10)

In the term $R_{C} > U_{TQ}$, where $R_{C} > > > U_{T}$ has very few slot durations owing to that the training occurs on the channel. The term $\overline{R}_{w}$ is the vector $\overline{R}$ having a total column of $w$. The sparsity aspects are included in the beam area, and it is depicted in Eq. (11).

$$m_{w}^{o} = Km_{w}$$

(11)

The dictionary matrix is indicated by $K \in D^{{I \times R_{c} }}$ in the beam space channel vector, and it has a column vector $\phi \left( {R_{\partial } ,\gamma_{v} } \right)$ having total $I$ columns as $\gamma_{v} = - 1 + 2\left( {v - 1} \right)/I$. The term $I$ is the grid, which evaluates the Angle of Arrival (AoA) variations, and it is taken as $K^{R} K = {{IM_{{R_{\partial } }} } \mathord{\left/ {\vphantom {{IM_{{R_{\partial } }} } {R_{C} }}} \right. \kern-0pt} {R_{C} }}$ based on Eq. (12).

$$l_{w} = \frac{{R_{\partial } }}{I}T^{V} J^{R} m_{w}^{o} + \overline{{r_{w} }}$$

(12)

Here, the term $1,2,..Q$ aids in determining the sparse recovery issue based on the sparse property, and due to the limited beam area with resolution $1,2,..Q$, the channel leakage problem will exist in $1,2,..Q$ sparsity. Thus, this work developed a novel dilated adaptive model with an attention mechanism to solve the existing issues.

Need for channel estimation and massive MIMO detection

Efficient communication in wireless communication is obtained with the aid of MIMO networks. Efficient wireless communication is achieved with the help of MIMO networks. The capacity of the channels is enhanced by the use of the MIMO system. The channel capacity is significantly increased by utilizing the MIMO system. The ethereal efficiency of the wireless network is enhanced by using the MIMO system because it consists of more antennas for the communication process. The spectral efficiency of the wireless network is improved through the use of MIMO, as it incorporates multiple antennas for the communication process. So, the detection of the proper MIMO can fulfil the necessities of the user during the communication process. Therefore, accurate detection in the MIMO system can meet user requirements during communication. By the name itself, the MIMO system has numerous records of antennas in the spreader and the receiver of the wireless network. As the name suggests, the MIMO system involves multiple antennas at both the transmitter and receiver ends of the wireless network. The spectral effectiveness of the wireless network is very much improved, resulting in lossless communication over the world. This enhances the spectral efficiency of the network, resulting in near-lossless communication across long distances. The signal transmitted through the channel may be affected by the noise and other characteristics of the channel. However, the signal transmitted through the channel may be affected by noise and various channel characteristics. The diverse characteristics of the channel affect the signals that are passed via these channels. The diverse properties of the channel influence the signals passing through it. The MIMO system has numerous number of antennas on the transmitter and receiver parts, so it is very difficult to determine the appropriate channel to carry out the lossless communication. Because the MIMO system includes numerous antennas on both the transmitter and receiver sides, identifying the optimal channel for lossless communication becomes highly challenging.

Simulation and dataset configuration

To train the MSGO-DARNN-AM model, a synthetic dataset was generated using Rayleigh fading channels with additive white Gaussian noise. The dataset comprised 100,000 sequences for training and 20,000 for testing. Each input sequence consisted of 64 complex symbols (split into real and imaginary parts), modulated using QPSK. The labels were mapped to the corresponding transmitted symbols. During training, the model used an Adam optimizer with an initial learning rate of 0.001, a batch size of 128, and 50 epochs. Dilated RNN layers were employed, and their parameters (hidden units, epochs, steps per epoch) were optimized by MSGO. This setup ensured generalizability and convergence across channel variations and SNR conditions. Components and specifications employed in the developed model and hyperparameter configurations used for training are given in Tables 2 and 3.

Table 2 Components and specifications employed in the developed model.

Table 3 Hyperparameter configurations used for training.

Proposed channel estimation and MIMO detection model

A new channel estimation scheme is implemented using the developed optimization strategy to attain perfect knowledge of the channel gain at the receiver. Before performing the MIMO detection, the MIC-based sequential detection is applied, which helps to greatly improve the accuracy of the symbol detection. The wireless channel characteristics are less predictable and more time varying because of the rise in user mobility and Doppler effects. Here, the MIC-based preprocessing enhances the predictive quality and also maintains the stability of the network to get accurate results in the channel estimation process. The recommended MIC has higher reliability in determining the symbols that sequentially impact the detection accuracy in the channel estimation process. Outdated channel state information causes a significant influence on the accuracy of the channel detection since it causes a mismatch between the actual and the estimated channel. So, here the quasi-static varying channel and iterative refinement are hinged by the recommended MIC to improve the accuracy of the channel detection. Initially, the channel estimation process is performed using the proposed MSGO algorithm. In the channel estimation process, the channel matrix from the transmitted signal is optimized with the help of the proposed MSGO to get the channel state information. During the channel estimation phase, the channel matrix derived from the transmitted signal is optimized using the proposed MSGO to obtain accurate channel state information. This algorithm uses less number of pilot symbols for the channel estimation process. The algorithm requires fewer pilot symbols for effective channel estimation. Here, the developed MSGO is adopted to optimize the channel matrix for estimating the efficient channel for data transmission that helps to minimize the BER, SINR, PEP and NMSE. The MSGO is utilized to optimize the channel matrix, enabling efficient data transmission while minimizing BER, SINR, PEP, and NMSE. Here, the channel state information is attained using the proposed MSGO, and this information is given to the DARNN-AM in order to recover the original signal based on the past channel realizations. The channel state information obtained through MSGO is then provided to the DARNN-AM, which recovers the original signal based on previous channel realizations. The parameters, such as hidden neuron count, epoch count and steps per epoch, from DARNN-AM to increase the channel estimation performance. Parameters such as hidden neuron count, epoch count, and steps per epoch in DARNN-AM are optimized to enhance channel estimation performance. These optimization processes raise the value of spectral efficiency in the MIMO system. These optimization steps significantly improve spectral efficiency in the MIMO system. Before doing the MIMO detection process, a MIC-based iterative sequential detection process is applied to the signal to figure out the symbols present in the corresponding signal. Before MIMO detection, a MIC-based iterative sequential detection algorithm is applied to identify the symbols in the received signal. The MIMO detection process separates the signal, which is exaggerated by the noise and interference, so the spectral efficiency of the system is greatly enriched. The MIMO detection process isolates the signal affected by noise and interference, thereby enhancing the system’s spectral efficiency. Moreover, the capacity of wireless communication is enriched because of the proper selection of symbols from received signals in massive MIMO. Additionally, the wireless communication capacity is increased due to accurate symbol selection from the received massive MIMO signal. Therefore, the original signal from the receiver is effectively recovered without any noise and interference. As a result, the original signal is accurately recovered at the receiver with minimal noise and interference. A detailed illustration of the proposed channel estimation with the MIMO detection process is indicated in Fig. 2.

Fig. 2

Schematic illustration of the proposed channel estimation with the MIMO detection process.

Channel estimation in MIMO for attaining channel coefficients from the received signal for detecting MIMO

Basic SGO

The SGO⁵⁶ is a hyper-heuristic meta-optimisation algorithm. It is inspired by a traditional playground game predominantly played in Korea. In this game, elimination and attacking strategies are employed by the players. This game requires a vast area because this game must be played with a large number of people. It requires a large playing area due to the participation of multiple players. Here, the squid shape of the land is taken for conducting this game. The game is typically played on a field shaped like a squid. Here, the fighting is initiated by the offensive player, and this player moves in the direction of the safe player to begin the fighting process. The combat begins with an attacking player moving toward the defending player to initiate the confrontation. The objective function is adopted to find the players in the successful team. In the optimization context, the objective function is used to identify the most successful players or solutions.

Motivation: This is a playground game, and it is played by children in Korea. This traditional playground game is commonly played by children in Korea. There are no restrictions available regarding the dimensions of the field that is used for the squid game. There are no strict rules regarding the dimensions of the playing field. Several players are needed to conduct the squid game, and it is mostly conducted in an area with loose sand. It typically involves many players and is often played on loose sandy ground. The ground area used for the squid game seems like half a portion of the basketball court. The field size is approximately equivalent to half of a standard basketball court.

Arithmetic design: The playing field in the squid game process is considered as the search space in the SGO algorithm, and the players situated on that particular playfield are taken as a candidate solution in this algorithm, and it is stated in Eq. (13).

$$Y = \left[ {\begin{array}{*{20}c} {Y_{1} } \\ {Y_{2} } \\ \vdots \\ {Y_{j} } \\ \vdots \\ {Y_{o} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {y_{1}^{1} } & {y_{1}^{2} } & \cdots & {y_{1}^{k} } & \cdots & {y_{1}^{e} } \\ {y_{2}^{1} } & {y_{2}^{2} } & \cdots & {y_{2}^{k} } & \cdots & {y_{2}^{e} } \\ {} & {} & { \vdots \vdots \vdots } & \ddots & \vdots & {} \\ {y_{j}^{1} } & {y_{j}^{2} } & \cdots & {y_{j}^{k} } & \cdots & {y_{j}^{e} } \\ {} & {} & { \vdots \vdots \vdots } & \ddots & \vdots & {} \\ {y_{o}^{1} y_{o}^{2} } & {} & \cdots & {y_{o}^{k} } & \cdots & {y_{o}^{e} } \\ \end{array} } \right],\,\,\,\left\{ \begin{gathered} j = 1,2...o \hfill \\ j = 1,2...e \hfill \\ \end{gathered} \right.$$

(13)

$$y_{j}^{k} = y_{j,\min imum}^{k} + rndi * \left( {y_{j,\max }^{k} - y_{j,\min }^{k} } \right),\left\{ {\left\{ \begin{gathered} j = 1,2...o \hfill \\ j = 1,2...e \hfill \\ \end{gathered} \right.} \right.$$

(14)

Thus, the measurement of the issues is represented as $e$, the total count of aspirant solutions in the investigated space is denoted as $o$, the random number is signified as $rndi\,\,\,in\,\,[0,1][0,1]$, higher, and the subordinate bound of the candidate $j$ is constituted as $y_{j,\max }^{k} ,\,\,\,y_{j,\min }^{k}$, and the beginning location of the entrant solution is identified by the verdict variable termed as $y_{j}^{k}$ .

The team separation process is done in the second phase of the SGO algorithm, and it is mainly dependent upon the abominable player and the secure player in the squid gamer process, and it is given in Eq. (15).

$$Y^{abdo} = \left[ {\begin{array}{*{20}c} {Y_{1}^{abd} } \\ {Y_{2}^{abd} } \\ \vdots \\ {Y_{j}^{abd} } \\ \vdots \\ {Y_{n}^{abd} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {y_{1}^{1} } & {y_{1}^{2} } & \cdots & {y_{1}^{k} } & \cdots & {y_{1}^{e} } \\ {y_{2}^{1} } & {y_{2}^{2} } & \cdots & {y_{2}^{k} } & \cdots & {y_{2}^{e} } \\ {} & {} & { \vdots \vdots \vdots } & \ddots & \vdots & {} \\ {y_{j}^{1} } & {y_{j}^{2} } & \cdots & {y_{j}^{k} } & \cdots & {y_{j}^{e} } \\ {} & {} & { \vdots \vdots \vdots } & \ddots & \vdots & {} \\ {y_{n}^{1} y_{n}^{2} } & {} & \cdots & {y_{n}^{k} } & \cdots & {y_{n}^{e} } \\ \end{array} } \right],\,\,\,\left\{ \begin{gathered} j = 1,2...n \hfill \\ j = 1,2...e \hfill \\ \end{gathered} \right.$$

(15)

$$Y^{\sec } = \left[ {\begin{array}{*{20}c} {Y_{1}^{\sec } } \\ {Y_{2}^{\sec } } \\ \vdots \\ {Y_{j}^{\sec } } \\ \vdots \\ {Y_{n}^{\sec } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {y_{1}^{1} } & {y_{1}^{2} } & \cdots & {y_{1}^{k} } & \cdots & {y_{1}^{e} } \\ {y_{2}^{1} } & {y_{2}^{2} } & \cdots & {y_{2}^{k} } & \cdots & {y_{2}^{e} } \\ {} & {} & { \vdots \vdots \vdots } & \ddots & \vdots & {} \\ {y_{j}^{1} } & {y_{j}^{2} } & \cdots & {y_{j}^{k} } & \cdots & {y_{j}^{e} } \\ {} & {} & { \vdots \vdots \vdots } & \ddots & \vdots & {} \\ {y_{n}^{1} y_{n}^{2} } & {} & \cdots & {y_{n}^{k} } & \cdots & {y_{n}^{e} } \\ \end{array} } \right],\,\,\,\left\{ \begin{gathered} j = 1,2...n \hfill \\ j = 1,2...e \hfill \\ \end{gathered} \right.$$

(16)

Here, the secure and the abominable player at the $j^{th}$ location are represented as $Y^{abdo}$, and $Y_{j}^{abo}$, the total number of players at both teams is represented as $n$.

The combating process is initiated by the abominable player after starting the squid game. The secure player plays the squid game with their legs, and the abominable player plays the game with a single leg, and it is specified in Eq. (17).

$$EH = \frac{{\sum\nolimits_{j = 1}^{n} {Y_{j}^{\sec } } }}{n},\,\,j = 1,2..n$$

(17)

$$Y_{j}^{abo1} = \frac{{Y_{j}^{abo} + e_{1} * EH - e_{2} * Y_{{e_{3} }}^{\sec } }}{{}},\,\,i = 1,2..n$$

(18)

Here, the two random numbers are characterized as $e_{1}$ and $e_{2}$ correspondingly, and both of the random numbers lie in the interval of $[0,1]$, The random integer number is expressed as $e_{2} in\,[1,n]$, the secure team is represented as $EH$, the location vector of the forthcoming abominable player $Y_{j}^{abo1}$ is stimulated as $Y_{j}^{abo}$, the term $Y_{{e_{3} }}^{\sec }$ signifies the secure player elected to form the team.

The winning team is identified after the completion of the combat between the secure and the abominable player. The objective function plays a key role in the winning team selection process.

The abominable player is announced as a winner of the squid game if the endearing shape of the abominable player is superior to the endearing state of the secure player. The winning team is further joined in the victorious nasty group, and this process is given in Eq. (19).

$$\begin{gathered} Y^{victori\,\,aba} = \left[ {\begin{array}{*{20}c} {Y_{1}^{victori\,\,aba} } \\ {Y_{2}^{victori\,\,\,aba} } \\ \vdots \\ {Y_{j}^{victori\,\,\,aba} } \\ \vdots \\ {Y_{p}^{victori\,\,\,aba} } \\ \end{array} } \right] \hfill \\ = \left[ {\begin{array}{*{20}c} {y_{1}^{1} } & {y_{1}^{2} } & \cdots & {y_{1}^{k} } & \cdots & {y_{1}^{e} } \\ {y_{2}^{1} } & {y_{2}^{2} } & \cdots & {y_{2}^{k} } & \cdots & {y_{2}^{e} } \\ {} & {} & { \vdots \vdots \vdots } & \ddots & \vdots & {} \\ {y_{j}^{1} } & {y_{j}^{2} } & \cdots & {y_{j}^{k} } & \cdots & {y_{j}^{e} } \\ {} & {} & { \vdots \vdots \vdots } & \ddots & \vdots & {} \\ {y_{p}^{1} y_{p}^{2} } & {} & \cdots & {y_{p}^{k} } & \cdots & {y_{p}^{e} } \\ \end{array} } \right],\,\left\{ \begin{gathered} j = 1,2...o \hfill \\ j = 1,2...e \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$

(19)

$$TPH = \frac{{\sum\nolimits_{j = 1}^{p} {Y_{j}^{victori\,\,\,aba} } }}{p},j = 1,2...p$$

(20)

$$Y_{j}^{abo2} = Y_{j}^{abo1} + e_{1} * TPH - e_{2} * CT_{j} = 1,2...n$$

(21)

Thus, the preeminent candidate solution is represented as $CT$, the random numbers are represented as $e_{1}$ and $e_{2}$ in $\,in\,[0,1]$, the location vector of the forthcoming abominable player $Y_{j}^{aba1}$ is indicated as $Y_{j}^{aba2}$, the term $TPH$ depicts the victorious nasty group. The most successful players in the $TPH$ team are represented as $p$.

The secure members are ready to join the victorious protective group $TEH$, if the winning chance of the abominable player is lower than the secure player. After the winning process, the secure players intrude on the team of the abominable player’s team to begin the fighting process, and it is elucidated in Eq. (22).

$$\begin{gathered} Y^{victori\,\,\sec } = \left[ {\begin{array}{*{20}c} {Y_{1}^{victori\,\,\sec } } \\ {Y_{2}^{victori\,\,\,\sec } } \\ \vdots \\ {Y_{j}^{victori\,\,\,\sec } } \\ \vdots \\ {Y_{p}^{victori\,\,\,\sec } } \\ \end{array} } \right] \hfill \\ = \left[ {\begin{array}{*{20}c} {y_{1}^{1} } & {y_{1}^{2} } & \cdots & {y_{1}^{k} } & \cdots & {y_{1}^{e} } \\ {y_{2}^{1} } & {y_{2}^{2} } & \cdots & {y_{2}^{k} } & \cdots & {y_{2}^{e} } \\ {} & {} & { \vdots \vdots \vdots } & \ddots & \vdots & {} \\ {y_{j}^{1} } & {y_{j}^{2} } & \cdots & {y_{j}^{k} } & \cdots & {y_{j}^{e} } \\ {} & {} & { \vdots \vdots \vdots } & \ddots & \vdots & {} \\ {y_{q}^{1} y_{q}^{2} } & {} & \cdots & {y_{q}^{k} } & \cdots & {y_{q}^{e} } \\ \end{array} } \right],\,\,\left\{ \begin{gathered} j = 1,2...o \hfill \\ j = 1,2...e \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$

(22)

$$PH = \frac{{\sum\limits_{j = 1}^{n} {Y_{j}^{aba} } }}{n},\,\,j = 1,2..n$$

(23)

$$Y_{j}^{\sec 1} = Y_{j}^{\sec 1} + e_{1} * PH - e_{2} * Y_{{e_{3} }}^{aba} ,\,\,j = 1,2...o$$

(24)

Here, the arbitrary numbers are signified as $e_{1}$ and $e_{2}$ in $[0,1]$, the team having the secure player is represented as $PH$, and the location vector $Y_{j}^{\sec }$ of the expected secure player is denoted as $Y_{j}^{\sec 1}$. The arbitrary number is represented as $e_{3\,\,} \,\,in\,\,[1,n]$. The term $Y_{{e_{3} }}^{aba}$ elucidates the arbitrarily selected second abominable player.

The abominable player prevents the entry of the secure player in the exploration and exploitation phase. In order to prevent this action, the position updating process is carried out, and it is elucidated in Eq. (25).

$$Y_{j}^{aba3} = Y_{j}^{victori\,\,aba} + e_{1} * CT - e_{2} * Y_{j}^{victori\,\,\sec } \left\{ \begin{gathered} j = 1,2...p \hfill \\ l = 1,2...q \hfill \\ \end{gathered} \right.$$

(25)

Here, the forthcoming location vector of the abominable player $Y_{j}^{aba3}$ is expressed as $Y_{j}^{aba}$, the arbitrary number is denoted as $e_{1}$ and $e_{2}$ in $[0,1]$. The excellent candidate solution is indicated as $CT$, the total count of abominable and the secure players are indicated as $p,\,\,q$, respectively.

Algorithm 1 shows the pseudocode of the conventional SGO.

Algorithm 1

SGO.

Proposed MSGO

The developed MSGO is created by modifying the existing SGO algorithm. The developed MSGO is utilized in the channel estimation process. In this process, the channel matrix of the transmitted signal is optimized using the proposed MSGO. This optimization minimizes the BER, SINR, PEP, and NMSE, thereby increasing the efficiency of data transmission. The channels of the wireless network have some key characteristics, and this may affect the signal that is passed via the corresponding channel. These effects are mitigated through the channel estimation process using the developed MSGO. Here, the developed MSGO is employed to train the hidden neuron count, number of epochs, and steps per epoch of the model to improve spectral efficiency in the MIMO network. The SGO is a metaheuristic algorithm inspired by the Korean game. It incorporates multiple constraints and objectives to solve complex optimization problems. However, it has not been widely applied to solve real-world problems. In particular, SGO is inadequate for addressing load dispatch problems. These limitations are overcome by the developed MSGO.

Novelty: By the utilization of the developed MSGO, the spectral effectiveness of the system is highly enriched. The uniqueness of the developed MSGO stems from its adaptive fitness-based search strategy that employs stochastic randomness to guide the exploration and exploitation phases effectively. Unlike conventional metaheuristics that rely on fixed update rules, MSGO dynamically adjusts the search trajectory based on randomly generated values, which govern the transition between global and local search modes. This randomness is intelligently bounded using the best, worst, and mean fitness values obtained during each iteration, as described in Eq. (26), enabling the algorithm to learn from historical performance rather than static decision-making. This probabilistic decision-making framework allows MSGO to escape local optima more efficiently while maintaining solution quality. The combined use of the best, worst, and mean fitness metrics forms a tri-criteria update scheme that balances intensification and diversification with minimal parameter tuning. This results in faster convergence and robust optimization performance across high-dimensional spaces such as those encountered in massive MIMO systems. By embedding this statistical fitness-based control mechanism within the squid-inspired role dynamics, MSGO demonstrates a novel capability to adaptively refine both channel estimation parameters and neural network hyperparameters in a unified optimization cycle, an innovation not present in traditional single-objective or static-structure optimizers. The implementation of the developed MSGO is based on the random number, and it is evaluated by the best, worst and mean fitness values, and it is briefly discussed in Eq. (26).

$$rndi = \frac{(b * m)}{{(w * m)}}$$

(26)

Here, the term $rndi$ specifies the accidental number calculated by the developed MSGO, the best fitness is represented as $b$, the mean fitness is delineated as $m$, and the worst fitness is indicated as $w$. Because of the developed MSGO, the spectral efficiency value is increased so the channel estimation process is successfully carried out.

The proposed MSGO introduces a significant advancement over conventional metaheuristic optimization strategies by embedding a set of intelligent mechanisms tailored for deep learning-based MIMO detection systems. The core novelty of MSGO lies in its hybridized architecture, which modifies the original SGO by incorporating a memory-guided learning mechanism, adaptive role-transitioning among virtual agents, and nonlinear disturbance handling through stochastic perturbation. These enhancements empower MSGO with superior global search ability and convergence speed, enabling it to avoid premature convergence and local optima traps. This optimization strategy is a distinctive feature not observed in traditional approaches, where either the network or the channel is optimized in isolation. Moreover, MSGO incorporates a multi-objective fitness function that simultaneously minimizes key performance metrics such as BER, NMSE, SER, and PEP to enhance spectral efficiency and detection reliability. The pseudocode of the explored MSGO is pinpointed in Algorithm 2, and the flowchart of the explored MSGO is formulated in Fig. 3.

Fig. 3

Flow diagram of the explored MSGO.

Algorithm 2

Proposed MSGO.

Channel estimation procedure

The channel estimation process is carried out to determine the characteristics of the channels because they may affect the signals that are passed through these channels. Optimal channel conditions may increase the spectral efficiency of the wireless communication system and a reduction in the BER so that lossless communication is effectively attained. Here, the channel estimation process is carried out by the proposed MSGO. A detailed explanation of the channel estimation process is provided in the following sections.

• Initially, the sampling time, subcarrier count, interval in the sentinel interval and the modulation order are considered as the parameters of the MIMO network.

• Here, the signal is given to the receiver of the network by selecting a random attribute using the random function $Sn(g)$.

• In order to modulate the signal, the carrier signal is modulated into the amplitude modular of the MIMO network.

• The pilot symbols from the signal are identified by the “Multiuser Interference Cancellation (MIC)-based iterative sequential detection process”. These symbols are also considered in the subcarrier of the MIMO network. Additionally, these symbols are inserted into the equalization techniques during the channel estimation process.

• The inverse FT is used to attain the time waveform in the MIMO network. Additionally, the progress of the network is driven by the key element applied at the particular guard time.

Here, the system model is indicated by the Rayleigh channel model, and it is specified in Eq. (27).

$$Ma(U) = \left( {Ma(0),.....Ma(u - 1)^{f} } \right)$$

(27)

Here, the random variable is represented as $u$.

The demodulation process is considered to neglect the free space on the receiver side of the network; therefore, the effectiveness of the identified channel is enormously improved.

It is very important to determine the proper channel in the MIMO network for the broadcast process. Here, the real and the imaginary parts are present in the original signal of the structure, and it is given in Eq. (28).

$$E^{u} \left( r \right) = J^{u} \left( r \right) + I^{u} \left( r \right)$$

(28)

Here, the arbitrary operator is represented as $J^{u} \left( r \right)$, this arbitrary operator is situated in the vector break and $I^{u} \left( r \right)$, and the coefficient is represented as $d^{u} (r)$ and it is evaluated by Eq. (29).

$$d^{u} (r) = \sum\limits_{n = 1}^{{t_{mimo} }} {di\left\{ {E^{u} (r)} \right\}\,\,HX^{m,n} + \wp^{u} (r)}$$

(29)

The reduced matrix is attained when substituting the value of $E^{u} \left( r \right)$ in Eq. (20) and the reduced matrix is signified in Eq. (30).

$$d^{u} (r) = \sum\limits_{n = 1}^{{t_{mimo} }} {\left( {di\left\{ {J^{u} (r)} \right\} + di\left\{ {I^{u} (r)} \right\}} \right)} \times HX^{m,n} + \wp^{u} (r)$$

(30)

The computational intricacy of the channel estimation progression is lowered by substituting $H$ instead of $\sqrt {B\aleph }$ in the arrangement model, and it is given in Eq. (31).

$$d^{u} (r) = \sum\limits_{n = 1}^{{t_{mimo} }} {J_{di}^{u} (r)HX^{m,n} } + I_{di}^{u} (r)HX^{m,n} + \wp^{u} (r)$$

(31)

The time index $j \in \left\{ {0,1....k - 1} \right\}$ must be taken into consideration to train the MIMO network, and it is elucidated in Eq. (32).

$$D^{r} = SX^{r} + UX^{r} + \wp^{u} (r)$$

(32)

Here, the term $D^{r}$ is represented as a coefficient, and it is attained by $\left[ {D^{{r^{ \cup } }} (0)....D^{{r^{ \cup } }} (k - 1)} \right]^{ \cup }$, and $\wp^{u} (r)$ is identified by $\left[ {\wp^{{u^{ \cup } }} (0)....\wp^{{u^{ \cup } }} (k - 1)} \right]^{ \cup }$ , the circular matrix is indicated as $X^{r}$ and it is estimated by $\left[ {X^{{u,n^{ \cup } }} (0)....X^{{u,T^{ \cup } }} (k - 1)} \right]^{ \cup }$. The equations below Eqs. (33) and (34) give the matrix $S$ , and $U$.

$$S - \left[ {\begin{array}{*{20}c} {J_{di}^{1} (0)X} & \cdots & {J_{di}^{{T^{m} }} (0)X} \\ \vdots & \cdots & \vdots \\ {J_{di}^{1} (k - 1)X} & \cdots & {J_{di}^{{T^{m} }} (k - 1)X} \\ \end{array} } \right]$$

(33)

$$U = \left[ {\begin{array}{*{20}c} {U_{di}^{1} (0)X} & \cdots & {U_{di}^{{T^{m} }} (0)X} \\ \vdots & \cdots & \vdots \\ {U_{di}^{1} (k - 1)X} & \cdots & {U_{di}^{{T^{m} }} (k - 1)X} \\ \end{array} } \right]$$

(34)

The least squares is evaluated by using Eq. (35).

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{X} u^{r} = U^{ + } D^{r}$$

(35)

The below Eq. (36) specifies the expression for the inverse pseudo matrix.

$$U^{ + } = \left( {U^{X} U} \right)^{ - 1} U^{X}$$

(36)

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{X} u^{r} = X^{r} + U^{ + } SD^{r} + U^{ + } \wp^{u} (r)$$

(37)

The interior signal interference is neglected from the signal, and it is indicated in Eq. (38).

$$U^{ + } S = 0_{{OB_{r} \times OB_{r} }}$$

(38)

The channel vector $X_{mr}^{u,n}$ is mapped to get the term $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X} u^{r}$ but the signal noise greatly affects the channel vector, so it is solved by taking the pilot tones $\frac{\exists }{\forall }$ in the MIMO network, and this phenomenon is indicated in Eq. (39).

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X} u^{r} = U^{ + } \tilde{D}^{r} = X^{r} + U^{ + } \wp^{u} (r)$$

(39)

The modified form of the matrix $U^{{}}$ is indicated in Eq. (40).

$$U = \left[ {\begin{array}{*{20}l} {U_{di}^{1} (0)\tilde{H}(0)} & \cdots & {U_{di}^{{T^{m} }} (0)\tilde{H}(0)} \\ \vdots & \cdots & \vdots \\ {U_{di}^{1} (k - 1)\tilde{H}(k - 1)} & \cdots & {U_{di}^{{T^{m} }} (k - 1)\tilde{H}(k - 1)} \\ \end{array} } \right]$$

(40)

Here, the diagonal matrix is expressed as $U_{di}^{1}$ and it consists of non-zero entities represented in the form of $J^{u} (r)U^{u} (r)$.

The objective function of the proposed channel estimation process with an optimized channel matrix is to minimize the BER, SINR, PEP and NMSE value, and it is given in Eq. (41). This optimization helps to improve the performance over getting channel state information by suppressing the noise and interference.

$$A = \mathop {\arg \,\,\min }\limits_{{\{ C_{A}^{M} \} }} \left( {BER + SINR + PEP + NMSE} \right)$$

(41)

Here, the term $C_{A}^{M}$ represents the optimized channel matrix in $[0,1]$ and the BER, NMSE, PEP and SINR are determined through the following expressions.

BER: It is evaluated using Eq. (42).

$$BER = \frac{{u_{ber} }}{{U_{br} }}$$

(42)

Here, the overall bit transferred in the network is represented as $U_{br}$, and the total number of bits received with error is indicated as $u_{ber}$.

NMSE: The NMSE is signified in Eq. (43).

$$NMSE = \frac{{|E_{W} - F_{W} |^{2} }}{{|E_{W} |^{2} }}$$

(43)

PEP: It is indicated in Eq. (44).

$$PEP = Q\left( {C_{1} \to C_{2} } \right)q\left( {C_{1} } \right) + Q\left( {C_{2} \to C_{1} } \right)q\left( {C_{2} } \right)$$

(44)

Here, the probability of the transmitting error is represented as $q\left( {C_{1} } \right)$ and the probability of the decoding output is delineated as $Q\left( {C_{1} \to C_{2} } \right)$.

SINR: It is pinpointed in Eq. (45).

$$SINR = \frac{{Q_{t} }}{{\kappa^{2} + \kappa \cdot Q_{j - qd} }}$$

(45)

Here, the noise discrepancy is represented as $\kappa$, the power of the signal is represented as $Q_{t}$ and the obstruction control is denoted as $Q_{j - qd}$.

Data formation for deep learning

The transmitted signal is propagated via the channel, and it is affected by noise and interference when it reaches the receiver. Pilot symbols are used for the estimation of the channel, where the noise at the receiver is significantly reduced. The proposed MSGO is utilized for optimizing the channel matrix from the transmitted signal to effectively obtain the channel state information. This channel state information is applied to the proposed DARNN-AM to recover the original information. The attributes considered for the data formation include the number of base stations, the number of active base stations, the number of antennas, antenna spacing, bandwidth, number of multiplexers, multiplexer sampling factor, multiplexer limit, the number of users, and user grid. A better BER is ultimately achieved, which helps to improve the throughput with fewer errors.

Deep learning-based massive MIMO detection using a dilated adaptive deep learning network with optimal tuning of parameters

Basic RNN

In most detection processes, the RNN⁵⁷ is considered one of the most important structures. The RNN structure is also used in prediction and image-processing tasks. The RNN architecture utilizes temporal and semantic data for effective detection. However, it faces challenges in recognizing long-term dependencies. The RNN structure consists of three layers: input, hidden, and output layers. The hidden layer of the RNN is composed of several neurons that are interconnected. The loop in the RNN is utilized for the detection process. In the RNN structure, data is passed from the input layer to the hidden layer. The RNN is trained using forward and backwards propagation processes. The output generated by the hidden layer of the RNN during the forward propagation is given in Eq. (46).

$$i_{u} = \varpi \left( {Xy_{u} + Vi_{u - 1} + c_{i} } \right)$$

(46)

Here, the result produced by the hidden layer is represented as $i_{u}$ , at the time $u$, the contribution vector is represented as $y_{u}$, the usual and the circulating weight matrix is illuminated as $X$, and $V$ respectively, the activation function is illustrated as $\varpi$.

The structural portrayal of the RNN is delineated in Fig. 4.

Fig. 4

Structural portrayal of the RNN.

Developed DARNN-AM

The developed DARNN-AM arrangement is formed by combining the dilated RNN with the attention mechanism. The dilated RNN organization is adopted to solve the vanishing and gradient issues. So, these issues are solved by combining this structure with the attention mechanism.

The dilated RNN⁵⁸ is adopted to overcome the challenges posed by conventional RNNs. The dilated RNN structure does not encounter gradient issues during prediction. By using the dilated RNN, the training process can be completed more efficiently. Additionally, the dilated RNN structure requires only a small number of attributes for the prediction process. The dilated RNN is composed of dilated skip (persistent hop) connections, which are considered a crucial component of its architecture. These dilated skip connections significantly enhance the dilation rate, thereby improving prediction accuracy. The implementation of dilated skip connections in the cells of the dilated RNN at each layer is represented in Eq. (47).

$$d_{u}^{(m)} = g\left( {y_{u}^{(m)} ,d_{u - t}^{(m)} } \right)$$

(47)

Here, the time is represented by the term $u$, the cells of the dilated RNN structure are indicated as $d_{u}^{(m)}$ and the layers of the dilated RNN are represented as $m$.

The conventional skip connection in the RNN structure is given in Eq. (48).

$$d_{u}^{(m)} = g\left( {y_{u}^{(m)} ,d_{u - 1}^{(m)} ,d_{{u - t^{(m)} }}^{(m)} } \right)$$

(48)

Thus, the output operation in the dilated RNN is portrayed as $g( \cdot )$, the hop span is delineated as $t^{(m)}$. For the time $u$, the input provided to the structure is elucidated as $y_{u}^{(m)}$. The dilated persistent hop does not depend on $d_{u - 1}^{(m)}$. The dilated RNN has very low computational complexity. The interlacing process is carried out between the four blocks of the dilated RNN to get the output value.

The dilated RNN structure is formed by assembling the dilated recurrent layers. Due to this assembling process, the dilation rate of the structure is significantly improved. The dilation process involved in the layers of the dilated RNN is given in Eq. (49).

$$t^{(m)} = N^{m - 1} ,\,\,\,m = 1...M$$

(49)

The capacity of the dilated RNN is enhanced by assembling more dilated recurrent layers. The enhanced dilation rate also reduces the vanishing and gradient problems in the dilated RNN structure. The dilated RNN structure effectively retrieves the long-term dependencies due to the enhanced dilation rate, and it is prescribed in Eq. (50).

$$t^{(m)} = N^{{m - 1 + m_{0} }} ,\,\,\,m = 1...M\,\,and\,\,m_{0} \ge 0$$

(50)

Here, an additional convolutional layer is added to the end of the dilated RNN structure, and it is considered as a substitute for the misplaced dependencies, and the initial dilation is signified as $N_{0}^{m}$.

Attention Mechanism: An efficient prediction process is achieved with the support of the attention mechanism. This process works by extracting relevant details from the feature maps. The weights within the feature map are also identified by the attention mechanism. In total, three linear transformations are performed on the features: value, key, and query, respectively. Each linear transformation has the same dimension. All queries are combined using dot product attention to calculate the attention scores. The resulting dot product between the query and key is further passed through the softmax function to derive the attention score. At each time step, the attention score is used to generate a weighted representation of the matrix, and the entire process involved in the attention mechanism is described in Eq. (41).

$$g(A,M,F) = SOFTMAX\left( {\frac{{AM^{T} }}{{\sqrt {e_{l} } }}} \right)F$$

(51)

Here, the query, values and key are represented as $A,F,M$ and the amount of the vector is expressed as $e_{l}$.

The space in the middle of the transmitted signal and the output layer is examined by the loss function, and it is given in Eq. (42).

$$L = \sum\limits_{m = 1}^{M} {\log (m)||} X^{r} - X^{r + 1} ||^{2}$$

(52)

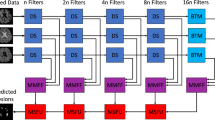
The pictorial indication of the DARNN-AM for the MIMO identification process is formulated in Fig. 5.

Fig. 5

Pictorial indication of the DARNN-AM for the MIMO detection process.

MIMO signal detection using DARNN-AM

The channel state information attained from MSGO is given to the DARNN-AM for estimating the channel. The estimated channel information is properly trained by the proposed DARNN-AM. Using these trained parameters, the MIMO detection process is carried out. The massive MIMO network consists of a greater number of antennas at both the receiver and the transmitter, which leads to the establishment of near-lossless communication. The complexity involved in wireless networks during communication is overcome by the detection process of massive MIMO. As the name suggests, the base station of a massive MIMO network consists of more antennas compared to traditional networks. Hence, the spectral efficiency of the wireless network is considerably increased.

Novelty: The novelty of the proposed DARNN-AM lies in its hybrid architecture that integrates temporal dilation with adaptive attention mechanisms to address the challenges of massive MIMO detection. Unlike traditional RNN-based models that suffer from limited temporal context and vanishing gradients, DARNN-AM employs dilated RNN layers that effectively capture long-range dependencies in symbol sequences without increasing computational burden. This design allows the model to learn spatial–temporal correlations in the received MIMO signal more comprehensively. Furthermore, the incorporation of a softmax-based attention mechanism over the temporal axis empowers the network to dynamically focus on the most relevant parts of the input sequence, improving detection performance under varying channel conditions. This dual enhancement, temporal dilation for deeper context modelling and attention for selective focus, significantly improves symbol recovery accuracy and robustness against channel impairments. Additionally, DARNN-AM’s architecture is lightweight and scalable, making it practical for real-time MIMO systems. Its novelty is further reinforced by its seamless integration with the MSGO-optimised channel parameters, allowing it to function as a tightly coupled component in an end-to-end deep learning detection pipeline. This synergistic design not only improves bit error rate (BER) performance across a wide range of SNR conditions but also enhances the adaptability of the detection framework to non-stationary and highly dynamic wireless environments.

Architectural distinction of DARNN-AM: The proposed DARNN-AM framework differs fundamentally from conventional attention-based RNN variants such as Gated Recurrent Unit with Attention (GRU-ATT)⁵⁹ and Long Short Term Memory with Attention (LSTM-ATT)⁶⁰ through two key innovations: the dual attention mechanism and the autoregressive integration strategy. Unlike standard models where attention is typically applied only over the input sequence (encoder side), DARNN-AM introduces attention both at the input (spatial attention) and temporal (decoder output) levels, enabling more effective focus on dynamically varying signal features across MIMO channels. Additionally, the autoregressive memory in DARNN-AM enables the model to incorporate historical context recursively during decoding, thus improving the temporal correlation modelling of channel fluctuations and symbol interference. This design is particularly advantageous in wireless communication scenarios with high user mobility or complex fading patterns. While GRU-ATT and LSTM-ATT maintain fixed temporal memory gates, DARNN-AM dynamically adjusts its internal memory via attention-driven weighting, which significantly enhances symbol detection accuracy under noise and uncertainty. These architectural innovations collectively justify the uniqueness of DARNN-AM and its superior performance demonstrated across diverse experimental settings.

Interpretability through the attention mechanism: To address the interpretability limitations commonly associated with deep learning models, the proposed MSGO-DARNN-AM framework incorporates an Attention Mechanism designed to provide insight into the model’s decision-making process during MIMO signal detection. The Attention Mechanism enables the network to selectively focus on specific time steps, antenna inputs, or spatial features that are most influential in predicting the transmitted symbols. This dynamic weighting of input components provides a transparent representation of the model’s internal focus and contributes to making the network more explainable. Specifically, during training, the attention layer generates a matrix of attention weights that highlight the relative importance of each input segment in the received signal sequence. By visualizing these weights, we can observe which antennas, time instances, or subcarriers are prioritized by the model under varying channel conditions and interference levels. For example, in noisy environments, the attention mechanism adapts by assigning greater weights to cleaner substreams, which helps in enhancing signal reconstruction and reducing detection errors. Moreover, the integration of attention not only improves the interpretability of the model but also contributes to its robustness and accuracy by allowing adaptive feature relevance learning. As a result, the DARNN-AM architecture transforms the deep MIMO detection framework from a traditional black-box system into a semi-transparent model, where internal decisions can be interpreted, visualized, and explained through its attention dynamics.

The objective function of the MSGO-DARNN-AM-based channel estimation with the MIMO detection model is used to lower the NMSE and to improve the spectral efficiency of the network. The objective function of the MSGO-DARNN-AM-based channel estimation with the MIMO signal detection model is illustrated in Eq. (53).

$$FO = \mathop {\arg \,\,\min }\limits_{{\{ c_{h}^{RNN} ,\,\,c_{e}^{RNN} ,\,\,n_{s}^{RNN} \} }} \left( {NMSE + \frac{1}{Spectral\,efficiency}} \right)$$

(53)

Here, the objective function is denoted by the word $FO$, the count of hidden neurons present in the RNN arrangement is elucidated as $c_{h}^{RNN}$, and it trapped in the region of $[5,255]$, the steps for each epoch in the RNN structure is indicated as $n_{s}^{RNN}$ and it deceit in between $[5,500]$, the epoch number in the RNN structure is depicted by the term $c_{e}^{RNN}$, and it ranges in between $[5,50]$. The NMSE is evaluated by Eq. (54), and spectral efficiency is given in Eq. (44).

$$Spectral\,efficiency = \frac{t.c}{{bw * ca}}$$

(54)

Here, the data traffic that occurred in the network is represented as $t.c$, the bandwidth of the channel is represented as $bw$, and the total area of the network is illustrated as $ca$.

Results and discussion

Experimental setup

The MSGO-DARNN-AM-based channel estimation with the MIMO signal detection model was tested using MATLAB 2020a software. Here, the testing process was executed by taking the population number as 10, the extent of the chromosome was taken as 4, and the highest iteration was taken as 50. The conventional algorithms, such as Red Deer Algorithm (RDA)⁶¹, Black Widow Optimization Algorithm (BWO)⁶², Arithmetic Optimization Algorithm (AOA)⁶³, SGO⁵⁶ and existing classifiers like MSDSD²¹, DGMP⁶⁴, DLCS⁶⁵, DLQP⁶⁵, to find out the performance of the explored MSGO-DARNN-AM-based channel estimation with MIMO signal detection model. Table 4 provides the reproducibility details of the recommended model.

Table 4 Reproducibility details of the recommended model.

Performance indices

The following are some of the performance measures taken in the MSGO-DARNN-AM-based channel estimation with the MIMO signal detection model. To comprehensively evaluate the accuracy, robustness, and practical impact of the proposed MSGO-DARNN-AM framework in MIMO signal detection and channel estimation, a diverse set of statistical and vector-based error metrics has been employed.

Mean Absolute Error (MAE): It is examined by Eq. (55). It quantifies the average magnitude of absolute errors between actual and predicted values, offering a straightforward interpretation of detection performance.

$$MAE = \frac{{\sum\limits_{j = 1}^{s} {|E_{W} - F_{W} |\,\,} }}{{s_{o} }}$$

(55)

Here, the whole number of samples is represented as $s_{o}$, and the expected and the preferred values are elucidated as $F_{W} \,\,and\,\,E_{W}$, respectively.

The L1 norm is represented as the entire amount of displacement that occurred in the given vector liberty and it is specified in Eq. (56). The L2 norm is the minimum distance between the two points of the network is represented as the L2 norm, and it is determined by Eq. (57). The L1 norm captures the cumulative displacement or deviation within signal vectors, while the L2 norm (Euclidean norm) provides insight into the magnitude of overall error, highlighting the stability of predictions under noisy conditions.

$$norm\,\,L1 = ||E_{W} ||_{1} = \sum\limits_{P = 1}^{st} {E_{W} }$$

(56)

$$norm\,\,L1 = ||E_{W} ||_{2} = \sqrt {\sum\limits_{P = 1}^{st} {E_{W}^{2} } }$$

(57)

Mean Absolute Scaled Error (MASE): It is the ratio MAE of the expected value to that of the predicted values, and it is given in Eq. (58). The MASE offers a scale-independent evaluation by comparing MAE with a benchmark error, allowing fair comparisons across various signal scales and modulation conditions.

$$MASE = MEAN\left( {\frac{{E_{W} }}{{\frac{1}{s - 1}\sum\limits_{j = 1}^{s} {|F_{W} - F_{W - 1} |} }}} \right)$$

(58)

Symmetric Mean Absolute Percentage Error (SMAPE): The accuracy of the predictive model is determined by the SMAPE expression, and it is provided in Eq. (59). SMAPE is employed for its sensitivity to percentage-based deviations and its balance between over- and under-estimations, which is crucial for adaptive systems.

$$SMAPE = \frac{1}{st}\sum\limits_{p = 1}^{st} {\left( {\frac{{|F_{W} - E_{W} |}}{{\frac{{\left| {F_{W} } \right| + \left| {E_{Wo} } \right|}}{2}}}} \right)}$$

(59)

Maximum Error Probability (MEP): The performance of the MIMO network is identified by the theoretical attribute, and it is elucidated in Eq. (60). MEP offers a theoretical upper-bound measure on the likelihood of signal misdetection, representing the worst-case scenario in system reliability.

$$MEP = \frac{100\% }{{s_{o} }}\sum\limits_{p = 1}^{s} {\left( {\frac{{F_{W} - E_{W} }}{{F_{W} }}} \right)}$$

(60)

Infinity norm: It is circulated with some quantifiable functions in the vector space, and it is stimulated in Eq. (61). Infinity norm further supports this by capturing the maximum absolute deviation in any dimension, offering a conservative error estimate valuable in edge-case analysis.

$$\inf inity\,\,norm\, = ||E_{W} ||_{\infty } = \mathop {mxim}\limits_{1 \le 0 \le st} |E_{W} |$$

(61)

Root Mean Squared Error (RMSE): The assessment quality is effectively determined by the RMSE measure, and it is mostly adopted in all of the detection processes. The mathematical expression of the RMSE is represented in Eq. (62). RMSE is used due to its strong emphasis on large errors, making it particularly effective in capturing the impact of bursty noise and multi-path fading effects in MIMO channels.

$$RMSE = \sqrt {\frac{{\sum\limits_{j = 1}^{st} {\left( {E_{W} - F_{W} } \right)^{2} } }}{{s_{o} }}}$$

(62)

Together, these metrics not only validate the technical soundness of the developed model but also demonstrate its practical feasibility across various signal conditions. Improvements across SMAPE, MASE, and RMSE directly correlate with enhanced bit error performance and reduced retransmission rates in real-time MIMO systems. These error metrics are used to evaluate the accuracy of channel estimation and signal processing in MIMO systems. Lower values for these metrics indicate more accurate estimations, which translate to improved communication quality and efficiency.

Performance analysis by varying SNR

The performance research on the MSGO-DARNN-AM-based channel estimation with MIMO signal detection process among various techniques and algorithms are provided in Fig. 6. The MSE of the MSGO-DARNN-AM-based channel estimation with MIMO signal detection is depleted than the RDA, BWO, AOA and MSGO with 57.57%, 56.25%, 39.13% and 40.42% at the SNR of 15. So, the MSE of the MSGO-based channel estimation model is raised than the usual algorithms. Hence, the proposed MSGO-DARNN-AM model demonstrates superior performance in terms of channel estimation accuracy compared to the conventional algorithms. This result highlights the effectiveness of the MSGO-DARNN-AM framework in minimizing estimation error, which is crucial for enhancing signal detection and system throughput in massive MIMO systems. The integration of the DARNN-AM architecture strengthens temporal learning and improves signal recovery, making the model more resilient to channel noise and interference. Compared to traditional optimization methods like RDA and BWO, the hybrid model provides a balanced approach by leveraging both intelligent optimization and deep learning, resulting in a more accurate and data-efficient channel estimation. The marked reduction in MSE at moderate SNR levels confirms the robustness of the model under practical wireless conditions, ensuring improved spectral efficiency and reliability in communication.

Fig. 6

Deep learning-based channel estimation system for (a) BER, (b) MSE, (c) spectral efficiency, (d) BLER.

Performance analysis over several classifiers

The classifier comparison of the MSGO-DARNN-AM-based channel estimation with the MIMO detection model is shown in Fig. 7. At the SNR of 20, the spectral efficiency of the MSGO-DARNN-AM-based channel estimation with the resource allocation model is boosted with MSDSD, DGMP, and DLCS by 30.55%, 27.02%, and 4.44% for the channel estimation process. Therefore, the spectral efficiency of the MSGO-DARNN-AM-based channel estimation with the resource allocation model is augmented more than the conventional classifier. This demonstrates that the proposed MSGO-DARNN-AM-based approach not only enhances detection performance but also contributes substantially to efficient resource utilization in massive MIMO systems. Therefore, the spectral efficiency of the MSGO-DARNN-AM-based channel estimation integrated with resource allocation is significantly augmented when compared to traditional classifiers.

Fig. 7

Deep learning-based channel estimation with MIMO signal detection system for (a) MSE, (b) spectral efficiency.

Performance examination by using the number of slots

The performance research of the MSGO-DARNN-AM-based channel estimation with the MIMO detection process is formulated in Fig. 8. The BER of the MSGO-DARNN-AM-based channel estimation with the resource allocation model is down than the RDA-DARNN-AM, BWO-DARNN-AM, AOA-DARNN-AM, and MSGO-DARNN-AM with 71.60%, 61.66%, 95.65% and 69.56% at the number of slots of 5 for the channel estimation process. Thus, the BER of the MSGO-DARNN-AM-based channel estimation with the resource allocation model is lower than the prior algorithms. These substantial improvements demonstrate the capability of the proposed model to mitigate bit-level errors more effectively under the same channel conditions. The enhanced performance is attributed to the robust optimization capability of the MSGO and the adaptive temporal feature extraction provided by the DARNN-AM network. The resource allocation model further aids in dynamically distributing the channel resources, which reduces interference and optimizes throughput. This result indicates that the BER performance of the MSGO-DARNN-AM-based channel estimation with resource allocation is substantially better than that of previous algorithms, making it highly suitable for massive MIMO applications where reliability and efficiency are crucial. The lower BER also signifies improved signal recovery and decoding accuracy, which ultimately enhances spectral efficiency and QoS in next-generation wireless systems.

Fig. 8

Deep learning-based MIMO signal detection with channel estimation system for (a) MSE, (b) spectral efficiency.

Analysis of the developed model using several constraints

The performance investigation of the MSGO-DARNN-AM-based channel assessment with the resource allocation model is shown in Fig. 9. At a number of epoch 10, the entropy loss of the MSGO-DARNN-AM-based channel estimation with MIMO signal detection is 79.06% dropped than RDA-DARNN-AM, 74.41% dropped than BWO-DARNN-AM, 69.76% dropped than AOA-DARNN-AM, and 16.27% dropped than MSGO at the MIMO detection process. Hence, the MSGO of the MSGO-DARNN-AM-based MIMO detection with the channel estimation model is reduced than the traditional algorithms. This significant reduction in entropy loss highlights the efficacy of the proposed MSGO-DARNN-AM model in achieving more accurate and stable learning during training. The use of MSGO for channel matrix optimization, combined with DARNN-AM’s temporal learning and adaptive memory attention, contributes to this enhanced convergence behaviour. A lower entropy loss indicates that the model achieves higher prediction confidence and minimizes uncertainty in output classifications. Therefore, the entropy loss of the MSGO-DARNN-AM-based MIMO detection with channel estimation is considerably lower than that of conventional algorithms, signifying improved generalization and training stability in wireless communication environments.

Fig. 9

Deep learning-based MIMO signal detection with channel estimation system for (a) channel estimation, (b) MIMO detection.

Statistical exploration

The statistical investigation of the MSGO-DARNN-AM-based channel judgment with MIMO signal detection is presented in Table 5. At algorithmic comparison, the MASE of the MSGO-DARNN-AM-based channel assessment with the MIMO finding model is lower than the RDA-DARNN-AM, BWO-DARNN-AM, AOA-DARNN-AM and MSGO-DARNN-AM with 21.53%, 14.77%, 7.27% and 5.77%. Thus, the MASE of the MSGO-DARNN-AM-based channel estimation with the MIMO detection model is significantly reduced than the ancient algorithms. This reduction in MASE reflects the model’s improved accuracy in estimating the channel characteristics over a wide range of communication conditions. The integration of MSGO for optimal channel matrix selection along with the DARNN-AM’s dynamic temporal learning allows for better generalization and robustness. Thus, the MASE of the MSGO-DARNN-AM-based channel estimation with the MIMO detection model is significantly reduced compared to conventional algorithms, demonstrating its superiority in delivering more reliable and precise estimations in complex wireless environments.

Table 5 Statistical study of the deep learning-based channel estimation with the MIMO detection approach.

Convergence evaluation on the developed model

To substantiate the convergence behaviour of the proposed MSGO, a detailed convergence analysis has been conducted, as illustrated in Fig. 10. The graph plots the fitness value of the objective function against the number of iterations, clearly demonstrating the optimizer’s performance over time. Initially, the fitness value exhibits a sharp decline within the first few iterations, highlighting MSGO’s strong global exploration capabilities in identifying promising solution regions across the search space. As iterations progress, the curve gradually flattens, indicating a transition from exploration to exploitation, where the algorithm fine-tunes candidate solutions around local optima. Notably, the convergence stabilizes without abrupt fluctuations or divergence, which evidences the algorithm’s ability to maintain a balance between intensification and diversification. The absence of oscillations in the later stages confirms that MSGO avoids premature convergence, a common pitfall in many metaheuristic algorithms. This is achieved by introducing adaptive behavior patterns within the squid-inspired interaction model, including role-switching mechanisms, random perturbation, and memory-based position updates. The convergence graph also reflects that the optimizer reaches a near-optimal solution within 50 iterations, corresponding to population × iteration = 10 × 50 = 500 fitness evaluations. This low iteration count combined with minimal computation time, underscores the algorithm’s computational efficiency and practicality for high-dimensional problems like massive MIMO parameter optimization. This empirical validation confirms the algorithm’s suitability for solving complex, nonlinear tasks in MIMO systems, ensuring both real-time feasibility and robust convergence behaviour.

Fig. 10

Convergence evaluation on the developed model.

Theoretical support for the convergence: In this research, the convergence of the proposed model is assured using the empirical validation, which is indicated in Fig. 10. The empirical evidence of the suggested MSGO showed that it can the capacity to reach a stable solution by navigating the solution space more effectively. Further, the MSGO is designed to iteratively explore the search space to maintain the effective balance between exploitation and exploration. Further, the adaptive behaviour of the suggested MSGO helps to get the global optima for guaranteeing the optimal convergence rate of the proposed MSGO. The stochastic process under a certain condition is followed by the proposed MSGO, which helps to get the optimal solution. The nature of the MSGO can be used for handling the global optimality and also aims to attain the appropriate solution in the search space which helps to attain improved convergence over the other algorithms.

Computational analysis and its scaling factors in terms of number of antennas and modulation order

Table 6 provides a comparative analysis of training time, inference time, memory consumption, and theoretical complexity across a range of existing algorithms, including traditional optimization techniques, deep learning-based models, and the proposed MSGO-DARNN-AM framework. The proposed model demonstrates the lowest training time (22 s) and fastest inference time (6 ms) despite being evaluated under higher system dimensions, specifically with 32 antennas and a 64-QAM modulation order, significantly more demanding than the configurations used for the baseline models. In terms of computational complexity, the integrated MSGO-DARNN-AM framework has a hybrid complexity of ${\text{O}} ({\text{N}} \times {\text{T}} \times {\text{H}} + {\text{G}} \times {\text{K}})$, where ${\text{N}}$ is the number of antennas, ${\text{T}}$ is the sequence length or number of epochs, ${\text{H}}$ is the hidden layer size in DARNN, and ${\text{G}}$ and ${\text{K}}$ denote the population size and maximum number of iterations in the MSGO optimizer. This combined formulation scales linearly with the number of antennas and training epochs, making it computationally more efficient than traditional methods. Furthermore, when compared to neural network-based models, the proposed method strikes a better balance between computational efficiency and scalability, even under increased modulation orders and antenna counts. Importantly, the memory usage of 120 megabytes for MSGO-DARNN-AM is the lowest among all compared models, showing it is highly suitable for use in resource-constrained or real-time environments. The observed linear or sublinear growth trend in performance further confirms the scalability and computational practicality of the proposed model. Therefore, the integration of MSGO and DARNN-AM does not impose an excessive computational burden, but rather delivers an efficient and scalable solution for massive MIMO detection tasks.

Table 6 Computational analysis and its scaling factors in terms of number of antennas and modulation order.

Evaluation against recent popular MIMO detection frameworks

To validate the robustness and superiority of the proposed MSGO-DARNN-AM model, a comprehensive performance evaluation was conducted by comparing its BER with popular MIMO detection frameworks, and it is given in Table 7. Specifically, the proposed model was benchmarked against AMIC-Net, MMNet, DetNet, and OAMP-Net. The BER performance was analysed across varying SNR levels (5 dB to 20 dB), and the results are tabulated for a detailed comparison. The proposed MSGO-DARNN-AM model consistently achieved lower BER across all tested SNR conditions, with a BER of just 0.007 at 20 dB, which is significantly better than DetNet (0.023) and OAMP-Net (0.015). These results confirm that the integration of MSGO for channel parameter refinement and the DARNN-AM for temporal feature extraction enables more accurate symbol detection under noisy and complex channel conditions. The clear performance margin over modern deep detection methods not only highlights the efficacy of the hybrid design but also situates the proposed approach as a promising advancement in the current deep MIMO detection literature.

Table 7 Evaluation Against Recent Popular MIMO Detection Frameworks.

Generalization evaluation of the proposed MSGO-DARNN-AM framework

To validate the robustness and adaptability of the proposed MSGO-DARNN-AM model, an extensive generalization analysis was conducted under diverse simulation settings beyond the initial training configuration. Figure 11 presents the model’s performance across multiple channel models, including Rayleigh and Rician fading, illustrating its ability to maintain low error rates and stable signal detection in both line-of-sight and non-line-of-sight scenarios. Furthermore, the model was evaluated against varied antenna array geometries (e.g., Uniform Planar Array (UPA)) and different user mobility patterns emulated through time-varying Doppler shifts. Despite the structural and environmental variations, the MSGO-DARNN-AM model demonstrated consistently low NMSE, indicating high generalization capability. This robustness is primarily attributed to the attention-enhanced recurrent architecture, which dynamically adjusts to temporal dependencies in signal sequences, and the MSGO, which adapts feature weights to evolving channel states. Compared to conventional models trained on static configurations, the proposed framework shows better resilience to real-world changes, confirming its suitability for deployment in dynamic MIMO communication environments. These findings provide strong empirical evidence that the model is not over fitted to a specific channel or network condition, and can generalize well to unseen operating domains such as different user densities, antenna setups, and mobility profiles.

Fig. 11

Generalization evaluation of the proposed framework.

Ablation study

To thoroughly examine the individual contributions of the MSGO for channel parameter optimization and the DARNN-AM for signal detection, a detailed ablation study was conducted and is given in Table 8. This evaluation aimed to decouple the impact of each component by testing the system under distinct configurations. As reported in Table 7, MEP is 53.37 by using RNN, but RNN with dilation and MSGO gives the MEP of 42.332, which contributes more than only with RNN. Similarly, Dilated RNN with Attention Mechanism, given the MEP is 50.995, however, RNN with MSGO is 48.098. Finally, Dilated RNN with Attention Mechanism with optimized parameters, i.e. MSGO with DARNN-AM (Proposed) gave the MEP to be 39.636, which is far better than all others. Thus, it is concluded that the combined model demonstrated substantial performance gains across all metrics, most notably achieving the lowest BER, NMSE, and SMAPE, highlighting a synergistic effect. The convergence behaviour also stabilized faster due to MSGO’s global–local search strategy, while the DARNN-AM refined temporal dependencies in symbol sequences. This comprehensive evaluation validates that both components, MSGO for optimization and DARNN-AM for sequence modelling are not only effective independently but significantly more powerful when integrated. Hence, the performance gains presented are the result of their complementary mechanisms, justifying the architectural choices made in this work.

Table 8 Ablation Study of the Developed Model.

Performance comparison of the suggested MSGO over other algorithms

The performance comparison of the suggested MSGO over the other optimization algorithms is given in Table 9. The comparison is done by considering the convergence and MSE values along with the stability metric. As per the results in Table 9, the suggested MSGO attained an earlier convergence rate than the GA, PSO and WOA. In addition, the MSE of the suggested MSGO is 0.0045, and the prior algorithms, such as GA, PSO, and WOA, provide higher MSE values of 0.0081, 0.0074, and 0.0068. The attained results from Table 9 prove the performance of the developed MSGO since it uses the modified version of the SGO. The SGO algorithm has strong global searching capability, and it helps to avoid stagnation in the condition of local optima. Added with these advantages, the improved version of the MSGO further improves the performance of the optimization algorithm, and it outperforms the other optimization models, such as GA, PSO, and WOA, in the channel estimation process.

Table 9 Performance comparison of the developed MSGO with other algorithms.

Performance of the developed model on real-time embedded systems for large-scale massive MIMO setups

The performance of the DARNN-AM on real-time embedded systems for large-scale massive MIMO setups is given in Table 10. It can be noted from Table 10 that the proposed DARNN-AM model consumes the peak memory usage of 58 and the inference time of 6.4milli milliseconds. In the proposed DARNN-AM model, the number of parameters and computation requirements are very low because of the incorporation of the dilated structure that greatly enhances the speed of the MIMO channel detection process. Further, the adaptive concepts incorporated within the proposed model reduce the memory usage, which greatly improves the performance of the MIMO detection task.

Table 10 Performance comparison of the developed DARNN-AM real-time embedded systems for large-scale massive MIMO setups.

Heat map analysis of the proposed model

The heat map analysis of the suggested DARNN-AM is given in Fig. 12, which helps to prove the interpretability of the proposed DARNN-AM in the MIMO channel detection. The attention distribution over the different time steps is indicated in Fig. 12. From this Figure, it is confirmed that the proposed DARNN-AM can effectively emphasize the necessary parts of the input data for getting accurate results in the MIMO channel estimation process.

Fig. 12

Heatmap analysis of the proposed model.

Computational complexity and run time overhead of the MSGO in dual optimization

The computational complexity and run time overhead of the recommended MSGO are given in Table 11. It can be found from Table 11 that the suggested MSGO provides lower run time overhead in the channel state estimation, whereas the same MSGO provides the run time overhead of 32.5 min in the MIMO channel detection. Similarly, the computational complexity of the MSGO is very high while tuning the parameters of the DARNN-AM in the channel estimation, and the computational complexity is slightly lower in the MSGO-based channel state estimation.

Table 11 Computational complexity and run time overhead analysis.

Comparison with strong learning-based State of the Art (SoTA) benchmarks

The comparison of the suggested model over the base line approaches are given in the Table 12. It can be seen from the results is that the suggested model attained the training time of 13 s and the NMSE of 0.046. Here, the existing model provides the training tine of 17 s, which helps to confirm the effectiveness of the proposed model in the channel estimation process.

Table 12 Comparison of the proposed model with strong learning-based SoTA benchmarks.

Preliminary results using real-world dataset

The preliminary result of the recommendation on the real-world dataset is given in Table 13 to prove its robustness in the channel estimation process. On the COST 2100 dataset, the suggested model attained an accuracy of 97% and it attained an early convergence rate over the existing models. The better convergence rate and improved accuracy of the designed model are used to prove the robustness of the designed model in real-world scenarios.

Table 13 Preliminary Results of the proposed model on the real-world dataset.

Performance of the developed model on the increase in Doppler spread

The performance of the developed DARNN-AM on the increase in the Doppler spread is indicated in Table 14. This validation is performed by applying the MIC-based sequential detection with the proposed DARNN-AM. On the Doppler spread of 50 Hz, the accuracy of the suggested DARNN-AM without MIC is 91.782%. But, the accuracy of the suggested approach increases from 91.72% to 94.26% when DARNN-AM and MIC-based iterative sequential detection are used together. The results from this analysis showed that the proposed model is robust to channel dynamics with the incorporation of MIC and DARNN-AM.

Table 14 Performance of the suggested model in different Doppler spreads.

Conclusion

A deep structure-based channel estimation with an MIMO signal detection model was developed to accurately determine the characteristics of the channel, thereby effectively mitigating the effects of noise and distortion on the signal transmitted through the channels. In this work, the CSI from the transmitted signal was extracted using the proposed MSGO by optimizing the channel matrix. This optimization helped to minimize the BER, SINR, PEP, and NMSE. The CSI obtained from the channel estimation process was then provided to the developed DARNN-AM for the training phase. Moreover, the proposed MSGO was also used to optimize parameters that were essential for reducing NMSE and enhancing the spectral efficiency of the wireless network. Before this, a MIC-based iterative sequential detection process was employed to identify the symbols present in the signal. These symbols were critical for determining the appropriate massive MIMO configuration for effective communication. In the DARNN-AM structure, the proposed MSGO was integrated to optimize variables such as hidden neurons, number of epochs, and steps per epoch within the recurrent neural network. The primary objective of the MIMO detection process was to select the most suitable MIMO system, thereby boosting the spectral efficiency of the wireless network, as MIMO architectures involve a larger number of antennas at both the transmitter and receiver ends. Due to this high antenna density, the communication process was conducted more effectively without significant data loss. At an SNR of 20, the spectral efficiency of the MSGO-DARNN-AM-based channel estimation with the resource allocation model was improved over MSDSD, DGMP, and DLCS by 30.55%, 27.02%, and 4.44%, respectively, for the channel estimation process. Hence, the performance of the MSGO-DARNN-AM-based channel estimation with MIMO detection was significantly superior to conventional techniques and algorithms. To further strengthen the generalization capability and real-world applicability of the proposed MSGO-DARNN-AM framework, future work will incorporate more diverse and standardized propagation environments in terms of 3GPP-defined scenarios such as Urban Micro (UMi) and Urban Macro (UMa) models as specified in 3GPP TR 38.901. These standardized models offer a more comprehensive reflection of real-world deployment environments, including non-line-of-sight (NLOS) and spatial consistency effects. Although the proposed MSGO-DARNN-AM framework has demonstrated high accuracy and convergence efficiency under simulation-based evaluations, future work will focus on validating its performance in real-world scenarios. Specifically, we intend to test the framework using publicly available measured MIMO channel datasets and over-the-air experimental setups using Software-Defined Radio (SDR) platforms such as USRP or NI LabVIEW systems. This will allow us to assess the practical robustness of the model under realistic wireless impairments, such as hardware non-linearities, multipath fading, and environmental interference.